Extremal Graphs for Sombor Index with Given Parameters
Abstract
:1. Introduction
2. Preliminaries
3. Connected Graphs with Given Parameters
3.1. Extremal Graphs with Regard to in Terms of Order n and Chromatic Number c
3.2. Extremal Graphs with Regard to in Terms of Order n and Girth g
3.3. Extremal Graphs with Regard to in Terms of Matching Number
4. Bipartite Graphs with Given Parameters
4.1. Extremal Bipartite Graphs with Regard to in Terms of Matching Number
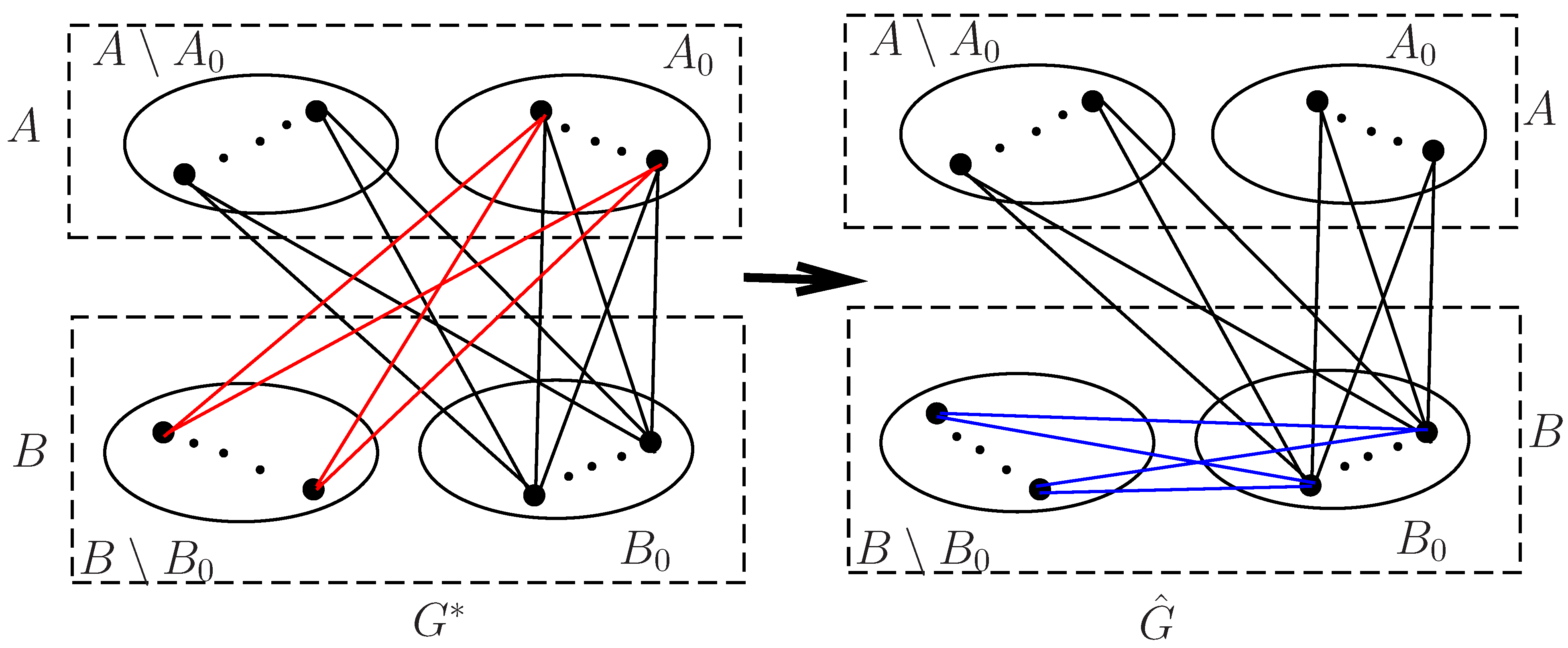
4.2. Extremal Bipartite Graphs with Regard to in Terms of Connectivity k
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gutman, I. Geometric approach to degree-based topological indices: Sombor indices. MATCH Commun. Math. Comput. Chem. 2021, 86, 11–16. [Google Scholar]
- Réti, T.; Doslic, T.; Ali, A. On the Sombor index of graphs. Contrib. Math. 2021, 3, 11–18. [Google Scholar]
- Liu, H.C.; You, L.H.; Tang, Z.K.; Liu, J.B. On the reduced Sombor index and its applications. MATCH Commun. Math. Comput. Chem. 2021, 86, 729–753. [Google Scholar]
- Wang, F.X.; Wu, B. The Proof of a Conjecture on the Reduced Sombor Index. MATCH Commun. Math. Comput. Chem. 2022, 88, 583–591. [Google Scholar] [CrossRef]
- Wang, F.X.; Wu, B. The reduced Sombor index and the exponential reduced Sombor index of a molecular tree. J. Math. Anal. Appl. 2022, 515, 126442. [Google Scholar] [CrossRef]
- Sun, X.; Du, J. On Sombor index of trees with fixed domination number. Appl. Math. Comput. 2022, 421, 126946. [Google Scholar] [CrossRef]
- Zhou, T.; Lin, Z.; Miao, L. The Sombor index of trees and unicyclic graphs with given matching number. arXiv 2021, arXiv:2103.04645. [Google Scholar] [CrossRef]
- Zhou, T.; Lin, Z.; Miao, L. The Sombor index of trees and unicyclic graphs with given maximum degree. arXiv 2021, arXiv:2103.07947. [Google Scholar]
- Das, K.C.; Gutman, I. On Sombor index of trees. Appl. Math. Comput. 2022, 412, 12675. [Google Scholar] [CrossRef]
- Liu, H.; Gutman, I.; You, L.; Huang, Y. Sombor index:review of extremal results and bounds. J. Math. Chem. 2022, 60, 771–798. [Google Scholar] [CrossRef]
- Aashtab, A.; Akbari, S.; Madadinia, S.; Noei, M.; Salehi, F. On the graphs with minimum Sombor index. MATCH Commun. Math. Comput. Chem. 2022, 88, 553–559. [Google Scholar] [CrossRef]
- Liu, H.; You, L.; Huang, Y. Extremal Sombor indices of tetracyclic (chemical) graphs. MATCH Commun. Math. Comput. Chem. 2022, 88, 573–581. [Google Scholar] [CrossRef]
- Ning, W.; Song, Y.; Wang, K. More on Sombor index of graphs. Mathematics 2022, 10, 301. [Google Scholar] [CrossRef]
- Horoldagva, B.; Xu, C. On Sombor index of graphs. MATCH Commun. Math. Comput. Chem. 2021, 86, 703–713. [Google Scholar]
- Das, K.C.; Cevik, A.S.; Cangul, I.N.; Shang, Y. On Sombor index. Symmetry 2021, 13, 140. [Google Scholar] [CrossRef]
- Ghanbari, N.; Alikhani, S. Sombor index of certain graphs. Iran. J. Math. Chem. 2021, 12, 27–37. [Google Scholar]
- Deng, H.; Tang, Z.; Wu, R. Molecular trees with extremal values of Sombor indices. Int. J. Quantum Chem. 2021, 121, e26622. [Google Scholar] [CrossRef]
- Cruz, R.; Gutman, I.; Rada, J. Sombor index of chemical graphs. Appl. Math. Comput. 2021, 399, 126018. [Google Scholar] [CrossRef]
- Liu, H.; Chen, H.; Xiao, Q.; Fang, X.; Tang, Z. More on Sombor indices of chemical graphs and their applications to the boiling point of benzenoid hydrocarbons. Int. J. Quantum Chem. 2021, 121, 26689. [Google Scholar] [CrossRef]
- Liu, H.; You, L.; Huang, Y. Ordering chemical graphs by Sombor indices and its applications. MATCH Commun. Math. Comput. Chem. 2022, 87, 5–22. [Google Scholar] [CrossRef]
- Filipovski, S. Relations between Sombor index and some degree-based topological indices. Iran. J. Math. Chem. 2021, 12, 19–26. [Google Scholar]
- Rada, J.; Rodriguez, J.M.; Sigarreta, J.M. General properties on Sombor indices. Discrete Appl. Math. 2021, 299, 87–97. [Google Scholar] [CrossRef]
- Wang, F.X.; Wu, B. The k-Sombor index of trees. Asia-Pac. J. Oper. Res. 2023. [Google Scholar] [CrossRef]
- Chen, H.; Li, W.; Wang, J. Extremal Values on the Sombor Index of Trees. MATCH Commun. Math. Comput. Chem. 2022, 87, 23–49. [Google Scholar] [CrossRef]
- Milovanović, I.; Milovanović, E.; Matejić, M. On some mathematical properties of Sombor indices. Bull. Int. Math. Virtual Inst. 2021, 11, 341–353. [Google Scholar]
- Xu, K.; Das, K.C. Some extremal graphs with respect to inverse degree. Discrete Appl. Math. 2016, 203, 171–183. [Google Scholar] [CrossRef]
- Bondy, J.A.; Murty, U.S.R. Graph Theory with Applications; Macmillan Press: New York, NY, USA, 1976. [Google Scholar]
- Das, K.C.; Shang, Y. Some extremal graphs with respect to Sombor index. Mathematics 2021, 9, 1202. [Google Scholar] [CrossRef]
- Li, S.; Song, Y. On the sum of all distances in bipartite graphs. Discrete Appl. Math. 2014, 169, 176–185. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Meng, J.; Wang, N. Extremal Graphs for Sombor Index with Given Parameters. Axioms 2023, 12, 203. https://doi.org/10.3390/axioms12020203
Zhang W, Meng J, Wang N. Extremal Graphs for Sombor Index with Given Parameters. Axioms. 2023; 12(2):203. https://doi.org/10.3390/axioms12020203
Chicago/Turabian StyleZhang, Wanping, Jixiang Meng, and Na Wang. 2023. "Extremal Graphs for Sombor Index with Given Parameters" Axioms 12, no. 2: 203. https://doi.org/10.3390/axioms12020203
APA StyleZhang, W., Meng, J., & Wang, N. (2023). Extremal Graphs for Sombor Index with Given Parameters. Axioms, 12(2), 203. https://doi.org/10.3390/axioms12020203




