Communication in Weighted Networks: A Game Theoretic Approach
Abstract
1. Introduction
2. Preliminaries
2.1. Cooperative TU-Games
2.2. Graphs
2.3. Communication Situations
3. The Weighted Mixed Value
4. Characterizing the Weighted Mixed Value
- (a)
- Let us prove that satisfies mixed component efficiency. Given , a vector of weights and , by definitionAs the weighted Shapley value is efficient:
- (b)
- As the weighted mixed value is clearly linear (in the game), to prove that satisfies weighted mixed fairness, it is sufficient to see that the property holds for communication situations of the form with the unanimity game of the coalition . Suppose is the vector of weights. Then,where is the pseudogame in whichThus, for and ,is zero, or is the weighted Shapley value of a linear combination of unanimity games, such that l belongs to in all of them. If the difference is zero, the result is trivial. In another case, taking into account that the weighted Shapley value of each player or link is proportional to his, her or its weight, we haveandand, thus, the result is proved.
- (c)
- Let us prove that satisfies weighted balanced contributions. For , andandare both zero, or the weighted Shapley value of a linear combination of unanimity games . The property trivially holds if both quantities vanish. In another case, as the weighted Shapley value assigns to each player a quantity proportional to his weight, we have thatand thus the result.
- (d)
- The proof of satisfies weighted mixed balanced contributions follows immediately from the previous one, considering two players and a link and reproduces the argument.
- (e)
- To prove that satisfies weighted balanced link contributions we use the linearity (in the game) of the mixed weighted value and, thus, it is sufficient to prove that the property holds for with, the characteristic function of the unanimity game of . Suppose and is a vector of weights. Aswe have, for that is a linear combination of unanimity games such that in all of them. Thusis the value of i in all unanimity games in which is present. However, in these unanimity games j is also present as it is incident on the different arcs . By symmetry, the variation of value of jcorresponds to the same unanimity games and, thus, both values are proportional to the weights, which completes the proof.
5. Conclusions and Final Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Shapley, L.S. A value for n-person games. Ann. Math. Stud. 1953, 28. [Google Scholar]
- Myerson, R.B. Graphs and cooperation in games. Math. Oper. Res. 1977, 2, 225–229. [Google Scholar] [CrossRef]
- Myerson, R.B. Conference structures and fair allocation rules. Int. J. Game Theory 1980, 9, 169–182. [Google Scholar] [CrossRef]
- Meessen, R. Communication Games. Master’s Thesis, University of Nijmegen, Nijmegen, The Netherlands, 1988. [Google Scholar]
- Borm, P.; Owen, G.; Tijs, S. On the position value for communication situations. SIAM J. Discret. Math. 1992, 5, 305–320. [Google Scholar] [CrossRef]
- González-Arangüena, E.; Manuel, C.; Owen, G.; del Pozo, M. The within groups and the between groups Myerson values. Eur. J. Oper. Res. 2017, 257, 586–600. [Google Scholar] [CrossRef]
- Li, D.L.; Shan, E. The position value and the structures of graphs. Appl. Math. Comput. 2019, 356, 190–197. [Google Scholar] [CrossRef]
- Li, D.L.; Shan, E.F. The Myerson value on local structures of coalitions. J. Oper. Res. Soc. China 2019, 7, 461–473. [Google Scholar] [CrossRef]
- Manuel, C.; Ortega, E.; del Pozo, M. Marginality and Myerson values. Eur. J. Oper. Res. 2020, 284, 301–312. [Google Scholar] [CrossRef]
- Shan, E.; Shi, J.; Lv, W. A note on the position value for hypergraph communication situations. In Complexity and Approximation; Springer: Berlin/Heidelberg, Germany, 2020; pp. 230–237. [Google Scholar]
- Wang, G.; Cai, L.; Shan, E. The efficient proportional Myerson values for hypergraph games. Math. Probl. Eng. 2021, 2021, 1468979. [Google Scholar] [CrossRef]
- Feltkamp, V.; Nouweland, A. Controlled Communication Networks. In Operations Research’92; Springer: Berlin/Heidelberg, Germany, 1993; pp. 413–415. [Google Scholar]
- López, S.; Owen, G.; Saboya, M. The impact of intermediaries on a negotiation: An approach from game theory. Cent. Eur. J. Oper. Res. 2022, 30, 837–859. [Google Scholar] [CrossRef]
- Shapley, L.S. Additive and Non-Additive Set Functions; Princeton University: Princeton, NJ, USA, 1953. [Google Scholar]
- Slikker, M. A characterization of the position value. Int. J. Game Theory 2005, 33, 505–514. [Google Scholar] [CrossRef]
- Harsanyi, J.C. A Bargaining Model for the Cooperative n-Person Game; Stanford University: Stanford, CA, USA, 1959. [Google Scholar]
- Navarro, F. Necessary players, Myerson fairness and the equal treatment of equals. Ann. Oper. Res. 2019, 280, 111–119. [Google Scholar] [CrossRef]
- Béal, S.; Rémila, E.; Solal, P. Fairness and fairness for neighbors: The difference between the Myerson value and component-wise egalitarian solutions. Econ. Lett. 2012, 117, 263–267. [Google Scholar] [CrossRef]
- Yokote, K.; Kongo, T.; Funaki, Y. The balanced contributions property for equal contributors. Games Econ. Behav. 2018, 108, 113–124. [Google Scholar] [CrossRef]
- Yokote, K.; Kongo, T. The balanced contributions property for symmetric players. Oper. Res. Lett. 2017, 45, 227–231. [Google Scholar] [CrossRef]
- Yokote, K.; Kongo, T.; Funaki, Y. Relationally equal treatment of equals and affine combinations of values for TU games. Soc. Choice Welf. 2019, 53, 197–212. [Google Scholar] [CrossRef]
- Casajus, A. Weakly balanced contributions and solutions for cooperative games. Oper. Res. Lett. 2017, 45, 616–619. [Google Scholar] [CrossRef]
- Ghintran, A.; González-Arangüena, E.; Manuel, C. A probabilistic position value. Ann. Oper. Res. 2012, 201, 183–196. [Google Scholar] [CrossRef]
- Shan, E.; Zhang, G.; Shan, X. The degree value for games with communication structure. Int. J. Game Theory 2018, 47, 857–871. [Google Scholar] [CrossRef]
- Manuel, C.; Ortega, E.; Pozo, M.D. Marginality and the position value. In TOP; Springer: Berlin/Heidelberg, Germany, 2022; pp. 1–16. [Google Scholar]
- Zhang, G.; Shan, E.; Qu, S. Characterizations of the Position Value for Hypergraph Communication Situations. In Proceedings of the East Asia Game Theory International Conference, Fuzhou, China, 7–9 March 2019; pp. 27–42. [Google Scholar]
- Manuel, C.M.; Martín, D. A monotonic weighted Shapley value. Group Decis. Negot. 2020, 29, 627–654. [Google Scholar] [CrossRef]
- Haeringer, G. A new weight scheme for the Shapley value. Math. Soc. Sci. 2006, 52, 88–98. [Google Scholar] [CrossRef]
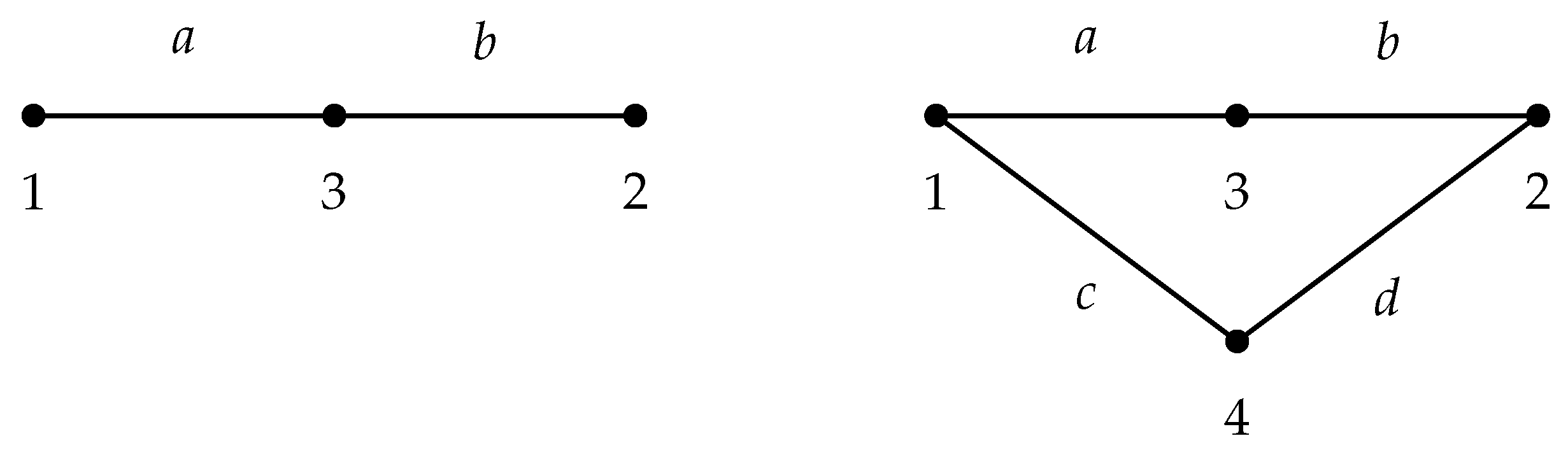
| Weighted Mixed Value | Mixed Value | Myerson Value | Position Value | |
|---|---|---|---|---|
| Component efficiency | × | × | √ | √ |
| Mixed component efficiency | √ | √ | × | × |
| Fairness | √ * | √ | √ | × |
| Mixed fairness | √ * | √ | × | × |
| Weighted mixed fairness | √ | × | × | × |
| Balanced contributions | √ * | √ | √ | × |
| Mixed balanced contributions | √ * | √ | × | × |
| Weighted mixed balanced contributions | √ | × | × | × |
| Balanced link contributions | √ * | √ | × | √ |
| Weighted balanced link contributions | √ | × | × | × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gavilán, E.C.; Manuel, C.; Martín, D. Communication in Weighted Networks: A Game Theoretic Approach. Axioms 2023, 12, 180. https://doi.org/10.3390/axioms12020180
Gavilán EC, Manuel C, Martín D. Communication in Weighted Networks: A Game Theoretic Approach. Axioms. 2023; 12(2):180. https://doi.org/10.3390/axioms12020180
Chicago/Turabian StyleGavilán, Elena C., Conrado Manuel, and Daniel Martín. 2023. "Communication in Weighted Networks: A Game Theoretic Approach" Axioms 12, no. 2: 180. https://doi.org/10.3390/axioms12020180
APA StyleGavilán, E. C., Manuel, C., & Martín, D. (2023). Communication in Weighted Networks: A Game Theoretic Approach. Axioms, 12(2), 180. https://doi.org/10.3390/axioms12020180







