FedGR: Federated Graph Neural Network for Recommendation Systems
Abstract
1. Introduction
2. Related Work
2.1. Social Recommendation
2.2. Graph Neural Network for Recommendation Systems
2.2.1. For General Recommendation
2.2.2. For Sequential Recommendation
2.3. Privacy-Protection Recommendation
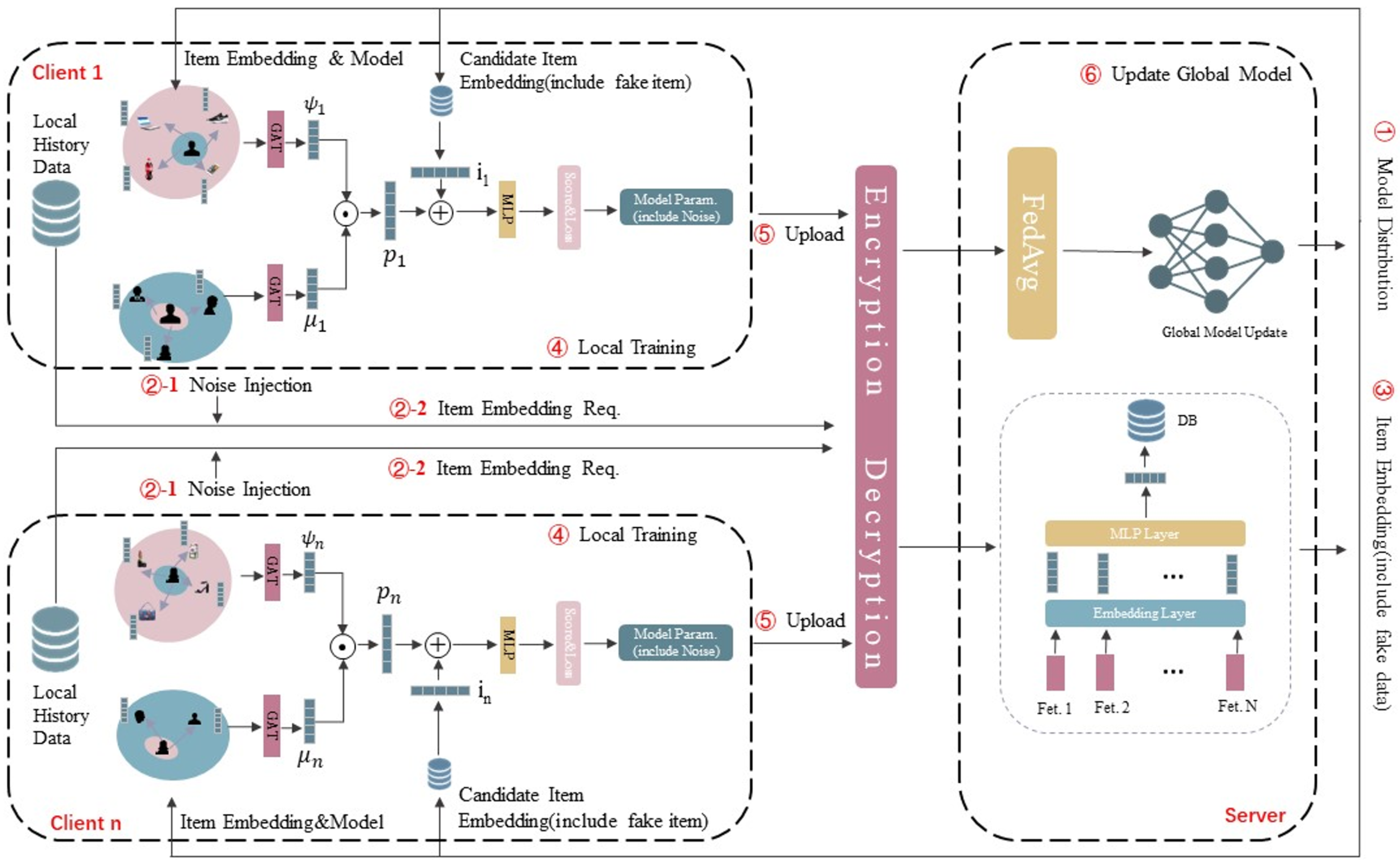
3. Proposed Framework
3.1. Model Overview
3.2. Item Model
| Algorithm 1 Item Embedding |
Input: feature set of item i
|
3.3. User Model
3.3.1. Item Graph Representation
| Algorithm 2 Item Graph Representation |
Input: Input of the user–item graph and the embedding representation of the corresponding item (obtained from the server side)
|
3.3.2. Social Aggregation
| Algorithm 3 Social Representation |
Input: input social graph/user–friend–item graph/friends item-embedding set
|
3.4. Security Model
4. Experiment
4.1. Experimental Settings
4.1.1. Datasets
4.1.2. Evaluation Metrics
4.1.3. Parameter Settings
4.1.4. Baselines
- SoReg [28]: A factor analysis recommendation algorithm based on the probability matrix decomposition.
- SocialMF [29]: Introducing trust propagation in matrix decomposition, the user indicates that friends close to that user indicate.
- GraphRec [2]: Graph neural networks are used to learn user embeddings and item embeddings from user history product graphs and social graphs.
- GCMC+SN [25]: A graph-neural-network-based recommendation model is used to generate embeddings for each user in the social network using the node2vec technique.
- FeSoG [30]: A social recommendation system with privacy protection, using local differential privacy (LDP) and pseudo-item labeling as a means of user data privacy protection.
- FedMF [26]: The representation of each user is computed by matrix factorization, and homomorphic encryption is used to protect the user data from disclosure.
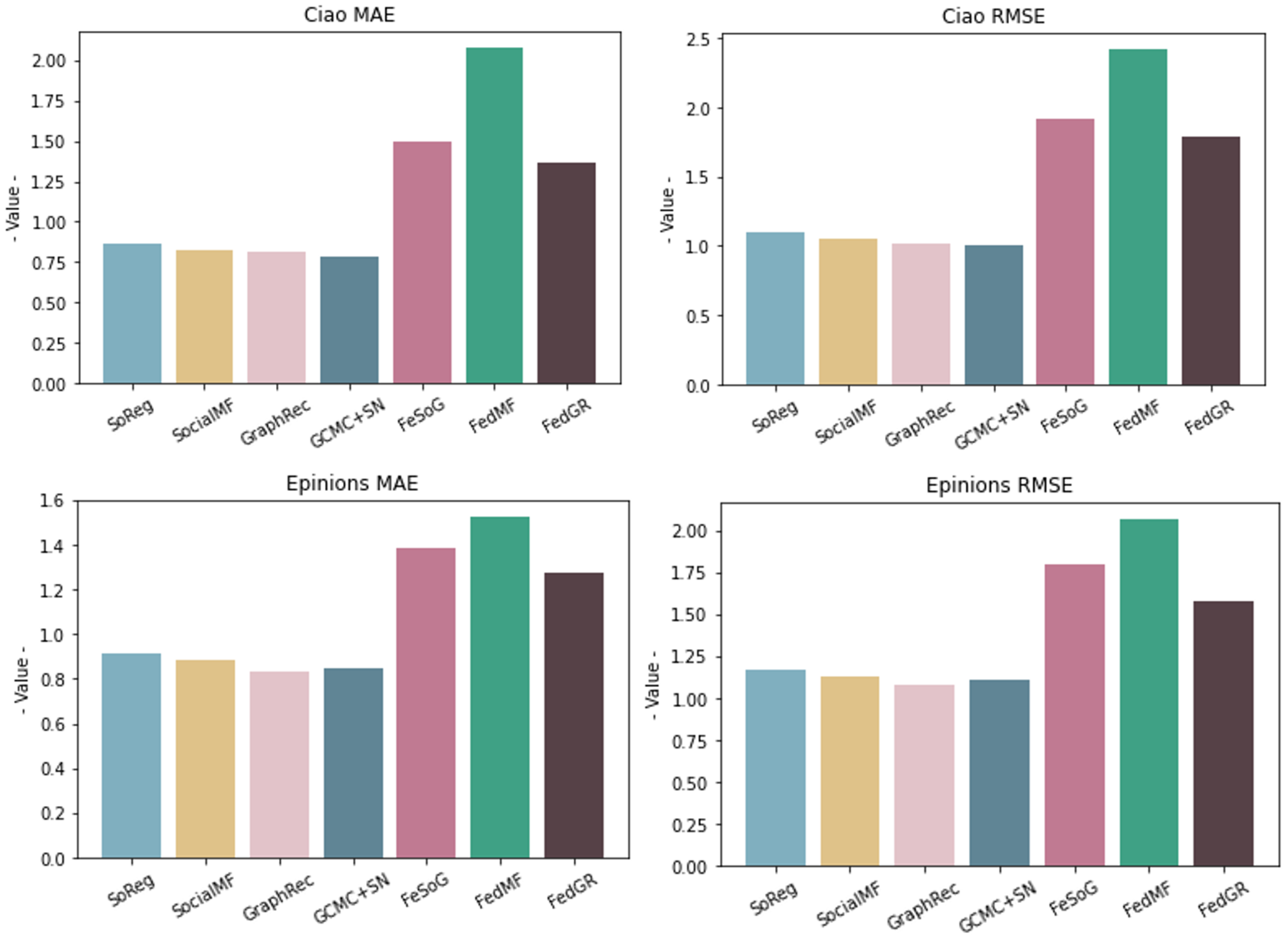
4.2. Quantitative Results
4.3. Analysis of Parameters
5. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Qiu, R.; Li, J.; Huang, Z.; Yin, H. Rethinking the item order in session-based recommendation with graph neural networks. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management, Beijing, China, 3–7 November 2019; pp. 579–588. [Google Scholar]
- Fan, W.; Ma, Y.; Li, Q.; He, Y.; Zhao, E.; Tang, J.; Yin, D. Graph neural networks for social recommendation. In Proceedings of the The World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019; pp. 417–426. [Google Scholar]
- Wang, D.; Cui, P.; Zhu, W. Structural deep network embedding. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1225–1234. [Google Scholar]
- Nasiri, E.; Berahmand, K.; Li, Y. Robust graph regularization nonnegative matrix factorization for link prediction in attributed networks. Multimed. Tools Appl. 2023, 82, 3745–3768. [Google Scholar] [CrossRef]
- Wu, L.; Sun, P.; Fu, Y.; Hong, R.; Wang, X.; Wang, M. A neural influence diffusion model for social recommendation. In Proceedings of the 42nd International ACM SIGIR Conference on Research and Development in Information Retrieval, Paris, France, 21–25 July 2019; pp. 235–244. [Google Scholar]
- Xu, G.; Wu, X.; Liu, J.; Liu, Y. A community detection method based on local optimization in social networks. IEEE Netw. 2020, 34, 42–48. [Google Scholar] [CrossRef]
- Berahmand, K.; Mohammadi, M.; Saberi-Movahed, F.; Li, Y.; Xu, Y. Graph regularized nonnegative matrix factorization for community detection in attributed networks. IEEE Trans. Netw. Sci. Eng. 2023, 10, 372–385. [Google Scholar] [CrossRef]
- Xu, G.; Dong, J.; Ma, C.; Liu, J.; Cliff, U.G.O. A Certificateless Signcryption Mechanism Based on Blockchain for Edge Computing. IEEE Internet Things J. 2022. [Google Scholar] [CrossRef]
- Wu, C.; Wu, F.; Cao, Y.; Huang, Y.; Xie, X. Fedgnn: Federated graph neural network for privacy-preserving recommendation. arXiv 2021, arXiv:2102.04925. [Google Scholar]
- Dwork, C. Differential privacy: A survey of results. In Proceedings of the International Conference on Theory and Applications of Models of Computation, Xi’an, China, 25–29 April 2008; pp. 1–19. [Google Scholar]
- Gentry, C. Fully homomorphic encryption using ideal lattices. In Proceedings of the Forty-First Annual ACM Symposium on Theory of Computing, Bethesda, MD, USA, 2009, 31 May–2 June 2009; pp. 169–178. [Google Scholar]
- Hao, M.; Li, H.; Luo, X.; Xu, G.; Yang, H.; Liu, S. Efficient and privacy-enhanced federated learning for industrial artificial intelligence. IEEE Trans. Ind. Inform. 2019, 16, 6532–6542. [Google Scholar] [CrossRef]
- Xu, G.; Li, W.; Liu, J. A social emotion classification approach using multi-model fusion. Future Gener. Comput. Syst. 2020, 102, 347–356. [Google Scholar] [CrossRef]
- Ma, H.; Yang, H.; Lyu, M.R.; King, I. Sorec: Social recommendation using probabilistic matrix factorization. In Proceedings of the 17th ACM Conference on Information and Knowledge Management, Napa Valley, CA, USA, 26–30 October 2008; pp. 931–940. [Google Scholar]
- Jamali, M.; Ester, M. A matrix factorization technique with trust propagation for recommendation in social networks. In Proceedings of the Fourth ACM Conference on Recommender Systems, Barcelona, Spain, 26–30 September 2010; pp. 135–142. [Google Scholar]
- Fan, W.; Ma, Y.; Li, Q.; Wang, J.; Cai, G.; Tang, J.; Yin, D. A graph neural network framework for social recommendations. IEEE Trans. Knowl. Data Eng. 2020, 34, 2033–2047. [Google Scholar] [CrossRef]
- Wu, L.; Li, J.; Sun, P.; Hong, R.; Ge, Y.; Wang, M. Diffnet++: A neural influence and interest diffusion network for social recommendation. IEEE Trans. Knowl. Data Eng. 2020, 34, 4753–4766. [Google Scholar] [CrossRef]
- Berg, R.v.d.; Kipf, T.N.; Welling, M. Graph convolutional matrix completion. arXiv 2017, arXiv:1706.02263. [Google Scholar]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. Adv. Neural Inf. Process. Syst. 2016, 29. [Google Scholar]
- Ying, R.; He, R.; Chen, K.; Eksombatchai, P.; Hamilton, W.L.; Leskovec, J. Graph convolutional neural networks for web-scale recommender systems. In Proceedings of the 24th ACM Sigkdd International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 974–983. [Google Scholar]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Wang, W.; Zhang, W.; Liu, S.; Liu, Q.; Zhang, B.; Lin, L.; Zha, H. Beyond clicks: Modeling multi-relational item graph for session-based target behavior prediction. In Proceedings of the The Web Conference 2020, Taipei, Taiwan, 20–24 April 2020; pp. 3056–3062. [Google Scholar]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Velickovic, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. Stat 2017, 1050, 20. [Google Scholar]
- Ammad-Ud-Din, M.; Ivannikova, E.; Khan, S.A.; Oyomno, W.; Fu, Q.; Tan, K.E.; Flanagan, A. Federated collaborative filtering for privacy-preserving personalized recommendation systems. arXiv 2019, arXiv:1901.09888. [Google Scholar]
- Chai, D.; Wang, L.; Chen, K.; Yang, Q. Secure federated matrix factorization. IEEE Intell. Syst. 2020, 36, 11–20. [Google Scholar] [CrossRef]
- Mills, J.; Hu, J.; Min, G. Communication-efficient federated learning for wireless edge intelligence in IoT. IEEE Internet Things J. 2019, 7, 5986–5994. [Google Scholar] [CrossRef]
- Ma, H.; Zhou, D.; Liu, C.; Lyu, M.R.; King, I. Recommender systems with social regularization. In Proceedings of the Fourth ACM International Conference on Web Search and Data Mining, Hong Kong, China, 9–12 February 2011; pp. 287–296. [Google Scholar]
- Guo, H.; Tang, R.; Ye, Y.; Li, Z.; He, X. DeepFM: A factorization-machine based neural network for CTR prediction. arXiv 2017, arXiv:1703.04247. [Google Scholar]
- Liu, Z.; Yang, L.; Fan, Z.; Peng, H.; Yu, P.S. Federated social recommendation with graph neural network. ACM Trans. Intell. Syst. Technol. (TIST) 2022, 13, 1–24. [Google Scholar] [CrossRef]
- Wu, S.; Sun, F.; Zhang, W.; Xie, X.; Cui, B. Graph neural networks in recommender systems: A survey. ACM Comput. Surv. 2022, 55, 1–37. [Google Scholar] [CrossRef]
- Reddi, S.; Charles, Z.; Zaheer, M.; Garrett, Z.; Rush, K.; Konečnỳ, J.; Kumar, S.; McMahan, H.B. Adaptive federated optimization. arXiv 2020, arXiv:2003.00295. [Google Scholar]




| Symbol | Definitions and Descriptions |
|---|---|
| embedding of user i | |
| embedding of item j | |
| friends embedding of user | |
| user i’s rating score for item j, in [0,1,2,3,4,5] | |
| weighting factor of item j to user i | |
| weighting factor of friend j and user i | |
| product of the item embeddings of user i and the corresponding score embeddings | |
| collection of historical interaction item IDs for user i | |
| collection of noise item IDs added by user i | |
| a set of features of item i, = | |
| a set of features embedding representation of item j, = | |
| embedding representation learned by user i in the user–item graph | |
| the embedding representation learned by user i friends in the user–item graph | |
| embedding representation learned by user i in the social graph | |
| history item graph of user i | |
| social relation graph of user i | |
| friends item graph of user i | |
| history item embedding set of user i | |
| friends history item embedding set of uer i | |
| user i’s rating of item j embedding | |
| user i obtains the set of item IDs from the server |
| Datasets | Ciao | Epinions |
|---|---|---|
| Users | 2248 | 22,168 |
| Items | 16,862 | 296,277 |
| Ratings | 36,065 | 920,075 |
| Social Connections | 57,545 | 355,812 |
| Rating Scale | [1,5] | [1,5] |
| Method | Ciao MAE | Ciao RMSE | Epinions MAE | Epinions RMSE |
|---|---|---|---|---|
| SoReg | 0.8627 | 1.1021 | 0.9119 | 1.1703 |
| SocialMF | 0.8270 | 1.0501 | 0.8837 | 1.1328 |
| GraphRec | 0.8141 | 1.0133 | 0.8326 | 1.0814 |
| SoRGCMC+SN | 0.7824 | 1.0031 | 0.8480 | 1.1070 |
| FeSoG | 1.4937 | 1.9136 | 1.3847 | 1.7969 |
| FedMF | 2.0792 | 2.4216 | 1.5254 | 2.0685 |
| FedGR | 1.3650 | 1.7941 | 1.2773 | 1.5806 |
| Improvement (%) | 8.6 | 6.2 | 7.7 | 12.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, C.; Ren, X.; Xu, G.; He, B. FedGR: Federated Graph Neural Network for Recommendation Systems. Axioms 2023, 12, 170. https://doi.org/10.3390/axioms12020170
Ma C, Ren X, Xu G, He B. FedGR: Federated Graph Neural Network for Recommendation Systems. Axioms. 2023; 12(2):170. https://doi.org/10.3390/axioms12020170
Chicago/Turabian StyleMa, Chuang, Xin Ren, Guangxia Xu, and Bo He. 2023. "FedGR: Federated Graph Neural Network for Recommendation Systems" Axioms 12, no. 2: 170. https://doi.org/10.3390/axioms12020170
APA StyleMa, C., Ren, X., Xu, G., & He, B. (2023). FedGR: Federated Graph Neural Network for Recommendation Systems. Axioms, 12(2), 170. https://doi.org/10.3390/axioms12020170






