Third-Order Neutral Differential Equation with a Middle Term and Several Delays: Asymptotic Behavior of Solutions
Abstract
1. Introduction
2. Main Results
2.1. Nonexistence of Solutions in
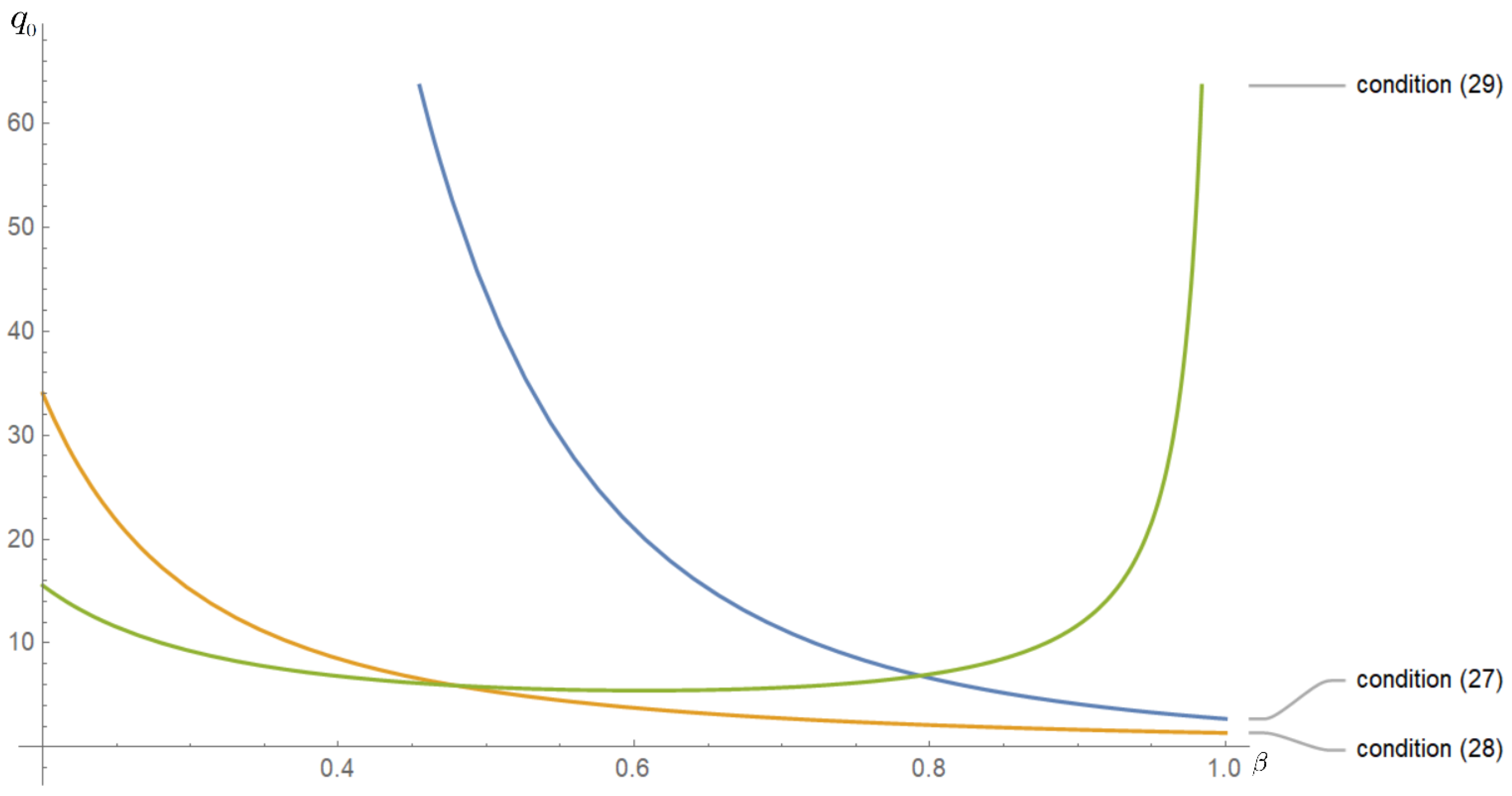
2.2. Asymptotic Behavior
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hale, J.K. Functional Differential Equations, Oxford Applied Mathematical Sciences; Springer: New York, NY, USA, 1971; Volume 3. [Google Scholar]
- Rihan, F.A. Delay Differential Equations and Applications to Biology; Springer Nature Singapore Pte Ltd.: Singapore, 2021. [Google Scholar]
- Li, T.; Baculíková, B.; Džurina, J.; Zhang, C. Oscillation of fourth-order neutral differential equations with p-Laplacian like operators. Bound. Value Probl. 2014, 2014, 56. [Google Scholar] [CrossRef]
- Liu, Q.; Bohner, M.; Grace, S.R.; Li, T. Asymptotic behavior of even-order damped differential equations with p-Laplacian like operators and deviating arguments. J. Inequal. Appl. 2016, 2016, 321. [Google Scholar] [CrossRef]
- Zhang, C.; Agarwal, R.P.; Li, T. Oscillation and asymptotic behavior of higher-order delay differential equations with p-Laplacian like operators. J. Math. Anal. Appl. 2014, 409, 1093–1106. [Google Scholar] [CrossRef]
- Ferreira, J.M.; Ford, N.J.; Malique, M.A.; Pinelas, S.; Yan, Y. Analytical and numerical treatment of oscillatory mixed differential equations with differentiable delays and advances. J. Comput. Appl. Math. 2011, 235, 5112–5130. [Google Scholar] [CrossRef]
- Lima, P.M.; Teodoro, M.F.; Ford, N.J.; Lumb, P.M. Finite element solution of a linear mixed-type functional differential equation. Numer. Algorithms 2010, 55, 301–320. [Google Scholar] [CrossRef]
- Lima, P.M.; Ford, N.J.; Lumb, P.M. Computational methods for a mathematical model of propagation of nerve impulses in myelinated axons. Appl. Numer. Math. 2014, 85, 38–53. [Google Scholar] [CrossRef]
- Baculíková, B. Oscillatory behavior of the second order noncanonical differential equations. Electron. J. Qual. Theory Differ. Equ. 2019, 89, 1–11. [Google Scholar] [CrossRef]
- Baculíková, B. Oscillation of second-order nonlinear noncanonical differential equations with deviating argument. Appl. Math. Lett. 2019, 91, 68–75. [Google Scholar] [CrossRef]
- Džrina, J.; Jadlovská, I. A note on oscillation of second-order delay differential equations. Appl. Math. Lett. 2017, 69, 126–132. [Google Scholar] [CrossRef]
- Chatzarakis, G.E.; Moaaz, O.; Li, T.; Qaraad, B. Some oscillation theorems for nonlinear second-order differential equations with an advanced argument. Adv. Differ. Equ. 2020, 2020, 160. [Google Scholar] [CrossRef]
- Bohner, M.; Grace, S.R.; Jadlovská, I. Sharp oscillation criteria for second-order neutral delay differential equations. Math. Meth. Appl. Sci. 2020, 43, 10041–10053. [Google Scholar] [CrossRef]
- Grace, S.R.; Dzurina, J.; Jadlovská, I.; Li, T. An improved approach for studying oscillation of second-order neutral delay differential equations. J. Inequal. Appl. 2018, 2018, 193. [Google Scholar] [CrossRef] [PubMed]
- Moaaz, O.; Elabbasy, E.M.; Qaraad, B. An improved approach for studying oscillation of generalized Emden–Fowler neutral differential equation. J. Inequal. Appl. 2020, 2020, 69. [Google Scholar] [CrossRef]
- Moaaz, O.; Anis, M.; Baleanu, D.; Muhib, A. More effective criteria for oscillation of second-order differential equations with neutral arguments. Mathematics 2020, 8, 986. [Google Scholar] [CrossRef]
- Selvarangam, S.; Madhan, M.; Thandapani, E.; Pinelas, S. Improved oscillation conditions for third-order neutral type difference equations. Electron. J. Diff. Equ. 2017, 2017, 1–13. [Google Scholar]
- Yeniçerioğlu, A.F.; Pinelas, S.; Yan, Y. On the behavior of the solutions for linear autonomous mixed type difference equation. Rend. Del Circ. Mat. Palermo Ser. 2 2020, 69, 787–801. [Google Scholar] [CrossRef]
- Vidhyaa, K.S.; Dharuman, C.; Thandapani, E.; Pinelas, S. Oscillation theorems for third order nonlinear delay difference equations. Math. Bohem. 2019, 144, 25–37. [Google Scholar] [CrossRef]
- Baculíková, B.; Džurina, J. Oscillation of third-order neutral differential equations. Math. Comp. Modell. 2010, 52, 215–226. [Google Scholar] [CrossRef]
- Baculíková, B.; Džurina, J. On the asymptotic behavior of a class of third order nonlinear neutral differential equations. Open Math. 2010, 8, 1091–1103. [Google Scholar] [CrossRef]
- Thandapani, E.; Li, T. On the oscillation of third-order quasi-linear neutral functional differential equations. Arch. Math. 2011, 47, 181–199. [Google Scholar]
- Aktas, M.F.; Tiryaki, A.; Zafer, A. Oscillation criteria for third-order nonlinear functional differential equations. Appl. Math. Lett. 2010, 23, 756–762. [Google Scholar] [CrossRef]
- Grace, S.R. Oscillation criteria for third-order nonlinear delay differential equations with damping. Opusc. Math. 2015, 35, 485–497. [Google Scholar] [CrossRef]
- Tiryaki, A.; Aktas, M.F. Oscillation criteria of a certain class of third-order nonlinear delay differential equations with damping. J. Math. Anal. Appl. 2007, 325, 54–68. [Google Scholar] [CrossRef]
- Moaaz, O.; Elabbasy, E.M.; Shaaban, E. Oscillation criteria for a class of third order damped differential equations. Arab J. Math. Sci. 2018, 24, 16–30. [Google Scholar] [CrossRef]
- Moaaz, O.; Baleanu, D.; Muhib, A. New aspects for non-existence of kneser solutions of neutral differential equations with odd-order. Mathematics 2020, 8, 494. [Google Scholar] [CrossRef]
- Kiguradze, I.; Chanturia, T. Asymptotic Properties of Solutions of Nonautonomous Ordinary Differential Equations; Kluwer Acad. Publ.: Drodrcht, The Netherlands, 1993. [Google Scholar]
- Philos, C.G. On the existence of nonoscillatory solutions tending to zero at ∞ for dif ferential equations with positive delays. Arch. Math. 1981, 36, 168–178. [Google Scholar] [CrossRef]
- Kitamura, Y.; Kusano, T. Oscillation of first-order nonlinear differential equations with deviating arguments. Proc. Am. Math. Soc. 1980, 78, 64–68. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almarri, B.; Moaaz, O.; Anis, M.; Qaraad, B. Third-Order Neutral Differential Equation with a Middle Term and Several Delays: Asymptotic Behavior of Solutions. Axioms 2023, 12, 166. https://doi.org/10.3390/axioms12020166
Almarri B, Moaaz O, Anis M, Qaraad B. Third-Order Neutral Differential Equation with a Middle Term and Several Delays: Asymptotic Behavior of Solutions. Axioms. 2023; 12(2):166. https://doi.org/10.3390/axioms12020166
Chicago/Turabian StyleAlmarri, Barakah, Osama Moaaz, Mona Anis, and Belgees Qaraad. 2023. "Third-Order Neutral Differential Equation with a Middle Term and Several Delays: Asymptotic Behavior of Solutions" Axioms 12, no. 2: 166. https://doi.org/10.3390/axioms12020166
APA StyleAlmarri, B., Moaaz, O., Anis, M., & Qaraad, B. (2023). Third-Order Neutral Differential Equation with a Middle Term and Several Delays: Asymptotic Behavior of Solutions. Axioms, 12(2), 166. https://doi.org/10.3390/axioms12020166







