On the Uniqueness of Lattice Characterization of Groups

Abstract

We analyze the problem of the uniqueness of characterization of groups by their weak congruence lattices. We discuss the possibility that the same algebraic lattice L acts as a weak congruence lattice of a group in more than one way, so that the corresponding diagonals are represented by different elements of L. If this is impossible, that is, if L can be interpreted as a weak congruence lattice of a group in a single way, we say that L is a sharp lattice. We prove that groups in many classes have a sharp weak congruence lattice. In particular, we analyze connections among isomorphisms of subgroup lattices of groups and isomorphisms of their weak congruence lattices. Summing up, we prove that there is a one-to-one correspondence between many known classes of groups and lattice-theoretic properties associated with each of these classes. Finally, an open problem is formulated related to the uniqueness of the element corresponding to the diagonal in the lattice of weak congruences of a group.

1. Introduction

1.1. Historical Background

Important tools for structural investigations of algebras are subalgebra and congruence lattices. Generally, these lattices are lattice-theoretically independent and are therefore investigated separately. Both lattices provide important properties of algebras, in particular, varieties are well characterized by congruence lattices. Concerning groups, congruences form modular lattices embeddable into the lattices of subgroups. Still, the corresponding sublattice in general could not be identified only by lattice properties. Consequently, investigations are mostly applied to the lattice of subgroups as a whole. These lattices have been used for characterizing various classes of groups from the beginning of the 20th century; among numerous experts, we mention those which are relevant for the present research: Dedekind, Baer [1], Iwasawa [2], Ore [3], and Suzuki [4]. The results about groups in the framework of subgroup lattices, as the basic starting structure for us, are collected in the mentioned book [4] by Suzuki, as well as in the more recent book [5] by Schmidt; there is also a nicely written survey paper [6] by Pàlfy. Among recently published papers dealing with the characterization of groups by the subgroup lattices, we also mention [7] by Shareshian and Woodroofe, [8] by De Falco, De Giovanni, and Musella, and [9] by Ferrara and Trombetti.

Our research of groups is also situated in the framework of lattices. We use the lattice of weak congruences, which contains, up to isomorphism, both the above-mentioned lattices as sublattices. In universal algebra, weak congruence relations were introduced in [10] (for details, see monograph [11]). Weak congruences of an algebra $\mathcal{A}$ are congruences on subalgebras considered as relations on the whole algebra $\mathcal{A}$. They form an algebraic lattice $\mathsf{Wcon}\left(\mathcal{A}\right)$ under inclusion. If this algebra is a group G, then each element of $\mathsf{Wcon}\left(G\right)$ uniquely corresponds to a normal subgroup of some subgroup of G and vice versa. Moreover, $\mathsf{Sub}\left(G\right)\cong \downarrow \Delta$ and $\mathsf{Con}\left(G\right)=\uparrow \Delta$, where $\Delta$ is the diagonal relation of G generating an ideal and a filter in $\mathsf{Wcon}\left(G\right)$; analogously, for a subgroup H of G, $\mathsf{Sub}\left(H\right)\cong \downarrow {\Delta }_H$ and $\mathsf{Con}\left(H\right)=[{\Delta }_H,H^2]$ (an interval sublattice). This holds in the weak congruence lattice of every algebra; for groups, $\uparrow \Delta$ is additionally embeddable into $\downarrow \Delta$.

Our previous research of groups by weak congruence lattices is presented in papers [12,13]. More recently, a special lattice-theoretic approach to groups via weak congruence lattices is given in [14,15,16]; the results consist of characterizations, that is, necessary and sufficient conditions for $\mathsf{Wcon}\left(G\right)$—under which G belongs to a particular class of groups (Dedekind, Hamiltonian, abelian, solvable, etc.). Here, we use the lattice-theoretic approach from these papers, in particular lattices with normal elements, a class of algebraic lattices that possess the main properties of weak congruence lattices of groups.

Through the present research, we show that in the case of groups, lattices of weak congruences characterize groups more precisely than lattices of subgroups. This applies not only to many classes of groups but also to single groups.

1.2. Review of Results

In our previous papers on the same topic, we analyzed groups with particular algebraic properties, characterizing them via their weak congruence lattices. In the present paper, we are more concentrated on lattice properties of the weak congruence lattices of groups. We analyze order isomorphisms and also the role, as well as uniqueness, of special elements in these lattices.

First, we extend the notion of projectivity, i.e., the isomorphism between subgroup lattices of two groups, replacing lattices of subgroups by weak congruence lattices. We call the corresponding isomorphism a w-projectivity. If it exists, these groups are said to be weak congruence lattice isomorphic. We deal with the connection between projectivity and w-projectivity, i.e., we give conditions under which each of these properties implies the other. One of the basic sufficient conditions for these implications is the uniqueness of the element in the weak congruence lattice of a group, representing the diagonal relation in this lattice. If the element is unique, the lattice in question can be interpreted as a weak congruence lattice of a group in a single way. We say that such lattices are sharp. We analyze the algebraic properties of a group and lattice-theoretic properties of the weak congruence lattice, under which this lattice is sharp.

We recall a definition of a class of groups (see e.g., [17,18]) as a set-theoretic collection of groups closed under isomorphism and containing a trivial group. We list the classes that are characterized here and in previous investigations and we relate these classes to particular classes of lattices.

Finally, summing up the results, we prove that there is a one-to-one correspondence between all classes of groups that we list and lattice properties that determine the corresponding lattices of weak congruences.

Since it is not known whether the weak congruence lattice of each group is sharp, we formulate this question as an open problem.

2. Preliminaries

2.1. Lattices with Normal Elements

We list lattice notions that we use and their basic properties. For more about general notions, see, e.g., books [19,20,21]. For lattices with normal elements, in addition to what is given here, see papers [14,16].

If $a\in L$, then a is a codistributive element if for all $x,y\in L$, $a\wedge (x\vee y)=(a\wedge x)\vee (a\wedge y).$ We also use a distributive element as a dual notion.

For $a\in L$, $m_a$ is the map $L\to \downarrow a$, defined by $m_a\left(x\right):=x\wedge a$, and by $n_a$, we denote the dual map $L\to \uparrow a$, i.e., such that $n_a\left(x\right):=x\vee a$. Observe that a is a codistributive element in a lattice L if and only if $m_a$ is an endomorphism on L. The kernel of $m_a$ is here denoted by ${\phi }_a$.

Dual properties hold for a distributive element.

We consider a lattice L to be algebraic, and the mentioned element a is assumed to be codistributive. For $x\in L$, $\overline{x}$ is the top element of the ${\phi }_a$-class to which x belongs; we also denote by $T_a\subseteq L$ the set of all the top elements:

$$\overline{x}:=\bigvee {\left[x\right]}_{{\phi }_a};T_a=\{\overline{x}\mid x\in L\}.$$

(1)

$T_a$ is a lattice under the order from L, a meet-subsemilattice of L. The classes under ${\phi }_a$ are specific intervals in L: for $x\in L$, there is $b\in \downarrow a$, such that ${\left[x\right]}_{{\phi }_a}=[b,\overline{b}]$.

Concerning notation, let us mention that for any $x\in L$, ${\left[x\right]}_{{\phi }_a}=[b,\overline{b}]=[x\wedge a,\overline{x}]$, where $x\wedge a=b\in \downarrow a$ and, obviously, for any y in this interval, we have $y\wedge a=b$, and $\overline{y}=\overline{b}$.

As usual, we denote by ACC and DCC the Ascending and Descending Chain Condition of a lattice L, respectively.

If $X\ne \varnothing$, then ${\Delta }_X$ is a diagonal of X: ${\Delta }_X:=\{(x,x)\mid x\in X\}.$

A lattice L with a bottom element 0 is atomic if, for every $b\in L$, $b>0$, there is an atom a such that $b⩾a>0$. A lattice L with a bottom element 0 is atomistic if every element is a join of atoms. If a lattice L with a bottom element is atomic and it has a single atom x, then x is a monolith in L.

The following is introduced in [16], with the motivation to capture lattice properties of group notions and to formulate them in pure lattice-theoretic terms.

We say that a codistributive element a in an algebraic lattice L is a full codistributive element of L if

(a) $T_a$ is closed under joins and (b) for every $b\in \downarrow a$, $b=\bigvee c_i$, $i\in I$, so that for every i intervals $[0,c_i]$ and $[c_i,{\overline{c}}_i]$ are isomorphic under $x\mapsto \overline{x}\vee c_i$.

Proposition 1 

([16]). If a is a full codistributive element in L, then:

(i) 

Every $b\in \downarrow a$ is a full codistributive element in the sublattice $\downarrow \overline{b}$.

(ii) 

The map $\xi :\downarrow a⟶T_a$, $x\mapsto \overline{x}$ is a lattice isomorphism.

Let a be a full codistributive element in L, and $x\in L$. Then, the element $x_a\in \downarrow a$ is defined by:

$$x_a:=\bigvee (y\in \downarrow a\mid \overline{y}⩽x).$$

(2)

In addition, let $n,b\in \downarrow a$, $n⩽b$. If $n=x_a$, for some $x\in [b,\overline{b}]$, then n is said to be normal in$\downarrow b$, and we denote it by $n◂b$ (the sign is filled in to thus indicate the difference from the normality among groups).

As introduced in [16], we say that a lattice L is a lattice with normal elements determined by a if it is an algebraic lattice in which a is a fixed full codistributive element, we call it the main codistributive element, and the following postulates ((Pi)–(Pv)) hold.

(Pi) 

For every $x\in \downarrow a$, ${\left[x\right]}_{{\phi }_a}$ is a modular lattice; in particular, ${\left[0\right]}_{{\phi }_a}=\left\{0\right\}$, as the only one-element ${\phi }_a$-class.

(Pii) 

For every $x\in L$, $x=\overline{x_a}\vee (x\wedge a)$.

(Piii) 

For all $x,y\in \downarrow a$, if $x<y$ and $x\cancel{◂}y$, then there are $x_i\in \downarrow a,i\in I$, forming the antichain $x,x_i,i\in I$ so that:

(a) 

$\overline{x_i}\vee y=\overline{x}\vee y$ for all $i\in I$;

(b) 

$x\wedge \left({\bigwedge }_{i\in I}{x}_i\right)◂y$; moreover, it is the greatest element in $\downarrow x$ which is normal in $\downarrow y$.

(Piv) 

The map $f:L\to T_a$, such that $f\left(x\right)=\overline{x_a}$ satisfies the following:

(a) 

if $\chi =\mathsf{ker}f$, then $\chi$-classes are closed under joins in L.

(b) 

f is compatible with joins in ${\phi }_a$-classes.

(Pv) 

Let $b,c\in \downarrow a$, $b◂c$. Furthermore, let $\{d_i,i\in I\}$ be the set of all elements in $[\overline{b},\overline{b}\vee c]$ such that:

(a)

$d_i$ is normal in $[\overline{b},\overline{b}\vee c]$, for every $i\in I$;

(b)

$[\overline{d_i},\overline{c}]$ is a modular lattice for every $i\in I$;

(c)

$[\overline{d_i},\overline{d_i}\vee c]$ does not have an interval sublattice isomorphic with Q given in Figure 1.

Then, $\{d_i,i\in I\}$ has a bottom element.

Lemma 1 

([16]). Let $n,b\in \downarrow a,n⩽b$. Then, $n◂b$ if and only if $[\overline{n},\overline{n}\vee b]\cap T_a=\left\{\overline{n}\right\}$.

Let $b,c\in \downarrow a$ so that $b◂c$. We define $c/b:=\overline{b}\vee c$. Here, $c/b$ is the quotient (of c modulo b).

Obviously, every $x\in L$ is a quotient: if ${\left[x\right]}_{{\phi }_a}=[b,\overline{b}]$, where $b\in \downarrow a$, then by $\left(Piii\right)$$x_a◂b$, and $x=\overline{x_a}\vee b$, so $x=b/x_a$. In addition, for every $x\in L$, the quotient representation is well-defined. Indeed, by the definition of $x_a$ and by postulate $\left(Piii\right),$ the quotient representation is unique, since $x=c/b=e/d$ implies $b=d$ and $c=e$.

Theorem 1 

([12,16]). Let L be a lattice with normal elements determined by a. The following are equivalent:

(a) 

for every $n\in \downarrow a$, $n◂a$;

(b) 

the map $g:\uparrow a⟶\downarrow a$, $x\mapsto x_a$ is an isomorphism;

(c) 

for $b\in \downarrow a$, $\uparrow \overline{b}$ is a lattice with normal elements determined by $\overline{b}\vee a$;

(d) 

L is a modular lattice.

Proposition 2 

([16]). In a lattice L with normal elements determined by a, for $b\in \downarrow a$, the map $g_b:[b,\overline{b}]\to \downarrow a$, $g_b\left(x\right):=x_a$ is an embedding; $g_b\left([b,\overline{b}]\right)$ is a modular sublattice of $\downarrow b$, consisting of all normal elements in $\downarrow b$.

L is an A-lattice if it is a modular lattice with normal elements determined by a in which $\downarrow a$ does not have an interval sublattice which is isomorphic with the lattice Q in Fig. 1 (Q represents the subgroup lattice of the quaternion group, which is uniquely determined by the subgroup lattice).

2.2. Groups

By $H⩽G$ (or $H<G$ if $H\ne G$) and $H⊲G$, we denote that H is a subgroup and a normal subgroup of G, respectively. $\mathsf{Sub}\left(G\right)$ is the algebraic lattice of all subgroups of G, ordered by the set inclusion. ${\mathsf{Sub}}_{\mathsf{n}}\left(G\right)$ is a complete modular sublattice of $\mathsf{Sub}\left(G\right)$, consisting of all normal subgroups of G. A group of whose subgroups are all normal is a Dedekind group, which may be abelian and nonabelian, i.e., Hamiltonian.

According to [5], if G and $G_1$ are groups, then an isomorphism from $\mathsf{Sub}\left(G\right)$ to $\mathsf{Sub}\left(G_1\right)$ is a projectivity from G to $G_1$. If such an isomorphism exists, then G and $G_1$ are here said to be subalgebra lattice isomorphic.

A group satisfies the maximal condition for subgroups if every strictly ascending chain of subgroups $G_1\subset G_2\subset G_3\subset \cdots$ is finite. Groups fulfilling this condition are known to be finitely generated. Such are, e.g., cyclic groups and, more generally, locally cyclic groups, i.e., groups for which every finite subset generates a cyclic subgroup.

Theorem 2 

(Ore [3], Schmidt [5], p. 13). (i) A group G is locally cyclic if and only if the lattice $\mathsf{Sub}\left(G\right)$ of subgroups of G is distributive.

(ii) A group G is cyclic if and only if $\mathsf{Sub}\left(G\right)$ is a distributive lattice satisfying the ACC.

A group G is simple if it does not have proper normal subgroups (different from G and from $\left\{e\right\}$). We say that a simple group G is fully simple if all its proper subgroups are simple. A Tarski monster group is an infinite group G, such that every proper subgroup of G is a cyclic group whose order is a fixed prime number p (also called a Tarski p-group), see, e.g., [5], p. 82. Since it is simple, a Tarski monster group is fully simple. The existence of such groups was proved in 1979 by Olshanskii; actually, they are effectively constructed (see [22,23] and the book [22]). A finite group is said to be semisimple if it has no nontrivial normal abelian subgroups (Robinson, [24], p. 89).

According to [18], and also [17], a class of groups $\mathfrak{C}$ is a collection of groups with the property that if $G\in \mathfrak{C}$, then every group isomorphic to G is also in $\mathfrak{C}$; it is assumed to also contain the trivial, one-element group. A closely related notion to a class of groups is a group theoretical property, or simply property of groups: such is every property that is preserved under the isomorphism of groups. Observe that there is a one-to-one correspondence between the group classes and the group theoretical properties. Clearly, classes can be ordered under inclusion. In this investigation, we deal with numerous classes of groups, showing that these classes can be characterized by lattice-theoretic properties of their weak congruence lattices. Some of the characterizations are presented in this paper, and others in our previous papers.

For more details about all above-mentioned and other notions related to groups, see, e.g., books [17,24,25,26,27,28].

2.3. Weak Congruences

A weak congruence of a group G is a symmetric and transitive subuniverse of $G^2$. Thus, the collection $\mathsf{Wcon}\left(G\right)$ of all weak congruences on G is a lattice which is the set union of all congruences on all subgroups of G, and it also contains, up to an isomorphism, the subgroup lattice as the principal ideal generated by the diagonal of G. For details see [11] (also the references therein). In particular, groups are investigated in this context in [12,13,14]. Some basic facts ([11]): $\mathsf{Wcon}\left(G\right)$ is under inclusion an algebraic lattice in which the diagonal Δ is a full codistributive element. The set $T_{\Delta }$, defined by (1) as $T_a$, is the set of squares of subgroups of G, forming a complete sublattice of $\mathsf{Wcon}\left(G\right)$.

Theorem 3 

([16]). The lattice $\mathsf{Wcon}\left(G\right)$ of a group G is a lattice with normal elements determined by Δ. If $H,K$ are subgroups of G, then $H⊲K$ if and only if ${\Delta }_H◂{\Delta }_K$ in the lattice $\mathsf{Wcon}\left(G\right)$.

Corollary 1 

([16]). If H is a subgroup of a group G, then $H⊲G$ if and only if the principal filter $\uparrow \left(H^2\right)$ in $\mathsf{Wcon}\left(G\right)$ is a lattice with normal elements determined by $H^2\vee \Delta$ as the weak congruence lattice of $G/H$. Analogously, for subgroups $H,K$ of G, $H⊲K$ if and only if the interval $[H^2,K^2]$ in $\mathsf{Wcon}\left(G\right)$ is a lattice with normal elements determined with $H^2\vee {\Delta }_K$ as the weak congruence lattice of $K/H$.

Theorem 4 

([12,16]). The following are equivalent for a group G:

(i) 

G is a Dedekind group;

(ii) 

the lattice $\mathsf{Wcon}\left(G\right)$ of weak congruences of G is modular.

Theorem 5 

([16]). A group G is abelian if and only if $\mathsf{Wcon}\left(G\right)$ is an A-lattice.

In [16], we gave characterizations of particular classes of groups in terms of lattice commutators, e.g., solvable and supersolvable groups. Finite nilpotent groups are characterized by lower semimodularity of $\mathsf{Wcon}\left(G\right)$ in [14].

Theorem 6 

([12]). A group G is locally cyclic if and only if the lattice $\mathsf{Wcon}\left(G\right)$ is distributive. G is cyclic if and only if $\mathsf{Wcon}\left(G\right)$ is a distributive lattice fulfilling the ACC.

3. Results

3.1. w-Projectivity, Uniqueness of Main Codistributive Element, and Sharp Lattices with Normal Elements

Let G and $G_1$ be groups. We say that an isomorphism from $\mathsf{Wcon}\left(G\right)$ to $\mathsf{Wcon}\left(G_1\right)$ is a w-projectivity from G to $G_1$; if such an isomorphism exists, we say that G and $G_1$ are weak congruence lattice isomorphic. Recall that an isomorphism from $\mathsf{Sub}\left(G\right)$ to $\mathsf{Sub}\left(G_1\right)$ is a projectivity from G to $G_1$; in this case, G and $G_1$ are said to be subalgebra lattice isomorphic.

Recall that $\mathsf{Sub}\left(G\right)$ is an ideal sublattice of $\mathsf{Wcon}\left(G\right)$ up to the embedding which sends each subgroup H to the corresponding diagonal relation ${\Delta }_H$. Therefore, it is reasonable to analyze connections between projectivity and w-projectivity in terms of properties of these two groups and of the corresponding lattices.

Firstly, let us mention that projectivity does not necessarily imply w-projectivity: if there is an isomorphism from $\mathsf{Sub}\left(G\right)$ to $\mathsf{Sub}\left(G_1\right)$, then the weak congruence lattices of these two groups need not be isomorphic. For example, there are nonabelian groups with modular subgroup lattices which are lattice isomorphic with abelian groups ([5], p. 88); by our characterization of abelian groups (Theorem 5), the corresponding weak congruence lattices could not be isomorphic. In the present paper, we prove that, for some classes of groups, this implication (projectivity → w-projectivity) does hold.

Here, we also deal with the converse. Namely, we analyze the problem of whether, in general, w-projectivity implies projectivity:

Question. If groups G and $G_1$ are weak congruence lattice isomorphic, are they (or, under which conditions are they) subalgebra lattice isomorphic?

Denote by L the lattice with normal elements representing in such a case the weak congruence lattice of several groups. If the answer to Question 1 is yes, then:

(i) either L has a single main codistributive element, which corresponds to the diagonal relation of each of these groups, or (ii) there is a lattice automorphism on L, sending the element representing the diagonal of G onto the element corresponding to the diagonal relation of $G_1$.

In terms of lattices with normal elements, the negative answer to the Question would mean that there are different full codistributive elements in the lattices of weak congruences of some groups, corresponding to diagonals of two different groups. In addition, the ideals generated by these full codistributive elements are not isomorphic. Consequently, the groups G and $G_1$ would be weak congruence lattice isomorphic but not subalgebra lattice isomorphic, i.e., in such a case w-projectivity would not imply projectivity.

The problems we deal with are essentially lattice-theoretic; therefore, we analyze the uniqueness of full codistributive elements in lattices with normal elements related to groups, as we make precise in the following definition.

If G is a group and $L=\mathsf{Wcon}\left(G\right)$, then L is a lattice with normal elements determined by the element a corresponding to the diagonal relation of G. We say that L is a sharp lattice with normal elements if it is not isomorphic to the weak congruence lattice of some other group, whose diagonal is represented by some $b\ne a$. Note that the mentioned group is not necessarily different from G, meaning that the diagonal of the same group G could be represented by another element of L.

The above-mentioned particular case, where the diagonal of the same group is represented by two different elements $a,b\in L$, is illustrated by the following example.

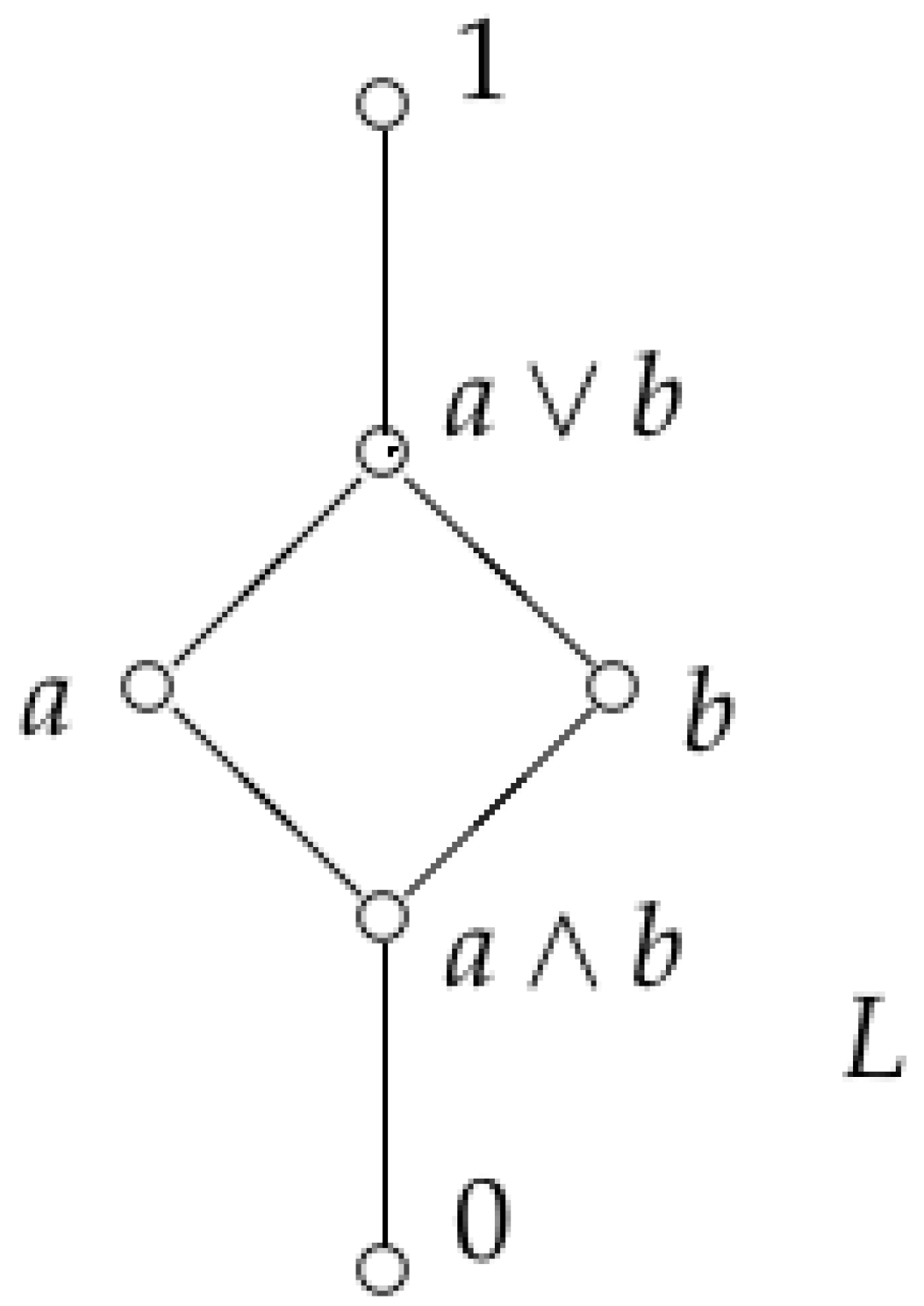
Example 1. 

The lattice L in Figure 2 is a lattice with normal elements determined by a and also by b.

L is the weak congruence lattice of any group G of order $p^2$, p-prime. Each of the two elements a and b can represent the diagonal relation Δ of G. Hence, each of the two different elements of L can represent the diagonal of the same group.

Next, we formulate the theorem illustrating our first reason for investigating the sharpness of weak congruence lattices for groups. Other reasons are related to classes of groups, as formulated in Section 3.4.

Theorem 7. 

Let G and $G_1$ be groups such that there exists a w-projectivity $f:\mathsf{Wcon}\left(G\right)⟶\mathsf{Wcon}\left(G_1\right)$. If $\mathsf{Wcon}\left(G\right)$ is sharp, then there is a projectivity $g:\mathsf{Sub}\left(G\right)⟶\mathsf{Sub}\left(G_1\right)$.

Proof. 

From the assumption that $\mathsf{Wcon}\left(G\right)$ is sharp, we have that $\mathsf{Wcon}\left(G_1\right)$ is sharp, too. Furthermore, $f\left({\Delta }_G\right)$ is the main codistributive element in $f\left(\mathsf{Wcon}\right(G\left)\right)$, and it plays the role of ${\Delta }_G$. Since $\mathsf{Wcon}\left(G_1\right)$ is sharp, there is only one element in this lattice that can be the diagonal relation of $G_1$, and that is ${\Delta }_{G_1}$. Hence, $f\left({\Delta }_G\right)={\Delta }_{G_1}$ has to hold. Now, this implies $f(\downarrow {\Delta }_G)=(\downarrow {\Delta }_{G_1})$, so $\downarrow {\Delta }_G\cong \downarrow {\Delta }_{G_1}$ under the restriction of f. This, of course, implies $\mathsf{Sub}\left(G\right)\cong \mathsf{Sub}\left(G_1\right)$, which completes the proof. □

Remark 1. 

Observe that the property of being sharp applies to lattices with normal elements fulfilling both a lattice-theoretic and an algebraic property:

-

They are determined by a unique full codistributive element;

-

They are lattices of weak congruences of groups in which these unique full codistributive elements correspond to the diagonal relation.

3.2. Auxiliary Results Related to Lattices with Normal Elements

In order to further investigate the sharpness of lattices of weak congruences of groups, in the sequel, we analyze relevant properties of lattices with normal elements. Dealing with lattice properties, we concentrate on the mentioned uniqueness of the full codistributive element.

Recall that, in any lattice, atoms are join-irreducible and coatoms are meet-irreducible elements. Additional similar properties of other elements in lattices with normal elements are as follows.

Lemma 2. 

If L is a lattice with normal elements determined by a, and $b\in L$ is a join-irreducible element, then either $b\in \downarrow a$, or $b\in T_a$.

Proof. 

Let $b\in L$ be join-irreducible and $b\notin \downarrow a$, $b\notin T_a$. From $b\notin \downarrow a$, we have $b>b\wedge a$. Furthermore, by $\left(Pii\right)$, $b=\overline{c}\vee (b\wedge a)$, where $c=\bigvee \{y\in \downarrow a\mid \overline{y}⩽b\}$; here, $\overline{c}<b$ holds from $b\notin T_a$. This implies b is join-reducible, contrary to the assumption. □

Lemma 3. 

Let L be a lattice with normal elements determined by a, then:

(i) 

Each element from $\downarrow a$ different from 0 and from a is meet-reducible in L. In addition, for every nonzero b fulfilling $b<a$, there is $c\notin \downarrow a$, such that $b<c$;

(ii) 

For every atom c of L, $\overline{c}$ is join-irreducible;

(iii) 

For every coatom d of the sublattice $\downarrow a$, $\overline{d}$ is meet-irreducible in L.

Proof. 

(i) If $b\in \downarrow a$, $b\ne a$, $b\ne 0$, then $b=\overline{b}\wedge a$ and $b<\overline{b}$, for otherwise, we have ${\left[b\right]}_{{\phi }_a}=\left\{b\right\}$, which implies $b=0$ by $\left(Pi\right)$. Hence, b is meet-reducible. Furthermore, every element $c\ne b$ of the class ${\left[b\right]}_{{\phi }_a}=[b,\overline{b}]$ fulfills $c\notin \downarrow a$ and $b<c$. Since $b<\overline{b}$, there is at least one such element.

(ii) First, let us notice that for an atom c in L, $c\in \downarrow a$ holds. Namely, if $c\notin \downarrow a$, then $c\wedge a<c$, so $c\wedge a=0$, and $c\in {\left[0\right]}_{{\phi }_a}=\left\{0\right\}$, hence $c=0$ by $\left(Pi\right)$. Moreover, for every $c\ne 0$, $c\in \downarrow a$, we have $c<\overline{c}$ for the same reason.

Assume $\overline{c}$ is join-reducible for an atom c. Then, $\overline{c}=x\vee y$ for some $x,y\in L$ such that $x<\overline{c}$, $y<\overline{c}$. Now, using the codistributivity of a, we have $c=\overline{c}\wedge a=(x\vee y)\wedge a=(x\wedge a)\vee (y\wedge a)$. Since c is an atom, it is join-irreducible, so $x\wedge a=c$ or $y\wedge a=c$ holds. (In fact, $x\wedge a=y\wedge a=c$ has to hold, for otherwise, if, say, $y\wedge a<c$, we have $y\wedge a=0$, hence $y\in {\left[0\right]}_{{\phi }_a}$, so $y=0$, which implies $\overline{c}=x$, contrary to the assumption above.) So, $x,y\in {\left[c\right]}_{{\phi }_a}=[c,\overline{c}]$.

Next we prove that $[c,\overline{c}]=\{c,\overline{c}\}$ holds in L. Notice that by Propositions 1(ii) and (2), $c_a=0$ and ${\left(\overline{c}\right)}_a=c$. Now, if $c<y<\overline{c}$ by Proposition 2, $0=c_a<y_a<{\left(\overline{c}\right)}_a=c$, contrary to the assumption that c is an atom in L.

Hence, $x,y\in \{c,\overline{c}\}$, and from $\overline{c}=x\vee y$, $c<\overline{c}$, we have $x=\overline{c}$ or $y=\overline{c}$, contrary to the assumption.

(iii) Let $d\prec a$ in $\downarrow a$. By Proposition 1(ii), $\overline{d}<1$. First, we show that $\uparrow \overline{d}=\{\overline{d},\overline{d}\vee a,1\}$ in L.

Using $\left(Pii\right)$, for every $x\in L$ such that $\overline{d}<x<1$, we have $\overline{d}<\overline{x_a}\vee (x\wedge a)<1$, and $d⩽x_a⩽a$. From $d\prec a$ in $\downarrow a$, we have $x_a=d$ or $x_a=a$, but $x_a=a$ implies $x=1$, contrary to the assumption, hence $x_a=d$ holds. Furthermore, $\overline{d}<x<1$ implies $d=\overline{d}\wedge a⩽x\wedge a⩽a$, that is $x\wedge a=d$ or $x\wedge a=a$; $x\wedge a=d$ implies $x<\overline{d}$, contrary to the assumption, so $x\wedge a=a$. Therefore $x=\overline{d}\vee a$, and $\uparrow \overline{d}=\{\overline{d},\overline{d}\vee a,1\}$ in L.

If $\overline{d}$ is meet-reducible in L, then $\overline{d}=x\wedge y$ for some $x,y\in L$, such that $\overline{d}<x$, $\overline{d}<y$, so $x,y\in \{\overline{d}\vee a,1\}$, which implies $x\wedge y>\overline{d}$, contrary to the assumption. □

Lemma 4. 

In a lattice L with normal elements determined by a, this element a does not have a relative complement in any principal ideal in L to which a belongs, except for $\downarrow a$.

Proof. 

Indeed, if $x\in L$ is a relative complement of a in $\downarrow (x\vee a)$, then $a\wedge x=0=a\wedge 0$, implying $x\in {\left[0\right]}_{{\phi }_a}$, i.e., $x=0$ by $\left(Pi\right)$, and $x\vee a=a$. □

Corollary 2. 

Let L be a lattice such that it can be determined as a lattice with normal elements by two of its elements, $a,b\in L$, $a\ne b$. Then, $0<a\wedge b$.

Proof. 

First, notice that $a\ne 0$, $b\ne 0$, for otherwise L is a trivial lattice. Now, if $a\wedge b=0$, then b is a relative complement of a in $\downarrow (a\vee b)$. Since $b\ne 0$ by Lemma 4, this is impossible. □

Proposition 3. 

A finite lattice L with normal elements determined by a cannot be determined as a lattice with normal elements by an element b, which is comparable with a, i.e., by some $b\in L$, $a<b$ or $b<a$.

Proof. 

Let L be a finite lattice with normal elements determined by a and let $b\in \uparrow a$, $b\ne a$. Assume that L is also a lattice with normal elements determined by b. By postulate $\left(Pii\right)$, $b=\overline{c}\vee a$, where $c=b_a$, as defined by $\left(2\right)$ and $c◂a$. Notice that $\overline{c}\ne 0$, for otherwise we would have $b=a$. Moreover, $\overline{c}<b$ holds, since if $\overline{c}=b$, then $b\in T_a$, and from $b\in {\left[a\right]}_{{\phi }_a}$, we obtain $b=1$, which implies L is a trivial lattice. By Lemma 3(i), since $0<\overline{c}<b$, there exists $x\notin \downarrow b$, such that $\overline{c}<x$. By the proof of Lemma 3(i), this element x is any element of the class ${\left[\overline{c}\right]}_{{\phi }_b}$ other than $\overline{c}$. (It is easy to see that $\overline{c}$ is the bottom element of this class and also the only element in ${\left[\overline{c}\right]}_{{\phi }_b}\cap \downarrow b$. Moreover, since $\overline{c}\ne 0$, the class has more than one element by $\left(Pi\right)$.) Moreover, since L is finite, there exists an element $d\in {\left[\overline{c}\right]}_{{\phi }_b}$ such that $\overline{c}\prec d$. So, we have $\overline{c}\prec d$, $d\notin \downarrow b$, $d\wedge b=\overline{c}$.

Furthermore, with respect to a as the main codistributive element of L, we have the following: $c<\overline{c}\prec d$, $c◂a$, so $c◂a\wedge d$. (The last implication is due to one of the basic properties of normal elements in lattices with normal elements, all proven in [16].) So, there exists $y\in [a\wedge d,\overline{a\wedge d}]$, such that $c=y_a$, that is, $y=\overline{c}\vee (a\wedge d)$, and $\overline{c}⩽y⩽d$ holds.

Moreover, from $\overline{c}\prec d$, $y=\overline{c}$ or $y=d$.

If $y=\overline{c}$, then $a\wedge d⩽\overline{c}$, so $a\wedge d⩽c$, and given $\overline{c}\prec d$, we obtain $a\wedge d=c$. Hence, we have $\overline{a\wedge d}\prec d$ in L. This is impossible, since $d\in {[a\wedge d]}_{{\phi }_a}$.

For $y=d$, we have $\overline{c}\vee (a\wedge d)=d$, so $b=\overline{c}\vee a⩾\overline{c}\vee (a\wedge d)=d$, contrary to the choice of d. This completes the proof.

This clearly also proves the other possibility, when $b<a$. □

Observe that Proposition 3 can be straightforwardly generalized to the case where finiteness of the lattice is replaced by the condition that it fulfills the ACC. The proof is similar.

Proposition 4. 

Let L be a lattice with normal elements determined by a and satisfying the ACC condition. Then, L cannot be determined as a lattice with normal elements by an element b comparable with a, i.e., by some $b\in L$ such that $a<b$ or $b<a$.

Furthermore, directly from Lemma 3, we obtain the following.

Proposition 5. 

Let L be an algebraic lattice and let A be the set of atoms in L. Let $\langle A\rangle$ be the sublattice of L generated by A and ${\langle A\rangle }^{*}$ the smallest complete sublattice of L that contains $\langle A\rangle$. Then, for every element $b\in L$ such that L is a lattice with normal elements determined by b, $\downarrow b$ contains the sublattice ${\langle A\rangle }^{*}$.

Proof. 

In Lemma 3(ii), we proved that for every atom c in a lattice L with normal elements determined by b, $c\in \downarrow b$ holds. Hence, $A\subseteq \downarrow b$, so $\langle A\rangle$ is obviously a sublattice in $\downarrow b$. Furthermore, since $\downarrow b$ is a complete sublattice in L, we have ${\langle A\rangle }^{*}⩽\downarrow b$. □

Corollary 3. 

Let L be a lattice with normal elements determined by a and satisfying the ACC condition. If $\downarrow a$ is an atomistic lattice, then L is uniquely determined by a.

Proof. 

By Proposition 5, ${\langle A\rangle }^{*}$ is a sublattice in $\downarrow a$, where A is a set of atoms in L. Since $\downarrow a$ is atomistic, we have ${\langle A\rangle }^{*}=\downarrow a$. Now, if L is also a lattice with normal elements determined by b for some $b\ne a$, then, by Proposition 5, ${\langle A\rangle }^{*}$ is a sublattice in $\downarrow b$, hence $a<b$ holds, contrary to Proposition 4 above. □

Next, we show that particular modular lattices can be uniquely extended to modular lattices with normal elements. Consequences for groups are formulated as Corollaries 4–6 and explicitly by Corollary 8.

Proposition 6. 

Let S be an algebraic modular lattice such that for all $x,y\in S$, $x⩽y$ the following holds:

If $\{z_i\mid i\in I\}$ is the set of all elements from $[x,y]$ such that the interval $[z_i,y]$ does not have an interval sublattice isomorphic to Q in Figure 1, then this set has a bottom element.

Then, there is a unique (up to isomorphism) modular lattice L with normal elements determined by the top element $1_S$ of S, in which $S=\downarrow 1_S$.

Proof. 

It is easy to see that $S\times S$ is an algebraic modular lattice. Its compact elements are exactly the pairs of compact elements in S. Now, let L be the following sublattice of $S\times S$:

$$L:=\left\{\right(u,v)\mid u,v\in S,u⩽v\}.$$

Consequently, L is an algebraic modular lattice with compact elements being all pairs $(a,b)$, where $a,b$ are compact in S and $a⩽b$.

First we prove $(0,1)$ is a full codistributive element in L. Let $(a,b),(u,v)\in L$. Then, $(0,1)\wedge \left(\right(a,b)\vee (u,v\left)\right)=(0,1)\wedge (a\vee u,b\vee v)=(0,b\vee v)=\left(\right(0,1)\wedge (a,b\left)\right)\vee \left(\right(0,1)\wedge (u,v\left)\right)$, hence $(0,1)$ is codistributive in L. To simplify the notation, we further denote $(0,1)$ by $\alpha$. So, the mapping $m_{\alpha }:L⟶L$, $(x,y)\mapsto (x,y)\wedge (0,1)=(0,y)$ is an endomorphsm of L, ${\phi }_{\alpha }=\mathsf{Ker}\left(m_{\alpha }\right)=\{((x,y),(u,y))\in L\times L\}$, and for every $(x,y)\in L$, ${\left[(x,y)\right]}_{{\phi }_{\alpha }}=\{(z,y)\mid z⩽y\}=[(0,y),(y,y)]$ in L. The set of top elements of ${\phi }_{\alpha }$ classes is $T_{\alpha }=\{(y,y)\mid y\in S\}$. This set is closed under arbitrary meets in L.

Let $(y_i,y_i)\in T_{\alpha }$ for $i\in I$. Then, ${\bigvee }_{i\in I}(y_i,y_i)=({\bigvee }_{i\in I}{y}_i,{\bigvee }_{i\in I}{y}_i)\in T_{\alpha }$, hence $T_{\alpha }$ is closed under arbitrary joins in L. Moreover, let $(0,w)\in \downarrow (0,1)$ in L. Since $w\in S$, it is a join of some compact elements in S, say, $w={\bigvee }_{i\in I}{w}_i$. Now, $(0,w)={\bigvee }_{i\in I}(0,w_i)$ in L, where $(0,w_i)$ are compact in L. It is easy to prove that $[(0,0),(0,w_i)]\cong [(0,w_i),(w_i,w_i)]$ under the map $(0,z)\mapsto (z,w_i)$ for all $i\in I$, so $(0,1)$ is a full codistributive element in L.

Next, we prove the postulates (Pi)–(Pv) for L.

(Pi) For every $(0,y)\in \downarrow (0,1)$, ${\left[(0,y)\right]}_{{\phi }_{\alpha }}=[(0,y),(y,y)]$ in L, hence it is a modular lattice since L is modular. Moreover, ${\left[(0,0)\right]}_{{\phi }_{\alpha }}=\left\{(0,0)\right\}$, and it is the only one-element ${\phi }_{\alpha }$-class (if $(x,y)\ne (0,0)$, then $y\ne 0$, hence $(0,y)\ne (y,y)$, so the class ${\left[(x,y)\right]}_{{\phi }_{\alpha }}$ has at least two elements).

(Pii) Notice that in L${(x,y)}_{\alpha }=\bigvee \{(0,z)\in \downarrow (0,1)\mid (z,z)⩽(x,y)\}$ holds, hence ${(x,y)}_{\alpha }=(0,x)$. Now, let $(x,y)\in L$. Then, $(x,y)=(x,x)\vee \left(\right(x,y)\wedge (0,1\left)\right)$.

(Piii) First, notice that in L$(0,y)$ is normal in $\downarrow (0,z)$ for all $(0,y),(0,z)\in \downarrow (0,1)$, such that $(0,y)⩽(0,z)$. Namely, $(0,y)={(y,z)}_{\alpha }$ and $(y,z)\in [(0,z),(z,z)]={\left[(0,z)\right]}_{{\phi }_{\alpha }}$. Therefore, this postulate trivially holds.

(Piv) In L, we have the following: $f:L⟶T_{\alpha }$, $(x,y)\mapsto (x,x)$; $\chi =\mathsf{Ker}\left(f\right)=\left\{\right((a,b),(u,v))\in L\times L\mid (a,a)=(u,u\left)\right\}=\left\{\right((a,b),(a,v))\in L\times L\}$. So, for $(a,b)\in L$, ${\left[(a,b)\right]}_{\chi }=\{(a,v)\in L\}=[(a,a),(a,1)]$. Let $(a,x_i)\in {\left[(a,b)\right]}_{\chi }$, $i\in I$; ${\bigvee }_{i\in I}(a,x_i)=(a,{\bigvee }_{i\in I}{x}_i)\in {\left[(a,b)\right]}_{\chi }$. The classes of $\chi$ are closed under joins in L.

Let $\left[\right(0,y),(y,y\left)\right]$ be an arbitrary ${\phi }_{\alpha }$-class. Let $(x_i,y)\in [(0,y),(y,y)]$ for $i\in I$; $f\left({\bigvee }_{i\in I}(x_i,y)\right)=f({\bigvee }_{i\in I}{x}_i,y)=({\bigvee }_{i\in I}{x}_i,{\bigvee }_{i\in I}{x}_i)={\bigvee }_{i\in I}\left(f(x_i,y)\right)$, which proves f is compatible with joins in ${\phi }_{\alpha }$-classes.

(Pv) First, notice that in an arbitrary lattice with normal elements determined by a, for $b,c\in \downarrow a$ such that $b◂c$, $d_i$ is normal in $[\overline{b},\overline{b}\vee c]$ if and only if $d_i=\overline{b}\vee n_i$ for some $n_i\in [b,c]$, $n_i◂c$. (This is proved in [16].)

Now, in the current lattice L: let $(0,x),(0,y)\in \downarrow (0,1)$, $x⩽y$ in S. This implies $(0,x)◂(0,y)$, as proved above. We consider the set of all elements $(x,z_i)$ in $\left[\right(x,x),(x,y\left)\right]$ fulfilling the conditions (a), (b), and (c) of the postulate (Pv), and this set should have a bottom element. Since $(x,z_i)=(x,x)\vee (0,z_i)$, where $(0,z_i)\in [(0,x),(0,y)]$ and $(0,z_i)◂(0,y)$, we conclude that every $(x,z_i)$ from the interval $\left[\right(x,x),(x,y\left)\right]$ is normal in this interval and, hence, satisfies the condition (a) from this postulate.

In condition (b), for every $\left[(x,z_i)\right]$, we consider the interval $[(z_i,z_i),(y,y)]$ in L. It is a modular lattice for every $(x,z_i)\in [(x,x),(x,y)]$, that is, for every $z_i\in [x,y]$, as a sublattice of L. So, condition (b) is also fulfilled for all elements $(x,z_i)$ of $\left[\right(x,x),(z,y\left)\right]$.

For condition (c), let $\{(x,z_i)\mid i\in I\}$ be the set of all elements from $\left[\right(x,x),(x,y\left)\right]$ such that the interval $[(z_i,z_i),(z_i,y)]$ in L does not have an interval sublattice isomorphic to Q in Figure 1. Now, the interval $[(z_i,z_i),(z_i,y)]$ in L does not have an interval sublattice isomorphic to Q if and only if the interval $[z_i,y]$ in S does not have an interval sublattice isomorphic to Q. Furthermore, if $\{z_i\mid i\in I\}$ is the set of all elements in S satisfying the previous condition, then this set has a bottom element, say $z=\bigwedge \{z_i\mid i\in I\}$. It is easy to see that the corresponding set in L has a bottom element, too, and $(x,z)=\bigwedge \{(x,z_i)\mid i\in I\}$ holds. Therefore, (Pv) holds for L, and L is a lattice with normal elements determined by $(0,1)$.

Now, it is easy to show that $S\cong \downarrow (0,1)$ under the map $x\mapsto (0,x)$.

In the end, we have to show uniqueness.

First, notice that, by Theorem 1, if L is a lattice that satisfies the conditions of this proposition, and it is determined by a, then $(\forall n\in \downarrow a)n◂a$. Now, using quotient representations, the elements of L are exactly $c/b$ for all $b,c\in \downarrow a$, $b⩽c$. Furthermore, let us assume that $L_1$ and $L_2$ are lattices that satisfy the conditions of this proposition. Let them be determined by elements a and b, respectively, so that $\downarrow a\cong S$ and $\downarrow b\cong S$. Let $\xi :\downarrow a⟶\downarrow b$ be the isomorphism induced by these two isomorphisms. Based on what we said above, every element in $L_1$ is of the form $y/x$ for some $x,y\in \downarrow a$, and the analogue holds in $L_2$. An isomorphism between lattices $L_1$ and $L_2$ is defined like this: $\chi :L_1⟶L_2$, $y/x\mapsto \xi \left(y\right)/\xi \left(x\right)$ (or, $\overline{x}\vee y\mapsto \overline{\xi \left(x\right)}\vee \xi \left(y\right)$). This proves the uniqueness of this lattice (up to isomorphism). □

Corollary 4. 

Let S be an algebraic modular lattice that does not have an interval sublattice isomorphic to Q in Figure 1. Then, there is a unique, up to isomorphism, A-lattice L determined by the top element $1_S$ of S, in which $S=\downarrow 1_S$.

Notice that the previous result also holds for every lattice S with fewer than five elements.

Corollary 5. 

Let S be a complete chain. Then, there is a unique, up to isomorphism, A-lattice L determined by the top element $1_S$ of S, in which $S=\downarrow 1_S$.

Proposition 7. 

Let L be an algebraic lattice determined as a lattice with normal elements by a and by b, for some $a,b\in L$, $a\ne b$. If L satisfies DCC condition and $a\wedge b$ is a monolith in L, then L is a six-element lattice, represented in Figure 2.

Proof. 

First, notice that $a\wedge b<b$ holds in L. Otherwise, we have $b=a\wedge b$, so b is an atom in L and $\downarrow b=\{0,b\}$. Since L is a lattice with normal elements determined by b, every element in L has a unique quotient representation $y/x$ for some $x,y\in \downarrow b$, $x⩽y$. This implies $L=\{b/b,b/0,0/0\}=\{0,b,1\}$. (Recall that $b\ne 0$, $b\ne 1$, for otherwise the lattice with normal elements is trivial.) So, L is a three-element lattice, there is no $a\ne b$ such that L is determined by a, too, which contradicts the assumption.

Similarly. $a\wedge b<a$ holds in L.

If we consider L as a lattice with normal elements determined by a, then $b\in {[a\wedge b]}_{{\phi }_a}$. By Proposition 2, ${[a\wedge b]}_{{\phi }_a}$ is embeddable into the ideal $\downarrow (a\wedge b)$, which has two elements. Therefore, ${[a\wedge b]}_{{\phi }_a}=\{a\wedge b,b\}$. Since the class is an interval, we have $a\wedge b\prec b$ in L (and also $\overline{a\wedge b}=b$ regarding congruence ${\phi }_a$).

Analogously, ${[a\wedge b]}_{{\phi }_b}=\{a\wedge b,a\}$, $a\wedge b\prec a$ in L and ${\overline{a\wedge b}}^{*}=a$, where ${\overline{a\wedge b}}^{*}$ denotes the top element of the class ${[a\wedge b]}_{{\phi }_b}$.

So, we have $0\prec a\wedge b\prec a$ and $0\prec a\wedge b\prec b$ in L. Furthermore, from the fact that $a\wedge b$ is a monolith in L and that L (or $\downarrow a$) satisfies DCC, we obtain $\downarrow a=\{0,a\wedge b,a\}$, a three-element chain. Now, we show $a\wedge b◂a$ regarding ${\phi }_a$.

Let $x=\overline{a\wedge b}\vee a=b\vee a$. So, $x\in {\left[a\right]}_{{\phi }_a}$, and, by definition, $x_a=\bigvee \{z\in \downarrow a\mid \overline{z}⩽x\}$. It is easy to see that $\overline{0}=0$, $\overline{a}=1$, and $\overline{a\wedge b}=b$, hence $x_a=a\wedge b$, which implies $a\wedge b◂a$.

Now, we have $\downarrow a=\{0,a\wedge b,a\}$ and $a\wedge b◂a$. Elements of L are exactly the quotients $0/0=0$, $(a\wedge b)/0=a\wedge b$, $(a\wedge b)/(a\wedge b)=b$, $a/(a\wedge b)=b\vee a$, $a/0=a$, and $a/a=1$. The lattice L is obviously isomorphic to the six-element lattice represented in Figure 2. □

Remark 2. 

The DCC condition for L can be slightly weakened, namely, it is enough to ask for $\downarrow a$ to satisfy the DCC and not to require it for the whole lattice.

3.3. Applications to Groups

The above lattice-theoretic results can be formulated for weak congruence lattices of concrete classes of groups, as follows.

Corollary 6. 

Let S be a finite chain. Then, the lattice L from Corollary 5 is a weak congruence lattice for a cyclic group G of order $p^n$ for some prime p. Moreover, $L\cong \left\{\right(p,q)\mid p,q\in S,p⩽q\}$, and L has a single coatom.

We also have the following.

Theorem 8. 

In the class of Dedekind groups, projectivity implies w-projectivity.

Proof. 

Let $G_1$ and $G_2$ be Dedekind groups and $\xi :\mathsf{Sub}\left(G_1\right)⟶\mathsf{Sub}\left(G_2\right)$ a projectivity. We have isomorphisms ${\chi }_1:\mathsf{Sub}\left(G_1\right)⟶\downarrow {\Delta }_1$, ${\chi }_2:\mathsf{Sub}\left(G_2\right)⟶\downarrow {\Delta }_2$, where ${\Delta }_1$ and ${\Delta }_2$ are elements corresponding to diagonal relations in $\mathsf{Wcon}\left(G_1\right)$ and $\mathsf{Wcon}\left(G_2\right)$. Furthermore, ${\chi }_2\circ \xi \circ {\left({\chi }_1\right)}^{-1}$ is an isomorphism between $\downarrow {\Delta }_1$ and $\downarrow {\Delta }_2$; let us denote this isomorphism by $\zeta$, $\zeta :\downarrow {\Delta }_1⟶\downarrow {\Delta }_2$. By Theorem 3, for all $a,b\in \downarrow {\Delta }_1$ such that $a⩽b$, $a◂b$ holds, and the same in $\downarrow {\Delta }_2$. It is easy to show now, using quotient representations, that the map $\mu :\mathsf{Wcon}\left(G_1\right)⟶\mathsf{Wcon}\left(G_2\right)$, $y/x\mapsto \zeta \left(y\right)/\zeta \left(x\right)$ is an isomorphism. □

Theorem 9. 

The weak congruence lattice $\mathsf{Wcon}\left(G\right)$ of a finite group G is modular, and it has a single coatom if and only if G is a cyclic group of order $p^n$, p-prime.

Proof. 

It is straightforward to check that the weak congruence lattice of a cyclic group G whose order is $p^n$, p-prime, fulfills the requirements of the theorem. Conversely, suppose a finite group G fulfills the requirements of the theorem. Then, it is a Dedekind group with a single maximal subgroup, which is normal. Such finite groups are cyclic p-groups, and their subgroups are linearly ordered by inclusion. □

The lattice of weak congruences of a cyclic group of order $p^n$, p-prime is represented in Figure 3.

Theorem 10. 

The weak congruence lattice of a cyclic group of order $p^n$, p-prime is sharp.

Proof. 

Straightforward, since the lattice represented in Figure 3 is a lattice with normal elements, determined as such only by the element denoted by $\Delta$. □

Next, we characterize several classes of simple groups.

The following introductory result related to simple groups is obvious.

Theorem 11. 

A group G is simple if and only if the diagonal Δ is a coatom in the lattice $\mathsf{Wcon}\left(G\right)$.

Proof. 

Directly, since $\uparrow \Delta$ is the congruence lattice of G. □

Theorem 12. 

The weak congruence lattice L of a finite simple group G is sharp (Figure 4).

Proof. 

We use the result from [29], by which a finite simple group G is a K-group, i.e., the lattice $\mathsf{Sub}\left(G\right)$ is complemented. The lattice $L=\mathsf{Wcon}\left(G\right)$ is sketched in Figure 4 as the weak congruence lattice of G, so the ideal $\downarrow \Delta$ is a complemented lattice. Suppose now that L is a lattice with normal elements determined by b for some $b\ne \Delta$. Since L is a finite lattice, by Proposition 4, b and $\Delta$ are incomparable in L. Then, $b\wedge \Delta \in \downarrow \Delta$ and $b\wedge \Delta <\Delta$. Since $\downarrow \Delta$ is a complemented lattice, $b\wedge \Delta$ has a complement ${\Delta }^{\prime }$ in $\downarrow \Delta$. So, $b\wedge \Delta \wedge {\Delta }^{\prime }=0$, hence $b\wedge {\Delta }^{\prime }=0$, and $(b\wedge \Delta )\vee {\Delta }^{\prime }=\Delta$. By assumption, L is a lattice with normal elements determined by b, so $b\wedge {\Delta }^{\prime }=0$ implies ${\Delta }^{\prime }\in {\left[0\right]}_{{\phi }_b}$, that is, ${\Delta }^{\prime }=0$. Furthermore, this implies $b\wedge \Delta =\Delta$, and $b⩾\Delta$. □

Similar arguments as for the finite simple groups above can be used for an analogue statement related to the symmetric group $S_n$, as follows. The corresponding weak congruence lattice is sketched in Figure 5.

Theorem 13. 

The weak congruence lattice L of the symmetric group $S_n$, $n\ne 4$ is a sharp lattice with normal elements.

Proof. 

See the proof of Theorem 12. □

In order to characterize semisimple groups, we introduce the following property of lattices with normal elements determined by a:

For every $b\in \downarrow a$ such that $b◂a$ and $b\ne 0$, $\downarrow \overline{b}$ is not an A-lattice.     $(*)$

Theorem 14. 

A finite group G is semisimple if and only if $\mathsf{Wcon}\left(G\right)$ fulfills the property $(*)$.

Proof. 

Indeed, by Theorem 5, $(*)$ is a lattice reformulation of the definiens for a semisimple group. Namely, $\downarrow \overline{b}$ is the weak congruence lattice of the normal subgroup corresponding to the element b, which represents its diagonal. □

Finally, any Tarski monster group, which is fully simple, also has the same sharpness property of the weak congruence lattice.

Theorem 15. 

The weak congruence lattice of any Tarski monster group is a sharp lattice with normal elements.

Proof. 

Indeed, the diagonal $\Delta$ is the only nontrivial codistributive element in the corresponding weak congruence lattice (see Figure 6). □

3.4. Classes of Groups and Classes of Lattices with Normal Elements

As defined in the Preliminaries, a class of groups is a set-theoretic collection of groups closed under group isomorphism and which contains a trivial group; clearly, this is a class in the ordinary set-theoretic sense.

In the sequel, we list the classes of groups characterized in papers [14,15,16] and also in the present one, omitting the full name of the class; e.g., instead of the class of all abelian groups, we write abelian groups:

Empty class of groups, all finite groups, Dedekind groups, abelian groups, Hamiltonian groups, finite nilpotent groups, solvable groups, supersolvable groups, cyclic groups, metabelian groups, perfect groups, T-groups, metacyclic groups, hyperabelian groups, hypercyclic groups, polycyclic groups, cocyclic groups, N-groups, $\tilde{N}$-groups, finite symmetric groups, finite simple groups, semisimple groups, and fully simple groups.

Let $\mathfrak{G}$ be the collection of all mentioned classes of groups. Clearly, the classes are not generally disjoint, and they can be ordered by inclusion.

Analogously, as for groups, we consider classes of lattices with normal elements, closed under lattice isomorphism. The classes are determined by lattice properties of weak congruence lattices of the corresponding groups. For example, we have the class of modular lattices with normal elements, A-lattices with normal elements, lower semimodular lattices with normal elements, and so on. We do not list these classes here; in the sequel, they appear along with the characterization of the corresponding class of groups in the related theorems in this paper and in [14,15,16].

We denote by $\mathfrak{L}$ the collection of the mentioned classes of lattices with normal elements that correspond to the mentioned classes of groups.

Theorem 16. 

There is a one-to-one correspondence between classes of groups in $\mathfrak{G}$ and classes of lattices with normal elements in $\mathfrak{L}$.

Proof. 

Indeed, for a group G in a class $\mathcal{G}$ from $\mathfrak{G}$, we have a characterization theorem of the form $G\in \mathcal{G}$ if and only if $\mathsf{Wcon}\left(G\right)$ has lattice properties which determine the corresponding class of lattices. □

Every class of groups (lattices) listed above corresponds to a group (lattice)-theoretic property. Therefore, by Theorem 16, (classes of) groups are characterized by the associated lattice properties.

Let us mention that nothing similar to the correspondence described by Theorem 16 exists if the weak congruence lattices are replaced by subgroup lattices. In this context, an analogous characterization can be established only for a rather small number of (classes of) groups.

Due to properties given in Theorems 16 and 7, there is an additional straightforward way to see how weak congruence lattices determine groups:

Theorem 17. 

Classes of groups in $\mathfrak{G}$ which have sharp lattices of weak congruences are closed under w-projectivity.

In other words, for many classes of groups, for many classes of groups, only groups from the same class can have isomorphic weak congruence lattices.

We conclude with an open problem.

Problem. Prove or find a counterexample for the claim: The weak congruence lattice of every group G, $\left|G\right|\ne p^2$, p - prime is sharp.

4. Conclusions

As a part of the investigation of groups by their weak congruence lattices, here, we presented some important related lattice problems. Namely, conditions are given under which weak congruence lattices of different groups are isomorphic and also how this isomorphism is related to the isomorphisms of subgroup lattices. In this framework, an important lattice problem is the uniqueness of the element representing the diagonal of the group. This problem is solved for some classes of groups but remains open in general.

In the future, we intend to deal with groups having linearly ordered infinite systems of subgroups, possibly indexed by ordinal numbers. These are mostly generalized solvable groups, and the technique we use will also be applied to some classes of infinite simple groups (characterized by the absence of the mentioned series of subgroups). Our task is to characterize such groups by the corresponding linearly ordered sublattices in their lattices of weak congruences.