Abstract
We define the notions of weakly -countably compactness and nearly -countably compactness denoted by -CC and -CC as generalizations of -compact spaces in the sense of Csaśzaŕ generalized topological spaces. To obtain a more general setting, we define -CC and -CC via hereditary classes. Using -open sets, -regular open sets, and -regular spaces, many results and characterizations have been presented. Moreover, we use the properties of functions to investigate the effects of some types of continuities on -CC and -CC. Finally, we define soft -CC and -CC as generalizations of soft -compactness in soft generalized topological spaces.
Keywords:
μ-countably compact; μℋ-countably compact; weakly μ-countably compact; nearly μ-countably compact MSC:
54A05; 54C05; 54D30
1. Introduction
In 2002, Csaśzaŕ introduced generalized topology [1]. Csaśzaŕ’s topology removes the intersection property of a finite number of open sets. Many authors have made different generalizations of compactness such as [2,3,4,5]. On the other hand, many generalizations have been done by using the notion of generalized topology as [6,7,8,9,10]. In particular, we introduce the notion of weakly (nearly) -countably compactness. Additionally, by using hereditary classes defined in 2007 [8], weakly (nearly) -countably compact spaces have been investigated in more general settings. The current paper has an application in soft set theory as can be seen in the last section. Similar applications can be made in fuzzy and set theories, which are in uncertainty in mathematics. In particular, many developments can be made as interactions between uncertainty and other disciplines of mathematics as fractional calculus or in function spaces. So, the reader can return to [11,12,13,14,15].
A subset of the power set of X is generalized topology on X, whenever and for all [8]. In this work, the notation stands for strong generalized topology, which means . A subset A is -open whenever and A is -closed if . The interior of A in is for all , and the closure is given by for all . Whenever (resp. , then A is called -regular open (resp. -regular closed) [8]. See that whenever , then A is -open [6]. We write the pair simply as . Now, let be a subset of , then is a generalized subspace topology of A in X whenever, for all , there is a subset such that [16]. Let and , then is a hereditary class on X whenever and , then for all . The pair is a generalized space with respect to [8]. Moreover, whenever for all , then is called an ideal on X.
Next, we give basic concepts of known generalizations of compactness and countable compactness in generalized topology. Nearly -countably compactness and -countably compactness have been discussed in Section 2. In -regular spaces, Theorem 4 shows that there is no difference between nearly -countably compact space and -countably compact space. In Section 3, weakly -countably compactness has been characterized by using -closed sets in Theorem 10. There have been some further results about subsets of weakly -countably compact spaces. Some examples are given to verify the new spaces. The main contribution in Section 4 is to characterize the continuity in the generalized topology of the discussed spaces. Theorems 23 and 24 show that continuity preserves such given spaces. Using different kinds of continuity, we obtain stronger results in several theorems in Section 4. As a consequence, we add Section 5 before the conclusions. The short section is about an applicable definition in soft theory that generalizes soft -compactness.
Definition 1 ([7]).
Let X be a set. The space is said to be μ-compact whenever , where for all , then there is a finite sub-collection such that .
Definition 2 ([17]).
Let X be a set. The space is said to be nearly μ-compact (denoted by -compact) whenever , where for all , then there is a finite sub-collection such that .
Definition 3 ([10]).
Let X be a set. The space is said to be weakly μ-compact (denoted by -compact) whenever , where for all , then there is finite sub-collection such that .
Definition 4 ([18]).
Let be a space with respect to . The pair is said to be weakly -compact (denoted by -compact) whenever , where for all , then there is a finite sub-collection such that ∈.
Definition 5 ([17]).
Let be a space with respect to . The pair is said to be nearly -compact (denoted by -compact) whenever , where for all , then there is a finite sub-collection such that ∈.
Definition 6 ([19]).
Let X be a set. The space is said to be μ-countably compact (denoted by μ-CC) whenever , where for all and Λ is a countable index set, then there is a finite sub-collection such that .
Definition 7 ([19]).
Let be a space. A subset A of X is said to be μ-CC set whenever , where for all and Λ is a countable index set, then there is a finite sub-collection such that .
Definition 8 ([19]).
Let be a space with respect to . The pair is said to be -countably compact (denoted by -CC) whenever , where for all and Λ is a countable index set, then there is a finite sub-collection such that ∈.
Definition 9 ([10]).
Let X be a set. The space is said to be μ-regular whenever, for each μ-open subset U of X and for each , there exist a μ-open subset V of X and a μ-closed subset F of X such that .
Definition 10 ([10]).
If and , then x is called -cluster point of C if for all and . The set is a -cluster point of C} if , then C is called -closed. The set C is -open if is -closed.
Lemma 1 ([10]).
If and , then .
Lemma 2 ([10]).
Let be a function. The following statements are equivalent:
- 1.
- f is -continuous;
- 2.
- , for all ;
- 3.
- , for all .
Definition 11.
Let be a function. If for each and , there exists containing t such that:
- 1.
- , then f is said to be strongly -continuous [20].
- 2.
- , then f is said to be super -continuous [20].
- 3.
- , then f is said to be -continuous [21].
- 4.
- , then f is said to be almost -continuous [22].
2. Nearly -Countably Compactness and Nearly -Countably Compactness
In this section, we introduce the notion of nearly -countably compact and the notion of nearly -countably compact. Some interesting examples are presented to investigate these spaces.
Definition 12.
Let X be a set. The space is said to be nearly μ-countably compact (denoted by -CC) whenever , where for all and Λ is a countable index set, then there is a finite sub-collection such that .
Corollary 1.
Every μ-CC space is -CC space.
Proof.
Let be a -CC space. Which means that , where for all and is a countable index set, then there is a finite sub-collection where , but for each ,
so . Thus, . □
The converse of Corollary 1 is not true as presented in Example 1.
Example 1.
Let be a space, where or is a countable}. Let , where for all and Λ is a countable index set, then we can find a finite sub-collection , so and for each . Thus is a -CC space. It is clear that is not μ-CC space.
Definition 13.
Let be a space with respect to . The pair is said to be nearly -countably compact (denoted by - CC) whenever , where for all and Λ is a countable index set, then there is a finite sub-collection such that ∈.
Theorem 1.
If X is a -CC space, then X is a -CC space.
Proof.
Let X be a -CC space. Which means that , where for all and is a countable index set, then there is a finite sub-collection where , but = . Hence, be -CC space. □
In Example 1, we show that the converse of Theorem 1 is not always true.
Example 2.
Let , and be μ-subbase where μ generated by such that and . Then, is not -CC space. However, it is -CC space. Since , where for all and Λ is a countable index set, then there is a finite sub-collection where ∈.
Theorem 2.
If X is a -CC space, then X is a -CC space.
Proof.
Let X be a -CC space. This means for , where for all and is a countable index set, then there is a finite sub-collection where ∈, but . Thus, . Hence, is a -CC space. □
The converse of Theorem 2 is not true, as presented in Example 3.
Example 3.
Let , , where and . Then, is -CC because for any proper μ-open set where , then ∈. However, that is not -CC because there is no finite sub-collection such that ∈
Theorem 3.
If a space is -CC, then for every countable cover of X by -open sets, there exists a finite sub-collection such that .
Proof.
Suppose is -CC and is the -open cover of X. Then, for all , there exists where . Since is -open, then there exists where . However, . Then, where . Since X is -CC, there exist where . However, . Hence, . □
Theorem 4.
Let be a μ-regular space. The following statements are equivalent:
- 1.
- is -CC.
- 2.
- is -CC.
Proof.
Suppose X is -regular and -CC and is the -open cover of X. Then, for all , there exists where . Since is -open, then there exists such that . However, . Then, the sub-collection is the -open cover of X. Since X is -CC, so there exist where . However, . Thus, . This mean is -CC.
It follows from Theorem 2. □
3. Weakly -Countably Compactness and Weakly -Countably Compactness
In this section, we introduce the notion of weakly -countably compactness and the notion of weakly -countably compactness. We also present a diagram to describe the relationships among different types of generalizations of -compactness and -compactness.
Definition 14.
Let X be a set. The space is said to be weakly μ-countably compact (denoted by - CC) whenever , where for all and Λ is a countable index set, then there is a finite sub-collection such that .
Theorem 5.
A space is -CC if and only if whenever , where is a μ-regular open subset for all , then there exists a finite subset such that .
Proof.
Necessity. It is straightforward and therefore omitted.
Sufficiency. Suppose , where for all and is a countable index set. It is clear that is -open, thus is a countable -regular open cover of X. So we can find a finite sub-collection of X where . It is clear that is -closed, thus . Hence, is -CC. □
Theorem 6.
Let be a space. The following statements are equivalent:
- 1.
- X is -CC;
- 2.
- For any countable collection of countable μ-closed subset of X such that , there exists a finite sub-collection such that ;
- 3.
- For any countable collection of countable μ-regular closed subsets of X such that , there exists a finite sub-collection such that .
Proof.
Suppose X is -CC and is a countable sub-collection of a -closed subset of X such that . Then, . Since X is -CC, there exists a finite sub-collection cover of X. Thus, . Hence,
. Thus,
Suppose is a countable of -open cover of X. Thus, is a countable of -closed subset of X.
Since , so . So, by the assumption that there exists a finite sub-collection of such that
.
Hence, . Therefore, X is -CC.
Suppose is a countable -open cover of X and so is a countable -regular open cover of X.
Thus, is a -regular closed subset of X such that
, so by the assumption that there exists a finite sub-collection of such that .
Hence, . It is clear that X is -CC.
It is obvious since -regular closed is -closed.
It is similar to since -regular closed is -closed. □
Theorem 7.
If a space is -CC, then every countable cover of X by -open sets has a finite sub-cover.
Proof.
Suppose is -CC and be -open countable cover of X. Then, for all , there exists such that . Since is a -open, then there exists where . However, X is -CC, so there exist where . □
Theorem 8.
Let be a μ-regular space. Then, is -CC if and only if is μ-CC.
Proof.
It is straightforward and therefore omitted. □
Definition 15.
Let be a space. A subset A of X is said to be weakly μ-countably compact set (denoted by -CC set) whenever , where for all and Λ is a countable index set, then there is a finite sub-collection such that .
Theorem 9.
A subset A of is -CC set if and only if, whenever , where is μ-regular open subset for all , then there exists a finite sub-collection such that .
Proof.
It is straightforward and therefore omitted. □
Theorem 10.
Let A be a subset of . The following statements are equivalent:
- 1.
- A is -CC;
- 2.
- For any countable collection of a μ-closed subset of X such that , there exists a finite sub-collection of such that ;
- 3.
- For any countable collection of μ-regular closed subsets of X such that , there exists a finite sub-collection of such that .
Proof.
Suppose A is -CC set and is a -closed countable collection of X such that . Then, . Since X is -CC, there exists a finite sub-collection cover of A such that . Thus, . Hence,
. Thus,
Suppose is a countable -open cover of A. Thus, is a -closed subset of X. By the assumption that , so there exists a finite sub-collection of such that
.
Hence, . Therefore, X is -CC.
Suppose where for all and is a countable index set, so . Thus, is a -regular closed subset of X. By the assumption that , so there exists a finite sub-collection of such that
.
Hence,
. It is clear that A is -CC set.
It is obvious since -regular closed is -closed.
It is similar to since -regular closed is -closed. □
Theorem 11.
Let A be a -CC subset of a space . Then, every cover of A by -open subsets of X has a finite subcover.
Proof.
It is straightforward and therefore omitted. □
Theorem 12.
Let and be countable. If A is -closed and B is -CC, then is -CC set.
Proof.
Let , where for all is a countable index set, and . Then, . Additionally, for all , there exists where . Since is a -open and is countable, then is a countable -open cover of B. However, B is -CC, so there exist and there exist such that . However, , thus . Hence, is a -CC set. □
Theorem 13.
Let . If A is -CC, then A is -CC set.
Proof.
Suppose that A is -CC set, and is a countable -open cover of A. Then, is a -open cover of A. However, A is -CC, so there exists a finite sub-collection of such that . It is clear that where . Hence, A is -CC set. □
Definition 16.
Let be a space with respect to . The pair is said to be weakly -countably compact (denoted by - CC) whenever , where for all and Λ is a countable index set, then there is a finite sub-collection such that ∈.
Example 4.
Let , , where and . Then, is -CC because for any proper μ-open set where , then ∈. However, that is not -CC because there is no finite sub-collection such that ∈
Example 5.
Let , , and μ generated by μ-subbase and . Then, is -CC, but not -CC.
Theorem 14.
A space with respect to is -CC if and only if for any countable μ-regular open cover of X, there exits a finite sub-collection such that .
Proof.
Necessity. It is straightforward and therefore omitted.
Sufficiency. Let , where for all and is a countable index set. It is clear that is -open, thus bis a countable -regular open cover of X. Then, there exists a finite sub-collection such that .
However, . Thus, . Hence, is -CC. □
Theorem 15.
If a space is -CC, then for every countable cover of X by -open sets there exists a finite sub-collection such that .
Proof.
Suppose is -CC and be a -open cover of X. Then, for all , there exists such that . Thus, there exists such that . Then, where . Since X is -CC, so there exist where . However, . Hence, . □
Theorem 16.
Let be a μ-regular space. The following statements are equivalent:
- 1.
- is -CC;
- 2.
- is -CC.
Proof.
Suppose X is a -regular, and -CC and are -open covers of X. Then, for all , there exists such that . Thus, there exists where . Then, the sub-collection is a countable -open cover of X. Since X is -CC, so there exist where . However, . Thus, . This means is -CC.
It is clear that .
Thus, . □
Theorem 17.
Let A be a -CC, then for every countable cover of A by -open sets there exits a finite sub-collection such that .
Theorem 18.
Let be subsets of a space and is countable. If A is -closed and B is -CC, then is -CC.
Proof.
Let be a countable -open cover of . Then, is a countable -open cover B. Since is a -open for all , there exists a -open set where . Thus, is a countable -open cover of B. However, B is -CC, so there exist and where .
Thus, . Hence, . This mean is -CC. □
Theorem 19.
Let be a space with respect to where is an ideal on X, then the union of two -CC sets is a -CC set.
Proof.
Suppose A and B are -CC sets of X. Let be any countable -open cover of of X, then there exist finite subsets where and .
Thus, . However, is a finite subset of and is an ideal on X. Then, . Hence, is -CC. □
Example 6 illustrates that being an ideal is a necessary condition.
Example 6.
Let , , and hereditary class A is subset of the set of all odd numbers or A is a subset of the set of all even numbers }. Let A be the set of all odd numbers and B be the set of all even numbers, then A and B are -CC sets. While is not -CC. Let where for all . Thus, , for some , where .
Theorem 20.
Let be a -CC space, then is a -CC space.
Proof.
Suppose is a -CC space. Then, for each countable -open cover of X, there exists a finite sub-collection of X such that . However, .
Thus, . Hence, . □
Lemma 3.
Let be a space such that , and be disjoint dense μ-subspaces of X such that . Consider the and generated by the finite intersection of elements of μ and , then if C is a μ-regular closed subset of and A is a μ-open subset of such that , then
Proof.
It is straightforward and therefore omitted. □
The converse of Theorem 20 is not true, as illustrated in Example 7.
Example 7.
Let and as they are in the above Lemma 3.20. It is proved that is not almost compact in [23], so it is not nearly μ-CC. We prove that is weakly μ-CC. Let be a countable μ-regular open cover of , so there is μ-regular closed in where and . Then, by Lemma 3.20, we obtain , then where for all and Λ is countable, since is μ-CC, then there exists a finite subset where . Hence, this shows that is weakly μ-CC.
Theorem 21.
If is a -CC space, then is a -CC space.
Proof.
Suppose is a -CC space. Which means that , where for all and is a countable index set, then there exists a finite where ∈.
However, . Hence, . □
Figure 1 shows the relationship between all types of generalization of -compact spaces studied in this paper.
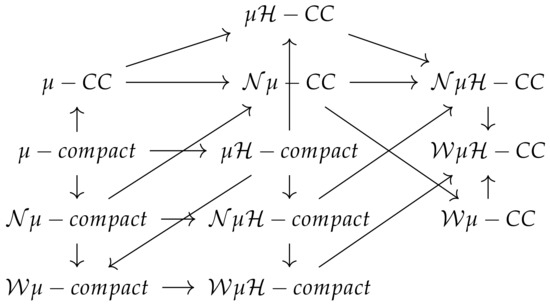
Figure 1.
The relationship between all types of generalization of -compact spaces.
4. Function Properties on -Countably Compact and -Countably Compact
Theorem 22.
Let be a -continuous function.
- 1.
- If A is a -CC subset of X, then is -CC.
- 2.
- If A is a -CC subset of X, then is -CC.
Proof.
Suppose , where for all and is a countable index set. Since f is -continuous, then , where for all and is a countable index set and A is a -CC set. Thus, there exist where . Thus, . Since f is -continuous and for all , then . Hence, is -CC.
Suppose , where for all and is a countable index set. Since f is -continuous, then , where for all and is a countable index set and A is -CC set. Thus, there exist where . Thus, . Since f is -continuous and for every subset B of Y,
then . Hence, is -CC. □
Theorem 23.
Let be a -continuous surjective function.
- 1.
- If X is a -CC, then is -CC.
- 2.
- If X is a -CC, then is -CC.
Proof.
Suppose , where for all and is a countable index set. Since f is -continuous, then , where for all and is a countable index set and X is -CC. Thus, there exist where . Thus, . Since f is -continuous and for all , then . Thus, is -CC. Hence, is -CC since f is surjective.
Suppose , where for all and is countable index set. Since f is -continuous, then , where for all and is a countable index set and X is -CC. Thus, there exist where . Thus, . Since f is -continuous, then where for all and is a countable index set and X is -CC. Thus, there exist where . Thus, . Since f is -continuous and for all , then . Thus, is -CC. Hence, is -CC since f is surjective. □
Theorem 24.
Let be a -continuous surjective.
- 1.
- If is -CC, then is -CC.
- 2.
- If is -CC, then is -CC.
Proof.
Suppose , where for all and is countable index set. Since f is -continuous, , where for all and is a countable index and X is -CC. Thus, there exist where . Since f is -continuous and for all , then . Since . Thus, . Since f is surjective, then . This means Y is -CC.
Suppose , where for all and is countable index set. Since f is -continuous, , where for all and is a countable index and X is -CC. Thus, there exist where . Since f is -continuous and for all , then
.
Since .
Thus, . Since f is surjective, then . This means Y is -CC. □
Theorem 25.
Let be a -open bijective function.
- 1.
- If is -CC, then is -CC.
- 2.
- If is -CC, then is -CC.
Proof.
Since is a -open bijective, then
is a -continuous surjective. By Theorem 24, so is a -CC(resp.-CC), then is -CC (resp.-CC). □
Theorem 26.
Let be a -continuous.
- 1.
- If A is -CC, then is -CC.
- 2.
- If A is -CC, then is -CC.
Proof.
Suppose , where for all and is a countable index set. Since f is -continuous, then , where for all and is a countable index and A is -CC set. Thus, there exist where . It is clear that .
Thus, . Thus,
.
Hence,
. This means is -CC.
It is clear that f is -continuous and for all , then
.
Since .
Thus .This means is -CC. □
Theorem 27.
Let be a -CC; if is strongly -continuous surjective, then is β-CC.
Proof.
Suppose , where for all and is a countable index set. Then, for all , there exists for some where . Since f is a strongly -continuous, then containing t such that . Since is countable index set, we obtain , where for all and is countable index set. Since is -CC, we obtain .
Thus, . Hence, is a -CC. □
Theorem 28.
Let be a -CC; if is super -continuous surjective, then is β-CC.
Proof.
Suppose , where for all and is a countable index set. Then, for all , there exists for some such that . Since f is a super -continuous, then containing t where . Since is a countable index set, we obtain where for all and is countable index set. Since is -CC, we obtain .
Thus, . Hence is a -CC. □
Theorem 29.
Let be a -CC; if is -continuous surjective, then is -CC.
Proof.
Suppose , where for all and is a countable index set. Then, for all , there exists for some where . Since f is a -continuous, then there exists containing t where . Since is a countable index set, we obtain , where for all and is a countable index set. Since is -CC, we obtain . Thus,
. Hence, is a -CC. □
Theorem 30.
Let be a -CC,
- 1.
- If is strongly - continuous surjective, then is β-CC.
- 2.
- If is super - continuous surjective, then is β-CC.
- 3.
- If is - continuous surjective, then is β-CC.
Proof.
It is straightforward and similar to Theorem 27, and therefore omitted. □
Theorem 31.
Let be almost - continuous surjective.
- 1.
- If is a -CC, then is also -CC.
- 2.
- If is a -CC, then is also -CC.
Proof.
Suppose , where for all and is countable index set. Since f is a almost - continuous, then . Thus for all is a countable index set, then there exists a finite sub-collection where ,
, it is clear that
, then
. Hence, Y is a -CC.
Suppose , where for all and is a countable index set. Since f is an almost -continuous, then .
Thus, for all is a countable index set, then there exist where .
Since , then
.
Thus , it is clear that
. Hence, Y is a -CC. □
5. Applications in Soft Set Theory
Recall that soft set theory is an important mathematical tool in uncertainty. The concepts defined in the current paper can be applied to furnish more work to obtain generalizations of covering properties of soft generalized topological spaces. In particular, we define soft -CC and soft -CC as generalizations of soft -compactness. Moreover, we provide an examined example to verify the new definitions as an applicable generalizations.
Definition 17 ([24]).
A soft set on the universe X is defined by the set of ordered pairs , where and G is the set of all possible parameters such that if . is said to be an approximate function of the soft set. The value of may be arbitrary. stands for the set of all soft sets.
Definition 18.
Let .
- 1.
- If for each , then is said to be an A-universal soft set, denoted by . If , then is said to be a universal soft set, denoted by [25].
- 2.
- The soft complement of , denoted by , is defined by the approximate function , where is the complement of the set for all [26].
Definition 19.
Let .
- 1.
- is a soft subset of , denoted by , if for all [27].
- 2.
- The soft union of and , denoted by , is defined by the approximate function [25].
- 3.
- The soft intersection of and , denoted by , is defined by the approximate function [26].
Definition 20 ([28]).
Let . A soft generalized topology (briefly. sGT) on , denoted by is a family of soft subsets of such that and if a family then .
Definition 21 ([28]).
Let be a sGTS. Every element of μ is called a soft μ-open set. The is a soft μ-open set. If be a soft subset of , then is called soft μ-closed if its soft complement is a soft μ-open.
Definition 22 ([28]).
Let be a sGTS and , then
(a) the soft union of all soft μ-open subsets of is said to be soft μ-interior of and denoted by .
(b) the soft intersection of all soft μ-closed subsets of is said to be soft μ-closure of and denoted by .
Definition 23 ([29]).
A sGTS is called soft μ-compact (denoted. soft μ-C) whenever , where is soft μ-open for all and Λ, then there is a finite sub-collection such that .
Definition 24.
Let be a sGTS and , then
- 1.
- the soft μ-regular open set if .
- 2.
- the soft μ-regular closed set if .
Definition 25.
A sGTS is called soft μ-countably compact (denoted soft μ-CC) whenever , where is soft μ-open for all and Λ countable index set, then there is a finite sub-collection such that .
Definition 26.
A sGTS is called soft nearly μ-countably compact (denoted soft -CC) whenever , where is soft μ-open for all and Λ is a countable index set, then there is a finite sub-collection such that .
Corollary 2.
Every soft μ-CC space is a soft -CC space.
Proof.
It is straightforward and therefore omitted. □
The converse of Corollary 2 is not true, as presented in Example 8.
Example 8.
Let and , let for each . Consider a sGT generated on sGTS by the soft basis . Then, only and are soft μ-regular open sets so a sGTS is soft -CC, but it is not soft -CC, since a family , where
,
,
⋮
is soft -open cover of sGTS with no finite soft -open sub-cover.
6. Conclusions
We have explored and examined the definition of weakly (nearly) -countably compact spaces in the sense of generalized topology given in [1]. Further, we studied the effect of hereditary classes on these spaces. The space presented in Example 1 is -CC, but not -CC. Some other results regarding subsets of such spaces have been presented. Observing that - countably compactness is a generalization of -compactness, Figure 1 is a summary to show the relations between these spaces studied in the paper and other spaces generalizing -compactness. Finally, we studied the effect of generalized continuity on these spaces. In particular, it is proved that the images and preimages of the new notions of spaces defined in this paper are preserved under -continuous functions. Stronger results are given if we use strongly -continuous functions and super -continuous functions. More varying results are given by using -continuous functions and almost -continuous functions.
As future research, some modifications can be made if we replace the generalized topology by a weaker framework as a weaker structure [30]. Moreover, we can study the effect of soft -regular sets on soft nearly -countably compact spaces defined in Section 5. To see some applications of generalizations of spaces in generalized topology, you can see [29,31,32].
Author Contributions
Conceptualization, Z.A. and A.B.; investigation, Z.A. and E.A.-Z., writing, review, and editing; A.B. and I.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the referees for their useful comments, and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Császár, A. Generalized topology, generalized continuity. Acta Math. Hung. 2002, 96, 351–357. [Google Scholar] [CrossRef]
- Vaughan, J. Countably compact and sequentially compact spaces. In Handbook Of Set-Theoretic Topology; Elsevier: Amsterdam, The Netherlands, 1984; pp. 569–602. [Google Scholar]
- James, R. Weakly compact sets. Trans. Am. Math. Soc. 1964, 113, 129–140. [Google Scholar] [CrossRef]
- Scarborough, C.; Stone, A. Products of nearly compact spaces. Trans. Am. Math. Soc. 1966, 124, 131–147. [Google Scholar] [CrossRef]
- Altawallbeh, Z.; Al-Momany, A. Nearly countably compact spaces. Int. Electron. J. Pure Appl. Math. 2014, 8, 59–65. [Google Scholar] [CrossRef]
- Császár, Á. Generalized open sets in generalized topologies. Acta Math. Hung. 2005, 106, 53–66. [Google Scholar] [CrossRef]
- Thomas, J.; John, S. μ-compactness in generalized topological spaces. J. Adv. Stud. Topol. 2012, 3, 18–22. [Google Scholar] [CrossRef]
- Császár, Á. Modification of generalized topologies via hereditary classes. Acta Math. Hung. 2007, 115, 29–36. [Google Scholar] [CrossRef]
- Carpintero, C.; Rosas, E.; Salas-Brown, M.; Sanabria, J. μ-compactness with respect to a hereditary class. Bol. Soc. Parana. MatemáTica 2016, 34, 231–236. [Google Scholar] [CrossRef]
- Sarsak, M. Weakly μ-compact spaces. Demonstr. Math. 2012, 45, 929–938. [Google Scholar] [CrossRef]
- Alb Lupaş, A. Applications of the Fractional Calculus in Fuzzy Differential Subordinations and Superordinations. Mathematics 2021, 9, 2601. [Google Scholar] [CrossRef]
- Mehmood, A.; Abdullah, S.; Al-Shomrani, M.; Khan, M.; Thinnukool, O. Some Results in Neutrosophic Soft Topology Concerning Neutrosophic Soft Open Sets. J. Funct. Spaces 2021, 2021, 544319. [Google Scholar] [CrossRef]
- An, T.; Vu, H.; Hoa, N. Hadamard-type fractional calculus for fuzzy functions and existence theory for fuzzy fractional functional integro-differential equations. J. Intell. Fuzzy Syst. 2019, 36, 3591–3605. [Google Scholar] [CrossRef]
- Guariglia, E. Riemann zeta fractional derivative—functional equation and link with primes. Adv. Differ. Equ. 2019, 2019, 1–15. [Google Scholar] [CrossRef]
- Guariglia, E. Fractional calculus, zeta functions and Shannon entropy. Open Math. 2021, 19, 87–100. [Google Scholar] [CrossRef]
- Sarsak, M. On μ-compact sets in μ-spaces, Questions and Answers in Gen. Topol 2013, 31, 49–57. [Google Scholar]
- Abuage, M.; Kiliçman, A.; Sarsak, M. nv-Lindelöfness. Malays. J. Math. Sci. 2017, 11, 73–86. [Google Scholar]
- Qahis, A.; AlJarrah, H.H.; Noiri, T. Weakly m-compact via a hereditary class. Bol. Soc. Parana. Matemática 2021, 39, 123–135. [Google Scholar] [CrossRef]
- Altawallbeh, Z.; Jawarneh, I. μ-Countably Compactness and μH-Countably Compactness. Commun. Korean Math. Soc. 2022, 37, 269–277. [Google Scholar]
- Min, W.; Kim, Y. Some strong forms of (g, g′)-continuity on generalized topological spaces. Honam Math. J. 2011, 33, 85–91. [Google Scholar] [CrossRef]
- Min, W. (δ,δ′)-continuity on generalized topological spaces. Acta Math. Hung. 2010, 129, 350–356. [Google Scholar] [CrossRef]
- Min, W. Almost continuity on generalized topological spaces. Acta Math. Hung. 2009, 125, 121. [Google Scholar] [CrossRef]
- Herrlich, H. T v-Abgeschlossenheit und T v-Minimalität. Math. Z. 1965, 88, 285–294. [Google Scholar] [CrossRef]
- Molodtsov, D. Soft Set Theory—First Results. Comp. Math. Appl. 1999, 37, 19–31. [Google Scholar] [CrossRef]
- Maji, P.; Biswas, R.; Roy, A. Soft set theory. Comput. Math. Appl. 2003, 45, 555–562. [Google Scholar] [CrossRef]
- Ali, M.; Feng, F.; Liu, X.; Min, W.; Shabir, M. On some new operations in soft set theory. Comput. Math. Appl. 2009, 57, 1547–1553. [Google Scholar] [CrossRef]
- Feng, F.; Li, C.; Davvaz, B.; Ali, M. Soft sets combined with fuzzy sets and rough sets: A tentative approach. Soft Comput. 2010, 14, 899–911. [Google Scholar] [CrossRef]
- Thomas, J.; Johna, S. On soft generalized topological spaces. J. New Results Sci. 2014, 3, 1–15. [Google Scholar]
- John, S.; Thomas, J. On soft μ-compact soft generalized topological spaces. J. Uncertain. Math. Sci. 2009, 57, 1547–1553. [Google Scholar]
- Császár, Á. Weak structures. Acta Math. Hung. 2011, 131, 193–195. [Google Scholar] [CrossRef]
- Min, W. On soft sets and generalized topologies in sense of cs∖’A SZ∖’A R. Int. J. Appl. Math. 2018, 31, 813. [Google Scholar] [CrossRef]
- Al-Saadi, H.; Min, W. On Soft Generalized Closed Sets in a Soft Topological Space with a Soft Weak Structure. Int. J. Fuzzy Log. Intell. Syst. 2017, 17, 323–328. [Google Scholar] [CrossRef][Green Version]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).