Finite-Time Stability of Impulsive Fractional Differential Equations with Pure Delays

Abstract

This paper introduces a novel concept of the impulsive delayed Mittag–Leffler-type vector function, an extension of the Mittag–Leffler matrix function. It is essential to seek explicit formulas for the solutions to linear impulsive fractional differential delay equations. Based on explicit formulas of the solutions, the finite-time stability results of impulsive fractional differential delay equations are presented. Finally, we present four examples to illustrate the validity of our theoretical results.

1. Introduction

In recent decades, researchers have found that fractional differential equations are appropriate for describing real-life problems with memory and genetic characteristics. Thus, the topic of fractional differential equations has received increasing attention. More details can be found in [1,2,3]. Impulsive fractional differential equations (IFDEs) are used to depict various practical dynamical systems, including the evolution of states that mutate into features at certain times, with the wide application of IFDE theory in the modeling of genetic phenomena and abrupt dynamical systems. The research on the existence, uniqueness and stability of IFDEs has attracted increasing attention [4,5,6,7,8,9].

At the same time, fractional delay differential equations (FDDEs) and impulsive fractional delay differential equations (IFDDEs) are often used to depict state changes that occurred in the time interval of the previous period. In [10], the authors presented the idea of a delayed matrix function and provided an explicit formula for FDDEs by the method of constant variation. In [11,12], the idea of an impulsive delayed solution vector function was developed. This notion aided the authors in finding the exact solutions of IFDDEs. In [13], the author obtained the exact solutions of higher-fractional-order nonhomogeneous delayed differential equations with Caputo-type derivatives by using the new generalized delay Mittag matrix function, Laplace transform and inductive construction.

The finite-time stability (FTS) of fractional differential equations has attracted much interest. After decades of research, FTS has contributed remarkable achievements in modern science and technology, chemical engineering, and other areas. Thus, we studied the FTS of a system, which is of great practical significance. Scholars have recently used the Lyapunov function, and Gronwall’s integral inequality to research the FTS of integer and fractional differential equations. In [14,15,16,17], the authors investigated finite-time stability by means of the generalized Gronwall inequality. Other related research can be found in [18,19,20,21]. Once we obtain the exact solution of the system, we can find a suitable method to obtain the sufficient conditions for FTS. Motivated by [12], we seek to construct an impulsive delayed solution vector function to express the explicit solution and study the FTS of IFDDEs.

In [22], the authors gave a representation of the solution of linear FDDEs:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \left\{\begin{array}{cc}& {(}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }v)\left(\xi \right)=Bv(\xi -\varsigma )+g\left(\xi \right),\varsigma >0,\xi \in (0,T],\hfill \\ & v\left(\xi \right)=\varpi \left(\xi \right),-\varsigma \le \xi \le 0,\hfill \\ & \left({\mathbb{I}}_{-{\varsigma }^{+}}^{1-\beta }v\right)(-{\varsigma }^{+})=\varpi (-\varsigma ),\varpi (-\varsigma )\in {\mathbb{R}}^n,\hfill \end{array}\right.\end{array}\end{array}$$

(1)

where ${}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }(0<\beta <1)$ denotes the Riemann–Liouville derivative (see Definition 2), ${\mathbb{I}}_{-{\varsigma }^{+}}^{1-\beta }(0<\beta <1)$ denotes the fractional integral (see Definition 1), $B\in {\mathbb{R}}^{n\times n}$, $T=k^{*}\varsigma$, $k^{*}\in \mathbb{N}:=\{0,1,2,\cdots \}$, $g\in C([-\varsigma ,T],{\mathbb{R}}^n)$, $\varsigma$ is a fixed delay time and ${}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }\varpi$ exists. For any $\xi \in [-\varsigma ,T]$, the solution $v\in C(\mathrm{\Omega },{\mathbb{R}}^n)\cap C([-\varsigma ,T],{\mathbb{R}}^n)$ of (1) is given by

$$\begin{array}{c}\hfill v\left(\xi \right)=e_{-\varsigma ,\beta }^{B{\xi }^{\beta }}\varpi (-\varsigma )+{\int }_{-\varsigma }^0{e}_{-\varsigma ,\beta }^{B{(\xi -\varsigma -s)}^{\beta }}{(}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }\varpi )\left(s\right)ds+{\int }_{-\varsigma }^{\xi }{e}_{-\varsigma ,\beta }^{B{(\xi -\varsigma -t)}^{\beta }}g\left(t\right)dt,\end{array}$$

(2)

where either $\mathrm{\Omega }=\left(\right(k-1)\varsigma ,k\varsigma ]$ for $0<\beta <\frac{1}{k+1}$ or $\mathrm{\Omega }=\left[\right(k-1)\varsigma ,k\varsigma ]$ for $\beta \ge \frac{1}{k+1}$.

In this paper, we deduce the general solution of linear IFDDEs:

$$\left\{\begin{array}{c}{(}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }v)\left(\xi \right)=Bv(\xi -\varsigma ),\xi \ne {\xi }_{𝚤},\varsigma >0,\xi \in (0,T],\hfill \\ v\left({\xi }_{𝚤}^{+}\right)=v\left({\xi }_{𝚤}^{-}\right)+C_{𝚤},\xi ={\xi }_{𝚤},𝚤=1,2,\cdots ,p(T,0),\hfill \\ v\left(\xi \right)=\varpi \left(\xi \right),-\varsigma \le \xi \le 0,\hfill \\ \left({\mathbb{I}}_{-{\varsigma }^{+}}^{1-\beta }v\right)(-{\varsigma }^{+})=\varpi (-\varsigma ),\varpi (-\varsigma )\in {\mathbb{R}}^n,\hfill \end{array}\right.$$

(3)

where $p(T,0)$ denotes the number of impulsive points belong to $(0,T)$ and the symbols $v\left({\xi }_{𝚤}^{+}\right)=\underset{ϵ\to 0^{+}}{lim}v({\xi }_{𝚤}+ϵ)$ and $v\left({\xi }_{𝚤}^{-}\right)=\underset{ϵ\to 0^{-}}{lim}v({\xi }_{𝚤}+ϵ)$ denote, respectively, the right and left limits of $v\left(\xi \right)$ at $\xi ={\xi }_{𝚤}$.

After that, we will give some new sufficient conditions to ensure that (4) is finite-time stable.

$$\left\{\begin{array}{c}{(}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }v)\left(\xi \right)=Bv(\xi -\varsigma )+g\left(\xi \right),\xi \ne {\xi }_{𝚤},\xi \in (0,T],\hfill \\ v\left({\xi }_{𝚤}^{+}\right)=v\left({\xi }_{𝚤}^{-}\right)+C_{𝚤},\xi ={\xi }_{𝚤},𝚤=1,2,\cdots ,p(T,0),\hfill \\ v\left(\xi \right)=\varpi \left(\xi \right),-\varsigma \le \xi \le 0,\hfill \\ \left({\mathbb{I}}_{-{\varsigma }^{+}}^{1-\beta }v\right)(-{\varsigma }^{+})=\varpi (-\varsigma ),\varpi (-\varsigma )\in {\mathbb{R}}^n.\hfill \end{array}\right.$$

(4)

This paper mainly has the following three aspects of innovation:

(i) The mathematical model is novel, and the newly constructed impulsive delay vector function is of great significance for extending from time-delay systems to impulsive time-delay systems.

(ii) Using the relationship between the Riemann–Liouville fractional derivative and the Caputo fractional derivative, the two are skillfully transformed to prove that the impulsive delay vector function is the fundamental solution of (3), which provides more ideas for future research.

(iii) The position of the pulse point in this paper is arbitrary, which renders the research more universal.

The rest of this paper is constituted as follows. Firstly, we review the symbols and definitions. Secondly, we construct an impulsive delayed solution vector function and give the explicit solutions of (3) and (4). Then, we give four practical conditions to guarantee that (4) is finite-time stable. Finally, we give three numerical examples to illustrate our theoretical results.

2. Preliminaries

Let $C([-\varsigma ,T],{\mathbb{R}}^n)$ be the space of a continuous function with ${\parallel v\parallel }_C={max}_{\xi \in [-\varsigma ,T]}\parallel v\left(\xi \right)\parallel$, $PC([-\varsigma ,T],{\mathbb{R}}^n)$$=\{v\in C(({\xi }_{𝚤},{\xi }_{𝚤+1}],{\mathbb{R}}^n),𝚤=1,2,\cdots ,p(T,0)$. There exist $v\left({\xi }_{𝚤}^{+}\right)$ and $v\left({\xi }_{𝚤}^{-}\right)$ with $v\left({\xi }_{𝚤}^{-}\right)=v\left({\xi }_{𝚤}\right)\}$ with ${\parallel v\parallel }_{PC}={sup}_{\xi \in [-\varsigma ,T]}\parallel v\left(\xi \right)\parallel$. For any $0<\gamma <1$, we denote $C_{\gamma }([a,b],{\mathbb{R}}^n)=\{v\in C((a,b],{\mathbb{R}}^n)|{(\xi -a)}^{\gamma }v\left(\xi \right)\in C([a,b],{\mathbb{R}}^n)\}$ with ${\parallel v\parallel }_{C_{\gamma }}={max}_{a\le \xi \le b}\parallel {(\xi -a)}^{\gamma }v\left(\xi \right)\parallel$. Let $\parallel v\parallel ={\sum }_{i=1}^n\left|v_i\right|$, $\parallel B\parallel ={max}_{1\le j\le n}{\sum }_{i=1}^n\left|b_{ij}\right|$ and ${\parallel \varpi \parallel }_C={max}_{\xi \in [-\varsigma ,0]}\parallel \varpi \left(\xi \right)\parallel$.

Definition 1 

(see [2]). Let $0<\beta <1$ and $y:[-\varsigma ,+\infty )\to {\mathbb{R}}^n$. The fractional integral of y is defined by

$$\begin{array}{c}\hfill {\mathbb{I}}_{-\varsigma }^{\beta }y\left(\xi \right)=\frac{1}{\mathrm{\Gamma }\left(\beta \right)}{\int }_{-\varsigma }^{\xi }\frac{y\left(t\right)}{{(\xi -t)}^{1-\beta }}dt,\xi >-\varsigma ,\end{array}$$

where $\mathrm{\Gamma }(·)$ is the Gamma function.

Definition 2 

(see [2]). Let $0<\beta <1$ and $y:[-\varsigma ,+\infty )\to {\mathbb{R}}^n$. The Riemann–Liouville fractional derivative of y is defined by

$$\begin{array}{c}\hfill {(}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }y)\left(\xi \right)=\frac{1}{\mathrm{\Gamma }(1-\beta )}\frac{d}{d\xi }{\int }_{-\varsigma }^{\xi }\frac{y\left(t\right)}{{(\xi -t)}^{\beta }}dt,\xi >-\varsigma .\end{array}$$

Definition 3 

(see [2]). Let $0<\beta <1$ and $y:[-\varsigma ,+\infty )\to {\mathbb{R}}^n$. The Caputo fractional derivative of y is defined by

$$\begin{array}{c}\hfill {(}^C{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }y)\left(\xi \right)=\frac{1}{\mathrm{\Gamma }(1-\beta )}{\int }_{-\varsigma }^{\xi }{(\xi -t)}^{-\beta }{y}^{\prime }\left(t\right)dt,\xi >-\varsigma .\end{array}$$

Definition 4 

(see [2]). If $0<\beta <1$, y is a function for which the Caputo fractional derivative ${(}^C{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }y)\left(\xi \right)$ exists together with the Riemann–Liouville fractional derivative ${(}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }y)\left(\xi \right)$. Then,

$$\begin{array}{c}\hfill {(}^C{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }y)\left(\xi \right)={(}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }y)\left(\xi \right)-\frac{y(-\varsigma )}{\mathrm{\Gamma }(1-\beta )}{(\xi +\varsigma )}^{-\beta }.\end{array}$$

(5)

In particular, when $y(-\varsigma )\equiv 0$, then ${(}^C{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }y)\left(\xi \right)={(}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }y)\left(\xi \right)$.

Definition 5. 

The delayed one-parameter Mittag–Leffler-type matrix function ${\mathbb{E}}_{-\varsigma }^{B{·}^{\beta }}:\mathbb{R}\to {\mathbb{R}}^{n\times n}$ is defined by

$${\mathbb{E}}_{-\varsigma }^{B{\xi }^{\beta }}=\left\{\begin{array}{c}\mathrm{\Theta },-\infty <\xi <-2\varsigma ,\hfill \\ E,-2\varsigma \le \xi \le -\varsigma ,\hfill \\ E+B\frac{{(\xi +\varsigma )}^{\beta }}{\mathrm{\Gamma }(\beta +1)}+B^2\frac{{\xi }^{2\beta }}{\mathrm{\Gamma }(2\beta +1)}+\cdots +B^{k+1}\frac{{(\xi -(k-1)\varsigma )}^{(k+1)\beta }}{\mathrm{\Gamma }\left(\right(k+1)\beta +1)},\hfill \\ (k-1)\varsigma <\xi \le k\varsigma ,k\in \mathbb{N},\hfill \end{array}\right.$$

(6)

where Θ is a zero matrix and E is an identity matrix.

Definition 6 

(see [22]). The delayed two-parameter Mittag–Leffler-type matrix function $e_{-\varsigma ,\alpha }^{B{·}^{\beta }}:\mathbb{R}\to {\mathbb{R}}^{n\times n}$ is defined by

$$e_{-\varsigma ,\alpha }^{B{\xi }^{\beta }}=\left\{\begin{array}{c}\mathrm{\Theta },-\infty <\xi <-\varsigma ,\hfill \\ E\frac{{(\xi +\varsigma )}^{\beta -1}}{\mathrm{\Gamma }\left(\beta \right)},-\varsigma \le \xi \le 0,\hfill \\ E\frac{{(\xi +\varsigma )}^{\beta -1}}{\mathrm{\Gamma }\left(\beta \right)}+B\frac{{\xi }^{2\beta -1}}{\mathrm{\Gamma }(\beta +\alpha )}+\cdots +B^k\frac{{(\xi -(k-1)\varsigma )}^{(k+1)\beta -1}}{\mathrm{\Gamma }(k\beta +\alpha )},\hfill \\ (k-1)\varsigma <\xi \le k\varsigma ,k\in \mathbb{N}.\hfill \end{array}\right.$$

(7)

Definition 7. 

For any $\xi \in \left(\right(k-1)\varsigma ,k\varsigma ]$ and $k=1,2,\cdots ,k^{*}$, the impulsive delayed Mittag–Leffler-type vector function $Q_{-\varsigma ,\beta }(·):\mathbb{R}\to {\mathbb{R}}^n$ is defined by

$$\begin{array}{c}\hfill Q_{-\varsigma ,\beta }\left(\xi \right)=\sum _{0<{\xi }_{𝚤}<\xi }{\mathbb{E}}_{-\varsigma }^{B{(\xi -{\xi }_{𝚤}-2\varsigma )}^{\beta }}{C}_{𝚤}.\end{array}$$

(8)

Definition 8. 

System (4) is finite-time stable with regard to $\{0,J,\varsigma ,\delta ,\eta \}$ if and only if ${\parallel \varpi \parallel }_C<\delta$ implies ${\parallel v\parallel }_{C_{\gamma }}<\eta$ and $\delta <\eta$, where $J:=\left(\right(k-1)\varsigma ,k\varsigma ]$ and $k=1,2,\cdots ,k^{*}$.

Lemma 1 

(see [12]). For any $\xi \in \left(\right(k-1)\varsigma ,k\varsigma ]$, $k=1,2,\cdots ,k^{*}$ and ${\xi }_{𝚤}\in (0,\xi )$, we have

$$\begin{array}{cc}\hfill & {\int }_{{\xi }_{𝚤}+(k-1)\varsigma }^{\xi }{(\xi -t)}^{-\beta }{(t-{\xi }_{𝚤}-(k-1)\varsigma )}^{(k-1)\beta -1}dt\hfill \\ \hfill & ={(\xi -{\xi }_{𝚤}-(k-1)\varsigma )}^{(k-2)\beta }\mathbb{B}[(k-1)\beta ,1-\beta ],\hfill \end{array}$$

where $\mathbb{B}[x,y]={\int }_0^1{s}^{x-1}{(1-s)}^{y-1}ds$.

Lemma 2 

(see [18]). For any $\xi \in \left(\right(k-1)\varsigma ,k\varsigma ]$, $k=1,2,\cdots ,k^{*}$ and $0<\gamma <1$, we obtain that

(i) For any $0<\beta <\frac{1}{k+1}$, one has

$$\begin{array}{c}\hfill {\parallel (\xi -(k-1)\varsigma )}^{\gamma }{e}_{-\varsigma ,\beta }^{B{\xi }^{\beta }}{\parallel \le (\xi -(k-1)\varsigma )}^{\beta +\gamma -1}{E}_{\beta ,\beta }{(\parallel B\parallel (\xi -(k-1)\varsigma )}^{\beta }).\end{array}$$

(ii) For any $\frac{1}{k+1}\le \beta <\frac{1}{2}$, one has

$$\begin{array}{c}\hfill {\parallel (\xi -(k-1)\varsigma )}^{\gamma }{e}_{-\varsigma ,\beta }^{B{\xi }^{\beta }}{\parallel \le (\xi -(k-1)\varsigma )}^{\gamma }\sum _{l=0}^k{\parallel B\parallel }^l\frac{{(\xi -(l-1)\varsigma )}^{(l+1)\beta -1}}{\mathrm{\Gamma }(l\beta +\beta )}.\end{array}$$

(iii) For any $\beta \ge \frac{1}{2}$, one has

$$\begin{array}{c}\hfill {\parallel (\xi -(k-1)\varsigma )}^{\gamma }{e}_{-\varsigma ,\beta }^{B{\xi }^{\beta }}\parallel \le {\xi }^{\beta +\gamma -1}{E}_{\beta ,\beta }(\parallel B\parallel {\xi }^{\beta }),\end{array}$$

where $E_{\beta ,\beta }\left(z\right)={\displaystyle \sum _{k=0}^{\infty }}\frac{z^k}{\mathrm{\Gamma }(k\beta +\beta )}$, $z\in \mathbb{R}$.

Lemma 3 

(see [18]). For any $\xi \in \left(\right(k-1)\varsigma ,k\varsigma ]$ and $k=1,2\cdots k^{*}$, we have

$$\begin{array}{ccc}& & {\int }_{-\varsigma }^0\parallel e_{-\varsigma ,\beta }^{B{(\xi -\varsigma -s)}^{\beta }}\parallel ds\hfill \\ & \le & \sum _{m=0}^k\frac{{\parallel B\parallel }^m}{\mathrm{\Gamma }\left(\right(m+1)\beta +1)}{(\xi -(m-1)\varsigma )}^{(m+1)\beta }-\sum _{m=1}^k\frac{{\parallel B\parallel }^{m-1}}{\mathrm{\Gamma }(m\beta +1)}{(\xi -(m-1)\varsigma )}^{m\beta }.\hfill \end{array}$$

Lemma 4 

(see [18]). For any $\xi \in \left(\right(k-1)\varsigma ,k\varsigma ]$, $k=1,2\cdots k^{*}$ and $\beta >1-\frac{1}{p}(p>1)$, we have

$$\begin{array}{ccc}& & {\int }_{-\varsigma }^0\parallel e_{-\varsigma ,\beta }^{B{(\xi -\varsigma -s)}^{\beta }}\parallel \parallel {(}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }\varpi )\left(s\right)\parallel ds\hfill \\ & \le & \sum _{m=0}^k\left(\frac{{\parallel B\parallel }^m{(\xi -(m-1)\varsigma )}^{(m+1)\beta -1-\frac{1}{p}}}{\mathrm{\Gamma }(m\beta +\beta ){(p(m+1)\beta -p+1)}^{\frac{1}{p}}}\right){\left({\int }_{-\varsigma }^0{\parallel {(}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }\varpi )\left(s\right)\parallel }^{q}ds\right)}^{\frac{1}{q}}.\hfill \end{array}$$

Lemma 5. 

For any $\xi \in \left(\right(k-1)\varsigma ,k\varsigma ]$ and $k=1,2\cdots k^{*}$, we have

$$\begin{array}{c}\hfill {\int }_{-\varsigma }^{\xi }\parallel e_{-\varsigma ,\beta }^{B{(\xi -\varsigma -s)}^{\beta }}\parallel ds\le \sum _{m=0}^k\frac{{\parallel B\parallel }^m}{\mathrm{\Gamma }\left(\right(m+1)\beta +1)}{(\xi -(m-1)\beta )}^{(m+1)\beta }.\end{array}$$

Proof. 

By (7), one has

$$\begin{array}{ccc}& & {\int }_{-\varsigma }^{\xi }\parallel e_{-\varsigma ,\beta }^{B{(\xi -\varsigma -s)}^{\beta }}\parallel ds\hfill \\ & \le & {\int }_{-\varsigma }^{\xi -k\varsigma }\parallel e_{-\varsigma ,\beta }^{B{(\xi -\varsigma -s)}^{\beta }}\parallel ds+{\int }_{\xi -k\varsigma }^{\xi -(k-1)\varsigma }\parallel e_{-\varsigma ,\beta }^{B{(\xi -\varsigma -s)}^{\beta }}\parallel ds+{\int }_{\xi -\varsigma }^{\xi }\parallel e_{-\varsigma ,\beta }^{B{(\xi -\varsigma -s)}^{\beta }}\parallel ds\hfill \\ & \le & {\int }_{-\varsigma }^{\xi -k\varsigma }\left(\frac{{(\xi -s)}^{\beta -1}}{\mathrm{\Gamma }\left(\beta \right)}+\parallel B\parallel \frac{{(\xi -\varsigma -s)}^{2\beta -1}}{\mathrm{\Gamma }\left(2\beta \right)}+\cdots +{\parallel B\parallel }^k\frac{{(\xi -k\varsigma -s)}^{(k+1)\beta -1}}{\mathrm{\Gamma }\left(\right(k+1\left)\beta \right)}\right)ds\hfill \\ & & +{\int }_{\xi -k\varsigma }^{\xi -(k-1)\varsigma }(\frac{{(\xi -s)}^{\beta -1}}{\mathrm{\Gamma }\left(\beta \right)}+\parallel B\parallel \frac{{(\xi -\varsigma -s)}^{2\beta -1}}{\mathrm{\Gamma }\left(2\beta \right)}\hfill \\ & & +\cdots +{\parallel B\parallel }^{k-1}\frac{{(\xi -(k-1)\varsigma -s)}^{k\beta -1}}{\mathrm{\Gamma }\left(k\beta \right)})ds+{\int }_{\xi -\varsigma }^{\xi }\frac{{(\xi -s)}^{\beta -1}}{\mathrm{\Gamma }\left(\beta \right)}ds\hfill \\ & =& \sum _{m=0}^k\frac{{\parallel B\parallel }^m}{\mathrm{\Gamma }\left(\right(m+1\left)\beta \right)}{\int }_{-\varsigma }^{\xi -m\varsigma }{(\xi -m\varsigma -s)}^{(m+1)\beta -1}ds\hfill \\ & =& \sum _{m=0}^k\frac{{\parallel B\parallel }^m}{\mathrm{\Gamma }\left(\right(m+1)\beta +1)}{(\xi -(m-1)\beta )}^{(m+1)\beta }.\hfill \end{array}$$

The proof is finished. □

3. The Solution of System (4)

In this section, we will establish the general solution of (3) by using (6)–(8).

Theorem 1. 

Let $\xi \in \left(\right(k-1)\varsigma ,k\varsigma ]$, and let ${\xi }_{𝚤}\in (0,\xi )$ be a fixed impulsive point. Then, we have

$$\begin{array}{c}\hfill {(}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }{\mathbb{E}}_{-\varsigma }^{B{(t-{\xi }_{𝚤}-2\varsigma )}^{\beta }}{C}_{𝚤})\left(\xi \right)=B{\mathbb{E}}_{-\varsigma }^{B{(\xi -{\xi }_{𝚤}-3\varsigma )}^{\beta }}{C}_{𝚤}.\end{array}$$

Proof. 

By Definition 4, we have

$$\begin{array}{c}\hfill {(}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }{\mathbb{E}}_{-\varsigma }^{B{(t-{\xi }_{𝚤}-2\varsigma )}^{\beta }})\left(\xi \right)={(}^C{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }{\mathbb{E}}_{-\varsigma }^{B{(t-{\xi }_{𝚤}-2\varsigma )}^{\beta }})\left(\xi \right),\end{array}$$

where we use the fact ${\mathbb{E}}_{-\varsigma }^{B(-\varsigma -{\xi }_{𝚤}-2\varsigma )}=0$. We will split down the entire proof into three steps.

(i) For ${\xi }_{𝚤}\in (\xi -\varsigma ,\xi ]$, we have

$$\begin{array}{c}\hfill {\mathbb{E}}_{-\varsigma }^{B{(\xi -{\xi }_{𝚤}-2\varsigma )}^{\beta }}{C}_{𝚤}=E{C}_{𝚤}.\end{array}$$

(9)

By Definition 3 and Equation (9), one has

$$\begin{array}{ccc}\hfill {(}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }{\mathbb{E}}_{-\varsigma }^{B{(t-{\xi }_{𝚤}-2\varsigma )}^{\beta }}{C}_{𝚤})\left(\xi \right)& =& {(}^C{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }{\mathbb{E}}_{-\varsigma }^{B{(t-{\xi }_{𝚤}-2\varsigma )}^{\beta }}{C}_{𝚤})\left(\xi \right)\hfill \\ & =& \frac{1}{\mathrm{\Gamma }(1-\beta )}{\int }_{-\varsigma }^{\xi }{(\xi -t)}^{-\beta }{\left(E{C}_{𝚤}\right)}^{\prime }dt\hfill \\ & =& B{\mathbb{E}}_{-\varsigma }^{B{(\xi -{\xi }_{𝚤}-3\varsigma )}^{\beta }}{C}_{𝚤}.\hfill \end{array}$$

(ii) For ${\xi }_{𝚤}\in (0,\xi -(k-1)\varsigma ]$, we have

$$\begin{array}{c}\hfill {\mathbb{E}}_{-\varsigma }^{B{(\xi -{\xi }_{𝚤}-2\varsigma )}^{\beta }}{C}_{𝚤}=\sum _{m=0}^{k-1}{B}^m\frac{{(\xi -{\xi }_{𝚤}-m\varsigma )}^{m\beta }}{\mathrm{\Gamma }(m\beta +1)}{C}_{𝚤}.\end{array}$$

(10)

By Definition 3, Lemma 1 and Equation (10), one has

$$\begin{array}{ccc}& & {(}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }{\mathbb{E}}_{-\varsigma }^{B{(t-{\xi }_{𝚤}-2\varsigma )}^{\beta }}{C}_{𝚤})\left(\xi \right)\hfill \\ & =& {(}^C{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }{\mathbb{E}}_{-\varsigma }^{B{(t-{\xi }_{𝚤}-2\varsigma )}^{\beta }}{C}_{𝚤})\left(\xi \right)\hfill \\ & =& \frac{B}{\mathrm{\Gamma }(1-\beta )\mathrm{\Gamma }\left(\beta \right)}{\int }_{{\xi }_{𝚤}+\varsigma }^{\xi }{(\xi -t)}^{-\beta }{(t-{\xi }_{𝚤}-\varsigma )}^{\beta -1}{C}_{𝚤}dt\hfill \\ & & +\frac{B^2}{\mathrm{\Gamma }(1-\beta )\mathrm{\Gamma }\left(2\beta \right)}{\int }_{{\xi }_{𝚤}+2\varsigma }^{\xi }{(\xi -t)}^{-\beta }{(t-{\xi }_{𝚤}-2\varsigma )}^{2\beta -1}{C}_{𝚤}dt\hfill \\ & & \cdots +\frac{B^{k-1}}{\mathrm{\Gamma }(1-\beta )\mathrm{\Gamma }\left(\right(k-1\left)\beta \right)}{\int }_{{\xi }_{𝚤}+(k-1)\varsigma }^{\xi }{(\xi -t)}^{-\beta }{(t-{\xi }_{𝚤}-(k-1)\varsigma )}^{(k-1)\beta -1}{C}_{𝚤}dt\hfill \\ & =& B\left(E{C}_{𝚤}+B^2\frac{{(\xi -{\xi }_{𝚤}-2\varsigma )}^{\beta }}{\mathrm{\Gamma }(\beta +1)}{C}_{𝚤}+\cdots +B^{k-1}\frac{{(\xi -{\xi }_{𝚤}-(k-1)\varsigma )}^{(k-2)\beta }}{\mathrm{\Gamma }\left(\right(k-2)\beta +1)}{C}_{𝚤}\right)\hfill \\ & =& B\sum _{m=0}^{k-2}{B}^m\frac{{(\xi -{\xi }_{𝚤}-(m+1)\varsigma )}^{m\beta }}{\mathrm{\Gamma }(m\beta +1)}{C}_{𝚤}\hfill \\ & =& B{\mathbb{E}}_{-\varsigma }^{B{(\xi -\xi 𝚤-3\varsigma )}^{\beta }}{C}_{𝚤}.\hfill \end{array}$$

(iii) For ${\xi }_{𝚤}\in (\xi -(n+1)\varsigma ,\xi -n\varsigma ]$, $n=2,\cdots ,k-2$, we have

$$\begin{array}{c}\hfill {\mathbb{E}}_{-\varsigma }^{B{(\xi -{\xi }_{𝚤}-2\varsigma )}^{\beta }}{C}_{𝚤}=\sum _{m=0}^n{B}^m\frac{{(\xi -{\xi }_{𝚤}-m\varsigma )}^{m\beta }}{\mathrm{\Gamma }(m\beta +1)}{C}_{𝚤}.\end{array}$$

(11)

By Definition 3, Lemma 1 and Equation (11), one has

$$\begin{array}{cc}& {(}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }{\mathbb{E}}_{-\varsigma }^{B{(t-{\xi }_{𝚤}-2\varsigma )}^{\beta }}{C}_{𝚤})\left(\xi \right)\hfill \\ =& {(}^C{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }{\mathbb{E}}_{-\varsigma }^{B{(t-{\xi }_{𝚤}-2\varsigma )}^{\beta }}{C}_{𝚤})\left(\xi \right)\hfill \\ =& \frac{1}{\mathrm{\Gamma }(1-\beta )}({\int }_{{\xi }_{𝚤}+\varsigma }^{{\xi }_{𝚤}+2\varsigma }{(\xi -t)}^{-\beta }B\frac{\beta {(t-{\xi }_{𝚤}-\varsigma )}^{\beta -1}}{\mathrm{\Gamma }(\beta +1)}{C}_{𝚤}dt+\hfill \\ & \cdots +{\int }_{{\xi }_{𝚤}+n\varsigma }^{\xi }{(\xi -t)}^{-\beta }\sum _{m=0}^n{B}^m\frac{m\beta {(t-{\xi }_{𝚤}-m\varsigma )}^{m\beta -1}}{\mathrm{\Gamma }(m\beta +1)}{C}_{𝚤}dt)\hfill \\ =& \frac{B}{\mathrm{\Gamma }(1-\beta )\mathrm{\Gamma }\left(\beta \right)}({\int }_{{\xi }_{𝚤}+\varsigma }^{\xi }{(\xi -t)}^{-\beta }{(t-{\xi }_{𝚤}-\varsigma )}^{\beta -1}{C}_{𝚤}dt\hfill \\ & +\frac{B^2}{\mathrm{\Gamma }(1-\beta )\mathrm{\Gamma }\left(2\beta \right)}{\int }_{{\xi }_{𝚤}+2\varsigma }^{\xi }{(\xi -t)}^{-\beta }{(t-{\xi }_{𝚤}-2\varsigma )}^{2\beta -1}{C}_{𝚤}dt\hfill \\ & \cdots +\frac{B^n}{\mathrm{\Gamma }(1-\beta )\mathrm{\Gamma }\left(n\beta \right)}{\int }_{{\xi }_{𝚤}+n\varsigma }^{\xi }{(\xi -t)}^{-\beta }{(t-{\xi }_{𝚤}-n\varsigma )}^{n\beta -1}{C}_{𝚤}dt)\hfill \\ =& B\left(E{C}_{𝚤}+B\frac{{(\xi -{\xi }_{𝚤}-2\varsigma )}^{\beta }}{\mathrm{\Gamma }(\beta +1)}{C}_{𝚤}+\cdots +B^{n-1}\frac{{(\xi -{\xi }_{𝚤}-(n-1)\varsigma -\varsigma )}^{(n-1)\beta }}{\mathrm{\Gamma }\left(\right(n-1)\beta +1)}{C}_{𝚤}\right)\hfill \\ =& B\sum _{m=0}^{n-1}{B}^m\frac{{(\xi -\varsigma -{\xi }_{𝚤}-m\varsigma )}^{m\beta }}{\mathrm{\Gamma }(m\beta +1)}{C}_{𝚤}\hfill \\ =& B{\mathbb{E}}_{-\varsigma }^{B{(\xi -{\xi }_{𝚤}-3\varsigma )}^{\beta }}{C}_{𝚤}.\hfill \end{array}$$

The proof is finished. □

Theorem 2. 

The impulsive delayed Mittag–Leffler-type vector function $Q_{-\varsigma ,\beta }(·)$ is the fundamental solution of (3).

Proof. 

By Definition 3 and Lemma 1, one has

$$\begin{array}{ccc}\hfill \left({}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }\sum _{0<{\xi }_{𝚤}<\xi }{\mathbb{E}}_{-\varsigma }^{B{(t-{\xi }_{𝚤}-2\varsigma )}^{\beta }}{C}_{𝚤}\right)\left(\xi \right)& =& \left({}^C{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }\sum _{0<{\xi }_{𝚤}<\xi }{\mathbb{E}}_{-\varsigma }^{B{(t-{\xi }_{𝚤}-2\varsigma )}^{\beta }}{C}_{𝚤}\right)\left(\xi \right)\hfill \\ & =& \frac{1}{\mathrm{\Gamma }(1-\beta )}{\int }_{-\varsigma }^{\xi }{(\xi -t)}^{-\beta }\sum _{0<{\xi }_{𝚤}<\xi }{\left({\mathbb{E}}_{-\varsigma }^{B{(t-{\xi }_{𝚤}-2\varsigma )}^{\beta }}\right)}^{\prime }{C}_{𝚤}\mathrm{d}t\hfill \\ & =& \left(\sum _{0<{\xi }_{𝚤}<\xi }{}^C{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }{\mathbb{E}}_{-\varsigma }^{B{(t-{\xi }_{𝚤}-2\varsigma )}^{\beta }}{C}_{𝚤}\right)\left(\xi \right)\hfill \\ & =& B\sum _{0<{\xi }_{𝚤}<\xi }{\mathbb{E}}_{-\varsigma }^{B{(\xi -{\xi }_{𝚤}-3\varsigma )}^{\beta }}{C}_{𝚤}.\hfill \end{array}$$

Let ${\xi }_{𝚤}\in (0,\xi )$ and $𝚤=1,2,\cdots ,p(T,0)$; we will prove $Q_{-\varsigma ,\beta }\left({\xi }_{𝚤}^{+}\right)=Q_{-\varsigma ,\beta }\left({\xi }_{𝚤}^{-}\right)+C_{𝚤}$.

$$\begin{array}{ccc}\hfill Q_{-\varsigma ,\beta }\left({\xi }_{𝚤}^{+}\right)& =& \sum _{k=1}^{𝚤}{\mathbb{E}}_{-\varsigma }^{B{({\xi }_{𝚤}^{+}-{\xi }_k-2\varsigma )}^{\beta }}{C}_k\hfill \\ & =& \sum _{k=1}^{𝚤-1}{\mathbb{E}}_{-\varsigma }^{B{({\xi }_{𝚤}^{-}-{\xi }_k-2\varsigma )}^{\beta }}{C}_k+C_{𝚤},{\xi }_{𝚤}^{+}\in ({\xi }_{𝚤},{\xi }_{𝚤+1}],\hfill \\ \hfill Q_{-\varsigma ,\beta }\left({\xi }_{𝚤}^{-}\right)& =& \sum _{k=1}^{𝚤-1}{\mathbb{E}}_{-\varsigma }^{B{({\xi }_{𝚤}^{-}-{\xi }_k-2\varsigma )}^{\beta }}{C}_k,{\xi }_{𝚤}^{-}\in ({\xi }_{𝚤-1},{\xi }_{𝚤}],\hfill \end{array}$$

which implies that $Q_{-\varsigma ,\beta }\left({\xi }_{𝚤}^{+}\right)=Q_{-\varsigma ,\beta }\left({\xi }_{𝚤}^{-}\right)+C_{𝚤}$. The proof is complete. □

Theorem 3. 

The solution $v\in PC(\mathrm{\Omega },{\mathbb{R}}^n)\cap PC([-\varsigma ,T],{\mathbb{R}}^n)$ of (3) has the form

$$\begin{array}{c}\hfill v\left(\xi \right)=e_{-\varsigma ,\beta }^{B{\xi }^{\beta }}\varpi (-\varsigma )+{\int }_{-\varsigma }^0{e}_{-\varsigma ,\beta }^{B{(\xi -\varsigma -s)}^{\beta }}{(}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }\varpi )\left(s\right)ds+\sum _{0<{\xi }_{𝚤}<\xi }{\mathbb{E}}_{-\varsigma }^{B{(\xi -{\xi }_{𝚤}-2\varsigma )}^{\beta }}{C}_{𝚤},\end{array}$$

where either $\mathrm{\Omega }=\left(\right(k-1)\varsigma ,k\varsigma ]$ for $0<\beta <\frac{1}{k+1}$ or $\mathrm{\Omega }=\left[\right(k-1)\varsigma ,k\varsigma ]$ for $\beta \ge \frac{1}{k+1}$.

Proof. 

The proof of this theorem is analogous to ([22], Theorem 3.2).

The general solution of (3) that satisfies $v\left(\xi \right)=\varpi \left(\xi \right)$, $-\varsigma \le \xi \le 0$ has the following form

$$\begin{array}{c}\hfill v\left(\xi \right)=e_{-\varsigma ,\beta }^{B{\xi }^{\beta }}c+{\int }_{-\varsigma }^0{e}_{-\varsigma ,\beta }^{B{(\xi -\varsigma -s)}^{\beta }}y\left(s\right)ds+Q_{-\varsigma ,\beta }\left(\xi \right),0\le \xi \le T.\end{array}$$

(12)

where c is an unknown vector and $y\in C([-\varsigma ,T],{\mathbb{R}}^n)$ is an unknown function. We choose a c satisfying $\left({\mathbb{I}}_{-{\varsigma }^{+}}^{1-\beta }z\right)(-{\varsigma }^{+})=\varpi (-\varsigma )$; then, one has

$$\begin{array}{c}\hfill e_{-\varsigma ,\beta }^{B{\xi }^{\beta }}c+{\int }_{-\varsigma }^0{e}_{-\varsigma ,\beta }^{B{(\xi -\varsigma -s)}^{\beta }}y\left(s\right)ds=\varpi \left(\xi \right),-\varsigma \le \xi \le 0.\end{array}$$

By (6), let $\xi =-\varsigma$, and we obtain $e_{-\varsigma ,\beta }^{B{(-2\varsigma -s)}^{\beta }}=\mathrm{\Theta }$ with $-\varsigma \le s\le 0$. For $-\varsigma \le \xi \le 0$, we have

$$\begin{array}{ccc}\hfill \varpi (-\varsigma )& =& \left({\mathbb{I}}_{-{\varsigma }^{+}}^{1-\beta }v\right)(-{\varsigma }^{+})\hfill \\ & =& \underset{\xi \to -{\varsigma }^{+}}{lim}\left({\mathbb{I}}_{-{\varsigma }^{+}}^{1-\beta }v\right)\left(\xi \right)\hfill \\ & =& \underset{\xi \to -{\varsigma }^{+}}{lim}\left(\frac{1}{\mathrm{\Gamma }(1-\beta )}{\int }_{-\varsigma }^{\xi }{(\xi -t)}^{-\beta }{e}_{-\varsigma ,\beta }^{B{t}^{\beta }}cdt\right)\hfill \\ & =& \underset{\xi \to -{\varsigma }^{+}}{lim}\frac{c}{\mathrm{\Gamma }(1-\beta )\mathrm{\Gamma }\left(\beta \right)}{\int }_{-\varsigma }^{\xi }{(\xi -t)}^{-\beta }{(t+\varsigma )}^{\beta -1}dt\hfill \\ & =& \underset{\xi \to -{\varsigma }^{+}}{lim}c=c,\hfill \end{array}$$

which implies that

$$\begin{array}{c}\hfill v\left(\xi \right)=e_{-\varsigma ,\beta }^{B{\xi }^{\beta }}\varpi (-\varsigma )+{\int }_{-\varsigma }^0{e}_{-\varsigma ,\beta }^{B{(\xi -\varsigma -s)}^{\beta }}y\left(s\right)ds+Q_{-\varsigma ,\beta }\left(\xi \right).\end{array}$$

For any $-\varsigma \le \xi \le 0$, one has

$$\begin{array}{c}\hfill e_{-\varsigma ,\beta }^{B{(\xi -\varsigma -s)}^{\beta }}=\begin{array}{c}\hfill \left\{\begin{array}{cc}& \mathrm{\Theta },\xi \le s\le 0,\hfill \\ & E\frac{{(\xi -s)}^{\beta -1}}{\mathrm{\Gamma }\left(\beta \right)},-\varsigma \le s\le \xi .\hfill \end{array}\right.\end{array}\end{array}$$

Thus, for any $-\varsigma \le \xi \le 0$, we have

$$\begin{array}{c}\hfill \varpi \left(\xi \right)=\frac{{(\xi +\varsigma )}^{\beta -1}}{\mathrm{\Gamma }\left(\beta \right)}\varpi (-\varsigma )+{\int }_{-\varsigma }^{\xi }\frac{{(\xi -s)}^{\beta -1}}{\mathrm{\Gamma }\left(\beta \right)}y\left(s\right)ds.\end{array}$$

(13)

Using Riemann–Liouville fractional differentiation on both sides of (13), we have

$$\begin{array}{ccc}\hfill {(}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }\varpi )\left(\xi \right)& =& \frac{1}{\mathrm{\Gamma }(1-\beta )}\frac{d}{d\xi }{\int }_{-\varsigma }^{\xi }{(\xi -t)}^{-\beta }(\frac{{(t+\varsigma )}^{\beta -1}}{\mathrm{\Gamma }\left(\beta \right)}\varpi (-\varsigma )\hfill \\ & & +{\int }_{-\varsigma }^t\frac{{(t-s)}^{\beta -1}}{\mathrm{\Gamma }\left(\beta \right)}y\left(s\right)ds)dt\hfill \\ & =& \frac{1}{\mathrm{\Gamma }(1-\beta )\mathrm{\Gamma }\left(\beta \right)}\frac{d}{d\xi }{\int }_{-\varsigma }^{\xi }y\left(s\right)\left({\int }_s^{\xi }{(\xi -t)}^{-\beta }{(t-s)}^{\beta -1}dt\right)ds\hfill \\ & =& \frac{d}{d\xi }{\int }_{-\varsigma }^{\xi }y\left(s\right)ds\hfill \\ & =& y\left(\xi \right).\hfill \end{array}$$

For any $\xi \in [0,T]$ and ${\xi }_{𝚤}\in (0,\xi )$, we have

$$\begin{array}{ccc}\hfill v\left({\xi }_{𝚤}^{+}\right)& =& e_{-\varsigma ,\beta }^{B{\left({\xi }_{𝚤}^{+}\right)}^{\beta }}\varpi (-\varsigma )+{\int }_{-\varsigma }^0{e}_{-\varsigma ,\beta }^{B{({\xi }_{𝚤}^{+}-\varsigma -s)}^{\beta }}{(}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }\varpi )\left(s\right)ds+\sum _{k=1}^{𝚤}{\mathbb{E}}_{-\varsigma }^{B{({\xi }_{𝚤}^{+}-{\xi }_k-2\varsigma )}^{\beta }}{C}_k\hfill \\ & =& e_{-\varsigma ,\beta }^{B{\left({\xi }_{𝚤}^{-}\right)}^{\beta }}\varpi (-\varsigma )+{\int }_{-\varsigma }^0{e}_{-\varsigma ,\beta }^{B{({\xi }_{𝚤}^{-}-\varsigma -s)}^{\beta }}{(}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }\varpi )\left(s\right)ds+\sum _{k=1}^{𝚤-1}{\mathbb{E}}_{-\varsigma }^{B{({\xi }_{𝚤}-{\xi }_k-2\varsigma )}^{\beta }}{C}_k+C_{𝚤}\hfill \\ & =& v\left({\xi }_{𝚤}^{-}\right)+C_{𝚤}.\hfill \end{array}$$

This proof is complete. □

Theorem 4. 

The solution $\tilde{v}\in C((0,T],{\mathbb{R}}^n)$ of (1) with $\tilde{v}\left(\xi \right)\equiv \mathbf{0}={(0,0,\cdots ,0)}^{\top },-\varsigma \le \xi \le 0$ can be written as

$$\begin{array}{c}\hfill \tilde{v}\left(\xi \right)={\int }_{-\varsigma }^{\xi }{e}_{-\varsigma ,\beta }^{B{(\xi -\varsigma -t)}^{\beta }}g\left(t\right)dt.\end{array}$$

Proof. 

The proof of this theorem is analogous to ([22], Theorem 3.3). □

Next, combined with Theorems 3 and 4, the solution of (4) can be obtained.

Theorem 5. 

The solution $v\in PC(\mathrm{\Omega },{\mathbb{R}}^n)\cap PC([-\varsigma ,T],{\mathbb{R}}^n)$ of (4) has the form

$$\begin{array}{ccc}\hfill v\left(\xi \right)& =& e_{-\varsigma ,\beta }^{B{\xi }^{\beta }}\varpi (-\varsigma )+{\int }_{-\varsigma }^0{e}_{-\varsigma ,\beta }^{B{(\xi -\varsigma -s)}^{\beta }}{(}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }\varpi )\left(s\right)ds+\sum _{0<{\xi }_{𝚤}<\xi }{\mathbb{E}}_{-\varsigma }^{B{(\xi -{\xi }_{𝚤}-2\varsigma )}^{\beta }}{C}_{𝚤}\hfill \\ & & +{\int }_{-\varsigma }^{\xi }{e}_{-\varsigma ,\beta }^{B{(\xi -\varsigma -t)}^{\beta }}g\left(t\right)dt.\hfill \end{array}$$

Proof. 

Equation (4) can be decomposed into (1) and (3) (where (1) satisfies $\tilde{v}\left(\xi \right)\equiv \mathbf{0},-\varsigma \le \xi \le 0$); thus, the solution of (4) can be manifested as $v\left(\xi \right)=v_0\left(\xi \right)+\tilde{v}\left(\xi \right)$, where $v_0\left(\xi \right)$ is a solution of (3) and $\tilde{v}\left(\xi \right)$ is a solution of (1) satisfying the zero initial condition. □

4. FTS of (4)

Now, we will give the results of FTS.

$\left[H_1\right]$$M={sup}_{-\varsigma \le s\le 0}\parallel {(}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }\varpi )\left(s\right)\parallel <\infty$.

$\left[H_2\right]$$0<N=({\int }_{-\varsigma }^0\parallel {(}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }\varpi )\left(s\right){{\parallel }^{q}ds)}^{\frac{1}{q}}<\infty$, $\frac{1}{q}=1-\frac{1}{p},p>1$.

$\left[H_3\right]$$\exists \kappa \in L^q([-\varsigma ,T],{\mathbb{R}}^{+})$, $\frac{1}{q}=1-\frac{1}{p}$, $p>1$ such that $\parallel g\left(\xi \right)\parallel \le \kappa \left(\xi \right)$ for $\xi \in [-\varsigma ,T]$ and $\psi \left(\xi \right):={\left({\int }_{-\varsigma }^{\xi }\kappa {\left(t\right)}^{q}dt\right)}^{\frac{1}{q}}<\infty$.

For every $\xi \in \left(\right(k-1)\varsigma ,k\varsigma ]$ and $k=1,2,\cdots k^{*}$, we define

$${\mathrm{\Psi }}_1\left(\xi \right)=\left\{\begin{array}{c}{(\xi -(k-1)\varsigma )}^{\beta +\gamma -1}{E}_{\beta ,\beta }{(\parallel B\parallel (\xi -(k-1)\varsigma )}^{\beta }),0<\beta <\frac{1}{k+1},\hfill \\ {(\xi -(k-1)\varsigma )}^{\gamma }\sum _{m=0}^k{\parallel B\parallel }^m\frac{{(\xi -(m-1)\varsigma )}^{(m+1)\beta -1}}{\mathrm{\Gamma }(m\beta +\beta )},\frac{1}{k+1}\le \beta <\frac{1}{2},\hfill \\ {\xi }^{\beta +\gamma -1}{E}_{\beta ,\beta }(\parallel B\parallel {\xi }^{\beta }),\beta \ge \frac{1}{2},\hfill \end{array}\right.$$

and

$$\begin{array}{ccc}& & {\mathrm{\Psi }}_2\left(\xi \right)=\sum _{m=0}^k\frac{{\parallel B\parallel }^m}{\mathrm{\Gamma }\left(\right(m+1)\beta +1)}{(\xi -(m-1)\varsigma )}^{(m+1)\beta }\hfill \\ & & -\sum _{m=1}^k\frac{{\parallel B\parallel }^{m-1}}{\mathrm{\Gamma }(m\beta +1)}{(\xi -(m-1)\varsigma )}^{m\beta },\hfill \\ & & {\mathrm{\Psi }}_3\left(\xi \right)=\sum _{m=0}^k\frac{{\parallel B\parallel }^m{(\xi -(m-1)\varsigma )}^{(m+1)\beta }}{\mathrm{\Gamma }\left(\right(m+1)\beta +1)},\hfill \\ & & {\mathrm{\Psi }}_4\left(\xi \right)=\sum _{m=0}^k\left(\frac{{\parallel B\parallel }^m}{\mathrm{\Gamma }(m\beta +\beta )}\frac{{(\xi -(m-1)\varsigma )}^{(m+1)\beta -1-\frac{1}{p}}}{{(p(m+1)\beta -p+1)}^{\frac{1}{p}}}\right).\hfill \end{array}$$

Theorem 6. 

Suppose that $\beta +\gamma -1>0$ and $\left[H_1\right]$ holds. If

$$\begin{array}{cc}\hfill & {\mathrm{\Psi }}_1\left(\xi \right)\delta +{(\xi -(k-1)\varsigma )}^{\gamma }(M{\mathrm{\Psi }}_2\left(\xi \right)\hfill \\ \hfill & +\sum _{0<{\xi }_{𝚤}<\xi }{E}_{\beta ,1}(\parallel B\parallel {(\xi -{\xi }_{𝚤}-2\varsigma )}^{\beta })\parallel C_{𝚤}{\parallel +\parallel g\parallel }_C{\mathrm{\Psi }}_3\left(\xi \right))<\eta ,\hfill \end{array}$$

(14)

then (4) is finite-time stable with regard to $\{0,J,\varsigma ,\delta ,\eta \}$.

Proof. 

By Lemmas 2, 3 and 5, we have

$$\begin{array}{ccc}& & {\parallel (\xi -(k-1)\varsigma )}^{\gamma }v\left(\xi \right)\parallel \hfill \\ & \le & {\parallel (\xi -(k-1)\varsigma )}^{\gamma }{e}_{-\varsigma ,\beta }^{B{\xi }^{\beta }}\parallel \parallel \varpi (-\varsigma )\parallel \hfill \\ & & +{(\xi -(k-1)\varsigma )}^{\gamma }{\int }_{-\varsigma }^0\parallel e_{-\varsigma ,\beta }^{B{(\xi -\varsigma -s)}^{\beta }}\parallel \parallel {(}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }\varpi )\left(s\right)\parallel ds\hfill \\ & & +{(\xi -(k-1)\varsigma )}^{\gamma }\sum _{0<{\xi }_{𝚤}<\xi }\parallel {\mathbb{E}}_{-\varsigma }^{B{(\xi -{\xi }_{𝚤}-2\varsigma )}^{\beta }}\parallel \parallel C_{𝚤}\parallel \hfill \\ & & +{(\xi -(k-1)\varsigma )}^{\gamma }{\int }_{-\varsigma }^{\xi }\parallel e_{-\varsigma ,\beta }^{B{(\xi -\varsigma -t)}^{\beta }}\parallel \parallel g\left(t\right)\parallel dt\hfill \\ & \le & {\mathrm{\Psi }}_1\left(\xi \right)\delta +{(\xi -(k-1)\varsigma )}^{\gamma }M{\mathrm{\Psi }}_2\left(\xi \right)\hfill \\ & & +{(\xi -(k-1)\varsigma )}^{\gamma }\sum _{0<{\xi }_{𝚤}<\xi }{E}_{\beta ,1}(\parallel B\parallel {(\xi -{\xi }_{𝚤}-2\varsigma )}^{\beta })\parallel C_{𝚤}\parallel \hfill \\ & & +{(\xi -(k-1)\varsigma )}^{\gamma }{\parallel g\parallel }_C\sum _{m=0}^k\frac{{\parallel B\parallel }^m}{\mathrm{\Gamma }\left(\right(m+1\left)\beta \right)}{\int }_{-\varsigma }^{\xi -m\varsigma }{(\xi -m\varsigma -t)}^{(m+1)\beta -1}dt\hfill \\ & \le & {\mathrm{\Psi }}_1\left(\xi \right)\delta +{(\xi -(k-1)\varsigma )}^{\gamma }(M{\mathrm{\Psi }}_2\left(\xi \right)\hfill \\ & & +\sum _{0<{\xi }_{𝚤}<\xi }{E}_{\beta ,1}(\parallel B\parallel {(\xi -{\xi }_{𝚤}-2\varsigma )}^{\beta })\parallel C_{𝚤}{\parallel +\parallel g\parallel }_C{\mathrm{\Psi }}_3\left(\xi \right))\hfill \\ & <& \eta .\hfill \end{array}$$

This proof is complete. □

Theorem 7. 

Suppose that $\beta >max\{1-\gamma ,1-\frac{1}{p}\}$ and $\left[H_2\right]$ and $\left[H_3\right]$ hold. If

$$\begin{array}{cc}\hfill & {\mathrm{\Psi }}_1\left(\xi \right)\delta +{(\xi -(k-1)\varsigma )}^{\gamma }({\mathrm{\Psi }}_4\left(\xi \right)N+{\mathrm{\Psi }}_4\left(\xi \right)\psi \left(\xi \right)\hfill \\ \hfill & +\sum _{0<{\xi }_{𝚤}<\xi }{E}_{\beta ,1}(\parallel B\parallel {(\xi -{\xi }_{𝚤}-2\varsigma )}^{\beta })\parallel C_{𝚤}\parallel )<\eta ,\hfill \end{array}$$

(15)

then (4) is finite-time stable with regard to $\{0,J,\varsigma ,\delta ,\eta \}$.

Proof. 

By Lemmas 2 and 4, we have

$$\begin{array}{cc}& {\parallel (\xi -(k-1)\varsigma )}^{\gamma }v\left(\xi \right)\parallel \hfill \\ \le & {\parallel (\xi -(k-1)\varsigma )}^{\gamma }{e}_{-\varsigma ,\beta }^{B{\xi }^{\beta }}\parallel \parallel \varpi (-\varsigma )\parallel \hfill \\ & +{(\xi -(k-1)\varsigma )}^{\gamma }{\int }_{-\varsigma }^0\parallel e_{-\varsigma ,\beta }^{B{(\xi -\varsigma -s)}^{\beta }}\parallel \parallel {(}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }\varpi )\left(s\right)\parallel ds\hfill \\ & +{(\xi -(k-1)\varsigma )}^{\gamma }\sum _{0<{\xi }_{𝚤}<\xi }\parallel {\mathbb{E}}_{-\varsigma }^{B{(\xi -{\xi }_{𝚤}-2\varsigma )}^{\beta }}\parallel \parallel C_{𝚤}\parallel \hfill \end{array}$$

$$\begin{array}{cc}& +{(\xi -(k-1)\varsigma )}^{\gamma }{\int }_{-\varsigma }^{\xi }\parallel e_{-\varsigma ,\beta }^{B{(\xi -\varsigma -t)}^{\beta }}\parallel \parallel g\left(t\right)\parallel dt\hfill \\ \le & {\mathrm{\Psi }}_1\left(\xi \right)\delta +{(\xi -(k-1)\varsigma )}^{\gamma }({\mathrm{\Psi }}_4\left(\xi \right)N+\sum _{0<{\xi }_{𝚤}<\xi }{E}_{\beta ,1}(\parallel B\parallel {(\xi -{\xi }_{𝚤}-2\varsigma )}^{\beta })\parallel C_{𝚤}\parallel \hfill \\ & +\sum _{m=0}^k\frac{{\parallel B\parallel }^m}{\mathrm{\Gamma }\left(\right(m+1\left)\beta \right)}{\int }_{-\varsigma }^{\xi -m\varsigma }{(\xi -m\varsigma -t)}^{(m+1)\beta -1}\kappa \left(t\right)dt)\hfill \\ \le & {\mathrm{\Psi }}_1\left(\xi \right)\delta +{(\xi -(k-1)\varsigma )}^{\gamma }({\mathrm{\Psi }}_4\left(\xi \right)N+\sum _{0<{\xi }_{𝚤}<\xi }{E}_{\beta ,1}(\parallel B\parallel {(\xi -{\xi }_{𝚤}-2\varsigma )}^{\beta })\parallel C_{𝚤}\parallel \hfill \\ & +\sum _{m=0}^k\frac{{\parallel B\parallel }^m}{\mathrm{\Gamma }\left(\right(m+1\left)\beta \right)}{\left({\int }_{-\varsigma }^{\xi -m\varsigma }{(\xi -m\varsigma -t)}^{p\left(\right(m+1)\beta -1)}dt\right)}^{\frac{1}{p}}{\left({\int }_{-\varsigma }^{\xi }\kappa {\left(t\right)}^{q}dt\right)}^{\frac{1}{q}})\hfill \\ \le & {\mathrm{\Psi }}_1\left(\xi \right)\delta +{(\xi -(k-1)\varsigma )}^{\gamma }({\mathrm{\Psi }}_4\left(\xi \right)N\hfill \\ & +\sum _{0<{\xi }_{𝚤}<\xi }{E}_{\beta ,1}(\parallel B\parallel {(\xi -{\xi }_{𝚤}-2\varsigma )}^{\beta })\parallel C_{𝚤}\parallel +{\mathrm{\Psi }}_4\left(\xi \right)\psi \left(\xi \right))\hfill \\ <& \eta .\hfill \end{array}$$

This proof is complete. □

Theorem 8. 

Suppose that $\beta >max\{\frac{1}{2},1-\gamma \}$ and $\left[H_1\right]$ holds. If

$$\begin{array}{cc}\hfill & {\mathrm{\Psi }}_1\left(\xi \right)\delta +M\varsigma {\xi }^{\gamma +\beta -1}{E}_{\beta ,\beta }(\parallel B\parallel {\xi }^{\beta })\hfill \\ \hfill & +{\xi }^{\gamma }\sum _{0<{\xi }_{𝚤}<\xi }{E}_{\beta ,1}(\parallel B\parallel {(\xi -{\xi }_{𝚤}-2\varsigma )}^{\beta })\parallel C_{𝚤}\parallel +{\xi }^{\gamma }{\parallel g\parallel }_C{\mathrm{\Psi }}_3\left(\xi \right)<\eta ,\hfill \end{array}$$

(16)

then (4) is finite-time stable with regard to $\{0,J,\varsigma ,\delta ,\eta \}$.

Proof. 

By Lemmas 2 and 5, we have

$$\begin{array}{cc}& {\parallel (\xi -(k-1)\varsigma )}^{\gamma }v\left(\xi \right)\parallel \hfill \\ \le & {\parallel (\xi -(k-1)\varsigma )}^{\gamma }{e}_{-\varsigma ,\beta }^{B{\xi }^{\beta }}\parallel \parallel \varpi (-\varsigma )\parallel \hfill \\ & +{(\xi -(k-1)\varsigma )}^{\gamma }{\int }_{-\varsigma }^0\parallel e_{-\varsigma ,\beta }^{B{(\xi -\varsigma -s)}^{\beta }}\parallel \parallel {(}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }\varpi )\left(s\right)\parallel ds\hfill \\ & +{(\xi -(k-1)\varsigma )}^{\gamma }\sum _{0<{\xi }_{𝚤}<\xi }\parallel {\mathbb{E}}_{-\varsigma }^{B{(\xi -{\xi }_{𝚤}-2\varsigma )}^{\beta }}\parallel \parallel C_{𝚤}\parallel \hfill \\ & +{(\xi -(k-1)\varsigma )}^{\gamma }{\int }_{-\varsigma }^{\xi }\parallel e_{-\varsigma ,\beta }^{B{(\xi -\varsigma -t)}^{\beta }}\parallel \parallel g\left(t\right)\parallel dt\hfill \\ \le & {\mathrm{\Psi }}_1\left(\xi \right)\delta +{\xi }^{\gamma }(\sum _{m=0}^k\frac{{\parallel B\parallel }^m{\xi }^{(m+1)\beta -1}}{\mathrm{\Gamma }(m\beta +\beta )}{\int }_{-\varsigma }^0{\parallel }^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }\varpi )\left(s\right)\parallel ds\hfill \\ & +\sum _{0<{\xi }_{𝚤}<\xi }{E}_{\beta ,1}(\parallel B\parallel {(\xi -{\xi }_{𝚤}-2\varsigma )}^{\beta })\parallel C_{𝚤}{\parallel +\parallel g\parallel }_C{\int }_{-\varsigma }^{\xi }\parallel e_{-\varsigma ,\beta }^{B{(\xi -\varsigma -t)}^{\beta }}\parallel dt)\hfill \\ \le & {\mathrm{\Psi }}_1\left(\xi \right)\delta +M\varsigma {\xi }^{\gamma +\beta -1}{E}_{\beta ,\beta }(\parallel B\parallel {\xi }^{\beta })\hfill \\ & +{\xi }^{\gamma }\sum _{0<{\xi }_{𝚤}<\xi }{E}_{\beta ,1}(\parallel B\parallel {(\xi -{\xi }_{𝚤}-2\varsigma )}^{\beta })\parallel C_{𝚤}\parallel +{\xi }^{\gamma }{\parallel g\parallel }_C{\mathrm{\Psi }}_3\left(\xi \right)\hfill \\ <& \eta .\hfill \end{array}$$

This proof is complete. □

Theorem 9. 

Suppose that $\beta >max\{\frac{1}{2},1-\gamma ,1-\frac{1}{p}\}$ and $\left[H_1\right]$ and $\left[H_3\right]$ hold. If

$$\begin{array}{c}{\mathrm{\Psi }}_1\left(\xi \right)\delta +{\xi }^{\gamma }\sum _{0<{\xi }_{𝚤}<\xi }{E}_{\beta ,1}(\parallel B\parallel {(\xi -{\xi }_{𝚤}-2\varsigma )}^{\beta })\parallel C_{𝚤}\parallel \hfill \\ +E_{\beta ,\beta }(\parallel B\parallel {\xi }^{\beta })\left(M\varsigma {\xi }^{\gamma +\beta -1}+{\xi }^{\gamma }\psi \left(\xi \right)\frac{{(\xi +\varsigma )}^{\beta -1+\frac{1}{p}}}{{(p(\beta -1)+1)}^{\frac{1}{p}}}\right)<\eta ,\hfill \end{array}$$

(17)

then (4) is finite-time stable with regard to $\{0,J,\varsigma ,\delta ,\eta \}$.

Proof. 

By Lemmas 2 and 5, we have

$$\begin{array}{cc}& {\parallel (\xi -(k-1)\varsigma )}^{\gamma }v\left(\xi \right)\parallel \hfill \\ \le & {\parallel (\xi -(k-1)\varsigma )}^{\gamma }{e}_{-\varsigma ,\beta }^{B{\xi }^{\beta }}\parallel \parallel \varpi (-\varsigma )\parallel \hfill \\ & +{(\xi -(k-1)\varsigma )}^{\gamma }{\int }_{-\varsigma }^0\parallel e_{-\varsigma ,\beta }^{B{(\xi -\varsigma -s)}^{\beta }}\parallel \parallel {(}^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }\varpi )\left(s\right)\parallel ds\hfill \\ & +{(\xi -(k-1)\varsigma )}^{\gamma }\sum _{0<{\xi }_{𝚤}<\xi }\parallel {\mathbb{E}}_{-\varsigma }^{B{(\xi -{\xi }_{𝚤}-2\varsigma )}^{\beta }}\parallel \parallel C_{𝚤}\parallel \hfill \\ & +{(\xi -(k-1)\varsigma )}^{\gamma }{\int }_{-\varsigma }^{\xi }\parallel e_{-\varsigma ,\beta }^{B{(\xi -\varsigma -t)}^{\beta }}\parallel \parallel g\left(t\right)\parallel dt\hfill \\ \le & {\mathrm{\Psi }}_1\left(\xi \right)\delta +{\xi }^{\gamma }(\sum _{m=0}^k\frac{{\parallel B\parallel }^m{\xi }^{(m+1)\beta -1}}{\mathrm{\Gamma }(m\beta +\beta )}{\int }_{-\varsigma }^0{\parallel }^{RL}{\mathbb{D}}_{-{\varsigma }^{+}}^{\beta }\varpi )\left(s\right)\parallel ds\hfill \\ & +\sum _{0<{\xi }_{𝚤}<\xi }{E}_{\beta ,1}(\parallel B\parallel {(\xi -{\xi }_{𝚤}-2\varsigma )}^{\beta })\parallel C_{𝚤}\parallel \hfill \\ & +\sum _{m=0}^k\frac{{\parallel B\parallel }^m}{\mathrm{\Gamma }(m\beta +\beta )}{\int }_{-\varsigma }^{\xi -m\varsigma }{(\xi -m\varsigma -t)}^{(m+1)\beta -1}\kappa \left(t\right)dt)\hfill \\ \le & {\mathrm{\Psi }}_1\left(\xi \right)\delta +{\xi }^{\gamma }(M\varsigma {\xi }^{\beta -1}{E}_{\beta ,\beta }(\parallel B\parallel {\xi }^{\beta })+\sum _{0<{\xi }_{𝚤}<\xi }{E}_{\beta ,1}(\parallel B\parallel {(\xi -{\xi }_{𝚤}-2\varsigma )}^{\beta })\parallel C_{𝚤}\parallel \hfill \\ & +\sum _{m=0}^k\frac{{\parallel B\parallel }^m{\xi }^{m\beta }}{\mathrm{\Gamma }(m\beta +\beta )}{\int }_{-\varsigma }^{\xi }{(\xi -t)}^{\beta -1}\kappa \left(t\right)dt)\hfill \\ \le & {\mathrm{\Psi }}_1\left(\xi \right)\delta +{\xi }^{\gamma }(M\varsigma {\xi }^{\beta -1}{E}_{\beta ,\beta }(\parallel B\parallel {\xi }^{\beta })+\sum _{0<{\xi }_{𝚤}<\xi }{E}_{\beta ,1}(\parallel B\parallel {(\xi -{\xi }_{𝚤}-2\varsigma )}^{\beta })\parallel C_{𝚤}\parallel \hfill \\ & +E_{\beta ,\beta }(\parallel B\parallel {\xi }^{\beta }\left){\left({\int }_{-\varsigma }^{\xi }{(\xi -t)}^{p(\beta -1)}dt\right)}^{\frac{1}{p}}\right({\int }_{-\varsigma }^{\xi }\kappa {\left(t\right)}^{q}dt{)}^{\frac{1}{q}}\hfill \\ \le & {\mathrm{\Psi }}_1\left(\xi \right)\delta +{\xi }^{\gamma }\sum _{0<{\xi }_{𝚤}<\xi }{E}_{\beta ,1}(\parallel B\parallel {(\xi -{\xi }_{𝚤}-2\varsigma )}^{\beta })\parallel C_{𝚤}\parallel \hfill \\ & +E_{\beta ,\beta }(\parallel B\parallel {\xi }^{\beta })\left(M\varsigma {\xi }^{\gamma +\beta -1}+{\xi }^{\gamma }\psi \left(\xi \right)\frac{{(\xi +\varsigma )}^{\beta -1+\frac{1}{p}}}{{(p(\beta -1)+1)}^{\frac{1}{p}}}\right)\hfill \\ <& \eta .\hfill \end{array}$$

This proof is complete. □

5. Example

Example 1. 

Let $\beta =0.6$, $\varsigma =0.3$, $k^{*}=3$, ${\xi }_1=0.2$ and ${\xi }_2=0.5$. Consider

$$\left\{\begin{array}{c}{(}^{RL}{\mathbb{D}}_{-0.3^{+}}^{\beta }v)\left(\xi \right)=Bv(\xi -0.3)+g\left(\xi \right),\xi \ne {\xi }_{𝚤},\xi \in (0,0.9],\hfill \\ v\left({\xi }_{𝚤}^{+}\right)=v\left({\xi }_{𝚤}^{-}\right)+C_{𝚤},\xi ={\xi }_{𝚤},𝚤=1,2,\hfill \\ \varpi \left(\xi \right)={(\xi +0.3,0.1(\xi +0.3))}^{\top },-0.3<\xi \le 0,\hfill \\ \left({\mathbb{I}}_{-0.3^{+}}^{0.4}v\right)(-0.3^{+})=\varpi (-0.3)={(0,0)}^{\top },\hfill \end{array}\right.$$

(18)

where

$$\begin{array}{c}\hfill v\left(x\right)=\left(\begin{array}{c}{v}_1\left(\xi \right)\hfill \\ v_2\left(\xi \right)\hfill \end{array}\right),B=\left(\begin{array}{c}0.10.1\hfill \\ 0.30.5\hfill \end{array}\right),C_{𝚤}=\left(\begin{array}{c}\frac{𝚤}{10}\hfill \\ \frac{𝚤}{20}\hfill \end{array}\right),g\left(\xi \right)=\left(\begin{array}{c}\xi \hfill \\ {\xi }^2\hfill \end{array}\right).\end{array}$$

(19)

By Theorem 5, for any $\xi \in [-0.3,0.9]$, one has

$$\begin{array}{ccc}\hfill v\left(\xi \right)& =& e_{-0.3,0.6}^{B{\xi }^{0.6}}\varpi (-0.3)+{\int }_{-0.3}^0{e}_{-0.3,0.6}^{B{(\xi -0.3-s)}^{0.6}}{(}^{RL}{\mathbb{D}}_{-0.3^{+}}^{0.6}\varpi )\left(s\right)ds\hfill \\ & & +\sum _{0<{\xi }_{𝚤}<\xi }{\mathbb{E}}_{-0.3}^{B{(\xi -{\xi }_{𝚤}-0.6)}^{0.6}}{C}_{𝚤}+{\int }_{-0.3}^{\xi }{e}_{-0.3,0.6}^{B{(\xi -0.3-t)}^{0.6}}g\left(t\right)dt,\hfill \end{array}$$

where

$$e_{-0.3,0.6}^{B{\xi }^{0.6}}=\left\{\begin{array}{c}E\frac{{(\xi +0.3)}^{-0.4}}{\mathrm{\Gamma }\left(0.6\right)}+B\frac{{\xi }^{0.2}}{\mathrm{\Gamma }\left(1.2\right)},\xi \in (0,0.3],\hfill \\ E\frac{{(\xi +0.3)}^{-0.4}}{\mathrm{\Gamma }\left(0.6\right)}+B\frac{{\xi }^{0.2}}{\mathrm{\Gamma }\left(1.2\right)}+B^2\frac{{(\xi -0.3)}^{0.8}}{\mathrm{\Gamma }\left(1.8\right)},\xi \in (0.3,0.6],\hfill \\ E\frac{{(\xi +0.3)}^{-0.4}}{\mathrm{\Gamma }\left(0.6\right)}+B\frac{{\xi }^{0.2}}{\mathrm{\Gamma }\left(1.2\right)}+B^2\frac{{(\xi -0.3)}^{0.8}}{\mathrm{\Gamma }\left(1.8\right)}+B^3\frac{{(\xi -0.6)}^{1.4}}{\mathrm{\Gamma }\left(2.4\right)},\xi \in (0.6,0.9],\hfill \end{array}\right.$$

and

$$\sum _{s<{\xi }_{𝚤}<\xi }{\mathbb{E}}_{-0.3}^{B{(\xi -{\xi }_{𝚤}-0.6)}^{0.6}}{C}_{𝚤}=\left\{\begin{array}{c}\left(\begin{array}{c}0\hfill \\ 0\hfill \end{array}\right),\xi \in [0,0.2],\hfill \\ \left(\begin{array}{c}\frac{1}{10}\hfill \\ \frac{1}{20}\hfill \end{array}\right),\xi \in (0.2,0.5],\hfill \\ \left(E+B\frac{{(\xi -0.5)}^{0.6}}{\mathrm{\Gamma }\left(1.6\right)}\right)\left(\begin{array}{c}\frac{1}{10}\hfill \\ \frac{1}{20}\hfill \end{array}\right)+\left(\begin{array}{c}\frac{2}{10}\hfill \\ \frac{2}{20}\hfill \end{array}\right),\xi \in (0.5,0.8],\hfill \\ \left(E+B\frac{{(\xi -0.5)}^{0.6}}{\mathrm{\Gamma }\left(1.6\right)}+B^2\frac{{(\xi -0.8)}^{1.2}}{\mathrm{\Gamma }\left(2.2\right)}\right)\left(\begin{array}{c}\frac{1}{10}\hfill \\ \frac{1}{20}\hfill \end{array}\right)\hfill \\ +\left(E+B\frac{{(\xi -0.8)}^{0.6}}{\mathrm{\Gamma }\left(1.6\right)}\right)\left(\begin{array}{c}\frac{2}{10}\hfill \\ \frac{2}{20}\hfill \end{array}\right),\xi \in [0.8,0.9].\hfill \end{array}\right.$$

Set $p=2$, $q=2$ and $\gamma =0.5$. We can obtain that $\parallel B\parallel =0.6$, ${\parallel g\parallel }_C=1.71$, $M=0.7659$, $N=0.4195$, $\psi \left(0.9\right)=0.9105$. Next, ${\mathsf{\Phi }}_1\left(0.9\right)=1.8211$, ${\mathsf{\Phi }}_2\left(0.9\right)=0.4479$, ${\mathsf{\Phi }}_3\left(0.9\right)=1.8181$, ${\mathsf{\Phi }}_4\left(0.9\right)=1.6056$. Choosing $\delta =0.331$, we present the FTS results of (18) in

Table 1. FTS results of (18) with $T=0.9$.

Theorem	${\parallel \mathit{\varpi }\parallel }_{\mathit{C}}$	$\mathit{\beta }$	T	$\mathit{\delta }$	${\parallel \mathit{z}\parallel }_{{\mathit{C}}_{\mathit{\gamma }}}$	$\mathit{\eta }$	FTS
6	0.33	0.6	0.9	0.331	2.7398	2.75	Yes
7	0.33	0.6	0.9	0.331	2.0187	2.03 (optimal)	Yes
8	0.33	0.6	0.9	0.331	4.3801	4.38	Yes
9	0.33	0.6	0.9	0.331	5.0680	5.07	Yes

.

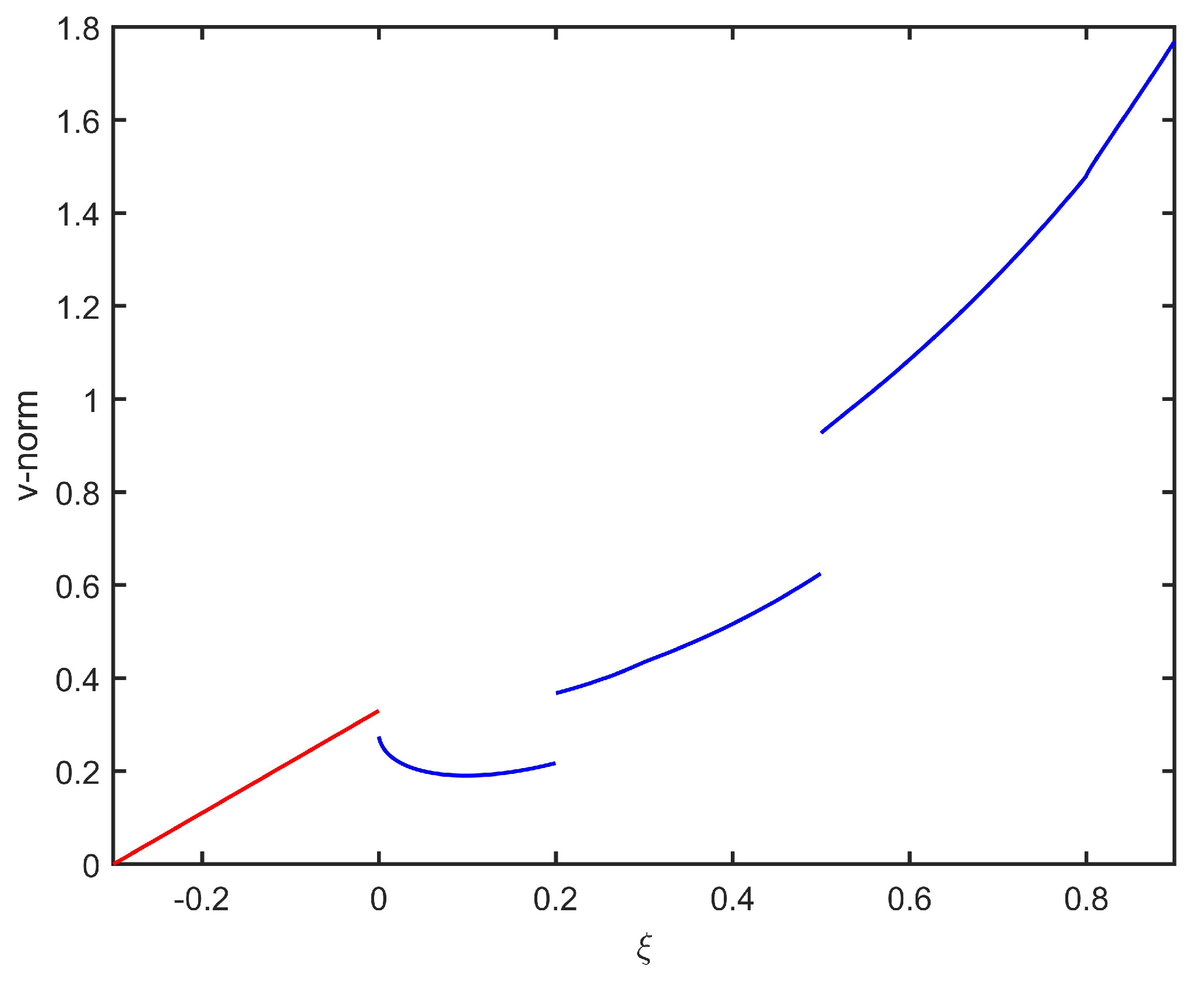
By Definition 8, we find an appropriate $\eta$, ensuring that ${\parallel z\parallel }_{C_{\gamma }}$ in (18) is no more than $\eta$ on J. So, through numerical simulation, we can use the explicit solution of (18) to find a suitable $\eta =1.770$ for a fixed $T=0.9$ (see Figure 1). Furthermore, by verifying the conditions in Theorems 6, 7, 8, 9 for $[-0.3,0.9]$, compared with the values of $\eta$ in Table 1, we can choose a better value of $\eta =2.03$.

Example 2. 

Let $\beta =0.7$, $\varsigma =0.2$, $k^{*}=3$, ${\xi }_1=0.2$ and ${\xi }_2=0.5$. Consider

$$\left\{\begin{array}{c}{(}^{RL}{\mathbb{D}}_{{-0.2}^{+}}^{\beta }v)\left(\xi \right)=Bv(\xi -0.2)+g\left(\xi \right),\xi \ne {\xi }_{𝚤},\xi \in (0,0.6],\hfill \\ v\left({\xi }_{𝚤}^{+}\right)=v\left({\xi }_{𝚤}^{-}\right)+C_{𝚤},\xi ={\xi }_{𝚤},𝚤=1,2,\hfill \\ \varpi \left(\xi \right)={(\xi +0.2,{(\xi +0.2)}^2)}^{\top },-0.2<\xi \le 0,\hfill \\ \left({\mathbb{I}}_{{-0.2}^{+}}^{0.3}v\right)\left({-0.2}^{+}\right)=\varpi (-0.2)={(0,0)}^{\top },\hfill \end{array}\right.$$

(20)

where

$$\begin{array}{c}\hfill v\left(x\right)=\left(\begin{array}{c}{v}_1\left(\xi \right)\hfill \\ v_2\left(\xi \right)\hfill \end{array}\right),B=\left(\begin{array}{c}0.10.1\hfill \\ 0.30.5\hfill \end{array}\right),C_{𝚤}=\left(\begin{array}{c}\frac{𝚤}{10}\hfill \\ \frac{𝚤}{20}\hfill \end{array}\right),g\left(\xi \right)=\left(\begin{array}{c}\xi \hfill \\ {\xi }^2\hfill \end{array}\right).\end{array}$$

(21)

By Theorem 5, for any $\xi \in [-0.2,0.6]$, one has

$$\begin{array}{ccc}\hfill v\left(\xi \right)& =& e_{-0.2,0.7}^{B{\xi }^{0.7}}\varpi (-0.2)+{\int }_{-0.2}^0{e}_{-0.2,0.7}^{B{(\xi -0.2-s)}^{0.7}}{(}^{RL}{\mathbb{D}}_{{-0.2}^{+}}^{0.7}\varpi )\left(s\right)ds\hfill \\ & & +\sum _{0<{\xi }_{𝚤}<\xi }{\mathbb{E}}_{-0.2}^{B{(\xi -{\xi }_{𝚤}-0.4)}^{0.7}}{C}_{𝚤}+{\int }_{-0.2}^{\xi }{e}_{-0.2,0.7}^{B{(\xi -0.2-t)}^{0.7}}g\left(t\right)dt,\hfill \end{array}$$

where

$$e_{-0.2,0.7}^{B{\xi }^{0.7}}=\left\{\begin{array}{c}E\frac{{(\xi +0.2)}^{-0.3}}{\mathrm{\Gamma }\left(0.7\right)}+B\frac{{\xi }^{0.4}}{\mathrm{\Gamma }\left(1.4\right)},\xi \in (0,0.2],\hfill \\ E\frac{{(\xi +0.2)}^{-0.3}}{\mathrm{\Gamma }\left(0.7\right)}+B\frac{{\xi }^{0.4}}{\mathrm{\Gamma }\left(1.4\right)}+B^2\frac{{(\xi -0.2)}^{1.1}}{\mathrm{\Gamma }\left(2.1\right)},\xi \in (0.2,0.4],\hfill \\ E\frac{{(\xi +0.2)}^{-0.3}}{\mathrm{\Gamma }\left(0.7\right)}+B\frac{{\xi }^{0.4}}{\mathrm{\Gamma }\left(1.4\right)}+B^2\frac{{(\xi -0.2)}^{1.1}}{\mathrm{\Gamma }\left(2.1\right)}+B^3\frac{{(\xi -0.4)}^{1.8}}{\mathrm{\Gamma }\left(2.8\right)},\xi \in (0.4,0.6],\hfill \end{array}\right.$$

and

$$\sum _{s<{\xi }_{𝚤}<\xi }{\mathbb{E}}_{-0.2}^{B{(\xi -{\xi }_{𝚤}-0.7)}^{0.7}}{C}_{𝚤}=\left\{\begin{array}{c}\left(\begin{array}{c}0\hfill \\ 0\hfill \end{array}\right),\xi \in [0,0.2],\hfill \\ \left(\begin{array}{c}\frac{1}{10}\hfill \\ \frac{1}{20}\hfill \end{array}\right),\xi \in (0.2,0.4],\hfill \\ \left(E+B\frac{{(\xi -0.4)}^{0.7}}{\mathrm{\Gamma }\left(1.7\right)}\right)\left(\begin{array}{c}\frac{1}{10}\hfill \\ \frac{1}{20}\hfill \end{array}\right),\xi \in (0.4,0.5],\hfill \\ \left(E+B\frac{{(\xi -0.4)}^{0.7}}{\mathrm{\Gamma }\left(1.7\right)}\right)\left(\begin{array}{c}\frac{1}{10}\hfill \\ \frac{1}{20}\hfill \end{array}\right)+\left(\begin{array}{c}\frac{2}{10}\hfill \\ \frac{2}{20}\hfill \end{array}\right),\xi \in [0.5,0.6].\hfill \end{array}\right.$$

Set $p=2$, $q=2$ and $\gamma =0.5$. We can get $\parallel B\parallel =0.6$, ${\parallel g\parallel }_C=0.96$, $M=0.8991$, $N=0.2587$, $\psi \left(0.6\right)=0.4574$. Next, ${\mathsf{\Phi }}_1\left(0.6\right)=1.3245$, ${\mathsf{\Phi }}_2\left(0.6\right)=0.2929$, ${\mathsf{\Phi }}_3\left(0.6\right)=1.2021$, ${\mathsf{\Phi }}_4\left(0.6\right)=2.1050$. Choosing $\delta =0.241$, we present the FTS results of (20) in

Table 2. FTS results of (20) with $T=0.6$.

Theorem	${\parallel \mathit{\varpi }\parallel }_{\mathit{C}}$	$\mathit{\beta }$	T	$\mathit{\delta }$	${\parallel \mathit{z}\parallel }_{{\mathit{C}}_{\mathit{\gamma }}}$	$\mathit{\eta }$	FTS
6	0.24	0.7	0.6	0.241	1.0661	1.07 (optimal)	Yes
7	0.24	0.7	0.6	0.241	1.1064	1.17	Yes
8	0.24	0.7	0.6	0.241	1.6471	1.65	Yes
9	0.24	0.7	0.6	0.241	1.3502	1.36	Yes

.

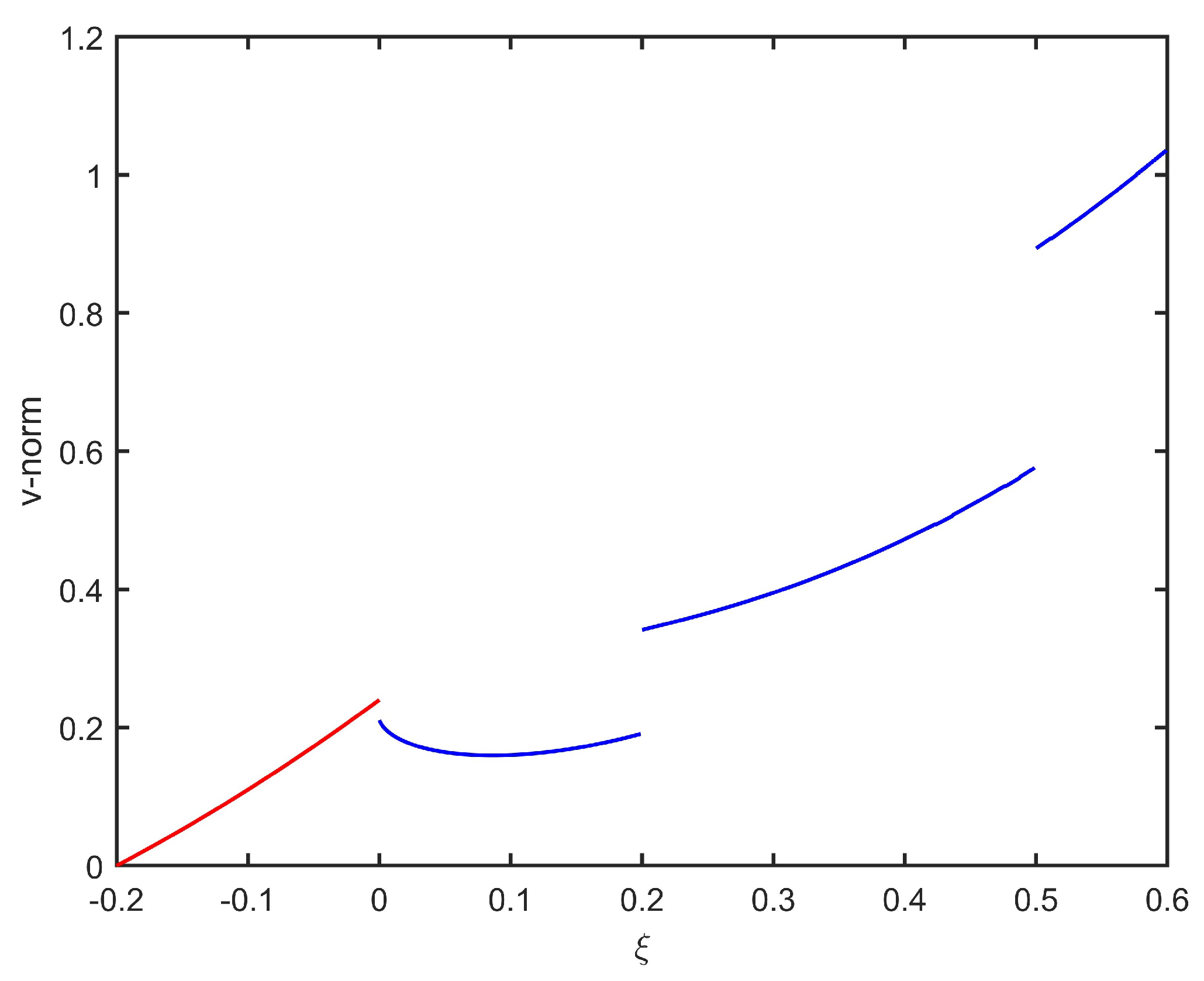
Like Example 1, we can choose a suitable $\eta =1.037$ for a fixed $T=0.6$ (see Figure 2). Furthermore, compared with the values of $\eta$ in Table 2, we can choose a better value of $\eta =1.07$.

Example 3. 

Let $\beta =0.6$, $\varsigma =0.2$, $k^{*}=3$, ${\xi }_1=0.2$ and ${\xi }_2=0.5$. Consider

$$\left\{\begin{array}{c}{(}^{RL}{\mathbb{D}}_{{-0.2}^{+}}^{\beta }v)\left(\xi \right)=Bv(\xi -0.2)+g\left(\xi \right),\xi \ne {\xi }_{𝚤},\xi \in (0,0.6],\hfill \\ v\left({\xi }_{𝚤}^{+}\right)=v\left({\xi }_{𝚤}^{-}\right)+C_{𝚤},\xi ={\xi }_{𝚤},𝚤=1,2,\hfill \\ \varpi \left(\xi \right)={(\xi +0.2,{(\xi +0.2)}^2)}^{\top },-0.2<\xi \le 0,\hfill \\ \left({\mathbb{I}}_{{-0.2}^{+}}^{0.3}v\right)\left({-0.2}^{+}\right)=\varpi (-0.2)={(0,0)}^{\top },\hfill \end{array}\right.$$

(22)

where

$$\begin{array}{c}\hfill v\left(x\right)=\left(\begin{array}{c}{v}_1\left(\xi \right)\hfill \\ v_2\left(\xi \right)\hfill \end{array}\right),B=\left(\begin{array}{c}0.10.1\hfill \\ 0.30.5\hfill \end{array}\right),C_{𝚤}=\left(\begin{array}{c}\frac{𝚤}{10}\hfill \\ \frac{𝚤}{20}\hfill \end{array}\right),g\left(\xi \right)=\left(\begin{array}{c}\xi \hfill \\ {\xi }^2\hfill \end{array}\right).\end{array}$$

(23)

By Theorem 5, for any $\xi \in [-0.2,0.6]$, one has

$$\begin{array}{ccc}\hfill v\left(\xi \right)& =& e_{-0.2,0.6}^{B{\xi }^{0.6}}\varpi (-0.2)+{\int }_{-0.2}^0{e}_{-0.2,0.6}^{B{(\xi -0.2-s)}^{0.6}}{(}^{RL}{\mathbb{D}}_{{-0.2}^{+}}^{0.6}\varpi )\left(s\right)ds\hfill \\ & & +\sum _{0<{\xi }_{𝚤}<\xi }{\mathbb{E}}_{-0.2}^{B{(\xi -{\xi }_{𝚤}-0.4)}^{0.6}}{C}_{𝚤}+{\int }_{-0.2}^{\xi }{e}_{-0.2,0.6}^{B{(\xi -0.2-t)}^{0.6}}g\left(t\right)dt,\hfill \end{array}$$

Set $p=2$, $q=2$ and $\gamma =0.5$. We can get $\parallel B\parallel =0.6$, ${\parallel g\parallel }_C=0.96$, $M=0.7612$, $N=0.2663$, $\psi \left(0.6\right)=0.4574$. Next, ${\mathsf{\Phi }}_1\left(0.6\right)=1.3834$, ${\mathsf{\Phi }}_2\left(0.6\right)=0.2998$, ${\mathsf{\Phi }}_3\left(0.6\right)=1.3167$, ${\mathsf{\Phi }}_4\left(0.6\right)=2.6823$. Choose $\delta =0.241$, we give the FTS results of (22) in

Table 3. FTS results of (22) with $T=0.6$.

Theorem	${\parallel \mathit{\varpi }\parallel }_{\mathit{C}}$	$\mathit{\beta }$	T	$\mathit{\delta }$	${\parallel \mathit{z}\parallel }_{{\mathit{C}}_{\mathit{\gamma }}}$	$\mathit{\eta }$	FTS
6	0.24	0.6	0.6	0.241	1.1198	1.12 (optimal)	Yes
7	0.24	0.6	0.6	0.241	1.4095	1.41	Yes
8	0.24	0.6	0.6	0.241	1.7294	1.73	Yes
9	0.24	0.6	0.6	0.241	1.8641	1.87	Yes

.

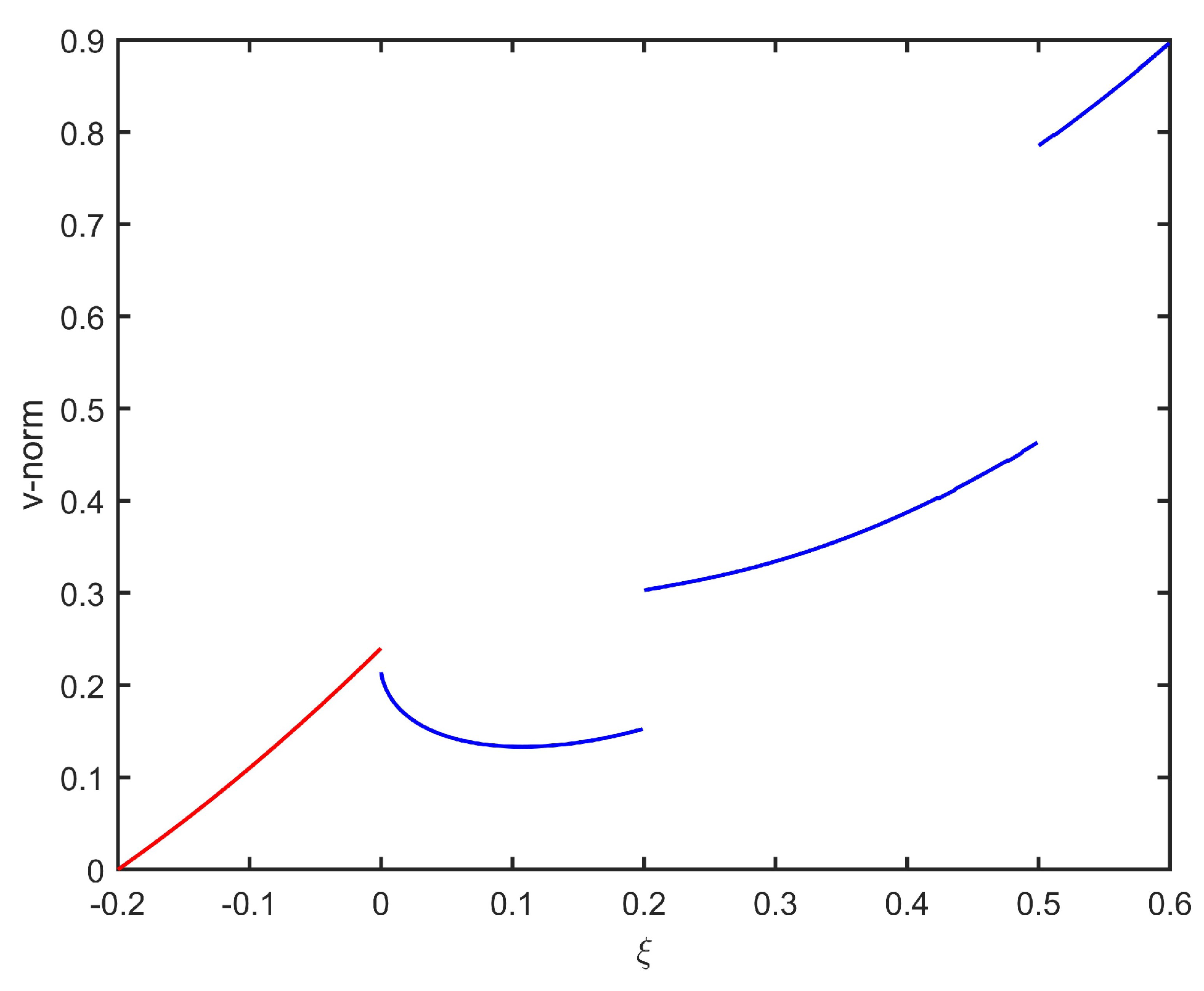
Like Example 2, we can choose a suitable $\eta =0.900$ for a fixed $T=0.6$ (see Figure 3). Furthermore, compared with the values of $\eta$ in Table 3, we can choose a better value $\eta =1.12$.

Comparing Example 1, Example 2 and Example 3, we find the following: When the order is the same, the time delay is different, and when the time delay is the same, the order is different, and the system is finite-time stable.

6. Conclusions

In this study, we introduce the Mittag–Leffler-type vector function with an impulsive delay, and give the explicit solution of the Riemann–Liouville fractional differential equation using the constant variation method. On this basis, by scaling the base solution matrix and the integral, we verify that the system is finite-time stable. Finally, the results are verified by four examples under different conditions. In the future, we may continue to study the other properties of the system, including stability or controllability. Due to the importance of impulsive differential equations, we believe that the results obtained by us will arouse the interest of many readers.