Multiplicative Consistent q-Rung Orthopair Fuzzy Preference Relations with Application to Critical Factor Analysis in Crowdsourcing Task Recommendation

Abstract

This paper presents a group decision-making (GDM) method based on q-rung orthopair fuzzy preference relations (q-ROFPRs). Firstly, the multiplicative consistent q-ROFPRs (MCq-ROFPRs) and the normalized q-rung orthopair fuzzy priority weight vectors (q-ROFPWVs) are introduced. Then, to obtain q-ROFPWVs, a goal programming model under q-ROFPRs is established to minimize their deviation from the MCq-ROFPRs and minimize the weight uncertainty. Further, a group goal programming model of ideal MCq-ROFPRs is constructed to obtain the expert weights using the compatibility measure between the ideal MCq-ROFPRs and the individual q-ROFPRs. Finally, a GDM method with unknown expert weights is solved by combining the group goal programming model and the simple q-rung orthopair fuzzy weighted geometric (Sq-ROFWG) operator. The effectiveness and practicality of the proposed GDM method are verified by solving the crucial factors in crowdsourcing task recommendation. The results show that the developed GDM method effectively considers the important measures of experts and identifies the crucial factors that are more reliable than two other methods.

1. Introduction

With the rise of the sharing economy on a global scale, traditional human resource service models are gradually changing. Crowdsourcing, a new flexible employment model, has become a new strategy for enterprises to optimize resource allocation and enhance innovation capabilities. Compared to traditional employment relationships, under the crowdsourcing model, companies do not establish formal full-time employment relationships with talents. Instead, companies can flexibly hire talents on demand based on their employment needs without the need for complex entry and exit processes. Due to the advantages of high employment flexibility, low employment costs, and low employment risks of the crowdsourcing model, as well as breaking the dependence of workers on commercial organizations, more and more enterprises and organizations facing external competition and internal resource shortages are seeking to use crowdsourcing platforms for production and innovation activities.

On knowledge-intensive crowdsourcing platforms, task publishers, problem solvers, and transaction data are growing exponentially. The high cost of information search and the lack of intelligent task recommendation mechanisms have had a negative impact on crowdsourcing participants [1,2]. How to activate the potential of structured and unstructured data elements and achieve efficient matching between massive tasks and public intellectual resources is a problem worth studying.

Preference relation (PR) is an important tool for experts to describe the critical degree of the factors in crowdsourcing task recommendation. With the q-rung orthopair fuzzy (q-ROF) set (q-ROFS) theory developing, the q-rung orthopair fuzzy preference relation (q-ROFPR) has the advantages of describing the uncertainty and preference information in crowdsourcing task recommendation.

Thus, we develop a group decision-making (GDM) method under q-ROFPRs for finding out the critical factors in crowdsourcing task recommendation and define the compatibility measure between q-ROFPRs to reflect the important measures of experts. The contributions are provided as follows:

(1) The implication relations and constraints between intuitionistic fuzzy sets (IFSs) and q-ROFSs are analyzed.

(2) We define the multiplicative consistent q-ROFPRs (MCq-ROFPRs) and the normalized q-rung orthopair fuzzy priority weight vectors (q-ROFPWVs) and provide the conversion method for q-ROFPWVs to construct MCq-ROFPRs.

(3) In decision-making problems, evaluators cannot always give MCq-ROFPRs when comparing alternatives, and it is necessary to establish a method to obtain the priority weight vectors (PWVs) of general q-ROFPR. Thus, a goal programming model for obtaining the PWVs is considered to minimize the difference between q-ROFPRs and MCq-ROFPRs and minimize the uncertainty of the PWVs based on the conversion method between q-ROFPWVs and MCq-ROFPRs.

(4) In some GDM problems, decision-makers cannot always subjectively provide expert groups’ weight vectors. In contrast, the judgmental ability of experts can not only provide feedback on the authority and expertise of experts but also objectively indicate the importance of the evaluator in the evaluation process [3]. In this paper, we extend the goal programming model to the overall goal planning model, use it to construct the ideal MCq-ROFPR, and combine the compatibility measures to obtain the objective weight vector of the expert group.

(5) A GDM method under q-ROFPRs is provided by combing the overall goal programming model and the simple q-ROF weighted geometric (Sq-ROFWG) operator. Considering the advantage of FPRs in expressing experts’ preferences for crowdsourcing recommendation influencing factors, the effectiveness and practicality of the developed GDM method are verified by solving crucial factors in crowdsourcing task recommendation.

The rest of this paper is organized as follows: Section 2 analyzes some existing literature and provides its drawbacks. Section 3 introduces some concepts of intuitionistic fuzzy preference relations (IFPRs) and multiplicative consistent IFPRs (MCIFPRs). Then, q-ROFPRs and MCq-ROCPRs are developed in Section 4. Next, Section 5 puts forward a goal programming model under MCq-ROFPRs for obtaining the PWVs of experts. The GDM method combining the group goal programming model and the Sq-ROFWG operator is developed in Section 6. An example of critical factor identification for crowdsourcing task recommendation illustrates the effectiveness of the developed GDM method in Section 7. Finally, some conclusions are made in Section 8.

2. Literature Review

In real-life decision problems, decision-makers need to select the best solution from a set of alternatives or arrive at a ranking of alternatives. A group of experts provides preference information on the alternatives, and then the decision-makers use reasonable decision-making methods to obtain credible and convincing decision results. The expert provides their preference for the alternatives based on their expertise. Preference relationship (PR) is an important tool for experts to describe preference information after comparing alternatives. The traditional PR mainly characterizes the preference degree between alternatives on a scale of 1/9~9 [4] and has been widely used in economic, environmental, and risk management fields [5,6,7,8,9]. At present, the research on multiplicative PRs (MPRs) [10], additive PRs (APRs) [11], fuzzy PRs (FPRs) [12], and linguistic PRs (LPRs) [13] is complete. FPRs use the membership value to characterize the PRs between experts for different solutions. LPRs, on the other hand, described experts’ preference information using a set of linguistic terms. Nowadays, the complexity of real decision-making problems increases with the continuous progress of society. When dealing with time-sensitive and complex decision problems, experts often do not know enough about the evaluated objects or solutions due to their knowledge limitations, resulting in three aspects of their perceptions: positive, negative, and hesitant. In such cases, experts do not necessarily fit their cognitive results when using the above PRs to characterize their preferences for the alternatives. IFSs are an extension of the fuzzy set [14], which has the advantage of containing information on membership, nonmembership, and hesitation at the same time. Thus, Xu [15] proposed the concept of IFPRs by incorporating IFSs into PRs. Compared with MPRs, APRs, FPRs, and LPRs, IFPRs can describe the fuzzy nature of the alternatives in a more delicate and reasonable way [16,17,18].

The concept of q-ROFSs was put forward by Yager [19], which is an extension of IFSs. We see that q-ROFSs continue the advantageous feature that IFSs contain three aspects of information, and the value area and information amount of membership and nonmembership are larger than those of IFSs. It ensures that any IFS is included in the scope of q-ROFS and enhances the flexibility of information representation for decision-makers. The existing research on q-ROFSs mainly includes operation laws, aggregation operators, and decision methods, where operation laws are the basis for calculating operators, operators are used to assemble multiple q-ROFSs with weights, and decision methods are used to solve realistic decision problems. The q-ROF decision methods have been widely applied in different fields. Yager [19] defined some operation laws and ordered weighted aggregation (OWA) operators for q-ROFSs. Liu and Wang [20] developed the q-ROF-weighted average (q-ROFWA) and weighted geometric (q-ROFWG) operators and applied them to multi-attribute decision-making (MADM) problems. Wei et al. [21] investigated some Heronian operators of q-ROFSs and applied them to select enterprise resource planning systems. Peng et al. [22] developed the exponential operation methods of q-ROFSs, and the developed q-ROF MADM methods have advantages in finding the optimal alternative without being counterintuitive. Riaz et al. [23] developed a q-ROF TOPSIS method to solve the transport policy selection problem. Alkan and Kahraman [24] analyzed the measures taken by countries in response to COVID-19, adopted a q-ROF TOPSIS method, and tried to find out the ideal government strategies against the COVID-19 pandemic. Arya and Kumar [25] defined the entropy and divergence measures of q-ROFSs and developed a comprehensive TODIM-VIKOR to measure the uncertainty of medical supplier selection problems.

In the above decision-making problems, using aggregation operators and decision-making methods of q-ROFSs, the decision information is provided with some common features. The evaluators provide attribute values for each alternative. However, in some decision-making problems, due to the limitations of obtaining knowledge information about the relevant attributes of the alternative set, the evaluator may prefer to provide evaluation information in the form of a two-by-two comparison of alternatives. It is called the preference relations (PRs) or comparison matrix. Thus, the experts do not need to determine the preference information of the alternative under each attribute, and the binary relationship obtained by two-by-two comparison appears to be relatively easy and refined [26,27].

Recently, the q-rung orthopair fuzzy information has been combined with PRs and has been used to develop the concepts of q-ROFPRs. Li et al. [28] defined some q-ROFPRs, including consistency, incompleteness, consistent incompleteness, and acceptable incompleteness. Zhang et al. [29,30] defined the q-ROFPRs with additive or multiplicative consistency. Zhang and Chen [31,32] completed the q-ROFPRs with additive or multiplicative consistency and developed some GDM methods with incomplete q-ROFPRs. However, experts’ weights are subjective, and the important measures of experts are not reflected in the above GDM methods. In addition, the group q-ROFPRs aggregated using individual q-ROFPRs may not satisfy multiplicative consistency.

Thus, we developed a GDM method in the q-ROFPR environment to find out the critical factors in crowdsourcing task recommendation.

3. Preliminaries

To express the importance measure between the two alternatives, the MPR is defined as follows:

Definition 1

[4]. Let $X=\left\{X_i\left|i\in \left[n\right]\right.\right\}$ be an alternative set and $\Omega ={\left(a_{ij}\right)}_{n\times n}$ be the MPR, where $a_{ij}$ denotes the preference degree of the alternative $X_i$ over $X_j$ by a scale of 1/9~9, satisfying

$$a_{ij}\in \left[1/9,9\right],a_{ij}=1/a_{ji},i,j\in \left[n\right].$$

(1)

Remark 1.

The symbol $\left[n\right]$ represents $\left[n\right]=\left\{1,2,\dots ,n\right\}$.

Further, Saaty [4] defined the consistency of MPR, which is used to measure the reliability and reasonableness of PRs.

Definition 2

[4]. Let PR $\Omega ={\left(a_{ij}\right)}_{n\times n}$ be an MCPR, then

$$a_{ij}=a_{ik}{a}_{kj},i,j,k\in \left[n\right].$$

(2)

Since $a_{ij}=1/a_{ji}$, the multiplicative consistency condition is $a_{ij}{a}_{jk}{a}_{ki}=a_{ik}{a}_{kj}{a}_{ji},i,j,k\in \left[n\right]$. Saaty [4] provided a sufficient condition for an MCPR $\Omega ={\left(a_{ij}\right)}_{n\times n}$, i.e., there exists a standard weight vector $w={\left(w_1,w_2,\dots ,w_n\right)}^T$, such that $a_{ij}=w_i/w_j$, where ${\displaystyle \sum _{i=1}^n{w}_i}=1,w_i\in \left[0,1\right]$.

Orlovsky [33] first used the membership function in fuzzy sets to express the relative importance among alternatives to deal with decision problems characterized by fuzzy uncertainty information. Further, Tanino [34] refined the definition of FPRs. The concept of fuzzy sets is provided below.

Definition 3

[35]. A fuzzy set $A$ on the universe $X$ is defined as follows:

$$A=\left\{〈x_i,{\mu }_A\left(x_i\right)〉\left|x_i\in X\right.\right\}$$

(3)

where ${\mu }_A:X\to \left[0,1\right]$ is the membership function, and the membership value ${\mu }_A\left(x_i\right)$ of $x_i$ is a fuzzy number (FN), which indicates the membership degree of the element $x_i$ belong to $A$.

Definition 4

[33]. Let $B={\left(b_{ij}\right)}_{n\times n}$ be an FPR on $X$, where $b_{ij}$ is the preference degree of the alternative $X_i$ and $X_j$, then

$$b_{ij}+b_{ji}=1,b_{ij}\in \left[0,1\right],i,j\in \left[n\right].$$

(4)

Definition 5

[33]. If an FPR $B={\left(b_{ij}\right)}_{n\times n}$ is an MCPR, then it satisfies the following conditions:

$$b_{ij}{b}_{jk}{b}_{ki}=b_{ik}{b}_{kj}{b}_{ji},i,j,k\in \left[n\right].$$

(5)

Similar to the PRs of 1/9 to 9 scales, the FPR satisfies the sufficient condition of multiplicative consistency if there is a standard weight vector $\omega ={\left({\omega }_1,{\omega }_2,\dots ,{\omega }_n\right)}^T$ such that

$$b_{ij}=\frac{{\omega }_i}{{\omega }_i+{\omega }_j},i,j,k\in \left[n\right]$$

(6)

The elements of both MPRs and FPRs are values of 1/9~9 or 0~1. In dealing with some decision problems of high complexity and uncertainty, evaluators prefer to express their preferences among alternatives in terms of certainty, negativity, and hesitation. Thus, IFPRs have been introduced [15,36].

Definition 6

[37,38]. An IFS $I$ on $X$ is defined as follows:

$$I=\left\{〈x_i,{\mu }_I\left(x_i\right),{\nu }_I\left(x_i\right)〉\left|x_i\in X\right.\right\}$$

(7)

where ${\mu }_I\left(x_i\right)$ and ${\nu }_I\left(x_i\right)$ denote the membership and nonmembership degrees of the elements $x_i$ belonging to the set $I$, respectively. ${\pi }_I\left(x_i\right)=1-{\mu }_I\left(x_i\right)-{\nu }_I\left(x_i\right)$ is the hesitation degree of the element $x_i$ belonging to the set $I$.

For convenience, $\left({\mu }_I\left(x_i\right),{\nu }_I\left(x_i\right)\right)$ is an intuitionistic fuzzy number (IFN) and is abbreviated as $\beta =\left({\mu }_I,{\nu }_I\right)$, where ${\mu }_I,{\nu }_I\in \left[0,1\right],{\mu }_I+{\nu }_I\le 1$. ${\pi }_I=1-{\mu }_I-{\nu }_I$ is the hesitation degree of $\beta$.

Definition 7

[15]. Let $R_I={\left({\tilde{r}}_{ij}\right)}_{n\times n}$ be an IFPR on the alternative set $X$, where ${\tilde{r}}_{ij}=\left({\mu }_{ij},{\nu }_{ij}\right)$ is an IFN, then

$${\mu }_{ij}={\nu }_{ji},{\nu }_{ij}={\mu }_{ji},{\mu }_{ii}={\nu }_{ii}=0.5,i,j\in \left[n\right]$$

(8)

where ${\mu }_{ij}$ denotes the preference degree of the alternative $X_i$ over $X_j$, ${\nu }_{ij}$ is the preference degree of the alternative $X_j$ over $X_i$, and ${\pi }_{ij}=1-{\mu }_{ij}-{\nu }_{ij}$ is the hesitation degree.

Liao and Xu [36] gave a general definition of MCIFPRs based on the membership values.

Definition 8

[31]. If an IFPR $R_I={\left({\tilde{r}}_{ij}\right)}_{n\times n}$ satisfies

$${\mu }_{ij}{\mu }_{jk}{\mu }_{ki}={\mu }_{kj}{\mu }_{ji}{\mu }_{ik},i,j,k\in \left[n\right]$$

(9)

then $R_I$ is an MCIFPR.

Because ${\mu }_{ij}={\nu }_{ji},{\nu }_{ij}={\mu }_{ji}$, its multiplicative consistency condition is ${\mu }_{ij}{\mu }_{jk}{\mu }_{ki}={\nu }_{ij}{\nu }_{jk}{\nu }_{ki},i,j,k\in \left[n\right]$.

Similar to FPRs, Wang [39] provided a normalized intuitionistic fuzzy weight vector (IFWV) and gave a conversion relation between the weight vector and the multiplicative consistency.

Definition 9

[38]. If a weight vector $\tilde{\omega }={\left({\tilde{\omega }}_1,{\tilde{\omega }}_2,\dots ,{\tilde{\omega }}_n\right)}^T$ satisfies ${\displaystyle \sum _{j\ne i}^n{\omega }_i^{\mu }}\le {\omega }_i^{\nu },{\omega }_i^{\mu }+n-2\ge {\displaystyle \sum _{j\ne i}^n{\omega }_i^{\nu }},i\in \left[n\right]$, then $\tilde{\omega }$ is a normalized IFWV, where ${\tilde{\omega }}_i=\left({\omega }_i^{\mu },{\omega }_i^{\nu }\right)$ is an IFN.

Theorem 1

[36]. If an IFPR $T_I={\left({\tilde{t}}_{ij}\right)}_{n\times n}$ satisfies the following conditions:

$$t_{ij}=\left(t_{ij}^{\mu },t_{ij}^{\nu }\right)=\left\{\begin{array}{l}\left(0.5,0.5\right),i=j\\ \left({\displaystyle \frac{2{\omega }_i^{\mu }}{{\omega }_i^{\mu }-{\omega }_i^{\nu }+{\omega }_j^{\mu }-{\omega }_j^{\nu }+2}},\frac{2{\omega }_j^{\mu }}{{\omega }_i^{\mu }-{\omega }_i^{\nu }+{\omega }_j^{\mu }-{\omega }_j^{\nu }+2}\right),i\ne j\end{array}\right.$$

(10)

then $T_I$ is an MCIFPR, where ${\tilde{\omega }}_i=\left({\omega }_i^{\mu },{\omega }_i^{\nu }\right)$ is the normalized IFWV in Definition 9.

If ${\tilde{\omega }}_i=\left({\omega }_i^{\mu },{\omega }_i^{\nu }\right)$ satisfies ${\omega }_i^{\mu }=1-{\omega }_i^{\nu }$ in Definition 1, then $R_I$ degenerates to an MCIFPR $B={\left(b_{ij}\right)}_{n\times n}={\left(t_{ij}^{\mu }\right)}_{n\times n}$, and $t_{ij}^{\mu }=1-t_{ij}^{\nu }={\omega }_i^{\mu }/\left({\omega }_i^{\mu }+{\omega }_j^{\mu }\right)$.

Yager [19] extended IFSs and introduced the concept of q-ROFSs. The q-ROFSs continue the advantageous features of IFSs and extend the information range consisting of membership and nonmembership values, which ensures that all IFSs are included in the scope of q-ROFSs.

Definition 10

[19]. Let $P$ be a q-ROFS on $X$, and then the q-ROFS is defined as follows:

$$P=\left\{〈x_i,{\rho }_P\left(x_i\right),{\sigma }_P\left(x_i\right)〉\left|x_i\in X\right.\right\}$$

(11)

where ${\rho }_P\left(x_i\right)$ and ${\sigma }_P\left(x_i\right)$ denote the membership and nonmembership degrees of the element $x_i$ belonging to the set $P$, respectively. ${\pi }_P\left(x_i\right)=\sqrt[q]{1-{\rho }_P^q\left(x_i\right)-{\sigma }_P^q\left(x_i\right)}$ is the hesitation degree.

For convenience, $\left({\rho }_P\left(x_i\right),{\sigma }_P\left(x_i\right)\right)$ is a q-ROFN, and the q-ROFN is abbreviated as $p=\left(\rho ,\sigma \right)$, where $\rho ,\sigma \in \left[0,1\right],{\rho }^2+{\sigma }^2\le 1$. ${\pi }_P=\sqrt[q]{1-{\rho }^q-{\sigma }^q}$ is the hesitation degree.

From Definitions 4 and 10, any IFN is a q-ROFN. For any two q-ROFNs $p_i=\left({\rho }_i,{\sigma }_i\right)\left(i=1,2\right)$. Yager [19] provided the partial order relation ${\rho }_1\le {\rho }_2,{\sigma }_1\ge {\sigma }_2\Rightarrow p_1\le p_2$. However, the partial order relation does not distinguish all the q-ROFNs.

Liu and Wang [20] defined the score and accuracy measures of q-ROFNs to sort them.

Definition 11

[20]. Let $p_1=\left({\rho }_1,{\sigma }_1\right)$ and $p_2=\left({\rho }_2,{\sigma }_2\right)$ be two q-ROFNs, then

(1) 

if $s\left(p_1\right)<s\left(p_2\right)$, then $p_1\prec p_2$;

(2) 

if $s\left(p_1\right)=s\left(p_2\right)$ and $h\left(p_1\right)<h\left(p_2\right)$, then $p_1\prec p_2$;

(3) 

if $s\left(p_1\right)=s\left(p_2\right)$ and $h\left(p_1\right)=h\left(p_2\right)$, then $p_1\sim p_2$, namely, ${\rho }_1={\rho }_2$ and ${\sigma }_1={\sigma }_2$;

where $s\left(p_i\right)={\rho }_i^2-{\sigma }_i^2$ and $h\left(p_i\right)={\rho }_i^2+{\sigma }_i^2$ are score and accuracy measures of $p_i\left(i=1,2\right)$, respectively.

According to Definition 11, if $p_1\le p_2$, then $p_1\underset{\_}{\prec }{p}_2$.

4. Multiplicative Consistent q-ROFPRs

From Definition 10, for any q-ROFN $p=\left(\rho ,\sigma \right)$ satisfying ${\rho }^q+{\sigma }^q\le 1$, if $\alpha =\left(\mu ,\nu \right)$ satisfying $\mu ={\rho }^q$,$\nu ={\sigma }^q$, and $\mu +\nu \le 1$, then $\alpha$ is an intuitionistic fuzzy number (IFN) according to Definition 6. Therefore, for a q-ROFN, its membership and nonmembership degrees can be converted into IFNs using $\phi \left(x\right)=x^q$.

The q-ROFSs are introduced into PRs, and the definition of q-ROFPRs is shown as follows:

Definition 12

[30]. Let $R_P={\left({\tilde{p}}_{ij}\right)}_{n\times n}={\left({\rho }_{ij},{\sigma }_{ij}\right)}_{n\times n}$ be a q-ROFPR on $X$, where ${\tilde{p}}_{ij}=\left({\rho }_{ij},{\sigma }_{ij}\right)$ is a q-ROFN, then

$${\rho }_{ij}={\sigma }_{ji},{\sigma }_{ij}={\rho }_{ji},{\rho }_{ii}={\sigma }_{ii}=\sqrt[q]{0.5},i,j\in \left[n\right]$$

(12)

where ${\rho }_{ij}$ denotes the preference degree of the alternative $X_i$ over $X_j$, ${\sigma }_{ij}$ is the preference degree of the alternative $X_j$ to $X_i$, ${\pi }_{ij}=\sqrt[q]{1-{\rho }_{ij}^q-{\sigma }_{ij}^q}$ is the degree of uncertainty and hesitation, and ${\pi }_{ii}=\sqrt[q]{1-{\rho }_{ii}^q-{\sigma }_{ii}^q}=0,i\in \left[n\right]$.

In Definition 12, ${\rho }_{ii}={\sigma }_{ii}=\sqrt[q]{0.5}$ means that the alternative $X_i$ is equally important relative to $X_i$. For IFPRs, ${\mu }_{ii}+{\nu }_{ii}=0.5={\rho }_{ii}^q={\sigma }_{ii}^q$ means that the alternative $X_i$ is equally important relative to $X_i$.

Similar to FPRs and IFPRs, the MCq-ROFPRs are defined as follows:

Definition 13

[30]. If the q-ROFPR $R_P={\left({\tilde{p}}_{ij}\right)}_{n\times n}$ satisfies

$${\rho }_{ij}^q{\rho }_{jk}^q{\rho }_{ki}^q={\rho }_{ik}^q{\rho }_{kj}^q{\rho }_{ji}^q,i,j,k\in \left[n\right]$$

(13)

then $R_P$ is an MCq-ROFPR.

Since ${\rho }_{ij}={\sigma }_{ji},{\sigma }_{ij}={\rho }_{ji},i,j\in \left[n\right]$, then the multiplicative consistency condition is equivalent to ${\rho }_{ij}^q{\rho }_{jk}^q{\rho }_{ki}^q={\sigma }_{ij}^q{\sigma }_{jk}^q{\sigma }_{ki}^q,i,j,k\in \left[n\right]$.

Similar to the intrinsic connection between IFSs and q-ROFSs, Theorem 2 further presents the connection between IFPRs and q-ROFPRs.

Theorem 2.

Let $R_I={\left({\tilde{r}}_{ij}\right)}_{n\times n}={\left({\mu }_{ij},{\nu }_{ij}\right)}_{n\times n}$ be an IFPR and $R_P={\left({\tilde{p}}_{ij}\right)}_{n\times n}={\left({\rho }_{ij},{\sigma }_{ij}\right)}_{n\times n}$ be a q-ROFPR, the function $\phi :\left[0,1\right]\to \left[0,1\right]$ satisfies $\phi \left(x\right)=x^q$, and ${\phi }^{-1}$ is its inverse function.

(1) When $R_P$ is an MCq-ROFPR, if $R_I$ satisfies ${\tilde{r}}_{ij}=\left(\phi \left({\rho }_{ij}\right),\phi \left({\sigma }_{ij}\right)\right)$, then $R_I$ is an MCIFPR.

(2) When $R_I$ is an MCIFPR, if $R_P$ satisfies ${\tilde{p}}_{ij}=\left({\phi }^{-1}\left({\mu }_{ij}\right),{\phi }^{-1}\left({\nu }_{ij}\right)\right)$, then $R_P$ is an MCq-ROFPR.

Proof. 

(1) Since $R_P$ is an MCq-ROFPR, then ${\rho }_{ij}^q{\rho }_{jk}^q{\rho }_{ki}^q={\sigma }_{ij}^q{\sigma }_{jk}^q{\sigma }_{ki}^q,i,j,k\in \left[n\right]$. If ${\tilde{r}}_{ij}=\left(\phi \left({\rho }_{ij}\right),\phi \left({\sigma }_{ij}\right)\right)$, in IFPR $R_I$, then

$${\mu }_{ij}{\mu }_{jk}{\mu }_{ki}=\phi \left({\rho }_{ij}\right)\phi \left({\rho }_{jk}\right)\phi \left({\rho }_{ki}\right)={\rho }_{ij}^q{\rho }_{jk}^q{\rho }_{ki}^q,$$

$${\nu }_{ij}{\nu }_{jk}{\nu }_{ki}=\phi \left({\sigma }_{ij}\right)\phi \left({\sigma }_{jk}\right)\phi \left({\sigma }_{ki}\right)={\sigma }_{ij}^q{\sigma }_{jk}^q{\sigma }_{ki}^q.$$

Therefore, ${\mu }_{ij}{\mu }_{jk}{\mu }_{ki}={\nu }_{ij}{\nu }_{jk}{\nu }_{ki}$, then $R_I$ satisfies consistent consistency.

(2) The proof is similar to (1).

Based on the partial order relations between q-ROFNs, we discuss the properties of q-ROFPRs. □

Property 1.

(Midpoint transferability) Let $R_P={\left({\tilde{p}}_{ij}\right)}_{n\times n}$ be an MCq-ROFPR,

(1) When $\lambda \ge \sqrt[q]{0.5}$, if ${\tilde{p}}_{ij}\ge \left(\lambda ,\sqrt[q]{1-{\lambda }^q}\right)$ and ${\tilde{p}}_{jk}\ge \left(\lambda ,\sqrt[q]{1-{\lambda }^q}\right)$, then ${\sigma }_{ik}={\rho }_{ki}\le \lambda$.

(2) When $\lambda \le \sqrt[q]{0.5}$, if ${\tilde{p}}_{ij}\le \left(\lambda ,\sqrt[q]{1-{\lambda }^q}\right)$ and ${\tilde{p}}_{jk}\le \left(\lambda ,\sqrt[q]{1-{\lambda }^q}\right)$, then ${\sigma }_{ki}={\rho }_{ik}\le \sqrt[q]{1-{\lambda }^q}$.

Proof. 

 

(1) When $\lambda \ge \sqrt[q]{0.5}$, $\sqrt[q]{1-{\lambda }^q}\le \sqrt[q]{0.5}$, then ${\rho }_{ji}\le \sqrt[q]{0.5}\le {\rho }_{ij}$ and ${\rho }_{kj}\le \sqrt[q]{0.5}\le {\rho }_{jk}$. Proving by the converse method, assume that ${\sigma }_{ik}={\rho }_{ki}\ge \lambda \ge \sqrt[q]{0.5}$, then ${\rho }_{ik}^q\le 0.5$. From Definition 13, ${\rho }_{ik}^q=\frac{{\rho }_{ij}^q{\rho }_{jk}^q}{{\rho }_{kj}^q{\rho }_{ji}^q}\cdot {\rho }_{ki}^q\ge 0.5$, contradicts the assumption. Therefore, ${\sigma }_{ik}={\rho }_{ki}\le \lambda$.

(2) The proof is similar to (1). □

Theorem 3.

Property 1(1) is equivalent to Property 1(2).

Proof. 

When $\lambda \le \sqrt[q]{0.5}$, $\sqrt[q]{1-{\lambda }^q}\ge \sqrt[q]{0.5}$, ${\tilde{p}}_{ij}\le \left(\lambda ,\sqrt[q]{1-{\lambda }^q}\right)$, ${\tilde{p}}_{jk}\le \left(\lambda ,\sqrt[q]{1-{\lambda }^q}\right)$, because ${\tilde{p}}_{ij}={\tilde{p}}_{ji}$, ${\tilde{p}}_{ij}\le \left(\lambda ,\sqrt[q]{1-{\lambda }^q}\right)$, ${\tilde{p}}_{jk}\le \left(\lambda ,\sqrt[q]{1-{\lambda }^q}\right)$ $\iff$ ${\tilde{p}}_{ji}\ge \left(\sqrt[q]{1-{\lambda }^q},\lambda \right)$, ${\tilde{p}}_{kj}\ge \left(\sqrt[q]{1-{\lambda }^q},\lambda \right)$.

Assume that $\sqrt[q]{1-{\lambda }^q}=\kappa \ge \sqrt[q]{0.5}$, Property 1(2) can be expressed in the following form: When $\kappa \ge \sqrt[q]{0.5}$, if ${\tilde{p}}_{kj}\ge \left(\kappa ,\sqrt[q]{1-{\kappa }^q}\right)$ and ${\tilde{p}}_{ji}\ge \left(\kappa ,\sqrt[q]{1-{\kappa }^q}\right)$, then ${\sigma }_{ki}={\rho }_{ik}\le \kappa$. Therefore, Property 1(2) is equivalent to Property 1(1). □

Theorem 4.

The equivalence of Property 1 is as follows: ${\rho }_{ij}\ge \lambda \ge \sqrt[q]{0.5}$, ${\rho }_{jk}\ge \lambda \ge \sqrt[q]{0.5}$ $\Rightarrow$ ${\sigma }_{ik}={\rho }_{ki}\le \lambda$.

Proof. 

In fact, ${\tilde{p}}_{ij}=\left({\rho }_{ij},{\sigma }_{ij}\right)$, ${\rho }_{ij}^q+{\sigma }_{ij}^q\le 1$. Therefore, ${\rho }_{ij}\ge \lambda \ge \sqrt[q]{0.5}\iff {\tilde{p}}_{ij}\ge \left(\lambda ,\sqrt[q]{1-{\lambda }^q}\right)$. □

Property 1(1) can be expressed equivalently in the following form: ${\rho }_{ij}\ge \lambda ,{\rho }_{jk}\ge \lambda \Rightarrow {\sigma }_{ik}={\rho }_{ki}\le \lambda$.

When $\lambda =\sqrt[q]{0.5}$, Property 1 degenerates to the following special form:

Property 2.

Let $R_P={\left({\tilde{p}}_{ij}\right)}_{n\times n}={\left({\rho }_{ij},{\sigma }_{ij}\right)}_{n\times n}$ be an MCq-ROFPR, then

$${\tilde{p}}_{ij}\ge \left(\sqrt[q]{0.5},\sqrt[q]{0.5}\right),{\tilde{p}}_{jk}\ge \left(\sqrt[q]{0.5},\sqrt[q]{0.5}\right)\Rightarrow {\sigma }_{ik}={\rho }_{ki}\le \sqrt[q]{0.5}$$

(14)

Property 2 shows that if the alternative $X_i$ is better than $X_j$, and the alternative $X_j$ is better than $X_k$, the preference degree of the alternative $X_k$ over $X_k$ is less than $\sqrt[q]{0.5}$.

In GDM problems, how consistent or divergent between experts or between experts and the expert group is important for the impact of the decision process. Definitions 14 and 15 will give the divergence and compatibility measures between the two PRs.

Definition 14.

Let $R={\left({\tilde{p}}_{ij}\right)}_{n\times n}={\left({\rho }_{ij},{\sigma }_{ij}\right)}_{n\times n}$ and $\overline{R}={\left({\overline{\mu }}_{ik},{\overline{\nu }}_{ik}\right)}_{n\times n}$ be two q-ROFPRs, the divergence measure between $R$ and $\overline{R}$ is defined as follows: $D\left(R,\overline{R}\right)={\left({\displaystyle \prod _{i\ne j}^n\frac{\max \left\{{\rho }_{ij},{\overline{\rho }}_{ij}\right\}}{\min \left\{{\rho }_{ij},{\overline{\rho }}_{ij}\right\}}\cdot \frac{\max \left\{{\sigma }_{ij},{\overline{\sigma }}_{ij}\right\}}{\min \left\{{\sigma }_{ij},{\overline{\sigma }}_{ij}\right\}}}\right)}^{\frac{1}{n\left(n-1\right)}}$.

Since ${\rho }_{ij}={\sigma }_{ji}$ and ${\overline{\rho }}_{ij}={\overline{\sigma }}_{ji}$, therefore,

$$D\left(R,\overline{R}\right)={\left({\displaystyle \prod _{i<j}^n\frac{\max \left\{{\rho }_{ij},{\overline{\rho }}_{ij}\right\}}{\min \left\{{\rho }_{ij},{\overline{\rho }}_{ij}\right\}}\cdot \frac{\max \left\{{\sigma }_{ij},{\overline{\sigma }}_{ij}\right\}}{\min \left\{{\sigma }_{ij},{\overline{\sigma }}_{ij}\right\}}}\right)}^{\frac{1}{n\left(n-1\right)}}$$

(15)

Theorem 5.

For any two q-ROFPRs $R$ and $\overline{R}$, the divergence measure $D\left(R,\overline{R}\right)$ satisfies $D\left(R,\overline{R}\right)\ge 1$, and when $D\left(R,\overline{R}\right)=1$, then $R=\overline{R}$.

Definition 15.

The compatibility measure between any two q-ROFPRs $R$ and $\overline{R}$ is $C\left(R,\overline{R}\right)=1/D\left(R,\overline{R}\right)$.

According to Definition 15 and Theorem 5, Corollary 1 is easily obtained.

Corollary 1.

(1) $0<C\left(R,\overline{R}\right)\le 1$; (2) $C\left(R,\overline{R}\right)=1$, when and only when $R=\overline{R}$; (3) $C\left(R,\overline{R}\right)=C\left(\overline{R},R\right)$.

The compatibility measure can be used to measure the gap between PRs. The higher the compatibility measure, the stronger the consistency degree between PRs. When two PRs are exactly equal, the compatibility measure is 1.

Property 3.

$R={\left({\rho }_{ij},{\sigma }_{ij}\right)}_{n\times n}$, $R^k={\left({\rho }_{ij}^k,{\sigma }_{ij}^k\right)}_{n\times n}$, and $R^l={\left({\rho }_{ij}^l,{\sigma }_{ij}^l\right)}_{n\times n}$ are three q-RPFPRs, if $R^k$ and $R^l$ satisfy ${\rho }_{ij}^l=1/{\rho }_{ij}^k,{\sigma }_{ij}^l=1/{\sigma }_{ij}^k,i<j$, then $C\left(R,R^k\right)=C\left(R,R^l\right)$.

Proof. 

Let ${\rho }_{ij}^k={\lambda }_{ij}^{\rho }{\rho }_{ij},{\sigma }_{ij}^k={\lambda }_{ij}^{\sigma }{\sigma }_{ij}$, then ${\rho }_{ij}^l={\rho }_{ij}/{\lambda }_{ij}^{\rho },{\sigma }_{ij}^l={\sigma }_{ij}/{\lambda }_{ij}^{\sigma }$. According to Definition 14, $D\left(R,R^k\right)=D\left(R,R^l\right)={\left({\displaystyle \prod _{i<j}^n\max \left\{{\lambda }_{ij}^{\rho },1/{\lambda }_{ij}^{\rho }\right\}\cdot \max \left\{{\lambda }_{ij}^{\sigma },1/{\lambda }_{ij}^{\sigma }\right\}}\right)}^{\frac{1}{n\left(n-1\right)}}$. Therefore, $C\left(R,R^k\right)=C\left(R,R^l\right)$. □

5. The Goal Programming Model under MCq-ROFPRs for q-ROFPWVs

This section defines the normalized q-ROFPWVs of MCq-ROFPRs, and the specific formula for q-ROFPWVs to construct MCq-ROFPRs is provided. In decision-making problems, evaluators may not always be able to give MCIFPR when comparing alternatives and thus need to study methods to obtain preference weight vectors corresponding to general PFPR. To this end, based on the conversion formula between PFPWV and MCIFPR, an objective planning model for obtaining the priority weight vector is considered to minimize the difference between PFPR and MCIFPR and minimize the uncertainty of the priority weight vector.

(1) MCq-ROFPRs based on normalized weight vectors

Definition 16.

If the weight vector $\tilde{\omega }={\left({\tilde{\omega }}_1,{\tilde{\omega }}_2,\dots ,{\tilde{\omega }}_n\right)}^T$ satisfies

$${\displaystyle \sum _{j\ne i}^n{\left({\omega }_j^{\rho }\right)}^q}\le {\left({\omega }_i^{\sigma }\right)}^q,{\left({\omega }_i^{\rho }\right)}^q+n-2\ge {\displaystyle \sum _{j\ne i}^n{\left({\omega }_j^{\sigma }\right)}^q},i\in \left[n\right]$$

(16)

then $\tilde{\omega }$ is the normalized q-ROFWV, and ${\tilde{\omega }}_i=\left({\tilde{\omega }}_i^{\rho },{\tilde{\omega }}_i^{\sigma }\right)$ is a q-ROFN.

Definition 17.

The function $g:\left[0,1\right]\times \left[0,1\right]\times \left[0,1\right]\times \left[0,1\right]\to \left[0,1\right]$ satisfies

$$g\left(x_1,x_2,x_3,x_4\right)=x_1^q+\left(1-x_2^q\right)+x_3^q+\left(1-x_4^q\right)$$

(17)

Theorem 6.

Let $\tilde{\omega }={\left({\tilde{\omega }}_1,{\tilde{\omega }}_2,\dots ,{\tilde{\omega }}_n\right)}^T$ be a normalized q-ROFWV, if $T_p={\left({\tilde{t}}_{ij}\right)}_{n\times n}$, it satisfies the following conditions:

$${\tilde{t}}_{ij}=\left(t_{ij}^{\rho },t_{ij}^{\sigma }\right)=\left\{\begin{array}{l}\left(\sqrt[q]{0.5},\sqrt[q]{0.5}\right),i=j\\ \left(\sqrt[q]{{\displaystyle \frac{2{\left({\omega }_i^{\rho }\right)}^q}{g\left({\omega }_i^{\rho },{\omega }_i^{\sigma },{\omega }_j^{\rho },{\omega }_j^{\sigma }\right)}}},\sqrt[q]{\frac{2{\left({\omega }_j^{\rho }\right)}^q}{g\left({\omega }_i^{\rho },{\omega }_i^{\sigma },{\omega }_j^{\rho },{\omega }_j^{\sigma }\right)}}\right),i\ne j\end{array}\right.$$

(18)

Then $T_p$ is an MCq-ROFPR.

Proof. 

First, prove that $T_p$ is a q-ROFPR, i.e., prove that ${\tilde{t}}_{ij}$ is a q-ROFN. When $i=j$, it obviously holds. When $i\ne j$, because ${\left({\omega }_i^{\rho }\right)}^q\le 1-{\left({\omega }_i^{\sigma }\right)}^q,{\left({\omega }_j^{\rho }\right)}^q\le 1-{\left({\omega }_j^{\sigma }\right)}^q$, according to Definition 17, then

$${\left(t_{ij}^{\rho }\right)}^q+{\left(t_{ij}^{\sigma }\right)}^q=\frac{2\left({\left({\omega }_i^{\rho }\right)}^q+{\left({\omega }_j^{\rho }\right)}^q\right)}{{\left({\omega }_i^{\rho }\right)}^q+1-{\left({\omega }_i^{\sigma }\right)}^q+{\left({\omega }_j^{\rho }\right)}^q+1-{\left({\omega }_j^{\sigma }\right)}^q}\le 1.$$

Therefore, ${\tilde{t}}_{ij}$ is a q-ROFN. Then $T_p$ is a q-ROFPR. Then, it should prove that $T_p$ satisfies the multiplicative consistency.

$${\left(t_{ij}^{\rho }{t}_{jk}^{\rho }{t}_{ki}^{\rho }\right)}^q=\frac{2{\left({\omega }_i^{\rho }{\omega }_j^{\rho }{\omega }_k^{\rho }\right)}^q}{g\left({\omega }_i^{\rho },{\omega }_i^{\sigma },{\omega }_j^{\rho },{\omega }_j^{\sigma }\right)g\left({\omega }_j^{\rho },{\omega }_j^{\sigma },{\omega }_k^{\rho },{\omega }_k^{\sigma }\right)g\left({\omega }_k^{\rho },{\omega }_k^{\sigma },{\omega }_i^{\rho },{\omega }_i^{\sigma }\right)}={\left(t_{ij}^{\sigma }{t}_{jk}^{\sigma }{t}_{ki}^{\sigma }\right)}^q.$$

□

Corollary 2.

For a q-ROFPR $R_P={\left({\tilde{p}}_{ij}\right)}_{n\times n}$, if there exists a normalized q-ROFWV $\tilde{\omega }={\left({\tilde{\omega }}_1,{\tilde{\omega }}_2,\dots ,{\tilde{\omega }}_n\right)}^T$ satisfying

$${\tilde{p}}_{ij}=\left({\rho }_{ij},{\sigma }_{ij}\right)=\left\{\begin{array}{l}\left(\sqrt[q]{0.5},\sqrt[q]{0.5}\right),i=j\\ \left(\sqrt[q]{{\displaystyle \frac{2{\left({\omega }_i^{\rho }\right)}^q}{g\left({\omega }_i^{\rho },{\omega }_i^{\sigma },{\omega }_j^{\rho },{\omega }_j^{\sigma }\right)}}},\sqrt[q]{\frac{2{\left({\omega }_j^{\rho }\right)}^q}{g\left({\omega }_i^{\rho },{\omega }_i^{\sigma },{\omega }_j^{\rho },{\omega }_j^{\sigma }\right)}}\right),i\ne j\end{array}\right.$$

(19)

then $R_P$ is an MCq-ROFPR.

Theorem 7.

Let $R_P={\left({\tilde{p}}_{ij}\right)}_{n\times n}$ be an MCq-ROFPR, and $\tilde{\omega }={\left({\tilde{\omega }}_1,{\tilde{\omega }}_2,\dots ,{\tilde{\omega }}_n\right)}^T$$\left({\tilde{\omega }}_i=\left({\omega }_i^{\rho },{\omega }_i^{\sigma }\right)\right)$ be the normalized q-ROFWV of $R_P$, if the IFWV $\tilde{\lambda }={\left({\tilde{\lambda }}_1,{\tilde{\lambda }}_2,\dots ,{\tilde{\lambda }}_n\right)}^T$ satisfies ${\tilde{\lambda }}_i=\left({\lambda }_i^{\rho },{\lambda }_i^{\sigma }\right)=\left({\left({\omega }_i^{\rho }\right)}^q,{\left({\omega }_i^{\sigma }\right)}^q\right)$, then $\tilde{\lambda }$ is a normalized IFWV.

(2) Priority weight vector based on the goal programming model

For a q-ROFPR $R_P={\left({\tilde{p}}_{ij}\right)}_{n\times n}$, if there exists a standardized q-ROFWV $\tilde{\omega }={\left({\tilde{\omega }}_1,{\tilde{\omega }}_2,\dots ,{\tilde{\omega }}_n\right)}^T$, then $R_P$ is an MCq-ROFPR. However, in some realistic decision problems, experts may not be able to propose an MCq-ROFPR. To obtain the standardized weight vector of $R_P$, we propose a goal programming model with the objective of minimizing the deviation between $R_P$ and $T_P$ and minimizing the hesitation of $T_P$. Finally, the corresponding standardized weight vector of $R_P$ is obtained [32].

From Theorem 6, an MCq-ROFPR $T_p={\left({\tilde{t}}_{ij}\right)}_{n\times n}$ can be constructed based on the standardized q-ROFWV $\tilde{\omega }$. The membership deviation and nonmembership deviation between $R_P$ and $T_P$ are ${\delta }_{ij}=\frac{2{\left({\omega }_i^{\rho }\right)}^q}{g\left({\omega }_i^{\rho },{\omega }_i^{\sigma },{\omega }_j^{\rho },{\omega }_j^{\sigma }\right)}-{\rho }_{ij}^q$, ${\gamma }_{ij}=\frac{2{\left({\omega }_j^{\rho }\right)}^q}{g\left({\omega }_i^{\rho },{\omega }_i^{\sigma },{\omega }_j^{\rho },{\omega }_j^{\sigma }\right)}-{\sigma }_{ij}^q$.

The smaller the membership deviation $\left|{\delta }_{ij}\right|$ and the nonmembership deviation $\left|{\gamma }_{ij}\right|$, the higher the consistency degree between $R_P$ and the MCq-ROFPR $T_P$.

In addition to considering the deviation values, the hesitancy of the elements of the MCq-ROFPR $T_P$ is ${\left({\pi }_{ij}\right)}^q=1-\frac{2\left({\left({\omega }_i^{\rho }\right)}^q+{\left({\omega }_j^{\rho }\right)}^q\right)}{g\left({\omega }_i^{\rho },{\omega }_i^{\sigma },{\omega }_j^{\rho },{\omega }_j^{\sigma }\right)}$.

For $0\le x<y\le 1$, the increase or decrease in the value $1-x/y$ is consistent with that of $y-x$. Therefore, ${\eta }_{ij}=g\left({\omega }_i^{\rho },{\omega }_i^{\sigma },{\omega }_j^{\rho },{\omega }_j^{\sigma }\right)-2\left({\left({\omega }_i^{\rho }\right)}^q+{\left({\omega }_j^{\rho }\right)}^q\right)$ should be considered for the hesitation of $T_P$. Furthermore, since

$$\begin{array}{l}\frac{1}{n^2}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{\eta }_{ij}}}\\ =\frac{1}{n^2}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\left({\left({\omega }_i^{\rho }\right)}^q-{\left({\omega }_i^{\sigma }\right)}^q+{\left({\omega }_j^{\rho }\right)}^q-{\left({\omega }_j^{\sigma }\right)}^q+2\right)-2\left({\left({\omega }_i^{\rho }\right)}^q+{\left({\omega }_j^{\rho }\right)}^q\right)}}\\ =\frac{1}{n^2}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n\left({\left(\tau \left({\tilde{\omega }}_i\right)\right)}^q+{\left(\tau \left({\tilde{\omega }}_j\right)\right)}^q\right)}}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left(\tau \left({\tilde{\omega }}_i\right)\right)}^q}=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left(1-{\left({\omega }_i^{\rho }\right)}^q-{\left({\omega }_i^{\sigma }\right)}^q\right)}\end{array},$$

and the hesitation value ${\eta }_{ij}$ is less than or equal to the hesitancy of the upper triangular element of $R_P={\left({\tilde{p}}_{ij}\right)}_{n\times n}$

$$\frac{1}{n}{\displaystyle \sum _{i=1}^n\left(1-{\left({\omega }_i^{\rho }\right)}^q-{\left({\omega }_i^{\sigma }\right)}^q\right)}\le \frac{2}{n\left(n-1\right)}{\displaystyle \sum _{1\le i<j\le n}^{}\left(1-{\rho }_{ij}^q-{\sigma }_{ij}^q\right)}$$

(20)

The lower the hesitation, the stronger the confidence of $T_P$.

Based on the above analysis, the following model (21) is constructed to minimize the deviation and minimize the hesitation:

$$\min T=\frac{{\displaystyle \sum _{i=1}^n\left(1-{\left({\omega }_i^{\rho }\right)}^q-{\left({\omega }_i^{\sigma }\right)}^q\right)}}{n}+{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j\ne i}^n\left(\left|{\delta }_{ij}\right|+\left|{\gamma }_{ij}\right|\right)}}$$

$$s.t.\left\{\begin{array}{c}2{\left({\omega }_i^{\rho }\right)}^q-g\left({\omega }_i^{\rho },{\omega }_i^{\sigma },{\omega }_j^{\rho },{\omega }_j^{\sigma }\right)\left({\rho }_{ij}^q+{\delta }_{ij}\right)=0,\\ 2{\left({\omega }_j^{\rho }\right)}^q-g\left({\omega }_i^{\rho },{\omega }_i^{\sigma },{\omega }_j^{\rho },{\omega }_j^{\sigma }\right)\left({\sigma }_{ij}^q+{\gamma }_{ij}\right)=0,\\ 0\le {\omega }_i^{\rho },{\omega }_i^{\sigma }\le 1,{\left({\omega }_i^{\rho }\right)}^q+{\left({\omega }_i^{\sigma }\right)}^q\le 1,\\ {\displaystyle \sum _{j\ne i}^n{\left({\omega }_j^{\rho }\right)}^q}\le {\left({\omega }_i^{\sigma }\right)}^q,{\left({\omega }_i^{\rho }\right)}^q+n-2\ge {\displaystyle \sum _{j\ne i}^n{\left({\omega }_j^{\sigma }\right)}^q}\\ \left(n-1\right){\displaystyle \sum _{i=1}^n\left(1-{\left({\omega }_i^{\rho }\right)}^q-{\left({\omega }_i^{\sigma }\right)}^q\right)}\le 2{\displaystyle \sum _{1\le i<j\le n}\left(1-{\rho }_{ij}^q-{\sigma }_{ij}^q\right)}\\ i,j\in \left[n\right],j\ne i\end{array}\right.$$

(21)

According to Definition 12, ${\rho }_{ij}={\sigma }_{ji},{\sigma }_{ij}={\rho }_{ji}\Rightarrow {\delta }_{ij}={\gamma }_{ji},i,j\in \left[n\right]$. Therefore, the model (21) only needs to consider the upper triangular element of the PR: $i,j\in J,J=\left\{\left(i,j\right):1\le i<j\le n\right\}$. Assume that

$${\delta }_{ij}^{+}=\frac{\left|{\delta }_{ij}\right|+{\delta }_{ij}}{2},{\delta }_{ij}^{-}=\frac{\left|{\delta }_{ij}\right|-{\delta }_{ij}}{2},{\gamma }_{ij}^{+}=\frac{\left|{\gamma }_{ij}\right|+{\gamma }_{ij}}{2},{\gamma }_{ij}^{-}=\frac{\left|{\gamma }_{ij}\right|-{\gamma }_{ij}}{2},i,j\in J$$

Then $\left|{\delta }_{ij}\right|={\delta }_{ij}^{+}+{\delta }_{ij}^{-},{\delta }_{ij}={\delta }_{ij}^{+}-{\delta }_{ij}^{-},\left|{\gamma }_{ij}\right|={\gamma }_{ij}^{+}+{\gamma }_{ij}^{-},{\gamma }_{ij}={\gamma }_{ij}^{+}-{\gamma }_{ij}^{-},{\delta }_{ij}^{+}\times {\delta }_{ij}^{-}=0,{\gamma }_{ij}^{+}\times {\gamma }_{ij}^{-}=0$.

Therefore, model (21) can be replaced with the following model (22):

$$\min T=\frac{{\displaystyle \sum _{i=1}^n\left(1-{\left({\omega }_i^{\rho }\right)}^q-{\left({\omega }_i^{\sigma }\right)}^q\right)}}{n}+{\displaystyle \sum _{1\le i<j\le n}\left({\delta }_{ij}^{+}+{\delta }_{ij}^{-}+{\gamma }_{ij}^{+}+{\gamma }_{ij}^{-}\right)}$$

$$s.t.\left\{\begin{array}{c}2{\left({\omega }_i^{\rho }\right)}^q-g\left({\omega }_i^{\rho },{\omega }_i^{\sigma },{\omega }_j^{\rho },{\omega }_j^{\sigma }\right)\left({\rho }_{ij}^q+{\delta }_{ij}^{+}-{\delta }_{ij}^{-}\right)=0,\\ 2{\left({\omega }_j^{\rho }\right)}^q-g\left({\omega }_i^{\rho },{\omega }_i^{\sigma },{\omega }_j^{\rho },{\omega }_j^{\sigma }\right)\left({\sigma }_{ij}^q+{\gamma }_{ij}^{+}-{\gamma }_{ij}^{-}\right)=0,\\ 0\le {\omega }_i^{\rho },{\omega }_i^{\sigma }\le 1,{\left({\omega }_i^{\rho }\right)}^q+{\left({\omega }_i^{\sigma }\right)}^q\le 1,\\ {\displaystyle \sum _{j\ne i}^n{\left({\omega }_j^{\rho }\right)}^q}\le {\left({\omega }_i^{\sigma }\right)}^q,{\left({\omega }_i^{\rho }\right)}^q+n-2\ge {\displaystyle \sum _{j\ne i}^n{\left({\omega }_j^{\sigma }\right)}^q}\\ \left(n-1\right){\displaystyle \sum _{i=1}^n\left(1-{\left({\omega }_i^{\rho }\right)}^q-{\left({\omega }_i^{\sigma }\right)}^q\right)}\le 2{\displaystyle \sum _{1\le i<j\le n}\left(1-{\rho }_{ij}^q-{\sigma }_{ij}^q\right)}\\ {\delta }_{ij}^{+},{\delta }_{ij}^{-},{\gamma }_{ij}^{+},{\gamma }_{ij}^{-}\ge 0,{\delta }_{ij}^{+}\times {\delta }_{ij}^{-}=0,{\gamma }_{ij}^{+}\times {\gamma }_{ij}^{-}=0\end{array}\right.$$

(22)

The normalized weight vector of $R_P$ can be obtained by solving the model (22): $\tilde{\omega }={\left({\tilde{\omega }}_1,{\tilde{\omega }}_2,\dots ,{\tilde{\omega }}_n\right)}^T$.

6. Group Decision-Making Method Based on the Group Goal Programming Model and the Sq-ROFWG Operator

6.1. Problem Description

In the GDM problem under q-ROFPRs with unknown expert weights, the alternative set is $X=\left\{X_i\left|i\in \left[n\right]\right.\right\}$, and the expert group is $E=\left\{e_k\left|k\in \left[m\right]\right.\right\}$. Based on the alternative information provided by the decision-makers, the expert $e_k\left(k\in \left[m\right]\right)$ makes a two-by-two comparison of the alternatives $X_i\left(i\in \left[n\right]\right)$ and $X_j\left(j\in \left[n\right]\right)$, provides the q-ROFPR $R_P^k={\left({\tilde{p}}_{ij}^k\right)}_{n\times n}\left(k\in \left[m\right]\right)$, where ${\tilde{p}}_{ij}^k=\left({\rho }_{ij}^k,{\sigma }_{ij}^k\right)\left(i,j\in \left[n\right];k\in \left[m\right]\right)$ is a q-ROFN. In order to obtain the ranking of the alternatives in $X$, the normalized q-ROFWV ${\tilde{\omega }}^{*}={\left({\tilde{\omega }}_1^{*},{\tilde{\omega }}_2^{*},\dots ,{\tilde{\omega }}_n^{*}\right)}^T$ is obtained. Thus, we propose a GDM method based on the Sq-ROFWG operator and goal programming model, apply it to solve the q-ROFWV, and finally obtain the optimal alternative.

6.2. Expert Weight Calculation

To solve the GDM problem, we need to determine the weight vector of the expert group first. Thus, the above individual goal programming model should be extended to a GDM method, and the overall normalized q-ROFWV $\tilde{\omega }={\left({\tilde{\omega }}_1,{\tilde{\omega }}_2,\dots ,{\tilde{\omega }}_n\right)}^T$ is obtained to construct an ideal MCq-ROFPR $\overline{R}={\left({\rho }_{ik},{\sigma }_{ik}\right)}_{n\times n}$. Then, we develop the compatibility measure between the individual q-ROFPR $R^l={\left({\tilde{p}}_{ij}^l\right)}_{n\times n}={\left({\rho }_{ij}^l,{\sigma }_{ij}^l\right)}_{n\times n}$ and the ideal MCq-ROFPR $R^l={\left({\tilde{p}}_{ij}^l\right)}_{n\times n}={\left({\rho }_{ij}^l,{\sigma }_{ij}^l\right)}_{n\times n}$ to obtain the weight vector of experts.

The consistency of each element of the ideal MCq-ROFPR $\overline{R}$ with the corresponding element of the individual q-ROFPR given by each expert should be high, i.e., the deviation should be minimized. Next, the overall goal programming model is constructed to obtain the ideal MCq-ROFPR $\overline{R}$. The standardized weight vector of $\overline{R}$ is $\tilde{\omega }={\left({\tilde{\omega }}_1,{\tilde{\omega }}_2,\dots ,{\tilde{\omega }}_n\right)}^T$. Inspired by the models (21) and (22), an overall programming model with the objective of minimizing the deviation among $\overline{R}$ and all individuals $R^l$ and minimizing the hesitation of the weight vector $\tilde{\omega }$ is constructed. In contrast to model (22), if the overall deviation is considered, only the relevant variables and objectives of the model (22) need to be adjusted, and the detailed adjustments are as follows:

$$\min T=\frac{{\displaystyle \sum _{i=1}^n\left(1-{\left({\tilde{\omega }}_i^{\rho }\right)}^q-{\left({\tilde{\omega }}_i^{\sigma }\right)}^q\right)}}{n}+{\displaystyle \sum _{l=1}^s{\displaystyle \sum _{1\le i<j\le n}\frac{\left({\delta }_{ij}^{+}+{\delta }_{ij}^{-}+{\gamma }_{ij}^{+}+{\gamma }_{ij}^{-}\right)}{s}}}$$

$${\omega }_i,{\eta }_{ij},{\rho }_{ij}^2,{\sigma }_{ij}^2,{\delta }_{ij}^{+},{\delta }_{ij}^{-},{\gamma }_{ij}^{+},{\gamma }_{ij}^{-}\to {\tilde{\omega }}_i,{\overline{\eta }}_{ij},{\left({\rho }_{ij}^l\right)}^q,{\left({\sigma }_{ij}^l\right)}^q,{\delta }_{ij}^{l+},{\delta }_{ij}^{l-},{\gamma }_{ij}^{l+},{\gamma }_{ij}^{l-},\begin{array}{c}\end{array}l\in \left[s\right]$$

Furthermore, the overall goal programming model (23) is constructed as follows:

$$\min T=\frac{{\displaystyle \sum _{i=1}^n\left(1-{\left({\tilde{\omega }}_i^{\rho }\right)}^q-{\left({\tilde{\omega }}_i^{\sigma }\right)}^q\right)}}{n}+{\displaystyle \sum _{l=1}^s{\displaystyle \sum _{1\le i<j\le n}\frac{\left({\delta }_{ij}^{l+}+{\delta }_{ij}^{l-}+{\gamma }_{ij}^{l+}+{\gamma }_{ij}^{l-}\right)}{s}}}$$

$$s.t.\left\{\begin{array}{c}2{\left({\tilde{\omega }}_i^{\rho }\right)}^q-g\left({\tilde{\omega }}_i^{\rho },{\tilde{\omega }}_i^{\sigma },{\tilde{\omega }}_j^{\rho },{\tilde{\omega }}_j^{\sigma }\right)\left({\left({\rho }_{ij}^l\right)}^q+{\delta }_{ij}^{l+}-{\delta }_{ij}^{l-}\right)=0,\\ 2{\left({\tilde{\omega }}_j^{\rho }\right)}^q-g\left({\tilde{\omega }}_i^{\rho },{\tilde{\omega }}_i^{\sigma },{\tilde{\omega }}_j^{\rho },{\tilde{\omega }}_j^{\sigma }\right)\left({\left({\sigma }_{ij}^l\right)}^q+{\gamma }_{ij}^{l+}-{\gamma }_{ij}^{l-}\right)=0,\\ 0\le {\tilde{\omega }}_i^{\rho },{\tilde{\omega }}_i^{\sigma }\le 1,{\left({\tilde{\omega }}_i^{\rho }\right)}^q+{\left({\tilde{\omega }}_i^{\sigma }\right)}^q\le 1,\\ {\displaystyle \sum _{j\ne i}^n{\left({\tilde{\omega }}_j^{\rho }\right)}^q}\le {\left({\tilde{\omega }}_i^{\sigma }\right)}^q,{\left({\tilde{\omega }}_i^{\rho }\right)}^q+n-2\ge {\displaystyle \sum _{j\ne i}^n{\left({\tilde{\omega }}_j^{\sigma }\right)}^q}\\ s\left(n-1\right){\displaystyle \sum _{i=1}^n\left(1-{\left({\tilde{\omega }}_i^{\rho }\right)}^q-{\left({\tilde{\omega }}_i^{\sigma }\right)}^q\right)}\le 2{\displaystyle \sum _{1\le i<j\le n}\left(1-{\displaystyle \sum _{l=1}^s\left({\left({\rho }_{ij}^l\right)}^q+{\left({\sigma }_{ij}^l\right)}^q\right)}\right)}\\ {\delta }_{ij}^{l+},{\delta }_{ij}^{l-},{\gamma }_{ij}^{l+},{\gamma }_{ij}^{l-}\ge 0,{\delta }_{ij}^{l+}\times {\delta }_{ij}^{l-}=0,{\gamma }_{ij}^{l+}\times {\gamma }_{ij}^{l-}=0\end{array}\right.$$

(23)

Because $2{\left({\tilde{\omega }}_i^{\rho }\right)}^q-g\left({\tilde{\omega }}_i^{\rho },{\tilde{\omega }}_i^{\sigma },{\tilde{\omega }}_j^{\rho },{\tilde{\omega }}_j^{\sigma }\right)\left({\left({\rho }_{ij}^l\right)}^q+{\delta }_{ij}^{l+}-{\delta }_{ij}^{l-}\right)=0,\left(i,j\right)\in J_l,l\in \left[s\right]$ is equivalent to

$$2{\left({\tilde{\omega }}_i^{\rho }\right)}^q-g\left({\tilde{\omega }}_i^{\rho },{\tilde{\omega }}_i^{\sigma },{\tilde{\omega }}_j^{\rho },{\tilde{\omega }}_j^{\sigma }\right){\displaystyle \sum _{l=1}^s\frac{{\left({\rho }_{ij}^l\right)}^q+{\delta }_{ij}^{l+}-{\delta }_{ij}^{l-}}{s}}=0,\left(i,j\right)\in J.$$

Similarly, $2{\left({\tilde{\omega }}_j^{\rho }\right)}^q-g\left({\tilde{\omega }}_i^{\rho },{\tilde{\omega }}_i^{\sigma },{\tilde{\omega }}_j^{\rho },{\tilde{\omega }}_j^{\sigma }\right)\left({\left({\sigma }_{ij}^l\right)}^q+{\gamma }_{ij}^{l+}-{\gamma }_{ij}^{l-}\right)=0,\left(i,j\right)\in J_l,l\in \left[s\right]$ is equivalent to

$$2{\left({\tilde{\omega }}_j^{\rho }\right)}^q-g\left({\tilde{\omega }}_i^{\rho },{\tilde{\omega }}_i^{\sigma },{\tilde{\omega }}_j^{\rho },{\tilde{\omega }}_j^{\sigma }\right){\displaystyle \sum _{l=1}^s\frac{{\left({\sigma }_{ij}^l\right)}^q+{\gamma }_{ij}^{l+}-{\gamma }_{ij}^{l-}}{s}}=0,\left(i,j\right)\in J.$$

And ${\overline{\delta }}_{ij}^{l+}=\frac{{\displaystyle \sum _{l=1}^s{\delta }_{ij}^{l+}}}{s},{\overline{\delta }}_{ij}^{l-}=\frac{{\displaystyle \sum _{l=1}^s{\delta }_{ij}^{l-}}}{s},{\overline{\gamma }}_{ij}^{l+}=\frac{{\displaystyle \sum _{l=1}^s{\gamma }_{ij}^{l+}}}{s},{\overline{\gamma }}_{ij}^{l-}=\frac{{\displaystyle \sum _{l=1}^s{\gamma }_{ij}^{l-}}}{s}$.

Based on the above analysis, model (23) can be converted into the model (24).

$$\min J=\frac{{\displaystyle \sum _{i=1}^n\left(1-{\left({\tilde{\omega }}_i^{\rho }\right)}^q-{\left({\tilde{\omega }}_i^{\sigma }\right)}^q\right)}}{n}+{\displaystyle \sum _{1\le i<j\le n}\left({\overline{\delta }}_{ij}^{l+}+{\overline{\delta }}_{ij}^{l-}+{\overline{\gamma }}_{ij}^{l+}+{\overline{\gamma }}_{ij}^{l-}\right)}$$

$$s.t.\left\{\begin{array}{c}2{\left({\tilde{\omega }}_i^{\rho }\right)}^q-g\left({\tilde{\omega }}_i^{\rho },{\tilde{\omega }}_i^{\sigma },{\tilde{\omega }}_j^{\rho },{\tilde{\omega }}_j^{\sigma }\right)\left({\displaystyle \sum _{l=1}^s{\left({\rho }_{ij}^l\right)}^q/s}\right)-{\delta }_{ij}^{l+}+{\delta }_{ij}^{l-}=0,\\ 2{\left({\tilde{\omega }}_j^{\rho }\right)}^q-g\left({\tilde{\omega }}_i^{\rho },{\tilde{\omega }}_i^{\sigma },{\tilde{\omega }}_j^{\rho },{\tilde{\omega }}_j^{\sigma }\right)\left({\displaystyle \sum _{l=1}^s{\left({\sigma }_{ij}^l\right)}^q}/s\right)-{\gamma }_{ij}^{l+}+{\gamma }_{ij}^{l-}=0,\\ 0\le {\tilde{\omega }}_i^{\rho },{\tilde{\omega }}_i^{\sigma }\le 1,{\left({\tilde{\omega }}_i^{\rho }\right)}^q+{\left({\tilde{\omega }}_i^{\sigma }\right)}^q\le 1,\\ {\displaystyle \sum _{j\ne i}^n{\left({\tilde{\omega }}_j^{\rho }\right)}^q}\le {\left({\tilde{\omega }}_i^{\sigma }\right)}^q,{\left({\tilde{\omega }}_i^{\rho }\right)}^q+n-2\ge {\displaystyle \sum _{j\ne i}^n{\left({\tilde{\omega }}_j^{\sigma }\right)}^q}\\ s\left(n-1\right){\displaystyle \sum _{i=1}^n\left(1-{\left({\tilde{\omega }}_i^{\rho }\right)}^q-{\left({\tilde{\omega }}_i^{\sigma }\right)}^q\right)}\le 2{\displaystyle \sum _{1\le i<j\le n}{\displaystyle \sum _{l=1}^s\left(1-\left({\left({\rho }_{ij}^l\right)}^q+{\left({\sigma }_{ij}^l\right)}^q\right)\right)}}\\ {\overline{\delta }}_{ij}^{l+},{\overline{\delta }}_{ij}^{l-},{\overline{\gamma }}_{ij}^{l+},{\overline{\gamma }}_{ij}^{l-}\ge 0,{\overline{\delta }}_{ij}^{l+}\times {\overline{\delta }}_{ij}^{l-}=0,{\overline{\gamma }}_{ij}^{l+}\times {\overline{\gamma }}_{ij}^{l-}=0\end{array}\right..$$

(24)

The model (24) is solved to obtain the overall normalized q-ROFWV $\tilde{\omega }={\left({\tilde{\omega }}_1,{\tilde{\omega }}_2,\dots ,{\tilde{\omega }}_n\right)}^T$$\left({\overline{\omega }}_i=\left({\overline{\omega }}_i^{\rho },{\overline{\omega }}_i^{\sigma }\right)\right)$, and the ideal q-ROFPR $\overline{R}={\left({\overline{\rho }}_{ij},{\overline{\sigma }}_{ij}\right)}_{n\times n}$ is constructed as

$$\overline{R}={\left({\overline{\rho }}_{ij},{\overline{\sigma }}_{ij}\right)}_{n\times n}=\left\{\begin{array}{l}\left(\sqrt[q]{0.5},\sqrt[q]{0.5}\right),i=j\\ \left(\sqrt[q]{{\displaystyle \frac{2{\left({\overline{\omega }}_i^{\rho }\right)}^q}{g\left({\tilde{\omega }}_i^{\rho },{\tilde{\omega }}_i^{\sigma },{\tilde{\omega }}_j^{\rho },{\tilde{\omega }}_j^{\sigma }\right)}}},\sqrt[q]{\frac{2{\left({\overline{\omega }}_j^{\rho }\right)}^q}{g\left({\tilde{\omega }}_i^{\rho },{\tilde{\omega }}_i^{\sigma },{\tilde{\omega }}_j^{\rho },{\tilde{\omega }}_j^{\sigma }\right)}}\right),i\ne j\end{array}\right..$$

(25)

The ideal MCq-ROFPR $\overline{R}={\left({\overline{\rho }}_{ij},{\overline{\sigma }}_{ij}\right)}_{n\times n}$ is constructed based on the overall goal programming model with the objective of minimizing the hesitancy of $\overline{R}$ and the deviation between $\overline{R}$ and all individuals $R^l$. Therefore, the compatibility measure between the individual PRs $R^l$ and the ideal $\overline{R}$ reflects the consistency degree between the expert and the group opinion and examines the expert’s judgment level. Therefore, the compatibility measure between individual PRs $R^l$ and ideal PR $\overline{R}$ is used to obtain the expert weights $\lambda ={\left({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_s\right)}^T$.

$${\lambda }_l=\frac{C\left(R^l,\overline{R}\right)}{{\displaystyle \sum _{l=1}^{s}C\left(R^l,\overline{R}\right)}},l\in \left[s\right]$$

(26)

6.3. Aggregation of Individual q-ROFPRs Using the Sq-ROFWG Operator

After obtaining the weight vectors of the expert group, using a reasonable q-ROF operator to aggregate the individual q-ROFPRs into a comprehensive q-ROFPR is one of the important steps to solve the GDM problem. Next, the aggregation operators are analyzed as follows:

Definition 18.

Let ${\alpha }_i=\left({\rho }_i,{\sigma }_i\right)\left(i\in \left[n\right]\right)$ be a set of q-ROFNs, whose weight vector is $\omega ={\left({\omega }_1,{\omega }_2,\dots ,{\omega }_n\right)}^T$, then

(1) The q-rung orthopair fuzzy weighted geometric (q-ROFWG) operator [20] is defined as follows:

$$q-ROFWG\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)=\left({\displaystyle \prod _{i=1}^n{\rho }_i^{{\omega }_i}},\sqrt[q]{1-{\displaystyle \prod _{i=1}^n{\left(1-{\sigma }_i^q\right)}^{{\omega }_i}}}\right)$$

(27)

(2) The symmetric q-rung orthopair fuzzy weighted geometric (SYq-ROFWG) operator is defined as follows:

$$SYq-ROFWG\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)=\left(\sqrt[q]{\frac{{\displaystyle \prod _{i=1}^n{\left({\rho }_i^q\right)}^{{\omega }_i}}}{{\displaystyle \prod _{i=1}^n{\left({\rho }_i^q\right)}^{{\omega }_i}}+{\displaystyle \prod _{i=1}^n{\left(1-{\rho }_i^q\right)}^{{\omega }_i}}}},\sqrt[q]{\frac{{\displaystyle \prod _{i=1}^n{\left({\sigma }_i^q\right)}^{{\omega }_i}}}{{\displaystyle \prod _{i=1}^n{\left({\sigma }_i^q\right)}^{{\omega }_i}}+{\displaystyle \prod _{i=1}^n{\left(1-{\sigma }_i^q\right)}^{{\omega }_i}}}}\right)$$

(28)

Let $R^l={\left({\tilde{p}}_{ij}^l\right)}_{n\times n}={\left({\rho }_{ij}^l,{\sigma }_{ij}^l\right)}_{n\times n}$ be the q-ROFPR provided by the expert group $e_l\left(l=1,2,\dots ,s\right)$, and ${\lambda }_l\left(l=1,2,\dots ,s\right)$ be the weights of $R^l$. Assume that all $R^l$ are MCq-ROFPRs, then they satisfy

$${\left({\rho }_{ij}^l\right)}^q{\left({\rho }_{jk}^l\right)}^q{\left({\rho }_{ki}^l\right)}^q={\left({\sigma }_{ij}^l\right)}^q{\left({\sigma }_{jk}^l\right)}^q{\left({\sigma }_{ki}^l\right)}^q$$

According to Definition 18, the q-ROFWG and SYq-ROFWG operator is used to assemble the individual PRs $R^l\left(l=1,2,\dots ,s\right)$ that satisfy the multiplicative consistency, and the analysis is as follows:

(1) The obtained integrated q-ROFPR $R_{q-ROFWG}={\left({\rho }_{ij}^{q-ROFWG},{\sigma }_{ij}^{q-ROFWG}\right)}_{n\times n}$ using the q-ROFWG operator satisfies

$${\rho }_{ij}^{q-ROFWG}={\displaystyle \prod _{l=1}^s{\left({\rho }_{ij}^l\right)}^{{\lambda }_l}},{\sigma }_{ij}^{q-ROFWG}=\sqrt[q]{1-{\displaystyle \prod _{l=1}^s{\left(1-{\left({\sigma }_{ij}^l\right)}^q\right)}^{{\lambda }_l}}}$$

(29)

then ${\left({\rho }_{ij}^{q-ROFWG}\right)}^q{\left({\rho }_{jk}^{q-ROFWG}\right)}^q{\left({\rho }_{ki}^{q-ROFWG}\right)}^q={\left({\sigma }_{ij}^{q-ROFWG}\right)}^q{\left({\sigma }_{jk}^{q-ROFWG}\right)}^q{\left({\sigma }_{ki}^{q-ROFWG}\right)}^q$ does not necessarily hold. Therefore, $R_{q-ROFWG}$ does not necessarily satisfy the multiplicative consistency.

(2) The obtained integrated PR $R_{SYPFWG}={\left({\rho }_{ij}^{SYPFWG},{\sigma }_{ij}^{SYPFWG}\right)}_{n\times n}$ using the SYq-ROFWG operator satisfies

$$\begin{array}{l}{\rho }_{ij}^{SYq-ROFWG}=\sqrt[q]{\frac{{\displaystyle \prod _{l=1}^s{\left({\left({\rho }_{ij}^l\right)}^q\right)}^{{\lambda }_l}}}{{\displaystyle \prod _{l=1}^s{\left({\left({\rho }_{ij}^l\right)}^q\right)}^{{\lambda }_l}}+{\displaystyle \prod _{l=1}^s{\left(1-{\left({\rho }_{ij}^l\right)}^q\right)}^{{\lambda }_l}}}},\\ {\sigma }_{ij}^{SYq-ROFWG}=\sqrt[q]{\frac{{\displaystyle \prod _{l=1}^s{\left({\left({\sigma }_{ij}^l\right)}^q\right)}^{{\lambda }_l}}}{{\displaystyle \prod _{l=1}^s{\left({\left({\sigma }_{ij}^l\right)}^q\right)}^{{\lambda }_l}}+{\displaystyle \prod _{l=1}^s{\left(1-{\left({\sigma }_{ij}^l\right)}^q\right)}^{{\lambda }_l}}}}\end{array}$$

(30)

then ${\left({\rho }_{ij}^{SYq-ROFWG}\right)}^q{\left({\rho }_{jk}^{SYq-ROFWG}\right)}^q{\left({\rho }_{ki}^{SYq-ROFWG}\right)}^q={\left({\sigma }_{ij}^{SYq-ROFWG}\right)}^q{\left({\sigma }_{jk}^{SYq-ROFWG}\right)}^q{\left({\sigma }_{ki}^{SYq-ROFWG}\right)}^q$ does not necessarily hold. Therefore, $R_{SYq-ROFWG}$ does not satisfy the multiplicative consistency.

Based on the above analysis, the integrated q-ROFPR obtained from individual MCq-ROFPRs using the q-ROFWG and SYq-ROFWG operators is not necessarily an MCq-ROFPR.

Therefore, we propose the simple q-ROF weighted geometric (Sq-ROFWG) operator.

Definition 19.

Let ${\alpha }_i=\left({\rho }_i,{\sigma }_i\right)\left(i\in \left[n\right]\right)$ be a set of q-ROFNs, whose weight vector is $\omega ={\left({\omega }_1,{\omega }_2,\dots ,{\omega }_n\right)}^T$. The Wq-ROFWG operator is defined as follows:

$$SPFWG\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)=\left({\displaystyle \prod _{i=1}^n{\rho }_i^{{\omega }_i}},{\displaystyle \prod _{i=1}^n{\sigma }_i^{{\omega }_i}}\right)$$

(31)

Theorem 8.

If the individual PRs $R^l\left(l\in \left[s\right]\right)$ are all MCq-ROFPRs, then the integrated matrix obtained using the Sq-ROFWG operator is still an MCq-ROFPR.

Proof. 

The integrated matrix obtained using the SYq-ROFWG is $R_{SYq-ROFWG}={\left({\rho }_{ij}^{SYq-ROFWG},{\sigma }_{ij}^{SYq-ROFWG}\right)}_{n\times n}$. From Definition 19, $R_{SYq-ROFWG}$ satisfies ${\rho }_{ij}^{SYq-ROFWG}={\displaystyle \prod _{l=1}^s{\left({\rho }_{ij}^l\right)}^{{\lambda }_l}}$ and ${\sigma }_{ij}^{SYq-ROFWG}={\displaystyle \prod _{l=1}^s{\left({\sigma }_{ij}^l\right)}^{{\lambda }_l}}$. Then

$$\begin{array}{l}{\left({\rho }_{ij}^{Sq-ROFWG}{\rho }_{jk}^{Sq-ROFWG}{\rho }_{ki}^{Sq-ROFWG}\right)}^q={\left({\displaystyle \prod _{l=1}^s{\left({\rho }_{ij}^l{\rho }_{jk}^l{\rho }_{ki}^l\right)}^{{\lambda }_l}}\right)}^q,\\ {\left({\sigma }_{ij}^{Sq-ROFWG}{\sigma }_{jk}^{Sq-ROFWG}{\sigma }_{ki}^{Sq-ROFWG}\right)}^q={\left({\displaystyle \prod _{l=1}^s{\left({\sigma }_{ij}^l{\sigma }_{jk}^l{\sigma }_{ki}^l\right)}^{{\lambda }_l}}\right)}^q.\end{array}$$

Since all $R^l\left(l\in \left[s\right]\right)$ satisfy the multiplicative consistency, then ${\left({\rho }_{ij}^l\right)}^q{\left({\rho }_{jk}^l\right)}^q{\left({\rho }_{ki}^l\right)}^q={\left({\sigma }_{ij}^l\right)}^q{\left({\sigma }_{jk}^l\right)}^q{\left({\sigma }_{ki}^l\right)}^q$. Thus,

$${\left({\rho }_{ij}^{Sq-ROFWG}\right)}^q{\left({\rho }_{jk}^{Sq-ROFWG}\right)}^q{\left({\rho }_{ki}^{Sq-ROFWG}\right)}^q={\left({\sigma }_{ij}^{Sq-ROFWG}\right)}^q{\left({\sigma }_{jk}^{Sq-ROFWG}\right)}^q{\left({\sigma }_{ki}^{Sq-ROFWG}\right)}^q.$$

Therefore, the integrated matrix obtained using the Sq-ROFWG operator is an MCq-ROFPR. □

Theorem 9.

If the individual PR $R^l\left(l\in \left[s\right]\right)$ and the ideal MCq-ROFPR $\overline{R}$ satisfy $D\left(R^l,\overline{R}\right)\le \tau$, then the integrated PR $R$ obtained from the Sq-ROFWG operator satisfies $D\left(R,\overline{R}\right)\le \tau$, where $\tau$ is the deviation threshold.

Proof. 

For any $x,y>0$, $\ln \frac{\max \left\{x,y\right\}}{\min \left\{x,y\right\}}=\left|\ln x-\ln y\right|$. From $D\left(R^l,\overline{R}\right)\le \tau$, then

$$e^{\ln D\left(R^l,\overline{R}\right)}=e^{\frac{1}{2n\left(n-1\right)}{\displaystyle \sum _{i<k}^n\ln \frac{\max \left\{{\rho }_{ik}^l,{\overline{\rho }}_{ik}\right\}}{\min \left\{{\rho }_{ik}^l,{\overline{\rho }}_{ik}\right\}}\cdot \frac{\max \left\{{\sigma }_{ik}^l,{\overline{\sigma }}_{ik}\right\}}{\min \left\{{\sigma }_{ik}^l,{\overline{\sigma }}_{ik}\right\}}}}=e^{\frac{1}{2n\left(n-1\right)}{\displaystyle \sum _{i<k}^n\left|\ln {\mu }_{ik}^l-\ln {\overline{\mu }}_{ik}\right|+\left|\ln {\nu }_{ik}^l-\ln {\overline{\nu }}_{ik}\right|}}\le e^{\ln \tau },$$

then

$$\left|{\displaystyle \sum _{l=1}^s{\lambda }_l\left(\ln {\rho }_{ik}^l-\ln {\overline{\rho }}_{ik}\right)}\right|\le \left|{\displaystyle \sum _{l=1}^s{\lambda }_l\left(\ln {\sigma }_{ik}^l-\ln {\overline{\sigma }}_{ik}\right)}\right|.$$

Furthermore,

$$\begin{array}{l}{e}^{\ln D\left(R,\overline{R}\right)}\\ =e^{\frac{1}{2n\left(n-1\right)}{\displaystyle \sum _{i<k}^n\left(\left|\ln {\displaystyle \prod _{l=1}^s{\left({\rho }_{ik}^l\right)}^{{\lambda }_l}}-\ln {\overline{\rho }}_{ik}\right|+\left|\ln {\displaystyle \prod _{l=1}^s{\left({\sigma }_{ik}^l\right)}^{{\lambda }_l}}-\ln {\overline{\sigma }}_{ik}\right|\right)}}\\ =e^{\frac{1}{2n\left(n-1\right)}{\displaystyle \sum _{i<k}^n\left(\left|{\displaystyle \sum _{l=1}^s{\lambda }_l\left(\ln {\rho }_{ik}^l-\ln {\overline{\rho }}_{ik}\right)}\right|+\left|{\displaystyle \sum _{l=1}^s{\lambda }_l\left(\ln {\sigma }_{ik}^l-\ln {\overline{\sigma }}_{ik}\right)}\right|\right)}}\\ \le e^{{\displaystyle \sum _{l=1}^s{\lambda }_l\left({\displaystyle \sum _{i<k}^n\frac{1}{2n\left(n-1\right)}\left(\left|\ln {\rho }_{ik}^l-\ln {\overline{\rho }}_{ik}\right|+\left|\ln {\sigma }_{ik}^l-\ln {\overline{\sigma }}_{ik}\right|\right)}\right)}}\\ ={\displaystyle \prod _{l=1}^s{\left(e^{\ln D\left(R^l,\overline{R}\right)}\right)}^{{\lambda }_l}}\le e^{\ln \tau }\end{array}.$$

Therefore, $D\left(R,\overline{R}\right)\le \tau$. □

According to Theorem 8, if all the individual q-ROFPRs satisfy the multiplicative consistency, then the combined q-ROFPRs obtained using the Sq-ROFWG operator still satisfy the multiplicative consistency. According to Theorem 9, if the compatibility measure between the individual PRs and the ideal MCq-ROFPRs is less than a given threshold, then the compatibility measure between the integrated PRs using the Sq-ROFWG operator and the ideal MCq-ROFPRs is still less than the given threshold. Therefore, the Sq-ROFWG operator is used as an aggregation operator to obtain the integrated q-ROFPRs.

6.4. GDM Method Based on the Group Goal Programming Model and the Sq-ROFWG Operator

Above all, the steps of the developed GDM method are as follows:

Step 1: Use the individual PRs $R^l={\left({\tilde{p}}_{ij}^l\right)}_{n\times n}\left(l\in \left[s\right]\right)$ provided by the expert group to construct the model (24) and solve it to obtain the $\tilde{\omega }={\left({\tilde{\omega }}_1,{\tilde{\omega }}_2,\dots ,{\tilde{\omega }}_n\right)}^T$. The ideal MCq-ROFPR $\overline{R}={\left({\overline{\mu }}_{ij},{\overline{\nu }}_{ij}\right)}_{n\times n}$ is obtained using Equation (25).

Step 2: calculate the divergence measure and compatibility measure between $R^l$ and $\overline{R}$ using Equation (15) and Definition 14.

$$C\left(R^l,\overline{R}\right)=\frac{1}{D\left(R^l,\overline{R}\right)},l\in \left[s\right]$$

(32)

The weight vector $\lambda ={\left({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_s\right)}^T$ of experts is calculated using Equation (26).

Step 3: combine the expert weight vector $\lambda$ and aggregate $R^l={\left({\tilde{p}}_{ij}^l\right)}_{n\times n}\left(l\in \left[s\right]\right)$ to obtain the combined PR $R={\left({\tilde{p}}_{ij}^k\right)}_{n\times n}$ using the Sq-ROFWG operator (Equation (31)).

Step 4: construct the goal programming model (22) to calculate the vector $\tilde{\omega }={\left({\tilde{\omega }}_1,{\tilde{\omega }}_2,\dots ,{\tilde{\omega }}_n\right)}^T$ based on the combined q-ROFPR $R={\left({\tilde{p}}_{ij}^k\right)}_{n\times n}$.

Step 5: rank the weight vectors to obtain the optimal alternative based on Definition 11.

7. A Numerical Example

In order to find out the critical factors of crowdsourcing task recommendation, assume that a group of three decision-makers formed an expert group $E=\left\{e_1,e_2,e_3\right\}$: a platform manager $e_1$, a system designer $e_2$, and a professor $e_3$ focused on crowdsourcing. The weight vector of decision-makers is unknown. The experts compared four factors: subject preference $X_1$, skill $X_2$, historical performance $X_3$, and social capital $X_4$. Before designing a recommendation system, it is necessary to use expert experience to identify critical factors in crowdsourcing task recommendation, serving the feature extraction of the recommendation system.

The experts $e_k\left(k=1,2,3\right)$ compare the influence factors $X_i$ and $X_j$$\left(i,j=1,2,3,4;i\ne j\right)$ and provide the q-ROFPRs $R_P^k={\left({\tilde{p}}_{ij}^k\right)}_{4\times 4}\left(k=1,2,3\right)$, where ${\tilde{p}}_{ij}^k=\left({\rho }_{ij}^k,{\sigma }_{ij}^k\right)$ is a q-ROFN. Next, assume that $q=3$, the four factors are ranked using the developed GDM method, and the steps are as follows:

$$R_P^1=\left[\begin{array}{cccc}\left(\sqrt[q]{0.5},\sqrt[q]{0.5}\right)& \left(0.60,0.70\right)& \left(0.70,0.60\right)& \left(0.65,0.70\right)\\ \left(0.70,0.60\right)& \left(\sqrt[q]{0.5},\sqrt[q]{0.5}\right)& \left(0.80,0.30\right)& \left(0.75,0.45\right)\\ \left(0.60,0.70\right)& \left(0.30,0.80\right)& \left(\sqrt[q]{0.5},\sqrt[q]{0.5}\right)& \left(0.75,0.60\right)\\ \left(0.70,0.65\right)& \left(0.45,0.75\right)& \left(0.60,0.75\right)& \left(\sqrt[q]{0.5},\sqrt[q]{0.5}\right)\end{array}\right]$$

$$R_P^2=\left[\begin{array}{cccc}\left(\sqrt[q]{0.5},\sqrt[q]{0.5}\right)& \left(0.75,0.55\right)& \left(0.80,0.50\right)& \left(0.80,0.50\right)\\ \left(0.55,0.75\right)& \left(\sqrt[q]{0.5},\sqrt[q]{0.5}\right)& \left(0.60,0.70\right)& \left(0.80,0.55\right)\\ \left(0.50,0.80\right)& \left(0.70,0.60\right)& \left(\sqrt[q]{0.5},\sqrt[q]{0.5}\right)& \left(0.75,0.55\right)\\ \left(0.50,0.80\right)& \left(0.55,0.80\right)& \left(0.55,0.75\right)& \left(\sqrt[q]{0.5},\sqrt[q]{0.5}\right)\end{array}\right]$$

$$R_P^3=\left[\begin{array}{cccc}\left(\sqrt[q]{0.5},\sqrt[q]{0.5}\right)& \left(0.75,0.55\right)& \left(0.75,0.60\right)& \left(0.80,0.35\right)\\ \left(0.55,0.75\right)& \left(\sqrt[q]{0.5},\sqrt[q]{0.5}\right)& \left(0.65,0.45\right)& \left(0.40,0.45\right)\\ \left(0.60,0.75\right)& \left(0.45,0.65\right)& \left(\sqrt[q]{0.5},\sqrt[q]{0.5}\right)& \left(0.40,0.65\right)\\ \left(0.35,0.80\right)& \left(0.45,0.40\right)& \left(0.65,0.40\right)& \left(\sqrt[q]{0.5},\sqrt[q]{0.5}\right)\end{array}\right]$$

Step 1: Substitute the q-ROFPRs $R_P^k={\left({\tilde{p}}_{ij}^k\right)}_{4\times 4}\left(k=1,2,3\right)$ into the model (24) and solve the normalized q-ROFWV.

$$\tilde{\omega }={\left(\left(0.5873,0.8196\right),\left(0.5061,0.8593\right),\left(0.4454,0.9238\right),\left(0.3999,0.9205\right)\right)}^T$$

The ideal MCq-ROFPR $\overline{R}={\left({\overline{\mu }}_{ij},{\overline{\nu }}_{ij}\right)}_{4\times 4}$ is obtained using Equation (21).

$$\overline{R}=\left[\begin{array}{cccc}\left(\sqrt[q]{0.5},\sqrt[q]{0.5}\right)& \left(0.5832,0.6091\right)& \left(0.7522,0.5705\right)& \left(0.7565,0.5151\right)\\ \left(0.6091,0.5832\right)& \left(\sqrt[q]{0.5},\sqrt[q]{0.5}\right)& \left(0.6882,0.6058\right)& \left(0.6929,0.5476\right)\\ \left(0.5705,0.7522\right)& \left(0.6058,0.6882\right)& \left(\sqrt[q]{0.5},\sqrt[q]{0.5}\right)& \left(0.6713,0.6028\right)\\ \left(0.5151,0.7565\right)& \left(0.5476,0.6929\right)& \left(0.6028,0.6713\right)& \left(\sqrt[q]{0.5},\sqrt[q]{0.5}\right)\end{array}\right]$$

Step 2: calculate the compatibility measures between $R_P^k\left(k=1,2,3\right)$ and $\overline{R}$ using Equations (15) and (32).

$$C\left(R^1,\overline{R}\right)=0.8470, C\left(R^2,\overline{R}\right)=0.8999, C\left(R^3,\overline{R}\right)=0.8091$$

The expert weight vector is calculated as $\lambda ={\left(0.3314,0.3521,0.3165\right)}^T$ using Equation (26).

Step 3: gather individual PRs $R_P^k\left(k=1,2,3\right)$ using the Sq-ROFWG operator (Equation (31)) to obtain the comprehensive q-ROFPR $R={\left({\tilde{p}}_{ij}^k\right)}_{4\times 4}$.

$$R=\left[\begin{array}{cccc}\left(\sqrt[q]{0.5},\sqrt[q]{0.5}\right)& \left(0.6965,0.5958\right)& \left(0.7499,0.5627\right)& \left(0.7468,0.4993\right)\\ \left(0.5958,0.6965\right)& \left(\sqrt[q]{0.5},\sqrt[q]{0.5}\right)& \left(0.6770,0.4596\right)& \left(0.6288,0.4829\right)\\ \left(0.5627,0.7499\right)& \left(0.4596,0.6770\right)& \left(\sqrt[q]{0.5},\sqrt[q]{0.5}\right)& \left(0.6147,0.5968\right)\\ \left(0.4993,0.7468\right)& \left(0.4829,0.6288\right)& \left(0.5968,0.6147\right)& \left(\sqrt[q]{0.5},\sqrt[q]{0.5}\right)\end{array}\right]$$

Step 4: Substitute $R={\left({\tilde{p}}_{ij}^k\right)}_{4\times 4}$ into the model (22) to obtain the normalized q-ROFWV.

$${\omega }^{*}={\left(\left(0.5765,0.8226\right),\left(0.4931,0.8530\right),\left(0.4019,0.9249\right),\left(0.3854,0.9174\right)\right)}^T$$

Step 5: Calculate the scores of the weight vector according to Definition 11.

$$s\left({\omega }_1^{*}\right)=-0.3651,s\left({\omega }_2^{*}\right)=-0.5008,s\left({\omega }_3^{*}\right)=-0.7262,s\left({\omega }_4^{*}\right)=-0.7148.$$

Then the ranking of influence factors is obtained as $X_3\prec X_4\prec X_2\prec X_1$. Therefore, the crucial factor in crowdsourcing task recommendation is $X_1$(subject preference).

In addition, the divergence measures between the individual q-ROFPRs $R_P^k\left(k=1,2,3\right)$ and the ideal MCq-ROFPR $\overline{R}$ are calculated using Definition 14.

$$D\left(R^1,\overline{R}\right)=1.1806,D\left(R^2,\overline{R}\right)=1.1112,D\left(R^3,\overline{R}\right)=1.2360.$$

The divergence between the combined q-ROFPR $R$ and $\overline{R}$ is $D\left(R,\overline{R}\right)=1.0755$, the compatibility measure is $C\left(R,\overline{R}\right)=0.9298$, which demonstrates the soundness of Theorem 9.

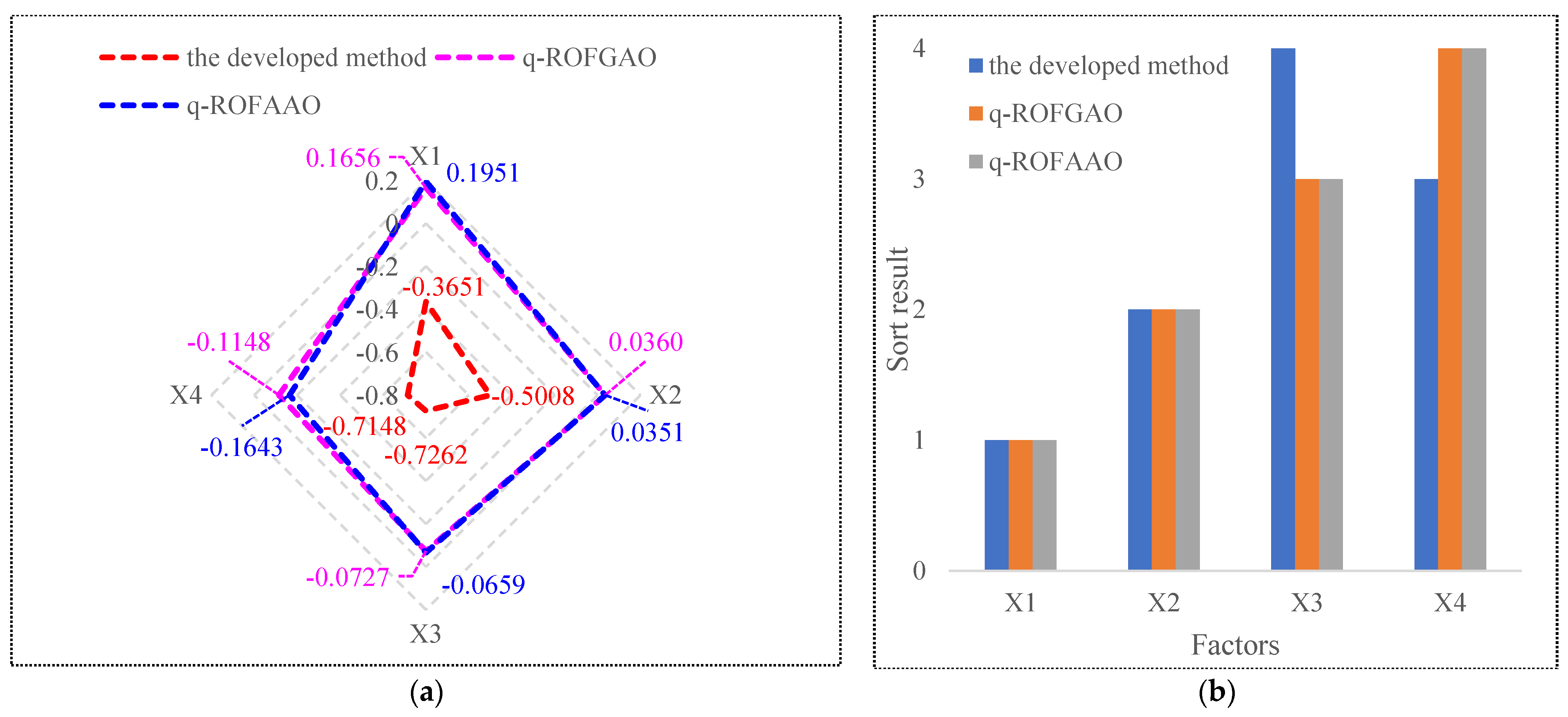
The q-ROFPR-based GDM method is compared with the q-ROF geometric averaging operator (q-ROFGAO) and the arithmetic averaging operator (q-ROFAAO) [28] to find the critical factors of crowdsourcing task recommendation. The scores and sort results obtained using the three different methods are presented in Figure 1. The scores of the q-ROFGAO method are 0.1656, 0.0360, −0.0727, and −0.1148, and the scores of the q-ROFAAO method are 0.1951, 0.0351, −0.0659, and −0.1643. The sorting results of the three methods are generally consistent, but there are differences in the sorting of X₃ and X₄. This is due to the objective weight vector of experts obtained by comparing the differences in individual and group FPRs. The proposed q-ROFPR-based GDM method uses objective weighting methods to identify critical factors in crowdsourcing task recommendation, which is more reliable than the q-ROFGAO and q-ROFAAO methods.

Finally, the managerial implications are provided as follows: in the problem of crowdsourcing task recommendation, all participants place greater emphasis on subject preference, then skill, social capital, and historical performance.

8. Conclusions

In the GDM process, q-ROFSs have a strong advantage in expressing the uncertainty of attributes. Meanwhile, q-ROFPRs play a very important role in expressing the PRs among the alternatives flexibly without scoring all alternatives under the corresponding attributes. However, in the existing MCq-ROFPR methods, experts’ weights are subjective, and the importance measures of experts are not reflected in the GDM methods. In addition, the group q-ROFPRs aggregated using individual q-ROFPRs may not satisfy multiplicative consistency.

Thus, we developed a GDM method under q-ROFPRs, considering the important measures of experts. Firstly, the implication relations and constraints between IFSs and q-ROFSs were analyzed. Then, we introduced the MCq-ROFPRs and the normalized q-ROFPWVs. Next, a goal programming model under q-ROFPRs was developed to obtain the q-ROFPWVs. Further, a GDM method under q-ROFPRs was provided by combing the overall goal programming model and the simple q-ROF weighted geometric (Sq-ROFWG) operator. Finally, the effectiveness and practicality of the developed GDM method were verified by identifying crucial factors in crowdsourcing task recommendation. The results show that the developed GDM method effectively considers the importance measures of experts and identifies the critical factors that are more reliable than the q-ROFGAO and q-ROFAAO methods in crowdsourcing task recommendation.

However, the developed GDM method only quantitatively estimates the preference degree of experts in finding out critical factors. In the future, we will use natural language processing and deep learning methods to evaluate the importance of influencing factors and improve the efficiency of crowdsourcing task recommendation.