Mass Generation via the Phase Transition of the Higgs Field
Abstract
1. Introduction
2. Derivation of the Higgs Potential from Catastrophe Theory
2.1. Method 1: Relying on Catastrophe Theory and Stable Isolated States
2.2. Method 2: Implementing a Shortcut
2.2.1. Utilizing a Familiarity Heuristic
2.2.2. Looking Back to Landau’s Theory of Phase Transitions
3. Discussion of Phase Transitions
3.1. The Higgs Phase Transition
3.2. The Maxwell Convention and Chemical Reactions
3.3. Overcoming the Energy Barrier
- (a)
- If the Gibbs free energy gained by the parts of the system is not sufficient to push any part up to at least point P (or B), then the perturbed system remains in the neighborhood of point I.
- (b)
- (c)
3.4. Star-Forming Phase Transitions
3.5. Peculiar -Transitions
4. Conclusions
- (a)
- Figure 1 shows the potential functions for Landau’s phenomenological theory of second-order phase transitions [1], including that ascribed to the Higgs field. As the control parameter is increased (to simulate time evolution), the potential develops two features that render it unphysical: two symmetric stable global minima appear on either side of the local maximum at , and they both continue to move away from in time.Thus, assuming an initial state at , as usual [4,5,6], the phase transition does not produce a unique or a universal final state. But these properties are required for the Higgs field at present [9,10,11,12,13,20]; and uniqueness of the final state is required for many phase transitions in solids and fluids [8,29,30,31,32,34,35,36,45,54].
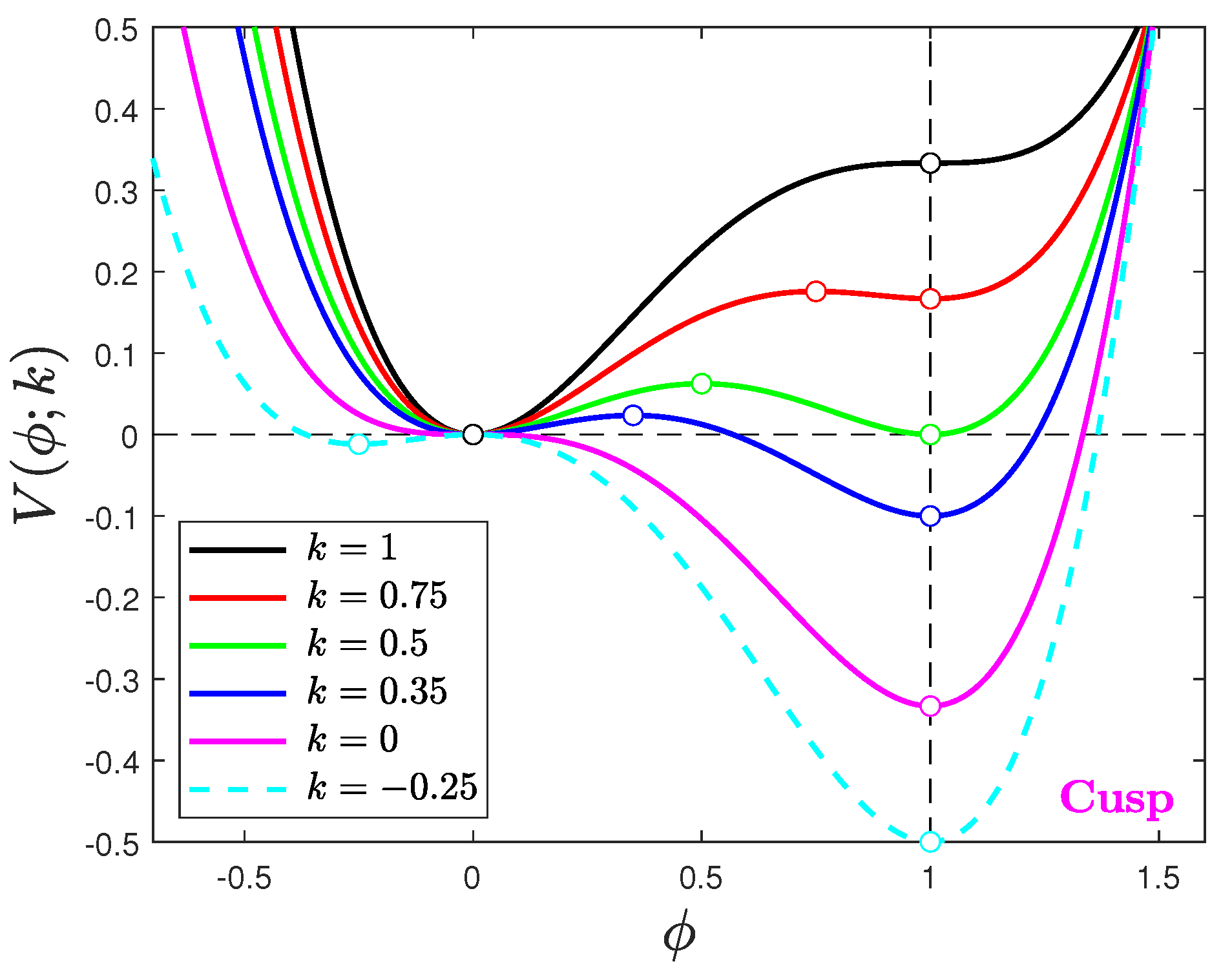
- (b)
- Figure 2 shows how to get around the problems highlighted above. The potential functions of the cusp catastrophe [4] are all shifted so that one minimum is always at (representing the initial state) and another minimum is constrained to always be at , making this (final) state universal [20]. The linear term of the cusp catastrophe (Equation (4)) precludes the appearance of another minimum at before the second-order critical point at is reached; and when such a minimum finally appears for , it is incapable of influencing the dynamics of the phase transition that took place spontaneously already for .The maximum that appears for represents a free-energy barrier between the two isolated stable states. External perturbations may drive a system from to , if they supply the requisite energy to overcome the intervening barrier (a first-order phase transition [2,3,30,31]), otherwise the system remains oscillating about . As the control parameter decreases toward (Figure 2), the barrier becomes shorter (just as in catalyzed chemical reactions [39,40,41,42,43]), and a second-order phase transition appears at , where the barrier disappears [29,32,45]. We believe that such a transition occurred in the massless Higgs field when it acquired its uniquely positive universal VEV [16,17,20] because we cannot imagine vacuum perturbations strong enough to overcome the energy barrier in the interval .Before the phase transition occurs, the Higgs field is induced to executing small amplitude oscillations about the minimum at that represents the equilibrium VEV of the massless state. Such oscillations generate evanescent particles with both positive and negative masses that do not survive long into the future. The observed particles of our times were all assigned masses after the Higgs field had settled to its universal VEV of 246.22 GeV [20,64].
- (c)
- Figure 3 shows the evolutionary path in the control plane of the cusp catastrophe. The path remains within the fold lines of the separatrix at all times (even for ), and exhibits a Maxwell critical point [37,38] for and a second-order critical point for .As the green curve in Figure 2 shows, a first-order stable minimum at becomes available for , but it is not necessarily accessible to a system located at via a first-order phase transition due to the intervening energy barrier. For the Higgs field, such a continuous line of first-order phase transitions was observed in the past (before the discovery of the Higgs boson and the measurement of its mass; see Refs. [16,17,46] and references therein); although the lattice simulations were using Landau’s even-symmetric potential and a Higgs mass of no more than GeV. For higher Higgs masses in non-perturbative simulations, the second-order critical point was replaced by a smooth crossover to the final massive state [16,17,46]. These doubtful results must have their origin in the unphysical potential used, and new simulations are needed to revisit the true nature of the Higgs phase transition.
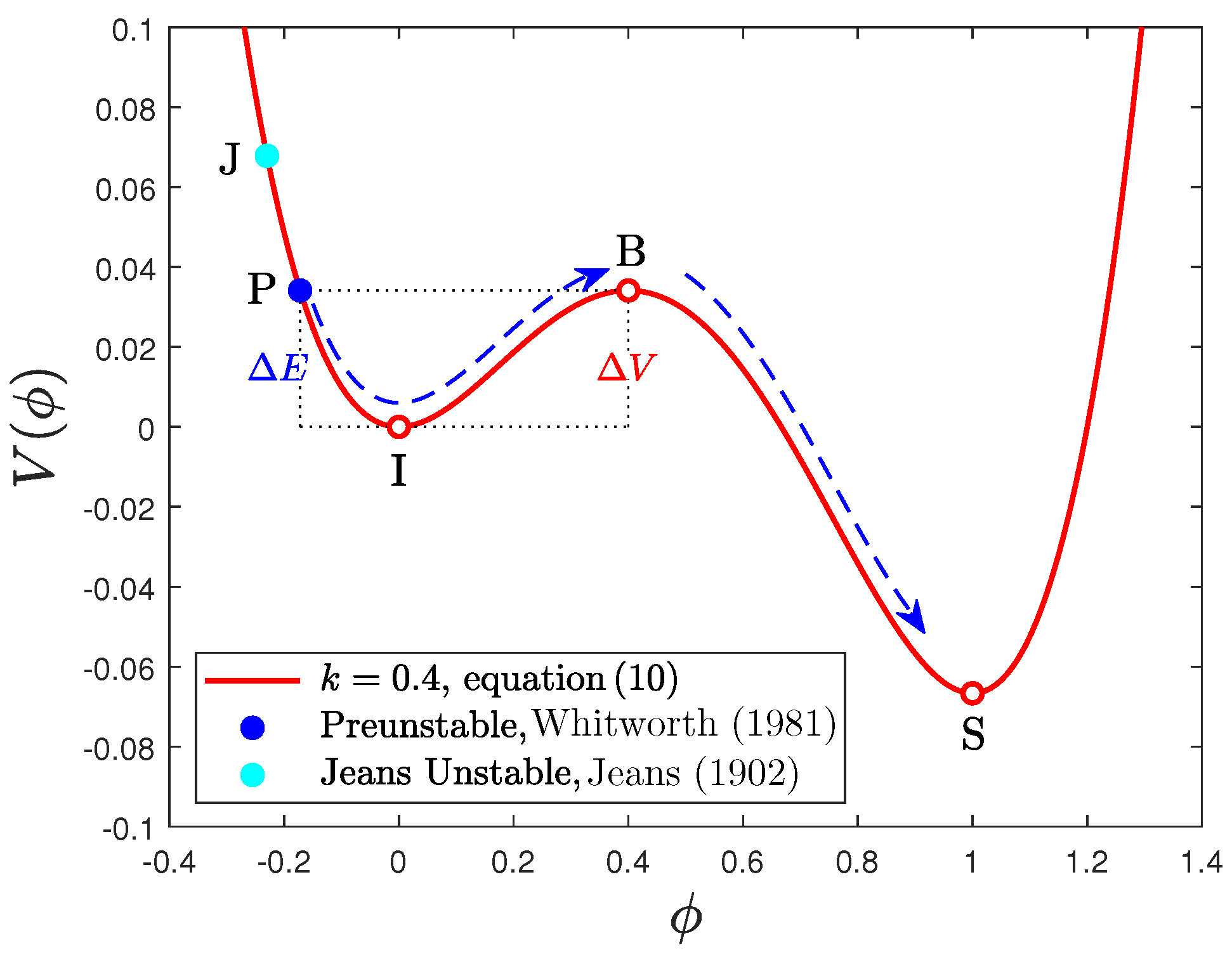
- (d)
- Figure 4 shows a schematic illustration of the various aspects of first-order phase transitions capable of overcoming the intervening energy barrier [3]. Basically, there are two separate evolutionary modes depending on the amount of energy deposited by acting external perturbations over time: (i) a strongly perturbed system (point J in Figure 4) is not impeded by the barrier any longer and makes the transition to the final equilibrium state S on a dynamical time [30,31,44]; and (ii) a system oscillating about point I, and perturbed gradually upward to point P (or B), gains enough energy to jump over the top of the barrier B and down to the final equilibrium state S [28,29,30].
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Potentials of Higher-Order Catastrophes
Appendix A.1. Swallowtail Potentials
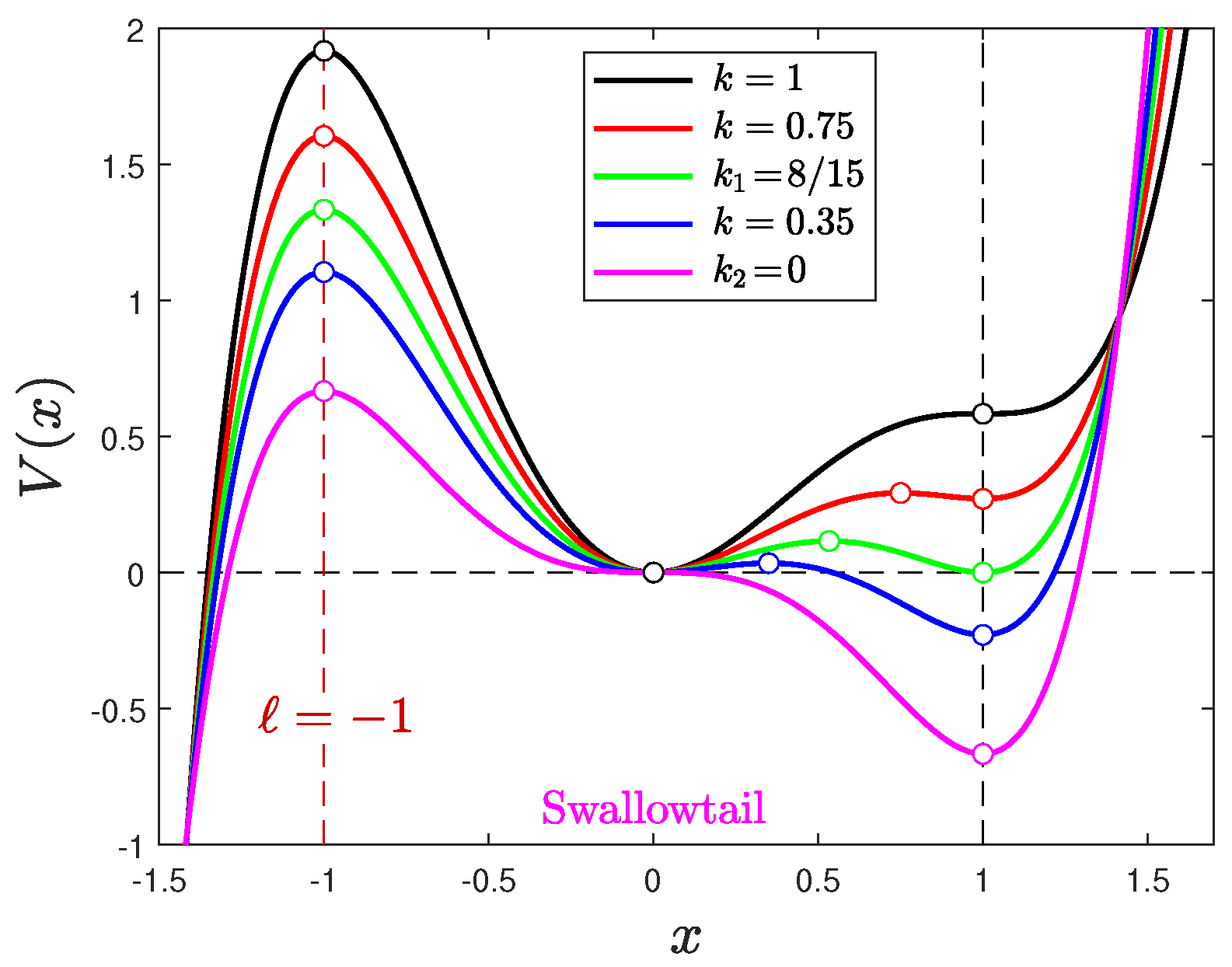
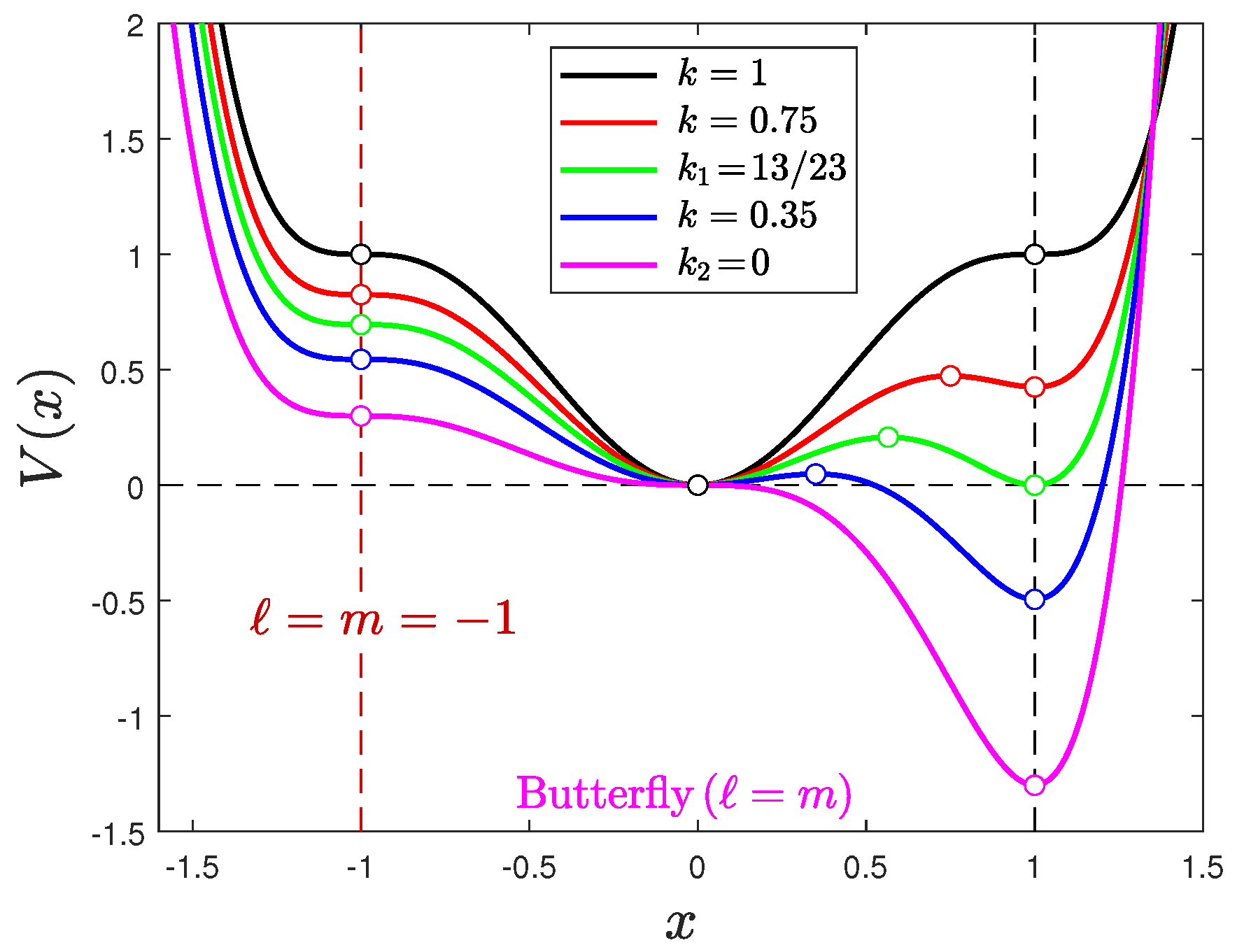
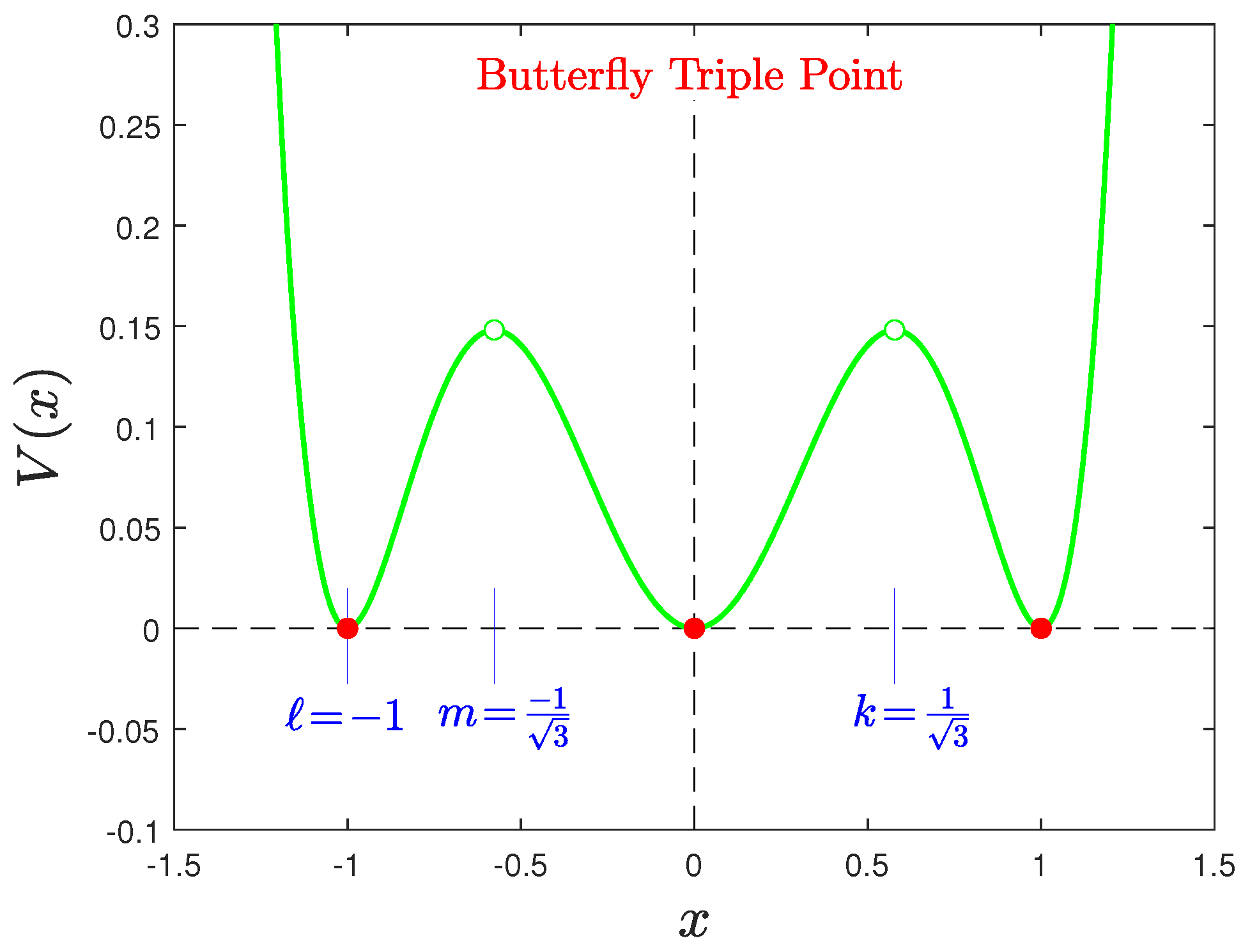
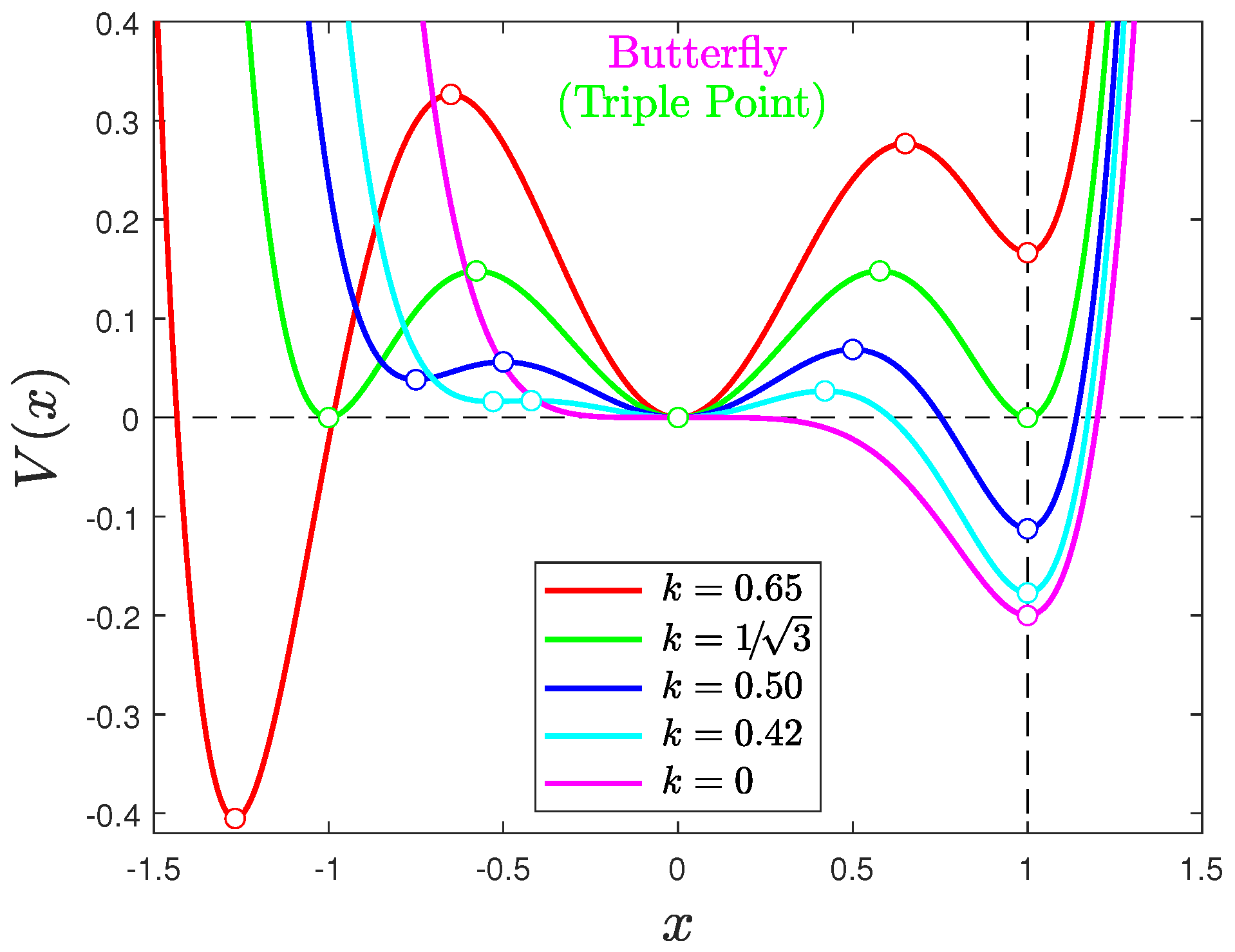
Appendix A.2. Butterfly and Triple-Point Potentials

| 1 | In contrast, Landau [1] was not thinking about isospin or null quantities when he formulated his theory. To him, symmetries were visible in the arrangement of atoms in a crystal or in the (mis)alignment of magnetic moments in magnetic materials. |
| 2 | In all fairness to Landau [1], Thom’s catastrophe theory [4] did not exist in Landau’s time, so he did not know that his Taylor expansion of the potential was not formally correct near the degenerate critical point. In fact, he was apparently lucky to get the rest of the perturbation () right when he correctly eliminated the cubic term (), albeit based on an inconclusive argument (that, for , the curve of phase transitions degenerates to a single point in the plane, where P is pressure); the counterargument is that functions and may have the same zeroes [5] and/or that . |
| 3 | |
| 4 | |
| 5 | The point or is where the evolutionary path crosses the B-axis in the control parameter plane (see Figure 3). |
| 6 | Recall that catastrophe theory is applicable only to gradient systems [6], so it does not account for time, and qualitative conventions have been invented to describe actual time evolution before and after a phase transition (or “catastrophe”). |
| 7 | Thus, not all butterfly phase-transition paths are covered in the present investigation. |
References
- Landau, L.D.; Lifshitz, E.G. Statistical Physics, 3rd ed.; Pergamon Press: New York, NY, USA, 1980; Volume 5, Part 1. [Google Scholar]
- Tohline, J.E.; Bodenheimer, P.H.; Christodoulou, D.M. The crucial role of cooling in the making of molecular clouds and stars. Astrophys. J. 1987, 322, 787. [Google Scholar] [CrossRef]
- Christodoulou, D.M.; Tohline, J.E. Phase transition time scales for cooling and isothermal media. Astrophys. J. 1990, 363, 197. [Google Scholar] [CrossRef]
- Thom, R. Structural Stability and Morphogenesis; Benjamin Press: Reading, PA, USA, 1975. [Google Scholar]
- Poston, T.; Stewart, I. Catastrophe Theory and Its Applications; Dover: New York, NY, USA, 1988. [Google Scholar]
- Gilmore, R. Catastrophe Theory for Scientists and Engineers; Dover: New York, NY, USA, 1981. [Google Scholar]
- Drazin, P.G.; Reid, W.H. Hydrodynamic Stability; Cambridge Univ. Press: Cambridge, UK, 1981. [Google Scholar]
- Christodoulou, D.M.; Kazanas, D.; Shlosman, I.; Tohline, J.E. Phase-transition theory of instabilities. IV. Astrophys. J. 1995, 446, 510. [Google Scholar] [CrossRef]
- Weinberg, S. The Quantum Theory of Fields, Vol. II; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Peskin, M.E.; Schroeder, D.V. An Introduction to Quantum Field Theory; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Perkins, D.H. Introduction to High Energy Physics, 4th ed.; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Bali, G.S. QCD forces and heavy quark bound states. Phys. Rep. 2001, 343, 1. [Google Scholar] [CrossRef]
- Griffiths, D. Introduction to Elementary Particles, 2nd ed.; Wiley-VCH: Weinheim, Germany, 2008. [Google Scholar]
- Goldstone, J. Field theories with “Superconductor” solutions. Nuovo Cim. 1961, 19, 154. [Google Scholar] [CrossRef]
- Weinberg, S. Gravitation and Cosmology; John Wiley & Sons: New York, NY, USA, 1972. [Google Scholar]
- D’Onofrio, M.; Rummukainen, K.; Tranberg, A. Sphaleron rate in the minimal Standard Model. Phys. Rev. Lett. 2014, 113, 141602. [Google Scholar] [CrossRef]
- D’Onofrio, M.; Rummukainen, K. Standard Model cross-over on the lattice. Phys. Rev. D 2016, 93, 025003. [Google Scholar] [CrossRef]
- Melia, F. A solution to the electroweak horizon problem in the Rh = ct universe. Eur. Phys. J. C 2018, 78, 739. [Google Scholar] [CrossRef]
- Melia, F. The electroweak horizon problem. Phys. Dark Univ. 2022, 37, 101057. [Google Scholar] [CrossRef]
- Cline, J.M. There is no electroweak horizon problem. Phys. Dark Univ. 2022, 37, 101059. [Google Scholar] [CrossRef]
- ATLAS Collaboration; Aad, G.; Abajyan, T.; Abbott, B.; Abdallah, J.; Abdel Khalek, S.; Abdelalim, A.A.; Abdinov, O.; Aben, R.; Abi, B.; et al. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 2012, 716, 1–29. [Google Scholar] [CrossRef]
- CMS Collaboration; Chatrchyan, S.; Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Aguilo, E.; Bergauer, T.; Dragicevic, M.; Erö, J.; et al. Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys. Lett. B 2012, 716, 30. [Google Scholar] [CrossRef]
- Particle Data Group; Zyla, P.A.; Barnett, R.M.; Beringer, J.; Dahl, O.; Dwyer, D.A.; Groom, D.E.; Lin, C.-J.; Lugovsky, K.S.; Pianori, E.; et al. Review of particle physics. Prog. Theor. Exp. Phys. 2020, 2020, 083C01. [Google Scholar] [CrossRef]
- Particle Data Group; Workman, R.L.; Burkert, V.D.; Crede, V.; Klempt, E.; Thoma, U.; Tiator, L.; Agashe, K.; Aielli, G.; Allanach, B.C.; et al. Review of particle physics. Prog. Theor. Exp. Phys. 2022, 2022, 083C01. [Google Scholar] [CrossRef]
- Godwin, A.N. Three dimensional pictures for Thom’s parabolic umbilic. Publ. Math. l’HÉS 1971, 40, 117. [Google Scholar] [CrossRef]
- Sun, Z.; Hu, J.; Wang, Y.; Ye, W.; Qian, Y. Manipulating self-focusing beams induced by high-dimensional parabolic umbilic beams. Res. Phys. 2023, 52, 106806. [Google Scholar] [CrossRef]
- Hui, D.; Hansen, J.S. The parabolic umbilic catastrophe and its application in the theory of elastic stability. Quart. Appl. Math. 1981, 39, 201. [Google Scholar] [CrossRef]
- Whitworth, A. Global gravitational stability for one-dimensional polytropes. Mon. Not. Roy. Astr. Soc. 1981, 195, 967. [Google Scholar] [CrossRef][Green Version]
- Christodoulou, D.M.; Kazanas, D.; Shlosman, I.; Tohline, J.E. Phase-transition theory of instabilities. I. Astrophys. J. 1995, 446, 472. [Google Scholar] [CrossRef]
- Tohline, J.E. Star formation: Phase transition, not Jeans instability. Astrophys. J. 1985, 292, 181. [Google Scholar] [CrossRef]
- Tohline, J.E.; Christodoulou, D.M. Star formation via the phase transition of an adiabatic gas. Astrophys. J. 1988, 325, 699. [Google Scholar] [CrossRef]
- Christodoulou, D.M.; Kazanas, D.; Shlosman, I.; Tohline, J.E. Phase-transition theory of instabilities. II. Astrophys. J. 1995, 446, 485. [Google Scholar] [CrossRef][Green Version]
- Schwikert, S.R.; Curran, T. Familiarity and recollection in heuristic decision making. J. Exp. Psychol. Gen. 2014, 143, 2341. [Google Scholar] [CrossRef] [PubMed]
- Huang, K. Statistical Mechanics, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1963. [Google Scholar]
- Pippard, A.B. Elements of Classical Thermodynamics; Cambridge University Press: Cambridge, UK, 1966. [Google Scholar]
- Stanley, H.E. Introduction to Phase Transitions and Critical Phenomena; Clarendon Press: Oxford, UK, 1971. [Google Scholar]
- Gilmore, R. Catastrophe time scales and conventions. Phys. Rev. A 1979, 20, 2510. [Google Scholar] [CrossRef]
- Clerk-Maxwell, J. On the dynamical evidence of the molecular constitution of bodies. J. Chem. Soc. 1875, 28, 493. [Google Scholar] [CrossRef]
- Espenson, J.H. Chemical Kinetics and Reaction Mechanisms, 2nd ed.; McGraw-Hill: New York, NY, USA, 1995. [Google Scholar]
- Steinfeld, J.I.; Francisco, J.S.; Hase, W.L. Chemical Kinetics and Dynamics, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Atkins, P.; de Paula, J. Physical Chemistry, 8th ed.; Freeman: New York, NY, USA, 2006. [Google Scholar]
- Berg, J.M.; Tymoczko, J.L.; Gatto, G.J., Jr.; Stryer, L. Biochemistry, 9th ed.; Freeman & Co.: New York, NY, USA, 2019. [Google Scholar]
- Wade, L.G.; Simek, J.W. Organic Chemistry, 10th ed.; Pearson: Upper Saddle River, NJ, USA, 2023. [Google Scholar]
- Jeans, J.H. The stability of a spherical nebula. Phil. Trans. Roy. Soc. Lond. A 1902, 199, 1. [Google Scholar]
- Bertin, G.; Radicati, L.A. The bifurcation from the Maclaurin to the Jacobi sequence as a second-order phase transition. Astrophys. J. 1976, 206, 815. [Google Scholar] [CrossRef]
- Aoki, Y.; Csikor, F.; Fodor, Z.; Ukawa, A. The end point of the first-order phase transition of the SU(2) gauge-Higgs model on a 4-dimensional isotropic lattice. Phys. Rev. D 1999, 60, 013001. [Google Scholar] [CrossRef]
- Rajaraman, R. Solitons and Instantons; North-Holland: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Coleman, S. Classical lumps and their quantum descendants. In New Phenomena in Subnuclear Physics; Zichichi, A., Ed.; The Subnuclear Series; Springer: Boston, MA, USA, 1977; Volume 13, p. 297. [Google Scholar]
- Jackiw, R. Quantum meaning of classical field theory. Rev. Mod. Phys. 1972, 49, 681. [Google Scholar] [CrossRef]
- Weber, S. Oscillation and collapse of interstellar clouds. Astrophys. J. 1976, 208, 113. [Google Scholar] [CrossRef]
- Hunter, J.H., Jr. The influence of initial velocity fields upon star formation. Astrophys. J. 1979, 233, 946. [Google Scholar] [CrossRef]
- Hunter, J.H., Jr.; Fleck, R.C. Star formation: The influence of velocity fields and turbulence. Astrophys. J. 1982, 256, 505. [Google Scholar] [CrossRef]
- Christodoulou, D.M.; Kazanas, D.E. Varying-G gravity. Mon. Not. Roy. Astr. Soc. 2023, 519, 1277. [Google Scholar] [CrossRef]
- Onsager, L. Crystal statistics. I. A two-dimensional model with an order-disorder transition. Phys. Rev. 1944, 65, 117. [Google Scholar] [CrossRef]
- Keller, K.; Dangelmayr, G.; Eikemeier, H. Phase diagrams and catastrophes, In Structural Stability in Physics; Güttinger, W., Eikemeier, H., Eds.; Springer: Berlin/Heidelberg, Germany, 1979; pp. 186–198. [Google Scholar]
- Madsen, A.; Als-Nielsen, J.; Hallmann, J.; Roth, T.; Lu, W. Critical behavior of the order-disorder phase transition in β-brass investigated by x-ray scattering. Phys. Rev. B 2016, 94, 014111. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Ellipsoidal Figures of Equilibrium; Yale University Press: New Haven, CT, USA, 1969. [Google Scholar]
- Bardeen, J.M. A reexamination of the post-Newtonian Maclaurin spheroids. Astrophys. J. 1971, 167, 425. [Google Scholar] [CrossRef]
- Hachisu, I.; Eriguchi, Y. Bifurcations and phase transitions of self-gravitating and uniformly rotating fluid. Mon. Not. Roy. Astr. Soc. 1983, 204, 583. [Google Scholar] [CrossRef]
- Hachisu, I.; Eriguchi, Y. Bifurcation points on the Maclaurin sequence. Publ. Astron. Soc. Jpn. 1984, 36, 497. [Google Scholar]
- Eriguchi, Y.; Hachisu, I. Maclaurin hamburger sequence. Astron. Astrophys. 1985, 148, 289. [Google Scholar]
- Hachisu, I. A versatile method for obtaining structures of rapidly rotating stars. Astrophys. J. Suppl. Ser. 1986, 61, 479. [Google Scholar] [CrossRef]
- Hachisu, I.; Tohline, J.E.; Eriguchi, Y. Fragmentation of rapidly rotating gas clouds. I. A universal criterion for fragmentation. Astrophys. J. 1987, 323, 592. [Google Scholar] [CrossRef]
- Particle Data Group; Amsler, C.; Doser, M.; Antonelli, M.; Asner, D.M.; Babu, K.S.; Baer, H.; Band, H.R.; Barnett, R.M.; Bergren, E.; et al. Review of particle physics. Phys. Lett. B 2008, 667, 1. [Google Scholar] [CrossRef]
- Bugis, I.; Hassen Kareem, M. Application of swallowtail catastrophe theory to transient stability assessment of multi-machine power system. J. Theor. Appl. Infor. Tech. 2013, 55, 390. [Google Scholar]
- Zannotti, A.; Diebel, F.; Denz, C. Dynamics of the optical swallowtail catastrophe. Optica 2017, 4, 1157. [Google Scholar] [CrossRef]
- Teng, H.; Qian, Y.; Lan, Y.; Cui, W. Swallowtail-type diffraction catastrophe beams. Optics Express 2021, 29, 3786. [Google Scholar] [CrossRef]
- Suzui, H.; Uchiyama, K.; Uchida, K.; Horisaki, R.; Hori, H.; Naruse, M. Mathematical modeling of morphological changes in photochromic crystals by catastrophe theory. J. Appl. Phys. 2023, 133, 055110. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Christodoulou, D.M.; Kazanas, D. Mass Generation via the Phase Transition of the Higgs Field. Axioms 2023, 12, 1093. https://doi.org/10.3390/axioms12121093
Christodoulou DM, Kazanas D. Mass Generation via the Phase Transition of the Higgs Field. Axioms. 2023; 12(12):1093. https://doi.org/10.3390/axioms12121093
Chicago/Turabian StyleChristodoulou, Dimitris M., and Demosthenes Kazanas. 2023. "Mass Generation via the Phase Transition of the Higgs Field" Axioms 12, no. 12: 1093. https://doi.org/10.3390/axioms12121093
APA StyleChristodoulou, D. M., & Kazanas, D. (2023). Mass Generation via the Phase Transition of the Higgs Field. Axioms, 12(12), 1093. https://doi.org/10.3390/axioms12121093







