Probabilistic Interval Ordering Prioritized Averaging Operator and Its Application in Bank Investment Decision Making
Abstract
1. Introduction
- (1)
- The PIOGPA operator introduces the probability parameter and priority and can reflect the importance degrees and priority relationships of attributes;
- (2)
- The PIOGPA operator is more flexible and robust. It considers the priority between different attributes and can manage the influence of extreme data or biased data and obtain more reasonable decision results;
- (3)
- The PIOGPA operator is more applicable in addressing uncertain problems. It can adjust the critical attributes in time and determine the new critical attribute weight.
2. Basic Concepts
- (1)
- when , ;
- (2)
- when , ;
- (3)
- when , .
3. Probabilistic Interval Ordering Averaging Operator with Attribute Priority
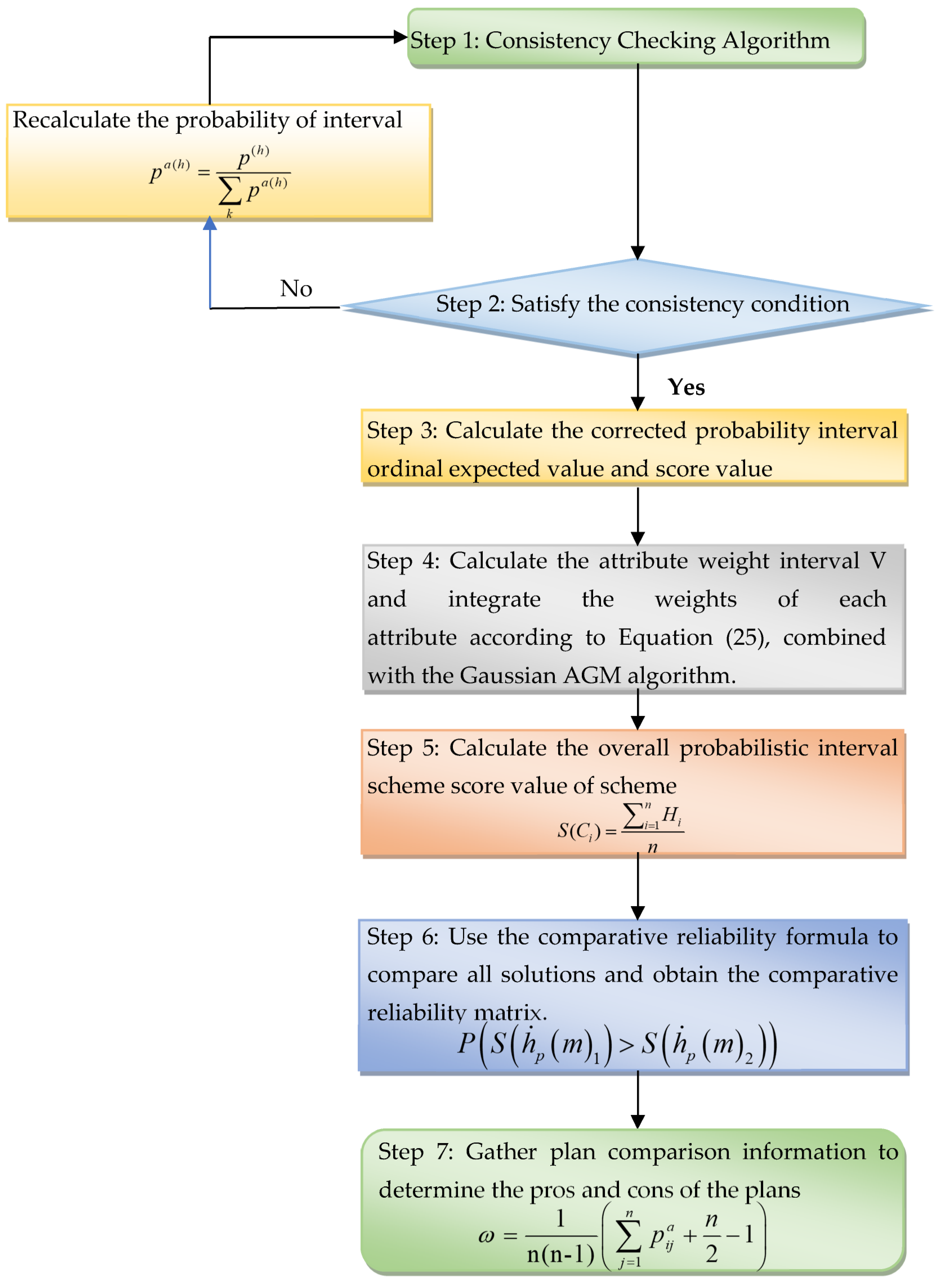
4. MADM Method Based on the PIOGPA Operator
4.1. Consistency Algorithm
- (1)
- when , , is better than ;
- (2)
- when , , is as good as ;
- (3)
- when , , is not as good as .
4.2. MADM Steps Based on the PIOGPA Operator
5. Case Study
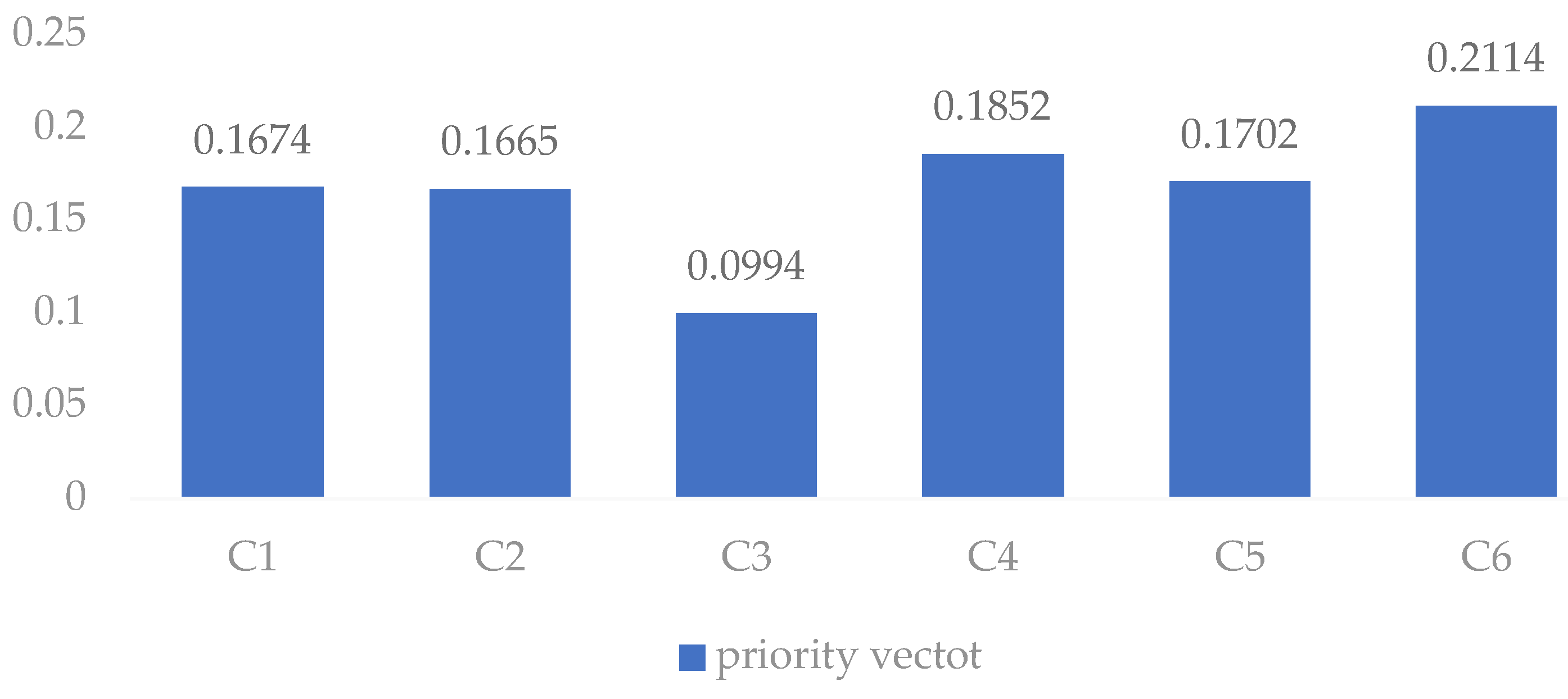
5.1. Case Analysis
5.2. Comparative Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, P.; Liu, Q.; Kang, B. An improved OWA-Fuzzy AHP decision model for multi-attribute decision making problem. J. Intell. Fuzzy Syst. 2021, 40, 9655–9668. [Google Scholar] [CrossRef]
- Zeng, S.; Chen, S.M.; Fan, K.Y. Interval-valued intuitionistic fuzzy multiple attribute decision making based on nonlinear programming methodology and TOPSIS method. Inform. Sci. 2020, 506, 424–442. [Google Scholar] [CrossRef]
- Ferreira, L.; Borenstein, D.; Santi, E. Hybrid fuzzy MADM ranking procedure for better alternative discrimination. Eng. Appl. Artif. Intell. 2016, 50, 71–82. [Google Scholar] [CrossRef]
- Mishra, A.R.; Chen, S.M.; Rani, P. Multiattribute decision making based on Fermatean hesitant fuzzy sets and modified VIKOR method. Inform. Sci. 2022, 607, 1532–1549. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Wang, H. Competency model for international engineering project manager through MADM method: The Chinese context. Expert Syst. Appl. 2023, 212, 118675. [Google Scholar] [CrossRef]
- Lei, F.; Cai, Q.; Wei, G.; Mo, Z.; Guo, Y. Probabilistic double hierarchy linguistic MADM for location selection of new energy electric vehicle charging stations based on the MSM operators. J. Intell. Fuzzy Syst. 2023, 44, 1–22. [Google Scholar] [CrossRef]
- Shahabi, R.S.; Basiri, M.H.; Qarahasanlou, A.N.; Mottahedi, A.; Dehghani, F. Fuzzy MADM-based model for prioritization of investment risk in Iran’s mining projects. Int. J. Fuzzy Syst. 2022, 24, 3189–3207. [Google Scholar] [CrossRef]
- Senapati, T.; Mesiar, R.; Simic, V.; Iampan, A.; Chinram, R.; Ali, R. Analysis of interval-valued intuitionistic fuzzy aczel–alsina geometric aggregation operators and their application to multiple attribute decision-making. Axioms 2022, 11, 258. [Google Scholar] [CrossRef]
- Dou, W. MADM framework based on the triangular Pythagorean fuzzy sets and applications to college public English teaching quality evaluation. J. Intell. Fuzzy Syst. 2023, 45, 4395–4414. [Google Scholar] [CrossRef]
- Sun, M.; Liang, Y.Y.; Pang, T.J. A weighted ranking method of dominance rough sets for interval ordered information systems. J. Chi. Comput. Syst. 2018, 39, 676–680. [Google Scholar]
- Ning, B.; Wei, G.; Lin, R.; Guo, Y. A novel MADM technique based on extended power generalized Maclaurin symmetric mean operators under probabilistic dual hesitant fuzzy setting and its application to sustainable suppliers selection. Expert Syst. Appl. 2022, 204, 117419. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inform. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K.T.; Stoev, S. Intuitionistic fuzzy sets. Fuzzy Sets. Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Khan, M.R.; Wang, H.; Ullah, K.; Karamti, H. Construction Material Selection by Using Multi-Attribute Decision Making Based on q-Rung Orthopair Fuzzy Aczel–Alsina Aggregation Operators. Appl. Sci. 2022, 12, 8537. [Google Scholar] [CrossRef]
- Khan, M.R.; Ullah, K.; Karamti, H.; Khan, Q.; Mahmood, T. Multi-attribute group decision-making based on q-rung orthopair fuzzy Aczel–Alsina power aggregation operators. Eng. Appl. Artif. Intell. 2023, 126, 106629. [Google Scholar] [CrossRef]
- Feng, F.; Zhang, C.; Akram, M.; Zhang, J. Multiple attribute decision making based on probabilistic generalized orthopair fuzzy sets. Granul. Comput. 2023, 8, 863–891. [Google Scholar] [CrossRef]
- Garg, H. Linguistic Pythagorean fuzzy sets and its applications in multiattribute decision-making process. Int. J. Intell. Syst. 2018, 33, 1234–1263. [Google Scholar] [CrossRef]
- Gorzałczany, M.B. A method of inference in approximate reasoning based on interval-valued fuzzy sets. Fuzzy Sets. Syst. 1987, 21, 1–17. [Google Scholar] [CrossRef]
- Ruan, C.; Chen, X. Probabilistic Interval-Valued Fermatean Hesitant Fuzzy Set and Its Application to Multi-Attribute Decision-Making. Axioms 2023, 12, 979. [Google Scholar] [CrossRef]
- Su, Z.; Xu, Z.; Zhao, H.; Hao, Z.; Chen, B. Entropy measures for probabilistic hesitant fuzzy information. IEEE Access 2019, 7, 65714–65727. [Google Scholar] [CrossRef]
- Krishankumar, R.; Ravichandran, K.S.; Kar, S.; Gupta, P.; Mehlawat, M.K. Interval-valued probabilistic hesitant fuzzy set for multi-criteria group decision-making. Soft Comput. 2019, 23, 10853–10879. [Google Scholar] [CrossRef]
- Mandal, P.; Ranadive, A.S. Multi-granulation interval-valued fuzzy probabilistic rough sets and their corresponding three-way decisions based on interval-valued fuzzy preference relations. Granul. Comput. 2019, 4, 89–108. [Google Scholar] [CrossRef]
- Li, W.; Zhan, T. Multi-Granularity Probabilistic Rough Fuzzy Sets for Interval-Valued Fuzzy Decision Systems. Int. J. Fuzzy Syst. 2023, 1–13. [Google Scholar] [CrossRef]
- Senapati, T.; Yager, R.R. Fermatean fuzzy weighted averaging/geometric operators and its application in multi-criteria decision-making methods. Eng. Appl. Artif. Intell. 2019, 85, 112–121. [Google Scholar] [CrossRef]
- Wei, G. Pythagorean fuzzy interaction aggregation operators and their application to multiple attribute decision making. J. Intell. Fuzzy Sys. 2017, 33, 2119–2132. [Google Scholar] [CrossRef]
- Ruan, C.Y.; Chen, X.J.; Zeng, S.Z.; Shahbaz, A.; Bander, A. Fermatean Fuzzy Power Bonferroni Aggregation Operators and Their Applications to Multi-Attribute Decision Making. Soft Comput. 2023. accepted. [Google Scholar]
- Deb, N.; Sarkar, A.; Biswas, A. Development of Archimedean power Heronian mean operators for aggregating linguistic q-rung orthopair fuzzy information and its application to financial strategy making. Soft Comput. 2023, 27, 11985–12020. [Google Scholar] [CrossRef]
- Rahman, K.; Abdullah, S.; Ahmed, R.; Ullah, M. Pythagorean fuzzy Einstein weighted geometric aggregation operator and their application to multiple attribute group decision making. J. Intell. Fuzzy Syst. 2017, 33, 635–647. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R. Fermatean fuzzy Einstein aggregation operators-based MULTIMOORA method for electric vehicle charging station selection. Expert Syst. Appl. 2021, 182, 115267. [Google Scholar] [CrossRef]
- Yager, R.R. Prioritized aggregation operators. Int. J. Approx. Reason. 2008, 48, 263–274. [Google Scholar] [CrossRef]
- Gao, H. Pythagorean fuzzy Hamacher prioritized aggregation operators in multiple attribute decision making. J. Intell. Fuzzy Syst. 2018, 35, 2229–2245. [Google Scholar] [CrossRef]
- Wei, C.; Tang, X. Generalized prioritized aggregation operators. Int. J. Intell. Syst. 2012, 27, 578–589. [Google Scholar] [CrossRef]
- Yu, D. Multi-Criteria Decision Making Based on Generalized Prioritized Aggregation Operators under Intuitionistic Fuzzy Environment. Int. J. Fuzzy Syst. 2013, 15, 47–54. [Google Scholar]
- He, Y.; Xu, Z.; Jiang, W. Probabilistic interval reference ordering sets in multi-criteria group decision making. Int. J. Uncertain. Fuzz. Knowl. Based Syst. 2017, 25, 189–212. [Google Scholar] [CrossRef]
- Khan, M.S.A.; Abdullah, S.; Ali, A.; Amin, F. Pythagorean fuzzy prioritized aggregation operators and their application to multi-attribute group decision making. Granul. Comput. 2019, 4, 249–263. [Google Scholar] [CrossRef]
- Pérez-Arellano, L.A.; León-Castro, E.; Avilés-Ochoa, E.; Merigó, J.M. Prioritized induced probabilistic operator and its application in group decision making. Int. J. Mach. Learn. Cyb. 2019, 10, 451–462. [Google Scholar] [CrossRef]
- Ruan, C.Y.; Chen, X.J.; Han, L.N. Fermatean Hesitant Fuzzy Prioritized Heronian Mean Operator and Its Application in Multi-Attribute Decision Making. Comput. Mater. Con. 2023, 75, 3204–3222. [Google Scholar] [CrossRef]
- Costa, T.M.; Chalco-Cano, Y.; Osuna-Gómez, R.; Lodwick, W.A. Interval order relationships based on automorphisms and their application to interval optimization. Inform. Sci. 2022, 615, 731–742. [Google Scholar] [CrossRef]
- Hesamian, G. Measuring similarity and ordering based on interval type-2 fuzzy numbers. IEEE Trans. Fuzzy Syst. 2016, 25, 788–798. [Google Scholar] [CrossRef]
- Moukrim, A.; Quilliot, A.; Toussaint, H. An effective branch-and-price algorithm for the preemptive resource constrained project scheduling problem based on minimal interval order enumeration. Eur. J. Oper. Res. 2015, 244, 360–368. [Google Scholar] [CrossRef]
- González-Pachón, J.; Romero, C. Aggregation of partial ordinal rankings: An interval goal programming approach. Comput. Oper. Res. 2001, 28, 827–834. [Google Scholar] [CrossRef]
- Zapata, F.; Kreinovich, V.; Joslyn, C.; Hogan, E. Orders on intervals over partially ordered sets: Extending Allen’s algebra and interval graph results. Soft Comput. 2013, 17, 1379–1391. [Google Scholar] [CrossRef][Green Version]
- Pouzet, M.; Zaguia, I. Interval orders, semiorders and ordered groups. J. Math. Psychol. 2019, 89, 51–66. [Google Scholar] [CrossRef]
- Ghosh, D.; Debnath, A.K.; Pedrycz, W. A variable and a fixed ordering of intervals and their application in optimization with interval-valued functions. Int. J. Approx. Reason. 2020, 121, 187–205. [Google Scholar] [CrossRef]
- Nguyen, J.; Armisen, A.; Sánchez-Hernández, G.; Casabayó, M.; Agell, N. An OWA-based hierarchical clustering approach to understanding users’ lifestyles. Know. Based Syst. 2020, 190, 105308. [Google Scholar] [CrossRef]
- Verma, R.; Mittal, A. Multiple attribute group decision-making based on novel probabilistic ordered weighted cosine similarity operators with Pythagorean fuzzy information. Granul. Comput. 2023, 8, 111–129. [Google Scholar] [CrossRef]
- Huang, Z.; Weng, S.; Lv, Y.; Liu, H. Ranking Method of Intuitionistic Fuzzy Numbers and Multiple Attribute Decision Making Based on the Probabilistic Dominance Relationship. Symmetry 2023, 15, 1001. [Google Scholar] [CrossRef]
- Gao, F.J.; Wang, H.Y. Probabilistic interval decision-making based on priority. Stat. Decis. 2012, 04, 85–87. [Google Scholar]
- Nie, R.; Wang, J. Prospect theory-based consistency recovery strategies with multiplicative probabilistic linguistic preference relations in managing group decision making. Arabian J. Sci. Eng. 2020, 45, 2113–2130. [Google Scholar] [CrossRef]
- Liu, R.; Fei, L.; Mi, J. A Multi-Attribute Decision-Making Method Using Belief-Based Probabilistic Linguistic Term Sets and Its Application in Emergency Decision-Making. Comput. Model. Eng. Sci. 2023, 136, 2039–2067. [Google Scholar] [CrossRef]
- Qiu, D.S.; He, C.; Zhu, X.M. Interval number ranking method based on probability credibility. Control. Decis. 2012, 27, 1894–1898. [Google Scholar]
- Hantoobi, A.; Sendeyah. A Decision Modelling Approach for Security Modules of Delegation Methods in Mobile Cloud Computing using Probabilistic Interval Neutrosophic Hesitant Fuzzy Set; The British University in Dubai (BUiD): Dubai, United Arab Emirates, 2023. [Google Scholar]
- Song, J.; Ni, Z.W.; Wu, W.Y.; Jin, F.F.; Li, P. Multi-attribute decision making method based on probability dual hesitant fuzzy information correlation coefficient under unknown attribute weight information. Pattern Recogn. Artif. Intell. 2022, 35, 306–322. [Google Scholar]
- Xie, G.; Wang, K.; Wu, X.; Wang, J.; Li, T.; Peng, Y.; Zhang, H. A hybrid multi-stage decision-making method with probabilistic interval-valued hesitant fuzzy set for 3D printed composite material selection. Eng. Appl. Artif. Intell. 2023, 123, 106483. [Google Scholar] [CrossRef]
- Luo, S.H.; Fang, T.; Liu, J. Probabilistic interval-valued intuitionistic hesitant fuzzy Maclaurin symmetric averaging operator and decision method. Control. Decis. 2021, 36, 1249–1258. [Google Scholar]
- Fermé, E.; Hansson, S.O. AGM 25 years: Twenty-five years of research in belief change. J. Philos. Logic. 2011, 40, 295–331. [Google Scholar] [CrossRef]

| A1 | A2 | A3 | A4 | |
|---|---|---|---|---|
| C1 | [1,2]0.6, [2,3]0.3, [3,4]0.1 | [2,3]0.7, [3,4]0.1, [5,6]0.2 | [1,3]0.5, [3,4]0.3, [4,5]0.2 | [1,2]0.7, [3,4]0.1, [4,5]0.2 |
| C2 | [1,3]0.4, [3,4]0.4, [5,6]0.2 | [1,2]0.35, [2,3]0.65 | [2,3]0.4, [3,4]0.55, [4,5]0.05 | [1,3]0.55, [3,4]0.45 |
| C3 | [1,2]0.2, [2,3]0.8 | [2,3]0.9, [3,4]0.09, [4,5]0.01 | [3,4]0.9, [4,5]0.1 | [1,2]0.6, [2,3]0.3, [5,6]0.1 |
| C4 | [1,2]0.3, [3,4]0.6, [4,5]0.1 | [1,2]0.3, [3,4]0.7 | [1,2]0.55, [3,4]0.41, [4,5]0.04 | [1,2]0.7, [2,3]0.3 |
| C5 | [1,3]0.9, [3,4]0.08, [5,6]0.02 | [2,3]0.7, [3,4]0.2, [5,6]0.1 | [1,2]0.6, [3,4]0.25, [5,6]0.15 | [1,2]0.3, [2,3]0.5, [4,5]0.2 |
| C6 | [1,2]0.75, [3,4]0.25 | [1,2]0.6, [2,3]0.3, [3,4]0.1 | [1,2]0.8, [3,5]0.17, [5,6]0.03 | [1,2]0.6, [2,4]0.4 |
| A1 | A2 | A3 | A4 | |
|---|---|---|---|---|
| C1 | [1,2]0.6, [2,3]0.3, [3,4]0.1 | [2,3]0.7, [3,4]0.1, [5,6]0.2 | [1,3]0.5, [3,4]0.3, [4,5]0.2 | [1,2]0.7, [3,4]0.1, [4,5]0.2 |
| C2 | [1,3]0.4, [3,4]0.4, [5,6]0.2 | [1,2]0.35, [2,3]0.65 | [2,3]0.4, [3,4]0.55, [4,5]0.05 | [1,3]0.55, [3,4]0.45 |
| C3 | [1,2]0.2, [2,3]0.8 | [2,3]0.9, [3,4]0.09, [4,5]0.01 | [3,4]0.9, [4,5]0.1 | [1,2]0.6, [2,3]0.3, [5,6]0.1 |
| C4 | [1,2]0.3, [3,4]0.6, [4,5]0.1 | [1,2]0.3, [3,4]0.7 | [1,2]0.55, [3,4]0.41, [4,5]0.04 | [1,2]0.7, [2,3]0.3 |
| C5 | [1,3]0.9, [3,4]0.08, [5,6]0.02 | [2,3]0.7, [3,4]0.2, [5,6]0.1 | [1,2]0.6, [3,4]0.25, [5,6]0.15 | [1,2]0.3, [2,3]0.5, [4,5]0.2 |
| C6 | [1,2]0.75, [3,4]0.25 | [1,2]0.6, [2,3]0.3, [3,4]0.1 | [1,2]0.8, [3,5]0.17, [5,6]0.03 | [1,2]0.6, [2,4]0.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruan, C.; Gong, S.; Chen, X. Probabilistic Interval Ordering Prioritized Averaging Operator and Its Application in Bank Investment Decision Making. Axioms 2023, 12, 1007. https://doi.org/10.3390/axioms12111007
Ruan C, Gong S, Chen X. Probabilistic Interval Ordering Prioritized Averaging Operator and Its Application in Bank Investment Decision Making. Axioms. 2023; 12(11):1007. https://doi.org/10.3390/axioms12111007
Chicago/Turabian StyleRuan, Chuanyang, Shicheng Gong, and Xiangjing Chen. 2023. "Probabilistic Interval Ordering Prioritized Averaging Operator and Its Application in Bank Investment Decision Making" Axioms 12, no. 11: 1007. https://doi.org/10.3390/axioms12111007
APA StyleRuan, C., Gong, S., & Chen, X. (2023). Probabilistic Interval Ordering Prioritized Averaging Operator and Its Application in Bank Investment Decision Making. Axioms, 12(11), 1007. https://doi.org/10.3390/axioms12111007








