High-Performance Computational Method for an Extended Three-Coupled Korteweg–de Vries System
Abstract
:1. Introduction
2. Analysis of the Presented Methodology
2.1. The Sub Equation Method
2.2. Fundamental Plan of the q-HATM
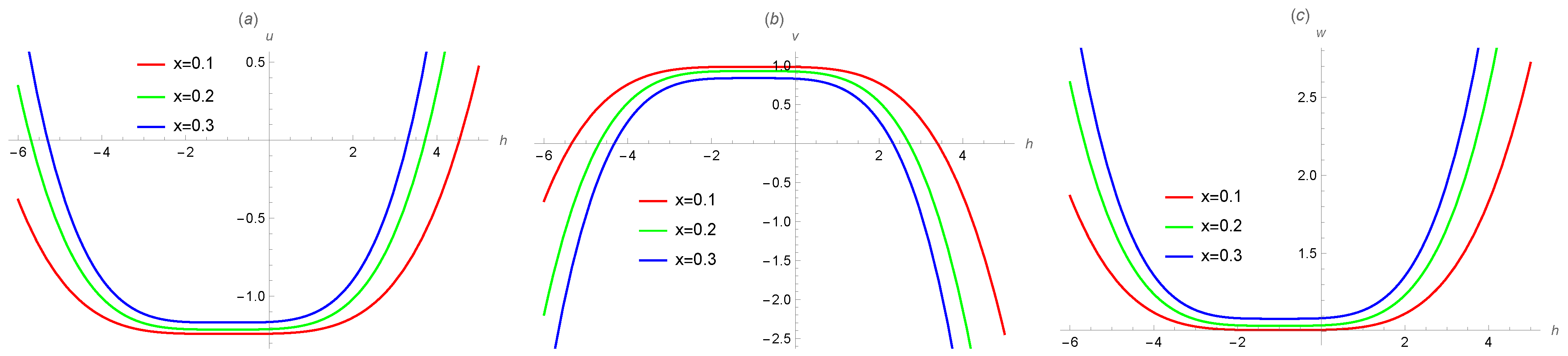
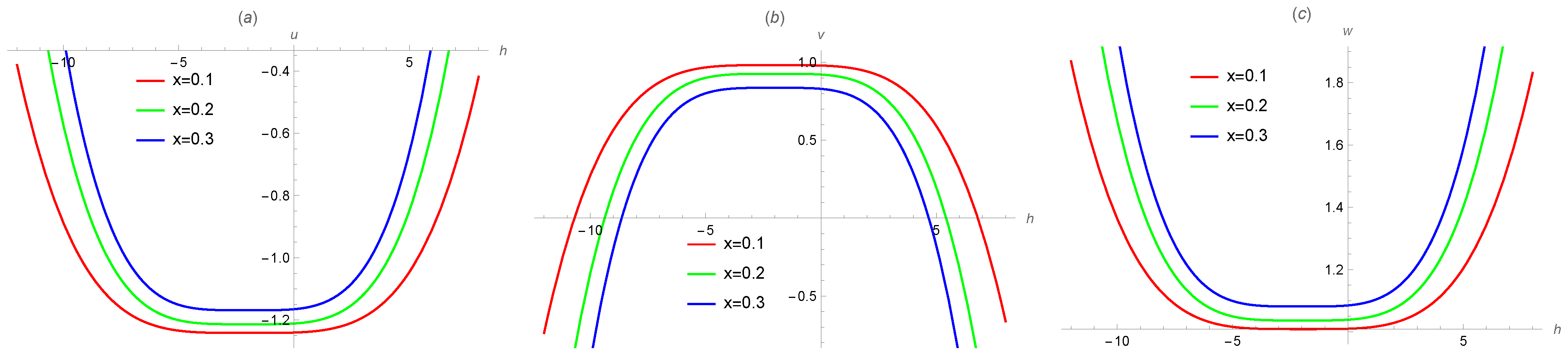
2.3. Convergence Analysis of the q-HATM
3. Applications of the Extended Three-Coupled Korteweg–de Vries System
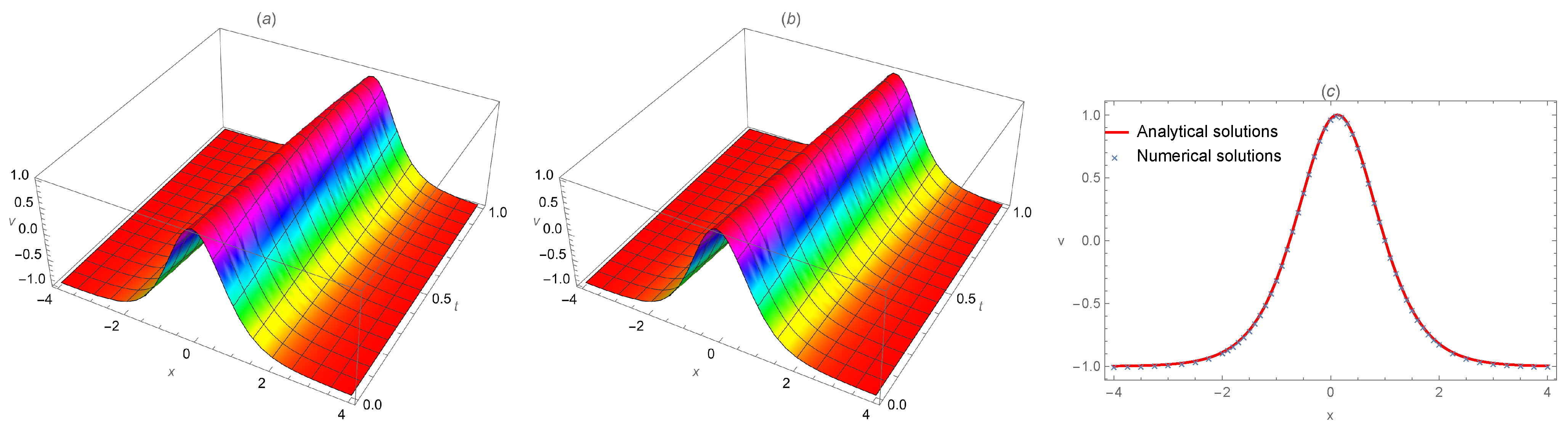
3.1. Analytical Solutions for Equation (1)
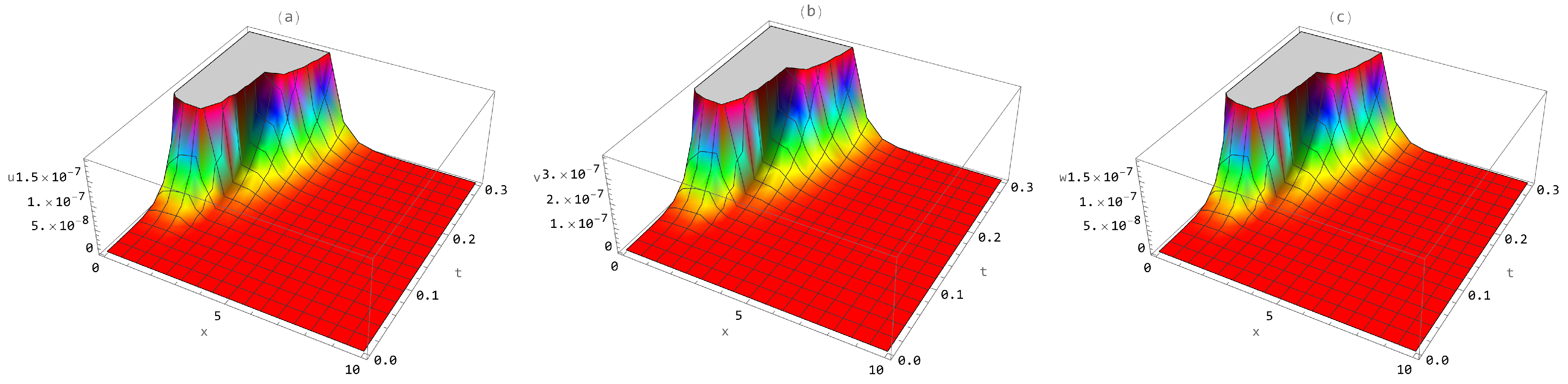
3.2. Numerical Solutions for Equation (1)
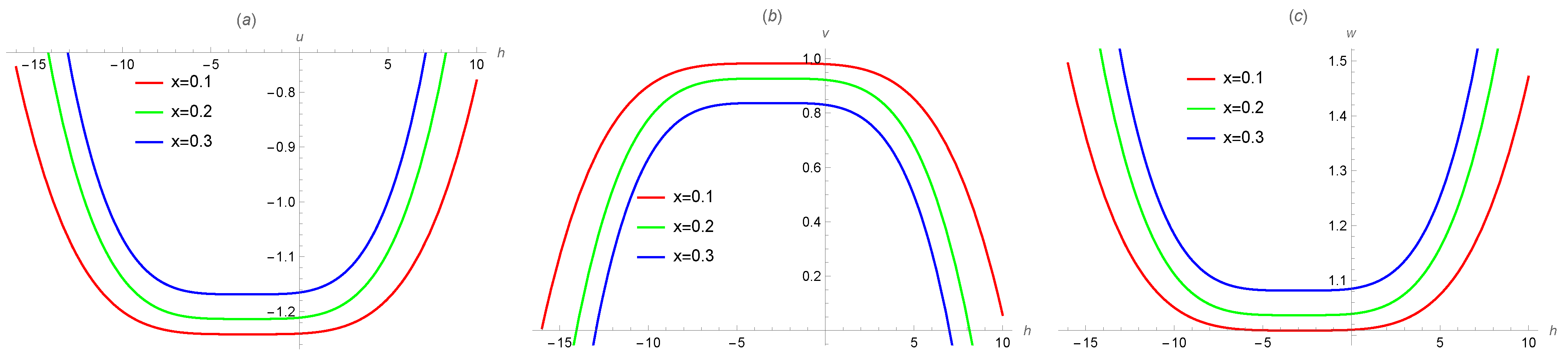
4. Numerical Results and Simulation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Leung, A.W. Systems of Nonlinear Partial Differential Equations: Applications to Biology and Engineering; Springer Science Business Media: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Inc, M.; Yusuf, A.; Aliyu, A.I.; Baleanu, D. Soliton solutions and stability analysis for some conformable nonlinear partial differential equations in mathematical physics. Opt. Quantum Electron. 2018, 50, 190. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Arnous, A.H. Exact Traveling Wave Solutions of Nonlinear PDEs in Mathematical Physics Using the Modified Simple Equation Method. Appl. Appl. Math. 2013, 8, 553–572. [Google Scholar]
- Boureghda, A. Numerical solution of the oxygen diffusion in absorbing tissue with a moving boundary. Commun. Numer. Methods Eng. 2006, 22, 933–942. [Google Scholar] [CrossRef]
- Botmart, T.; Alotaibi, B.M.; Shah, R.; El-Sherif, L.S.; El-Tantawy, S.A. A Reliable Way to Deal with the Coupled Fractional Korteweg-De Vries Equations within the Caputo Operator. Symmetry 2022, 14, 2452. [Google Scholar] [CrossRef]
- Aljahdaly, N.H.; Akgül, A.; Shah, R.; Mahariq, I.; Kafle, J. A comparative analysis of the fractional-order coupled Korteweg–De Vries equations with the Mittag–Leffler law. J. Math. 2022, 8876149–8876178. [Google Scholar] [CrossRef]
- Shah, N.A.; Alyousef, H.A.; El-Tantawy, S.A.; Shah, R.; Chung, J.D. Analytical investigation of fractional-order Korteweg-De-Vries-type equations under Atangana-Baleanu-Caputo operator: Modeling nonlinear waves in a plasma and fluid. Symmetry 2022, 14, 739. [Google Scholar] [CrossRef]
- Ma, W.-X. AKNS type reduced integrable bi-Hamiltonian hierarchies with four potentials. Appl. Math. Lett. 2023, 145, 108775. [Google Scholar] [CrossRef]
- Ma, W.-X. Four-component integrable hierarchies of Hamiltonian equations with (m+n+2)th-order Lax pairs. Theor. Math. Phys. 2023, 216, 1180–1188. [Google Scholar] [CrossRef]
- Liao, S. On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 2004, 147, 499–513. [Google Scholar] [CrossRef]
- Liao, S. Series solution of nonlinear eigenvalue problems by means of the homotopy analysis method. Nonlinear Anal. Real World Appl. 2009, 10, 2455–2470. [Google Scholar] [CrossRef]
- Liao, S.; Tan, Y. A general approach to obtain series solutions of nonlinear differential equations. Stud. Appl. Math. 2007, 119, 297–354. [Google Scholar] [CrossRef]
- Liao, S.J. An approximate solution technique which does not depend upon small parameters: A special example. Int. J. Non-Linear Mech. 1995, 30, 371–380. [Google Scholar] [CrossRef]
- El-Tawil, M.A.; Huseen, S.N. The Q-homotopy analysis method (QHAM). Int. J. Appl. Math. Mech. 2012, 8, 51–75. [Google Scholar]
- Zhao, Y.; Lin, Z.; Liu, Z. The improved homotopy analysis method for the Thomas–Fermi equation. Appl. Math Comput. 2012, 218, 8363–8369. [Google Scholar] [CrossRef]
- Mesloub, S.; Alsaud, H. Exploring the Efficiency of the q-Homotopy Analysis Transform Method for Solving a Fractional Initial Boundary Value Problem with a Nonlocal Condition. Axioms 2023, 12, 790. [Google Scholar] [CrossRef]
- Shah, R.; Khan, H.; Baleanu, D. Fractional Whitham–Broer–Kaup equations within modified analytical approaches. Axioms 2019, 8, 125. [Google Scholar] [CrossRef]
- Malagi, N.S.; Veeresha, P.; Prasannakumara, B.C.; Prasanna, G.D.; Prakasha, D.G. A new computational technique for the analytic treatment of time-fractional Emden Fowler equations. Math. Comput. Simul. 2021, 190, 362–376. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G. A novel technique for (2+1)-dimensional time-fractional coupled Burgers equations. Math. Comput. Simul. 2019, 166, 324–345. [Google Scholar] [CrossRef]
- El-Tawil, M.A.; Huseen, S.N. On Convergence of q-Homotopy Analysis Method. Int. J. Contemp. Math. Sci. 2013, 8, 481–497. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Kumar, D. An efficient technique for nonlinear time-fractional Klein-Fock-Gordon equation. Appl. Math. Comput. 2020, 364, 124637. [Google Scholar] [CrossRef]
- Gao, X.Y.; Guo, Y.J.; Shan, W.-R.; Zhou, T.Y. Singular manifold, auto-Bäcklund transformations and symbolic-computation steps with solitons for an extended three-coupled Korteweg-de Vries system. Int. J. Geom. Methods Mod. Phys. 2022, 19, 2250229. [Google Scholar] [CrossRef]
- Gao, X.Y.; Guo, Y.J.; Shan, W.R.; Zhou, T.Y. Report on an extended three-coupled Korteweg-de Vries system. Ric. Mat. 2023. [Google Scholar] [CrossRef]
- Gao, X.Y.; Guo, Y.J.; Shan, W.R. Hetero-Bäcklund transformation, bilinear forms and N solitons for a generalized three-coupled Korteweg-de Vries system. Qual. Theory Dyn. Syst. 2021, 20, 87–98. [Google Scholar] [CrossRef]
- Ray, S.; Sahoo, S. New Exact Solutions of Fractional Zakharov-Kuznetsov and Modified Zakharov-Kuznetsov Equations Using Fractional Sub-Equation Method. Commun. Theor. Phys. 2015, 63, 25–30. [Google Scholar] [CrossRef]
- Senol, M. Analytical and approximate solutions of (2+1)-dimensional time-fractional Burgers-Kadomtsev-Petviashvili equation. Commun. Theor. Phys. 2020, 72, 055003. [Google Scholar] [CrossRef]
- Adel, M. Numerical simulations for the variable order two-dimensional reaction sub-diffusion equation: Linear and Nonlinear. Fractals 2022, 30, 2240019. [Google Scholar] [CrossRef]
- Odibat, Z.M.; Shawagfeh, N.T. Generalized Taylor’s formula. Appl. Math. Comput. 2007, 186, 286–293. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Nikonorov, Y.G. On the integral mean value theorem. Sib. Math. J. 1993, 34, 150–152. [Google Scholar] [CrossRef]
- Magrenan, A.A. A new tool to study real dynamics: The convergence plane. Appl. Math. Comput. 2014, 248, 215–224. [Google Scholar] [CrossRef]


| t | x | Numerical | Exact | Absolute Error |
|---|---|---|---|---|
| 0.1 | −10 | −0.25000001 | −0.25000001 | |
| −5 | −0.25016025 | −0.25016025 | ||
| 0 | −1.24610392 | −1.24610390 | ||
| 5 | −0.25020576 | −0.25020576 | ||
| 10 | −0.25000001 | −0.25000000 | ||
| 0.2 | −10 | −0.25000001 | −0.25000001 | |
| −5 | −0.25014142 | −0.25014142 | ||
| 0 | −1.23453776 | −1.23453633 | ||
| 5 | −0.25023315 | −0.25023315 | ||
| 10 | −0.25000001 | −0.25000001 |
| t | x | Numerical | Exact | Absolute Error |
|---|---|---|---|---|
| 0.1 | −10 | −0.99999999 | −0.99999999 | |
| −5 | −0.99967950 | −0.99967950 | ||
| 0 | 0.99220785 | 0.99220780 | ||
| 5 | −0.99958848 | −0.99958848 | ||
| 10 | −0.99999998 | −0.99999998 | ||
| 0.2 | −10 | −0.99999999 | −0.99999999 | |
| −5 | −0.99971716 | −0.99971716 | ||
| 0 | 0.96907552 | 0.96907266 | ||
| 5 | −0.99953370 | −0.99953370 | ||
| 10 | −0.99999998 | −0.99999998 |
| t | x | Numerical | Exact | Absolute Error |
|---|---|---|---|---|
| 0.1 | −10 | 1.99999999 | 1.99999999 | |
| −5 | 1.99983975 | 1.99983975 | ||
| 0 | 1.00389608 | 1.00389610 | ||
| 5 | 1.99979424 | 1.99979424 | ||
| 10 | 1.99999999 | 1.99999999 | ||
| 0.2 | −10 | 1.99999999 | 1.99999999 | |
| −5 | 1.99985858 | 1.99985858 | ||
| 0 | 1.01546224 | 1.01546367 | ||
| 5 | 1.99976685 | 1.99976685 | ||
| 10 | 1.99999999 | 1.99999999 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Feng, X. High-Performance Computational Method for an Extended Three-Coupled Korteweg–de Vries System. Axioms 2023, 12, 990. https://doi.org/10.3390/axioms12100990
Wang P, Feng X. High-Performance Computational Method for an Extended Three-Coupled Korteweg–de Vries System. Axioms. 2023; 12(10):990. https://doi.org/10.3390/axioms12100990
Chicago/Turabian StyleWang, Panpan, and Xiufang Feng. 2023. "High-Performance Computational Method for an Extended Three-Coupled Korteweg–de Vries System" Axioms 12, no. 10: 990. https://doi.org/10.3390/axioms12100990
APA StyleWang, P., & Feng, X. (2023). High-Performance Computational Method for an Extended Three-Coupled Korteweg–de Vries System. Axioms, 12(10), 990. https://doi.org/10.3390/axioms12100990






