An Interval Type 2 Fuzzy Decision-Making Framework for Exploring Critical Issues for the Sustenance of the Tea Industry

Abstract

The purpose of the present study is to propose an interval-valued type 2 fuzzy set (IT2FS)-based analytic hierarchy process (AHP) framework to unfold the critical challenging factors influencing the sustenance and growth of the Indian tea industry. The current work follows an expert opinion-based group decision-making approach. The challenging factors have been identified through a literature review and finalized after a pilot study based on the opinions of professionals, consumers, and experts. Finally, the critical challenging factors and sub-factors have been figured out through analysis of the responses of the experts. To offset the subjective bias, an IT2FS-based granular analysis has been carried out. The findings reveal that market diversification and productivity are the central issues. Additionally, it is important to give attention to improving the quality of the products, increasing the use of modern technology and organic farming, and developing a variety of products. The result shows a considerable level of consistency in the group decision-making (CR < 0.1) for all pairwise comparisons. The present work shall be of use to formulate appropriate strategies and policy decisions. It shows a robust application of IT2FS-AHP for complex decision-making in real life.

1. Introduction

Complex real-life problems pose decision-making dilemmas for analysts due to the presence of a set of conflicting criteria. In such type of intricate situations, the selection of an appropriate course of action or choosing the best possible alternative requires setting the goal precisely, effectively assessing the effects of the conflicting objectives and judiciously prioritizing the criteria (by calculating their weights) to formulate the best possible decision [1]. MCDM is a sub-domain of applied operations research that provides the decision makers with a sizeable number of models for dealing with complex problems dealing with multiple objectives or criteria. The decision-makers first set their goals to select the alternatives and criteria. Then, the MCDM models formulate the decision-making problems in terms of a set of available alternative options and criteria. Prioritization of the criteria on the basis of their weights is a very important and critical task. The calculation of the criteria weights can be performed in two ways: using objective information (derived from the decision matrix) and using subjective opinions or ratings given by the decision-makers or domain experts. Historically, the literature has been contributed notably by researchers and analysts in this regard. There are umpteen methods available for calculating criteria weights, such as the entropy method, CRITIC, the IVEP method, LOPCOW, and SPC, which were developed primarily for using objective information. Additionally, there is a variety of methods developed primarily to calculate the criteria weights using subjective opinions like the analytic hierarchy process (AHP), the SWARA method, the best–worst method, PIPRECIA, FUCOM, LMAW, and the vital-immaterial mediocre method (VIMM).

The AHP method has been widely considered in past studies as an appropriate technique for criteria weight calculation due to the soundness of the model [2]. The AHP constructs a hierarchical MCDM structure based on decision-making goals and objectives, criteria and sub-criteria, and alternatives [3,4]. The AHP provides a sound mechanism to test and validate the reliability of the decision-maker’s judgments by calculating the consistency ratio (CR) and setting reference values. A lower value of CR is an indication of a higher consistency wherein 0.10 is the reference level. In effect, the AHP provides a powerful mechanism to deal with decision-making bias and maintain group harmony [5]. There are some criticisms of the AHP method as the possibility of misinterpretation of true priorities, the complexity of calculating a greater number of criteria, and the possibility of rank reversal issues in some occasions, especially due to the inclusion of indifferent criteria [6]. However, because of its inherent strength, researchers have been applying the AHP to various problems. A plethora of research has been conducted that used the AHP to derive the criteria weights and compare the alternatives; for instance, the identification of the challenges of biomass energy industries [7], the assessment of root causes for landslide [8], facility location selection [9,10], the assessment of utilities of blockchain technology for sustainable supply chain management [11], the identification of the barriers of retail supply chain management [12], critical success factors for quality management in the digital age [13], municipal solid waste management [14], the measurement of sustainability performance [15], among others.

Most of the real-life situations need more precise information [16,17,18,19,20]. The decisions are taken under uncertainty and are often influenced by subjective bias [21,22]. To deal with such situations, a new domain of data analysis was introduced by [23], which propounded the use of ordinary fuzzy sets (FS), aka type 1 fuzzy sets. Unlike the crisp set, the FS considers a variable degree of memberships of the elements from the universe of discourse. The FS has been used in numerous real-life complex problems, and a wide number of extensions have been made to date. In continuation with the concept of FS, type 2 fuzzy sets (T2 FS) were developed by Zadeh [24] in recognition of the need to handle uncertainties associated with the membership function. Later, several scientists and researchers worked on T2 FS for further expansion of the field and the development of various operations and concepts [25,26,27]. In T2 FS, the grades of membership are also considered fuzzy [28]. In other words, the T2 FS describes the fuzziness of fuzzy sets. The membership function of T2 FS is three-dimensional in nature, which helps to analyze uncertain situations in a better way with greater accuracy and additional degrees of freedom, especially while dealing with linguistic uncertainties [29].

Although the T2 FS provides a computationally intensive analysis, for simplification, interval type 2 fuzzy sets (IT2 FS) were introduced. The secondary membership function of the IT2 FS is an interval set in nature. The IT2 FS provides an efficient yet simple process of data analysis under uncertainties [30] with a wide range of applications [31]. It is also advantageous, as the mathematical operations for IT2 FS are grounded on the concepts of FS [32]. To represent all the human inputs that are subjective in nature, fuzzy set theory is the natural way of expressing linguistic subjective inputs received from the experts in the decision-making process. We have used interval type 2 fuzzy sets for the reason that in complex decision-making situations. The IT2 FS allows the incorporation of linguistic uncertainties, where it is difficult to determine an exact membership function for a fuzzy set. While the membership function of ordinary fuzzy sets is two-dimensional, the membership functions of type 2 fuzzy sets are three-dimensional, which makes it possible to directly model uncertainties associated with the subjective judgments of decision-makers. It is the third dimension that provides additional degrees of freedom that make it possible to model complex decision-making.

The IT2 FS has been applied by researchers in solving critical real-life issues. Some of the recent applications are found in green supplier selection [33], facility location planning [34,35], project management [36], and quality control [37]. Researchers have used IT2 FS to extend the applications of the AHP method in various practical problems. Kahraman et al. [38] first extended the fuzzy AHP model of Buckley [39] using IT2 FS. Later, Oztaysi [40] demonstrated the application of IT2 FS-AHP in a group decision-making situation to solve the problem of the selection of ERP. Gradually, the IT2 FS-AHP has been found in numerous cases to deal with several practical problems. Examples include a selection of suitable location for wind farm using IT2 FS-AHP with GIS [41], warehouse location selection using ordered weighted average and Bonferroni mean [42], green supplier selection for home appliance product manufacturing [43], portfolio design for investment decision-making [44], a comparison of e-learning platforms on the basis of critical factors [45], a SCOR model-based performance evaluation of supply chain management for humanitarian operations [46], industrial process design [47], vaccine selection [48], the design of an after-sales support system [49], blockchain project evaluation [50], and green human resource management [51].

The aim of this study is to show the potential applicability of type 2 fuzzy sets in multi-criteria selection problems using the decision process leading to the sustainable development of the Indian Tea Industry as a case example. The subjective judgment, selection, and preferences of decision-makers greatly influence the AHP results. Decision-maker’s requirements for evaluating alternatives always contain ambiguity and multiplicity of meaning. Furthermore, it is also recognized that the human assessment of qualitative attributes is always subjective and thus imprecise. In such a complex situation, the IT2 FS allows the incorporation of linguistic uncertainties, where it is difficult to determine an exact membership function for a fuzzy set. While the membership function of ordinary fuzzy sets is two-dimensional, the membership functions of type 2 fuzzy sets are three-dimensional, making it possible to directly model uncertainties associated with decision-makers’ subjective judgments. In the present work, we have built an intelligent decision analysis model using IT2 FS-AHP for discerning the critical issues for the sustenance of the Indian tea industry. Since strategic decision-making is subject to the influence of a number of conditions imposed by the uncertain external environment, the use of the IT2 FS is deemed fit for our objective. Further, the AHP is a well-versed model with extensive applications in complex decision-making. We prefer to use the IT2 FS-based AHP for deriving the weights of strategic issues. The AHP allows the decision-makers to combine their intuition, belief, experience, and knowledge, and it is useful in group decision-making set-up handling both quantitative and qualitative aspects [52].

After a review of the past studies on the tea industry, especially in the Indian context, the researchers have noticed that there is a scantiness of a granular analysis on critical strategic issues vis-à-vis sustainability. The extant literature shows some studies on the subject matter. For example, in [53], the researchers used multi-agent-based decision modeling under imprecision and market dynamics to analyze the effect of socio-political and CSR conditions. The authors [54] investigated the strategic implications of the rise in domestic consumption of tea for the entire value chain in the Indian context. Paul et al. [55] emphasized the need to embrace circular supply chain practices for the tea industry and proposed a blockchain and RFID-enabled system architecture. Wenner [56] discussed various industrial issues of the Indian tea industry. The Indian tea industry is an age-old business. Over the years, there have been notable changes in the operating environment, which necessitates bridging the gap in the requisite skill set through upskilling. In this regard, the researchers [57] conducted a study on skill development and its impact on overall performance enhancement.

The novelty and contributions of the present paper can be elaborated as follows. From the literature review, it is seen that there is a need to carry out a comprehensive evaluation of the critical factors for the subsistence of the age-old Indian tea industry. The Indian tea industry is at a crossroads, primarily for three reasons: a rise in domestic consumption and global competition, technological advancement, and the need for sustainable development. In this regard, the current work fills the gap in the literature by providing a robust and granular group decision analysis framework for discerning the critical strategic issues for Indian tea industries. Furthermore, the use of IT2 FS-AHP is still limited to specific engineering and managerial applications. The current work extends the domain of application of IT2 FS-AHP for industry analysis.

The rest of the paper is structured as follows. In the next section (Section 2), some preliminary concepts of FS, T2 FS, and IT2 FS are explained. Section 3 presents the methodological steps of the IT2 FS-AHP. The case study on the Indian tea industry is briefly described in Section 4. Section 5 exhibits the major findings of the data analysis. In Section 6, a short discussion is made based on the findings. At the end, Section 7 concludes the paper.

2. Definitions

In this section, we discuss various preliminary definitions of fuzzy sets and IT2 FS [23,24,26,27,28,29,58,59,60].

2.1. Fuzzy Set (FS)

A fuzzy set $X$ in the universe of information U can be defined as a set of elements, which can be represented as:

$$X=\left\{\left(x,\mu (x)|x\in U\right)\right\}$$

(1)

Here, $\mu (x)$ represents the degree of membership of $x$ in $X$ such that the values lie between 0 (no membership) and 1 (complete membership).

2.2. Type 2 Fuzzy Set (T2 FS)

A type 2 fuzzy set $\tilde{A}$ in $X$ is a fuzzy set where the membership function is itself a fuzzy set. The membership function is known as the type 2 membership function. A T2 FS $\tilde{A}$ is defined as:

$$\tilde{A}=\left\{\left((x,u),{\mu }_{\tilde{A}}(x,u)\right);\forall x\in X,\forall u\in J_x\subseteq [0,1]\right\}$$

(2)

where $0\le {\mu }_{\tilde{A}}(x,u)\le 1$ is the type 2 membership function (secondary), while $J_x$ is the primary membership function.

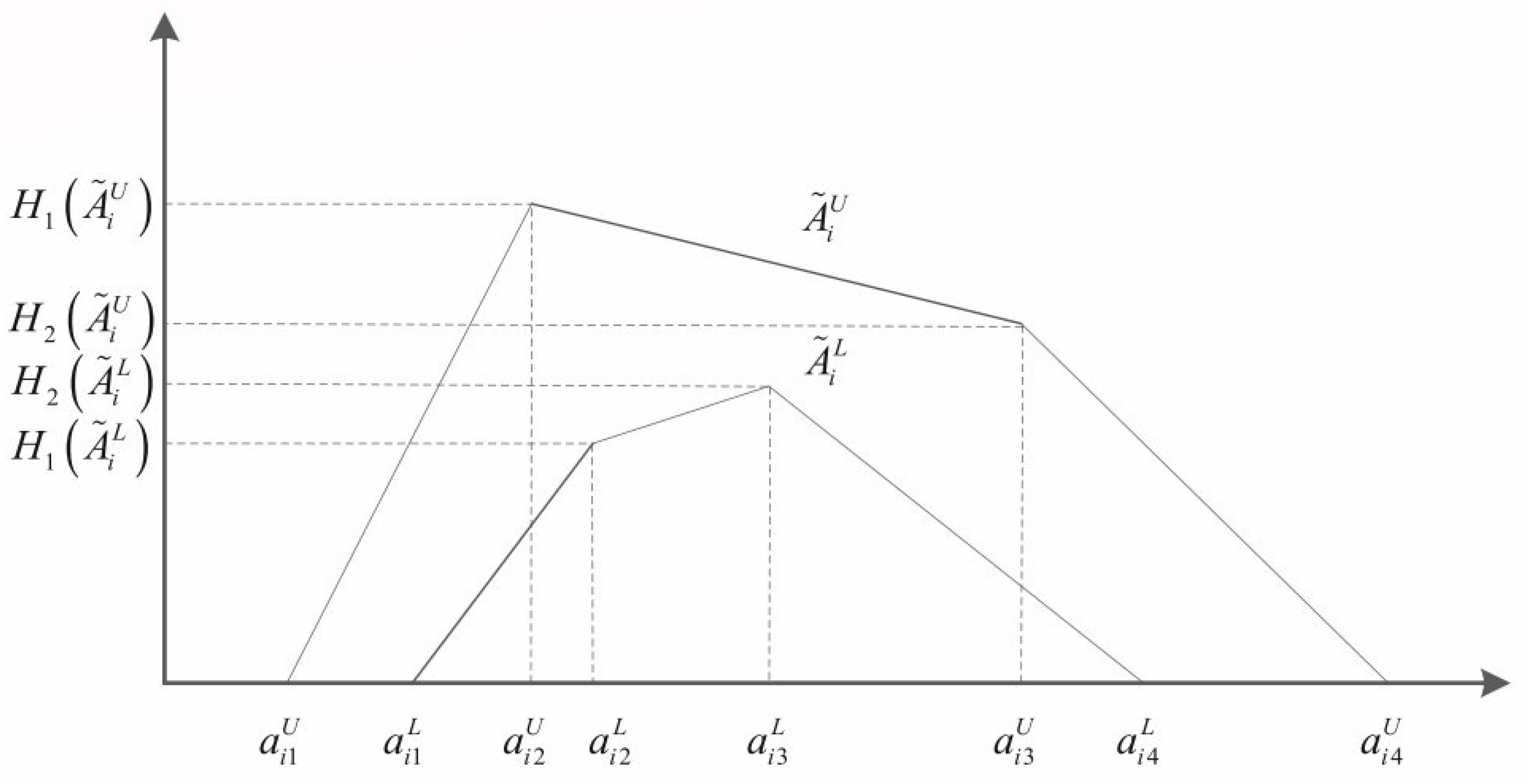
2.3. Interval Type 2 Fuzzy Set (IT2 FS)

The IT2 FS is a special variant of T2 FS when ${\mu }_{\tilde{A}}(x,u)=1$ for all $x\in X$. For an IT2 FS $\tilde{\tilde{A}}$, the following definition holds true [33,39].

$$\tilde{\tilde{A}}={\displaystyle \underset{x\in X}{\int }{\displaystyle \underset{u\in J_x}{\int }\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$(x,u)$}\right.}}$$

(3)

The IT2FS is defined as the footprint of uncertainty, i.e., the primary membership function [35]. The trapezoidal IT2 FS is defined as [38,61,62]:

$$\begin{array}{l}\tilde{\tilde{A}}=\left({\tilde{A}}_i^u,{\tilde{A}}_i^l\right)=((a_{i1}^u,a_{i2}^u,a_{i3}^u,a_{i4}^u;H_1({\tilde{A}}_i^u),H_2({\tilde{A}}_i^u)),\\ (a_{i1}^l,a_{i2}^l,a_{i3}^l,a_{i4}^l;H_1({\tilde{A}}_i^l),H_2({\tilde{A}}_i^l)))\end{array}$$

(4)

Figure 1 shows the pictorial representation of the trapezoidal IT2 FS.

It may be noted that the upper and lower membership functions, i.e., ${\tilde{A}}_i^u,{\tilde{A}}_i^l$, are type 1 fuzzy sets, where $a_{i1}^u,a_{i2}^u,a_{i3}^u,a_{i4}^u,a_{i1}^l,a_{i2}^l,a_{i3}^l,a_{i4}^l$ are the reference points of the IT2FS with the conditions $a_{i1}^u<a_{i2}^u<a_{i3}^u<a_{i4}^u$ and $a_{i1}^l<a_{i2}^l<a_{i3}^l<a_{i4}^l$. $H_k({\tilde{A}}_i^u)\in [0,1]$ and $H_k({\tilde{A}}_i^l)\in [0,1]$, where $k=1,2$, are the membership values of the elements $a_{k+1}^u$ and $a_{k+1}^l$ in the upper and lower trapezoidal membership functions (${\tilde{A}}_i^u$ and ${\tilde{A}}_i^l$), respectively.

The IT2 FS is a bounded convex fuzzy set with a universe of discourse as the entire real line. ${\tilde{\tilde{A}}}_1$ and ${\tilde{\tilde{A}}}_2$ are two IT2 fuzzy numbers (IT2 FN). Some of the fundamental operations (needed to understand the analysis carried out in the present work) are mentioned below. For more details and operations on the trapezoidal IT2FS, the work of [61] may be consulted.

$$\begin{array}{l}{\tilde{\tilde{A}}}_1=((a_{11}^u,a_{12}^u,a_{13}^u,a_{14}^u;H_1({\tilde{A}}_1^u),H_2({\tilde{A}}_1^u)),(a_{11}^l,a_{12}^l,a_{13}^l,a_{14}^l;H_1({\tilde{A}}_1^l),H_2({\tilde{A}}_1^l)))\\ {\tilde{\tilde{A}}}_2=((a_{21}^u,a_{22}^u,a_{23}^u,a_{24}^u;H_1({\tilde{A}}_2^u),H_2({\tilde{A}}_2^u)),(a_{21}^l,a_{22}^l,a_{23}^l,a_{24}^l;H_1({\tilde{A}}_2^l),H_2({\tilde{A}}_2^l)))\end{array}$$

Then, the following definitions hold true [63]:

Addition:

$$\begin{array}{l}{\tilde{\tilde{A}}}_1+{\tilde{\tilde{A}}}_2=((a_{11}^u+a_{21}^u,a_{12}^u+a_{22}^u,a_{13}^u+a_{23}^u,a_{14}^u+a_{24}^u;\min (H_1({\tilde{A}}_1^u),H_1({\tilde{A}}_2^u)),\min (H_2({\tilde{A}}_1^u),H_2({\tilde{A}}_2^u))),\\ (a_{11}^l+a_{21}^l,a_{12}^l+a_{22}^l,a_{13}^l+a_{23}^l,a_{14}^l+a_{24}^l;\min (H_1({\tilde{A}}_1^l),H_1({\tilde{A}}_2^l)),\min (H_2({\tilde{A}}_1^l),H_2({\tilde{A}}_2^l))))\end{array}$$

(5)

Subtraction:

$$\begin{array}{l}{\tilde{\tilde{A}}}_1-{\tilde{\tilde{A}}}_2=((a_{11}^u-a_{21}^u,a_{12}^u-a_{22}^u,a_{13}^u-a_{23}^u,a_{14}^u-a_{24}^u;\min (H_1({\tilde{A}}_1^u),H_1({\tilde{A}}_2^u)),\min (H_2({\tilde{A}}_1^u),H_2({\tilde{A}}_2^u))),\\ (a_{11}^l-a_{21}^l,a_{12}^l-a_{22}^l,a_{13}^l-a_{23}^l,a_{14}^l-a_{24}^l;\min (H_1({\tilde{A}}_1^l),H_1({\tilde{A}}_2^l)),\min (H_2({\tilde{A}}_1^l),H_2({\tilde{A}}_2^l))))\end{array}$$

(6)

Multiplication:

$$\begin{array}{l}{\tilde{\tilde{A}}}_1\otimes {\tilde{\tilde{A}}}_2=((a_{11}^u\times a_{21}^u,a_{12}^u\times a_{22}^u,a_{13}^u\times a_{23}^u,a_{14}^u\times a_{24}^u;\min (H_1({\tilde{A}}_1^u),H_1({\tilde{A}}_2^u)),\min (H_2({\tilde{A}}_1^u),H_2({\tilde{A}}_2^u))),\\ (a_{11}^l\times a_{21}^l,a_{12}^l\times a_{22}^l,a_{13}^l\times a_{23}^l,a_{14}^l\times a_{24}^l;\min (H_1({\tilde{A}}_1^l),H_1({\tilde{A}}_2^l)),\min (H_2({\tilde{A}}_1^l),H_2({\tilde{A}}_2^l))))\end{array}$$

(7)

Division:

$$\frac{{\tilde{\tilde{A}}}_1}{{\tilde{\tilde{A}}}_2}=\left(\begin{array}{l}(\frac{a_{11}^u}{a_{24}^u},\frac{a_{12}^u}{a_{23}^u},\frac{a_{13}^u}{a_{22}^u},\frac{a_{14}^u}{a_{21}^u};\min (H_1({\tilde{A}}_1^u),H_1({\tilde{A}}_2^u)),\min (H_2({\tilde{A}}_1^u),H_2({\tilde{A}}_2^u))),\\ (\frac{a_{11}^l}{a_{24}^l},\frac{a_{12}^l}{a_{23}^l},\frac{a_{13}^l}{a_{22}^l},\frac{a_{14}^l}{a_{21}^l};\min (H_1({\tilde{A}}_1^l),H_1({\tilde{A}}_2^l)),\min (H_2({\tilde{A}}_1^l),H_2({\tilde{A}}_2^l)))\end{array}\right)$$

(8)

Inverse:

$$\begin{array}{l}\frac{1}{{\tilde{\tilde{A}}}_1}=((\frac{1}{a_{14}^u},\frac{1}{a_{13}^u},\frac{1}{a_{12}^u},\frac{1}{a_{11}^u};H_1({\tilde{A}}_1^u),H_2({\tilde{A}}_1^u)),\\ (\frac{1}{a_{14}^l},\frac{1}{a_{13}^l},\frac{1}{a_{12}^l},\frac{1}{a_{11}^l};H_1({\tilde{A}}_1^l),H_2({\tilde{A}}_1^l)))\end{array}$$

(9)

Division by a number $n(n>0)$:

$$\begin{array}{l}\frac{{\tilde{\tilde{A}}}_1}{n}=((\frac{1}{n}\times a_{11}^u,\frac{1}{n}\times a_{12}^u,\frac{1}{n}\times a_{13}^u,\frac{1}{n}\times a_{14}^u;H_1({\tilde{A}}_1^u),H_2({\tilde{A}}_1^u)),\\ (\frac{1}{n}\times a_{11}^l,\frac{1}{n}\times a_{12}^l,\frac{1}{n}\times a_{13}^l,\frac{1}{n}\times a_{14}^l;H_1({\tilde{A}}_1^l),H_2({\tilde{A}}_1^l)))\end{array}$$

(10)

Multiplication by a crisp value $n$:

$$\begin{array}{l}n{\tilde{\tilde{A}}}_1=((n{a}_{11}^u,n{a}_{12}^u,n{a}_{13}^u,n{a}_{14}^u;H_1({\tilde{A}}_1^u),H_2({\tilde{A}}_1^u)),\\ (n{a}_{11}^l,n{a}_{12}^l,n{a}_{13}^l,n{a}_{14}^l;H_1({\tilde{A}}_1^l),H_2({\tilde{A}}_1^l)))\end{array}$$

(11)

Geometric mean:

$$\tilde{\tilde{R}}=\sqrt[n]{{\tilde{\tilde{A}}}_1\otimes {\tilde{\tilde{A}}}_2\otimes .......\otimes {\tilde{\tilde{A}}}_n}$$

(12)

where the $n^{th}$ root of the T2 FN $\tilde{\tilde{R}}$ is defined as:

$$\sqrt[n]{\tilde{\tilde{R}}}=\left(\begin{array}{l}(\sqrt[n]{r_1^u,}\sqrt[n]{r_2^u},\sqrt[n]{r_3^u},\sqrt[n]{r_4^u};H_1({\tilde{R}}^u),H_2({\tilde{R}}^u)),\\ (\sqrt[n]{r_1^l,}\sqrt[n]{r_2^l},\sqrt[n]{r_3^l},\sqrt[n]{r_4^l};H_1({\tilde{R}}^l),H_2({\tilde{R}}^l))\end{array}\right)$$

(13)

3. The IT2 FS-AHP Method

The Fuzzy Analytic Hierarchy Process (FAHP) is the development of the traditional AHP to incorporate the uncertainties associated with linguistic variables. The fuzzy AHP method allows a more accurate description of the problem in the decision-making process. Generally, it is impossible to express the decision-makers’ uncertain preferences through crisp inputs. Therefore, the FAHP is proposed to remove the uncertainness of the AHP method, where the fuzzy comparison ratios are used. The introduction of fuzzy numbers in the fuzzy AHP and interval type 2 trapezoidal fuzzy numbers allows us to model imprecise, uncertain, and ambiguous information that we commonly encounter in real-world problems. The method used also incorporated the fuzzy AHP and IT2 fuzzy set by applying the weights obtained from the fuzzy AHP to the expected value. As described before, unlike type 1 FS, the T2 FS works with a three-dimensional membership function to deal with the uncertainties with better accuracy and lower computational complexities [43]. The IT2 FS has been applied to many problems in the literature, and successful results have been obtained. In fact, this integration method was capable of handling fuzzy MCDM problems with a more comprehensible approach by the knowledge of the interval type 2 fuzzy set. The uncertainties of employing T2FNs mean making fewer assumptions during the decision-making process, so it should lead to more realistic solutions to real-life decision-making problems. In this section, a brief description of the computational steps is provided. Detailed explanations can be found in [38,61].

Step 1: Define the problem and establish its goal. In this case, the goal is to prioritize the critical issues to overcome the challenging factors for the tea industry. Let there be $n$ number of issues. Hence, the pairwise comparison matrix is of $n\times n$ order.

Step 2: Structure the hierarchy from the top through the in-between levels by determining the criteria and, finally, at the bottom level, there is a list of the alternatives available (see Figure 2).

Step 3: Construct the pairwise comparison matrices ($\tilde{\tilde{A}}$) of the criteria and the alternatives using the fuzzy comparison scale below (see

Table 1. Type 2 fuzzy scale of importance for the linguistic variables.

Linguistic Variables	Trapezoidal Interval Type 2 Fuzzy Scales
Absolute Importance	(7,8,9,9;1,1) (7.2,8.2,8.8,9;0.8,0.8)
Very Important	(5,6,8,9;1,1) (5.2,6.2,8.8,8.8;0.8,0.8)
Fair Importance	(3,4,6,7;1,1) (3.2,4.2,5.8,6.8;0.8,0.8)
Slight Importance	(1,2,4,5;1,1) (1.2,2.2,3.8,4.8;0.8,0.8)
Equal Importance	(1,1,1,1;1,1) (1,1,1,1;1,1)

). The pairwise comparison matrix is given as:

$$\tilde{\tilde{A}}={\left(\begin{array}{cccc}1& {\tilde{\tilde{a}}}_{12}& ....& {\tilde{\tilde{a}}}_{1n}\\ \frac{1}{{\tilde{\tilde{a}}}_{12}}& 1& ....& {\tilde{\tilde{a}}}_{2n}\\ ....& ....& ....& ....\\ \frac{1}{{\tilde{\tilde{a}}}_{1n}}& \frac{1}{{\tilde{\tilde{a}}}_{2n}}& ....& 1\end{array}\right)}_{n\times n}$$

(14)

Step 4: Check the consistency of the pairwise comparison matrix. Let $\tilde{\tilde{A}}=\left[{\tilde{\tilde{a}}}_{ij}\right]$ be the positive reciprocal matrix and $A=\left[a_{ij}\right]$ represent the defuzzified values of the elements of $\tilde{\tilde{A}}$. Then, the consistency in the values of $A$ is an indicator of the consistency of $\tilde{\tilde{A}}$.

Step 5: Calculate the mean of each row and then compute the fuzzy weights by the normalization matrix $\tilde{\tilde{N}}$.

Step 6: Apply the procedural steps of the classical AHP method to determine the best possible alternative. In order to find the crisp weight, the defuzzification value for an IT2 FS trapezoidal fuzzy number is given by [38]:

$$\begin{array}{l}DFTr(\tilde{\tilde{A}})=\frac{1}{2}(\frac{1}{4}((a_4^U-a_1^U)+(H_2({\tilde{A}}^U)\ast a_2^U-a_1^U)+(H_1({\tilde{A}}^U)\ast a_3^U-a_1^U))+a_1^U\\ +\frac{1}{4}((a_4^L-a_1^L)+(H_2({\tilde{A}}^L)\ast a_2^L-a_1^L)+(H_1({\tilde{A}}^L)\ast a_3^L-a_1^L))+a_1^L)\end{array}$$

(15)

4. Case Study

In this paper, we aim to investigate the critical issues that stand as barriers to the sustenance of Indian tea industries. India is the second largest source of tea in the world. Additionally, the Indian market shows a domestic consumption of 80% of the tea being produced in the country. The tea production in India showed a year-on-year increase of USD 19.77 million during April–June 2022. Despite a high volume of consumption and production, the Indian tea industry has been suffering from various issues that retarded its future potential. The issues stem from technical, managerial, and social perspectives.

In the month of November 2022, the Tea Board of India sought a special financial relief package of INR 10,000 million from the Ministry of Commerce and Industry for a period of five years starting in 2022–2023 for the tea industry under crisis. Officials from the Tea Board acknowledged that Indian tea had not been successful in establishing itself on a global scale and that one of its key brands, Darjeeling Tea, was severely under stress and required assistance from the government. The tea industry in India lacks effectively organized production systems and competitiveness in production, marketing, logistics, and product forms.

In response to the Tea Board of India’s demands, the Government of India approved the Scheme Modalities and Guidelines of the “Tea Development & Promotion Scheme” for execution during the 15th Finance Commission with a cash outlay of INR 9677.8 million. It is quite imperative that the Indian tea industry must redefine its business strategies and reposition its products in tune with the contemporary market dynamics. Strong actions must be taken to restructure the tea business, clarifying the duties of various bodies, such as the Tea Board and Producers’ Organizations, establishing policy, and developing good cooperation with labor.

In the recent past, there have been some studies conducted to explore the challenges of the Indian tea industry and suggest recommendations for policy implementation. For example, the authors [64] mentioned some of the barriers to be a stagnancy of production, climate change, a lack of awareness of modern farming, such as organic farming, training, and labor issues. In [65], the authors added issues like increasing cost and competition, changes in market demand, the use of obsolete technologies, improper marketing mix, and land issues. Singh et al. [66] pointed out the issue of price fluctuation as a challenge in front of Indian tea industries.

The present work is different from the past studies in the sense that it provides an expert opinion-based comprehensive evaluation of the operational challenges for achieving sustainability in the Indian tea industry. Further, it provides a better framework using IT2 FS to offset the subjective bias while being applied to analyzing the opinions. In this work, we first approached a group of 30 managers, government officials, and tea experts for detailed discussions on various issues. We also relied on field observations and discussions with the farmers to figure out various challenges. Finally, we refer to past studies to come out with a list of barriers for further investigations. The barriers are grouped under five broad factors such as production and productivity (F1), market diversification (F2), social environment (F3), administration and policy reforms (F4), and research and development (F5). Figure 2 provides the complete list of challenging factors identified for further investigation and prioritization through expert group decision-making.

To prioritize the barriers based on their relative weights in the second phase, we formed a group of five experts. The experts who took part in the study were spread across varying extents of association in the tea industry, expertise levels, and experience. The group of experts comprised a tea export and processing expert (E1), an academic expert (E2), an experienced consumer (E3), a plantation owner (E4), and an experienced plantation professional (E5). The insightful comments were of extreme help in the progress of the study. The current work intends to give a strategy execution of the remedy that would assist the Indian tea industry in overcoming the current crisis and establishing itself as a leader in the sector. All the responses were anonymous and used only for the purpose of study and research. The responses were recorded in a type 2 fuzzy linguistic scale (see Table 1) to form the pairwise comparison matrices as a first step of the IT2 FS-AHP. The first phase of the AHP was to determine the objective and criteria, and the second aimed to compare a pair of criteria on a single property. This is an effort to concentrate on an effective judgment of the criteria. The criteria were compared based on the experts’ opinions. To turn subjective evaluations of the participants into quantitative data, we used the trapezoidal type 2 fuzzy scale. The process was continued with the steps of obtaining the comparison matrix, normalizing the matrix, and calculating the priority vector and consistency ratio (CR). A CR is used to conclude whether comparison matrices are acceptable. It is calculated based on the consistency index (CI), which is the index of consistency of judgments across all pair-wise comparisons. A CR equal to or less than 0.10 indicates comparisons to be consistent, and so matrices are acceptable.

5. Data Analysis and Findings

In this section, we present the findings of data analysis carried out step by step. The responses of the experts in the type 2 fuzzy linguistic scale were recorded, and the type 2 fuzzy numbers were tabulated. The responses in terms of the type 2 fuzzy numbers for the pairwise comparison matrix are given in

Table A1. Pairwise comparison of the factor production and productivity with other main factors (experts’ opinions).

		Production and Productivity	Market Diversification	Social Environment	Administration and Policy Reforms	Research and Development
Production and productivity	Expert 1	(1,1,1,1;1,1) (1,1,1,1;1,1)	(0.2,0.26,0.45,0.83;1,1) (0.2,0.25,0.5,1;0.8,0.8)	(3,4,6,7;1,1) (3.2,4.2,5.8,6.8;0.8,0.8)	(5,6,8,9;1,1) (5.2,6.2,7.8,8.8;0.8,0.8)	(2,3,5,6;1,1) (2.2,3.2,4.8,5.8;0.8,0.8)
	Expert 2	(1,1,1,1;1,1) (1,1,1,1;1,1)	(0.14,0.16,0.25,0.33;1,1) (0.14,0.17,0.23,0.31;0.8,0.8)	(0.12,0.14,0.2,0.25;1,1) (0.128,0.147,0.19,0.23;0.8,0.8)	(0.2,0.25,0.5,1;1,1) (0.2,0.26,0.45,0.83;0.8,0.8)	(0.12,0.14,0.2,0.25;1,1) (0.128,0.147,0.19,0.23;0.8,0.8)
	Expert 3	(1,1,1,1;1,1) (1,1,1,1;1,1)	(1,1,1,1;1,1) (1,1,1,1;1,1)	(0.14,0.16,0.25,0.33;1,1) (0.14,0.17,0.23,0.31;0.8,0.8)	(7,8,9,9;1,1) (7.2,8.2,8.8,9;0.8,0.8)	(0.2,0.25,0.5,1;1,1) (0.2,0.26,0.45,0.83;0.8,0.8)
	Expert 4	(1,1,1,1;1,1) (1,1,1,1;1,1)	(3,4,6,7;1,1) (3.2,4.2,5.8,6.8;0.8,0.8)	(7,8,9,9;1,1) (7.2,8.2,8.8,9;0.8,0.8)	(0.2,0.25,0.5,1;1,1) (0.2,0.26,0.45,0.83;0.8,0.8)	(1,1,1,1;1,1) (1,1,1,1;1,1)
	Expert 5	(1,1,1,1;1,1) (1,1,1,1;1,1)	(1,2,4,5;1,1) (1.2,2.2,3.8,4.8;0.8,0.8)	(2,3,5,6;1,1) (2.2,3.2,4.8,5.8;0.8,0.8)	(1,1,1,1;1,1) (1,1,1,1;1,1)	(0.2,0.25,0.5,1;1,1) (0.2,0.26,0.45,0.83;0.8,0.8)

,

Table A2. Pairwise comparison of the factor market diversification with other main factors (experts’ opinions).

		Production and Productivity	Market Diversification	Social Environment	Administration and Policy Reforms	Research and Development
Market diversification	Expert 1	(1,2,4,5;1,1) (1.2,2.2,3.8,4.8;0.8,0.8)	(1,1,1,1;1,1) (1,1,1,1;1,1)	(4,5,7,8;1,1) (4.2,5.2,6.8,7.8;0.8,0.8)	(7,8,9,9;1,1) (7.2,8.2,8.8,9;0.8,0.8)	(5,6,8,9;1,1) (5.2,6.2,7.8,8.8;0.8,0.8)
	Expert 2	(3,4,6,7;1,1) (3.2,4.2,5.8,6.8;0.8,0.8)	(1,1,1,1;1,1) (1,1,1,1;1,1)	(1,2,4,5;1,1) (1.2,2.2,3.8,4.8;0.8,0.8)	(0.2,0.25,0.5,1;1,1) (0.2,0.26,0.45,0.83;0.8,0.8)	(1,2,4,5;1,1) (1.2,2.2,3.8,4.8;0.8,0.8)
	Expert 3	(1,1,1,1;1,1) (1,1,1,1;1,1)	(1,1,1,1;1,1) (1,1,1,1;1,1)	(3,4,6,7;1,1) (3.2,4.2,5.8,6.8;0.8,0.8)	(0.11,0.11,0.12,0.14;1,1) (0.112,0.113,0.121,0.138;0.8,0.8)	(0.2,0.25,0.5,1;1,1) (0.2,0.26,0.45,0.83;0.8,0.8)
	Expert 4	(3,4,6,7;1,1) (3.2,4.2,5.8,6.8;0.8,0.8)	(1,1,1,1;1,1) (1,1,1,1;1,1)	(7,8,9,9;1,1) (7.2,8.2,8.8,9;0.8,0.8)	(7,8,9,9;1,1) (7.2,8.2,8.8,9;0.8,0.8)	(1,2,4,5;1,1) (1.2,2.2,3.8,4.8;0.8,0.8)
	Expert 5	(0.2,0.25,0.5,1;1,1) (0.2,0.26,0.45,0.83;0.8,0.8)	(1,1,1,1;1,1) (1,1,1,1;1,1)	(1,2,4,5;1,1) (1.2,2.2,3.8,4.8;0.8,0.8)	(0.2,0.25,0.5,1;1,1) (0.2,0.26,0.45,0.83;0.8,0.8)	(1,2,4,5;1,1) (1.2,2.2,3.8,4.8;0.8,0.8)

,

Table A3. Pairwise comparison of the factor social environment with other main factors (experts’ opinions).

		Production and Productivity	Market Diversification	Social Environment	Administration and Policy Reforms	Research and Development
Social environment	Expert 1	(0.14,0.16,0.25,0.33;1,1) (0.14,0.17,0.23,0.31;0.8,0.8)	(0.12,0.14,0.2,0.25;1,1) (0.128,0.147,0.19,0.23;0.8,0.8)	(1,1,1,1;1,1) (1,1,1,1;1,1)	(0.2,0.25,0.5,1;1,1) (0.2,0.26,0.45,0.83;0.8,0.8)	(0.2,0.25,0.5,1;1,1) (0.2,0.26,0.45,0.83;0.8,0.8)
	Expert 2	(4,5,7,8;1,1) (4.2,5.2,6.8,7.8;0.8,0.8)	(0.2,0.25,0.5,1;1,1) (0.2,0.26,0.45,0.83;0.8,0.8)	(1,1,1,1;1,1) (1,1,1,1;1,1)	(2,3,5,6;1,1) (2.2,3.2,4.8,5.8;0.8,0.8)	(1,1,1,1;1,1) (1,1,1,1;1,1)
	Expert 3	(3,4,6,7;1,1) (3.2,4.2,5.8,6.8;0.8,0.8)	(0.14,0.16,0.25,0.33;1,1) (0.14,0.17,0.23,0.31;0.8,0.8)	(1,1,1,1;1,1) (1,1,1,1;1,1)	(0.11,0.11,0.12,0.14;1,1) (0.112,0.113,0.121,0.138;0.8,0.8)	(0.2,0.25,0.5,1;1,1) (0.2,0.26,0.45,0.83;0.8,0.8)
	Expert 4	(0.11,0.11,0.12,0.14;1,1) (0.112,0.113,0.121,0.138;0.8,0.8)	(0.11,0.11,0.12,0.14;1,1) (0.112,0.113,0.121,0.138;0.8,0.8)	(1,1,1,1;1,1) (1,1,1,1;1,1)	(0.11,0.11,0.12,0.14;1,1) (0.112,0.113,0.121,0.138;0.8,0.8)	(0.11,0.12,016,0.20;1,1) (0.113,0.128,0.161,0.19:0.8,0.8)
	Expert 5	(0.16,0.2,0.33,0.5;1,1) (0.17,0.20,0.31,0.45,0.8,0.8)	(0.2,0.25,0.5,1;1,1) (0.2,0.26,0.45,0.83;0.8,0.8)	(1,1,1,1;1,1) (1,1,1,1;1,1)	(0.2,0.25,0.5,1;1,1) (0.2,0.26,0.45,0.83;0.8,0.8)	(0.14,0.16,0.25,0.33;1,1) (0.14,0.17,0.23,0.31;0.8,0.8)

,

Table A4. Pairwise comparison of the factor administration and policy reform with other main factors (experts’ opinions).

		Production and Productivity	Market Diversification	Social Environment	Administration and Policy Reforms	Research and Development
Administration and policy reforms	Expert 1	(0.11,0.12,0.16,0.20;1,1) (0.113,0.128,0.161,0.19:0.8,0.8)	(0.11,0.11,0.12,0.14;1,1) (0.112,0.113,0.121,0.138;0.8,0.8)	(0.2,0.25,0.5,1;1,1) (0.2,0.26,0.45,0.83;0.8,0.8)	(1,1,1,1;1,1) (1,1,1,1;1,1)	(0.2,0.25,0.5,1;1,1) (0.2,0.26,0.45,0.83;0.8,0.8)
	Expert 2	(1,2,4,5;1,1) (1.2,2.2,3.8,4.8;0.8,0.8)	(1,2,4,5;1,1) (1.2,2.2,3.8,4.8;0.8,0.8)	(0.16,0.2,0.33,0.5;1,1) (0.17,0.20,0.31,0.45,0.8,0.8)	(1,1,1,1;1,1) (1,1,1,1;1,1)	(0.2,0.25,0.5,1;1,1) (0.2,0.26,0.45,0.83;0.8,0.8)
	Expert 3	(0.11,0.11,0.12,0.14;1,1) (0.112,0.113,0.121,0.138;0.8,0.8)	(7,8,9,9;1,1) (7.2,8.2,8.8,9;0.8,0.8)	(7,8,9,9;1,1) (7.2,8.2,8.8,9;0.8,0.8)	(1,1,1,1;1,1) (1,1,1,1;1,1)	(5,6,8,9;1,1) (5.2,6.2,7.8,8.8;0.8,0.8)
	Expert 4	(1,2,4,5;1,1) (1.2,2.2,3.8,4.8;0.8,0.8)	(0.11,0.11,0.12,0.14;1,1) (0.112,0.113,0.121,0.138;0.8,0.8)	(7,8,9,9;1,1) (7.2,8.2,8.8,9;0.8,0.8)	(1,1,1,1;1,1) (1,1,1,1;1,1)	(1,1,1,1;1,1) (1,1,1,1;1,1)
	Expert 5	(1,1,1,1;1,1) (1,1,1,1;1,1)	(1,2,4,5;1,1) (1.2,2.2,3.8,4.8;0.8,0.8)	(2,3,5,6;1,1) (2.2,3.2,4.8,5.8;0.8,0.8)	(1,1,1,1;1,1) (1,1,1,1;1,1)	(0.2,0.25,0.5,1;1,1) (0.2,0.26,0.45,0.83;0.8,0.8)

and

Table A5. Pairwise comparison of the factor research and development with other main factors (experts’ opinions).

		Production and Productivity	Market Diversification	Social Environment	Administration and Policy Reforms	Research and Development
Research and development	Expert 1	(0.16,0.2,0.33,0.5;1,1) (0.17,0.20,0.31,0.45,0.8,0.8)	(0.11,0.12,0.16,0.20;1,1) (0.113,0.128,0.161,0.19:0.8,0.8)	(1,2,4,5;1,1) (1.2,2.2,3.8,4.8;0.8,0.8)	(1,2,4,5;1,1) (1.2,2.2,3.8,4.8;0.8,0.8)	(1,1,1,1;1,1) (1,1,1,1;1,1)
	Expert 2	(4,5,7,8;1,1) (4.2,5.2,6.8,7.8;0.8,0.8)	(0.2,0.25,0.5,1;1,1) (0.2,0.26,0.45,0.83;0.8,0.8)	(1,1,1,1;1,1) (1,1,1,1;1,1)	(1,2,4,5;1,1) (1.2,2.2,3.8,4.8;0.8,0.8)	(1,1,1,1;1,1) (1,1,1,1;1,1)
	Expert 3	(1,2,4,5;1,1) (1.2,2.2,3.8,4.8;0.8,0.8)	(1,2,4,5;1,1) (1.2,2.2,3.8,4.8;0.8,0.8)	(1,2,4,5;1,1) (1.2,2.2,3.8,4.8;0.8,0.8)	(0.11,0.12,0.16,0.20;1,1) (0.113,0.128,0.161,0.19:0.8,0.8)	(1,1,1,1;1,1) (1,1,1,1;1,1)
	Expert 4	(1,1,1,1;1,1) (1,1,1,1;1,1)	(0.2,0.25,0.5,1;1,1) (0.2,0.26,0.45,0.83;0.8,0.8)	(5,6,8,9;1,1) (5.2,6.2,7.8,8.8;0.8,0.8)	(1,1,1,1;1,1) (1,1,1,1;1,1)	(1,1,1,1;1,1) (1,1,1,1;1,1)
	Expert 5	(1,2,4,5;1,1) (1.2,2.2,3.8,4.8;0.8,0.8)	(1,2,4,5;1,1) (1.2,2.2,3.8,4.8;0.8,0.8)	(3,4,6,7;1,1) (3.2,4.2,5.8,6.8;0.8,0.8)	(1,2,4,5;1,1) (1.2,2.2,3.8,4.8;0.8,0.8)	(1,1,1,1;1,1) (1,1,1,1;1,1)

(see Appendix A).

Next, the opinions of the experts are aggregated using the geometric mean. For example, when the market diversification is compared with the production and productivity, the expert opinions are aggregated as follows. e1, e2, e3, e4, and e5 are the opinions of the experts. Then, the aggregated response can be derived as:

$$\begin{array}{l}GM={(e_1\ast e_2\ast e_3\ast e_4\ast e_5)}^{\frac{1}{5}}\\ =(({(1\ast 3\ast 1\ast 3\ast 0.2)}^{\frac{1}{5}},{(2\ast 4\ast 1\ast 4\ast 0.25)}^{\frac{1}{5}},\\ {(4\ast 6\ast 1\ast 6\ast 0.5)}^{\frac{1}{5}},{(5\ast 7\ast 1\ast 7\ast 1)}^{\frac{1}{5}};\\ \min (1,1,1,1,1),\min (1,1,1,1,1))\\ ({(1.2\ast 3.2\ast 1\ast 3.2\ast 0.2)}^{\frac{1}{5}},{(2.2\ast 4.2\ast 1\ast 4.2\ast 0.26)}^{\frac{1}{5}},\\ {(3.8\ast 5.8\ast 1\ast 5.8\ast 0.45)}^{\frac{1}{5}},{(4.8\ast 6.8\ast 1\ast 6.8\ast 0.83)}^{\frac{1}{5}};\\ \min (0.8,0.8,0.8,0.8,0.8),\min (0.8,0.8,0.8,0.8,0.8)))\\ =(1.1,1.51,2.3,3;1,1)(1.91,1.58,2.24,2.83;0.8,0.8)\end{array}$$

Using the component-wise geometric mean, the expert opinions are aggregated and incorporate the opinion of each expert from various sectors of the Indian tea industry ranging from production to export, as given in

Table 2. Aggregated expert opinion matrix (pairwise comparison of the primary factors).

Factor	Production and Productivity
Production and Productivity	(1,1,1,1;1,1) (1,1,1,1;1,1)
Market Diversification	(1.1,1.51,2.3,3;1,1) (1.19,1.58,2.24,2.83;0.8,0.8)
Social Environment	(0.49,0.588,0.83,1.05;1,1) (0.51,0.609,0.806,1.0;0.8,0.8)
Administration and Policy Reforms	(0.41,0.55,0.78,0.93;1,1) (0.44,0.58,0.77,0.94;0.8,0.8)
Research and Development	(1.19,1.31,2.05,2.51;1,1) (1,1.38,1.98,2.4;0.8,0.8)
Factor	Market Diversification
Production and Productivity	(0.084,0.183,0.989,3.187;1,1) (0.640,0.836,1.110,1.33;0.8,0.8)
Market Diversification	(1,1,1,1;1,1) (1,1,1,1;1,1)
Social Environment	(0.149,0.17,0.27,0.40;1,1) (0.151,0.18,0.25,0.45;0.8,0.8)
Administration and Policy Reforms	(0.61,0.82,1.15,1.34;1,1) (0.66,0.87,1.13,1.31;0.8,0.8)
Research and Development	(0.33,0.49,0.9,1.37;1,1) (0.36,0.53,0.86,1.24;0.8,0.8)
Factor	Social Environment
Production and Productivity	(0.93,1.16,1.68,1.98;1,1) (0.98,1.22,1.60,1.83;0.8,0.8)
Market Diversification	(2.42,3.64,5.70,6.6;1,1) (2.68,3.86,5.49,6.4;0.8,0.8)
Social Environment	(1,1,1,1;1,1) (1,1,1,1;1,1)
Administration and Policy Reforms	(1.25,1.57,2.31,3;1,1) (1.31,1.6,2.7,2.81;0.8,0.8)
Research and Development	(1.71,2.49,3.77,4.3;1,1) (1.88,2.80,3.65,4.24;0.8,0.8)
Factor	Administration and Policy Reforms
Production and Productivity	(1.06,1.24,1.78,2.4;1,1) (0.98,1.22,1.60,1.83;1,1)
Market Diversification	(0.73,0.84,1.19,1.62;1,1) (0.74,0.87,1.1,1.5;0.8,0.8)
Social Environment	(0.24,0.29,0.44,0.65;1,1) (0.25,0.30,0.47,0.59;0.8,0.8)
Administration and Policy Reforms	(1,1,1,1;1,1) (1,1,1,1;1,1)
Research and Development	(0.64,0.99,1.59,1.90;1,1) (0.721,1.06,1.54,1.83
Factor	Research and Development
Production and Productivity	(0.39,0.48,0.75,1.08;1,1) (0.40,0.50,0.71,0.98;0.8,0.8)
Market Diversification	(1,1.64,3.03,4.07;1,1) (1.12,1.76,2.86,3.81;0.8,0.8)
Social Environment	(0.22,0.26,0.39,0.58;1,1) (0.229,0.27,0.37,0.52;0.8,0.8)
Administration and Policy Reforms	(0.52,0.62,1,1.55;1,1) (0.524,0.64,0.93,1.38;0.8,0.8)
Research and Development	(1,1,1,1;1,1) (1,1,1,1;1,1)

.

Now, we move to carry out the process of the normalization to obtain the normalized matrix $\tilde{\tilde{N}}$. The elements are obtained using the formula given below.

$$n_{ij}=\frac{a_{ij}}{{\displaystyle \sum _{i=1}^n{a}_{ij}}}$$

(16)

The sample calculation is as follows.

$$\begin{array}{l}{n}_{11}=\frac{a_{11}}{{\displaystyle \sum _{i=1}^5{a}_{i1}}}=\frac{(1,1,1,1;1,1)(1,1,1,1;1,1)}{(4.09,4.44,6.96,8.49;1,1)(4.14,5.14,6.75,8.17;0.8,0.8)}\\ =(0.118,0.144,0.202,0.239;1,1)(0.122,0.147,0.194,0.242;0.8,0.8)\end{array}$$

Then, the criteria weights are calculated using the simple arithmetic mean, where N represents the order of the normalized matrix. We have:

$$C_i=\frac{{\displaystyle \sum _{j=1}^n{n}_{ij}}}{N}$$

(17)

Next, the obtained criteria weights are defuzzified to obtain the score values ($d_i$). Then, the defuzzified score values are normalized using the following expression.

$$S_i=\frac{d_i}{{\displaystyle \sum _{i=1}^n{d}_i}}$$

(18)

The criteria weights and their defuzzified values for the pairwise comparisons (used in the present problem) are given in Appendix B (

Table A6. Criteria weights and defuzzified values (pairwise comparison of the primary factors).

	F1	F2	F3	F4	F5	Criterion Weight	d
F1	(0.118,0.144,0.202,0.239;1,1) (0.122,0.147,0.194,0.242;0.8,0.8)	(0.012,0.042,0.371,1.467;1,1) (0.120,0.192,0.325,0.473;0.8,0.8)	(0.055,0.080,0.170,0.271;1,1) (0.060,0.084,0.153,0.233;0.8,0.8)	(0.140,0.207,0.408,0.654;1,1) (0.145,0.214,0.360,0.496;0.8,0.8)	(0.047,0.078,0.188,0.345;1,1) (0.052,0.085,1.70,0.299;0.8,0.8)	(0.140,0.188,0.413,0.599;1,1) (0.122,0.203,0.385,0.580;0.8,0.8)	0.3118
F2	(0.130,0.217,0.464,0.716;1,1) (0.146,0.232,0.435,0.684;0.8,0.8)	(0.137,0.232,0.376,0.460;1,1) (0.188,0.230,0.293,0.356;0.8,0.8)	(0.143,0.252,0.578,0.903;1,1) (0.165,0.267,0.524,0.815;0.8,0.8)	(0.096,0.140,0.273,0.441;1,1) (0.110,0.152,0.247,0.406;0.8,0.8)	(0.121,0.266,0.758,1.300;1,1) (0.146,0.300,0.686,1.64;0.8,0.8)	(0.083,0.1178,0.2276,0.356;1,1) (0.0878,0.1228,0.212,0.3006;0.8,0.8)	0.5752
F3	(0.058,0.084,0.167,0.251;1,1) (0.062,0.09,0.157,0.242;0.8,08)	(0.20,0.039,0.101,0.184;1,1) (0.028,0.041,0.073,0.160;0.8,0.8)	(0.059,0.069,0.101,0.137;1,1) (0.061,0.069,0.095,0.127;0.8,0.8)	(0.032,0.048,0.101,0.177;1,1) (0.037,0.053,0.106,0.160;0.8,0.8)	(0.027,0.042,0.098,0.185;1,1) (0.030,0.046,0.089,0.159;0.8,0.8)	(0.075,0.0564,0.1136,0.1868;1,1) (0.0436,0.0598,0.104,0.169;0.8,0.8)	0.0970
F4	(0.048,0.079,0.157,0.222;1,1) (0.054,0.085,0.150,0.227;0.8,0.8)	(0.084,0.190,0.432,0.617;1,1) (0.124,0.200,0.331,0.466;0.8,0.8)	(0.074,0.109,0.234,0.410;1,1) (0.080,0.111,0.258,0.358;0.8,0.8)	(0.132,0.167,0.229,0.272;1,1) (0.148,0.175,0.225,0.271;0.8,0.8)	(0.063,0.100,0.250,0.495;1,1) (0.068,0.109,0.223,0.422;0.8,0.8)	(0.080,0.129,0.2604,0.4032;1,1) (0.0948,0.136,0.2374,0.3488;0.8,0.8)	0.2019
F5	(0.140,0.188,0.413,0.599;1,1) (0.122,0.203,0.385,0.580;0.8,0.8)	(0.045,0.114,0.338,0.630;1,1) (0.068,0.122,0.252,0.441;0.8,0.8)	(0.101,0.172,0.382,0.588;1,1) (0.115,0.194,0.348,0.540;0.8,0.8)	(0.085,0.165,0.365,0.518;1,1) (0.107,0.186,0.346,0.496,0.8,0.8)	(0.121,0.162,0.250,0.319;1,1) (0.13,0.17,0.240,0.306;0.8,0.8)	(0.098,0.1602,0.3496,0.5308;1,1) (0.1084,0.175,0.3142,0.4726;0.8,0.8)	0.2463

F1: Production and Productivity; F2: Market Diversification; F3: Social Environment; F4: Administration and Policy Reforms; F5: Research and Development.

,

Table A7. Criteria weights and defuzzified values (pairwise comparison of the sub-factors under F1).

	F11	F12	F13	F14	F15	Criterion Weight	d
F11	(0.0398,0.0452,0.0621,0.0763;1,1) (0.0408,0.0465,0.0598,0.0729;0.8,0.8)	(0.0162,0.0214,0.0468,0.0844;1,1) (0.0173,0.0238,0.0442,0.0736;0.8,0.8)	(0.0086,0.0112,0.0246,0.0405;1,1) (0.0088,0.0123,0.0218,0.0363;0.8,0.8)	(0.0079,0.0106,0.0219,0.0351;1,1) (0.0076,0.0099,0.0165,0.0241;0.8,0.8)	(0.5677,0.7111,0.9317,1.0539;1,1) (0.06015,0.7502,0.8898,1.0297;0.8,0.8)	(0.12804,0.1599,0.21742,0.25804;1,1) (0.02693,0.16854,0.20642,0.24732;0.8,0.8)	0.3017
F12	(0.1989,0.2712,0.4966,0.6865;1,1) (0.2119,0.2881,0.4667,0.6418;0.8,0.8)	(0.1475,0.1783,0.2924,0.4219;1,1) (0.1531,0.1858,0.2743,0.3874;0.8,0.8)	(0.01837,0.02807,0.5906,0.8600;1,1) (0.2011,0.3037,0.5487,0.7963;0.8,0.8)	(0.2363,0.3788,0.7659,1.1236;1,1) (0.2496,0.3516,0.5889,0.8186;0.8,0.8)	(0.0162,0.0222,0.0518,0.1171;1,1) (0.0167,0.0238,0.0455,0.0950;0.8,0.8)	(0.012345,0.17571,0.43946,0.64182;1,1) (0.16648,0.2306,0.38482,0.54782;0.8,0.8)	0.5194
F13	(0.1193,0.1808,0.3724,0.5339;1,1) (0.1304,0.1952,0.3470,0.4959;0.8,0.8)	(0.0206,0.0285,0.0731,0.1329;1,1) (0.0214,0.0316,0.0631,0.1201;0.8,0.8)	(0.0612,0.0702,0.0984,0.1229;1,1) (0.0629,0.0723,0.0946,0.1171;0.8,0.8)	(0.0656,0.0758,0.1094,0.1404;1,1) (0.0594,0.0676,0.0866,0.1050;0.8,0.8)	(0.0114,0.0142,0.0259,0.0386;1,1) (0.0177,0.0156,0.0233,0.0355;0.8,0.8)	(0.05562,0.0739,0.13584,0.19374;1,1) (0.05,0.07646,0.12292,0.17472;0.8,0.8)	0.1651
F14	(0.151,0.2260,0.4345,0.6102;1,1) (0.1712,0.2416,0.4069,0.5688;0.8,0.8)	(0.0177,0.0250,0.0585,0.01055;1,1) (0.0196,0.0273,0.0521,0.0891;0.8,0.8)	(0.0612,0.0702,0.0984,0.1229;1,1) (0.2011,0.3037,0.5487,0.7963;0.8,0.8)	(0.0656,0.0758,0.1094,0.1404;1,1) (0.0594,0.0676,0.0866,0.1050;0.8,0.8)	(0.0162,0.0222,0.0518,0.01171;1,1) (0.0167,0.0238,0.0455,0.0950;0.8,0.8)	(0.06234,0.08384,0.15052,0.17915;1,1) (0.0936,0.1328,0.22796,0.33084;0.8,0.8)	0.2709
F15	(0.0044,0.0050,0.0074,0.0107;1,1) (0.0046,0.0053,0.0072,0.0101;0.8,0.8)	(0.1475,0.3565,1.1696,2.1097;1,1) (0.1838,0.4088,1.0425,1.8597;0.8,0.8)	(0.1837,0.2807,0.5906,0.8600;1,1) (0.02011,0.3037,0.5487,0.7963;0.8,0.8)	(0.0656,0.1515,0.4376,0.7022;1,1) (0.1901,0.2840,0.5023,0.7137;0.8,0.8)	(0.0811,0.0889,0.1035,0.1171;0.8,0.8) (0.0835,0.0915,0.1011,0.1144;0.8,0.8)	(0.09646,0.17652,0.46174,0.75994;1,1) (0.09642,0.21866,0.44036,0.69884;0.8,0.8)	0.6740

F11: increased area under protection; F12: comprehensive product quality gradation programs; F13: use of high-yielding clones for plantation; F14: use of organic fertilizers and pesticides; F15: adaptation of modern farming techniques.

,

Table A8. Criteria weights and defuzzified values (pairwise comparison of the sub-factors under F2).

	F21	F22	F23	F24	F25	Criterion Weight	d
F21	(0.0707,0.0825,0.1233,0.3333;1,1) (0.0727,0.0853,0.1174,0.1535;0.8,0.8)	(0.1200,0.1481,0.2267,0.2994;1,1) (0.1259,0.1543,0.2159,0.2824;0.8,0.8)	(0.0140,0.0213,0.0676,0.1879;1,1) (0.0146,0.0231,0.0576,0.8379;0.8,0.8)	(0.2058,0.25,0.3461,0.409;1,1) (0.2142,0.2628,0.3283,0.2982;0.8,0.8)	(0.05,0.0754,0.1488,0.2075;1,1) (0.0540,0.0837,0.1342,0.5213;0.8,0.8)	(0.0921,0.1154,0.1825,0.28742;1,1) (0.0962,0.1218,0.1706,0.4186;0.8,0.8)	0.1783
F22	(0.0707,0.0825,0.1233,0.3333;1,1) (0.0727,0.0853,0.1174,0.1535;0.8,0.8)	(0.1200,0.1481,0.2267,0.2994;1,1) (0.1259,0.1543,0.2159,0.2824;0.8,0.8)	(0.0701,0.1709,0.5412,0.9398;1,1) (0.0878,0.1957,0.4867,0.1745;0.8,0.8)	(0.0882,0.125,0.2307,0.3181;1,1) (0.0952,0.1346,0.2164,0.3421;0.8,0.8)	(0.0714,0.1179,0.2976,0.6289;1,1) (0.0772,0.1280,0.2626,0.1947;0.8,0.8)	(0.8408,0.1288,0.2839,0.5039;1,1) (0.0917,0.1395,0.2598,0.2294;0.8,0.8)	0.2052
F23	(0.0707,0.1650,0.4932,1.6666;1,1) (0.0873,0.1876,0.4463,0.0211;0.8,0.8)	(0.0240,0.0370,0.113,0.2994;1,1) (0.0251,0.0401,0.0971,0.0875;0.8,0.8)	(0.0701,0.0854,0.1353,0.1879;1,1) (0.07320,0.0889,0.12809,0.0401;0.8,0.8)	(0.1176,0.1562,0.2692,0.3636;1,1) (0.125,0.1666,0.2537,0.0438;0.8,0.8)	(0.05,0.0754,0.1488,0.2075,1,1) (0.0540,0.0837,0.1342,0.0866;0.8,0.8)	(0.06648,0.1038,0.2319,0.545;1,1) (0.0729,0.1133,0.2118,0.0558;0.8,0.8)	0.1670
F24	(0.0077,0.0090,0.014,0.0466,1,1) (0.0081,0.0096,0.0142,1.0442;0.8,0.8)	(0.0168,0.0237,0.0566,0.0988;1,1) (0.0176,0.0262,0.0496,1.355;0.8,0.8)	(0.0084,0.01196,0.0270,0.0469;1,1) (0.0093,0.0130,0.0243,1.1871;0.8,0.8)	(0.0294,0.03125,0.0384,0.0454;1,1) (0.0297,0.03205,0.03731,0.3947;0.8,0.8)	(0.0392,0.0518,0.0714,0.0880;1,1) (0.0432,0.0556,0.0706,0.6281;0.8,0.8)	(0.0203,0.0255,0.0414,0.6514;1,1) (0.0215,0.0272,0.9218;0.8,0.8)	0.1436
F25	(0.2121,0.3300,0.7398,2.3333;1,1) (0.2329,0.3583,0.6813,2.1096;0.8,0.8)	(0.1200,0.2962,0.9070,1.497;1,1) (0.1511,0.3395,0.8207,2.242;0.8,0.8)	(0.2105,0.3418,0.8119,1.315;1,1) (0.2342,0.3736,0.7429,2.3847;0.8,0.8)	(0.2058,0.25,0.3461,0.4090;1,1) (0.2142,0.2628,0.3283,1.4736;0.8,0.8)	(0.3571,0.4716,0.5952,0.6289;1,1) (0.3863,0.4923,0.5837,1.6256)	(0.2211,0.3379,0.68,1.236;1,1) (0.24374,0.3653,0.6313,1.9671;0.8,0.8)	0.6855

F21: concentrated work on creating and disseminating an “Indian Tea” brand; F22: geographical diversification of markets and consolidation of existing primary markets; F23: a comprehensive exporter rating and reliability management; F24: targeting value-addition and niche segment opportunities in specific markets; F25: reignite the demand for tea in both home and foreign markets.

,

Table A9. Criteria weights and defuzzified values (pairwise comparison of the sub-factors under F3).

	F31	F32	F33	F34	F35	Criterion Weight	d
F31	(0.3367,0.4545,0.5813,0.6211;1,1) (0.3665,0.4737,0.5737,0.6165;0.8,0.8)	(0.1212,0.2985,0.9111,1.506;1,1) (0.1526,0.3416,0.8248,1.36054;0.8,0.8)	(0.1,0.1764,0.4545,0.75;1,1) (0.1134,0.1951,0.4137,0.6744;0.8,0.8)	(0.2941,0.4366,0.8426,1.145;1,1) (0.3265,0.4686,0.7914,1.0771;0.8,0.8)	(0.2058,0.2580,0.375,0.45;1,1) (0.2155,0.2715,0.3548,0.4326;0.8,0.8)	(0.2606,0.3248,0.6329,0.8944;1,1) (0.2349,0.3501,0.5916,0.8322;0.8,0.8)	0.4917
F32	(0.0673,0.1136,0.2906,0.6211;1,1) (0.0733,0.1231,0.2581,0.5117;0.8,0.8)	(0.1212,0.1492,0.2277,0.3012;1,1) (0.1272,0.1552,0.2170,0.2834;0.8,0.8)	(0.05,0.1176,0.3636,0.625;1,1) (0.0618,0.1341,0.3275,0.5581;0.8,0.8)	(0.0980,0.1091,0.1404,0.1636;1,1) (0.0102,0.1115,0.1364,0.1584;0.8,0.8)	(0.1176,0.1612,0.2916,0.4;1,1) (0.1257,0.1721,0.2741,0.375;0.8,0.8)	(0.0812,0.1301,0.2627,0.4221;1,1) (0.0796,0.1392,0.2426,0.3773;0.8,0.8)	0.2073
F33	(0.0538,0.0909,0.1918,0.3105;1,1) (0.0623,0.0947,0.1778,0.2774;0.8,0.8)	(0.0242,0.0373,0.1138,0.3012;1,1) (0.02544,0.0403,0.0976,0.2352;0.8,0.8)	(0.05,0.0588,0.0909,0.125;1,1) (0.0515,0.0609,0.0862,0.1162;0.8,0.8)	(0.0980,0.1091,0.1404,0.1636;1,1) (0.0102,0.1115,0.1364,0.1584;0.8,0.8)	(0.0882,0.1290,0.25,0.35;1,1) (0.095,0.1390,0.2338,0.3269;0.8,0.8)	(0.0842,0.0301,0.2318,0.35115;1,1) (0.0692,0.1373,0.1428,0.0383;0.8,0.8)	0.1279
F34	(0.0471,0.0727,0.1453,0.2049;1,1) (0.0513,0.0805,0.1319,0.1911;0.8,0.8)	(0.1212,0.1492,0.2277,0.3012;1,1) (0.1272,0.1552,0.2170,0.2834;0.8,0.8)	(0.05,0.0588,0.0909,0.125;1,1) (0.0515,0.0609,0.0862,0.1162;0.8,0.8)	(0.0980,0.1091,0.1404,0.1636;1,1) (0.0102,0.1115,0.1364,0.1584;0.8,0.8)	(0.1470,0.1935,0.3333,0.45;1,1) (0.1556,0.2052,0.3145,0.423;0.8,0.8)	(0.0786,0.1166,0.1875,0.2489;1,1) (0.0791,0.1226,0.1772,0.2344;0.8,0.8)	0.1482
F35	(0.0370,0.05,0.0697,0.0869;1,1) (0.0410,0.0535,0.0694,0.0850;0.8,0.8)	(0.0145,0.0208,0.0455,0.0753;1,1) (0.0162,0.0228,0.0412,0.0651;0.8,0.8)	(0.15,0.2325,0.5454,0.875;1,1) (0.1649,0.2560,0.5,0.7906;0.8,0.8)	(0.0107,0.0131,0.0224,0.0327;1,1) (0.011,0.0142,0.0219,0.0300;0.8,0.8)	(0.0294,0.03225,0.0416,0.05;0.8,0.8) (0.0299,0.0331,0.0403,0.0480;0.8,0.8)	(0.0536,0.06973,0.14492,0.22398,1,1) (0.526,0.07592,0.13456,0.20374;0.8,0.8)	0.1146

F31: dignified working conditions by providing basic welfare benefits; F32: adequate pay protection in addition to regular work; F33: facilities for education, housing, and health services for children and families; F34: social security schemes for tea garden workers; F35: emergence of worker collaboration.

,

Table A10. Criteria weights and defuzzified values (pairwise comparison of the sub-factors under F4).

	F41	F42	F43	F44	F45	Criterion Weight	d
F41	(0.0105,0.1277,0.0183,0.2293;1,1) (0.1101,0.1322,0.1766,0.2188;0.8,0.8)	(0.08,0.1428,0.3846,0.6667;1,1) (0.0909,0.1584,0.3478,0.5918;0.8,0.8)	(0.0769,0.1904,0.64,1.1904;1,1) (0.0965,0.2189,0.5705,1.0434;0.8,0.8)	(0.261,0.3246,0.3831,0.4;1,1) (0.2785,0.3344,0.3802,0.3984;0.8,0.8)	(0.1333,0.24,0.6060,0.9677;1,1) (0.1524,0.2655,0.5542,0.8787;0.8,0.8)	(0.1123,0.2051,0.4064,0.6908;1,1) (0.1456,0.2218,0.4058,0.6262;0.8,0.8)	0.3361
F42	(0.0168,0.0255,0.0605,0.1146;1,1) (0.0187,0.0264,0.0547,0.0984;0.8,0.8)	(0.04,0.0476,0.0769,0.1111;1,1) (0.0413,0.0495,0.0726,0.01020;0.8,0.8)	(0.0153,0.0238,0.08,0.2308;1,1) (0.016,0.0258,0.0675,0.1804;0.8,0.8)	(0.0365,0.0519,0.0957,0.132;1,1) (0.0389,0.0568,0.0874,0.1235;0.8,0.8)	(0.0133,0.02,0.0606,0.16129;1,1) (0.0138,0.0215,0.0519,0.1257;0.8,0.8)	(0.0243,0.0337,0.0747,0.1499;1,1) (0.0257,0.0360,0.0668,0.1076;0.8,0.8)	0.0623
F43	(0.02105,0.0319,0.0917,0.2293;1,1) (0.0220,0.0343,0.0795,0.1816;0.8,0.8)	(0.08,0.1428,0.3846,0.6667;1,1) (0.0909,0.1584,0.3478,0.5918;0.8,0.8)	(0.0769,0.0952,0.16,0.2380;1,1) (0.0804,0.0995,0.1501,0.2173;0.8,0.8)	(0.0522,0.0811,0.1915,0.4;1,1) (0.0557,0.0869,0.1711,0.3306;0.8,0.8)	(0.0667,0.08,0.1212,0.1612;1,1) (0.0693,0.0829,0.1154,0.1515;0.8,0.8)	(0.0593,0.0862,0.1898,0.3390;1,1) (0.0636,0.09241,0.1727,0.294563;0.8,0.8)	0.1556
F44	(0.1052,0.1277,0.1834,0.2293;1,1) (0.1101,0.1322,0.1766,0.2188;0.8,0.8)	(0.12,0.1904,0.4615,0.7778;1,1) (0.1322,0.2079,0.4202,0.6938;0.8,0.8)	(0.0769,0.01904,0.64,1.1904;1,1) (0.0965,0.2189,0.5705,1.043;0.8,0.8)	(0.2610,0.3246,0.3831,0.4;1,1) (0.2785,0.3344,0.3802,0.3984;0.8,0.8)	(0.1333,0.24,0.6060,0.9677;1,1) (0.1524,0.2655,0.5542,0.8787;0.8,0.8)	(0.1392,0.18034,0.4548,0.7130;1,1) (0.1539,0.2317,0.4203,0.6465;0.8,0.8)	0.3512
F45	(0.2105,0.3831,0.9174,1.3761;1,1) (0.2422,0.4232,0.8480,1.2691;0.8,0.8)	(0.04,0.0952,0.3076,0.5556;1,1) (0.0495,0.1089,0.2753,0.4897;0.8,0.8)	(0.0766,0.0952,0.16,0.2380,1,1) (0.0804,0.0995,0.1501,0.2173;0.8,0.8)	(0.0417,0.0649,0.1264,0.2;1,1) (0.0473,0.0668,0.1178,0.1792;0.8,0.8)	(0.0667,0.08,0.1212,0.1612;1,1) (0.0693,0.0829,0.1154,0.1515;0.8,0.8)	(0.0787,0.1307,0.3012,0.4661;1,1) (0.0882,0.1429,0.2777,0.4255;0.8,0.8)	0.2284

F41: growth of the plantation with an emphasis on small tea growers; F42: regulatory and auction reforms; F43: improving supply chains; F44: policy to stop low-quality imports into the market from other nations; F45: promotion of tea in worldwide festivals and events.

and

Table A11. Criteria weights and defuzzified values (pairwise comparison of the sub-factors under F5).

	F51	F52	F53	F54	F55	Criterion Weight	d
F51	(0.0754,0.0892,0.014,0.1953;1,1) (0.0779,0.0926,0.1325,0.1808;0.8,0.8)	(0.0754,0.0892,0.014,0.1953;1,1) (0.0779,0.0926,0.1325,0.1808;0.8,0.8)	(0.0509,0.0719,0.1314,0.2057;1,1) (0.055,0.0729,0.1233,0.1835;0.8,0.8)	(0.0483,0.0801,0.1915,0.3984;1,1) (0.0526,0.0860,0.1709,0.3304,0.8,0.8)	(0.1142,0.1515,0.2592,0.3478;1,1) (0.1213,0.1614,0.2446,0.3277;0.8,0.8)	(0.0728,0.0963,0.1220,0.2685;1,1) (0.0769,0.1011,0.1607,0.2406;0.8,0.8)	0.1359
F52	(0.0754,0.0892,0.014,0.1953;1,1) (0.0779,0.0926,0.1325,0.1808;0.8,0.8)	(0.0754,0.0892,0.014,0.1953;1,1) (0.0779,0.0926,0.1325,0.1808;0.8,0.8)	(0.0509,0.0719,0.1314,0.2057;1,1) (0.0559,0.0729,0.1233,0.1835;0.8,0.8)	(0.0483,0.0801,0.1915,0.3984;1,1) (0.0526,0.0860,0.1709,0.3304,0.8,0.8)	(0.1142,0.1515,0.2592,0.3478;1,1) (0.1213,0.1614,0.2446,0.3277;0.8,0.8)	(0.07285,0.0963,0.122,0.2685;1,1) (0.0771,0.1011,0.1607,0.2406;0.8,0.8)	0.1359
F53	(0.1509,0.2678,0.7002,1.1718;1,1) (0.1714,0.2965,0.636,1.0492;0.8,0.8)	(0.1509,0.2678,0.7002,1.1718;1,1) (0.1714,0.2965,0.636,1.0492;0.8,0.8)	(0.3184,0.3597,0.3984,0.4115;1,1) (0.3291,0.3648,0.3979,0.40783;0.8,0.8)	(0.2415,0.3205,0.3831,0.3984,1,1) (0.2632,0.3310,0.3797,0.3980;0.8,0.8)	(0.2,0.2424,0.3333,0.3913;1,1) (0.208,0.2546,0.316547,0.3781;0.8,0.8)	(0.2123,0.2916,0.5030,0.7089;1,1) (0.2286,0.3086,0.47322,0.6564;0.8,0.8)	0.4033
F54	(0.0754,0.1785,0.5602,0.9765;1,1) (0.0935,0.2038,0.5035,0.8683;0.8,0.8)	(0.0754,0.1785,0.5602,0.9765;1,1) (0.0935,0.2038,0.5035,0.8683;0.8,0.8)	(0.3184,0.3597,0.3984,0.4115;1,1) (0.3291,0.3648,0.3979,0.40783;0.8,0.8)	(0.2415,0.3205,0.3831,0.3984,1,1) (0.2632,0.3310,0.3797,0.3980;0.8,0.8)	(0.2,0.2424,0.3333,0.3913;1,1) (0.208,0.2546,0.316547,0.3781;0.8,0.8)	(0.1821,0.2559,0.4470,0.6308;1,1) (0.1974,0.2716,0.4202,0.5841;0.8,0.8)	0.3564
F55	(0.009,0.0125,0.028,0.0488;1,1) (0.0099,0.0136,0.0251,0.0416;0.8,0.8)	(0.009,0.0125,0.028,0.0488;1,1) (0.0099,0.0136,0.0251,0.0416;0.8,0.8)	(0.035,0.039,0.0478,0.0576;1,1) (0.0368,0.0412,0.0481,0.0562;0.8,0.8)	(0.0265,0.03526,0.04597,0.0557;1,1) (0.0294,0.0374,0.0459,0.0549;0.8,0.8)	(0.0285,0.0303,0.0370,0.0434;1,1) (0.0289,0.03105,0.035971,0.0420;0.8,0.8)	(0.0216,0.0259,0.0373,0.0508;1,1) (0.0229,0.0273,0.03603,0.0472;0.8,0.8)	0.0321

F51: workshops and training on modern techniques; F52: reducing the input costs and increasing profitability; F53: improvement of tea quality and production of specialty tea; F54: development of processing and packaging units near gardens; F55: stress-tolerant cultivators.

).

Now, we move to calculate the normalized scores for the primary and secondary factors.

Table 3. Normalized scores (primary factors).

Primary Factors	Normalized Score
Production and Productivity (F1)	0.2177
Market Diversification (F2)	0.4016
Social Environment (F3)	0.0677
Administration and Policy Reforms (F4)	0.1410
Research and Development (F5)	0.1720

exhibits the normalized score values of the primary factors.

In Table 3, it is seen that market diversification emerges as the dominant issue, while the experts believe that the social environment is not a compelling challenge compared with the other primary factors. To further introspect the normalized scores of all the sub-factors, each primary factor is also calculated (

Table 4. Normalized scores (sub-factors under the main factor production and productivity).

Sub-Factors	Normalized Score
Increased area under protection (F11)	0.156
Comprehensive product quality upgradation programs (F12)	0.269
Use of high-yielding clones for plantation (F13)	0.086
Use of organic fertilizers and pesticides (F14)	0.140
Adaptation of modern farming techniques (F15)	0.349

The order of preference is ${\mathrm{F}}_{15}\succ {\mathrm{F}}_{12}\succ {\mathrm{F}}_{11}\succ {\mathrm{F}}_{14}\succ {\mathrm{F}}_{13}$.

,

Table 5. Normalized scores (sub-factors under the main factor of market diversification).

Sub-Factor	Normalized Score
Concentrated work on creating and disseminating an “Indian Tea” brand (F21)	0.129
Geographical diversification of markets and consolidation of existing primary markets (F22)	0.149
A comprehensive exporter rating and reliability management (F23)	0.121
Targeting value-addition and niche segment opportunities in specific markets (F24)	0.104
Reignite the demand for tea in both home and foreign markets (F25)	0.497

Based on the normalized scores, the order of preference is ${\mathrm{F}}_{25}\succ {\mathrm{F}}_{22}\succ {\mathrm{F}}_{21}\succ {\mathrm{F}}_{23}\succ {\mathrm{F}}_{24}$.

,

Table 6. Normalized scores (sub-factors under the main factor of social environment).

Sub-Factor	Normalized Score
Dignified working conditions by providing basic welfare benefits (F31)	0.4511
Adequate pay protection in addition to regular work (F32)	0.1902
Facilities for education, housing, and health services for children and families (F33)	0.1173
Social security schemes for tea garden workers (F34)	0.1359
Emergence of worker collaboration (F35)	0.1051

The order of preference is ${\mathrm{F}}_{31}\succ {\mathrm{F}}_{32}\succ {\mathrm{F}}_{34}\succ {\mathrm{F}}_{33}\succ {\mathrm{F}}_{35}$.

,

Table 7. Normalized scores (sub-factors under the main factors of administration and policy reforms).

Sub-Factor	Normalized Score
Growth of the plantation with an emphasis on small tea growers (STG) (F41)	0.2965
Regulatory and auction reforms (F42)	0.0550
Improving supply chains (F43)	0.1373
Policy to stop low-quality imports into the market from other nations (F44)	0.3098
Promotion of tea in worldwide festivals and events (F45)	0.2015

The order of preference is ${\mathrm{F}}_{44}\succ {\mathrm{F}}_{41}\succ {\mathrm{F}}_{45}\succ {\mathrm{F}}_{43}\succ {\mathrm{F}}_{42}$.

and

Table 8. Normalized scores (sub-factors under the main factor of research and development).

Sub-Factor	Normalized Score
Workshops and training on modern techniques (F51)	0.1277
Reducing input cost and improve the profitability (F52)	0.1278
Improvement of tea quality and production of specialty teas (F53)	0.3792
Development of processing and packaging units near gardens (F54)	0.3351
Stress-tolerant cultivators (F55)	0.0302

The order of preference is ${\mathrm{F}}_{53}\succ {\mathrm{F}}_{54}\succ {\mathrm{F}}_{52}\succ {\mathrm{F}}_{51}\succ {\mathrm{F}}_{55}$.

).

Now, we proceed to find out the global weight (in terms of the global normalized score values of the sub-factors). The global weight of a sub-factor $F_{ij}$ can be found as:

$$W_{ij}=S_i{S}_{j(i)}$$

(19)

where $S_i$ is the normalized score value of the $i^{th}$ primary factor to which the $j^{th}$ sub-factor belongs and $S_{j(i)}$ is the normalized score value of $j^{th}$ sub-factor local to the $i^{th}$ primary factor. Accordingly, all sub-factors are ranked. The sub-factor that holds the highest global weight (i.e., global normalized score value) is ranked first.

Table 9. Aggregate ranking of the sub-factors.

		Local	Global
Sub-factor under F1	Score (F1)	Normalized Score	Normalized Score	Rank
F11	0.2177	0.156	0.03400	12
F12		0.269	0.05856	5
F13		0.086	0.01861	19
F14		0.140	0.03054	13
F15		0.349	0.07598	2
Sub-factor under F2	Score (F2)
F21	0.4016	0.129	0.05189	7
F22		0.149	0.05972	4
F23		0.121	0.04859	8
F24		0.104	0.04181	10
F25		0.497	0.19951	1
Sub-factor under F3	Score (F3)	Normalized Score
F31	0.0677	0.4511	0.03054	14
F32		0.1902	0.01288	20
F33		0.1173	0.00794	22
F34		0.1359	0.00920	21
F35		0.1051	0.00712	24
Sub-factor under F4	Score (F4)	Normalized Score
F41	0.141	0.2965	0.04180	11
F42		0.0550	0.00775	23
F43		0.1373	0.01935	18
F44		0.3098	0.04368	9
F45		0.2015	0.02841	15
Sub-factor under F5	Score (F5)	Normalized Score
F51	0.172	0.1277	0.02197	17
F52		0.1278	0.02198	16
F53		0.3792	0.06523	3
F54		0.3351	0.05763	6
F55		0.0302	0.00519	25

provides the ranking order of the sub-factors.

To check the reliability of the derived calculations using the IT2 FS-AHP based on pairwise comparisons of the primary factors and the sub-factors and to ensure harmony in decision-making among the experts, the consistency index (CI) and consistency ratio (CR) are calculated. We use the random index (RI) table suggested by [67], which is given in

Table 10. Random index table.

Matrix Size (n)	1	2	3	4	5	6	7	8	9	10
Random Index (R.I.)	0.00	0.00	0.58	0.90	1.12	1.24	1.32	1.41	1.45	1.49

.

The values of the CI and CR are found as follows [68]:

$$\mathrm{CI}=\frac{{\lambda }_{\max }-m}{m-1}$$

(20)

${\lambda }_{\max }$ is the highest eigenvalue of the pairwise comparison matrix. ${\lambda }_{\max }$ is given as:

$${\lambda }_{\max }={\displaystyle \sum _{j=1}^m\frac{{(\Omega .\mathrm{V})}_j}{m.v_j}}$$

(21)

$m$ is the number of independent rows in the matrix, $\Omega$ is the pairwise comparison matrix, and $\mathrm{V}$ represents the matrix eigenvector. For a perfectly consistent case, $\mathrm{CI}=0$. For an increasing number of pairwise comparisons, there is a rise in the inconsistencies. The CR measures the consistency and is calculated as:

$$\mathrm{CR}=\frac{\mathrm{CI}}{\mathrm{RI}}$$

(22)

Saaty [67] recommended a CR value < 0.1, indicating a good consistency. In this work, we calculate the CI and CR values for all pairwise comparison matrices (in our case, $n=5$ and RI = 1.12), which are recorded in

Table 11. CI and CR values for the pairwise comparisons.

Pairwise Comparison among	Λ (max)	CI	CR
Primary/main factors (F1 to F5)	5.0800	0.0202	0.0180 < 0.1
Sub-factors of F1	5.4230	0.1058	0.0940 < 0.1
Sub-factors of F2	5.3393	0.0848	0.0757 < 0.1
Sub-factors of F3	5.2425	0.0606	0.0541 < 0.1
Sub-factors of F4	5.2249	0.0562	0.0502 < 0.1
Sub-factors of F5	5.1180	0.0295	0.0263 < 0.1

.

Clearly, there is a consistency noticed for all pairwise comparisons. Hence, our IT2 FS-AHP provides a considerably reliable result.

In summary, it is seen that market diversification and concern for improving productivity stand out as the critical primary issues. Among the sub-factors, creating a demand pull and embracing technology to bring in product variety while enhancing quality and diversification emerge as the dominant challenges. The CR values affirm that the experts’ opinions were in harmony and consistent.

6. Discussion

From the analysis of the responses, it is seen that market diversification (F2) holds the highest weight among the primary factors, followed by production and productivity (F1). The result supports the views of [64,65], as there is a need to understand and respond to the changing needs of the global market by embracing modern technologies and enhancing the efficiencies of operations. However, the result suggests that the experts comparatively did not advocate much for a social environment (F3), which does not support the views of [53]. While plowing the sub-factors, we observed that the experts felt the need to rejuvenate the demand and create a pull factor for increasing the quantum of export of tea and domestic consumption (F25) over the other sub-factors. The second important sub-factor that stands apart is the requirement for the adaptation of modern technologies and techniques for farming (F15), which reinstates the opinions of [55,64,65]. The other three important sub-factors in the list of the top five challenging factors are the need to grow specialty tea on a plantation (F53), the diversification of geographical markets for tea (F22), and the upgradation of the product quality (F12). However, stress management (F55), worker collaboration (F35), and regulatory and auction reform (F42) hold their positions in the bottom priority challenges. The tea industry in India has been regulated and governed. Perhaps this is why the experts did not pay much attention to these challenges. Therefore, it is seen that the findings support the fragmented views of the past studies to give a comprehensive understanding of the key challenges of the tea industry. The Indian tea industry has a direct impact on the 1.2 million people responsible for the production of tea leaves, making them available to the end consumer. The people of each segment have a very subjective approach, which comes with their expertise in the industry. In order to provide the holistic development of the entire tea industry, we need to cater to the demand of all sections: plantation farmers, packaging units, policymakers, and consumers. Further, all CR values are within the prescribed value of 0.1, suggesting the validity of the pairwise comparison. Hence, it may be concluded that the current work is of use to the decision-makers to obtain a comprehensive picture of the tea industry.

The fuzzy AHP is widely used in the decision-making process and can be seen as an advanced analytical method developed to overcome the limitations of the traditional AHP process. The work is further developed to the fuzzy AHP using interval type 2 fuzzy sets instead of type 1 fuzzy sets in the decision problem for sustainable development of the tea industry. Using interval type 2 fuzzy sets for handling fuzzy group decision-making problems and making more flexible decisions can be made since interval type 2 fuzzy sets are more suitable to represent uncertainties than type 1 fuzzy sets. Earlier studies in the field of the tea industry were primarily focused on a particular section of the tea industry such as social factors, policy-making, and administrative reforms. In our work, we have built an intelligent decision analysis model considering all the factors using the IT2FS-AHP for discerning the critical issues for the sustenance of the Indian tea industry. Since strategic decision-making is subject to the influence of a number of conditions imposed by the uncertain external environment, the use of the IT2FS is deemed fit for our objective.

Based on the findings of the current work, a number of implications for further decision-making can be drawn. Firstly, the result suggests that there is a need to overhaul the process of tea plantations using advanced technologies and mechanisms. A thorough review of the policies needs to be carried out to bring the changes in the processes and appropriate strategic decisions regarding collaboration, location, training, and regulatory framework. Secondly, it is visible that to stay ahead of the global competition, the Indian tea industry needs to enhance its quality, venture into new markets, and adopt aggressive promotions. In this regard, a change in the marketing mix is important. Thirdly, understanding the tastes and preferences of the consumers’ needs to be assessed holistically. Fourthly, an emphasis needs to be put on building a robust supply chain, especially the distribution channel.

7. Conclusions

The Indian tea industry is at a crossroads. An age-old industry is struggling to hold its position at the global platform. Though there has been a considerable increase in domestic consumption, the Indian tea industry has been suffering from retarded growth. In this context, the present work puts forth an IT2 FS-based AHP framework to figure out the dominant primary challenges and secondary factors. The challenging factors and their sub-factors were identified through a literature review and a pilot survey (focused group discussion). Then, a group of five experts were interviewed to record their rating on the primary factors and their corresponding sub-factors. To offset the subjective bias, an IT2 FS-based approach has been selected for granular analysis. The results advocate for focusing on market diversification (F2) and production and productivity (F1) as the top challenges. Further, the findings emphasize on adaptation of modern technologies and techniques for farming, the rejuvenation of the demand by creating a pull factor, the improvement of product line and depth, the enhancement of product quality, and diversification into various markets. It is observed that there is considerable consistency in group decision-making for all pairwise comparisons, as in all cases the CR value was <0.1. The model (IT2 FS-AHP) has an apparent limitation of computational complexity of the order of $\frac{n(n-1)}{2}$, where n is the number of pairwise comparisons. The number of ranking methods for trapezoidal interval type 2 fuzzy sets is very limited. In a future study, we plan to work with bigger data sets and extend various ranking methods.

However, the current work has some scope for further extensions. For example, a causal model can be established through a large-scale empirical survey to discern the interrelationship of various challenging factors. Secondly, a future study may be designed to work on the sentiments of the consumers of Indian tea using advanced natural language processing (NLP) and text mining algorithms, and an attempt may be made to examine the linkage with the challenges. Thirdly, from a global perspective, a comparative analysis of Indian tea products with their global counterparts may be planned. Fourthly, from a technical point of view, the developed algorithm may be modified using the other variants of fuzzy such as picture fuzzy sets, spherical fuzzy sets, q-rung orthopair fuzzy sets, and rough sets. Fifthly, the IT2 FS can be applied to extend the recently developed Full Consistency Method (FUCOM), which shows a lesser computational complexity. Sixthly, a possible future study shall focus on developing a new approach for validation and sensitivity analysis. Seventh, in the current work, the validity is tested by means of a CR, but the present work can be compared with extended versions of the other group decision-making models used for finding out criteria weights. Lastly, the extension of the interval fuzzy AHP to the generalized type 2 fuzzy AHP can be developed in future research directions.

Nevertheless, the IT2 FS-AHP enables the analyst to carry out a granular-level analysis under uncertainty, which can be applied to solve other complex real-life issues pertaining to engineering, social science, business management, and basic science domains. The findings of the present work reveal some useful implications for future strategies.