The Clustering Coefficient for Graph Products

Abstract

The clustering coefficient of a vertex v, of degree at least 2, in a graph $\Gamma$ is obtained using the formula $C\left(v\right)=\frac{2t\left(v\right)}{\mathrm{deg}\left(v\right)\left(\mathrm{deg}\right(v)-1)},$ where $t\left(v\right)$ denotes the number of triangles of the graph containing v as a vertex, and the clustering coefficient of $\Gamma$ is defined as the average of the clustering coefficient of all vertices of $\Gamma$, that is, $C(\Gamma )=\frac{1}{\left|V\right|}{\sum }_{v\in V}C\left(v\right)$, where V is the vertex set of the graph. In this paper, we give explicit expressions for the clustering coefficient of corona and lexicographic products, as well as for the Cartesian sum; such expressions are given in terms of the order and size of factors, and the degree and number of triangles of vertices in each factor.

1. Introduction

Leonhard Euler introduced graph theory in his well-known discussion of the Königsberg Bridge Problem in 1736, when he gave a representation of the situation by means of a graph (see reference [1]). However, such an article remained isolated for almost a century until there was a revival of interest in the problems of graph theory, mainly in England. In 1857, Arthur Cayley used his knowledge of these topics to represent and study the structure and properties of some alkanes and their isomers. In this way, his first contribution was knowing the different isomers of the alkanes as a function of the number of carbons that they contain. Moreover, his work allowed us to know exactly the number of isomers of the alkane with n carbons once the number of isomers of the alkane with n − 1 carbons is known (see references [2,3]). At present, the representation of some systems by means of graphs has allowed us to analyze complex structures, both their structure and properties, and summarize them in terms of some numerical parameters called (topological) indices (see reference [4]); these indices, which are graph invariants, carry information on the structure of the graph. Thus, graphs are used as models for studying computer interconnections, social networks, social structures, neural networks, and networks of interactions of species in trophic networks, to name a few (see reference [5]).

It is precisely in social networks, in a story published in 1929, that the six degrees of separation hypothesis arose, which says that any two people can be connected through a chain of acquaintances with, at most, five intermediaries (see reference [6]). This hypothesis led to the emergence of the small-world phenomenon, which is the notion that the world can be seen as a somewhat “small” social network; that is, every person can be reached through a small set of intermediaries from any other person (see reference [7]). One of the best known studies was carried out in the 1960s by S. Milgram, who performed the so-called Small-world experiment (see reference [8]). After this, the concept of small-world was transferred, in a natural way, to graphs. Thus, in 1998, Watts and Strogatz proposed a model to generate random graphs with the properties of a small-world, introducing the clustering coefficient as a parameter for their model (see reference [9]).

Clustering in graphs is a topic that has caught the attention of many people in recent years, due to the fact that this invariant gives information about its local and global structure. Depending on the situation, the clustering coefficient grants: the classification of graphs that display interactions between elements (scale-free and small-world) (see references [10,11]); and the identification of species in an ecosystem that are most relevant or important from a biological viewpoint (see references [12,13]). Moreover, there are some papers devoted to the clustering coefficient, for example, in reference [14] the authors present some expressions for this parameter of the tensor product of arbitrary graphs, regular graphs, and strongly regular graphs. In reference [15] it is shown that the global clustering coefficient of the tensor and Cartesian product for two complete graphs with m vertices approach 1 and $1/2$, respectively, as $m\to \infty$. It is worth mentioning that the computation of this parameter is very hard when considering graphs with many vertices and edges (see references [16,17]).

As other structures, graphs can also be operated in such a way from two, given a third one is obtained (a graph product). Among these binary operations, there are some that are well known and that have been studied and investigated from different perspectives, for example: the total Roman domination number of the lexicographic product of graphs is studied in reference [18]; the exact value of the edge irregularity strength of the corona product of paths is determined in reference [19]; explicit expressions for the F-index of different types of corona product are derived in reference [20]; the super fair dominating sets of the corona and lexicographic product of two graphs are characterized in reference [21]; some tight bounds and closed formulas for the strong metric dimension of the Cartesian sum of graphs, in terms of some parameters of the factors, are obtained in reference [22]; and explicit expressions for the Schultz index of the Cartesian, corona, and lexicographic product, and the Cartesian sum, are given in reference [23].

In this work, we compute the number of triangles for the corona and lexicographic products, as well as for the Cartesian sum. Such expressions are given in terms of the order and size of factors, and the degree and number of triangles of vertices in each factor, and we use them to give explicit expressions for their clustering coefficient.

2. Preliminaries

In this section, we establish some notation and recall some definitions used throughout this paper.

By graph we mean a simple and finite graph $\Gamma =(V,E)$; given two vertices $u,v\in V$, we say that they are neighbors or adjacent if they form an edge, that is $uv\in E$. The set of neighbors of v is denoted by $N\left(v\right)$. The degree of $v\in V$ is the number of vertices that are its neighbors, that is,

$$\mathrm{deg}\left(v\right)=\left|N\right(v\left)\right|.$$

A graph $\Gamma$ is a tree if it is connected and contains no cycles. $\Gamma$ is called bipartite if V can be written as the disjoint union of two non-empty subsets such that every edge has one endpoint in each subset. The cycle graph of order $n\ge 3$, denoted by ${\mathrm{C}}_n$, is the graph with the vertex set $V\left({\mathrm{C}}_n\right)=\{v_1,\cdots ,v_n\}$ and edge set

$$E\left({\mathrm{C}}_n\right)=\{v_1{v}_2,v_2{v}_3,\cdots ,v_{n-1}{v}_n,v_n{v}_1\}.$$

The complete graph of order $n\ge 1$, denoted by ${\mathrm{K}}_n$, is the graph with the vertex set $V\left({\mathrm{K}}_n\right)=\{v_1,\cdots ,v_n\}$ and edge set

$$E\left({\mathrm{K}}_n\right)=\{v_i{v}_j:i,j=1,\cdots ,n,\mathrm{and}i\ne j\}.$$

We say that three vertices, $u,v$, and w, of a graph $\Gamma$ produce a triangle if the subgraph induced by them is isomorphic to ${\mathrm{K}}_3$, the number of triangles of $\Gamma$ that contain v is denoted by $t\left(v\right)$; thus,

$$t\left(v\right)=\left|\right\{uw\in E:vu,vw\in E\left\}\right|.$$

For more concepts related to graphs, see reference [24].

Below, we state the definition of the graph invariant that concerns us in this paper.

Definition 1.

Let $\Gamma =(V,E)$ be a graph and $v\in V$. The  clustering coefficient of v is defined using the formula

$$C\left(v\right)=\left\{\begin{array}{cc}\frac{2t\left(v\right)}{\mathrm{deg}\left(v\right)\left(\mathrm{deg}\right(v)-1)},\hfill & if\mathrm{deg}\left(v\right)\ge 2;\hfill \\ 0,\hfill & otherwise.\hfill \end{array}\right.$$

And the  clustering coefficient of Γ is defined by

$$C(\Gamma )=\frac{1}{\left|V\right|}\sum _{v\in V}C\left(v\right).$$

In the literature, it is common to refer to the clustering coefficient of a vertex as local clustering and to that of the graph as global clustering.

Example 1.

I. 

Let Γ be the graph shown in Figure 1. Observe that, for the vertex v, we have $\mathrm{deg}\left(v\right)=4$ and $t\left(v\right)=3$; thus, $C\left(v\right)=\frac{1}{2}$. Moreover, by doing the right calculations, we get $C(\Gamma )=\frac{17}{36}$.

II. 

If Γ is a tree, a bipartite graph, or a cycle of order $\ge 4$, it does not contain triangles; thus, for any vertex v we have $t\left(v\right)=0$ and, consequently, $C\left(v\right)=0$, obtaining $C(\Gamma )=0$.

III. 

For the complete graph ${\mathrm{K}}_n=(V,E)$ and $v\in V$, it is clear that it forms a triangle with any pair of distinct vertices. Thus, $t\left(v\right)=\frac{(n-1)(n-2)}{2}$, which implies $C\left(v\right)=1$ and $C(\Gamma )=1$. And, reciprocally, if any vertex v of a graph Γ satisfies $C\left(v\right)=1$, then $\Gamma \cong {\mathrm{K}}_n$.

3. The Clustering Coefficient for Graph Products

In this section, for some graph products, we compute the number of triangles containing a vertex in terms of some parameters associated with the vertices of each entry to give an expression of the local and global clustering.

3.1. The Corona Product

Recall that, given two graphs, ${\Gamma }_1=(V_1,E_1)$ and ${\Gamma }_2=(V_2,E_2)$, the corona product of ${\Gamma }_1$ with ${\Gamma }_2$ is defined as the graph $\Gamma =(V,E)$ given by taking one copy of ${\Gamma }_1$ and $|V_1|$ copies of ${\Gamma }_2$, joining the r-th vertex of ${\Gamma }_1$ to every vertex in the r-th copy of ${\Gamma }_2$. That is,

$$\begin{array}{cc}\hfill V& =\left(V_1\times \left\{v_0\right\}\right)\cup \left(V_1\times V_2\right)\mathrm{and}\hfill \\ \hfill E& =E_1\cup \{(u_r,v_i)(u_r,v_j):v_i{v}_j\in E_2\}\cup \{(u_r,v_0)(u_r,v_i):v_i\in V_2\},\hfill \end{array}$$

where $V_1\times \left\{v_0\right\}$ are considered as the vertices of the copy of ${\Gamma }_1$ and $V_1\times V_2$ are those of the $|V_1|$ copies of ${\Gamma }_2$. This graph is denoted by ${\Gamma }_1\odot {\Gamma }_2$. Figure 2 shows the corona product of ${\mathrm{K}}_5$ with ${\mathrm{K}}_4$.

Proposition 1.

Let ${\Gamma }_1=(V_1,E_1)$ and ${\Gamma }_2=(V_2,E_2)$ be two graphs with $|E_2|=m_2$. If $(u,v)$ is a vertex of ${\Gamma }_1\odot {\Gamma }_2$, then

$$t(u,v)=\left\{\begin{array}{cc}{t}_1\left(u\right)+m_2,\hfill & ifv=v_0;\hfill \\ t_2\left(v\right)+\mathrm{deg}\left(v\right),\hfill & otherwise,\hfill \end{array}\right.$$

where $t_1\left(u\right)$ and $t_2\left(v\right)$ denote the number of triangles containing the vertices u and v in ${\Gamma }_1$ and ${\Gamma }_2$, respectively.

Proof. 

Let $(x,y),(w,z)\in V$ such that they form a triangle with $(u,v)$. We proceed by cases. If $v=v_0$, then $(u,v_0)(x,y)\in E$ if and only if $y=v_0$ and $ux\in E_1$ or $u=x$, analogously for $(w,z)$. Moreover, $(x,y)(w,z)\in E$ if and only if $y=z=v_0$ and $xw\in E_1$ or $x=w$ and $yz\in E_2$. Thus, $(u,v_0),(x,y),(w,z)$ form a triangle when $u,x,w$ create a triangle in ${\Gamma }_1$ or $yz\in E_2$. In this way, the number of triangles for $(u,v_0)$ is $t_1\left(u\right)+m_2$.

Now suppose $v\ne v_0$. Then, $(u,v)(x,y)\in E$ if and only if $u=x$ and $vy\in E_2$ or $u=x$ and $y=v_0$, analogously for $(w,z)$. And $(x,y)(w,z)\in E$ if and only if $x=w=u$ and $yz\in E_2$ or $y=v_0$ or $z=v_0$, but not both. Thus, $(u,v),(x,y),(w,z)$ form a triangle if $v,y,z$ do it in ${\Gamma }_2$ or $y=v_0$ and $vz\in E_2$. Consequently, the number of triangles for $(u,v)$ is $t_2\left(v\right)+\mathrm{deg}\left(v\right)$. □

Under the conditions of the above proposition, the subsequent result follows immediately.

Theorem 1.

Let ${\Gamma }_1=(V_1,E_1)$ and ${\Gamma }_2=(V_2,E_2)$ be two graphs with $|V_1|=n_1$, $|E_1|=m_1$, $|V_2|=n_2$, and $|E_2|=m_2$. If ${\Gamma }_1\odot {\Gamma }_2=(V,E)$ and $(u,v)\in V$, then

I.

The local clustering of $(u,v)$ is given by

$$C(u,v)=\left\{\begin{array}{cc}\frac{2\left(t_1\left(u\right)+m_2\right)}{(\mathrm{deg}\left(u\right)+n_2)(\mathrm{deg}\left(u\right)+n_2-1)},\hfill & if v=v_0;\hfill \\ \frac{2\left(t_2\left(v\right)+\mathrm{deg}\left(v\right)\right)}{\left(\mathrm{deg}\right(v)+1)\mathrm{deg}\left(v\right)},\hfill & otherwise,\hfill \end{array}\right.$$

II.

And the global clustering by

$$\begin{array}{c}C({\Gamma }_1\odot {\Gamma }_2)=\frac{1}{n_1+n_1{n}_2}(\sum _{u\in V_1}\frac{2\left(t_1\left(u\right)+m_2\right)}{(\mathrm{deg}\left(u\right)+n_2)(\mathrm{deg}\left(u\right)+n_2-1)}\\ +n_1\sum _{v\in V_2}\frac{2\left(t_2\left(v\right)+\mathrm{deg}\left(v\right)\right)}{\left(\mathrm{deg}\right(v)+1)\mathrm{deg}\left(v\right)}).\end{array}$$

Example 2.

Consider two complete graphs, ${\mathrm{K}}_r$ and ${\mathrm{K}}_s$, of order r and s, respectively, and let $\Gamma =(V,E)$ be the corona product of ${\mathrm{K}}_r$ with ${\mathrm{K}}_s$. For $(u,v)\in V$

$$\mathrm{deg}(u,v)=\left\{\begin{array}{cc}r+s-1,\hfill & if v=v_0;\hfill \\ s,\hfill & otherwise.\hfill \end{array}\right.$$

According to Proposition 1, we have that the number of triangles containing $(u,v)$ is

$$t(u,v)=\left\{\begin{array}{cc}\frac{(r-1)(r-2)+(s-1)s}{2},\hfill & if v=v_0;\hfill \\ \frac{(s-1)s}{2},\hfill & otherwise.\hfill \end{array}\right.$$

The first part of the last theorem implies

$$C(u,v)=\left\{\begin{array}{cc}\frac{(r-1)(r-2)+(s-1)s}{(r+s-1)(r+s-2)},\hfill & if v=v_0;\hfill \\ 1,\hfill & otherwise,\hfill \end{array}\right.$$

obtaining

$$C({\Gamma }_1\odot {\Gamma }_2)=\frac{1}{s+1}\left(\frac{(r-1)(r-2)+(s-1)s}{(r+s-1)(r+s-2)}+s\right).$$

It is worth noting that, even when the first graph is not complete, it is enough that the second one is so that the value of the clustering coefficient of the vertices whose second entry is other than $v_0$ is 1. Figure 2 shows the corona product of ${\mathrm{K}}_5$ with ${\mathrm{K}}_4$.

3.2. The Lexicographic Product

The lexicographic product of two graphs, ${\Gamma }_1=(V_1,E_1)$ and ${\Gamma }_2=(V_2,E_2)$, is defined as the graph $\Gamma =(V,E)$ with $V=V_1\times V_2$ and

$$E=\{(u,v)(x,y):ux\in E_1\}\cup \{(x,v)(x,y):vy\in E_2\}.$$

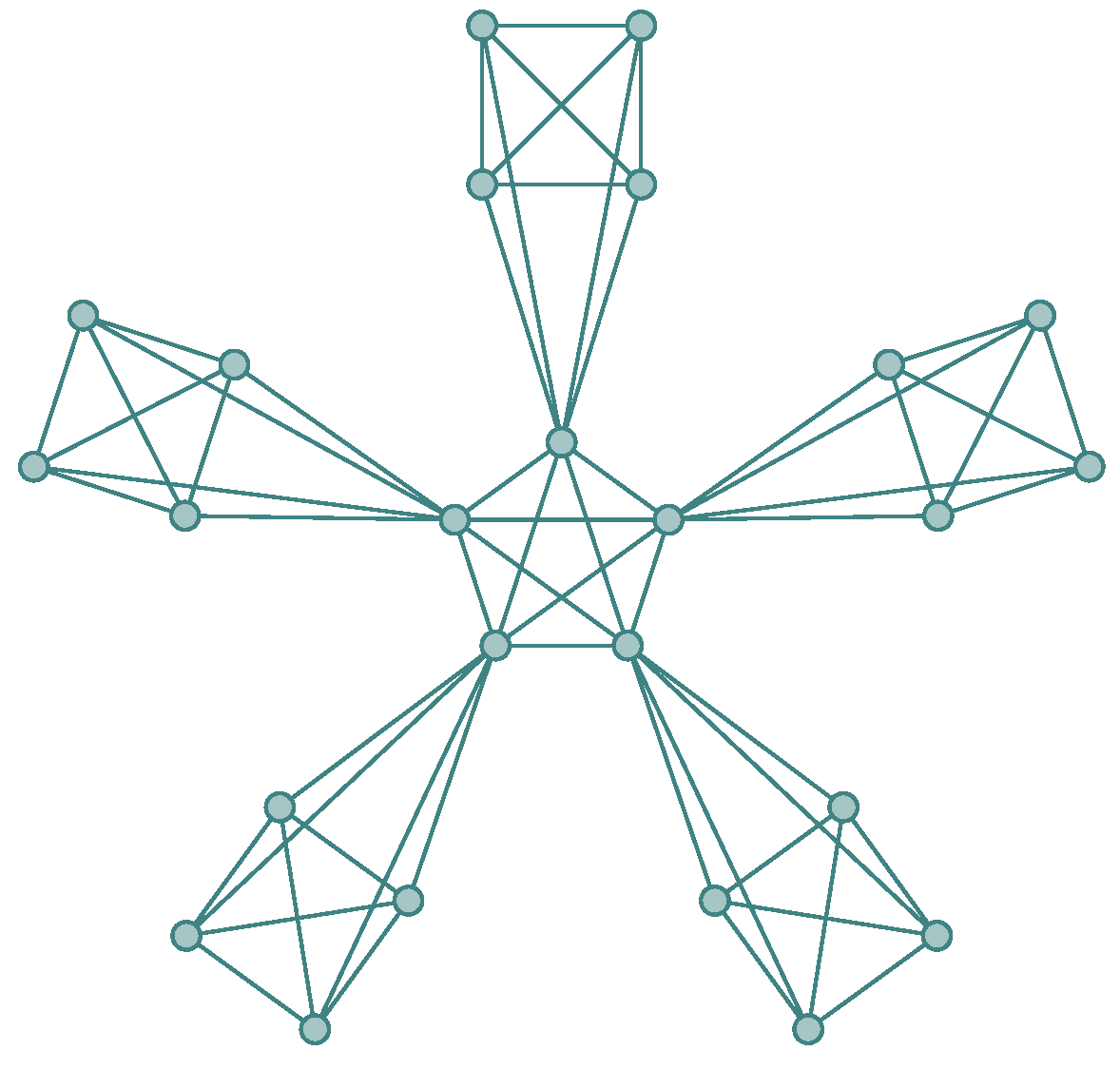
We denote this graph by ${\Gamma }_1\circ {\Gamma }_2$. Observe that ${\Gamma }_1\circ {\Gamma }_2$ can obtained by taking $|V_1|$ copies of ${\Gamma }_2$ and joining the vertices of ${\Gamma }_{2,u}$ with every vertex of ${\Gamma }_{2,x}$ (the corresponding copies to vertices u and x, respectively) if $ux\in E_1$. Figure 3 shows a representation of the lexicographic product of ${\mathrm{S}}_3$ and ${\mathrm{P}}_3$.

Note that the edge set of the lexicographic product is precisely the union of two sets. Assume that an edge of the first set is incident to one of the second ones, say $(u,v)(x,y)$ to $(u,v)(u,z)$. Thus, $ux\in E_1$ and $vz\in E_2$. We may note that $(x,y)(u,z)\in E$ is the only edge incident to them, and it belongs to the first set. This implies that the only way of creating a triangle with edges in both sets is that two of them belong to the first set and the other to the second one. In this way, we consider triangles of three types.

∘

Type 1: the three edges belong to the first set.

∘

Type 2: two edges are in the first set and the other in the second one.

∘

Type 3: the three edges are in the second set.

In contrast to the corona product case, we compute the number of triangles of each type separately to make our calculations clearer.

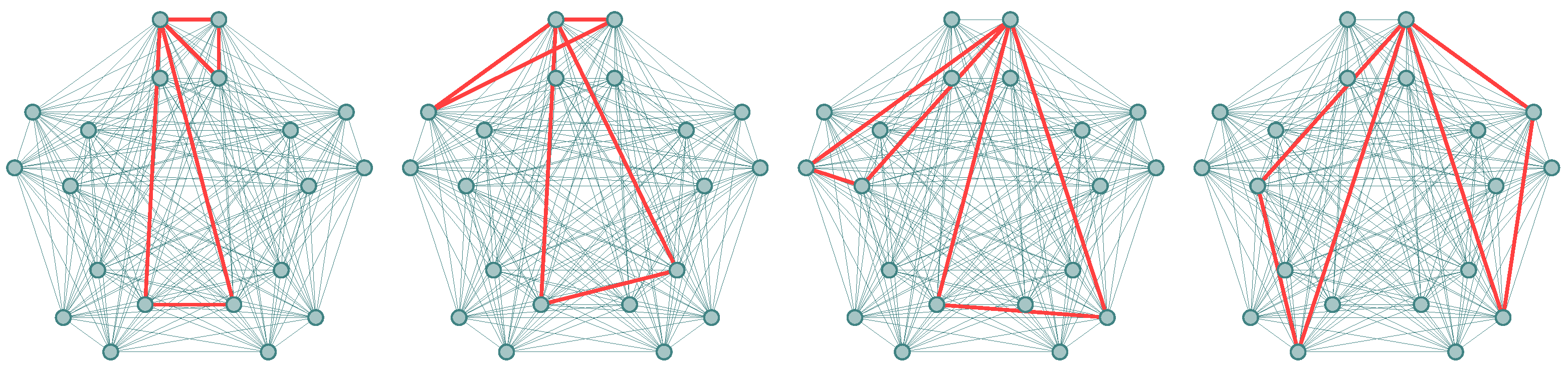
Before starting with our computations, we present some of these triangles in an example to illustrate some of our reasonings. The first graph of Figure 4 shows some triangles of type 1 in the lexicographic product of ${\mathrm{K}}_5$ and ${\mathrm{K}}_4$, they are produced by vertices whose first entries are adjacent in ${\mathrm{K}}_4$. The second one shows triangles of type 2, they are formed by vertices such that two of them have the same first entry, the second entries are adjacent in ${\mathrm{K}}_5$, and the first entry of these vertices form an edge with the first of the third one. And the last one displays triangles of type 3; they are formed by vertices that have the same first entry and the second entries are adjacent in ${\mathrm{K}}_5$.

Throughout this subsection, $n_1$ and $n_2$ denote the order of ${\Gamma }_1$ and ${\Gamma }_2$, respectively, $m_1$ and $m_2$ the size of ${\Gamma }_1$ and ${\Gamma }_2$, respectively, and $(u,v)$ a vertex of ${\Gamma }_1\circ {\Gamma }_2$.

Lemma 1.

Under the above conditions, the number of triangles of type 1 containing $(u,v)$ as a vertex is given by $t_1\left(u\right)n_2^2$.

Proof. 

Let $(x,y)$ and $(w,z)$ be two vertices such that they form a triangle of type 1 with $(u,v)$. Then, $ux,uw,xw\in E_1$, that is, $u,x$, and w, produce a triangle in ${\Gamma }_1$. Since y and z can be any of the vertices of ${\Gamma }_2$, there are $n_2^2$ triangles of type 1 in $\Gamma$ determined by this one in ${\Gamma }_1$. Therefore, there are $n_2^2{t}_1\left(u\right)$ triangles of this type containing $(u,v)$. □

Following lemma gives the number of triangles of type 2.

Lemma 2.

Under the initial conditions, there are $\mathrm{deg}\left(u\right)(n_2\mathrm{deg}\left(v\right)+m_2)$ triangles of type 2 in Γ, having $(u,v)$ as a vertex.

Proof. 

Let $(x,y),(w,z)\in V$ such that they form a triangle of type 2 with $(u,v)$. Then, $(u,v)(x,y)$ or $(x,y)(w,z)$ belong to the second set of edges. If $(u,v)(x,y)$ is in the second set, then $u=x$ and $vy\in E_2$, that is, $y\in N\left(v\right)$ and $(u,v)(w,z)$ is an edge that belongs to the first set, which implies $uw\in E_1$. Thus, w can be taken as any neighbor of u and z any vertex of ${\Gamma }_2$. On the other hand, if $(x,y)(w,z)$ is in the second set of edges, $x=w$ and $yz\in E_2$, since $(u,v)(x,y)$ and $(u,v)(x,z)$ are edges in the first set, x can be any neighbor of u; therefore, $yz$ can be any edge of ${\Gamma }_2$. Hence, the number of triangles of type 2 is $\mathrm{deg}\left(u\right)(n_2\mathrm{deg}\left(v\right)+m_2)$. □

Next, we characterize the triangles of type 3 by those in the second factor.

Lemma 3.

The number of triangles of type 3 in Γ, containing $(u,v)$ as a vertex, is $t_2\left(v\right)$.

Proof. 

Let $(x,y),(w,z)\in V$ such that they form a triangle of type 3 with $(u,v)$. Then $u=x=w$ and $vy,vz,yz\in E_2$, that is, $v,y$, and z are the vertices of a triangle in ${\Gamma }_2$. Thus, the triangle with vertices $(u,v),(u,y)$, and $(u,z)$ is determined by the last one.

Therefore, there are $t_2\left(v\right)$ triangles of type 3 containing $(u,v)$. □

To summarize, we have the following proposition.

Proposition 2.

The number of triangles of ${\Gamma }_1\circ {\Gamma }_2$ having $(u,v)$ as a vertex is given by

$$t(u,v)=n_2^2{t}_1\left(u\right)+\mathrm{deg}\left(u\right)(n_2\mathrm{deg}\left(v\right)+m_2)+t_2\left(v\right).$$

The next result follows immediately from the last one.

Theorem 2.

Let ${\Gamma }_1=(V_1,E_1)$ and ${\Gamma }_2=(V_2,E_2)$ be two graphs with $|V_1|=n_1$, $|E_1|=m_1$, $|V_2|=n_2$, and $|E_2|=m_2$. If ${\Gamma }_1\circ {\Gamma }_2=(V,E)$ and $(u,v)\in V$, then

I.

The clustering coefficient of $(u,v)$ is given by

$$C(u,v)=\frac{2\left(n_2^2{t}_1\left(u\right)+\mathrm{deg}\left(u\right)(n_2\mathrm{deg}\left(v\right)+m_2)+t_2\left(v\right)\right)}{(\mathrm{deg}\left(v\right)+n_2\mathrm{deg}\left(u\right))(\mathrm{deg}\left(v\right)+n_2\mathrm{deg}\left(u\right)-1)},$$

II.

And the clustering coefficient of ${\Gamma }_1\circ {\Gamma }_2$ by the formula

$$C({\Gamma }_1\circ {\Gamma }_2)=\frac{1}{n_1{n}_2}\sum _{u\in V_1}\sum _{v\in V_2}\frac{2\left(n_2^2{t}_1\left(u\right)+\mathrm{deg}\left(u\right)(n_2\mathrm{deg}\left(v\right)+m_2)+t_2\left(v\right)\right)}{(\mathrm{deg}\left(v\right)+n_2\mathrm{deg}\left(u\right))(\mathrm{deg}\left(v\right)+n_2\mathrm{deg}\left(u\right)-1)}.$$

Example 3.

Again, we consider two complete graphs ${\mathrm{K}}_r$ and ${\mathrm{K}}_s$. If $(u,v)$ is a vertex of ${\mathrm{K}}_r\circ {\mathrm{K}}_s$, Proposition 2 implies that

$$\begin{array}{cc}\hfill t(u,v)& =s^2\frac{(r-1)(r-2)}{2}+(r-1)\left(s(s-1)+\frac{s(s-1)}{2}\right)+\frac{(s-1)(s-2)}{2}\hfill \\ \hfill & =\frac{r^2{s}^2-3rs+2}{2}.\hfill \end{array}$$

According to the above theorem, we obtain $C(u,v)=1$, for every vertex. Therefore,

$$C({\mathrm{K}}_r\circ {\mathrm{K}}_s)=1,$$

which coincides with the fact that ${\mathrm{K}}_r\circ {\mathrm{K}}_s$ is the complete graph of $rs$ vertices.

3.3. The Cartesian Sum

Given two graphs ${\Gamma }_1=(V_1,E_1)$ and ${\Gamma }_2=(V_2,E_2)$, the Cartesian sum of them is defined as the graph $\Gamma =(V,E)$ with $V=V_1\times V_2$ and

$$E=\{(u,v)(x,y):ux\in E_1\mathrm{or}vy\in E_2\}.$$

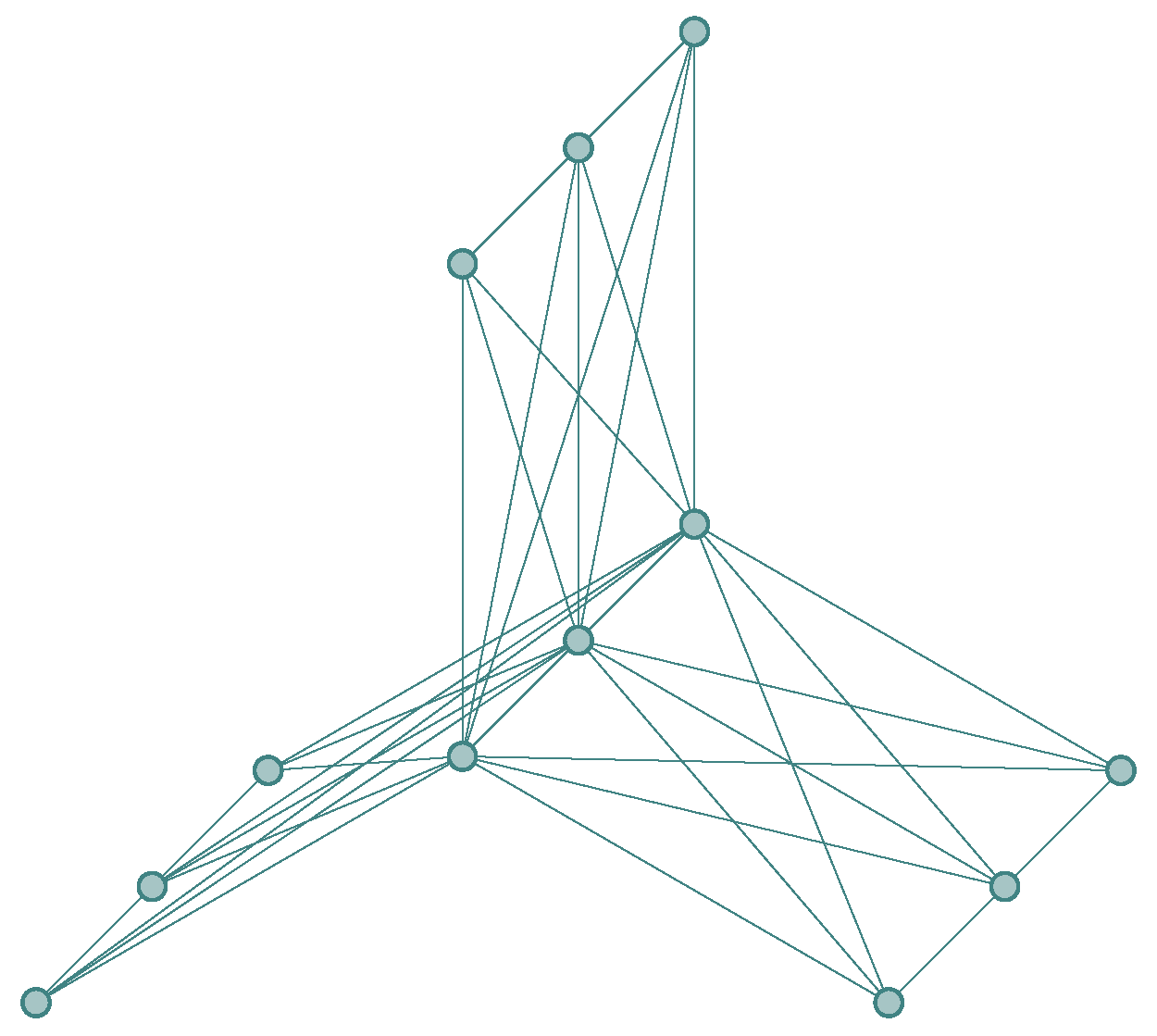
This graph is denoted by ${\Gamma }_1\oplus {\Gamma }_2$. We may observe that ${\Gamma }_1\circ {\Gamma }_2$ is a subgraph of ${\Gamma }_1\oplus {\Gamma }_2$. Thus, the Cartesian sum can be obtained with the lexicographic product plus the edges obtained by joining the vertex v of the i-th copy with the vertex y of any other copy, whenever $vy\in E_2$. Figure 5 shows a representation of the Cartesian sum of ${\mathrm{S}}_3$ and ${\mathrm{P}}_3$.

To compute the number of triangles of a vertex in the Cartesian sum, we observe that two vertices form an edge if and only if there is an edge between the vertices of the first or the second entries; thus, we consider four types of triangles.

∘

Type 1: there are three edges between the first entries.

∘

Type 2: two edges are formed with the first entries and one with the second.

∘

Type 3: one edge is formed with the first entries and two with the second.

∘

Type 4: the three edges are formed between the second entries.

In order to make clearer our calculations, we compute the number of triangles of each type and those of the intersections between different types.

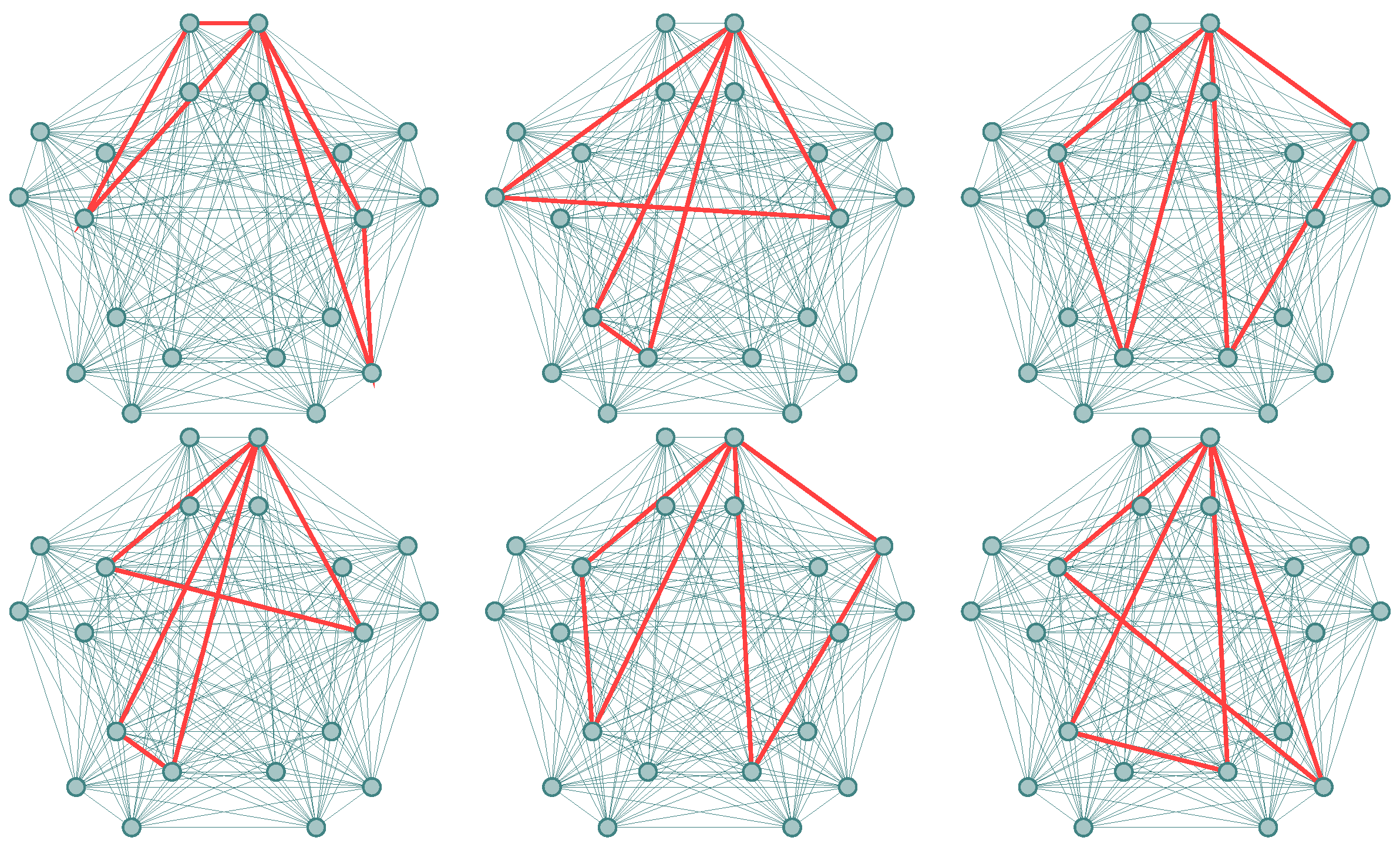
As in the lexicographic product, before starting our computations, we present examples of these triangles that help to illustrate some of our reasonings. Since ${\mathrm{K}}_r\circ {\mathrm{K}}_s\cong {\mathrm{K}}_{rs}$, then ${\mathrm{K}}_r\oplus {\mathrm{K}}_s$ is also isomorphic to ${\mathrm{K}}_{rs}$. The first graph of Figure 6 shows some triangles of type 1 in the Cartesian sum of ${\mathrm{K}}_5$ and ${\mathrm{K}}_4$; they are produced by vertices whose first entries form a triangle in ${\mathrm{K}}_4$. The second one shows triangles of type 2; they are produced by vertices such that their first entries form two edges in ${\mathrm{K}}_4$ and one edge is formed with the second entries in ${\mathrm{K}}_5$. The third graph displays triangles of type 3; they are formed by vertices such that their second entries form two edges in ${\mathrm{K}}_5$ and one edge is formed with the first entries in ${\mathrm{K}}_4$. And the last one exhibits triangles of type 4 which are formed by vertices such that their second entries are in a triangle in ${\mathrm{K}}_5$.

Throughout this subsection, $n_1$ and $n_2$ denote the order of ${\Gamma }_1$ and ${\Gamma }_2$, respectively, $m_1$ and $m_2$ the size of ${\Gamma }_1$ and ${\Gamma }_2$, respectively, and $(u,v)$ a vertex of the Cartesian sum ${\Gamma }_1\oplus {\Gamma }_2$.

Lemma 4.

For the vertex $(u,v)$ there are $n_2^2{t}_1\left(u\right)$ triangles of type 1 which contain it.

Proof. 

Let $(x,y)$ and $(w,z)$ be two vertices such that $(u,v),(x,y)$, and $(w,z)$ form a triangle of type 1, so $ux,uw,xw\in E_1$. Thus, this triangle is induced by a triangle of ${\Gamma }_1$. Note that a triangle in ${\Gamma }_1$ given by $u,x$, and w induces the triangles $(u,v)$, $(x,y)$, and $(w,z)$ for any $y,z\in V_2$. Consequently, the number of triangles induced is $n_2^2$. Therefore, there are $n_2^2{t}_1\left(u\right)$ triangles of type 1 containing $(u,v)$. □

Analogous arguments can be used for triangles of type 4, obtaining the following.

Lemma 5.

For the vertex $(u,v)$ there are $n_1^2{t}_2\left(v\right)$ triangles of type 4 which contain it.

Next, we compute the number of triangles of type 2.

Lemma 6.

The number of triangles of type 2 containing $(u,v)$ as a vertex is

$$m_2{\mathrm{deg}}^2\left(u\right)+n_2\mathrm{deg}\left(v\right)\sum _{x\in N\left(u\right)}\mathrm{deg}\left(x\right)-t_1\left(u\right)\left[{\mathrm{deg}}^2\left(v\right)+2\left(\sum _{z\in N\left(v\right)}\mathrm{deg}\left(z\right)-t_2\left(v\right)\right)\right].$$

Proof. 

Consider two vertices $(x,y)$ and $(w,z)$ such that $(u,v),(x,y)$, and $(w,z)$ form a triangle of type 2. We have the following two cases.

• Case 1: $ux,uw\in E_1$ and $yz\in E_2$. Note that x and w can be any neighbor of u and they can even coincide, since $y\ne z$. Moreover, $yz$ can be any edge of ${\Gamma }_2$, thus, there are $m_2{\mathrm{deg}}^2\left(u\right)$ of these triangles.
• Case 2: $ux,xw\in E_1$ and $vz\in E_2$. Notice that x can be any neighbor of u, and for each x any of its neighbors can be w, even the same u, since $vz\in E_2$. In addition, z can be any vertex adjacent to v and y any vertex of ${\Gamma }_2$, but when $u,x$, and w form a triangle in ${\Gamma }_1$, there are triangles counted twice for each $y\in N\left(v\right)$, and since z is also any neighbor of v, the number of the triangles counted two times is $t_1\left(u\right){\mathrm{deg}}^2\left(v\right)$. Thus, we get $n_2\mathrm{deg}\left(v\right){\sum }_{x\in N\left(u\right)}\mathrm{deg}\left(x\right)-t_1\left(u\right){\mathrm{deg}}^2\left(v\right)$ triangles.

Observe that these cases may occur simultaneously; when this happens we have $ux,uw\in E_1$ and $xw\in E_1$, then $u,x,w$ produce a triangle in ${\Gamma }_1$. Furthermore, $yz,vz\in E_2$ or $yz,vy\in E_2$, which can be read into 2-walks starting at v, but when $v,y$, and z form a triangle in ${\Gamma }_2$, such walks are counted twice; this implies that the number of these triangles is $t_1\left(u\right)2({\sum }_{z\in N\left(v\right)}\mathrm{deg}\left(z\right)-t_2\left(v\right))$. Hence, the number of triangles of type 2 is

$$m_2{\mathrm{deg}}^2\left(u\right)+n_2\mathrm{deg}\left(v\right)\sum _{x\in N\left(u\right)}\mathrm{deg}\left(x\right)-t_1\left(u\right)\left[{\mathrm{deg}}^2\left(v\right)+2\left(\sum _{z\in N\left(v\right)}\mathrm{deg}\left(z\right)-t_2\left(v\right)\right)\right].$$

 □

A similar analysis can be done for triangles of type 3, obtaining the next result.

Lemma 7.

The number of triangles of type 3 containing $(u,v)$ as a vertex is

$$m_1{\mathrm{deg}}^2\left(v\right)+n_1\mathrm{deg}\left(u\right)\sum _{y\in N\left(v\right)}\mathrm{deg}\left(y\right)-t_2\left(v\right)\left[{\mathrm{deg}}^2\left(u\right)+2\left(\sum _{w\in N\left(u\right)}\mathrm{deg}\left(w\right)-t_1\left(u\right)\right)\right].$$

Now, before starting to count triangles that have been considered in two or more cases, we present examples of these. The first graph of Figure 7 shows some triangles that are, at the same time, of type 1 and type 2 in the Cartesian sum of ${\mathrm{K}}_5$ and ${\mathrm{K}}_4$; they are produced by vertices whose first entries form a triangle in ${\mathrm{K}}_4$ and their second entries form at least one edge in ${\mathrm{K}}_5$. The second one shows triangles of type 1 and type 3; they are produced by vertices such that their first entries form a triangle in ${\mathrm{K}}_4$ and at least two edges are formed by the second entries in ${\mathrm{K}}_5$. The third graph displays triangles of type 1 and type 4; they are formed by vertices such that their first entries form a triangle in ${\mathrm{K}}_4$ and the second entries form also a triangle in ${\mathrm{K}}_5$. The fourth one shows triangles of type 2 and type 3; they are produced by vertices such that the first entries of two of them form an edge in ${\mathrm{K}}_4$ and the second entries form another in ${\mathrm{K}}_5$, and the other two edges are formed by one between the first entries and another between the second ones. The fifth graph displays triangles of type 2 and type 4 that are formed by vertices, such that their first entries form at least two edges in ${\mathrm{K}}_4$ and the second ones are in a triangle in ${\mathrm{K}}_5$. And the last one shows triangles of type 3 and type 4 which are produced by vertices, such that their first entries form at least one edge in ${\mathrm{K}}_4$ and the second ones are in a triangle in ${\mathrm{K}}_5$.

Lemma 8.

The number of triangles of type 1 and 2 that contain $(u,v)$ is

$$t_1\left(u\right)\left[2m_2+2n_2\mathrm{deg}\left(v\right)-{\mathrm{deg}}^2\left(v\right)-2\left(\sum _{z\in N\left(v\right)}\mathrm{deg}\left(z\right)-t_2\left(v\right)\right)\right].$$

Proof. 

Suppose that $(x,y)$ and $(w,z)$ form a triangle with $(u,v)$, which is both types 1 and 2. Then, $ux,uw,xw\in E_1$, that is, u, x, and w are vertices of a triangle in ${\Gamma }_1$. Moreover, $yz\in E_2$, $vy\in E_2$ or $vz\in E_2$. We proceed by cases.

• Case 1: if $yz\in E_2$, there is no restriction for y and z, so that $yz$ can be any edge of ${\Gamma }_2$, counted twice, since it can be considered $yz$ or $zy$.
• Case 2: if $vy\in E_2$, y can be any neighbor of v and z any vertex of ${\Gamma }_2$.
• Case 3: if $vz\in E_2$, the reasoning is analogous to the last case.

Note that, if y and z are both adjacent to v, they are counted in both cases $\mathrm{deg}\left(v\right)$ times. In addition, if $yz,vz\in E_2$, the first and third situations happen at the same time, or if $yz,vy\in E_2$ the first and second happen; this can be interpreted as a 2-walk starting at v. But if $v,y$, and z form a triangle in ${\Gamma }_2$, these walks are counted twice. Therefore, the number of triangles that are of type 1 and 2 is

$$t_1\left(u\right)\left[2m_2+2n_2\mathrm{deg}\left(v\right)-{\mathrm{deg}}^2\left(v\right)-2\left(\sum _{z\in N\left(v\right)}\mathrm{deg}\left(z\right)-t_2\left(v\right)\right)\right].$$

 □

Analogous arguments lead to the next result.

Lemma 9.

The number of triangles of type 3 and 4 that contain $(u,v)$ is

$$t_2\left(v\right)\left[2m_1+2n_1\mathrm{deg}\left(u\right)-{\mathrm{deg}}^2\left(u\right)-2\left(\sum _{w\in N\left(u\right)}\mathrm{deg}\left(w\right)-t_1\left(u\right)\right)\right].$$

Next, we state the correspondent result for triangles of types 1 and 3.

Lemma 10.

For the vertex $(u,v)$, the number of triangles of types 1 and 3 which contain it is

$$t_1\left(u\right)\left[{\mathrm{deg}}^2\left(v\right)+2\left(\sum _{y\in N\left(v\right)}\mathrm{deg}\left(y\right)-2t_2\left(v\right)\right)\right].$$

Proof. 

Suppose that $(u,v)$, $(x,y)$, and $(w,z)$ form a triangle of type 1, then $ux,uw,xw\in E_1$ and the vertices $u,x$, and w produce a triangle in ${\Gamma }_1$. Since the triangle of the former vertices is also of type 3, we have that $vy,vz\in E_2$, $vy,yz\in E_2$, or $vz,yz\in E_2$, again by cases.

• Case 1: if $vy,vz\in E_2$; then y and z can be any neighbor of v, they may even be the same.
• Case 2: if $vy,yz\in E_2$, this can be treated as a 2-walk starting at v.
• Case 3: if $vz,yz\in E_2$, the reasoning is analogous to the last one.

In addition, if $vy$, $vz$, and $yz$ occur at the same time, then $v,y$, and z create a triangle in ${\Gamma }_2$, and since the triangle given by the edges $vy$, $yz$, and $vz$ is the same as that formed by $vz$, $zy$, and $vy$, such a triangle is counted twice. Hence, the number of triangles of types 1 and 3 is

$$t_1\left(u\right)\left({\mathrm{deg}}^2\left(v\right)+2\left(\sum _{y\in N\left(v\right)}\mathrm{deg}\left(y\right)-2t_2\left(v\right)\right)\right).$$

 □

A similar reasoning shows the following result.

Lemma 11.

For the vertex $(u,v)$, the number of triangles of types 2 and 4 which contain it is

$$t_2\left(v\right)\left[{\mathrm{deg}}^2\left(u\right)+2\left(\sum _{x\in N\left(u\right)}\mathrm{deg}\left(x\right)-2t_1\left(u\right)\right)\right].$$

Now, we formulate the statement for triangles of types 1 and 4.

Lemma 12.

The number of triangles of types 1 and 4 that have $(u,v)$ as a vertex is $2t_1\left(u\right)t_2\left(v\right)$.

Proof. 

Suppose that the vertices $(u,v)$, $(x,y)$, and $(w,z)$ give rise to a triangle of type 1 and 4, then $ux,uw,xw\in E_1$ and $vy,vz,yz\in E_2$, that is, $u,x$, and w form a triangle in ${\Gamma }_1$ and $v,y$, and z form the same in ${\Gamma }_2$. Note that $(u,v)$, $(x,z)$, and $(w,y)$ is also a triangle of both types 1 and 4 and it is induced by the same triangles in ${\Gamma }_1$ and ${\Gamma }_2$; thus, for each triangle in ${\Gamma }_1$ and each triangle in ${\Gamma }_2$, there are two triangles of type 1 and 4 in $\Gamma$. Therefore, the number of these triangles is $2t_1\left(u\right)t_2\left(v\right)$. □

We continue with triangles of types 2 and 3.

Lemma 13.

The number of triangles of type 2 and 3 that have $(u,v)$ as a vertex is

$$\begin{array}{c}{\mathrm{deg}}^2\left(u\right)\left(\sum _{y\in N\left(v\right)}\mathrm{deg}\left(y\right)-t_{{\Gamma }_2}\left(v\right)\right)+{\mathrm{deg}}^2\left(v\right)\left(\sum _{x\in N\left(u\right)}\mathrm{deg}\left(x\right)-t_1\left(u\right)\right)\\ +\sum _{x\in N\left(u\right)}\mathrm{deg}\left(x\right)\sum _{z\in N\left(v\right)}\mathrm{deg}\left(z\right)-2[t_1\left(u\right)t_2\left(v\right)\\ +t_1\left(u\right)\left(\sum _{y\in N\left(v\right)}\mathrm{deg}\left(y\right)-t_2\left(v\right)\right)+t_2\left(v\right)\left(\sum _{x\in N\left(u\right)}\mathrm{deg}\left(x\right)-t_1\left(u\right)\right)].\end{array}$$

Proof. 

Let $(x,y)$ and $(w,z)$ be two vertices such that they form a triangle of types 2 and 3 with $(u,v)$. Since such a triangle is of type 2, we have: $ux,uw\in E_1$ and $yz\in E_2$, $ux,xw\in E_1$ and $vz\in E_2$, or $uw,xw\in E_1$ and $vy\in E_2$, and, for type 3: $vy,vz\in E_2$ and $xw\in E_1$, $vy,yz\in E_2$ and $uw\in E_1$, or $vz,yz\in E_2$ and $ux\in E_1$. In this way, we obtain nine cases from which we analyze just three of them, since the others are contained in one of these. The cases are as follows.

• Case 1: $ux,uw\in E_1$ and $vy,yz\in E_2$. For this case, note that x and w can be any neighbor of u, while z is any neighbor of y which, in turn, can be any neighbor of v; this situation can be interpreted as the 2-walk $v-y-z$, but if $v,y$, and z form a triangle in ${\Gamma }_2$, the triangle produced by $(u,v),(x,y)$, and $(w,z)$, considering such a 2-walk, is counted twice, since it is the same as the triangle formed by $(u,v),(w,z)$, and $(x,y)$ with the 2-walk $v-z-y$. Thus, there are ${\mathrm{deg}}^2\left(u\right)\left({\sum }_{y\in N\left(v\right)}\mathrm{deg}\left(y\right)-t_2\left(v\right)\right)$ triangles.
• Case 2: $ux,xw\in E_1$ and $vy,vz\in E_2$. Here, the reasoning is analogous to the last one, obtaining ${\mathrm{deg}}^2\left(v\right)\left({\sum }_{x\in N\left(u\right)}\mathrm{deg}\left(x\right)-t_1\left(u\right)\right)$ triangles.
• Case 3: $ux,xw\in E_1$ and $vz,yz\in E_2$. In this case, observe that w can be any neighbor of x which, in turn, can be any neighbor of u, which is considered as the 2-walk $u-x-w$, while y can be any neighbor of z which, in turn, can be any neighbor of v, obtaining the 2-walk $v-z-y$, but, as in the first case, when $u,x$, and w form a triangle in ${\Gamma }_1$ and when $v,y$, and z form a triangle in ${\Gamma }_2$, the 2-walks $u-x-w$, $u-w-x$, $v-y-z$, and $v-z-y$ determine the two triangles counted twice. Thus, there are ${\sum }_{x\in N\left(u\right)}\mathrm{deg}\left(x\right){\sum }_{y\in N\left(v\right)}\mathrm{deg}\left(y\right)-2t_1\left(u\right)t_2\left(v\right)$ triangles.

Now, we count the triangles when the first and second cases happen at the same time; in this situation, $u,x$, and w form a triangle in ${\Gamma }_1$, as well as $v,y$, and z forming it in ${\Gamma }_2$; thus, there are $2t_1\left(u\right)t_2\left(v\right)$ triangles.

When the second and third cases occur simultaneously, $v,y$, and z create a triangle in ${\Gamma }_2$, while w can be any neighbor of x which, in turn, can be any neighbor of u, obtaining the 2-walk $u-x-w$, and again, when $u,x$, and w form a triangle in ${\Gamma }_1$, the 2-walks $u-x-w$ and $u-w-x$ determine the same triangle in $\Gamma$, which must be counted twice, since the cases $uw,xw\in E_1$ and $vy,vz\in E_2$, and $uw,xw\in E_1$ and $vz,yz\in E_2$ are then the same as the second and third cases, respectively, obtaining $2t_2\left(v\right)\left({\sum }_{x\in N\left(u\right)}\mathrm{deg}\left(x\right)-t_1\left(u\right)\right)$ triangles.

When the first and third cases take place at the same time, an analogous reasoning shows that there are $2t_2\left(v\right)\left({\sum }_{y\in N\left(v\right)}\mathrm{deg}\left(y\right)-t_2\left(v\right)\right)$ triangles.

Finally, if the three cases happen at the same time, $u,x$, and w form a triangle in ${\Gamma }_1$ and $v,y$, and z form it in ${\Gamma }_2$, counting $2t_1\left(u\right)t_2\left(v\right)$ triangles.

Therefore, the number of triangles of type 2 and 3 which contain $(u,v)$ as a vertex is

$$\begin{array}{c}{\mathrm{deg}}^2\left(u\right)\left(\sum _{y\in N\left(v\right)}\mathrm{deg}\left(y\right)-t_2\left(v\right)\right)+{\mathrm{deg}}^2\left(v\right)\left(\sum _{x\in N\left(u\right)}\mathrm{deg}\left(x\right)-t_1\left(u\right)\right)\\ +\sum _{x\in N\left(u\right)}\mathrm{deg}\left(x\right)\sum _{z\in N\left(v\right)}\mathrm{deg}\left(z\right)-2[t_1\left(u\right)t_2\left(v\right)\\ +t_1\left(u\right)\left(\sum _{y\in N\left(v\right)}\mathrm{deg}\left(y\right)-t_2\left(v\right)\right)+t_2\left(v\right)\left(\sum _{x\in N\left(u\right)}\mathrm{deg}\left(x\right)-t_1\left(u\right)\right)].\end{array}$$

 □

Now, we count considered triangles of three types.

Lemma 14.

For the vertex $(u,v)$, the number of triangles of type 1, 2, and 3 which contain it is

$$t_1\left(u\right)\left[{\mathrm{deg}}^2\left(v\right)+2\left(\sum _{y\in N\left(v\right)}\mathrm{deg}\left(y\right)-2t_2\left(v\right)\right)\right].$$

Proof. 

We may note that, if a triangle is of type 1 and 3, it is automatically of type 2; thus, the number of these triangles is given by

$$t_1\left(u\right)\left[{\mathrm{deg}}^2\left(v\right)+2\left(\sum _{y\in N\left(v\right)}\mathrm{deg}\left(y\right)-2t_2\left(v\right)\right)\right].$$

 □

Similar considerations can be carried out in order to obtain the next result.

Lemma 15.

For the vertex $(u,v)$, the number of triangles of type 2, 3, and 4 which contain it is

$$t_2\left(v\right)\left[{\mathrm{deg}}^2\left(u\right)+2\left(\sum _{x\in N\left(u\right)}\mathrm{deg}\left(x\right)-2t_1\left(u\right)\right)\right].$$

The results of the next lemma follow from the subsequent reasoning: a triangle that is of type 1 and 4, is automatically of types 2 and 3.

Lemma 16.

For the vertex $(u,v)$, the number of triangles of type 1, 2, and 4; 1, 3, and 4; and 1, 2, 3, and 4 which contain it is $2t_1\left(u\right)t_2\left(v\right)$.

To sum up, we have the next result.

Proposition 3.

The number of triangles in ${\Gamma }_1\oplus {\Gamma }_2$ that contain the vertex $(u,v)$ is

$$\begin{array}{cc}\hfill t(u,v)=& t_1\left(u\right)\left[n_2^2+2\left(\sum _{y\in N\left(v\right)}\mathrm{deg}\left(y\right)-m_2\right)\right]+{\mathrm{deg}}^2\left(u\right)\left(m_2+t_2\left(v\right)-\sum _{y\in N\left(v\right)}\mathrm{deg}\left(y\right)\right)\hfill \\ \hfill & +n_1\mathrm{deg}\left(u\right)\left(\sum _{y\in N\left(v\right)}\mathrm{deg}\left(y\right)-2t_2\left(v\right)\right)+t_2\left(v\right)\left[n_1^2+2\left(\sum _{x\in N\left(u\right)}\mathrm{deg}\left(x\right)-m_1\right)\right]\hfill \\ \hfill & +{\mathrm{deg}}^2\left(v\right)\left(m_1+t_1\left(u\right)-\sum _{x\in N\left(u\right)}\mathrm{deg}\left(x\right)\right)+n_2\mathrm{deg}\left(v\right)\left(\sum _{x\in N\left(u\right)}\mathrm{deg}\left(x\right)-2t_1\left(u\right)\right)\hfill \\ \hfill & -\sum _{x\in N\left(u\right)}\mathrm{deg}\left(x\right)\sum _{y\in N\left(v\right)}\mathrm{deg}\left(y\right)-2t_1\left(u\right)t_2\left(v\right).\hfill \end{array}$$

The following theorem is an immediate consequence of the aforementioned.

Theorem 3.

Let ${\Gamma }_1=(V_1,E_1)$ and ${\Gamma }_2=(V_2,E_2)$ be two graphs, with $|V_1|=n_1$, $|E_1|=m_1$, $|V_2|=n_2$, and $|E_2|=m_2$. If $\Gamma =(V,E)$ denotes the Cartesian sum of ${\Gamma }_1\circ {\Gamma }_2$ and $(u,v)\in V$, then

I.

The local clustering of $(u,v)$ is given by

$$C(u,v)=\frac{2t(u,v)}{\left(n_1\mathrm{deg}\left(v\right)+n_2\mathrm{deg}\left(u\right)-\mathrm{deg}\left(u\right)\mathrm{deg}\left(v\right)\right)\left(n_1\mathrm{deg}\left(v\right)+n_2\mathrm{deg}\left(u\right)-\mathrm{deg}\left(u\right)\mathrm{deg}\left(v\right)-1\right)};$$

II.

And the global clustering of ${\Gamma }_1\oplus {\Gamma }_2$ is given by the formula

$$\frac{1}{n_1{n}_2}\sum _{i=1}^{n_1}\sum _{j=1}^{n_2}\frac{2t(u,v)}{\left(n_1\mathrm{deg}\left(v\right)+n_2\mathrm{deg}\left(u\right)-\mathrm{deg}\left(u\right)\mathrm{deg}\left(v\right)\right)\left(n_1\mathrm{deg}\left(v\right)+n_2\mathrm{deg}\left(u\right)-\mathrm{deg}\left(u\right)\mathrm{deg}\left(v\right)-1\right)},$$

where $t(u,v)$ is given as in the above proposition.

Example 4.

Consider the two complete graphs ${\mathrm{K}}_r$ and ${\mathrm{K}}_s$. Our computations in Proposition 3 show that, for every vertex of ${\Gamma }_1\oplus {\Gamma }_2$, we obtain

$$\begin{array}{cc}\hfill t(u,v)=& \frac{(r-1)(r-2)}{2}\left[s^2+2\left({(s-1)}^2-\frac{s(s-1)}{2}\right)\right]\hfill \\ \hfill & +{(r-1)}^2\left[\frac{s(s-1)}{2}+\frac{(s-1)(s-2)}{2}-{(s-1)}^2\right]\hfill \\ \hfill & +r(r-1)\left({(s-1)}^2-2\frac{(s-1)(s-2)}{2}\right)\hfill \\ \hfill & +\frac{(s-1)(s-2)}{2}\left[r^2+2\left({(r-1)}^2-\frac{r(r-1)}{2}\right)\right]\hfill \\ \hfill & +{(s-1)}^2\left(\frac{r(r-1)}{2}+\frac{(r-1)(r-2)}{2}-{(r-1)}^2\right)\hfill \\ \hfill & +s(s-1)\left({(r-1)}^2-2\frac{(r-1)(r-2)}{2}\right)\hfill \\ \hfill & -{(r-1)}^2{(s-1)}^2-2\frac{(r-1)(r-2)}{2}\frac{(s-1)(s-2)}{2}\hfill \\ \hfill =& \frac{r^2{s}^2-3rs+2}{2},\hfill \end{array}$$

according to the first part of the above theorem, we obtain $C(u,v)=1$ for every vertex. Hence,

$$C({\mathrm{K}}_r\oplus {\mathrm{K}}_s)=1,$$

which obviously coincides with the observation we have already made that ${\mathrm{K}}_r\oplus {\mathrm{K}}_s$ is isomorphic to ${\mathrm{K}}_{rs}$.

4. Conclusions

In this work, we study the clustering coefficient of some graph products (corona, lexicographic, and Cartesian sum) by computing the number of triangles formed in a vertex in each product. For the lexicographic product and Cartesian sum, we observe that these triangles can be classified into three or four types, respectively, and the computation of this number is carried out by counting the number of triangles of each type. We note that this calculation can be easier or harder, depending on the product considered and the specific type of triangle.

As mentioned in the introduction, this invariant ($C(\Gamma )$) has a lot of applications in areas as diverse as biology, sociology, or computer science, to name a few. Thus, the results obtained in this paper may be used in problems in these fields or in other areas that involve these concepts.