Existence Results for a Class of Fractional Differential Beam Type Equations

Abstract

Fractional differential beam type equations are considered. By using an efficient approach, we prove the existence and uniqueness of continuous solutions. An iterative scheme for approximating the solution is given. Some examples are presented.

1. Introduction

Deformations of an elastic beam can be modeled by equations of the form

$${\vartheta }^{\left(4\right)}\left(\varsigma \right)=h(\varsigma ,\vartheta \left(\varsigma \right),{\vartheta }^{\prime }\left(\varsigma \right),{\vartheta }^{″}\left(\varsigma \right),{\vartheta }^{‴}\left(\varsigma \right)),0<\varsigma <1,$$

depending on how the beam is supported at the boundary (for more details, see, e.g., [1]).

This kind of equation has been investigated by many authors (see, e.g., [2,3,4,5,6,7,8,9,10,11], and references therein).

For instance, in [2], Aftabizadeh considered the problem

$$\left\{\begin{array}{cc}{\vartheta }^{\left(4\right)}\left(\varsigma \right)=h(\varsigma ,\vartheta \left(\varsigma \right),{\vartheta }^{″}\left(\varsigma \right)),\hfill & 0<\varsigma <1,\hfill \\ \vartheta \left(0\right)={\vartheta }^{″}\left(0\right)=\vartheta \left(1\right)={\vartheta }^{″}\left(1\right)=0.\hfill \end{array}\right.$$

(1)

where $h\in C\left([0,1]\times {\mathbb{R}}^2,\mathbb{R}\right)$ satisfying some appropriate conditions. By transforming problem (1) into a second-order boundary value problem, and applying known results, the author proved an existence results.

Minhós et al. [12] proved the existence of a solution for

$$\left\{\begin{array}{cc}{\vartheta }^{\left(4\right)}\left(\varsigma \right)=h(\varsigma ,\vartheta \left(\varsigma \right),{\vartheta }^{\prime }\left(\varsigma \right),{\vartheta }^{″}\left(\varsigma \right),{\vartheta }^{‴}\left(\varsigma \right)),\hfill & 0<\varsigma <1,\hfill \\ \vartheta \left(0\right)={\vartheta }^{″}\left(0\right)={\vartheta }^{\prime }\left(1\right)={\vartheta }^{‴}\left(1\right)=0,\hfill \end{array}\right.$$

where $h\in C\left([0,1]\times {\mathbb{R}}^4,\mathbb{R}\right)$ satisfying a Nagumo-type condition. The proof is based on the degree theory.

Dang and Ngo [13] studied the problem

$$\left\{\begin{array}{cc}{\vartheta }^{\left(4\right)}\left(\varsigma \right)=h(\varsigma ,\vartheta \left(\varsigma \right),{\vartheta }^{\prime }\left(\varsigma \right),{\vartheta }^{″}\left(\varsigma \right),{\vartheta }^{‴}\left(\varsigma \right)),\hfill & 0<\varsigma <1,\hfill \\ \vartheta \left(0\right)={\vartheta }^{\prime }\left(0\right)={\vartheta }^{″}\left(1\right)={\vartheta }^{‴}\left(1\right)=0,\hfill \end{array}\right.$$

(2)

where $h\in C\left([0,1]\times {\mathbb{R}}^4,\mathbb{R}\right).$

They have proved that problem (2) admits a unique solution. Their method consists of reducing the problem to an operator equation, then proving the contraction of the operator.

Currently, many researchers from various fields have become interested in the topic of fractional calculus based on integrals and derivatives of fractional order. It has numerous applications in the widespread field of science and engineering (see, for instance [14,15,16,17,18] and references therein). Fractional calculus offers superior tools to cope with the time-dependent effects noticed compared to integer-order calculus, which forms the mathematical foundation of most mathematical systems. As a result, fractional calculus is crucial to model real-life problems and finding mathematical solutions is a great challenge. Since fractional differential equations are used to model real-life problems, many mathematical methods (numerical/analytical/exact) are being developed to obtain the solutions to fractional differential equations/models/systems.

Throughout this paper, we refer to ${\mathbb{D}}^{\gamma }$ $(\gamma >0)$, for the Riemann–Liouville fractional derivative (see Definition 2).

In [19], the authors studied the problem

$$\left\{\begin{array}{cc}{\mathbb{D}}^{\gamma }\vartheta \left(\varsigma \right)+h(\varsigma ,\vartheta \left(\varsigma \right))=0,\hfill & 0<\varsigma <1,\hfill \\ \vartheta \left(0\right)={\vartheta }^{\prime }\left(0\right)={\vartheta }^{″}\left(0\right)={\vartheta }^{″}\left(1\right)=0,\hfill \end{array}\right.$$

where $3<\gamma \le 4$ and $h\in C\left(\right[0,1]\times [0,\infty ),[0,\infty \left)\right)$.

Existence results of positive solutions are obtained for the above problem by means of lower and upper solution methods.

In [20], the author proved some existence results for

$$\left\{\begin{array}{cc}{\mathbb{D}}^{\gamma }\vartheta \left(\varsigma \right)=h(\varsigma ,\vartheta \left(\varsigma \right),{\vartheta }^{\prime }\left(\varsigma \right),{\vartheta }^{″}\left(\varsigma \right)),\hfill & 0<\varsigma <1,\hfill \\ {\mathbb{D}}^{\gamma -3}\vartheta \left(0\right)={\displaystyle \underset{\varsigma \to 0}{lim}}{t}^{4-\gamma }\vartheta \left(\varsigma \right)=\vartheta \left(1\right)={\vartheta }^{\prime }\left(1\right)=0,\hfill \end{array}\right.$$

where $3<\gamma <4$ and $h\in C((0,1)\times [0,\infty )\times {\mathbb{R}}^2,[0,\infty ))$, which need not to be a Caratheodory function. An approximating of the solution is also obtained.

The approach relies on the Schäuder fixed-point theorem.

In [21], by using the Schäuder fixed point theorem, the authors proved the existence of a unique positive solution to the problem

$$\left\{\begin{array}{cc}{\mathbb{D}}^{\alpha }\left({\mathbb{D}}^{\beta }\vartheta \right)\left(\varsigma \right)+h\left(\varsigma \right){\vartheta }^{\sigma }=0,\hfill & 0<\varsigma <1,\hfill \\ {\displaystyle \underset{\varsigma \to 0^{+}}{lim}}{\varsigma }^{1-\alpha }{\mathbb{D}}^{\beta }\vartheta \left(\varsigma \right)=\vartheta \left(1\right)=0,\hfill \end{array}\right.$$

where $\alpha ,\beta \in (0,1]$ with $\alpha +\beta >1$ and $h\in C\left(\right(0,1),[0,\infty \left)\right)$ satisfying some appropriate conditions.

More related existence results can be found in [22,23,24,25,26,27,28] and their references.

In this paper, motivated by the previous cited works, we are interested in the study of the following fractional beam type problem:

$$\left\{\begin{array}{cc}{\mathbb{D}}^{\alpha }\left({\mathbb{D}}^{\beta }\vartheta \right)\left(\varsigma \right)+h(\varsigma ,\vartheta \left(\varsigma \right))=0,\hfill & 0<\varsigma <1,\hfill \\ \vartheta \left(0\right)={\mathbb{D}}^{\beta }\vartheta \left(0\right)={\left({\mathbb{D}}^{\beta }\vartheta \right)}^{\prime }\left(0\right)={\mathbb{D}}^{\beta }\vartheta \left(1\right)=0,\hfill \end{array}\right.$$

(3)

where $2<\alpha \le 3,$ $0<\beta \le 1$ and $h\in C\left([0,1]\times {\mathbb{R}}^2,\mathbb{R}\right)$ satisfying some sufficient conditions.

Our goal is to address the existence and uniqueness of a solution for the above problem. The convergence of an iterative process to the unique solution is also proposed. The method consists at reducing the problem to an operator equation, then proving the contraction of the operator.

2. Preliminary Results

Definition 1

([15,16,17,18]). Let $\gamma >0$ and $\vartheta :\left(0,\infty \right)\to \mathbb{R}$ be a measurable function. Then, ${\mathbb{I}}^{\gamma }\vartheta$ is defined by

$${\mathbb{I}}^{\gamma }\vartheta \left(\varsigma \right):=\frac{1}{\mathsf{\Gamma }\left(\gamma \right)}{\int }_0^{\varsigma }{\left(\varsigma -\sigma \right)}^{\gamma -1}\vartheta \left(\sigma \right)d\sigma ,\varsigma >0,$$

where Γ is the Euler Gamma function.

Definition 2

([15,16,17,18]). Let $\gamma >0$ and $\left[\gamma \right]$ its integer part. Let $\vartheta :\left(0,\infty \right)\to \mathbb{R}$ be a given function, then ${\mathbb{D}}^{\gamma }\vartheta$ is defined by

$${\mathbb{D}}^{\gamma }\vartheta \left(\varsigma \right):=\frac{1}{\mathsf{\Gamma }\left(n-\gamma \right)}{\left(\frac{d}{d\varsigma }\right)}^n{\int }_0^{\varsigma }{\left(\varsigma -\sigma \right)}^{n-\gamma -1}\vartheta \left(\sigma \right)d\sigma ={\left(\frac{d}{d\varsigma }\right)}^n{\mathbb{I}}^{n-\gamma }\vartheta \left(\varsigma \right),$$

where $n=\left[\gamma \right]+1.$

Lemma 1

([15,16,17,18]). Let $\delta >0$ and $\vartheta \in C\left(0,1\right)\cap L^1\left(0,1\right)$. Then,

(i) 

${\mathbb{D}}^{\gamma }{\mathbb{I}}^{\delta }\vartheta ={\mathbb{I}}^{\delta -\gamma }\vartheta$ and ${\mathbb{D}}^{\delta }{\mathbb{I}}^{\delta }\vartheta =\vartheta ,$ where $0<\gamma <\delta .$

(ii) 

${\mathbb{D}}^{\gamma }\vartheta \left(\varsigma \right)=0$ if and only if $\vartheta \left(\varsigma \right)=a_1{\varsigma }^{\gamma -1}+a_2{\varsigma }^{\gamma -2}+...+a_m{\varsigma }^{\gamma -m},$

where $m=⌈\gamma ⌉$ is the ceiling function and $a_i\in \mathbb{R}.$

(iii) 

If ${\mathbb{D}}^{\gamma }\vartheta \in C\left(0,1\right)\cap L^1\left(0,1\right),$ then

$${\mathbb{I}}^{\gamma }{\mathbb{D}}^{\gamma }\vartheta \left(\varsigma \right)=\vartheta \left(\varsigma \right)+a_1{\varsigma }^{\gamma -1}+a_2{\varsigma }^{\gamma -2}+\dots +a_m{\varsigma }^{\gamma -m},$$

where $m=⌈\gamma ⌉$ is the ceiling function and $a_i\in \mathbb{R}.$

Lemma 2

([28]). Let $2<\alpha \le 3$ and $\varphi \in C\left(\right[0,1],\mathbb{R}).$ The problem,

$$\left\{\begin{array}{c}{\mathbb{D}}^{\alpha }\vartheta \left(\varsigma \right)+\varphi \left(\varsigma \right)=0,0<\varsigma <1,\hfill \\ \vartheta \left(0\right)={\vartheta }^{\prime }\left(0\right)=\vartheta \left(1\right)=0,\hfill \end{array}\right.$$

admits a unique solution

$$\vartheta \left(\varsigma \right)={\int }_0^1{\mathbb{G}}_{\alpha }\left(\varsigma ,\sigma \right)\varphi \left(\sigma \right)d\sigma ,$$

where

$${\mathbb{G}}_{\alpha }\left(\varsigma ,\sigma \right):=\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}\left\{\begin{array}{cc}{\varsigma }^{\alpha -1}{\left(1-\sigma \right)}^{\alpha -1}-{\left(\varsigma -\sigma \right)}^{\alpha -1},\hfill & for0\le \sigma \le \varsigma \le 1,\hfill \\ {\varsigma }^{\alpha -1}{\left(1-\sigma \right)}^{\alpha -1},\hfill & for0\le \varsigma \le \sigma \le 1.\hfill \end{array}\right.$$

Remark 1.

Note that ${\mathbb{G}}_{\alpha }(\varsigma ,\sigma )\ge 0,$ for all $(\varsigma ,\sigma )\in \left[0,1\right]\times \left[0,1\right].$

For $2<\alpha \le 3,$ define ${\mathbb{V}}_{\alpha }$ on the space $C\left(\right[0,1],\mathbb{R})$ by

$${\mathbb{V}}_{\alpha }\varphi \left(\varsigma \right):={\int }_0^1{\mathbb{G}}_{\alpha }\left(\varsigma ,\sigma \right)\varphi \left(\sigma \right)d\sigma ,\mathrm{for}0\le \varsigma \le 1.$$

(4)

For $\varphi \in C\left(\right[0,1],\mathbb{R}),$ we let

$$∥\varphi ∥:=\underset{\varsigma \in [0,1]}{sup}\left|\varphi \left(\varsigma \right)\right|.$$

It is clear that ${\mathbb{V}}_{\alpha }\varphi \in C([0,1],\mathbb{R}).$

Lemma 3

Let $2<\alpha \le 3$ and $0<\beta \le 1.$ Then, for $\varphi \in C\left(\right[0,1],\mathbb{R}),$

$$∥{\mathbb{I}}^{\beta }\left({\mathbb{V}}_{\alpha }\varphi \right)∥\le \frac{\beta }{\alpha \mathsf{\Gamma }\left(\alpha +\beta +1\right)}∥\varphi ∥.$$

Proof. 

Let $\varphi$ be a continuous function on $[0,1]$. Since ${\mathbb{G}}_{\alpha }(\varsigma ,\sigma )\ge 0,$ it follows from (4) that

$$\left|{\mathbb{V}}_{\alpha }\varphi \left(\varsigma \right)\right|\le ∥\varphi ∥{\int }_0^1{\mathbb{G}}_{\alpha }\left(\varsigma ,\sigma \right)d\sigma ,\mathrm{for}\varsigma \in [0,1].$$

By using Lemma 2, we obtain

$${\int }_0^1{\mathbb{G}}_{\alpha }\left(\varsigma ,\sigma \right)d\sigma =\frac{1}{\mathsf{\Gamma }\left(\alpha +1\right)}{\varsigma }^{\alpha -1}(1-\varsigma ).$$

Hence,

$$\left|{\mathbb{V}}_{\alpha }\varphi \left(\varsigma \right)\right|\le \frac{∥\varphi ∥}{\mathsf{\Gamma }\left(\alpha +1\right)}{\varsigma }^{\alpha -1}(1-\varsigma ),\mathrm{for}\varsigma \in [0,1].$$

(5)

By using (5) and the substitution $\sigma =\varsigma s,$ we obtain

$$\begin{array}{ccc}\hfill \left|{\mathbb{I}}^{\beta }\left({\mathbb{V}}_{\alpha }\varphi \right)\left(\varsigma \right)\right|& \le & \frac{∥\varphi ∥}{\mathsf{\Gamma }\left(\beta \right)\mathsf{\Gamma }\left(\alpha +1\right)}{\int }_0^{\varsigma }{(\varsigma -\sigma )}^{\beta -1}{\sigma }^{\alpha -1}(1-\sigma )d\sigma \hfill \\ & =& \frac{∥\varphi ∥}{\mathsf{\Gamma }\left(\beta \right)\mathsf{\Gamma }\left(\alpha +1\right)}{\int }_0^{\varsigma }{(\varsigma -\sigma )}^{\beta -1}({\sigma }^{\alpha -1}-{\sigma }^{\alpha })d\sigma \hfill \\ & =& \frac{∥\varphi ∥}{\mathsf{\Gamma }\left(\alpha +1\right)}(\frac{\mathsf{\Gamma }\left(\alpha \right)}{\mathsf{\Gamma }\left(\alpha +\beta \right)}{\varsigma }^{\alpha +\beta -1}-\frac{\mathsf{\Gamma }\left(\alpha +1\right)}{\mathsf{\Gamma }\left(\alpha +\beta +1\right)}{\varsigma }^{\alpha +\beta })\hfill \\ & =& \frac{∥\varphi ∥}{\mathsf{\Gamma }\left(\alpha +\beta \right)}\theta \left(\varsigma \right),\hfill \end{array}$$

where

$$\theta \left(\varsigma \right):={\varsigma }^{\alpha +\beta -1}(\frac{1}{\alpha }-\frac{1}{\alpha +\beta }\varsigma ).$$

Since $\theta \left(\varsigma \right)\le \theta \left(1\right),$ for all $\varsigma \in [0,1],$ we deduce that

$$\left|{\mathbb{I}}^{\beta }\left({\mathbb{V}}_{\alpha }\varphi \right)\left(\varsigma \right)\right|\le \frac{∥\varphi ∥}{\mathsf{\Gamma }\left(\alpha +\beta \right)}(\frac{1}{\alpha }-\frac{1}{\alpha +\beta }),\mathrm{for}\varsigma \in [0,1].$$

Therefore,

$$∥{\mathbb{I}}^{\beta }\left({\mathbb{V}}_{\alpha }\varphi \right)∥\le \frac{\beta }{\alpha \mathsf{\Gamma }\left(\alpha +\beta +1\right)}∥\varphi ∥.$$

 □

3. Main Results

Let $2<\alpha \le 3$ and $0<\beta \le 1.$ For $\mathcal{A}>0,$ we let

$${\mathcal{E}}_{\mathcal{A}}=\{(\varsigma ,\sigma )\in {\mathbb{R}}^2:0\le \varsigma \le 1,\left|\sigma \right|\le \frac{\beta \mathcal{A}}{\alpha \mathsf{\Gamma }\left(\alpha +\beta +1\right)}\},$$

and we denote by

$${\mathbb{B}}_{\mathcal{A}}:=\{\psi \in C([0,1],\mathbb{R}):∥\psi ∥\le \mathcal{A}\}.$$

Theorem 1.

Consider h in $C\left(\right[0,1]\times \mathbb{R},\mathbb{R})$ and assume that for some $\mathcal{A}>0$ and $L>0,$ we have

(i) 

$\left|h(\varsigma ,\sigma )\right|\le \mathcal{A},$ for any $(\varsigma ,\sigma )\in {\mathcal{E}}_{\mathcal{A}}.$

(ii) 

$\left|h(\varsigma ,{\sigma }_2)-h(\varsigma ,{\sigma }_1)\right|\le L\left|{\sigma }_2-{\sigma }_1\right|,$ for any $(\varsigma ,{\sigma }_i)\in {\mathcal{E}}_{\mathcal{A}},$ $i=1,2.$

(iii) 

$p:={\displaystyle \frac{\beta L}{\alpha \mathsf{\Gamma }\left(\alpha +\beta +1\right)}}<1.$

Then, problem (3) admits a unique solution $\vartheta \in C\left(\right[0,1],\mathbb{R})$ with

$$∥\vartheta ∥\le \frac{\beta \mathcal{A}}{\alpha \mathsf{\Gamma }\left(\alpha +\beta +1\right)}.$$

(6)

Proof. 

Define T on $C\left(\right[0,1],\mathbb{R})$ by

$$T\varphi \left(\varsigma \right):=h(\varsigma ,{\mathbb{I}}^{\beta }\left({\mathbb{V}}_{\alpha }\varphi \right)\left(\varsigma \right)),\varsigma \in [0,1],$$

where ${\mathbb{V}}_{\alpha }\varphi$ is defined by (4) and ${\mathbb{I}}^{\beta }$ is given by Definition 1.

Assume that T has a fixed point $\varphi .$ Then, by ([18], Theorem 2.4), (4) and Lemma 2,

$$\vartheta \left(\varsigma \right):={\mathbb{I}}^{\beta }\left({\mathbb{V}}_{\alpha }\varphi \right)\left(\varsigma \right),$$

is a continuous solution of problem (3). Conversely, if $\vartheta$ is a continuous solution of problem (3), then $\varphi \left(\varsigma \right):=h(\varsigma ,\vartheta (\varsigma \left)\right)$ satisfies $T\varphi \left(\varsigma \right)=\varphi \left(\varsigma \right).$

Thus, solving problem (3) is equivalent to finding a fixed point for the operator $T.$

We claim that T maps ${\mathbb{B}}_{\mathcal{A}}$ into itself. Note that $T\varphi \in C\left(\right[0,1],\mathbb{R}).$

On the other hand, due to Lemma 3, we obtain

$$∥{\mathbb{I}}^{\beta }\left({\mathbb{V}}_{\alpha }\varphi \right)∥\le \frac{\beta \mathcal{A}}{\alpha \mathsf{\Gamma }\left(\alpha +\beta +1\right)},\mathrm{for}\varphi \in {\mathbb{B}}_{\mathcal{A}}.$$

So, for $\varsigma \in [0,1],$ $(\varsigma ,{\mathbb{I}}^{\beta }\left({\mathbb{V}}_{\alpha }\varphi \right)\left(\varsigma \right))\in {\mathcal{E}}_{\mathcal{A}},$ and therefore $T\left({\mathbb{B}}_{\mathcal{A}}\right)\subset {\mathbb{B}}_{\mathcal{A}},$ by assumption (i).

Next, for ${\varphi }_1,{\varphi }_2\in {\mathbb{B}}_{\mathcal{A}},$ we have

$$\begin{array}{ccc}\hfill \left|T{\varphi }_2\left(\varsigma \right)-T{\varphi }_1\left(\varsigma \right)\right|& =& \left|h(\varsigma ,{\mathbb{I}}^{\beta }\left({\mathbb{V}}_{\alpha }{\varphi }_2\right)\left(\varsigma \right))-h(\varsigma ,{\mathbb{I}}^{\beta }\left({\mathbb{V}}_{\alpha }{\varphi }_1\right)\left(\varsigma \right))\right|\hfill \\ & \le & L∥{\mathbb{I}}^{\beta }\left({\mathbb{V}}_{\alpha }{\varphi }_2\right)-{\mathbb{I}}^{\beta }\left({\mathbb{V}}_{\alpha }{\varphi }_1\right)∥\hfill \\ & =& L∥{\mathbb{I}}^{\beta }\left({\mathbb{V}}_{\alpha }({\varphi }_2-{\varphi }_1)\right)∥\hfill \\ & \le & \frac{\beta L}{\alpha \mathsf{\Gamma }\left(\alpha +\beta +1\right)}∥{\varphi }_2-{\varphi }_1∥.\hfill \end{array}$$

Since $\frac{\beta L}{\alpha \mathsf{\Gamma }\left(\alpha +\beta +1\right)}<1$, we deduce that T is a contraction on ${\mathbb{B}}_{\mathcal{A}}.$

Hence, by the Banach’s fixed point Theorem, there exists a unique ${\phi }_0\in {\mathbb{B}}_{\mathcal{A}}$ such that

$${\phi }_0\left(\varsigma \right)=h(\varsigma ,{\mathbb{I}}^{\beta }\left({\mathbb{V}}_{\alpha }{\phi }_0\right)\left(\varsigma \right)),\mathrm{for}\varsigma \in [0,1].$$

Therefore, problem (3) admits a unique solution $\vartheta \left(\varsigma \right):={\mathbb{I}}^{\beta }\left({\mathbb{V}}_{\alpha }{\phi }_0\right)\left(\varsigma \right)\in C([0,1],\mathbb{R})$ satisfying (6). □

To study the positivity, we denote by

$${\mathcal{E}}_{\mathcal{A}}^{+}=\{(\varsigma ,\sigma )\in {\mathbb{R}}^2:0\le \varsigma \le 1,0\le \sigma \le \frac{\beta \mathcal{A}}{\alpha \mathsf{\Gamma }\left(\alpha +\beta +1\right)}\}.$$

Corollary 1.

Consider h in $C\left(\right[0,1]\times \mathbb{R},[0,\infty \left)\right)$ and assume that for some $\mathcal{A}>0$ and $L>0,$ we have

(i) 

$0\le h(\varsigma ,\sigma )\le \mathcal{A}$ for any $(\varsigma ,\sigma )\in {\mathcal{E}}_{\mathcal{A}}^{+}.$

(ii) 

$\left|h(\varsigma ,{\sigma }_2)-h(\varsigma ,{\sigma }_1)\right|\le L\left|{\sigma }_2-{\sigma }_1\right|,$ for any $(\varsigma ,{\sigma }_i)\in {\mathcal{E}}_{\mathcal{A}}^{+},$ $i=1,2.$

(iii) 

$p:={\displaystyle \frac{\beta L}{\alpha \mathsf{\Gamma }\left(\alpha +\beta +1\right)}}<1.$

Then, problem (3) admits a unique $\vartheta \in C\left(\right[0,1],[0,\infty \left)\right)$ satisfying

$$0\le \vartheta \left(\varsigma \right)\le \frac{\beta \mathcal{A}}{\alpha \mathsf{\Gamma }\left(\alpha +\beta +1\right)},for\varsigma \in [0,1].$$

Theorem 2.

(Iterative method) Under the same hypotheses of Theorem 1, let ϑ be the unique solution of problem (3) and consider the following iterative process:

$${\varphi }_0\in {\mathbb{B}}_{\mathcal{A}}and{\varphi }_{k+1}\left(\varsigma \right):=T{\varphi }_k\left(\varsigma \right)=h(\varsigma ,{\mathbb{I}}^{\beta }\left({\mathbb{V}}_{\alpha }{\varphi }_k\right)\left(\varsigma \right)),fork=0,1,...;\varsigma \in [0,1].$$

Then,

$$∥{\mathbb{I}}^{\beta }\left({\mathbb{V}}_{\alpha }{\varphi }_k\right)-\vartheta ∥\le \frac{\beta }{\alpha \mathsf{\Gamma }\left(\alpha +\beta +1\right)}\frac{p^k}{(1-p)}∥{\varphi }_1-{\varphi }_0∥,$$

where $p:={\displaystyle \frac{\beta L}{\alpha \mathsf{\Gamma }\left(\alpha +\beta +1\right)}}.$

In particular,

$$\underset{k\to \infty }{lim}∥{\mathbb{I}}^{\beta }\left({\mathbb{V}}_{\alpha }{\varphi }_k\right)-\vartheta ∥=0.$$

Proof. 

Let $\varphi \in {\mathbb{B}}_{\mathcal{A}}$ such that $T\left(\varphi \right)=\varphi .$

It is known from the Banach contraction principle (see, for instance ([29], Theorem 1.1)) that the sequence ${\left({\varphi }_k\right)}_{k\ge 0}$ converges to $\varphi$ and we have

$$∥{\varphi }_k-\varphi ∥\le \frac{p^k}{1-p}∥{\varphi }_1-{\varphi }_0∥.$$

Therefore, by using Lemma 3, we deduce

$$\begin{array}{ccc}\hfill ∥{\mathbb{I}}^{\beta }\left({\mathbb{V}}_{\alpha }{\varphi }_k\right)-\vartheta ∥& =& ∥{\mathbb{I}}^{\beta }\left({\mathbb{V}}_{\alpha }{\varphi }_k\right)-{\mathbb{I}}^{\beta }\left({\mathbb{V}}_{\alpha }\varphi \right)∥\hfill \\ & =& ∥{\mathbb{I}}^{\beta }({\mathbb{V}}_{\alpha }({\varphi }_k-\varphi )∥\hfill \\ & \le & \frac{\beta }{\alpha \mathsf{\Gamma }\left(\alpha +\beta +1\right)}∥{\varphi }_k-\varphi ∥\hfill \\ & \le & \frac{\beta }{\alpha \mathsf{\Gamma }\left(\alpha +\beta +1\right)}\frac{p^k}{1-p}∥{\varphi }_1-{\varphi }_0∥.\hfill \end{array}$$

Since $p:={\displaystyle \frac{\beta L}{\alpha \mathsf{\Gamma }\left(\alpha +\beta +1\right)}}<1,$ we deduce that

$$\underset{k\to \infty }{lim}∥{\mathbb{I}}^{\beta }\left({\mathbb{V}}_{\alpha }{\varphi }_k\right)-\vartheta ∥=0.$$

 □

Example 1.

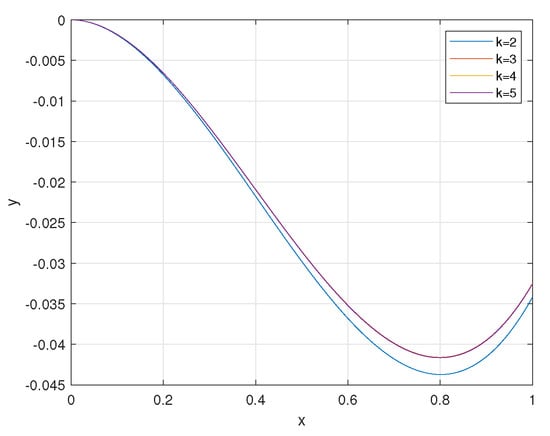
For $\alpha =\frac{5}{2}$ and $\beta =\frac{1}{2}$ consider

$$\left\{\begin{array}{c}{\mathbb{D}}^{\frac{5}{2}}\left({\mathbb{D}}^{\frac{1}{2}}\vartheta \right)\left(\varsigma \right)=e^{\vartheta \left(\varsigma \right)},0<\varsigma <1,\hfill \\ \vartheta \left(0\right)={\mathbb{D}}^{\frac{1}{2}}\vartheta \left(0\right)={\left({\mathbb{D}}^{\frac{1}{2}}\vartheta \right)}^{\prime }\left(0\right)={\mathbb{D}}^{\frac{1}{2}}\vartheta \left(1\right)=0.\hfill \end{array}\right.$$

(7)

We have ${\mathcal{A}}_0:=\frac{\beta }{\alpha \mathsf{\Gamma }\left(\alpha +\beta +1\right)}=\frac{1}{30}.$

On can easy verify that the assumptions in Theorem 1 hold, for example, with $\mathcal{A}=2$ and $L=e^{\frac{1}{30}}.$

Hence, problem (7) admits a unique continuous solution ϑ satisfying

$$∥\vartheta ∥\le \frac{1}{15}.$$

Take ${\varphi }_0\left(\varsigma \right)=1.$ Then, graphs of ${\vartheta }_k\left(\varsigma \right):={\mathbb{I}}^{\frac{1}{2}}\left({\mathbb{V}}_{\frac{5}{2}}{\varphi }_k\right)\left(\varsigma \right),$ the successive approximation of $\vartheta ,$ are presented in Figure 1.

Figure 1. Approximation of the solution for Example 1.

Example 2.

For $\alpha =\frac{5}{2}$ and $\beta =\frac{1}{2}$, consider

$$\left\{\begin{array}{c}{\mathbb{D}}^{\frac{5}{2}}\left({\mathbb{D}}^{\frac{1}{2}}\vartheta \right)\left(\varsigma \right)+sin\left(\vartheta \left(\varsigma \right)\right)=0,0<\varsigma <1,\hfill \\ \vartheta \left(0\right)={\mathbb{D}}^{\frac{1}{2}}\vartheta \left(0\right)={\left({\mathbb{D}}^{\frac{1}{2}}\vartheta \right)}^{\prime }\left(0\right)={\mathbb{D}}^{\frac{1}{2}}\vartheta \left(1\right)=0.\hfill \end{array}\right.$$

(8)

Observe that 0 is a solution of problem (8).

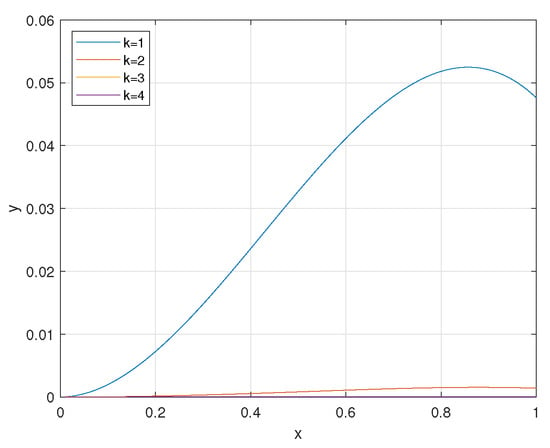
We have ${\mathcal{A}}_0:=\frac{\beta }{\alpha \mathsf{\Gamma }\left(\alpha +\beta +1\right)}=\frac{1}{30}.$ By Applying Theorem 1 with $\mathcal{A}=1,$ $L=1,$ we obtain the uniqueness of the zero solution. Take ${\varphi }_0\left(\varsigma \right)=1.$ Some iterations of the sequence ${({\vartheta }_k:={\mathbb{I}}^{\frac{1}{2}}\left({\mathbb{V}}_{\frac{5}{2}}{\varphi }_k\right))}_{k\ge 0}$ are depicted in Figure 2.

Figure 2. Approximation of $\vartheta \equiv 0$.

Example 3.

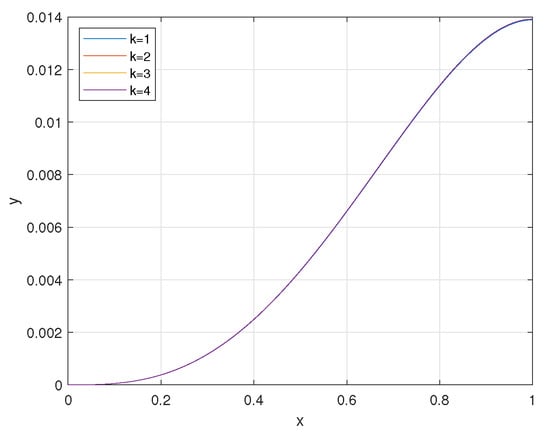
For $\alpha =3,$ $\beta =1$ consider

$$\left\{\begin{array}{c}{\vartheta }^{\left(4\right)}\left(\varsigma \right)+\sqrt{1+\vartheta \left(\varsigma \right)}=0,0<\varsigma <1,\hfill \\ \vartheta \left(0\right)={\vartheta }^{\prime }\left(0\right)={\vartheta }^{\prime \prime }\left(0\right)={\vartheta }^{\prime }\left(1\right)=0.\hfill \end{array}\right.$$

(9)

In this example, ${\mathcal{A}}_0:=\frac{\beta }{\alpha \mathsf{\Gamma }\left(\alpha +\beta +1\right)}=\frac{1}{72}.$

Assumptions in Theorem 1 are valid with $\mathcal{A}=2$ and $L=\frac{1}{2}.$ Therefore, by Corollary 1 problem (9) admits a unique solution $\vartheta \in C\left(\right[0,1],\mathbb{R})$ with

$$0\le \vartheta \left(\varsigma \right)\le \frac{1}{36},\mathrm{for}\varsigma \in [0,1].$$

Approximation of the solution can be achieved by the sequence ${({\vartheta }_k:={\mathbb{I}}^1\left({\mathbb{V}}_3{\varphi }_k\right))}_{k\ge 0}$ with ${\varphi }_0\left(\varsigma \right)=1.$ Some iterations are depicted in Figure 3.

Figure 3. Approximation of the solution regarding Example 3.

4. Conclusions

In this work, we presented a new approach to study a class of Riemann–Liouville fractional differential equations of beam type. Under suitable conditions, we have proved the existence and uniqueness of continuous solutions by reducing the problem to an operator equation, then proving the contraction of the operator. Some examples with numerical approximation are given. In future works, we can extend this problem to more fractional derivatives, such as the Hadamard fractional derivative, $\psi$-Hilfer and Quantum Fractional Derivatives.