A Superbundle Description of Differential K-Theory

Abstract

We construct a model of differential K-theory using superbundles with a $\mathbb{Z}/2\mathbb{Z}$-graded connection and a differential form on the base manifold and prove that our model is isomorphic to the Freed–Lott–Klonoff model of differential K-theory.

1. Introduction

In algebraic topology, K-theory is an example of exotic cohomology theory that satisfies all Eilenberg–Steenrod axioms but the dimension axiom. It is one of a few cohomology theories whose elements are known to be represented by geometric cocycles, namely vector bundles over the base space. K-theory was first introduced by Grothendieck in the 1950s, and since then, many applications have been found in areas such as algebraic geometry, topology, and operator algebras. See, for example, [1].

Differential K-theory refines K-theory by taking into account the differential structure of vector bundles, as well as the connections on those bundles. This allows it to capture more subtle differential-geometric information than ordinary K-theory. It has found applications in mathematics and physics, particularly in the study of anomalies in quantum field theory [2], classifying D-brane charges and Ramond-Ramond fields in type IIA and IIB superstring theories [3,4,5] as well as formulating T-duality [6], and more recently in the classification of topological phases of matter [7].

Among various descriptions of differential K-theory, the model by Freed–Lott [8] and Klonoff [9] is the most geometric. It uses vector bundles with connection and an odd differential form for its cocycle data. It was shown by Simons and Sullivan [10] that the odd differential form is not necessary and differential K-theory is codified by vector bundles with connection, and the Simons–Sullivan model is naturally isomorphic to the Freed–Lott and Klonoff model [11,12].

It has been communicated in the mathematical literature that a differential K-theory can equivalently be described using superbundles with a $\mathbb{Z}/2\mathbb{Z}$-graded connection and odd differential forms (see [8,9,13]). Even though this is a convincing statement, there is no literature actually justifying this equivalence. Furthermore, there is not much literature comprehensively describing the underlying topological K-theory using superbundles as cocycles.

This paper is to fill the aforementioned gap in the literature. Namely, we give a superbundle description of the Freed–Lott and Klonoff model of differential K-theory and show that such a description is isomorphic to the Freed–Lott and Klonoff model using ordinary vector bundles with connection.

Our work is going to be useful in the context of differential K-theory using superbundles with $\mathbb{Z}/2\mathbb{Z}$-graded connection. More specifically it will add clarity in comparison to the index-theoretic model by Bunke and Schick [14,15,16] as well as to the physical applications mentioned above.

This paper is organized as follows. Section 2 provides necessary preliminaries for our discussion of the main theorem. It also serves purposes of establishing notations as well as providing a comprehensive review of topological K-theory with superbundles as cocycles. Section 3 constructs a model of differential K-theory using superbundles with $\mathbb{Z}/2\mathbb{Z}$-graded connecion and proves that it is isomorphic to the Freed–Lott and Klonoff model.

2. Review of K-Theory

In this section, we review the group completion and topological K-theory including its superbundle description. The purpose of this section is to give a brief expository account about these topics while establishing notations and terminologies we will use later in the paper. In the first two subsections, we shall closely follow Atiyah ([17], Chapter 2), Karoubi ([18], Chapter 2), and Luke–Mishchenko ([19], Chapter 2.6) to enhance the self-containedness and the readability of this paper. We refer the reader to these references for more comprehensive details.

2.1. Group Completion of Abelian Monoids

We shall begin by reviewing the group completion as in Karoubi ([18], p. 52). Let $(A,+)$ be an abelian monoid. Then, we can associate an abelian group $K\left(A\right)$ with A and a homomorphism of the underlying monoids $\alpha :A\to K\left(A\right)$, having the following universal property: For any abelian group G, and any homomorphism of the underlying monoids $\gamma :A\to G$, there is a unique group homomorphism $\kappa :K\left(A\right)\to G$ such that $\gamma =\kappa \alpha$. That is, we have the following commutative diagram.

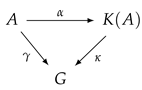
There are various possible constructions of $\alpha$ and $K\left(A\right)$, which are the same up to isomorphism. Here, we list three constructions.

• Let $F\left(A\right)$ be the free abelian group generated by the elements $a\in A$ and denote by $\left[a\right]$ the image of $a\in A$ under the inclusion map $A\hookrightarrow F\left(A\right)$. Define $S\left(A\right)\subseteq F\left(A\right)$ as the subgroup generated by the elements of the form $\left[a\right]+\left[a^{\prime }\right]-[a+a^{\prime }]$, $a,a^{\prime }\in A$. Then $K\left(A\right):=F\left(A\right)/S\left(A\right)$ and $\alpha :A\to K\left(A\right)$ is defined by $\alpha \left(a\right):=\left[a\right]$.
• Define $K\left(A\right):=A\times A/{\sim }_1$, where ${\sim }_1$ is the equivalence relation defined by

  $$(a,b){\sim }_1(a^{\prime },b^{\prime }) if there is p\in A such that a+b^{\prime }+p=b+a^{\prime }+p,$$

  and $\alpha \left(a\right):=(a,0)$.
• Define $K\left(A\right):=A\times A/{\sim }_2$, where ${\sim }_2$ is the equivalence relation defined by

  $$(a,b){\sim }_2(a^{\prime },b^{\prime }) if there are p,q\in M such that (a,b)+(p,p)=(a^{\prime },b^{\prime })+(q,q),$$

  and $\alpha \left(a\right):=(a,0)$.

In each of the these three constructions, every element of $K\left(A\right)$ can be written as $\alpha \left(a\right)-\alpha \left(b\right)$ where $a,b\in M$, and $-\left(\alpha \right(a)-\alpha (b\left)\right)=\alpha \left(b\right)-\alpha \left(a\right)$.

Remark 1

([17], p. 42). The third construction of the group completion can also be described as following. Let $\Delta :A\to A\times A$ be the diagonal homomorphism of abelian monoids. Then, $K\left(A\right)$ is the group of all cosets of $\Delta \left(A\right)$ in $A\times A$ with the interchange of factors in $A\times A$ induces an inverse in $K\left(A\right)$.

Proposition 1.

The groups $K\left(A\right)$ constructed from the three constructions above are isomorphic.

Proof. 

(1) ⇔ (2): ([19], pp. 127–128) Let $x\in F\left(A\right)/S\left(A\right)$. Then, $x={\sum }_{i=1}^p{n}_i\left[a_i\right]$ for $a_i\in A$ and $n_i\in \mathbb{Z}$. Then, we can split the sum into two parts $x={\sum }_{i=1}^{p_1}{n}_i\left[a_i\right]-{\sum }_{j=1}^{p_2}{m}_j\left[b_j\right]$ with $n_i,m_j\in {\mathbb{Z}}^{+}$. Using the definition of the subgroup $S\left(A\right)$, we have

$$x=\left[\sum _{i=1}^{p_1}\left(\underset{n_i\mathrm{times}}{\underbrace{a_i+\cdots +a_i}}\right)\right]-\left[\sum _{j=1}^{p_2}\left(\underset{m_j\mathrm{times}}{\underbrace{b_j+\cdots +b_j}}\right)\right]=\left[{\zeta }_1\right]-\left[{\zeta }_2\right],$$

where we used the definition of $S\left(A\right)$ to combine the formal sum of the elements in $F\left(A\right)$. Define the map $\phi :F\left(A\right)/S\left(A\right)\to A\times A/{\sim }_1$ with $\phi \left(x\right):=[{\zeta }_1,{\zeta }_2]$. We claim that $\phi$ is a group isomorphism.

First, we show that $\phi$ is well-defined. Let $x=y$ in $F\left(A\right)/S\left(A\right)$ with $\phi \left(x\right)=[{\zeta }_1,{\zeta }_2]$ and $\phi \left(y\right)=[{\xi }_1,{\xi }_2]$. We want to show that $[{\zeta }_1,{\zeta }_2]=[{\xi }_1,{\xi }_2]$ in $K\left(A\right)$. From the assumption, we have $\left[{\zeta }_1\right]-\left[{\zeta }_2\right]=\left[{\xi }_1\right]-\left[{\xi }_2\right]$, or $\left[{\zeta }_1\right]+\left[{\xi }_2\right]=\left[{\xi }_1\right]+\left[{\zeta }_2\right]$ in $F\left(A\right)/S\left(A\right)$. This implies that $[{\zeta }_1+{\xi }_2]-[{\xi }_1+{\zeta }_2]=0$ and the left side element should be a linear combination of the generators of $S\left(A\right)$, i.e.,

$$[{\zeta }_1+{\xi }_2]-[{\xi }_1+{\zeta }_2]=\sum _k{\lambda }_k(\left[{\eta }_k\right]+\left[{\rho }_k\right]-[{\eta }_k+{\rho }_k]).$$

Without loss of generality, we can consider that ${\lambda }_k=\pm 1$. By rearranging negative summands on the other side, we have $[{\zeta }_1+{\xi }_2+\theta ]=[{\xi }_1+{\zeta }_2+\theta ]$ for some $\theta \in A$, which implies that $({\zeta }_1,{\zeta }_2){\sim }_1({\xi }_1,{\xi }_2)$. Thus, $[{\zeta }_1,{\zeta }_2]=[{\xi }_1,{\xi }_2]$ and the mapping $\phi$ is well-defined. Note that $\phi$ is a group homomorphism with the inverse $\psi :A\times A/{\sim }_1\to F\left(A\right)/S\left(A\right)$ with $\psi \left([{\zeta }_1,{\zeta }_2]\right):=\left[{\zeta }_1\right]-\left[{\zeta }_2\right]$. Hence, $\phi$ is a group isomorphism.

(2) ⇔ (3): Let $(a,b){\sim }_1(a^{\prime },b^{\prime })$. Then, $a+b^{\prime }+p=b+a^{\prime }+p$ for some p. Let $P=b^{\prime }+p$ and $Q=b+p$. Then, we have $a+P=a^{\prime }+Q$ and $b+P=b+b^{\prime }+p=b^{\prime }+Q$. That is, $(a+b)+(P,P)=(a^{\prime },b^{\prime })+(Q,Q)$ and so $(a,b){\sim }_2(a^{\prime },b^{\prime })$. Conversely, if $(a,b){\sim }_2(a^{\prime },b^{\prime })$, then we have $a+p=a^{\prime }+q$ and $b^{\prime }+q=b+p$ for some $p,q$. By adding these two equations, we get $a+b^{\prime }+(p+q)=a^{\prime }+b+(p+q)$ which implies that $(a,b){\sim }_2(a^{\prime },b^{\prime })$. So the relation ${\sim }_1$ and ${\sim }_2$ are equal and the quotients $A\times A/{\sim }_1$ and $A\times A/{\sim }_2$ are identical. □

2.2. Topological K-Theory via Vector Bundles

Let B be a compact Hausdorff space and $\mathrm{Vect}\left(B\right)$ the set of all isomorphism classes of vector bundles on B. The definition of topological K-theory is given by taking the group completion on the isomorphism classes of vector bundles. Note that $\left(\mathrm{Vect}\right(B),+)$ is an abelian monoid with the addition induced from the direct sum. This operation is well-defined since the isomorphism classes of $E\oplus F$ depends only on the isomorphism classes of E and F. In this situation, the group $K\left(A\right)$, where $A=\mathrm{Vect}\left(B\right)$, is called the Grothendieck group of $\mathrm{Vect}\left(B\right)$. We will write $K\left(B\right)$ for the group $K\left(\mathrm{Vect}\right(B\left)\right)$. To avoid excessive notation, we may write E for a class in $\mathrm{Vect}\left(B\right)$, and $\left[E\right]$ for the image of E in $K\left(B\right)$.

It follows that every element of $K\left(B\right)$ is of the form $[E,F]$ or $\left[E\right]-\left[F\right]$. The addition of $K\left(B\right)$ is induced from the semigroup $\mathrm{Vect}\left(B\right)\times \mathrm{Vect}\left(B\right)$ and the inverse is induced from the interchange of factors. That is,

$$[E,F]+[E^{\prime },F^{\prime }]:=[E\oplus E^{\prime },F\oplus F^{\prime }],$$

and $-[E,F]=[F,E]$.

Let G be a bundle such that $F\oplus G$ is trivial. We write $\underline{n}$ for the trivial bundle of dimension n. Let $F\oplus G=\underline{n}$. Then, $\left[E\right]-\left[F\right]=\left[E\right]+\left[G\right]-(\left[F\right]+\left[G\right])=[E\oplus G]-\left[\underline{n}\right]$. Thus, every element of $K\left(B\right)$ can be written in the form $\left[H\right]-\left[\underline{n}\right]$.

Definition 1.

Two bundles E and F are said to be stably equivalent if there is a trivial bundle $\underline{n}$ such that $E\oplus \underline{n}\cong F\cong \underline{n}$.

Proposition 2.

$\left[E\right]=\left[F\right]$ in $K\left(B\right)$ if and only if E and F are stably equivalent.

In general, we have $[E,F]=[E^{\prime },F^{\prime }]$ if and only if there is a bundle G such that $E\oplus F^{\prime }\oplus G\cong F\oplus E^{\prime }\oplus G$.

2.3. Topological K-Theory via Superbundles

See Varadarajan ([20], Chapter 3), Berline–Getzler–Vergne ([21], p. 38 and p. 294), and Atiyah ([17], Section 2) for references. Let B be a compact Hausdorff space.

Definition 2

([21], p. 38). A superspace V is a $\mathbb{Z}/2\mathbb{Z}$-graded vector space $V=V^{+}\oplus V^{-}$.

Definition 3

([21], p. 39). A superbundle on B is a bundle $E=E^{+}\oplus E^{-}$ where $E^{+}$ and $E^{-}$ are two vector bundles on B.

So superbundles are vector bundles whose fibers are superspaces.

Example 1.

An ungraded vector space V is implicitly $\mathbb{Z}/2\mathbb{Z}$-graded with $V^{+}=V$ and $V^{-}=0$. A vector bundle E is identified with the superbundle such that $E^{+}=E$ and $E^{-}=0$.

Let V, W be two superspaces.

Definition 4

([20], p. 83). A linear map $f:V\to W$ is called grade-preserving if $f\left(V^{+}\right)\subseteq W^{+}$ and $f\left(V^{-}\right)\subseteq W^{-}$. A morphism in the category of superspaces is a grade-preserving linear map. A superspace isomorphism is a bijective superspace homomorphism.

From the definition, if $f:V^{+}\oplus V^{-}\to W^{+}\oplus W^{-}$ is a superspace isomorphism, then we can write $f=f^{+}\oplus f^{-}$, where $f^{+}:V^{+}\to W^{+}$ and $f^{-}:V^{-}\to W^{-}$ are linear isomorphisms. Let $\left[f\right]$ be a superspace isomorphism class of $f=f^{+}\oplus f^{-}$ on $V^{+}\oplus V^{-}$. Then, $\left[f\right]$ can be represented by $(\left[f^{+}\right],\left[f^{-}\right])$, where $\left[f^{+}\right]$ and $\left[f^{-}\right]$ represent linear isomorphism classes on $V^{+}$ and $V^{-}$, respectively. Similarly, we define the morphisms of super bundles.

Definition 5.

A morphism in the category of superbundles is a grade-preserving linear map of vector bundles. A superbundle isomorphism is a bijective superbundle homomorphism.

We will use ${\left[E\right]}_s$ to denote the isomorphism class of superbundles represented by a superbundle E. Let ${\mathrm{Vect}}_s\left(B\right)$ be the set of all superbundle isomorphism classes on B. Then, we can naturally identify ${\mathrm{Vect}}_s\left(B\right)=\mathrm{Vect}\left(B\right)\times \mathrm{Vect}\left(B\right)$. Using this identification, we define an equivalence relation on ${\mathrm{Vect}}_s\left(B\right)$ to define the K-group.

Definition 6

([21], p. 294). Let ${\left[E\right]}_s,{\left[F\right]}_s\in {\mathit{Vect}}_s\left(B\right)$ with ${\left[E\right]}_s=(\left[E^{+}\right],\left[E^{-}\right])$ and ${\left[F\right]}_s=(\left[F^{+}\right],\left[F^{-}\right])$. We define an equivalence relation on ${\mathit{Vect}}_s\left(B\right)$ that ${\left[E\right]}_s\sim {\left[F\right]}_s$ if there are two vector bundles G and H such that

$$\begin{array}{cc}\hfill E^{+}\oplus G& \cong F^{+}\oplus H,\hfill \\ \hfill E^{-}\oplus G& \cong F^{-}\oplus H.\hfill \end{array}$$

(1)

The equivalence class ${\left[\left[E\right]\right]}_s$ is called the difference bundle of E, which is denoted by ${\left[(\left[E^{+}\right],\left[E^{-}\right])\right]}_s$. For the sake of simplicity, we will just write ${\left[E\right]}_s={[E^{+},E^{-}]}_s$ for the difference bundle. If G is a vector bundle, we will associate to it the difference bundle ${\left[G\right]}_s:={[G,0]}_s$.

Definition 7

([21], p. 294). The K-theory of B is defined as the abelian group of all difference bundles, denoted by $K{\left(B\right)}_s$.

The sum in the group is induced by the sum in ${\mathrm{Vect}}_s\left(B\right)$. That is,

$$\begin{array}{c}\hfill {\left[E\right]}_s+{\left[F\right]}_s:=[E^{+}\oplus F^{+},E^{-}\oplus F^{-}].\end{array}$$

i.e., the representative of the sum is the sums of even parts and odd parts, respectively. The additive identity is ${\left[0\right]}_s$ and the interchange of the components in ${\mathrm{Vect}}_s\left(B\right)$ induces the inverse $-{\left[E\right]}_s:=[E^{-},E^{+}]$. We can also identify ${\left[E\right]}_s=\left[E^{+}\right]-\left[E^{-}\right]$ as the difference. Since the addition is defined on equivalence classes, we should check that the operation does not depend on the representatives. That is,

Proposition 3.

The addition of $K{\left(B\right)}_s$ is well-defined.

Proof. 

Let ${\left[E_i\right]}_s,{\left[F_i\right]}_s\in K{\left(B\right)}_s$ with ${\left[E_i\right]}_s={\left[F_i\right]}_s$ for $i=1,2$. We want to show that ${\left[E_1\right]}_s+{\left[E_2\right]}_s={\left[F_1\right]}_s+{\left[F_2\right]}_s$, i.e., ${[E_1^{+}\oplus E_2^{+},E_1^{-}\oplus E_2^{-}]}_s={[F_1^{+}\oplus F_2^{+},F_1^{-}\oplus F_2^{-}]}_s$. From the assumption, we have

$$\begin{array}{cc}\hfill E_i^{+}\oplus G_i& \cong F_i^{+}\oplus H_i,\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill E_i^{-}\oplus G_i& \cong F_i^{-}\oplus H_i\hfill \end{array}$$

(3)

for some bundles $G_i$ and $H_i$ for $i=1,2$. By taking direct sum of two equations in (2) and (3), we get

$$(E_1^{\pm }\oplus E_2^{\pm })\oplus (G_1\oplus G_2)\cong (F_1^{\pm }\oplus F_2^{\pm })\oplus (H_1\oplus H_2),$$

that is, $E_1+E_2{\sim }_s{F}_1+F_2$. Hence, ${\left[E_1\right]}_s+{\left[E_2\right]}_s={\left[E_1\right]}_s+{\left[F_2\right]}_s$ in $K{\left(B\right)}_s$. □

Proposition 4.

$K{\left(B\right)}_s$ and $K\left(B\right)$ are isomorphic as groups.

Proof. 

Let $f:K{\left(B\right)}_s\to K\left(B\right)$ and $g:K\left(B\right)\to K{\left(B\right)}_s$ be two maps defined by $f\left({\left[E\right]}_s\right):=[E^{+},E^{-}]$ and $g\left([E,F]\right):={[E,F]}_s$.

We first show that f is well-defined. Suppose that $E=E^{+}\oplus E^{-}$ and $F=F^{+}\oplus F^{-}$ are two superbundles such that ${\left[E\right]}_s={\left[F\right]}_s$. We want to show that $[E^{+},E^{-}]=[F^{+},F^{-}]$ in $K\left(B\right)$. From the assumption, we have $E^{\pm }\oplus G\cong F^{\pm }\oplus H$ for some bundles G and H. This implies that

$$E^{+}\oplus F^{-}\oplus (G\oplus H)\cong E^{-}\oplus F^{+}\oplus (G\oplus H)$$

by adding the two equations. Hence, $[E^{+},E^{-}]=[F^{+},F^{-}]$.

Next, we show that g is well-defined. Let $[E_1,F_1]=[E_2,F_2]\in K\left(B\right)$. We want to show that ${[E_1,F_1]}_s={[E_2,F_2]}_s$. From the assumption, there is a bundle $ϵ$ such that $E_1\oplus F_2\oplus ϵ\cong E_2\oplus F_1\oplus ϵ$. Let $G:=F_2\oplus ϵ$ and $H:=F_1\oplus ϵ$. Then, we have $E_1\oplus G\cong E_2\oplus H$. Additionally,

$$F_1\oplus G=F_1\oplus F_2\oplus ϵ\cong F_2\oplus F_1\oplus ϵ=F_2\oplus H.$$

This implies that ${[E_1,F_1]}_s={[E_2,F_2]}_s$. It is straight-forward to see that f and g are inverses to each other and preserve the group structure. □

The above proposition shows that on the topological level, the two definitions of K-theory group via superbundles or vector bundles are isomorphic and so we can use them interchangably. That is, if $\xi$ is an element of a K-theory of B, we can either interpret $\xi$ as a formal difference of two vector bundle isomorphism classes, or equivalence class of a superbundle isomorphism classes.

3. A Superbundle Description of Differential K-Theory

In this section, we review the Freed–Lott and Klonoff model of differential K-theory (Section 3.1). After that we give a superbundle description of the Freed–Lott and Klonoff model and prove that it is isomorphic to the Freed–Lott and Klonoff model using ordinary vector bundles (Section 3.2).

We shall briefly review notations and terminologies which will be frequently used in this section. We will use the notation ${\Omega }^{•}\left(B\right)$ to denote the de Rham complex on a smooth manifold B and d the differential of the complex. For a smooth vector bundle with connection $(E,{\nabla }^E)$ over B, we shall write $\mathrm{ch}\left({\nabla }^E\right)$ the total Chern character form ${\sum }_{n=0}^{\infty }\frac{1}{n!}\mathrm{tr}\left(R_{{\nabla }^E}^n\right)$ where $R_{{\nabla }^E}$ is the curvature form of the connection ${\nabla }^E$. It is the Chern–Weil theorem that the de Rham cohomology class of the total Chern character form is independent of the choice of the connection. Furthermore, for connections ${\nabla }_0$ and ${\nabla }_1$ on E and a path $\gamma$ (which exists because the space of connections on E is an affine space) joining them, it is a standard fact that $d\mathrm{cs}\left(\gamma \right)=\mathrm{ch}\left({\nabla }_1\right)-\mathrm{ch}\left({\nabla }_0\right)$, where $\mathrm{cs}\left(\gamma \right)$ is the Chern–Simons form of a path $\gamma$ defined by ${\int }_{[0,1]}\mathrm{ch}\left({\nabla }_t\right)$, where ${\nabla }_t$ is a connection on $E\times [0,1]$ over $B\times [0,1]$ interpolating the connections ${\nabla }_t$ on E for $t\in [0,1]$. It is also well-known (cf. Simons and Sullivan ([10], p. 583, Proposition 1.1)) that $\mathrm{cs}\left(\alpha \right)-\mathrm{cs}\left(\gamma \right)\in \mathrm{Im}\left(d\right)$ for two paths of connections $\alpha$ and $\gamma$ beginning at ${\nabla }_0$ and ending at ${\nabla }_1$. Therefore, for any path of connections on E beginning at ${\nabla }_0$ and ending at ${\nabla }_1$, there is only one Chern–Simons form modulo d-exact forms. We may write $\mathrm{CS}({\nabla }_0,{\nabla }_1):=\mathrm{cs}\left(\gamma \right)$ mod $\mathrm{Im}\left(d\right)$.

3.1. Differential K-Theory via Vector Bundles

The differential K-theory group ${\widehat{K}}_{\mathrm{FLK}}\left(B\right)$ is the abelian group defined as follows.

Definition 8

(Freed–Lott [8] and Klonoff [9]). The generators of ${\widehat{K}}_{\mathit{FLK}}\left(B\right)$ are quadruples

$$\mathcal{E}=(E,h^E,{\nabla }^E,\varphi ),$$

where

• E is a complex vector bundle on B.
• $h^E$ is a hermitian metric on E.
• ${\nabla }^E$ is an $h^E$-compatible connection on E.
• $\varphi \in {\Omega }^{\mathit{odd}}\left(B\right)/\mathit{Im}\left(d\right)$.

Definition 9.

The ${\widehat{K}}_{\mathit{FLK}}\left(B\right)$-relation is defined as $\mathcal{E}\sim \mathcal{F}$ if there is a vector bundle isomorphism $\phi :E\to F$ covering the identity map on B such that $\mathit{CS}({\nabla }^E,{\phi }^{*}{\nabla }^F)={\varphi }^E-{\varphi }^F$.

Remark 2.

In this section, all equalities involving the CS forms including Definitions 9 and 12 are under modulo $\mathit{Im}\left(d\right)$.

An addition + between two equivalence class of ${\widehat{K}}_{\mathrm{FLK}}$-generators is defined by

$$\left[(E,h^E,{\nabla }^E,{\varphi }^E)\right]+\left[(F,h^F,{\nabla }^F,{\varphi }^F)\right]=\left[(E\oplus F,h^E\oplus h^F,{\nabla }^E\oplus {\nabla }^F,{\varphi }^E+{\varphi }^F)\right].$$

The addition + is well-defined and the set of all equivalence classes of ${\widehat{K}}_{\mathrm{FLK}}\left(B\right)$-generators forms a commutative monoid $(\mathfrak{M},+)$.

Definition 10.

The (even) differential K-group of B, denoted by ${\widehat{K}}_{\mathit{FLK}}\left(B\right)$, is the Grothendieck group of the commutative monoid $(\mathfrak{M},+)$.

As in the topological K-group case (see Section 2.3), a typical element of ${\widehat{K}}_{\mathrm{FLK}}\left(B\right)$ is in the form $[\mathcal{E},\mathcal{F}]$, which we denote by the difference $\left[\mathcal{E}\right]-\left[\mathcal{F}\right]$. If $[\mathcal{E},\mathcal{F}]=[{\mathcal{E}}^{\prime },{\mathcal{F}}^{\prime }]$ in ${\widehat{K}}_{\mathrm{FLK}}\left(B\right)$, then there exists a ${\widehat{K}}_{\mathrm{FLK}}\left(B\right)$-generator $\mathcal{G}=(G,h^G,{\nabla }^G,{\varphi }^G)$ such that

$$\mathcal{E}+{\mathcal{F}}^{\prime }+\mathcal{G}\sim \mathcal{F}+{\mathcal{E}}^{\prime }+\mathcal{G}$$

in the abelian monoid $\mathfrak{M}$. This implies that there is a vector bundle isomorphism $\phi :E\oplus F^{\prime }\oplus G\to F\oplus E^{\prime }\oplus G$ covering the identity map on B such that

$$\begin{array}{cc}\hfill \mathrm{CS}({\nabla }^E\oplus {\nabla }^{F^{\prime }}\oplus {\nabla }^G,{\phi }^{*}({\nabla }^F\oplus {\nabla }^{E^{\prime }}\oplus {\nabla }^G))=& {\varphi }^{E\oplus F^{\prime }\oplus G}-{\varphi }^{F\oplus E^{\prime }\oplus G}\hfill \\ \hfill =& ({\varphi }^E+{\varphi }^{F^{\prime }}+{\varphi }^G)-({\varphi }^F+{\varphi }^{E^{\prime }}+{\varphi }^G)\hfill \\ \hfill =& {\varphi }^E+{\varphi }^{F^{\prime }}-({\varphi }^F+{\varphi }^{E^{\prime }}).\hfill \end{array}$$

So the differential form ${\varphi }^G$ does not play any role so we may omit it when using the generator $\mathcal{G}$.

3.2. Differential K-Theory via Superbundles

Alternatively, we can also define the generators with $\mathbb{Z}/2\mathbb{Z}$-graded vector bundles (see ([9], p. 39, Remark 4.21), Ortiz ([13], p. 20) and Ho ([22], p. 962, Section 2.5)).

Definition 11.

The generators of ${\widehat{K}}_{\mathit{FLK}}{\left(B\right)}_s$ are quadruples

$$\mathcal{E}=(E,h^E,{\nabla }^E,\varphi ),$$

where

• $E=E^{+}\oplus E^{-}$ is a superbundle on B.
• $h^E=h^{E^{+}}\oplus h^{E^{-}}$ is a hermitian metric on E.
• ${\nabla }^E={\nabla }^{E^{+}}\oplus {\nabla }^{E^{-}}$ is an $h^E$-compatible grade-preserving connection on E.
• $\varphi \in {\Omega }^{\mathit{odd}}\left(B\right)/\mathit{Im}\left(d\right)$.

We define $\mathrm{ch}({\nabla }^{E^{+}}\oplus {\nabla }^{E^{-}}):=\mathrm{ch}\left({\nabla }^{E^{+}}\right)-\mathrm{ch}\left({\nabla }^{E^{-}}\right)$. Given two connections ${\nabla }^E={\nabla }^{E^{+}}\oplus {\nabla }^{E^{-}}$ and ${\nabla }^{\tilde{E}}={\nabla }^{{\tilde{E}}^{+}}\oplus {\nabla }^{{\tilde{E}}^{-}}$ on the superbundle E, we define the Chern–Simons form $\mathrm{CS}({\nabla }^E,{\nabla }^{\tilde{E}})$ as the form interpolating two even forms and two odd forms simultaneously. Let $W=B\times I$ where $I=[0,1]$, and $p:W\to B$ be the projection map. Let $F=p^{*}E=F^{+}\oplus F^{-}$ where $F^{\pm }=p^{*}{E}^{\pm }\cong E^{\pm }\times I$. Let ${\nabla }_t^{F^{+}}$ be a connection on $F^{+}$ such that ${\nabla }_0^{F^{+}}=p^{*}{\nabla }^{E^{+}}$ over $\left\{0\right\}\times B$ and ${\nabla }_1^{F^{+}}=p^{*}{\nabla }^{{\tilde{E}}^{+}}$ over $\left\{1\right\}\times B$. We define ${\nabla }_t^{F^{-}}$ similarly on $F^{-}$ and ${\nabla }_t^F:={\nabla }_t^{F^{+}}\oplus {\nabla }_t^{F^{-}}$. Note that ${\nabla }_t^{F^{\pm }}$ interpolates ${\nabla }^{E^{\pm }}$ and ${\nabla }^{{\tilde{E}}^{\pm }}$. Since

$$\mathrm{ch}\left({\nabla }_t^F\right)=\mathrm{ch}({\nabla }_t^{F^{+}}\oplus {\nabla }_t^{F^{-}})=\mathrm{ch}\left({\nabla }_t^{F^{+}}\right)-\mathrm{ch}\left({\nabla }_t^{F^{-}}\right)\in {\Omega }^{\mathrm{even}}(B\times I),$$

we integrate over I to get

$$\begin{array}{cc}\hfill \mathrm{CS}({\nabla }^E,{\nabla }^{\tilde{E}}):=& {\int }_I\mathrm{ch}\left({\nabla }_t^F\right)\hfill \\ \hfill =& {\int }_I\mathrm{ch}\left({\nabla }_t^{F^{+}}\right)-{\int }_I\mathrm{ch}\left({\nabla }_t^{F^{-}}\right)\hfill \\ \hfill =& \mathrm{CS}({\nabla }^{E^{+}},{\nabla }^{{\tilde{E}}^{+}})-\mathrm{CS}({\nabla }^{E^{-}},{\nabla }^{{\tilde{E}}^{-}}).\hfill \end{array}$$

It is readily seen that

$$\begin{array}{cc}\hfill d\mathrm{CS}({\nabla }^E,{\nabla }^{\tilde{E}})=& d\mathrm{CS}({\nabla }^{E^{+}},{\nabla }^{{\tilde{E}}^{+}})-d\mathrm{CS}({\nabla }^{E^{-}},{\nabla }^{{\tilde{E}}^{-}})\hfill \\ \hfill =& (\mathrm{ch}\left({\nabla }^{E^{+}}\right)-\mathrm{ch}\left({\nabla }^{{\tilde{E}}^{+}}\right))-(\mathrm{ch}\left({\nabla }^{E^{-}}\right)-\mathrm{ch}\left({\nabla }^{{\tilde{E}}^{-}}\right))\hfill \\ \hfill =& (\mathrm{ch}\left({\nabla }^{E^{+}}\right)-\mathrm{ch}\left({\nabla }^{E^{-}}\right))-(\mathrm{ch}\left({\nabla }^{{\tilde{E}}^{+}}\right)-\mathrm{ch}\left({\nabla }^{{\tilde{E}}^{-}}\right))\hfill \\ \hfill =& \mathrm{ch}\left({\nabla }^E\right)-\mathrm{ch}\left({\nabla }^{\tilde{E}}\right).\hfill \end{array}$$

Definition 12.

The ${\widehat{K}}_{\mathit{FLK}}{\left(B\right)}_s$-relations are defined as $\mathcal{E}{\sim }_s\mathcal{F}$ if there exist two $\mathbb{Z}/2\mathbb{Z}$-graded hermitian vector bundles with metric compatible connections $(G,h^G,{\nabla }^G)$ and $(H,h^H,{\nabla }^H)$ over B of the form

$$G^{+}=G^{-},h^{G^{+}}=h^{G^{-}},{\nabla }^{G^{+}}={\nabla }^{G^{-}},H^{+}=H^{-},h^{H^{+}}=h^{H^{-}},{\nabla }^{H^{+}}={\nabla }^{H^{-}},$$

(4)

and a super bundle isomorphism $\phi :E\oplus G\to F\oplus H$ such that

$$\begin{array}{cc}\hfill \mathit{CS}({\nabla }^{E^{+}}\oplus {\nabla }^{G^{+}},{\left({\phi }^{+}\right)}^{*}({\nabla }^{F^{+}}\oplus {\nabla }^{H^{+}}))=& {\varphi }^E-{\varphi }^F,\hfill \\ \hfill \mathit{CS}({\nabla }^{E^{-}}\oplus {\nabla }^{G^{-}},{\left({\phi }^{-}\right)}^{*}({\nabla }^{F^{-}}\oplus {\nabla }^{H^{-}}))=& 0.\hfill \end{array}$$

We denote ${\widehat{K}}_{\mathrm{FLK}}{\left(B\right)}_s$-equivalence class by ${\left[\mathcal{E}\right]}_s$. Given the ${\widehat{K}}_{\mathrm{FLK}}{\left(B\right)}_s$-generator $\mathcal{E}$, let ${\mathcal{E}}^{+}=(E^{+},h^{E^{+}},{\nabla }^{E^{+}},{\varphi }^E)$ and ${\mathcal{E}}^{-}=(E^{-},h^{E^{-}},{\nabla }^{E^{-}},0)$. Then, we can identify ${\left[\mathcal{E}\right]}_s={[{\mathcal{E}}^{+},{\mathcal{E}}^{-}]}_s$ with even and odd parts of the generator.

The addition + between two equivalence classes of ${\widehat{K}}_{\mathrm{FLK}}{\left(B\right)}_s$-generators is defined as

$${\left[\mathcal{E}\right]}_s+{\left[\mathcal{F}\right]}_s:={[{\mathcal{E}}^{+}+{\mathcal{F}}^{+},{\mathcal{E}}^{-}+{\mathcal{F}}^{-}]}_s,$$

with the identity ${\left[0\right]}_s$ and $-{\left[\mathcal{E}\right]}_s:={[{\mathcal{E}}^{-},{\mathcal{E}}^{+}]}_s$.

Definition 13.

The differential K-group ${\widehat{K}}_{\mathit{FLK}}{\left(B\right)}_s$ is defined as the abelian group of all ${\widehat{K}}_{\mathit{FLK}}{\left(B\right)}_s$-equivalence classes.

The following is our main theorem showing that the two definitions of differential K-theory are equivalent.

Theorem 1.

${\widehat{K}}_{\mathit{FLK}}{\left(B\right)}_s$ and ${\widehat{K}}_{\mathit{FLK}}\left(B\right)$ are isomorphic as groups.

Proof. 

Let $f:{\widehat{K}}_{\mathrm{FLK}}{\left(B\right)}_s\to {\widehat{K}}_{\mathit{FLK}}\left(B\right)$ and $g:{\widehat{K}}_{\mathrm{FLK}}\left(B\right)\to {\widehat{K}}_{\mathrm{FLK}}{\left(B\right)}_s$ be two maps defined by $f\left({\left[\mathcal{E}\right]}_s\right):=[{\mathcal{E}}^{+},{\mathcal{E}}^{-}]$ and $g\left([\mathcal{E},\mathcal{F}]\right):={[\tilde{\mathcal{E}},\tilde{\mathcal{F}}]}_s$, where $\tilde{\mathcal{E}}=(E,h^E,{\nabla }^E,{\varphi }^E-{\varphi }^F)$ and $\tilde{\mathcal{F}}=(F,h^F,{\nabla }^F,0)$. Note that $[\tilde{\mathcal{E}},\tilde{\mathcal{F}}]=[\mathcal{E},\mathcal{F}]$ in ${\widehat{K}}_{\mathrm{FLK}}\left(B\right)$.

We first show that f is well-defined. Suppose that ${\left[\mathcal{E}\right]}_s={\left[\mathcal{F}\right]}_s\in {\widehat{K}}_{\mathrm{FLK}}{\left(B\right)}_s$. Then, there exist two $\mathbb{Z}/2\mathbb{Z}$-graded hermitian vector bundles with compatible connections $\mathcal{G}=(G,h^G,{\nabla }^G)$ and $\mathcal{H}=(H,h^H,{\nabla }^H)$ over B of the form (4) and a super bundle isomorphism $\phi :E\oplus G\to F\oplus H$ such that

$$\begin{array}{cc}\hfill \mathrm{CS}({\nabla }^{E^{+}}\oplus {\nabla }^{G^{+}},{\left({\phi }^{+}\right)}^{*}({\nabla }^{F^{+}}\oplus {\nabla }^{H^{+}}))=& {\varphi }^E-{\varphi }^F,\hfill \\ \hfill \mathrm{CS}({\nabla }^{E^{-}}\oplus {\nabla }^{G^{-}},{\left({\phi }^{-}\right)}^{*}({\nabla }^{F^{-}}\oplus {\nabla }^{H^{-}}))=& 0,\hfill \end{array}$$

where ${\phi }^{\pm }:E^{\pm }\oplus G^{\pm }\to F^{\pm }\oplus H^{\pm }$ are the vector bundle isomorphisms covering the identity. Let $\mathcal{P}:=\mathcal{G}+\mathcal{H}$ and $\psi :={\phi }^{+}\oplus {\left({\phi }^{-}\right)}^{-1}$ so that $\psi :E^{+}\oplus F^{-}\oplus P\to E^{-}\oplus F^{+}\oplus P$ is a vector bundle isomorphism. We can write that $\psi :(E^{+}\oplus G^{+})\oplus (F^{-}\oplus H^{-})\to (F^{+}\oplus H^{+})\oplus (E^{-}\oplus G^{-})$ is the isomorphism and from the assumption,

$$\begin{array}{cc}\hfill & \mathrm{CS}({\nabla }^{E^{+}}\oplus {\nabla }^{F^{-}}\oplus {\nabla }^P,{\psi }^{*}({\nabla }^{F^{+}}\oplus {\nabla }^{E^{-}}\oplus {\nabla }^P))\hfill \\ \hfill =& \mathrm{CS}(({\nabla }^{E^{+}}\oplus {\nabla }^{G^{+}})\oplus ({\nabla }^{F^{-}}\oplus {\nabla }^{H^{-}}),{\psi }^{*}(({\nabla }^{F^{+}}\oplus {\nabla }^{H^{+}})\oplus ({\nabla }^{E^{-}}\oplus {\nabla }^{G^{-}})))\hfill \\ \hfill =& \mathrm{CS}(({\nabla }^{E^{+}}\oplus {\nabla }^{G^{+}})\oplus ({\nabla }^{F^{-}}\oplus {\nabla }^{H^{-}}),{\left({\phi }^{+}\right)}^{*}({\nabla }^{F^{+}}\oplus {\nabla }^{H^{+}})\oplus {{\left({\phi }^{-}\right)}^{-1}}^{*}({\nabla }^{E^{-}}\oplus {\nabla }^{G^{-}}))\hfill \\ \hfill =& \mathrm{CS}({\nabla }^{E^{+}}\oplus {\nabla }^{G^{+}},{\left({\phi }^{+}\right)}^{*}({\nabla }^{F^{+}}\oplus {\nabla }^{H^{+}}))+\mathrm{CS}({\nabla }^{F^{-}}\oplus {\nabla }^{H^{-}},{{\left({\phi }^{-}\right)}^{-1}}^{*}({\nabla }^{E^{-}}\oplus {\nabla }^{G^{-}})),\hfill \\ \hfill =& {\varphi }^E-{\varphi }^F\hfill \end{array}$$

where we used the property of the Chern–Simons form (see ([9], p. 15, Corollary 2.15)) on the third equality. Hence, $[{\mathcal{E}}^{+},{\mathcal{E}}^{-}]=[{\mathcal{F}}^{+},{\mathcal{F}}^{-}]$ in ${\widehat{K}}_{\mathrm{FLK}}\left(B\right)$.

Next, we show that g is well-defined. Suppose that $[{\mathcal{E}}_1,{\mathcal{F}}_1]=[{\mathcal{E}}_2,{\mathcal{F}}_2]\in {\widehat{K}}_{\mathrm{FLK}}\left(B\right)$. Then, there is a ${\widehat{K}}_{\mathrm{FLK}}\left(B\right)$-generator $\mathcal{Q}$ and a vector bundle isomorphism $\phi :E_1\oplus F_2\oplus Q\to E_2\oplus F_1\oplus Q$ covering the identity map on B such that

$$\begin{array}{cc}\hfill \mathrm{CS}({\nabla }^{E_1}\oplus {\nabla }^{F_2}\oplus {\nabla }^Q,{\phi }^{*}({\nabla }^{E_2}\oplus {\nabla }^{F_1}\oplus {\nabla }^Q))=& ({\varphi }^{E_1}+{\varphi }^{F_2})-({\varphi }^{E_2}+{\varphi }^{F_1}).\hfill \end{array}$$

We want to show that ${[{\tilde{\mathcal{E}}}_1,{\tilde{\mathcal{F}}}_1]}_s={[{\tilde{\mathcal{E}}}_2,{\tilde{\mathcal{F}}}_2]}_s$ in ${\widehat{K}}_{\mathrm{FLK}}{\left(B\right)}_s$. That is, there exist two $\mathbb{Z}/2\mathbb{Z}$-graded hermitian vector bundles with compatible connections $(G,h^G,{\nabla }^G)$ and $(H,h^H,{\nabla }^H)$ over B of the form (4) and a super bundle isomorphism $\phi :E_1\oplus F_1\oplus G\to E_2\oplus F_2\oplus H$ such that

$$\begin{array}{cc}\hfill \mathrm{CS}({\nabla }^{E_1}\oplus {\nabla }^{G^{+}},{\left({\phi }^{+}\right)}^{*}({\nabla }^{E_2}\oplus {\nabla }^{H^{+}}))=& ({\varphi }^{E_1}-{\varphi }^{F_1})-({\varphi }^{E_2}-{\varphi }^{F_2}),\hfill \\ \hfill \mathrm{CS}({\nabla }^{F_1}\oplus {\nabla }^{G^{-}},{\left({\phi }^{-}\right)}^{*}({\nabla }^{F_2}\oplus {\nabla }^{H^{-}}))=& 0.\hfill \end{array}$$

Let $\mathcal{G}$ and $\mathcal{H}$ be two ${\widehat{K}}_{\mathrm{FLK}}\left(B\right)$-generators with $\mathcal{G}=(F_2\oplus Q,h^{F_2}\oplus h^Q,{\nabla }^{F_2}\oplus {\nabla }^Q,{\varphi }^Q)$ and $\mathcal{H}=(F_1\oplus Q,h^{F_1}\oplus h^Q,{\nabla }^{F_1}\oplus {\nabla }^Q,{\varphi }^Q)$. Then, $E_1\oplus G\cong E_2\oplus H$ and $F_1\oplus G\cong F_2\oplus H$. Let ${\phi }^{+}=\phi$ and ${\phi }^{-}:F_1\oplus F_2\oplus Q\to F_2\oplus F_1\oplus Q$ is the isomorphism of switching the first two components, and define the superbundle isomorphism $\phi :={\phi }^{+}\oplus {\phi }^{-}$. Then, we have

$$\begin{array}{cc}\hfill \mathrm{CS}({\nabla }^{E_1}\oplus {\nabla }^G,{\left({\phi }^{+}\right)}^{*}({\nabla }^{E_2}\oplus {\nabla }^H))=& \mathrm{CS}({\nabla }^{E_1}\oplus {\nabla }^{F_2}\oplus {\nabla }^Q,{\phi }^{*}({\nabla }^{E_2}\oplus {\nabla }^{F_1}\oplus {\nabla }^Q))\hfill \\ \hfill =& ({\varphi }^{E_1}+{\varphi }^{F_2})-({\varphi }^{E_2}+{\varphi }^{F_1})\hfill \\ \hfill =& ({\varphi }^{E_1}-{\varphi }^{F_1})-({\varphi }^{E_2}-{\varphi }^{F_2}),\hfill \\ \hfill =& {\varphi }^{{\tilde{\mathcal{E}}}_1}-{\varphi }^{{\tilde{\mathcal{E}}}_2},\hfill \\ \hfill \mathrm{CS}({\nabla }^{F_1}\oplus {\nabla }^G,{\left({\phi }^{-}\right)}^{*}({\nabla }^{F_2}\oplus {\nabla }^H))=& \mathrm{CS}({\nabla }^{F_1}\oplus {\nabla }^{F_2}\oplus {\nabla }^Q,{\left({\phi }^{-}\right)}^{*}({\nabla }^{F_2}\oplus {\nabla }^{F_1}\oplus {\nabla }^Q))\hfill \\ \hfill =& 0.\hfill \end{array}$$

This implies that ${[{\tilde{\mathcal{E}}}_1,{\tilde{\mathcal{F}}}_1]}_s={[{\tilde{\mathcal{E}}}_2,{\tilde{\mathcal{F}}}_2]}_s$ in ${\widehat{K}}_{\mathrm{FLK}}{\left(B\right)}_s$.

It is straight-forward to see that $g\circ f={\mathtt{id}}_{{\widehat{K}}_{\mathrm{FLK}}{\left(B\right)}_s}$. On the other hand,

$$(f\circ g)\left([\mathcal{E},\mathcal{F}]\right)=f\left({[\tilde{\mathcal{E}},\tilde{\mathcal{F}}]}_s\right)=[\tilde{\mathcal{E}},\tilde{\mathcal{F}}]\mathrm{in}{\widehat{K}}_{\mathrm{FLK}}\left(B\right).$$

Since $[\mathcal{E},\mathcal{F}]=[\tilde{\mathcal{E}},\tilde{\mathcal{F}}]$ in ${\widehat{K}}_{\mathrm{FLK}}\left(B\right)$, we have $f\circ g={\mathtt{id}}_{{\widehat{K}}_{\mathrm{FLK}}\left(B\right)}$, as well. Finally, we can check that

$$\begin{array}{cc}\hfill f({\left[\mathcal{E}\right]}_s+{\left[\mathcal{F}\right]}_s)=& f\left([{\mathcal{E}}^{+}+{\mathcal{F}}^{+},{\mathcal{E}}^{-}+{\mathcal{F}}^{-}]\right)=[{\mathcal{E}}^{+}+{\mathcal{F}}^{+},{\mathcal{E}}^{-}+{\mathcal{F}}^{-}]\hfill \\ \hfill =& [{\mathcal{E}}^{+},{\mathcal{E}}^{-}]+[{\mathcal{F}}^{+},{\mathcal{F}}^{-}]=f\left({\left[\mathcal{E}\right]}_s\right)+f\left({\left[\mathcal{F}\right]}_s\right),\hfill \\ \hfill g([{\mathcal{E}}_1,{\mathcal{F}}_1]+[{\mathcal{E}}_2,{\mathcal{F}}_2])=& g\left([{\mathcal{E}}_1+{\mathcal{E}}_2,{\mathcal{F}}_1+{\mathcal{F}}_2]\right)=[\widetilde{{\mathcal{E}}_1+{\mathcal{E}}_2},\widetilde{{\mathcal{F}}_1+{\mathcal{F}}_2}]\_s\hfill \\ \hfill =& {[\widetilde{{\mathcal{E}}_1},\widetilde{{\mathcal{F}}_1}]}_s+{[\widetilde{{\mathcal{E}}_2},\widetilde{{\mathcal{F}}_2}]}_s=g\left([{\mathcal{E}}_1,{\mathcal{F}}_1]\right)+g\left([{\mathcal{E}}_2,{\mathcal{F}}_2]\right).\hfill \end{array}$$

So f and g are group homomorphisms. □

4. Discussion

In this article, we have reviewed topological K-theory and its superbundle description. Based on that, we have constructed a model of differential K-theory using superbundles with $\mathbb{Z}/2\mathbb{Z}$-graded connection and a differential form on the base manifold. As our main theorem, we have proved that our model is isomorphic to the Freed–Lott–Klonoff model of differential K-theory.