Political Signed Temporal Networks: A Deep Learning Approach
Abstract
:1. Introduction
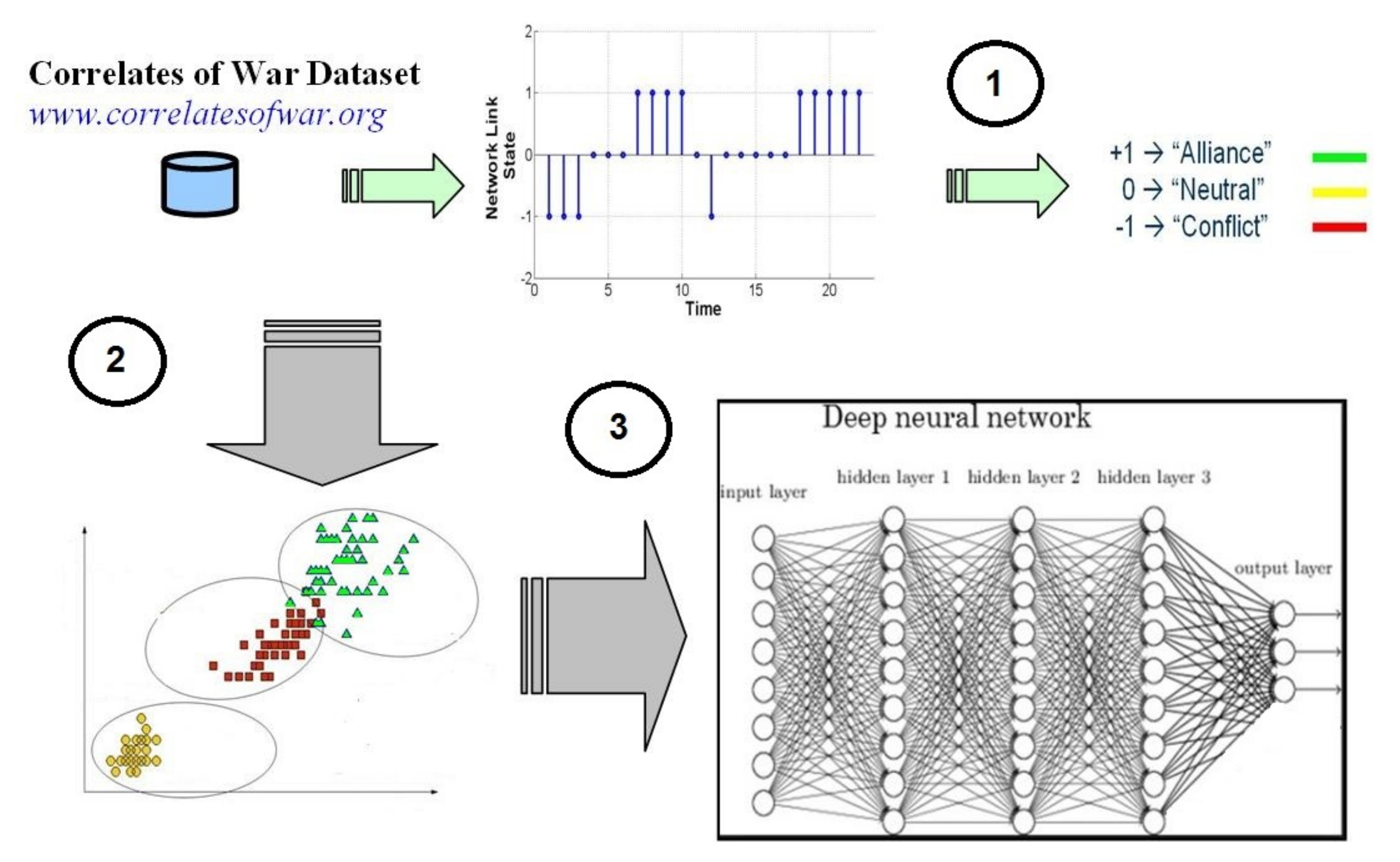
2. Proposed Approach
2.1. Theoretical Background and Main Steps of the Approach
2.2. The Correlates of War Data
3. Geometric and Information-Theoretic Measures
3.1. Inertias
3.2. Dispersion and Fisher Criterion
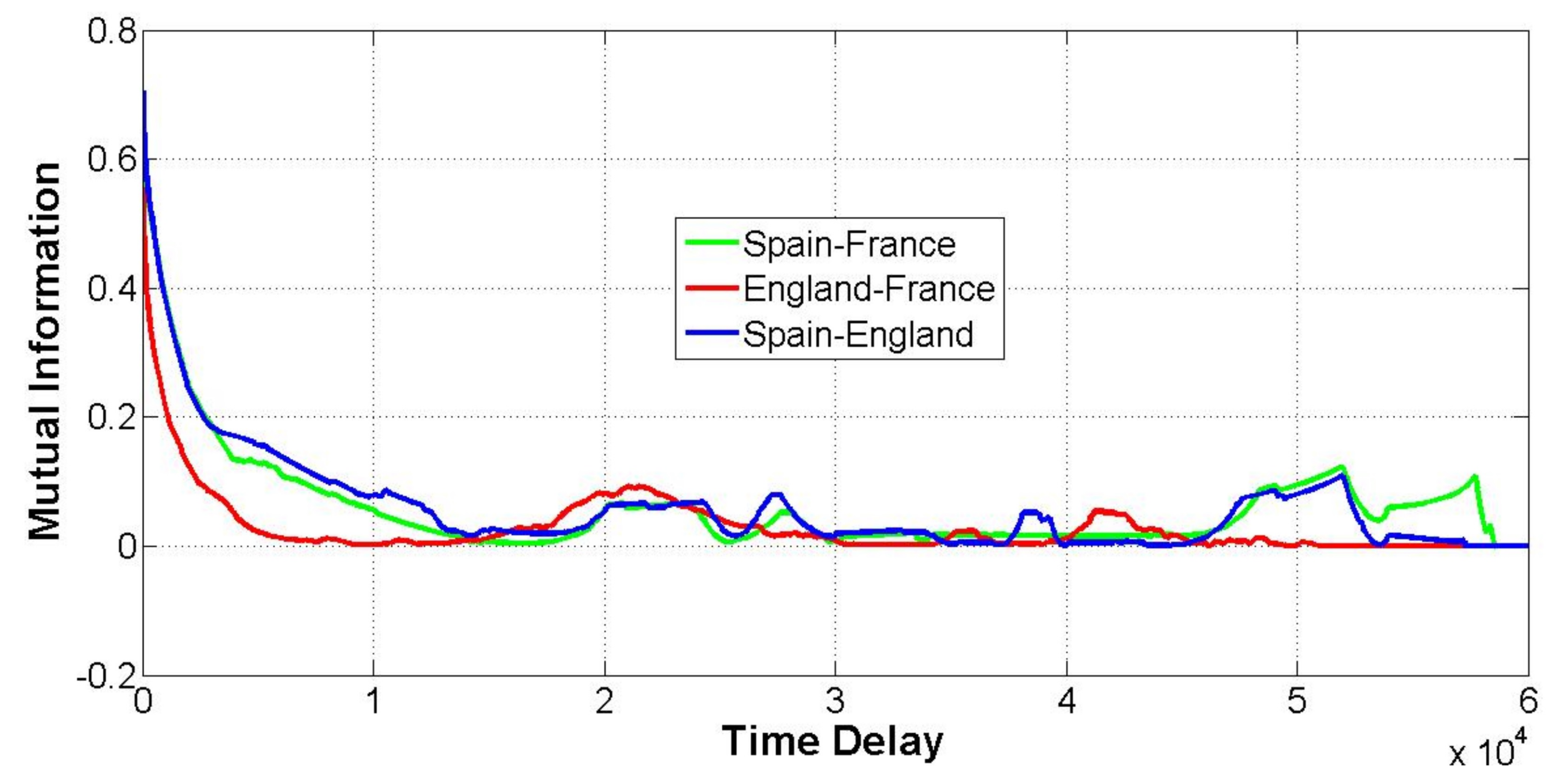
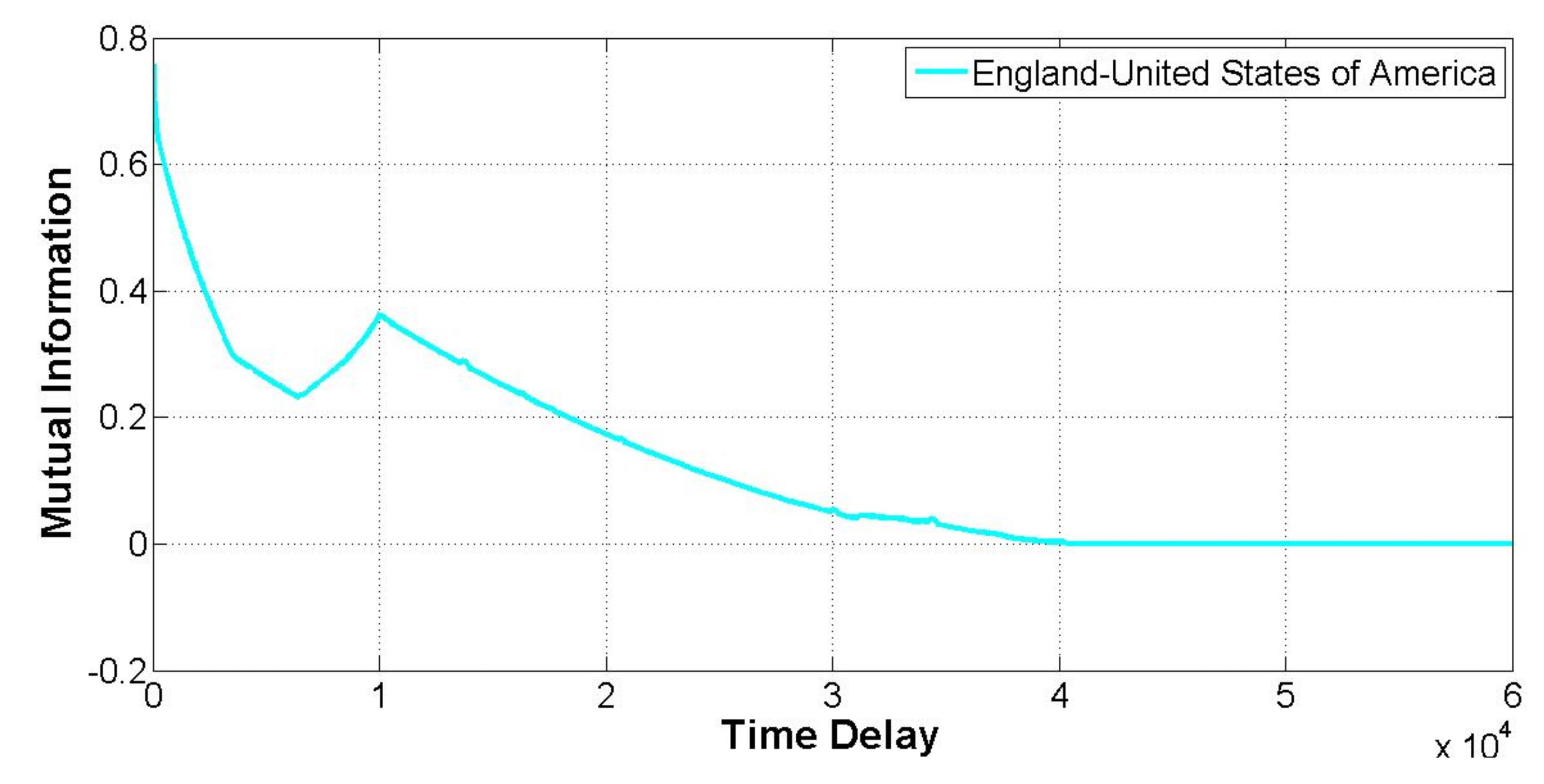
3.3. Mutual Information
4. Deep Networks
4.1. The Optimal Number of Regressors
4.2. Deep Networks Structure
4.3. Results from the Deep Learning Approach
5. Discussion
- The fact of employing information-theoretic measures such as mutual information provides substantial information not only with regards to the influence of certain historical events but especially in a better comprehension of international signed relations (e.g., to better understand the role and actions of the actors involved).
- The predictive model can capture with enough accuracy the regularities of international signed relations (i.e., an average accuracy ranging from 1 up to 5 errors each 10,000 predictions for the well-represented categories), including the prediction of conflictual events at the local level (i.e., the under-represented category Conflict achieving an average accuracy of 84 errors each 10,000 predictions) thus, outperforming state of the art approaches.
- Given the accuracy of the predictions obtained at the local level, our results suggest that this model might be extended by incorporating both temporal and topological aspects of networks to improve predictions of dynamical processes at regional and global levels aimed at achieving a complete understanding of the overall pattern of signed international relations.
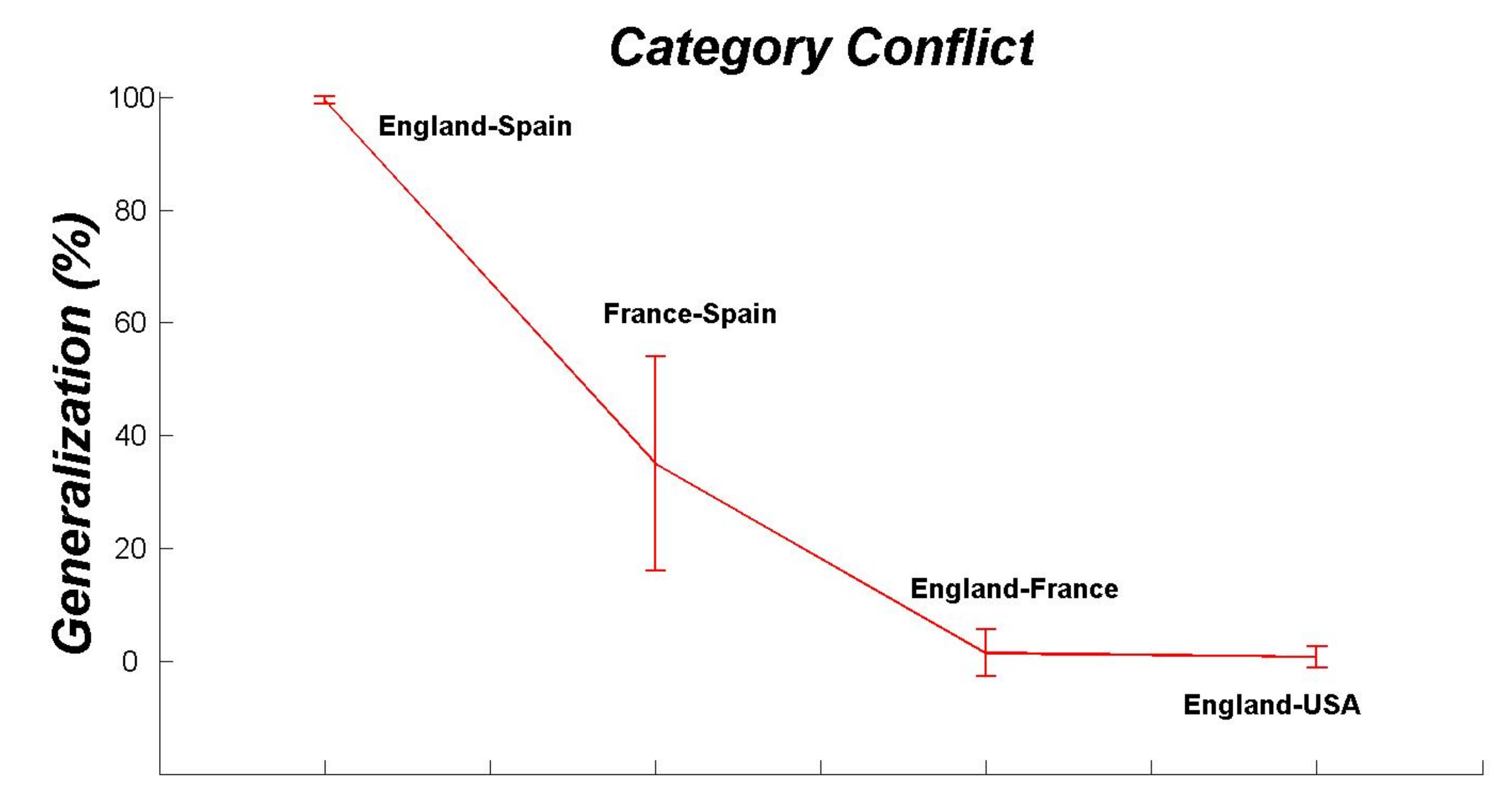
5.1. Under-Represented Samples: The Conflict Category
5.2. Global Patterns versus Pairwise Relationships
5.3. Influence of Historical Events
6. Conclusions
- The dispersion values obtained between the categories representing the states of the links have shown that the mechanisms (or strategies) employed by countries to generate alliances are, in general, more complex compared to those leading to a conflict. The overlapping rate of the categories of the international signed relations measured by the Fisher criterion, together with their prior probabilities, were good indicators of the expected generalization performance of the models.
- The interpretation of the time delayed mutual information permitted to show that the political relationships between countries are influenced to a great extent by past historical events, that is, the dependence on the past (the memory) of the stochastic processes driving link dynamics goes beyond to the previous state (Markov property). Furthermore, its correlations for a certain range of values of the delay across multiple links of the network evidenced the existence of historical events that directly or indirectly affected the political relationships between those countries, thus, potentially helping the interpretation of the strategies and actions of the actors involved.
- Deep learning machines can capture with enough accuracy (probability of error close to zero) the regularities of international signed relations, including the prediction of conflictual events at the local level, specifically, the prediction of those big events in two centuries of state-wise geopolitical information when the typical relationship between countries changed to a war or a conflict.
- The predictive capacities of the model are beyond strictly local predictions as the model can also provide accurate predictions at the regional or global levels of patterns belonging to the well-represented categories of the international signed relations.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dorogovtsev, S.N. Lectures on Complex Networks; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Newman, M.E.J. Networks: An introduction; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Newman, M.E.J. Network structure from rich but noisy data. Nat. Phys. 2018, 14, 542–545. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of `small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Elhesha, R.; Sarkar, A.; Boucher, J.; Kahveci, T. Identification of co-evolving temporal networks. BMC Genom. 2019, 20 (Suppl. 6), 434. [Google Scholar] [CrossRef]
- Masuda, N.; Holme, P. (Eds.) Temporal Network Epidemiology (Theoretical Biology), 1st ed.; Springer: Berlin/Heidelberg, Germany, 2017; Available online: https://link.springer.com/book/10.1007/978-981-10-5287-3 (accessed on 16 August 2022).
- Wang, W.; Wuang, L.; Gan, C. Epidemic Spreading Dynamics on Temporal Networks, Collection of Papers 2021. 2021. Available online: https://www.hindawi.com/journals/complexity/si/813208/ (accessed on 16 August 2022).
- Zhu, Z.; Sun, Y.; Kuang, Y.; Yuan, X.; Gu, H.; Zhu, J.; Xing, W. Contemporaneous symptom networks of multidimensional symptom experiences in cancer survivors: A network analysis. Cancer Med. 2022, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Akbar, M.A.; Leiva, V.; Rafi, S.; Qadri, S.F.; Mahmood, A.; Alsanad, A. Towards roadmapto implement blockchain in healthcare systems based on a matrity model. Softw. Evol. Process. 2022, e2500. [Google Scholar] [CrossRef]
- Riatz, M.T.; Alsanad, A.A.; Ahmad, S.; Akbar, M.A.; AlSuwaidan, L.; Al-AlShaikh, H.A.; Alsagri, H. A wireless controlled intelligent healthcare system for diplegia patients. Math. Biosci. Eng. 2022, 19, 456–472. [Google Scholar] [CrossRef]
- Jordan, G.; Winer, S.; Salem, T. The Current Status of Temporal Network Analysis for Clinical Science: Considerations as the Paradigm Shifts? Available online: https:/onlinelibrary.wiley.com/doi/10.1002/jclp.22957 (accessed on 15 August 2022).
- Centola, D. The spread of behavior in an online social network experiment. Science 2010, 329, 1194–1197. [Google Scholar] [CrossRef]
- Holme, P. Modern temporal network theory: A colloquium. Eur. Phys. J. B 2015, 88, 1–30. [Google Scholar] [CrossRef]
- Kossinets, G.; Watts, D.J. Empirical analysis of an evolving social network. Science 2006, 311, 88–90. [Google Scholar] [CrossRef]
- Maulana, A.; Situngkir, H.; Suroso, R. Dynamics of Polarization and Coalition Formation in Signed Political Elite Networks. In Complex Networks and Their Applications; Complex Networks 2021, Studies in Computational Intelligence; Benito, R.M., Cherifi, C., Cherifi, H., Moro, E., Rocha, L.M., Sales-Pardo, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2022; Volume 1015. [Google Scholar] [CrossRef]
- Musciotto, F.; Delpriori, S.; Castagno, P.; Pournaras, E. Mining social interactions in privacy-preserving temporal networks. In Proceedings of the IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM), San Francisco, CA, USA, 18–21 August 2016; pp. 1103–1110. [Google Scholar] [CrossRef]
- Bassett, D.S.; Wymbs, N.F.; Porter, M.A.; Mucha, P.J.; Carlson, J.M.; Grafton, S.T. Dynamic reconfiguration of human brain networks during learning. Proc. Natl. Acad. Sci. USA 2011, 108, 7641–7646. [Google Scholar] [CrossRef]
- Nasuha-Daud, N.; Hafizah-Ab-Hamid, S.; Saadoon, M.; Sahran, F.; Badrul-Anuar, N. Applications of link prediction in social networks: A review. J. Netw. Comput. Appl. 2020, 166, 102716. [Google Scholar] [CrossRef]
- Ai, J.; Cai, Y.; Su, Z.; Zhang, K.; Peng, D.; Chen, Q. Predicting user-item links in recommender systems based on similarity-network resource allocation. Chaos Solitons Fractals 2022, 158, 112032. [Google Scholar] [CrossRef]
- Cheng, Y.L.; Hsiao, C.H.; Wu, C.C. An ensemble model for link prediction based on graph embedding. Decis. Support Syst. 2022, 157, 113753. [Google Scholar] [CrossRef]
- Calderoni, F.; Catanese, S.; De Meo, P.; Ficara, A.; Fiumara, G. Robust link prediction in criminal networks: A case study of the Sicilian Mafia. Expert Syst. Appl. 2020, 161, 113666. [Google Scholar] [CrossRef]
- Boccaleti, S.; Bianconi, G.; Criado, R.; Del Genio, C.I.; Gómez-Gardenes, J.; Romance, M.; Sendina-Nadal, I.; Wang, Z.; Zanin, M. The Structure and Dynamics of Multilayer Networks. Phys. Rep. 2014, 544, 1–122. [Google Scholar] [CrossRef]
- Aref, S.; Wilson, M.C. Balance and frustration in signed networks. J. Complex Netw. 2019, 7, 163–189. [Google Scholar] [CrossRef]
- Aref, S.; Mason, A.J.; Wilson, M.C. A modeling and computational study of the frustration index in signed networks. Networks 2020, 75, 95–110. [Google Scholar] [CrossRef]
- Aref, S.; Neal, Z. Detecting coalitions by optimally partitioning signed networks of political collaboration. Sci. Rep. 2020, 10, 1506. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kirkley, A.; Cantwell, G.T.; Newman, M.E.J. Balance in signed networks. Phys. Rev. E 2019, 99, 0123120. [Google Scholar] [CrossRef]
- Antal, T.; Krapivsky, P.L.; Redner, S. Social Balance on Networks: The Dynamics of Friendship and Enmity. Phys. D Nonlinear Phenom. 2006, 224, 130. [Google Scholar] [CrossRef]
- Doreian, P.; Mrvar, A. Structural Balance and Signed International Relations. J. Soc. Struct. 2019, 16, 1–49. [Google Scholar] [CrossRef]
- Kunegis, J.; Schmidt, S.; Lommatzsch, A.; Lerner, J.; De Luca, E.W.; Albayrak, S. Spectral Analysis of Signed Graphs for Clustering, Prediction and Visualization. In Proceedings of the SIAM International Conference on Data Mining, SDM 2010, Columbus, OH, USA, 29 April–1 May 2010; pp. 559–570. [Google Scholar] [CrossRef]
- Musial, K.; Bródka, P.; De Meo, P. Analysis and Applications of Complex Social Networks. Complexity 2017, 2017, 3014163. [Google Scholar] [CrossRef]
- Xiang, B.B.; Ma, C.; Chen, H.S.; Zhang, H.F. Reconstructing signed networks via Ising dynamics. Chaos 2018, 28, 123117. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, H.V.; Alves, L.G.A.; Martins, A.F.; Lenzi, E.K.; Perc, M. The dynamical structure of political corruption networks. J. Complex Netw. 2018, 6, 989–1003. [Google Scholar] [CrossRef]
- Faustino, J.; Barbosa, H.; Ribeiro, E.; Menezes, R. A data-driven network approach for characterization of political parties’ ideology dynamics. Appl. Netw. Sci. 2019, 4, 48. [Google Scholar] [CrossRef]
- Arinik, N.; Figueiredo, R.; Labatut, V. Analysis of roll-calls in the European parliament by multiple partitioning of multiplex signed networks. Soc. Netw. 2019, 60, 83–102. [Google Scholar] [CrossRef]
- Tang, D.; Du, W.; Shekhtman, L.; Wang, Y.; Havlin, S.; Cao, X.; Yan, G. Predictability of real temporal networks. Natl. Sci. Rev. 2020, 7, 929–937. [Google Scholar] [CrossRef] [Green Version]
- Cranmer, S.J.; Menninga, E.J.; Mucha, P.J. Kantian Fractionalization Predicts the Conflict Propensity of the International System. Proc. Natl. Acad. Sci. USA 2014, 112, 11812–11816. [Google Scholar] [CrossRef]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Abarbanel, H. Analysis of Observed Chaotic Data; Springer: New York, NY, USA, 1996. [Google Scholar] [CrossRef]
- Lerner, J. Structural balance in signed networks: Separating the probability to interact from the tendency to fight. Soc. Netw. 2016, 45, 66–77. [Google Scholar] [CrossRef]
- Reid, M.; Wayman, F. Resort to War: 1816–2007; CQ Press: Washington, DC, USA, 2010. [Google Scholar]
- Takens, F. On the numerical determination of the dimension of an attractor. In Dynamical Systems and Turbulence, Annual Notes in Mathematics; Rand, D., Yound, L.S., Eds.; Springer: Berlin, Germany, 1981; Volume 898, pp. 366–381. [Google Scholar]
- Schmidhuber, J. Deep Learning in Neural Networks: An Overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- LeCunn, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Blayo, F.; Cheneval, Y.; Guérin-Dugué, A.; Chentouf, R.; Aviles-Cruz, C.; Madrenas, J.; Moreno, M.; Voz, J.L. Enhanced Learning for Evolutive Neural Architecture ESPRIT Basic Research Project Number 6891, Deliverable R3-B4-P, Task B4 (Benchmarks). 1995. Available online: https://cordis.europa.eu/project/id/6891/en (accessed on 16 August 2022).
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Blahut, R.E. Principles and Practice of Information Theory; Addison-Wesley Longman Publishing Co.: Boston, MA, USA, 1987. [Google Scholar]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134–1140. [Google Scholar] [CrossRef] [PubMed]
- Hegger, R.; Kantz, H.; Schreiber, T. Practical implementation of nonlinear time series methods: The TISEAN package. Chaos 1999, 9, 413–435. [Google Scholar] [CrossRef] [PubMed]
- Nørgaard, M.; Rvn, O.; Poulse, N.K.; Hansen, L.K. Neural Networks for Modelling and Control of Dynamic System; Springer: London, UK, 2000. [Google Scholar]
- Chinea, A. On the Theory of Deep Learning: A Theoretical Physics Perspective (Part I). 2020. Available online: https://www.preprints.org/manuscript/202010.0285/v1 (accessed on 1 January 2020).
- Anand, K.; Bianconi, G. Entropy measures for networks. Phys. Rev. E 2009, 80, 045102(R). [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall: Hoboken, NJ, USA, 1999. [Google Scholar]
- Efron, B. Bootstrap Methods: Another Look at the Jacknife. Ann. Stat. 1979, 7, 1–26. [Google Scholar] [CrossRef]
- Yedidia, J.; Weiss, Y. Generalized Belief Propagation. In Advances in Neural Information Processing Systems; 2001; pp. 689–695. Available online: https://proceedings.neurips.cc/paper/2000/hash/61b1fb3f59e28c67f3925f3c79be81a1-Abstract.html (accessed on 16 August 2022).
- Bishop, C.M. Pattern Analysis and Machine Learning; Springer: London, UK, 2006. [Google Scholar]
- Furtlehner, C.; Lasgouttes, J.-M.; de La Fortelle, A. A BeliefPropagation Approach to Traffic Prediction Using Probe Vehicles. In Proceedings of the 10th International IEEE Conference on Intelligent Transportation Systems, Bellevue, WA, USA, 30 September–3 October 2007; pp. 1022–1027. Available online: https://hal.inria.fr/hal-00175627 (accessed on 18 August 2022).
- Srivastava, A.; Chelmis, C.; Prasanna, V.K. Social influence computation and maximization in signed networks with competing cascades. In Proceedings of the IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM), Paris, France, 25–28 August 2015; pp. 41–48. [Google Scholar] [CrossRef]
- Huang, J.; Shen, H.; Cheng, X. SIGNLENS: A Tool for Analyzing People’s Polarization Social Relationship Based on Signed Graph Modeling. In Proceedings of the Fifteenth International AAAI Conference on Web and Social Media, Virtually, 7–10 June 2021; Volume 15. [Google Scholar]
- Bonchi, F.; Galimberti, E.; Gionis, A.; Ordozgoiti, B.; Ruffo, G. Discovering Polarized Communities in Signed Networks. arXiv 2019, arXiv:1910.02438. [Google Scholar] [CrossRef]

| Prior Probabilities | |||
|---|---|---|---|
| Network Link | Alliance | Neutral | Conflict |
| England–France | |||
| England–Spain | |||
| England–USA | =0.4010 | ||
| France–Spain | =0.6138 | ||
| Probability of Error | |||
|---|---|---|---|
| Network Link | Alliance | Neutral | Conflict |
| England–France | |||
| England–Spain | |||
| England–USA | |||
| France–Spain | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manrique de Lara, A.C.; Korutcheva, E. Political Signed Temporal Networks: A Deep Learning Approach. Axioms 2022, 11, 464. https://doi.org/10.3390/axioms11090464
Manrique de Lara AC, Korutcheva E. Political Signed Temporal Networks: A Deep Learning Approach. Axioms. 2022; 11(9):464. https://doi.org/10.3390/axioms11090464
Chicago/Turabian StyleManrique de Lara, Alejandro Chinea, and Elka Korutcheva. 2022. "Political Signed Temporal Networks: A Deep Learning Approach" Axioms 11, no. 9: 464. https://doi.org/10.3390/axioms11090464
APA StyleManrique de Lara, A. C., & Korutcheva, E. (2022). Political Signed Temporal Networks: A Deep Learning Approach. Axioms, 11(9), 464. https://doi.org/10.3390/axioms11090464






