Abstract
This paper develops a fractional-order model of COVID-19 with vaccination. The model is well designed by including both the efficacy and inefficacy of vaccinations in humans. Besides calculating the reproduction number, equilibrium points and the feasibility region are also determined. Stability analysis for the proposed model around equilibrium points is discussed. Fixed-point theory is employed to identify the singularity of the solution. Adomian decomposition and Laplace integral transformation are combined to obtain the solution. We present the solutions graphically to analyze the contributions of the disease dynamics based on different values of the fractional order. This study seeks an in-depth understanding of COVID-19 transmission to improve health outcomes.
AMS Classification:
34A08; 34D20; 65P99
1. Introduction
The World Health Organization issued a public health emergency of international concern on 30 January 2020 and a pandemic alert in March 2020 in response to the rapid and extensive spread of Coronavirus Disease 2019. Initially, the disease turned out to be an epidemic in mainland China first hitting Wuhan, in the province of Hubei [1]. India had the second-highest confirmed cases in the world. The direct transmission of SARS-CoV-2 was conclusively proven by clinical evidence in January 2020 [2]. Four consecutive lockdowns came into effect in India as a preventive measure. In the absence of vaccines, social distancing serves as the best control measure against COVID-19 [3].
As a part of the vaccination program, India has established a NEGVAC (National Expert Group on Vaccine Administration for COVID-19) committee to develop guidelines for the COVID-19 vaccine administration [4]. There have been vaccination campaigns conducted around the world to combat COVID-19. Several types of vaccines are available for COVID-19 [5]. Furthermore, India has exported 35,793,000 doses of vaccine internationally (commercial exports). Innovative technologies are tested during the development of vaccines to determine if they work. Vaccine development, which is dependent on public approval, determines the effectiveness of the vaccination program based on perception and beliefs surrounding the vaccine [6]. In addition, a significant portion of the population remains uncertain about the vaccine. The perception of the vaccine among people may change with the advent of awareness programs and the improvement of vaccine outcomes [7].
Fractional-order differential equations are the most effective tool for studying biological and engineering systems. Several fractional-order derivatives comprise numerical models of physical and biological systems [8,9]. There are numerous motivations to employ fractional order, but the main focus is on dealing with the memory dynamics evident in many biological systems. Differential equations derived using the fractional derivative have several applications to analyze various infectious disease transmission dynamics such as HIV/AIDS, TB, and others [10].
The results in [11] indicate that even in the absence of social distancing, only vaccination to people can significantly reduce the overall infected population. Other approaches related to vaccination strategies have been considered, for example, in [12]. Some fractional models have been considered [13] to derive the optimal control of COVID-19 transmission. In [14], the authors proposed the fraction model and dynamics of COVID-19 and numerical simulations are performed using Laguerre collocation technique. In [15], a generalized fractional-order SEIR model is proposed. Specifically, the paper shows that, according to real data from the USA, the considered fractional model has a good prediction ability for the epidemic trend in the next two weeks. In [16], numerical simulations of fractional-order modeling of COVID-19 in the case of Wuhan (China) were carried out. In particular, the Adams–Bashforth numerical scheme was used in simulations of the Caputo–Fabrizio fractional-order derivative.
The aim of this paper is to develop the fractional-order model to describe the dynamics of COVID-19 using the Caputo–Fabrizio fractional derivative. The main contribution of this paper is to prove the existence and uniqueness of the solution using fixed-point theory. In order to reduce infection in a community, this paper examines the dynamic behavior of the system with vaccination. A summary of the paper’s content is as follows. We formulate an SVEITR model for COVID-19 in Section 2. We calculate equilibrium points and the reproduction number in Section 3. Section 4 discusses the existence and uniqueness of the fractional system solution. The Adomian decomposition method with Laplace integral transform is employed to obtain the analytical solution whose graphical results appear in Section 5 and Section 6.
2. Mathematical Model
Let us consider the mathematical model for understanding the dynamics of COVID-19 spread with vaccination. The model is formulated based on assumptions involving six compartments: and represent the people who are likely to contract the infection and are vaccinated, is the exposed population, is the infected population, is individuals who are receiving treatment after infection, is the recovered population. The total population is . It is formulated as:
where : the recruitment rate of individuals susceptible to the disease, : the rate at which infectious agents transfer from exposed individuals to susceptible humans,
: the rate at which infection is transferred from infected persons to susceptible persons via objects or surfaces used by them,
: natural death rate,
: the removal rate of the treatment population to susceptible population,
: the rate of the exposed population getting infected,
: the rate of individuals receiving treatment after knowing symptoms,
d: disease-induced mortality rate,
: recovery rate,
: the removal rate of the treatment population to vaccinated population,
: vaccination rate,
: rate of vaccine inefficacy in people.
With as the initial conditions.
In the model, we apply the definitions of fractional derivatives [17]. The fractional derivatives and integrals are incorporated, and the time derivative takes the form of a Caputo–Fabrizio (CF) fractional derivative [18]. For and , the Caputo–Fabrizio derivative of fractional order for g is given by
where is a normalization function that depends on n and . Hence, we introduce an auxiliary parameter called for [19,20,21]. The transmission model is as follows:
with the same initial conditions.
3. Model Analysis
Theorem 1.
The closed set Ω is positively invariant under fractional system (2).
Proof.
From (2), we obtain
After some calculations, we have
Thus, then , . Therefore, the closed set is positively invariant. □
3.1. Equilibria Points
By equating each relationship in the fractional system with zero, this section determines the equilibrium points of the fractional system. The disease-free equilibrium exists when there is no disease; it is denoted by , where .
The endemic equilibrium is denoted by , , where
where .
3.2. Basic Reproduction Number
4. Stability of the System
This section examines the stability of the system.
Theorem 2.
The equilibrium point is locally asymptotically stable in the system (2).
Proof.
The reduced matrix of the system (2) is
The eigenvalues of the above matrix are negative. The remaining eigenvalues of the matrix obtained by the equation where
Hence the model (2) is locally asymptotically stable if . □
Theorem 3.
The equilibrium point is globally asymptotically stable in the system (2).
Proof.
Consider the Lyapunov function,
Therefore, . Hence proved. □
5. A Fractional Approach
The unique solution of the fractional system (2) is investigated and becomes
Using the fractional derivative theorem, we obtain
Theorem 4.
The kernel satisfies the Lipschitz condition and contraction if the holds.
Proof.
Let us consider for S and ,
Hence, where is bounded function. Hence,
Therefore, if the is a contraction and the Lipschitz condition is obtained. Similarly, we obtain the Lipschitz condition for all the relations.
where are all bounded functions if then are contractions.
Consider the following recursive forms, according to the system (5),
with the initial conditions.
Similarly, we obtain,
This can be written as
Next, we must prove the existence of the solution. □
Theorem 5.
The fractional system (2) gives the system of solutions if there exist such that i.
Proof.
We assume
where
The above equation can be obtained by repeating the method.
We obtain as r tends to ∞. Hence, this can be obtained for all functions. This completes the proof. □
Therefore,
Hence, . Therefore, . Similarly, we can obtain this result for all the equations in the model.
6. Numerical Simulation
An approximate method for the solution of the nonlinear problem is called the Adomian decomposition method [23] and provides solutions for both ordinary and fractional differential equations [24]. To obtain results, Laplace Transform is used for model (2)
The series of the solution is considered to be [25],
where is used as Adomian polynomial. After some manipulation, the system (11) becomes
After some manipulation, we obtain
The solution can be expressed as
7. Graphical Discussion

Table 1.
Values of the parameters for the fractional model (2).
Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 show the approximate solutions of various population compartments corresponding to different fractional orders. The density of the susceptible population is decreasing according to the corresponding fractional-order depicted in Figure 1. In Figure 2, the number of the vaccinated population was rapidly increasing. According to Figure 3 and Figure 4, the infected population density increases following exposure to infection. Figure 5 and Figure 6 show that the total number of people in treatment is on the rise, as many people have been cured of the disease through proper treatment, resulting in an increasing number of people in recovery.
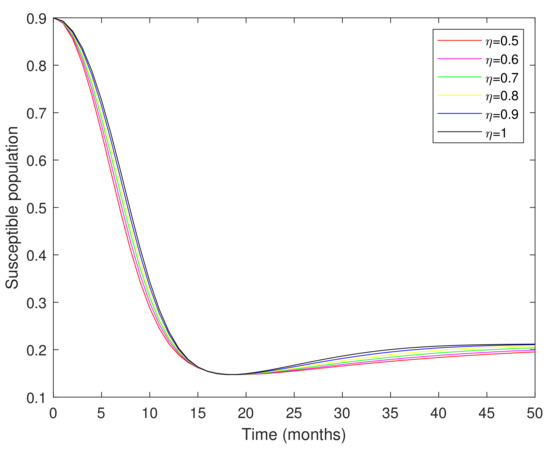
Figure 1.
Graphical representation of the susceptible population corresponding to different fractional orders.
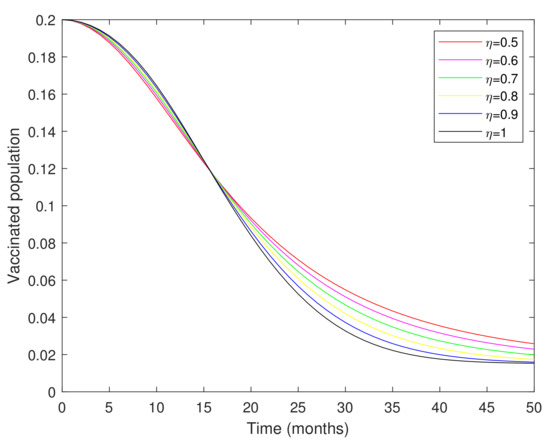
Figure 2.
Graphical representation of the vaccinated population corresponding to different fractional orders.
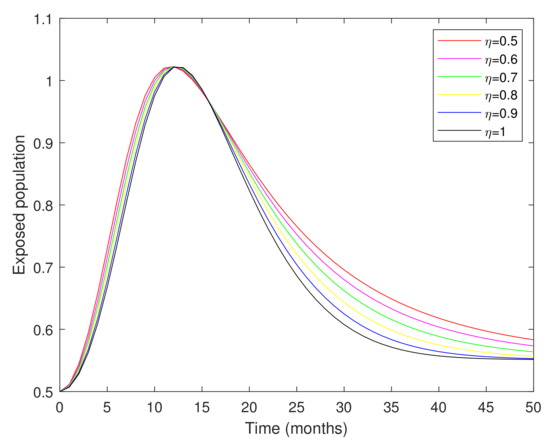
Figure 3.
Graphical representation of the exposed population corresponding to different fractional orders.
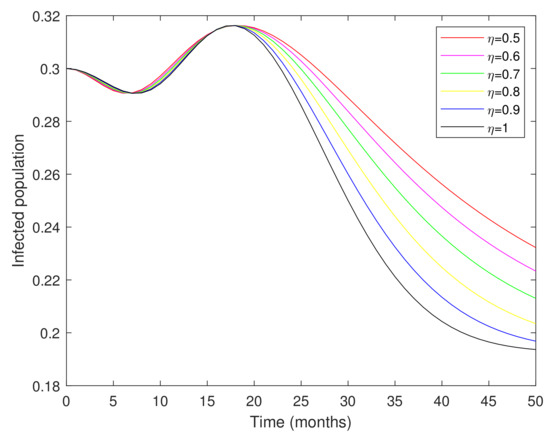
Figure 4.
Graphical representation of the infected population corresponding to different fractional orders.
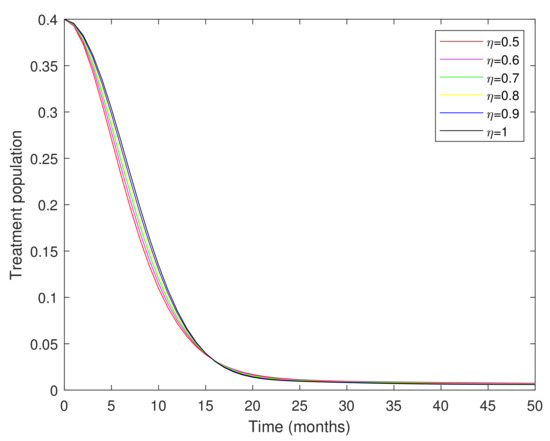
Figure 5.
Graphical representation of the treatment population corresponding to different fractional orders.
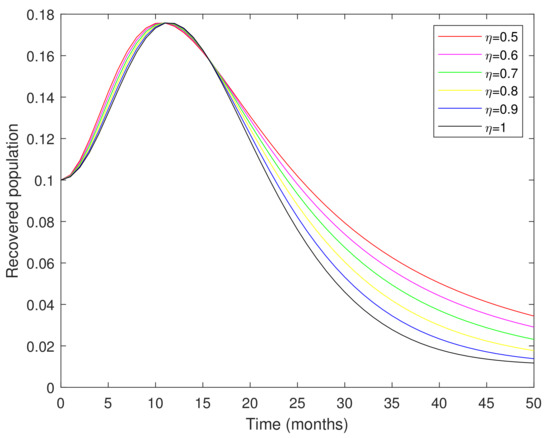
Figure 6.
Graphical representation of the recovered population corresponding to different fractional orders.
8. Conclusions
This paper presents an SVEITR COVID-19 model with a fractional-order derivative of Caputo–Fabrizio. We compute the reproduction number, equilibrium points, and feasible region. Fixed-point theory is applied to show that a unique solution exists for the fractional system. The Adomian method coupled with Laplace integral transform yields the approximate solution of the proposed model. The graphical presentation provides a better understanding of the dynamics, and the proposed technique compares favorably with the other method in terms of its speed of convergence. At the same time, COVID-19 is persistent and largely uncontrollable due to the continual change in the spread of information, a factor which will be explored in more depth in the future by bifurcation analysis, which combines fractional derivatives with optimal control. In future work, this model may be modified by introducing control variables to analyze optimal control strategies.
Author Contributions
All authors contribute equally to this article. All authors have read and agreed to the published version of the manuscript.
Funding
The research of JJ Nieto has been partially supported by the Agencia Estatal de Investigación (AEI) of Spain under Grant PID2020-113275GB-I00, cofinanced by the European Community fund FEDER, as well as Xunta de Galicia grant ED431C 2019/02 for Competitive Reference Research Groups (2019–2022).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Huang, C. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet 2020, 395, 497–506. [Google Scholar] [CrossRef]
- Li, Q. Early transmission dynamics in Wuhan, China of novel coronavirus-infected pneumonia. N. Engl. J. Med. 2020, 382, 1199–1207. [Google Scholar] [CrossRef] [PubMed]
- Laxminarayan, R.; Jameel, S. India’s Battle against COVID-19: Progress and Challenges. Am. Soc. Trop. Med. Hyg. 2020, 103, 1343–1347. [Google Scholar] [CrossRef] [PubMed]
- Vaccine Supply; Ministry of External Affairs, Government of India: New Delhi, India, 2021. Available online: https://www.mea.gov.in/vaccine-supply.htm (accessed on 28 May 2022).
- Sharma, J.; Varshney, S.K. India’s vaccine diplomacy aids global access to COVID-19 jabs. Nat. India 2021. Available online: https://www.nature.com/articles/nindia.2021.31 (accessed on 28 May 2022).
- Bhargava, R.; Jain, G. COVID-19 Vaccination drive: Impact on the acceptance of vaccine among the general population of India. J. Manag. Res. Anal. 2021, 8, 2, 61–69. [Google Scholar] [CrossRef]
- Das, B.; Padhye, A. Public Perception and Potential Acceptance of COVID-19 Vaccine in India. Public Health Rev.-Int. J. Public Health Res. 2021, 8, 2. [Google Scholar] [CrossRef]
- Baleanu, D.; Ghassabzade, F.A.; Nieto, J.J.; Jajarmi, A. On a new and generalized fractional model for a real cholera outbreak. Alex. Eng. J. 2022, 61, 9175–9186. [Google Scholar] [CrossRef]
- Ndairou, F.; Area, I.; Nieto, J.J.; Silva, C.J.; Torres, D.F.M. Fractional model of COVID-19 applied to Galicia, Spain and Portugal. Chaos Solitons Fractals 2021, 144, 110652. [Google Scholar] [CrossRef]
- Bushnaq, S.; Khan, S.A. Mathematical analysis of HIV/AIDS infection model with Caputo-Fabrizio fractional derivative. Cogent Math. Stat. 2018, 5, 1. [Google Scholar] [CrossRef]
- Saha, S.; Samanta, G.; Nieto, J.J. Impact of optimal vaccination and social distancing on COVID-19 pandemic. Math. Comput. Simul. 2022, 200, 285–314. [Google Scholar] [CrossRef]
- Couras, J.; Area, I.; Nieto, J.J.; Silva, C.J.; Torres, D.F.M. Optimal Control of Vaccination and Plasma Transfusion with Potential Usefulness for Covid-19. In Infosys Science Foundation Series in Mathematical Sciences; Springer: Singapore, 2021; pp. 509–525. [Google Scholar]
- Rosa, S.; Torres, D.F.M. Fractional Modelling and Optimal Control of COVID-19. Transm. Port. Axioms 2022, 11, 170. [Google Scholar] [CrossRef]
- Pandey, P.; Chu, Y. A novel fractional mathematical model of COVID-19 epidemic considering quarantine and latent time. Results Phys. 2021, 26, e104286. [Google Scholar] [CrossRef]
- Punj, V. COVID Vaccination Coverage Reaches 40.44 Cr in India; 46 Lakhs Doses Given Today; Mint: Mountain View, CA, USA, 2021. [Google Scholar]
- Xu, C.; Yu, Y.; Chen, Y.; Lu, Z. Forecast analysis of the epidemics trend of COVID-19 in the USA by a generalized fractional-order SEIR model. Nonlin. Dyn. 2020, 101, 1621–1634. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A. Fractional Integrals and Derivatives: Theory and Applications; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar]
- Caputo, M.; Fabrizio, M. On the Singular Kernels for Fractional Derivative, Some applications to Partial Differential Equations. Prog. Fract. Differ. Appl. 2021, 7, 79–82. [Google Scholar]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Losada, J.; Nieto, J.J. Properties of a new fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 87–92. [Google Scholar]
- Losada, J.; Nieto, J.J. Fractional Integral Associated to Fractional Derivatives with Nonsingular Kernels. Prog. Fract. Differ. Appl. 2021, 7, 137–143. [Google Scholar]
- Driessche, P.V.; Watmough, J. Reproduction numbers and subthreshold endemic equilibria for compartmental models of disease transmission. Math Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Suheil, A.; Khuri, A. Laplace decomposition algorithm applied to a class of nonlinear differential equations. J. Appl. Math. 2001, 1, 141–155. [Google Scholar]
- Kiymaz, O. An algorithm for solving initial value problems using Laplace Adomian decomposition method. Appl. Math. Sci. 2009, 3, 30, 1453–1459. [Google Scholar]
- Yadav, R.P.; Verma, R. A numerical simulation of fractional order mathematical modeling of COVID-19 disease in case of Wuhan China. Chaos Solitons Fract. 2020, 140, 110124. [Google Scholar] [CrossRef]
- Mandal, M.; Jana, S. A model based study on the dynamics of COVID-19: Prediction and Control. Chaos Solitons Fractals 2020, 136, 109889. [Google Scholar] [CrossRef] [PubMed]
- Vekumar, L.M.; Pandi-Perumal, S.R. Strategy for COVID-19 vaccination in India: The country with the second highest population and number of cases. NPJ Vaccines 2021, 6, 60. [Google Scholar]
- Malhotra, V.; Basu, S. Outcomes among 10,314 hospitalized COVID-19 patients at a tertiary care government hospital in Delhi, India. J. Med. Virol. 2021, 93, 4553–4558. [Google Scholar] [CrossRef] [PubMed]
- Chances of Hospitalization Only 0.6 Percentage after COVID Vaccination, India Today. 2021. Available online: https://www.indiatoday.in/coronavirus-outbreak/story/chances-of-hospitalisation-covid-vaccination-study-1803108-2021-05-16 (accessed on 29 May 2022).
- Jacob Koshy, Coronavirus|One in Five Indians Have Been Exposed To Coronavirus, ICMR Survey Finds, The Hindu. 2021. Available online: https://www.thehindu.com/news/national/coronavirus-one-in-five-indians-have-been-exposed-to-coronavirus-icmr-survey-finds/article61755028.ece (accessed on 29 May 2022).
- Chatterjee, K.; Chatterjee, K. Healthcare impact of COVID-19 epidemic in India: A Stochastic Mathematical model. Med. J. Armed Forces India 2020, 76, 147–155. [Google Scholar] [CrossRef] [PubMed]
- Kaul, R. COVID-19:7.3 Percentage of Active Cases in ICU’s Are on Ventilators, Says Centre. Hindusthan Times. 2021. Available online: https://www.hindustantimes.com/india-news/73-of-active-cases-in-icus-or-on-ventilators-says-ministry-101617995175222.html (accessed on 29 May 2022).
- COVID-19 in India: ’Recovery down to 91.22 Percentage Fatality Rate at 1.28 Percentage Says Health Minister Harsh Vardhan, Times Now Digital. 2021. Available online: https://www.timesnownews.com/india/article/covid-19-in-india-recovery-down-to-91-22-percent-fatality-rate-at-1-28-percent-health-minister-harsh-vardhan/742980 (accessed on 29 May 2022).
- Nidhi Sharma. India’s Fatality Rate Rises to 1.2 Percentage from 1 Percentage in over 3 Weeks. The Economic Times. 2021. Available online: https://economictimes.indiatimes.com/news/india/fatality-rate-rises-to-1-2-from-1-in-over-3-weeks/articleshow/83125217.cms (accessed on 29 May 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).