Group Acceptance Sampling Plan Based on New Compounded Three-Parameter Weibull Model
Abstract
:1. Introduction
2. Complementary Bell-G with Motivation
Complementary Bell Weibull Distribution
3. Designing of GASP under CBellW Model
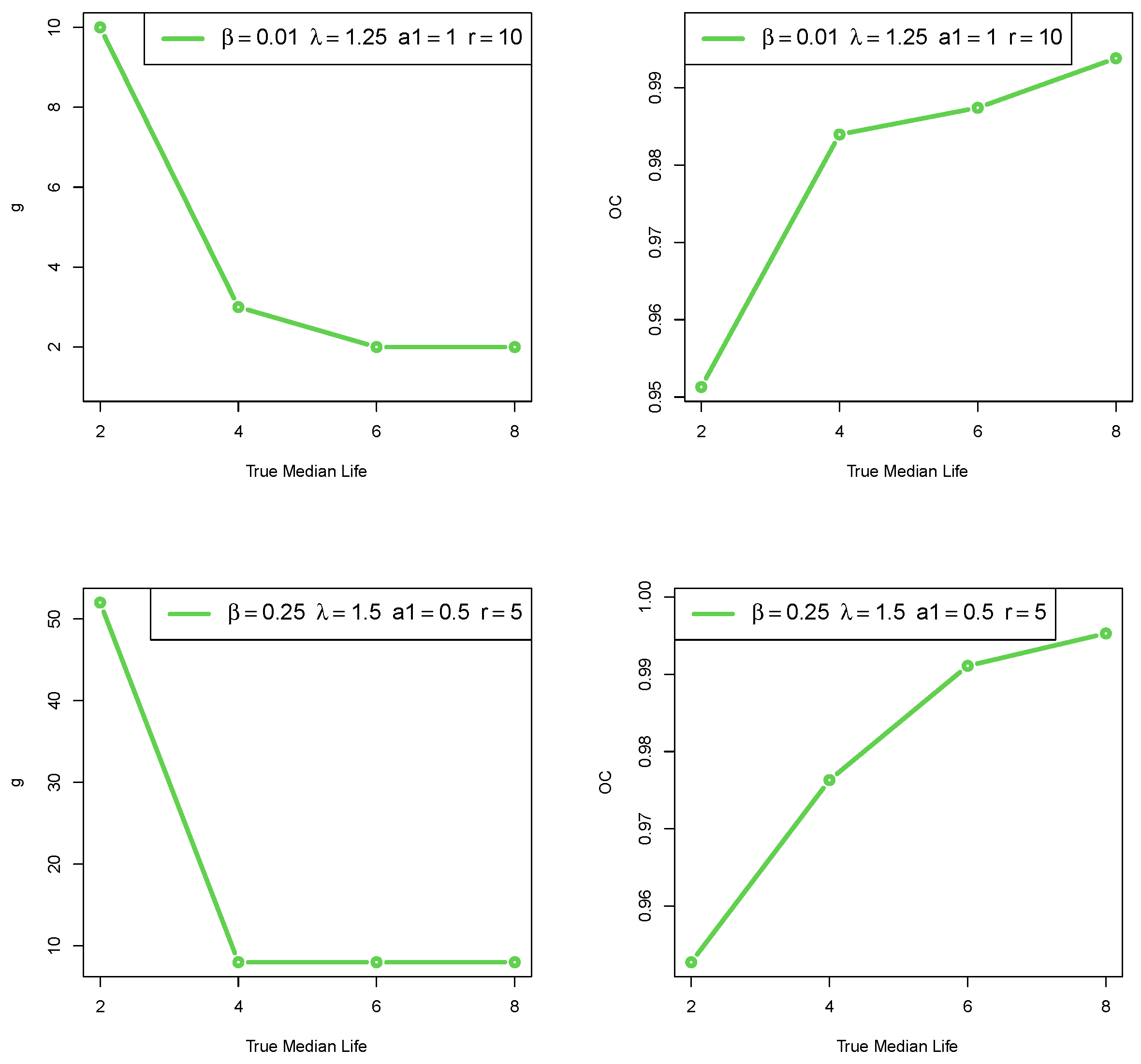
4. Discussion with Illustrative Examples
| 2 | 4 | 6 | 8 | |
| g | 10 | 3 | 2 | 2 |
| c | 5 | 3 | 2 | 2 |
| 0.9513 | 0.9839 | 0.9874 | 0.9938 |
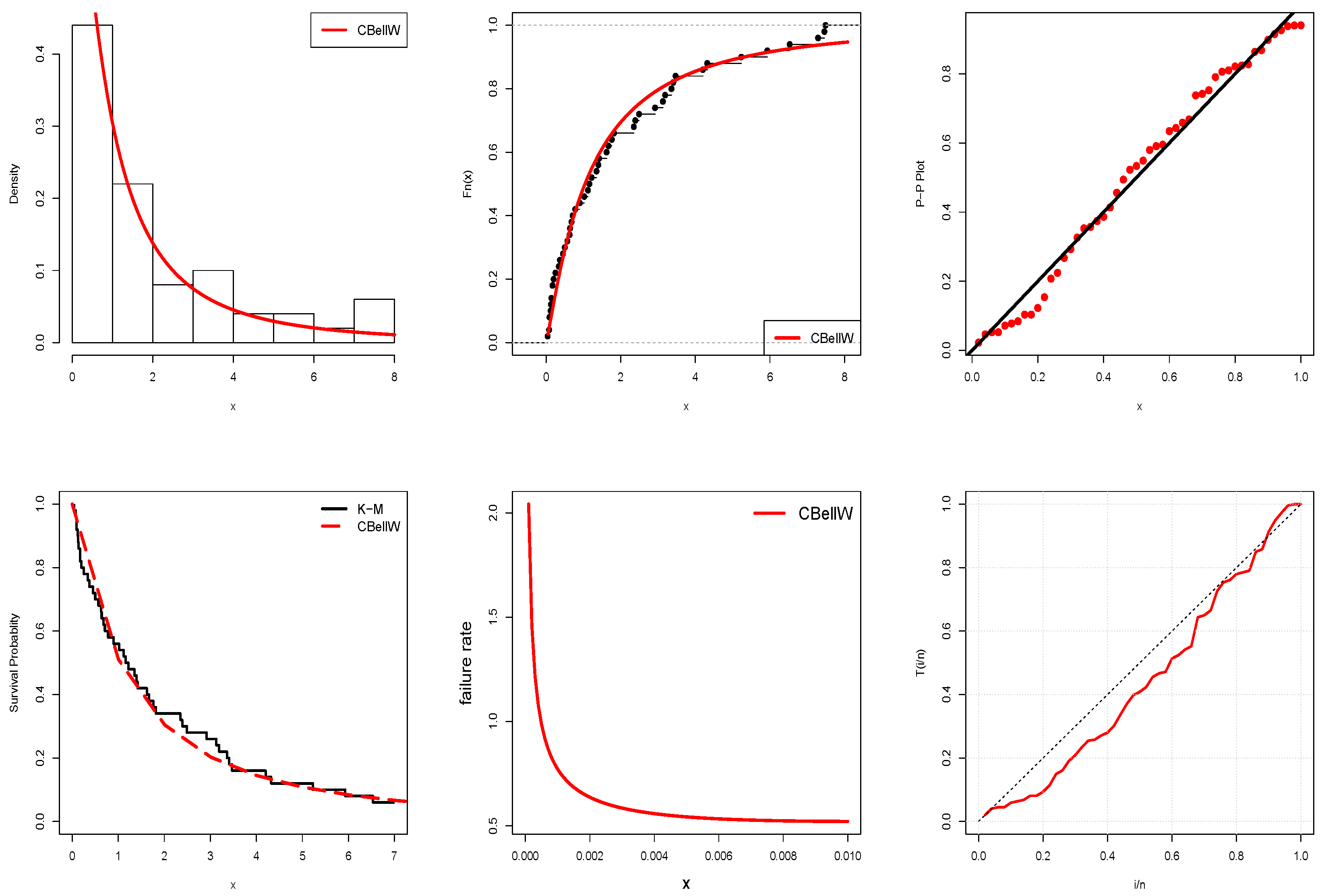
5. Application
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jun, C.H.; Balamurali, S.; Lee, S.H. Variables sampling plans for Weibull distributed lifetimes under sudden death testing. IEEE Trans. Reliab. 2006, 55, 53–58. [Google Scholar]
- Tripathi, H.; Dey, S.; Saha, M. Double and group acceptance sampling plan for truncated life test based on inverse log-logistic distribution. J. Appl. Stat. 2021, 48, 1227–1242. [Google Scholar] [CrossRef] [PubMed]
- Suseela, V.B.; Rao, B.S. Group Acceptance Sampling Plans For Life Tests Based On Exponentiated Inverted Weibull Distribution. Eur. J. Mol. Clin. Med. 2021, 8, 2713–2720. [Google Scholar]
- Yigiter, A.; Hamurkaroglu, C.; Danacloglu, N. Group acceptance sampling plans based on time truncated life tests for compound Weibull–exponential distribution. Int. J. Qual. Reliab. Manag. 2021. [Google Scholar] [CrossRef]
- Almarashi, A.M.; Khan, K.; Chesneau, C.; Jamal, F. Group Acceptance Sampling Plan Using Marshall–Olkin Kumaraswamy Exponential (MOKw–E) Distribution. Processes 2021, 9, 1066. [Google Scholar] [CrossRef]
- Aslam, M.; Kundu, D.; Jun, C.H.; Ahmad, M. Time truncated group acceptance sampling plans for generalized exponential distribution. J. Test. Eval. 2011, 39, 671–677. [Google Scholar] [CrossRef]
- Aslam, M.; Jun, C.H.; Lio, Y.L.; Ahmad, M.; Rasool, M. Group acceptance sampling plans for resubmitted lots under Burr-type XII distributions. J. Chin. Inst. Ind. Eng. 2011, 28, 606–615. [Google Scholar] [CrossRef]
- Aslam, M.; Ahmad, M.; Mughal, A.R. Group acceptance sampling plan for lifetime data using generalized Pareto distribution. Pak. J. Commer. Soc. Sci. (PJCSS) 2010, 4, 185–193. [Google Scholar]
- Castellares, F.; Ferrari, S.L.; Lemonte, A.J. On the bell distribution and its associated regression model for count data. Appl. Math. Model. 2018, 56, 172–185. [Google Scholar] [CrossRef]
- Tahir, M.H.; Cordeiro, G.M. Compounding of distributions: A survey and new generalized classes. J. Stat. Dist. Applic. 2016, 3, 13. [Google Scholar] [CrossRef]
- Maurya, S.K.; Nadarajah, S. Poisson generated family of distributions: A review. Sankhya B 2020, 83, 484–540. [Google Scholar] [CrossRef]
- Basu, A.P.; Klein, J.P. Some recent results in competing risks theory. Lect. Notes–Monogr. Ser. 1982, 2, 216–229. [Google Scholar]
- Khan, K.; Alqarni, A. A group acceptance sampling plan using mean lifetime as a quality parameter for inverse Weibull distribution. Adv. Appl. Stat. 2020, 649, 237–249. [Google Scholar] [CrossRef]
- Srinivasa, R.G. A group acceptance sampling plans for lifetimes following a generalized exponential distribution. Stochastics Qual. Control 2009, 24, 75–85. [Google Scholar] [CrossRef]
- Rao, G.S. A group acceptance sampling plans based on truncated life tests for Marshall–Olkin extended Lomax distribution. Electron. J. Appl. Stat. Anal. 2009, 3, 18–27. [Google Scholar] [CrossRef]
- Singh, S.; Tripathi, Y.M. Acceptance sampling plans for inverse Weibull distribution based on truncated life test. Life Cycle Reliab. Saf. Eng. 2017, 6, 169–178. [Google Scholar] [CrossRef]
- Aslam, M.; Shahbaz, M.Q. Economic reliability test plans using the generalized exponential distribution. J. Stat. 2007, 14, 53–60. [Google Scholar]
- Gomez–Deniz, E.; Iriarte, Y.A.; Gomez, Y.M.; Barranco–Chamorro, I.; Gomez, H.W. Statistical Inference for a General Family of Modified Exponentiated Distributions. Mathematics 2021, 9, 3069. [Google Scholar] [CrossRef]
- Fayomi, A.; Tahir, M.H.; Algarni, A.; Imran, M.; Jamal, F. A New Useful Exponential Model with Applications to Quality Control and Actuarial Data. Comput. Intell. Neurosci. 2022, 2022, 2489998. [Google Scholar] [CrossRef] [PubMed]

| 0.25 | 2 | 247 | 3 | 0.9670 | 7 | 3 | 0.9614 | 51 | 4 | 0.9803 | 3 | 5 | 0.9851 |
| 4 | 5 | 1 | 0.9548 | 1 | 1 | 0.9537 | 4 | 2 | 0.9876 | 1 | 2 | 0.9680 | |
| 6 | 5 | 1 | 0.9815 | 1 | 1 | 0.9823 | 2 | 1 | 0.9688 | 1 | 2 | 0.9919 | |
| 8 | 5 | 1 | 0.9900 | 1 | 1 | 0.9908 | 2 | 1 | 0.9828 | 1 | 2 | 0.9627 | |
| 0.1 | 2 | – | – | – | 73 | 4 | 0.9817 | 84 | 4 | 0.9678 | 5 | 5 | 0.9753 |
| 4 | 44 | 2 | 0.9872 | 4 | 2 | 0.986 | 7 | 2 | 0.9784 | 1 | 2 | 0.9680 | |
| 6 | 9 | 1 | 0.9669 | 2 | 1 | 0.9649 | 3 | 1 | 0.9536 | 1 | 2 | 0.9919 | |
| 8 | 9 | 1 | 0.9820 | 2 | 1 | 0.9817 | 3 | 1 | 0.9743 | 1 | 1 | 0.9627 | |
| 0.05 | 2 | – | – | – | 95 | 4 | 0.9763 | 110 | 4 | 0.958 | 7 | 5 | 0.9656 |
| 4 | 58 | 2 | 0.9832 | 5 | 2 | 0.9825 | 9 | 2 | 0.9723 | 2 | 3 | 0.9916 | |
| 6 | 11 | 1 | 0.9597 | 2 | 1 | 0.9649 | 9 | 2 | 0.9926 | 2 | 2 | 0.9839 | |
| 8 | 11 | 1 | 0.9781 | 2 | 1 | 0.9817 | 4 | 1 | 0.9659 | 1 | 1 | 0.9627 | |
| 0.01 | 2 | – | – | – | 146 | 4 | 0.9638 | 992 | 5 | 0.9771 | 10 | 5 | 0.9513 |
| 4 | 88 | 2 | 0.9746 | 7 | 2 | 0.9756 | 14 | 2 | 0.9572 | 3 | 3 | 0.9839 | |
| 6 | 88 | 2 | 0.9935 | 7 | 2 | 0.9944 | 14 | 2 | 0.9885 | 2 | 2 | 0.9874 | |
| 8 | 17 | 1 | 0.9663 | 3 | 1 | 0.9727 | 14 | 2 | 0.9954 | 2 | 2 | 0.9938 | |
| 0.25 | 2 | 52 | 2 | 0.9527 | 7 | 3 | 0.9845 | 27 | 3 | 0.9792 | 2 | 4 | 0.9803 |
| 4 | 8 | 1 | 0.9763 | 1 | 1 | 0.9804 | 3 | 1 | 0.9624 | 1 | 2 | 0.9906 | |
| 6 | 8 | 1 | 0.9911 | 1 | 1 | 0.9937 | 3 | 1 | 0.9855 | 1 | 1 | 0.9739 | |
| 8 | 8 | 1 | 0.9953 | 1 | 1 | 0.9970 | 3 | 1 | 0.9923 | 1 | 1 | 0.9873 | |
| 0.1 | 2 | – | – | – | 12 | 3 | 0.9735 | 45 | 3 | 0.9656 | 3 | 4 | 0.9706 |
| 4 | 13 | 1 | 0.9618 | 2 | 1 | 0.9612 | 4 | 1 | 0.9502 | 1 | 2 | 0.9906 | |
| 6 | 13 | 1 | 0.9855 | 2 | 1 | 0.9874 | 4 | 1 | 0.9807 | 1 | 1 | 0.9739 | |
| 8 | 13 | 1 | 0.9924 | 2 | 1 | 0.9940 | 4 | 1 | 0.9898 | 1 | 1 | 0.9873 | |
| 0.05 | 2 | – | – | – | 15 | 3 | 0.967 | 59 | 3 | 0.9552 | 4 | 4 | 0.961 |
| 4 | 17 | 1 | 0.9504 | 2 | 1 | 0.9612 | 16 | 2 | 0.9905 | 2 | 2 | 0.9813 | |
| 6 | 17 | 1 | 0.9811 | 2 | 1 | 0.9874 | 5 | 1 | 0.9759 | 1 | 1 | 0.9739 | |
| 8 | 17 | 1 | 0.9901 | 2 | 1 | 0.9940 | 5 | 1 | 0.9873 | 1 | 1 | 0.9873 | |
| 0.01 | 2 | – | – | – | 146 | 4 | 0.9889 | 463 | 4 | 0.9796 | 5 | 4 | 0.9515 |
| 4 | 171 | 1 | 0.9910 | 7 | 2 | 0.9935 | 24 | 2 | 0.9858 | 2 | 2 | 0.9813 | |
| 6 | 26 | 1 | 0.9713 | 3 | 1 | 0.9812 | 8 | 1 | 0.9617 | 2 | 2 | 0.9964 | |
| 8 | 26 | 1 | 0.9849 | 3 | 1 | 0.9911 | 8 | 1 | 0.9797 | 2 | 1 | 0.9748 | |
| Data-1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1.120 | 0.170 | 0.640 | 4.320 | 1.220 | 0.370 | 1.160 | 1.420 | 0.090 | 1.670 |
| 0.130 | 0.250 | 0.080 | 0.040 | 2.350 | 0.200 | 0.780 | 0.340 | 1.020 | 0.170 |
| 1.760 | 2.390 | 0.500 | 1.350 | 3.360 | 0.450 | 0.900 | 2.920 | 6.530 | 1.620 |
| 7.460 | 3.190 | 2.490 | 1.400 | 7.490 | 0.570 | 0.140 | 0.630 | 5.230 | 0.710 |
| 0.680 | 0.120 | 0.090 | 3.470 | 5.930 | 1.820 | 4.200 | 7.290 | 3.130 | 3.410 |
| Descriptive Summary | |||||||||
| n | Min | Max | Q1 | Q3 | Mean | Median | SD | S | K |
| 50 | 0.04 | 7.49 | 0.39 | 3.078 | 1.975 | 1.19 | 2.115767 | 1.3253 | 0.8032 |
| Data-2 | |||||||||
| 0.0251 | 0.0886 | 0.0891 | 0.2501 | 0.3113 | 0.3451 | 0.4763 | 0.565 | 0.5671 | 0.6566 |
| 0.6748 | 0.6751 | 0.6753 | 0.7696 | 0.8375 | 0.8391 | 0.8425 | 0.8645 | 0.8851 | 0.9113 |
| 0.912 | 0.9836 | 1.0483 | 1.0596 | 1.0773 | 1.1733 | 1.257 | 1.2766 | 1.2985 | 1.3211 |
| 1.3503 | 1.3551 | 1.4595 | 1.488 | 1.5728 | 1.5733 | 1.7083 | 1.7263 | 1.746 | 1.763 |
| 1.7746 | 1.8275 | 1.8375 | 1.8503 | 1.8808 | 1.8878 | 1.8881 | 1.9316 | 1.9558 | 2.0048 |
| 2.0408 | 2.0903 | 2.1093 | 2.133 | 2.21 | 2.246 | 2.2878 | 2.3203 | 2.347 | 2.3513 |
| 2.4951 | 2.526 | 2.9911 | 3.0256 | 3.2678 | 3.4045 | 3.4846 | 3.7433 | 3.7455 | 3.9143 |
| 4.8073 | 5.4005 | 5.4435 | 5.5295 | 6.5541 | 9.096 | ||||
| Descriptive Summary | |||||||||
| n | Min | Max | Q1 | Q3 | Mean | Median | SD | S | K |
| 76 | 0.0251 | 9.096 | 0.9048 | 2.2959 | 1.95924 | 1.73615 | 1.573981 | 1.97956 | 5.16079 |
| SE | SE | SE | K-S | p-Value | ||||
|---|---|---|---|---|---|---|---|---|
| Data-1 | 0.0201 | 0.0374 | 0.2916 | 0.0800 | 2.0975 | 0.4556 | 0.0776 | 0.9241 |
| Data-2 | 0.4255 | 0.2385 | 0.6734 | 0.1358 | 1.6316 | 0.3002 | 0.0834 | 0.6356 |
| 0.25 | 2 | 186 | 3 | 0.9684 | 44 | 4 | 0.984 | 38 | 4 | 0.9805 | 3 | 5 | 0.9781 |
| 4 | 5 | 1 | 0.9504 | 3 | 2 | 0.9875 | 4 | 2 | 0.9857 | 1 | 2 | 0.9626 | |
| 6 | 5 | 1 | 0.9787 | 1 | 1 | 0.9805 | 2 | 1 | 0.9642 | 1 | 2 | 0.9907 | |
| 8 | 5 | 1 | 0.9878 | 1 | 1 | 0.9899 | 2 | 1 | 0.9792 | 1 | 1 | 0.9591 | |
| 0.1 | 2 | – | – | – | 73 | 4 | 0.9735 | 62 | 4 | 0.9684 | 5 | 5 | 0.9638 |
| 4 | 36 | 2 | 0.9879 | 4 | 3 | 0.9833 | 6 | 2 | 0.9786 | 1 | 2 | 0.9626 | |
| 6 | 8 | 1 | 0.9661 | 2 | 1 | 0.9613 | 6 | 2 | 0.9939 | 1 | 2 | 0.9907 | |
| 8 | 8 | 1 | 0.9806 | 2 | 1 | 0.9798 | 3 | 1 | 0.9690 | 1 | 1 | 0.9591 | |
| 0.05 | 2 | – | – | – | 95 | 4 | 0.9657 | 81 | 4 | 0.9589 | – | – | – |
| 4 | 47 | 2 | 0.9842 | 5 | 2 | 0.9792 | 8 | 2 | 0.9716 | 2 | 3 | 0.9895 | |
| 6 | 10 | 1 | 0.9578 | 2 | 1 | 0.9613 | 8 | 2 | 0.9918 | 2 | 2 | 0.9815 | |
| 8 | 10 | 1 | 0.9758 | 2 | 1 | 0.9798 | 3 | 1 | 0.9690 | 1 | 1 | 0.9591 | |
| 0.01 | 2 | – | – | – | – | – | – | 625 | 5 | 0.978 | – | – | – |
| 4 | 72 | 2 | 0.9759 | 7 | 2 | 0.9710 | 12 | 2 | 0.9577 | 3 | 3 | 0.9815 | |
| 6 | 72 | 2 | 0.9934 | 7 | 2 | 0.9935 | 12 | 2 | 0.9878 | 2 | 2 | 0.9843 | |
| 8 | 15 | 1 | 0.9639 | 3 | 1 | 0.9699 | 12 | 2 | 0.9947 | 1 | 2 | 0.9928 | |
| 0.25 | 2 | – | – | – | – | – | – | – | – | – | – | – | – |
| 4 | 8 | 2 | 0.9668 | 7 | 3 | 0.9802 | 4 | 3 | 0.9790 | 2 | 4 | 0.9741 | |
| 6 | 8 | 2 | 0.9904 | 3 | 2 | 0.9703 | 2 | 2 | 0.9764 | 1 | 3 | 0.9845 | |
| 8 | 3 | 1 | 0.9618 | 3 | 2 | 0.9874 | 2 | 2 | 0.9898 | 1 | 2 | 0.9625 | |
| 0.1 | 2 | – | – | – | – | – | – | – | – | – | – | – | – |
| 4 | 72 | 3 | 0.9876 | 12 | 3 | 0.9662 | 6 | 3 | 0.9686 | 4 | 3 | 0.9615 | |
| 6 | 13 | 2 | 0.9845 | 4 | 2 | 0.9605 | 3 | 2 | 0.9648 | 2 | 3 | 0.9692 | |
| 8 | 13 | 2 | 0.9936 | 4 | 2 | 0.9833 | 3 | 2 | 0.9847 | 1 | 2 | 0.9725 | |
| 0.05 | 2 | – | – | – | – | – | – | – | – | – | – | – | – |
| 4 | 93 | 3 | 0.9840 | 15 | 3 | 0.9580 | 7 | 3 | 0.9635 | 7 | 5 | 0.9864 | |
| 6 | 17 | 2 | 0.9798 | 5 | 2 | 0.9509 | 4 | 2 | 0.9533 | 2 | 3 | 0.9692 | |
| 8 | 17 | 2 | 0.9917 | 5 | 2 | 0.9791 | 4 | 2 | 0.9797 | 2 | 3 | 0.9894 | |
| 0.01 | 2 | – | – | – | – | – | – | – | – | – | – | – | – |
| 4 | 143 | 3 | 0.9755 | 146 | 4 | 0.9848 | 28 | 4 | 0.9855 | 10 | 5 | 0.9806 | |
| 6 | 26 | 2 | 0.9693 | 23 | 3 | 0.9869 | 11 | 3 | 0.9882 | 3 | 3 | 0.9542 | |
| 8 | 26 | 2 | 0.9873 | 7 | 2 | 0.9709 | 5 | 2 | 0.9747 | 3 | 3 | 0.9842 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Algarni, A. Group Acceptance Sampling Plan Based on New Compounded Three-Parameter Weibull Model. Axioms 2022, 11, 438. https://doi.org/10.3390/axioms11090438
Algarni A. Group Acceptance Sampling Plan Based on New Compounded Three-Parameter Weibull Model. Axioms. 2022; 11(9):438. https://doi.org/10.3390/axioms11090438
Chicago/Turabian StyleAlgarni, Ali. 2022. "Group Acceptance Sampling Plan Based on New Compounded Three-Parameter Weibull Model" Axioms 11, no. 9: 438. https://doi.org/10.3390/axioms11090438
APA StyleAlgarni, A. (2022). Group Acceptance Sampling Plan Based on New Compounded Three-Parameter Weibull Model. Axioms, 11(9), 438. https://doi.org/10.3390/axioms11090438





