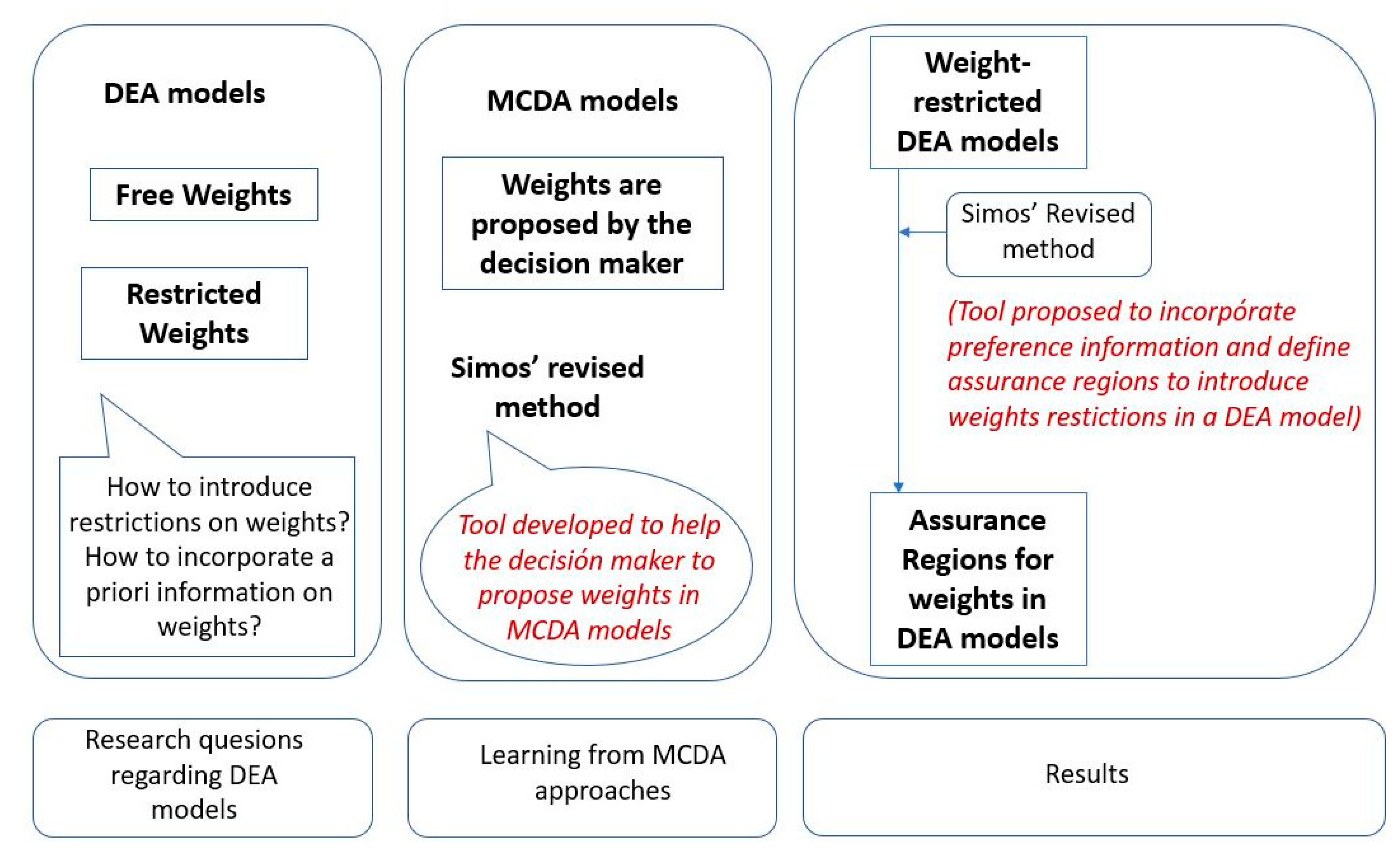
1. Introduction
The novelty of this study lies in the fact that whereas previous research has extensively applied DEA and MCDA in the fields of economics and management [
1,
2,
3], until now, it is the first time that a revised Simos’ Procedure has been used to obtain weight restrictions in a data envelopment analysis (DEA) model.
The originality of this study is to propose a new application of an intuitive approach for incorporating preference information in a weight-restricted DEA model based on MCDA methodologies.
The main target of this research is to propose an intuitive MCDA-based methodology to incorporate preference information in a weight-restricted DEA model.
Data envelopment analysis is one the most successful techniques in the field of operations research. DEA is a data-oriented approach for evaluating the relative efficiency of a homogenous set of decision-making units (DMUs).
The original DEA proposal contemplated the total freedom of variation of weights, thus putting the evaluated DMU in the best possible light.
Nevertheless, it should be noticed that this full weight flexibility leads to three main problems: weakness in discriminating power, unreasonable weight assignment, and contradiction with the prior available information (or preferences) of the decision-maker (DM).
When the number of DMUs is not large enough, compared to the number of inputs and outputs, a great number of DMUs can become efficient; that is, in these situations, DEA has low discriminating power.
As for the unreasonable weight assignment, a DMU can become efficient due to the extremely low weights of some of the inputs or outputs, meaning that these inputs or outputs are ignored in practice. Finally, the complete flexibility of weights can contradict existing prior information or expert opinions.
A usual way to restrict weight flexibility is through the introduction of weight restrictions. General references about the use of weight restrictions in DEA can be found in [
4,
5]. The most usual ways of introducing weight restrictions are absolute weight restrictions [
6], assurance regions [
7], virtual weight restrictions [
8], and cone-ratio models [
9]. Different approaches to tackle the problem of the complete flexibility of weights are using regression analysis [
10] or determining a common set of weights using an ideal decision-making unit [
11].
It is important to note that as pointed out by [
12], the introduction of weight restrictions in DEA models can constrain the problem in such a way that it becomes infeasible.
A multiple criteria decision making (MCDM) problem can be reformulated in terms of DEA by replacing DMU with alternatives, outputs with criteria to be maximized, and inputs with criteria to be minimized. These similarities between DEA and MCDM techniques have led some researchers to develop approaches that are combinations of DEA and MCDM models.
These approaches, by using the MCDM, allow for incorporating the preferences of the decision-maker through the restrictions to the weights of the criteria.
A large part of this research studies the possible contributions of the analytic hierarchy process (AHP) to establish restrictions on weights [
13] presented an analytical process, in which the lower and upper limits of the virtual weight restrictions are determined by the AHP method.
AHP is used to obtain the relative weights among the outputs for each input, where the lower and upper limits are the minimum and maximum weights reached by this output through all the inputs.
As it has been shown by [
14], another option is to integrate a DEA model with assurance regions and AHP. They considered the judgments of decision-makers who were familiar with the characteristics of the evaluated DMUs and used AHP to derive the weights of the criteria for each DM.
In that case, the maximum and minimum rates between the different weights proposed by each DM were used as the AR weights. Ref. [
15] used the judgment matrix of MACBETH (Measuring Attractiveness by a Categorical Based Evaluation Technique) to generate the weights, taking the minimum and maximum of these values as the lower and upper bounds in the virtual weight restrictions DEA model.
According to [
16], who used stability intervals based on PROMETHEE II (Preference Ranking Organization METHod for Enrichment of Evaluations) as absolute weight restrictions in DEA and the unicriterion net flow score of the PROMETHEE II matrix instead of the initial DEA evaluation matrix.
The relationship between TOPSIS (Technique for Order Preference by Similarity to the Ideal Solution) and DEA has been studied by [
17]. They constructed two hypothetical DMUs and called them “the ideal DMU” and “the nadir DMU”.
These DMUs were used as reference points to evaluate a set of information technology (IT) investment strategies, taking into account their Euclidean distance from these reference points. It should be taken into consideration that the best relative efficiency of the fuzzy ideal DMU and the worst relative efficiency of the fuzzy nadir DMU were determined and combined to rank the DMUs.
A different approach for combining DEA and TOPSIS is used by [
18].
In the first phase, DEA has been applied to shortlist the efficient DMUs having the desired characteristics (from the point of view of stakeholders) and then, the TOPSIS method is employed to rank those efficient DMUs while also identifying the best-performing DMU.
The use of used concepts from multi-attribute utility models with imprecise information in an additive DEA model has been applied by [
19]. In a first phase, they convert inputs and outputs into utility functions which are aggregated with a weighted sum. In a second phase, DMU choose the weights that minimize the difference of utility with the best DMU.
On the other hand, ref. [
20] proposed incorporating preference information in DEA by linking multiple criteria decision-making with an additive DEA model that takes into account criteria interactivity, by taking advantage of the Choquet multiple criteria preference aggregation model.
The literature review and theoretical background show a research gap that we decided to fill in this research: until now there has not been used a tool that has been exclusively designed to determine the weights for some multicriteria methods to introduce weight restrictions in DEA models.
Our paper also explores possible contributions of MCDA to DEA. The objective is to introduce weight restrictions that allow for the incorporation of the judgments of the decision-maker.
The particularity of our study is that the MCDA tool we use to build a restricted DEA is not a complete MCDA method (such as PROMETHEE) or a part of one (such as AHP or MACBETH), but a tool exclusively designed to determine the weights for some multicriteria methods.
Specifically, we use the revised Simos’ procedure [
21] to produce type I Assurance Regions for the DEA model.
The revised Simos’ procedure is used to give an appropriate value to the weights of criteria in outranking methods such as ELECTRE or PROMETHEE.
From our point of view, the advantage of this approach is that we are using a tool to think about how to incorporate a priori information about weights with a method simple enough for a DM who is not necessarily familiarized with multicriteria decision aiding or making.
This procedure is very well-adapted to contexts where several sets of weights are needed and, so, to proposing bounds to the weights.
Therefore, this study raises the following research question:
Can MCDA techniques be applied to incorporate preference information into DEA models?
A priori, the most logical answer to the above research question is the following hypothesis: The revised Simos’ method can be applied to find intervals of variation of input and output weights in a DEA model that reflect a priori information about weights.
The paper is organized as follows.
Section 2 presents data and methods, which include the data source, the basic DEA formulations, an introduction to weight restrictions with Assurance Regions in DEA models, the revised Simos’ procedure, and a subsection dedicated to explaining our proposed methodology including the proposed revised Simos’ procedure clarifying how to use the revised Simos’ procedure to obtain Type I Assurance Regions for DEA models (WR-RSP DEA).
Section 3 shows results comparison followed by a numerical example. Finally,
Section 4 is devoted to drawing some conclusions.
3. Results: Comparison and Numerical Example
In this section, we use a data set that was evaluated in the paper of [
22] to apply the methodology we have proposed in this paper.
Table 1 lists the criteria (inputs and outputs) and the normalized data used to choose the location of a solid waste management system in Oulu, Finland.
As stated in
Section 4, the first step should be to normalize the data by dividing by the mean.
The case has been discussed in [
2], as it is an application of the ELECTRE-III method to a municipal solid waste management system problem in the Oulu district of Northern Finland.
The objective was to find the most reasonable solution for waste management. The following waste treatment methods were considered: landfilling, incineration, and composting.
All methods considered were in accordance with Finnish environmental legislation. One of the targets was to recover 50% of municipal waste, which included a target for the level of recycling (30%).
The problem has been studied by [
22], who included 22 alternatives and eight criteria. The normalized data of [
22] are shown in
Table 1, and the criteria weights in [
22] are shown in
Table 2.
The alternatives were obtained by combination of the following three factors in different municipalities of Oulu: co-operation level, treatment method, and number of treatment sites.
The criteria are classified into inputs and outputs:
Inputs: Cost, Global (Global Effects), Health (Health Effects), Acidif. (Acidificative Re-leases), and Surface (Surface Water Dispersed Releases);
Outputs: Feasibility (Technical Reliability), Employees, and Resource (Resource Recovery).
Table 1.
Normalized data of [
22].
Table 1.
Normalized data of [
22].
| | INPUTS | OUTPUTS |
|---|
| | Cost | Global | Health | Acidif. | Surface | Feasibility | Employees | Resource |
|---|
| 1 | 0.8945 | 1.0657 | 1.2419 | 0.9874 | 1.3701 | 0.7120 | 0.9112 | 0.5107 |
| 2 | 1.0717 | 1.0395 | 1.1726 | 0.9874 | 1.3947 | 0.5696 | 1.1716 | 0.8670 |
| 3 | 1.2435 | 0.9267 | 1.3663 | 1.0140 | 1.2147 | 0.5696 | 1.5621 | 1.4610 |
| 4 | 0.8031 | 1.0794 | 0.8382 | 0.9883 | 0.9059 | 1.2816 | 0.6509 | 0.5107 |
| 5 | 0.9626 | 1.0264 | 0.6628 | 0.9883 | 0.8262 | 0.9968 | 0.9112 | 0.8670 |
| 6 | 1.1372 | 0.9075 | 1.0197 | 1.0173 | 0.7853 | 0.9256 | 1.1716 | 1.4941 |
| 7 | 0.7908 | 1.0817 | 0.8116 | 0.9883 | 0.8793 | 1.2816 | 0.6509 | 0.5107 |
| 8 | 0.9299 | 1.0263 | 0.6403 | 0.9883 | 0.8037 | 0.9968 | 0.9112 | 0.8670 |
| 9 | 1.1426 | 0.8997 | 1.0217 | 1.0198 | 0.7628 | 0.9256 | 1.4320 | 1.5338 |
| 10 | 0.7895 | 1.0828 | 0.7607 | 0.9883 | 0.8282 | 1.2816 | 0.5858 | 0.5107 |
| 11 | 0.9381 | 1.0264 | 0.5955 | 0.9883 | 0.7566 | 0.9968 | 0.8462 | 0.8670 |
| 12 | 1.1426 | 0.8973 | 1.0176 | 1.0206 | 0.7382 | 0.9256 | 1.1065 | 1.5602 |
| 13 | 0.8113 | 1.0808 | 1.0197 | 0.9883 | 1.1002 | 1.2816 | 0.7811 | 0.5107 |
| 14 | 0.9667 | 1.0277 | 0.8198 | 0.9883 | 1 | 0.9968 | 1.1065 | 0.8670 |
| 15 | 1.1576 | 0.9143 | 1.3215 | 1.0173 | 1.1002 | 0.9256 | 1.3018 | 1.4941 |
| 16 | 0.8236 | 1.0808 | 1.0197 | 0.9883 | 1.1002 | 1.2816 | 0.7811 | 0.5107 |
| 17 | 1.0035 | 1.0277 | 0.8198 | 0.9883 | 1 | 0.9968 | 1.1065 | 0.8670 |
| 18 | 1.1876 | 0.9143 | 1.3215 | 1.0173 | 1.1002 | 0.9256 | 1.3018 | 1.4941 |
| 19 | 0.7895 | 1.0966 | 1.0095 | 0.9899 | 1.1411 | 1.2816 | 0.4556 | 0.5107 |
| 20 | 0.9476 | 1.0354 | 0.8647 | 0.9916 | 1.0941 | 0.8544 | 1.1716 | 0.8670 |
| 21 | 1.1276 | 0.8816 | 1.3276 | 1.0264 | 1.0491 | 0.9968 | 1.0414 | 1.6594 |
| 22 | 1.3390 | 0.8816 | 1.3276 | 1.0281 | 1.0491 | 0.9968 | 1.0414 | 1.6594 |
In the paper of [
22], the weights were obtained by interviewing 113 experts (decision-makers). These weights are shown in
Table 2. In the original article [
22], all information concerning the construction of the criteria, alternatives, and the obtaining of performances and weights can be found. Minimizing criteria will be considered as inputs and maximizing criteria as outputs.
To develop the methodology proposed in this paper, and with the philosophy of considering a joint framework for DEA and multicriteria decision analysis, we used the Diviz software both for the DEA and for obtaining the weight restrictions from the revised Simos’ method. Diviz is a software for modelling, processing, and sharing algorithmic workflows in MCDA (Multicriteria Decision Aid) which has recently incorporated other tools such as DEA. Interested readers can find more information in [
27,
28].
We began by trying to reproduce, as accurately as possible, the original weights of [
22] with the revised Simos’ method. We did this separately for inputs and outputs. We begin with the inputs.
The first step was to rank the cards representing the criteria from the least important to the most important:
Next, we introduced white cards between successive criteria. The ranks of the criteria, once we introduced the white cards, were as indicated in
Table 3:
The criteria ratio weight was set at
z = 16 (the exact ratio was 16.875). Then, the weights proposed by the revised Simos’ method were as shown in
Table 4:
We can see that the values are very similar to those we wanted to simulate (i.e., those of [
22]).
As mentioned in
Section 4, we have to propose two values for the parameter
z:
zmin and
zmax. In our example, we set
zmin = 13 and
zmax = 19.
The weights proposed by the revised Simos’ method were as stated in
Table 5 and in
Table 6:
We used only the bounds for consecutive criteria (inputs). These bounds were:
It is always advisable to do a sensitivity analysis and see how the weights vary. In this case, we studied the changes when z = 11 and z = 22. The changes observed were minimal, only affecting the decimals.
Consequently, we decided to keep the above bounds with 0 decimal places. Expressing these restrictions with integer numbers also helps and simplifies the decision-maker’s thinking process. These were the final input restrictions:
Next, we generated the bounds for the outputs. As we did with the inputs, we began with the simulation of the original weights proposed by [
22]. The ranking of the outputs, from the least important to the most important, was:
After the decision-maker has established the ranking of the criteria (outputs, in this case), they are asked to introduce white cards between two successive cards (or subsets of
ex aequo cards) to represent the relative importance of two successive criteria. The ranks assigned to the criteria after this process are shown in
Table 7:
In this case, we set
z = 5 (the exact ratio was 5.2). The result that we have obtained is indicated in
Table 8:
Once we checked the similarity of the result, we set
zmin = 3 and
zmax = 7. As it is shown in
Table 9 and
Table 10, the weights resulting from the revised Simos’ method were:
The bounds for consecutive outputs were:
or, considering integer bounds:
As with the inputs, we also carried out a sensitivity analysis studying the possible changes with variation of z.
We analyzed what happened when
z = 2 and
z = 8. In this case, there were significant changes. The minimum and the maximum (integer) ratios were:
Thus, we had the assurance regions for the weights and could introduce these bounds into a CCR input-oriented DEA model.
We will now present a comparison of the results obtained with DEA depending on whether we introduce restrictions to the weights or not and which restrictions we introduce depending on the values obtained after applying the revised Simos’ method to calculate the assurance regions.:
DEA without restrictions on the weights
DEA + RSMI: DEA model with assurance regions provided by the revised Simos’ method after sensitivity analysis on inputs and outputs. That is to say,
z = 11 and
z = 22 in the Simos’ method for the inputs obtaining equations [
7] for the assurance regions for input values. For the outputs, we have
z = 2 and
z = 8 in the Simos’ method obtaining equations [
9] for the assurance regions of outputs.
DEA + RSMII: DEA model with assurance regions provided by revised Simos’ method after sensitivity analysis only on inputs and without sensitivity analysis on outputs. That means
z = 11 and
z = 22 in the Simos’ method for the inputs obtaining equations [
7] for the assurance regions for input values. While for the outputs, we have
z = 3 and
z = 7 in the Simos’ method obtaining equations [
8] for the assurance regions of outputs
We can observe that there is a large difference between the efficiency values obtained with the DEA without restrictions on the weights and the other two models where assurance regions have been set for the values of the weights. The first thing that is striking is that the unconstrained DEA model generates a large number of efficient DMUs. While the other models have only 2 or 1 efficient DMUs. The solutions of the models DEA + RSMI and DEA + RSMII are quite similar.
Finally,
Table 12 shows a comparison of the results obtained with the approach presented in this paper and the results obtained by [
16], we call this model PIIWCCR (PROMETHEE II weighted CCR), and [
15] on the same example:
Efficiencies obtained with models DEA + RSMI and DEA + RSMII and the one proposed on [
15] are similar (or at least not very different). Results obtained with our proposal (DEA + RSMI and DEA + RSMII) are better because they have greater discriminatory power (there are less efficient DMUS).
The efficiencies produced by the PIIWCCR model are significantly different from the ones obtained with the other approaches.
4. Conclusions
We have proposed, in this work, the use of the Revised Simos’ Procedure to generate assurance regions for the weights of a DEA model.
The restricted DEA model obtained showed a dramatic reduction in the number of efficient DMU’s. This improvement in the discriminatory power of the DEA is done through a set of realistic weights, in which the judgments of decision-makers have been incorporated.
The particularity of this work is that the MCDA tool we used to build the restricted DEA model is not a complete MCDA method or a part of one (as other authors have done with PROMETHEE, AHP, or MACBETH), but is a tool exclusively designed to determine the weights for some multicriteria methods. From our point of view, the advantage of this approach is that we are using a tool to think about how to incorporate a priori information about weights with a method which is simple enough for a DM not necessarily familiarized with decision-making or assistance.
The procedure is very well-adapted to contexts where several sets of weights are needed and, so, to propose bounds on the weights.
The method was tested on a classical example presented by [
22], and the results were compared with those obtained by other authors on the same example. The use of the Revised Simos’ Procedure to obtain weight restrictions for a DEA model demonstrated improved discrimination power, much greater than that of the other proposed approaches, while allowing for the incorporation of the judgments of decision-makers and working with realistic weights.
The improved theoretical foundations presented in this research, have proven to be useful to be applied to the specific case of study of choosing a solid waste management system using multicriteria decision analysis [
22]. As in the previous case study, the theoretical result proposed in this paper, based on using the Revised Simos’ Procedure to obtain weight restrictions in a Data Envelopment Analysis model, is suitable to be applied in the field of economics and management, being an intuitive and simple enough method for decision-makers who are not familiar with working with DEA models or multicriteria decision analysis.
Therefore, our theoretical contribution opens new avenues of research in the decision support systems in general, and more specifically in the area of economics and management decision support systems in particular.