Mathematical Analysis for the Evaluation of Settlement and Load-Bearing Capacity of a Soil Base Adjacent to an Excavation Pit

Abstract

The present paper states and provides an analytical solution for the problem of evaluating the settlement and load-bearing capacity of weighty soil layers of limited thickness resting upon incompressible soil bases and an excavation pit wall upon exposure of the foundation to a distributed load in the vicinity of a wall. The authors develop a method for determining the stressed state component in the reduced engineering problem based on the Ribere–Faylon trigonometric series and for accounting for the nonlinear deformation properties of soils, building on the analytical dependencies of S.S. Grigoryan and S.P. Timoshenko. In order to determine the relationship between stress and strain, the Hencky’s physical equation systems were used. They factor in the impact of average stresses σ_m on the shear modulus of elasticity G (σ_m) and volumetric modulus of elasticity K (σ_m). The obtained solutions make it possible to assess the deformation of soil bases and the load-bearing capacity with respect to nonlinear properties in a way that accurately corresponds to the actual performance of subsoils exposed to loading. The theoretical results are followed by numerical experiments to prove their validity.

1. Introduction

One of the critical problems in applied soil mechanics for high-rise construction involving substantial subsurfaces is quantitative assessment of the stress–strain state (SSS) of the soil massif adjacent to the deep excavation pit of the walls and subsurface structures and the factoring in of engineering–geological conditions. When the subsurface of a high-rise building interacts with the adjacent soil massif in the vicinity of the excavation pit walls and the foundation sublayer, a heterogeneous stress–strain state arises that is transformed in space—either during the construction stage or during the building’s operation. The main difficulties arise when the soil massif is heterogeneous and has elasto-plastic properties and when the additional load is applied in the proximity of an excavation pit.

The methods for forecasting the short-term and long-term settlements of foundations and soil bases were developed by such Russian scientists as N.A. Tsytovich [1], V.A. Florin [2], K.E. Egorov [3], N.M. Gersevanov [4], S.P. Timoshenko [5], Yu. K. Zaretsky [6], Z.G. Ter-Martirosyan [7], and others [8,9]. We can emphasize the work [10,11,12,13,14,15,16,17,18,19,20,21,22,23] where the methods for the analysis of foundation and soil-base settlement are described. Such analyses are based on a method of layered summation, without regard for changes in the deformation properties of soils, as a function of the stress level and thickness of the soil massif that do not correspond to the actual values of settlement in most cases. Due to this, methods for the quantitative assessment of the settlement and load-bearing capacity, factoring in the elasto-plastic properties of soils, of foundations and soil bases of finite width are gaining momentum and practical importance.

Presently, it is possible to obtain the nonlinear relationship between stresses and strains by means of numerical modelling of applied and boundary value problems using the hardening soil model and its varieties. Thus, it can be stated that there are no analytical solutions that allow the demonstration of the relationship between stresses and strains that describes the decaying and progressive parts; i.e., double-curved graphs. Such graphs have been drawn in laboratory tests on the formability of clayey soils by N.A. Tsytovich [1], S.S. Vyalov [24], Yu. K. Zaretsky [6], Z.G. Ter-Martirosyan [25,26,27,28], A.Z. Ter-Martirosyan [25,26,27,28], and others. Therefore, it is important to consider the nonlinear deformation properties of soils in analytical solutions based on the results of compression and triaxial tests. As the result, the changing values of the shear modulus and volumetric modulus as a function of stress can be determined at any point using Cartesian coordinates.

In the present paper, the authors propose an analytical solution for the problem of the stress–strain state of weighty soil layers of limited thickness resting upon an incompressible soil base and an excavation pit wall upon exposure of the foundation to a distributed load in the vicinity of the wall. To evaluate the settlement and load-bearing capacity, the authors applied Hencky’s equation system [7,29], which makes it possible to factor in both the linear and nonlinear behavior of soil exposed to additional loading and to divide the total vertical strain ε_z into the shear strain ε_γ and volumetric strain ε_v in the following manner:

$${\epsilon }_z=\frac{{\sigma }_z-{\sigma }_m}{G({\sigma }_m,{\tau }_i/{\tau }_i^{*})}+\frac{{\sigma }_m}{K};$$

(1)

where G (σ_m, τ_i/τ_i*) and K (σ_m) indicates the moduli of the shear and volumetric strains depending on the average stress σ_m, as well as the relationships between the acting τ_i and the ultimate value τ_i* of the shear stress intensity; i.e., τ_i/τ_i*, where τ_i* = σtgφ + c.

In the particular case where G = const and K = const, this equation is graded into Hooke’s equation. The parameters G (σ_m, τ_i/τ_i*) and K (σ_m) are determined according to the results of standard triaxial tests (Figure 1). The advantage of Hencky’s equation system [29] is obvious with respect to soil grounds. It makes it possible to determine linear strain as the sum of the shear and volumetric strains in the soil, which are essentially different (see Figure 1, upper left and lower right segments), and, as seen, they can describe not only the decaying dependencies ε_m–σ_m but also the continuous shear strains ε_i–σ_i of soil bases.

Moreover, Hencky’s equations make it possible to predict settlement for the condition where p < R as for the condition where p > R, which is required for the cases of settlement evaluation where R < p < p **.

2. Materials and Methods

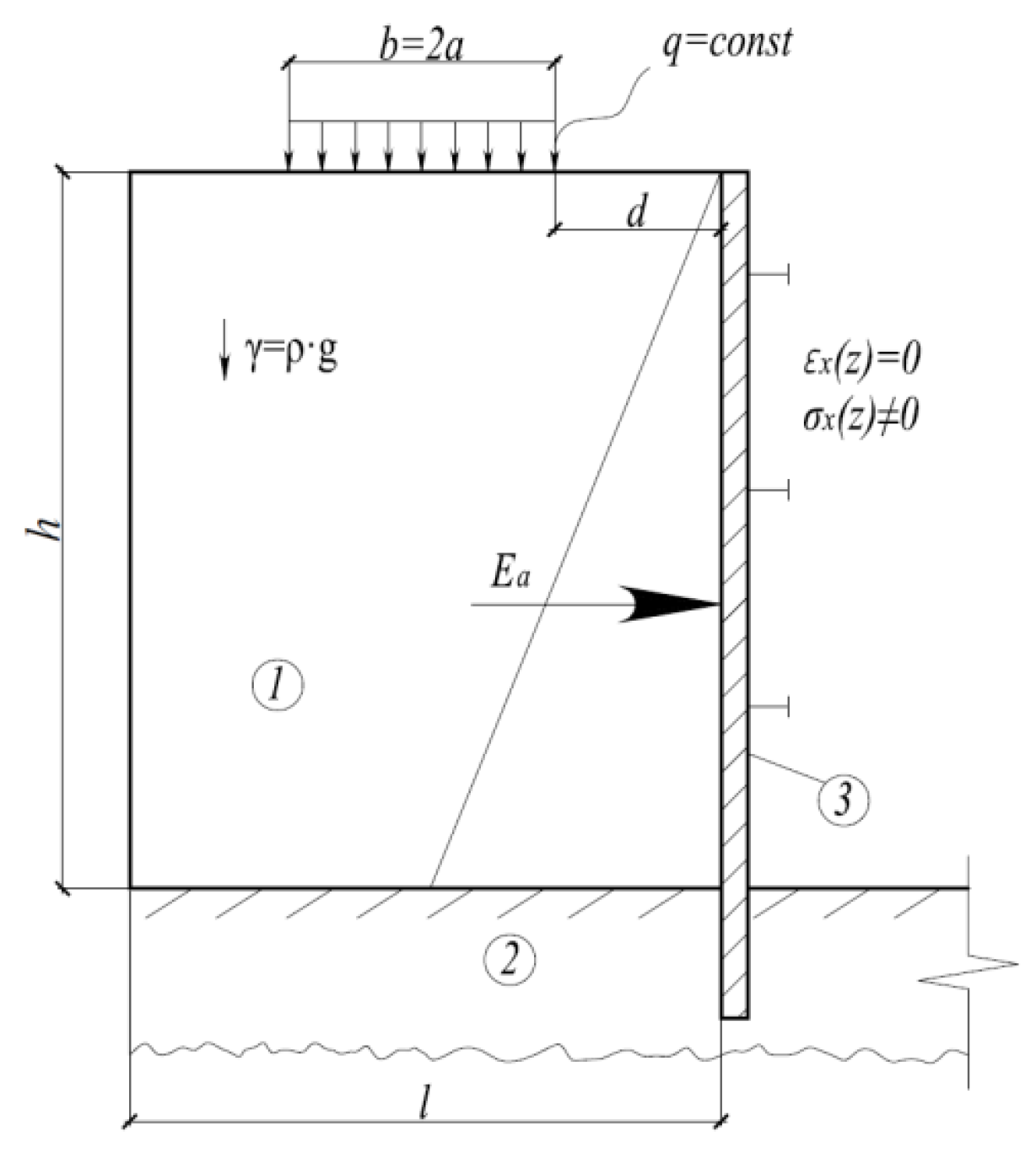
2.1. Theoretical Basis for Determination of the Settlement of a Weighty Soil Layer Resting upon an Incompressible Soil Base upon Exposure of the Foundation to a Distributed Load in the Vicinity of an Excavation Pit Wall

Consider the action of the distributed load q = const on the horizontal section of width b = 2a at a distance d from the edge of an envelope structure with a rectangular profile on a soil base resting on an incompressible soil layer. It is assumed that the vertical wall is fixed by struts, whereas vertical shifts in the soil are permitted (see Figure 2). It is known that, for the given problem, the components of the stressed state of the soil ground, being one quarter of a plane, can be determined using the Ribere–Faylon trigonometric series with the method developed by Z.G. Ter-Martirosyan in the following manner [30]:

$$\begin{array}{l}{\sigma }_y\left(x,y\right)=\frac{qa}{l}+\\ +\frac{4q}{\pi }{\displaystyle \sum _{m=1}^{\infty }\frac{\sin \frac{m\pi a}{l}}{m}\frac{\left[\left(\frac{m\pi h}{l}ch\frac{m\pi h}{l}+sh\frac{m\pi h}{l}\right)ch\frac{m\pi \left(y-h\right)}{l}-\frac{m\pi \left(y-h\right)}{l}sh\frac{m\pi \left(y-h\right)}{l}sh\frac{m\pi h}{l}\right]}{sh\frac{2m\pi h}{l}+\frac{2m\pi h}{l}}\cos \frac{m\pi x}{l}}\end{array}$$

(2)

$$\begin{array}{l}{\sigma }_x\left(x,y\right)=\frac{qa}{l}\frac{\nu }{1-\nu }-\\ -\frac{4q}{\pi }{\displaystyle \sum _{m=1}^{\infty }\frac{\sin \frac{m\pi a}{l}}{m}\frac{\left[\left(\frac{m\pi h}{l}ch\frac{m\pi h}{l}-sh\frac{m\pi h}{l}\right)ch\frac{m\pi \left(y-h\right)}{l}-\frac{m\pi \left(y-h\right)}{l}sh\frac{m\pi \left(y-h\right)}{l}sh\frac{m\pi h}{l}\right]}{sh\frac{2m\pi h}{l}+\frac{2m\pi h}{l}}}\cos \frac{m\pi x}{l}\end{array}$$

(3)

$${\tau }_{xy}\left(x,y\right)=-\frac{4q}{\pi }{\displaystyle \sum _{m=1}^{\infty }\frac{\sin \frac{m\pi a}{l}}{m}}\frac{\left[\frac{m\pi h}{l}ch\frac{m\pi h}{l}sh\frac{m\pi \left(y-h\right)}{l}-\frac{m\pi \left(y-h\right)}{l}ch\frac{m\pi \left(y-h\right)}{l}sh\frac{m\pi h}{l}\right]}{sh\frac{2m\pi h}{l}+\frac{2m\pi h}{l}}\sin \frac{m\pi x}{l}$$

(4)

$${\sigma }_m(x,y)=\frac{1+\nu }{3}\left[\frac{qa}{l}\frac{1}{1-\nu }+\frac{8q}{\pi }{\displaystyle \sum _{m=1}^{\propto }\frac{\sin \frac{m\pi a}{l}}{m}}\frac{\mathrm{s}h\frac{m\pi a}{l}ch\frac{m\pi (y-h)}{l}}{\mathrm{s}h\frac{2m\pi h}{l}+\frac{2m\pi h}{l}}\cos \frac{m\pi x}{l}\right]$$

(5)

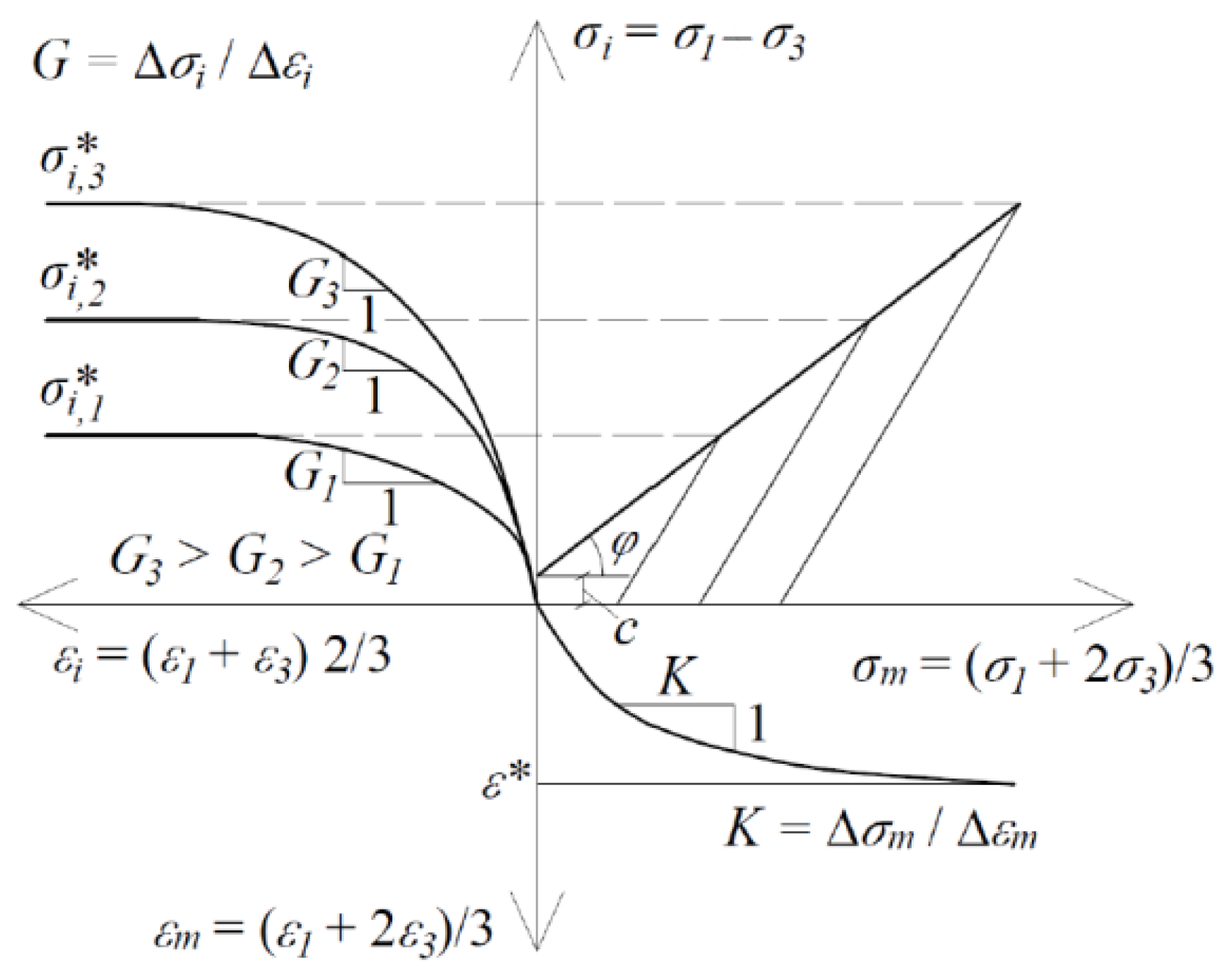
2.2. Hencky’s Physical Equation System

The strains of the soil base ε_z were determined as the sum of the shear and volumetric strains (ε_z = ε_zγ + ε_zν). Hencky’s physical equation system [29], which allows the determination of the linear and nonlinear dependencies of stresses on strains, has the following form:

$${\epsilon }_x=\chi ({\sigma }_x-{\sigma }_m)+{\chi }^{*}\cdot {\sigma }_m;{\gamma }_{xy}=2\chi \cdot {\tau }_{xy}$$

(6)

$${\epsilon }_y=\chi ({\sigma }_y-{\sigma }_m)+{\chi }^{*}\cdot {\sigma }_m;{\gamma }_{yz}=2\chi \cdot {\tau }_{yz}$$

(7)

$${\epsilon }_z=\chi ({\sigma }_z-{\sigma }_m)+{\chi }^{*}\cdot {\sigma }_m;{\gamma }_{zx}=2\chi \cdot {\tau }_{zx}$$

(8)

where

$$\chi =\frac{{\gamma }_i}{2{\tau }_i}=\frac{f({\tau }_i,{\sigma }_m,{\mu }_{\sigma })}{2{\tau }_i};$$

(9)

$${\chi }^{*}=\frac{{\epsilon }_m}{{\sigma }_m}=\frac{f^{*}({\tau }_i,{\sigma }_m,{\mu }_{\sigma })}{2{\tau }_i};$$

(10)

Hencky’s equations [29] at χ = 1/2G and χ* = 1/K, where G = E/2(1 + ν) and K = E/(1 − 2ν), can be graded into Hooke’s equation system.

2.3. Analytical Models of Soil Bases

The dependency proposed by the academician of the Russian Academy of Sciences (RAS) S.S. Grigoryan was assumed as an analytical model for determining nonlinear volumetric strains [24]. It is as follows:

$${\epsilon }_m({\sigma }_m)={\epsilon }^{*}(1-e^{-\alpha {\sigma }_m})$$

(11)

The tangent modulus of the volumetric strain K can be estimated by dividing the expression ε_m by σ_m; i.e.,

$$\frac{{\epsilon }_m}{{\sigma }_m}=\frac{1}{K}=\frac{{\epsilon }^{*}(1-e^{-\alpha {\sigma }_m})}{{\sigma }_m}$$

(12)

$$\frac{{\epsilon }_m}{{\sigma }_m}=\frac{1}{K}=\frac{{\epsilon }^{*}(1-e^{-\alpha {\sigma }_m})}{{\sigma }_m}$$

(13)

at σ_m→∞; ε_m→ ε*, but when α = 0, ε* = ε_m and we obtain the linear dependency K = ε_m/σ_m.

To describe the elasto-plastic properties of cohesive soil exposed to shear loading, we can use the dependency proposed by S.P. Timoshenko [5], which has the following form with regard to soil ground:

$${\gamma }_i=\frac{{\tau }_i}{G^o}\frac{{\tau }_i^{*}}{{\tau }_i^{*}-{\tau }_i}$$

(14)

where γ_i is the shearing strain intensity; τ_i are the acting values of the shearing stress intensity; τ_i* are the ultimate values of the shearing stress; and G^o is the shear modulus (elasticity modulus) for the initial part of the curve γ_i–τ_i.

$${\tau }_i^{*}=({\sigma }_m+{\sigma }_g)\cdot tg\phi +c_i$$

(15)

where φ_i and c_i are the ultimate values of the strength parameters determined under the limit line of the dependency τ_i–σ_m and σ_g is the residual stress.

The secant shear modulus can be calculated with the following formula:

$$G=G^o(1-\frac{{\tau }_i^{*}}{{\tau }_i^{*}-{\tau }_i})$$

(16)

In the simplest case involving the linear dependency of stresses on strains with the parameters G and K, the settlement can be determined with an analytical solution for the axis z. Then, we can write:

$$\frac{{\epsilon }_m}{{\sigma }_m}=\frac{1}{K}=\frac{{\epsilon }^{*}(1-e^{-\alpha {\sigma }_m})}{{\sigma }_m}$$

(17)

$$K=\frac{{\sigma }_m}{{\epsilon }_m}$$

(18)

To account for the nonlinear strain of a soil layer in the calculation of its vertical displacements, Hencky’s equation can be considered [29]:

$${\epsilon }_z=\frac{{\sigma }_z-{\sigma }_m}{G({\sigma }_m,{\tau }_i/{\tau }_i^{*})}+\frac{{\sigma }_m}{K};$$

(19)

Inserting G (σ_m, τ_i) and K (σ_m), we obtain nonlinear equations:

$${\epsilon }_{z,v}={\epsilon }^{*}(1-e^{-\alpha {\sigma }_m})$$

(20)

$${\epsilon }_{z,\gamma }=\frac{{\sigma }_z-{\sigma }_m}{2G_e({\sigma }_m,{\tau }_i/{\tau }_i^{*})};$$

(21)

where ${\tau }_i=\frac{{\sigma }_1-{\sigma }_3}{\sqrt{3}}=\frac{{\sigma }_z-{\sigma }_x}{\sqrt{3}}$ (at the axis of the distributed load center), τ_i* = (σ_m + σ_g)∙tgφ + c_i, and σ_zp and σ_xp are determined using Equations (2)–(5).

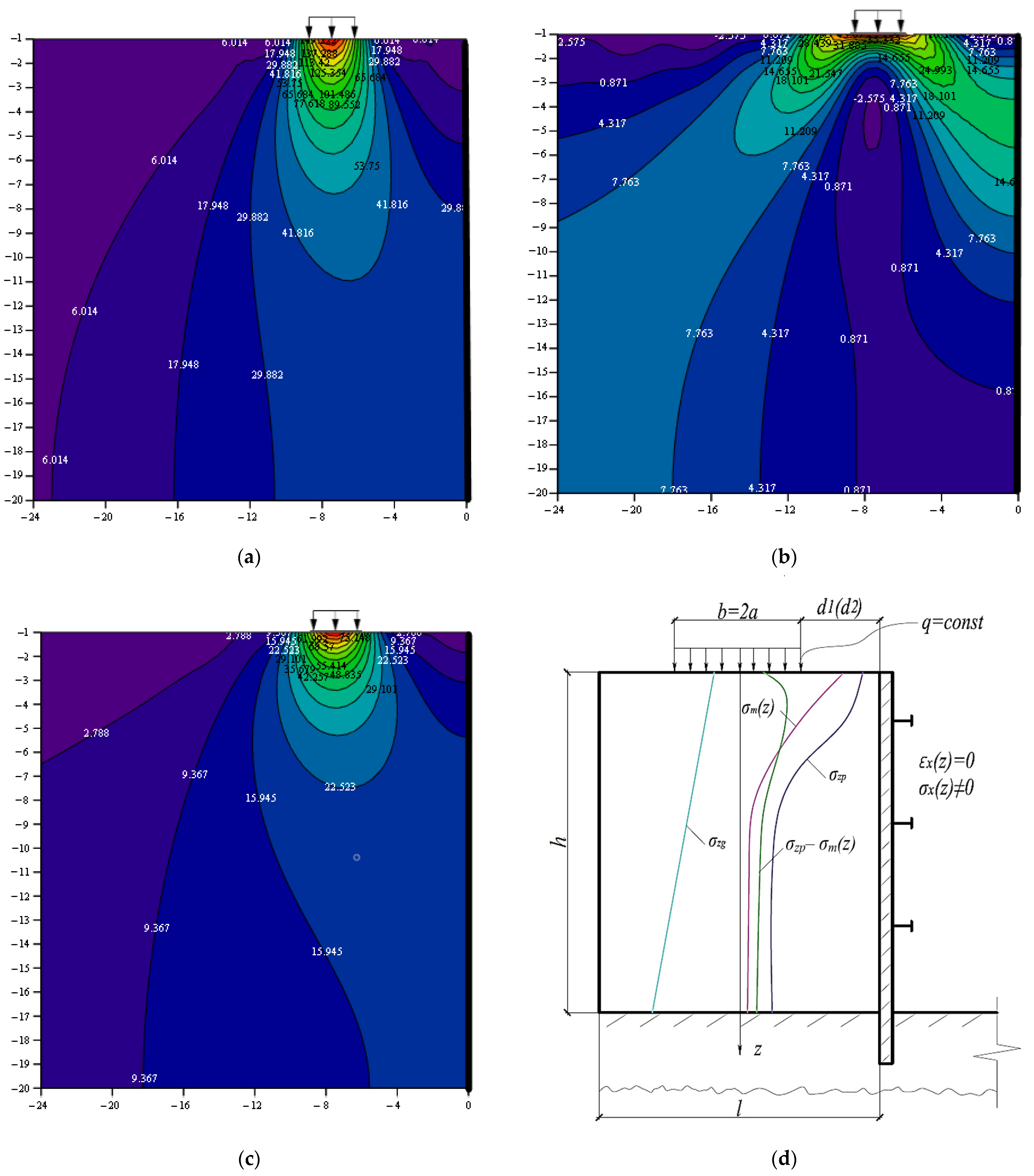
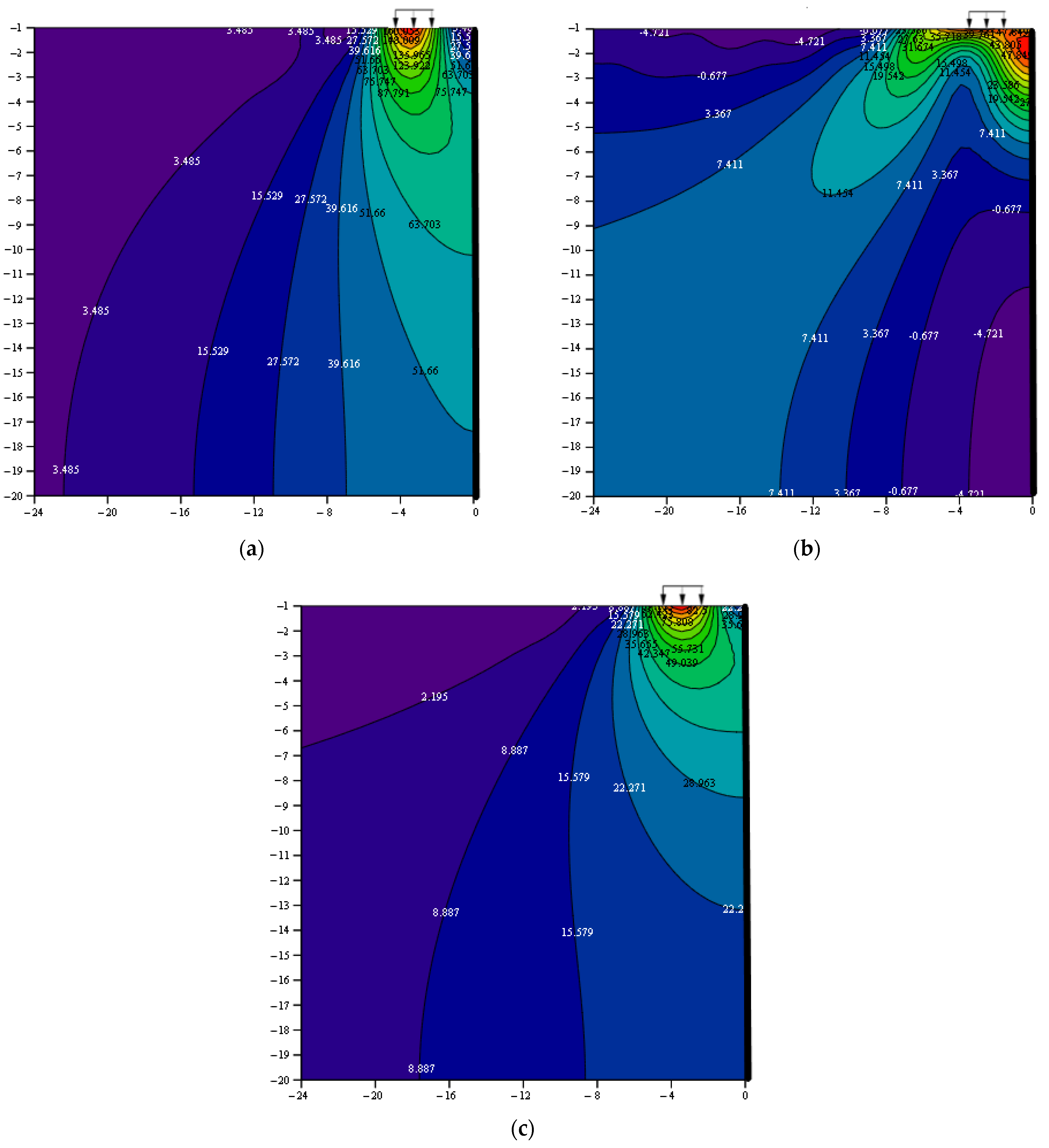
3. Results

Calculation using Equations (2)–(5) in the software complex MathCAD made it possible to determine the components of stresses along the entire plane at z > 0 and ±x according to the computational scheme (see Figure 2). For the isopoles, the stress component for the values q = 100 kPa, d₁ = 6 m, and b = 2a = 3 m are presented in Figure 3. Furthermore, results were obtained for the values q = 100 kPa, d₂ = 2 m, and b = 2a = 3 m (see Figure 4). The given values were randomly selected based on the experience of designing similar structures in order to quantify the proposed solution.

The settlement curves were drawn for the considered problem (see Figure 3 and Figure 4) with allowances made for the elasto-plastic properties of the soil base at various distance d (d₁, d₂) from the fence wall to the distributed load. The total deformation of a soil base with a thickness of h = 20 m at various values where x ≥ 0 can be calculated by means of the following integrals:

$$S={\displaystyle \underset{0}{\overset{h}{\int }}{\epsilon }_{z,vi}(dz)}+{\displaystyle \underset{0}{\overset{h}{\int }}{\epsilon }_{z,\gamma i}(dz)}=S_v+S_{\gamma }$$

(22)

Having analyzed Equations (20) and (21), it was concluded that the constituent of the volumetric strain ε_z,ν would be of the decaying type with a growth of σ_z and when σ_m → ∞; ε_z,ν → ε*. At the same time, with the increase in σ_z, the value of ε_z,γ would be initially of the linear type and then would progress to the intensive growth stage, as at τ_i → τ_i*; ε_z,γ → ∞. Therefore, the total value for the strain would have a double curvature; i.e., at the initial stage at τ_i < τ_i* ε_z, it would be of the decaying type and then at τ_i → τ_i* it would change to the stage of progressive deformation.

For comparison of settlement paths, we assumed the following distances from the fence wall to the point of application of the distributed load: d₁ = 6 m and d₂ = 2 m. The analysis of the total strain arising in a soil base ε_z = ε_z,ν + ε_z,γ along the different vertical lines was implemented for the center of the distributed load for each scenario (x₁ = −7.5; x₂ = −3.5). The parameters of the mechanical properties of the soils were assumed to be ε* = 0.003, α = 0.4, ν = 0.35, G_e = 7000 kPa, φ = 25°, and c = 14 kPa. The results are presented in Figure 5 and Figure 6.

Juxtaposing the total settlement of the soil base with various distances between the fence wall and the point of application of the distributed load, we obtained the combined dependency graph S − q (see Figure 7).

We also obtained the diagrams of the horizontal strains ε_x and vertical strains ε_y on the verticals with various distances d₁ = 6 m and d₂ = 2 m between the fence wall and the distributed load. In Figure 8 and Figure 9, a substantial difference in the total horizontal (a factor of 1.3) and vertical (twofold) strains of the right edge of a foundation with a distributed load q = 100 kPa with various distances d between the fence wall and the distributed load can be seen.

4. Discussion

From the analysis of the outlined results, it follows that the smaller the distance between the fence wall and the distributed load, the higher the value of the total strain is.

It is evident that, depending on the various parameters of the layers’ deformability, the total settlement of the soil base in general changes across a broad range from a decaying to progressive settlement (see Figure 10). The dependency curves S − q were obtained for the scenario where the distance between the fence wall and the distributed load is d₂ = 2 m.

Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10 show that the presented analytical method for the calculation of the settlement and load-bearing capacity of a soil base exposed to distributed loading at various distance from the edge of a excavation pit, implemented by means of the computational models of S.P. Timoshenko and S.S. Grigoryan, along with numerical methods, makes it possible to factor in the nonlinear character of soil behavior to the fullest extent and with a reasonable degree of confidence. Moreover, when designing excavation pits, it is necessary to take into account the distance from the edges to adjacent buildings and structures located within the influence zone of the new construction.

5. Conclusions

Summing up the obtained results, the following can be concluded:

• The selected geomechanical soil base model (its geometric parameters and initial and boundary conditions), as well as the computational model of the soil ground (linear, nonlinear, and rheological) and the type of physical equations used (Hooke’s system and Hencky’s system), have a significant impact on the type of settlement–load curve (S − q) and also on the load-bearing capacity of the soil ground.
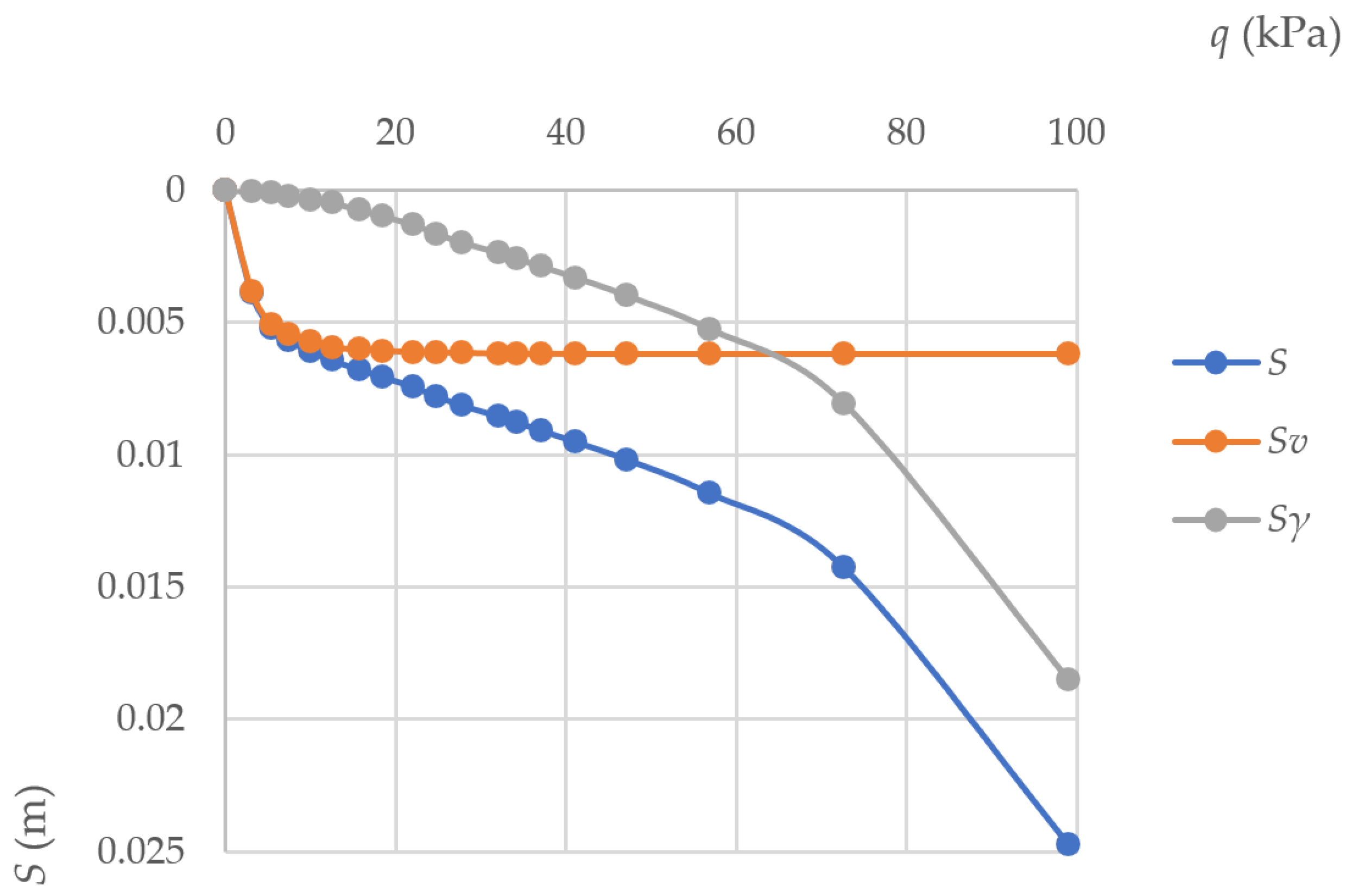
• The computational model applied in the present work, along with the elasto-plastic model for the shear strain and the nonlinear model for the volumetric strain in Hencky’s physical equation system, enabled us to present the linear soil deformation ε (σ, τ) in the form of the sum of the volumetric and shear constituents of this linear deformation (ε_z = ε_z,ν + ε_z,γ). In this case, the strain–stress curve (ε_z − σ_z) could develop along both the decaying path and progressive path (double-curved graph).
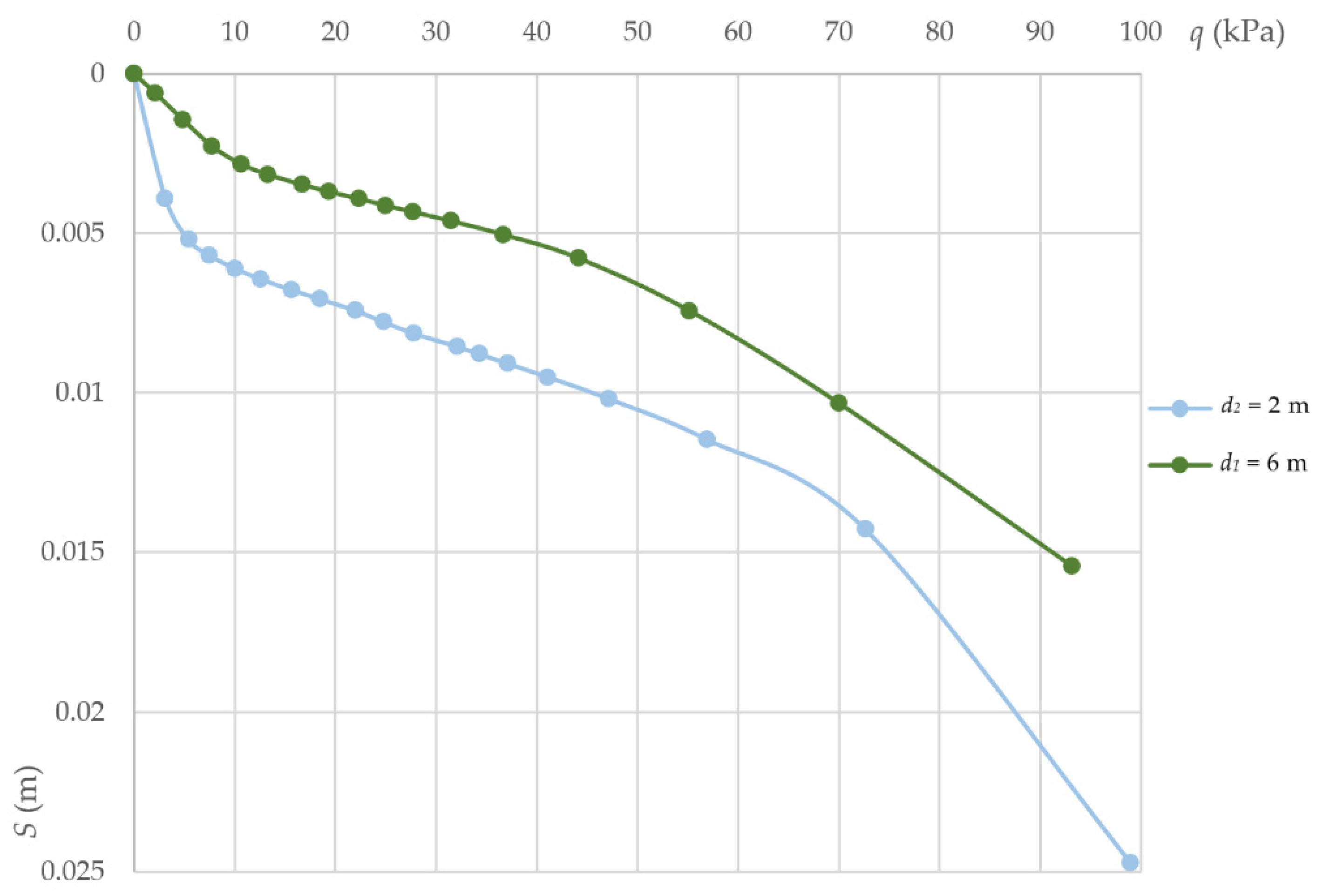
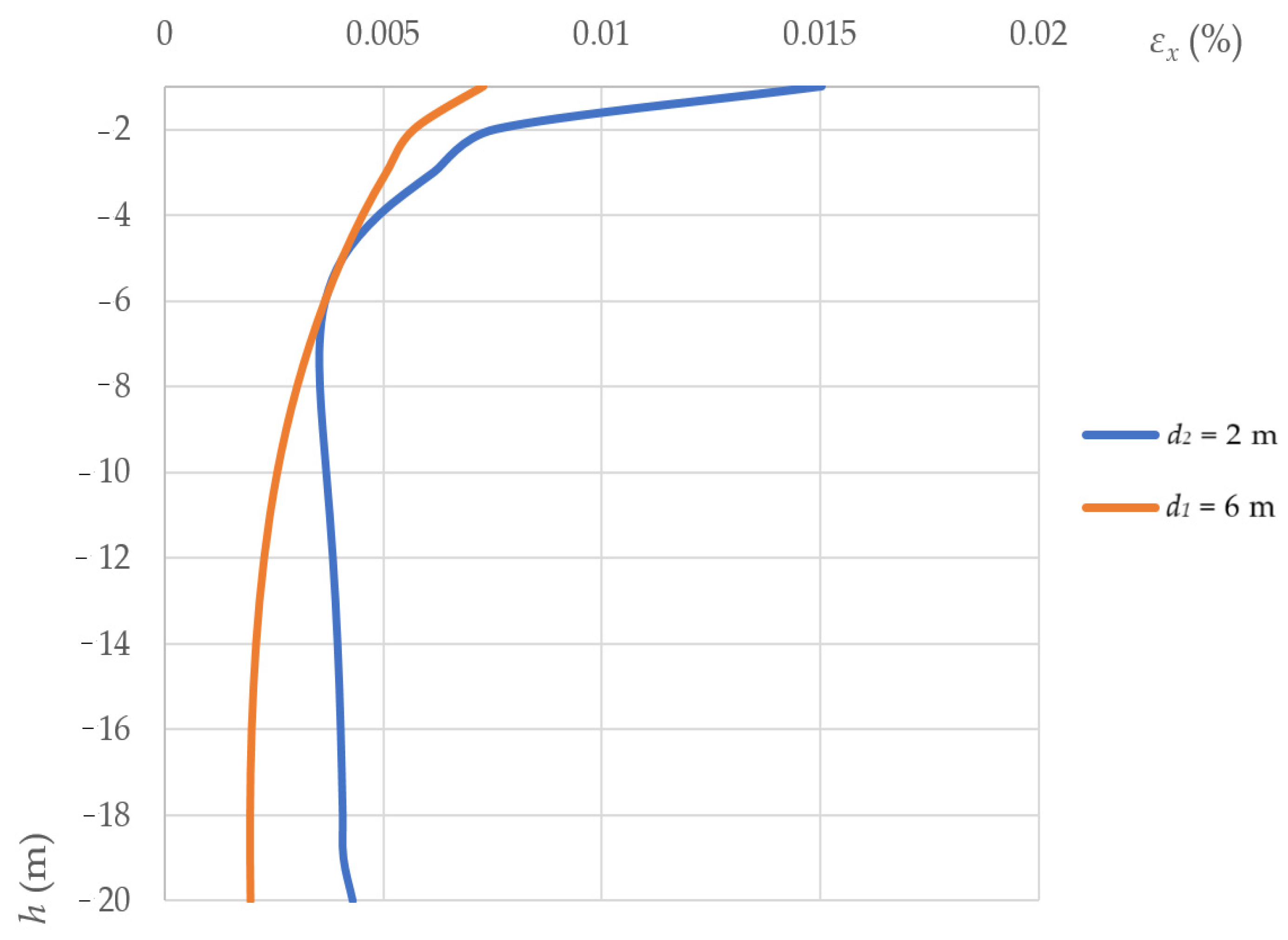
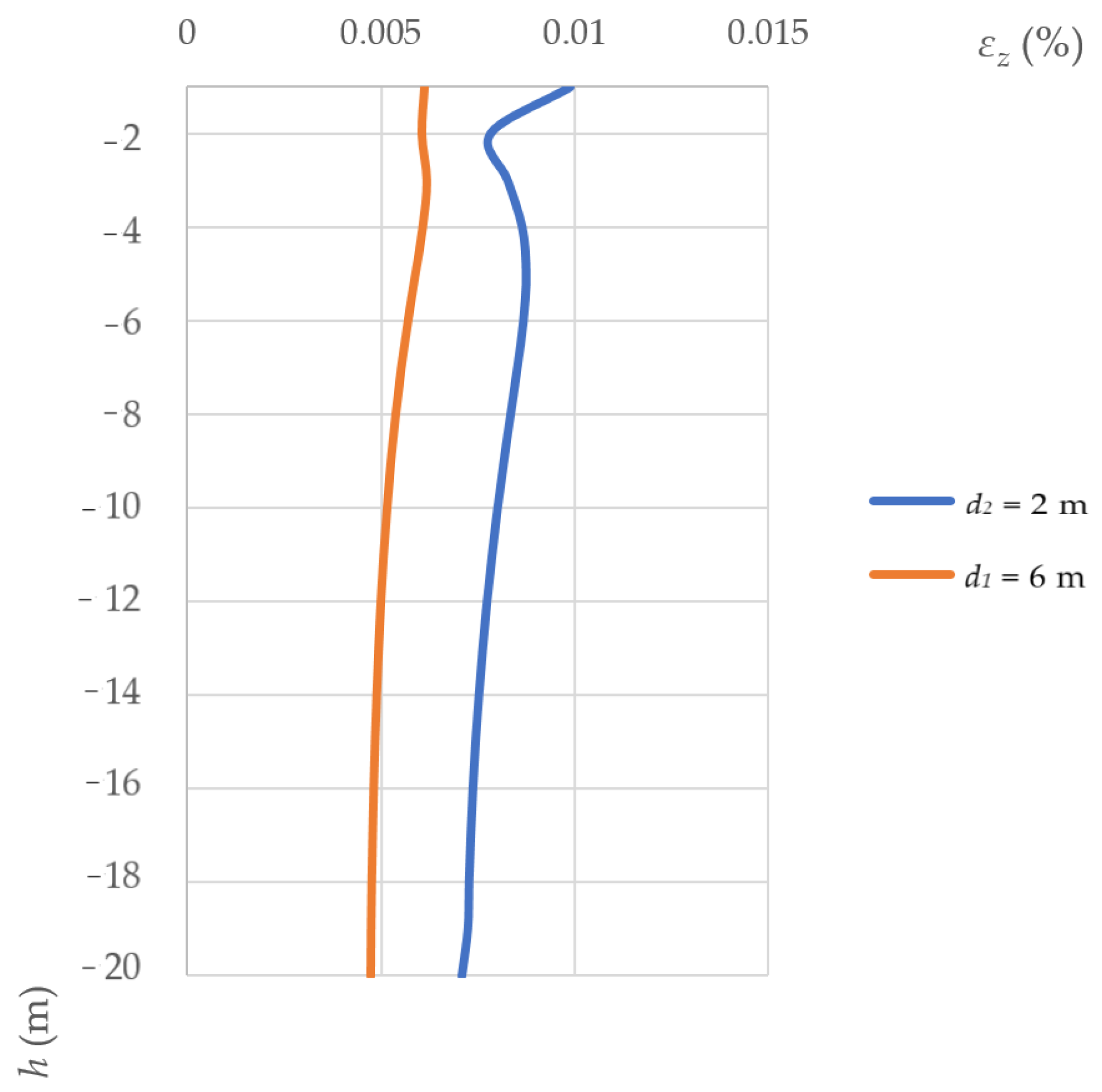
• The implemented strain analysis showed that, in the vicinity of the vertical excavation pit exposed to distributed load, the total foundation settlement was 1.6 times higher at the distance d₂ = 2 m than at d₁ = 6 m with the values for the deformation parameters of soils used in the calculation in this article. We also revealed a substantial difference in the total horizontal (a factor of 1.3) and vertical (twofold) strains at the right edge of the foundation exposed to a distributed load q = 100 kPa with various distances d between the fence wall and the distributed load. Thus, when designing excavation pits, it is necessary to take into account the distance from the edges to adjacent buildings and structures located within the influence zone of the new construction. This is done to avoid the development of strains in the foundation and soil base above the designed level.
• The analysis of existing methods describing the stress–strain state, as well as the calculation of the settlement and load-bearing capacity of soil bases exposed to additional loading—in particular, in the vicinity of excavation pits—showed that there are currently no analytical methods accounting for the elasto-plastic properties of soils. The presented analytical method for the calculation of the settlement and load-bearing capacity of soil bases exposed to distributed loading at various distances from the edge of an excavation pit, implemented by means of the computational models of S.P. Timoshenko and S.S. Grigoryan, along with numerical methods, makes it possible to factor in the nonlinear character of soil behavior to the fullest extent. It also makes it possible to predict the settlement and load-bearing capacity with a reasonable degree of confidence.