1.1. Introduction
This work is concerned with the question of global well-posedness for reaction-diffusion systems that are defined on a sequence of spatially bounded non-coincident spatial domains . The systems allow for discontinuity in the coefficients of the differential operators and in the components of the reaction vector fields, as well as interaction of species on overlapping subdomains. The vector field is required to satisfy a quasi-positivity condition to preserve nonnegativity, and also satisfy properties that help preserve total mass/concentration. Our concern is the establishment of a priori bounds and global existence of sup norm bounded weak solutions of these systems.
There has been a wealth of information for systems of this type with smooth coefficients on the differential operators and locally Lipschitz reaction vector fields in the case that
(i.e., the setting of only one domain). The majority of this work grew from a remark by R.H. Martin over 40 years ago [
1], when he noted that the solution to the system of initial value problems given by
is componentwise nonnegative, and exists for all
. He asked whether the same is true when spatial diffusion is added to the processes. In this setting, a bounded open subset
with smooth boundary is introduced, and the functions
u and
v above react and diffuse on
, subject to homogeneous Neumann boundary conditions and nonnegative initial data. The resulting system becomes
Here,
and
, where
. One of the interesting features of this system is that the solutions satisfy
for all
. That is, total mass is conserved. A full history of this problem can be found in [
2], along with a partial discussion of similar questions in the setting of systems with
unknowns having the fundamental properties of the system above. Here,
is locally Lipschitz and the system
preserves nonnegativity and gives rise to global solutions that are bounded for all
. It is well known that nonnegativity is preserved (regardless of initial data) if and only if
A simple additional property that guarantees global bounded solutions to (
2) and is satisfied by the simple two component system above is given by
When diffusion and homogeneous Neumann boundary conditions are added to (
2), the system becomes
Here,
for all
and
. Similar to above, it is a simple matter to show solutions are componentwise nonnegative, so long as they exist, but global existence is a very difficult question, even though similar to (
1), we have
for all
, so long as the solution exists. It turns out that growth conditions must be imposed on the vector field
f to guarantee global existence. Otherwise, finite time blow-up can occur in (
5). Recent work on this problem can be found in [
3,
4,
5,
6,
7,
8,
9]. In particular, the work in [
6] proves that (
3), (
4) and a requirement that the reaction vector field is at most quadratic, implies global existence and uniform sup norm bounds, independent of space dimension. We note that these results are very dependent on the spatial differential operators
being constant multiples of each other, and it is an open question whether they are true when this is not the case. In some sense, these results are best possible, since [
7] shows that if
then there exists a space dimension
n, a domain
with smooth boundary, and a vector field
f that satisfies (
3), (
4), and grows at the rate
, such that the solution to (
5) blows up in the sup norm in finite time. Finally, we note that there is a wealth of additional work in the setting when there are
domains related to traveling waves and interactions of species, and we note [
10,
11].
Global existence results related to (
3) and (
4) in the case of differential operators with discontinuous coefficients and discontinuous reaction vector fields have recently appeared in [
12]. There have also been a few results that extend the results on single domains to results coupled across multiple domains, and we list [
13,
14]. The work at hand differs from [
13,
14] by virtue of the fact that the diffusion and the reaction vector fields can be more complex, and of course, it differs from the work referred to above from the standpoint that the reaction-diffusion systems are set on
bounded domains in
, where diffusion takes place for a particular component on one domain, but can react with multiple components whose domains of diffusion intersect with this domain. The present work is an extension of work in [
12] for single domains with
diffusion.
Recall from above that our focus is on reaction-diffusion systems defined on a sequence of spatially bounded non-coincident spatial subdomains
, where
represents the number of domains, and
represents the spatial dimension. Problems of this type can arise in the modelling of biological systems, and have been studied as mathematical models. For example, one such system which is analyzed in [
13] models the interaction of two hosts and a vector population, where a disease is transmitted in a criss-cross fashion from one host through a vector to another host. It is assumed that the disease is benign for one host and lethal to the other.
In order to provide a more complete example of what we have in mind we provide three examples. Two of these examples are given below, and revisited in
Section 4, and the third example is introduced and discussed in
Section 4. The first example concerns the cross species spatial transmission of an infectious disease, and the second example concerns a hypothetical interaction of three species living on two overlapping domains. In the first case, we consider an infectious disease that can be transmitted across multiple species and multiple habitats. These are a major concern for animal husbandry, wildlife management, and human health [
15]. A species occupying a given habit may contract the disease from a second species occupying an overlapping habit and via dispersion transmit the disease to a third species whose habitat also overlaps the habitat of the first species. In the second setting, species
A,
B and
C interact through a reaction of the form
on overlapping domains
and
. Species
A lives on
, while species
B and
C live on
.
1.2. Two Illustrative Examples
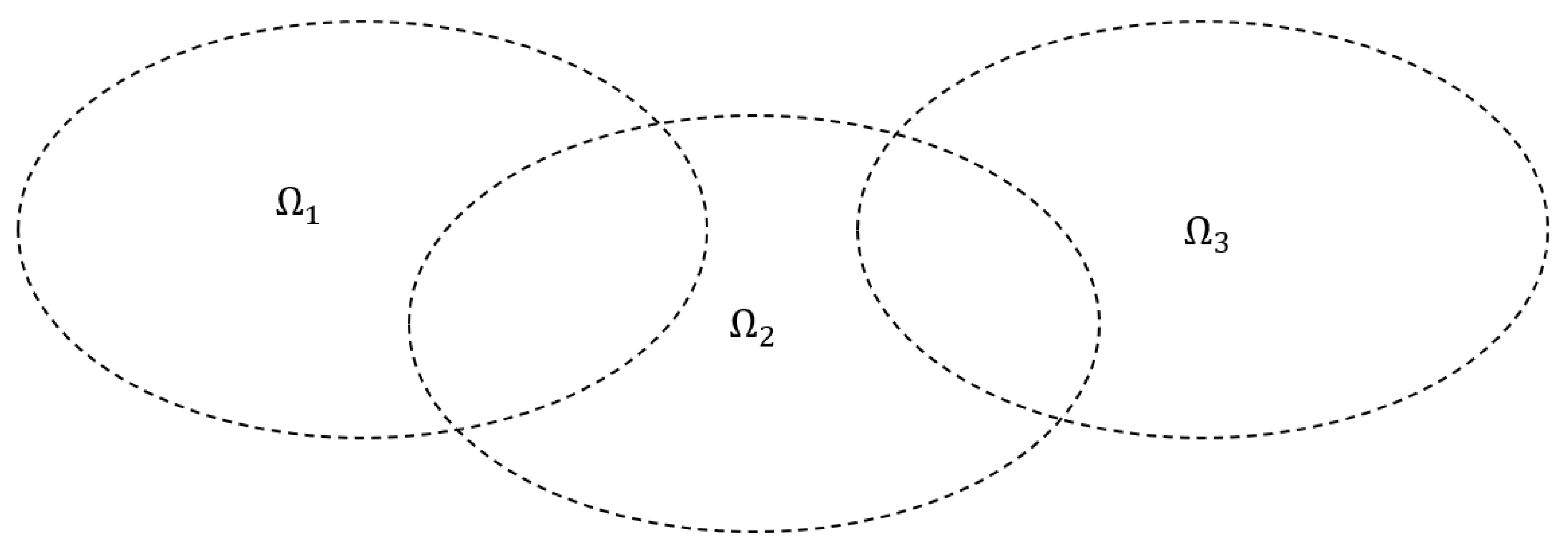
Consider a spatially distributed population. The dispersion of the population is modeled by Fickian diffusion. In this model, there are three populations confined to separate habitats
,
and
, such that
,
and
(see
Figure 1). The possibility of physically separated habitats for the vulnerable and resistant hosts are allowed, each of which intersects with the domain of the vector.
Suppose
and
are nonnegative functions,
and
are positive constants. Furthermore, the supports of
and
are contained in the intersection of
and
, respectively, and the supports of
and
are contained in the intersection of
and
, respectively. Finally, for each
,
is a positive bounded function that is bounded away from 0, and for each
,
is a positive constant.
We impose homogeneous Neumann boundary conditions on each domain
and
.
Finally, we specify continuous nonnegative initial data.
Here, the host with the disease is of benign effect, and is given by the first set of equations,
representing the susceptible and
representing the infectives. The incidence function is given by mass action kinetics and assumes a bilinear form. Because this disease is considered benign, we consider a constant recovery rate
with no mortality. The third set of equations with incidence term
describes the circulation of the disease through the second host. In this case, the disease can be fatal and there is no recovery term. The susceptible vector and infective vector populations are represented by
and
, respectively. The vector population can become infected via contact with infected members of the first and third populations. Consequently, the incidence term is written by a term of the form
. We assume a constant rate of recovery
with no mortality. Such a model could describe the invasion of a fatal disease into a host population
v occupying habitat
. The process would be initiated by the induction of this infection into another population
occupying a habitat
physically separated from
. The infection would not be fatal but would be sustainable in the second host population. The disease would be transmitted to the first via the action of a dispersing vector. It should be clear that such considerations could arise in livestock or wildlife management. For example transmission of brain worm infection from white tail deer to elk occurs via the action of vectors. The disease is benign in the deer population but fatal to the elk population [
16].
It can be shown that the system above preserves the nonnegativity of the initial data. In addition, on
the vector field
has a first component that is bounded above by a linear expression, and the components that clearly sum to zero. Similarly, on
the vector field
has a first component that is bounded above by a linear expression, and also sums to zero. The same mechanism can be seen on
since the function
has a first component that is bounded above by a linear expression, and a sum that is less than or equal to zero. We will apply our results to system (
7)–(
9), and a slightly more complex extension, in
Section 5.
The second example is easier to state. Here, species
A,
B and
C interact through a reaction of the form
on overlapping domains
and
. Species
A occupies
, while species
B and
C occupy
. If we define
(the characteristic function on
), and use
,
and
to denote the concentration densities of
A,
B and
C, then a possible model is given by
Here,
are positive bounded functions on
that are bounded away from 0,
and
,
and
are nonnegative and bounded. This system has a long history in the setting where
, and has appeared in many publications. One of the first was [
17], and a multitude of others following. Some of these are cited in [
2].
In the setting when
, we will see in
Section 4 that
,
and
are nonnegative. In addition, the reaction vector field
satisfies
This guarantees
for all
t > 0.
In addition, the component
is the only component associated with a species living on all of
, and it is clearly bounded above by
when
. The two components
and
corresponding to components associated with species living on all of
satisfy
We will see in
Section 4 that this structure is sufficient to guaranteed the system (
13) has a unique weak global solution which is sup norm bounded.
1.3. Notation and Assumptions
This work focusses on the analysis of reaction-diffusion systems with species on multiple domains. To this end, let be integers, and suppose are bounded domains with smooth boundaries for such that each lies locally on one side of . We define . Each domain represents a habitat which houses species of a population having a total of m species. Some of the habitats may overlap, and some may be completely contained in other habitats. We assume there is a mapping which defines species k to be uniquely associated with a habitat . Notationally, this results in each species being associated with an appropriate habitat by partitioning the set into N disjoint sets, where can be interpreted as meaning the ith species is associated with Finally, we denote the population density of species k on at time by .
We model the interactions of the species
across all habitats via a reaction-diffusion system given by
Here, is an unknown vector valued function.
Assumption A1. We assume the structure of the species and habitats described above, and for each , , for each , and there exists so that for all and . In addition, for each , denotes the outward unit normal vector to at a point on . For each we define the diagonal matrix for so that the entry given by the characteristic function , and let where , and for each , the function for bounded subsets and , and is locally Lipschitz in u, uniformly on for each . Finally, we define where such thatWe remark that for , the function has the same qualities as , except that for a given , only depends on component j of u if . The extension of as 0 outside is only done for convenience in development of estimates below. We remark that the homogeneous Neumann boundary conditions listed in (
14) can be replaced with nonhomogeneous boundary conditions. It is also possible to use some ideas from [
12] to include nondiagonal diffusion, nonlinear diffusion and semilinear boundary conditions. It is also possible to use other simple boundary conditions, including homogeneous Dirichlet boundary conditions. In all cases, it is possible to include convective terms provided
apriori estimates can be obtained. The interested reader is referred to [
12] for additional remarks in the setting of
, which can be extended with modification to the current setting.
We are primarily interested in systems which guarantee that solutions to (
14) are componentwise nonnegative, and total population is bounded for finite time. That is,
for each
, and there exists
such that
for each
. As noted earlier, there has been a wealth of work on systems of the form (
14) when the number of domains is
. The results we present in this work extend some of the work from the setting of
domain to
domains.
We start by imposing reasonable conditions on the vector field
f to guarantee the nonnegativity of solutions. To this end, we assume
Here,
is the set of componentwise nonnegative vectors in
. In the setting of
, condition (
16) is typically referred to as a quasi-positivity condition. It is not difficult to prove that solutions to (
14) are componentwise nonnegative regardless of the choice of bounded, componentwise nonnegative initial data if and only if (
16) holds. More general information related to nonnegativity of solutions in the case of
appears in [
18].
There are many conditions that can result in bounded total population. The one we assume is related to a well known dissipativity condition in the setting
that has been used in many of the references listed above (and we especially note [
2]). The analogous assumption in this setting requires that there exist
for each
,
and
so that
where
is the characteristic function on the set
S. It is possible for the constants
and
in (
17) can be replaced by functions depending on
t and
x, and we leave the details to the interested reader. We will see below that this assumption guarantees the estimate given in (
15).
It is well known in the
setting that assumptions (
16) and (
17) are not sufficient to guarantee the existence of global solutions to (
14) that are sup norm bounded on
for all
(cf [
7,
19]). In fact, when
, if
, then in the setting when
there exist constant diffusion
,
,
, bounded nonnegative initial data, and
f satisfying (
16) and (
17) with
, such that the solutions to (
14) blow up in the sup norm in finite time [
7]. As a result, we need at least one additional assumption to avoid sup norm blow up in this setting.
Recently, in the setting of
, work in [
12] proved solutions to (
14) cannot blow up in the sup norm provided there exist
so that
and there exists an
lower triangular matrix
A with positive diagonal entries, and a number
so that
We note that while there is considerable restriction on
r in (
19), there is no restriction on the size of
l in (
18). In the setting of
, it is tempting to simply rewrite the assumptions above, but the analysis does not lend itself to the full generalization of the second one. Instead, we amend the first assumption above to fit our setting, and use more care with the second assumption. To this end, for each
, we assume there exist
(without restriction on size) so that
and for each
there is an
lower triangular matrix
with positive entries on the diagonal, and
with
so that
Here,
denotes the vector whose entries are
components of
f such that
. Note that the right hand side of (
19) includes all components of
u whose habitats intersect with
.
Note that when components of the vector field are polynomial in nature, the value of
r in (
19) is more restrictive than the inequality indicates. This is because a polynomial bounded above by another polynomial that has a positive integer degree
, tells us the actual bound is of degree
. So, when
, the upper bound for
r above effectively restricts us to
, while in the setting of
,
r can be 2. This does not mean that the reaction terms can only be linear in nature. In deed, we can see in (
7) that there are quadratic reaction terms, but it is apparent that (
19) is satisfied with
.
The condition in (
19) has a long history in the setting of
, and was originally termed an
intermediate sum condition. As pointed out in [
12], this condition implies a much more general condition that actually leads to the result given in that work, but (
19) is far easier to recognize in systems, and it occurs naturally as a trade off of higher order terms related to different components.
In this work, we extend the results in [
12] by using (
16)– (
19) to prove that solutions to (
14) cannot blow up in the sup norm in finite time.
Section 2 contains some notation, definitions, and the statements of our main results. The proofs are given in
Section 3 and
Section 4, and some examples are stated in
Section 5. Finally, we pose an open question in Secton
Section 4.