A Simple Greedy Heuristic for Site Specific Management Zone Problem
Abstract
:1. Introduction
- Edaphic, such as salinity, nutrients;
- Biological, earthworms, microbes, etc;
- Anthropogenic, e.g., irrigation management, among others;
- Topographic, e.g., slope elevation;
- Meteorological, e.g., temperature, rainfall;
- How to divide the facility into regions,
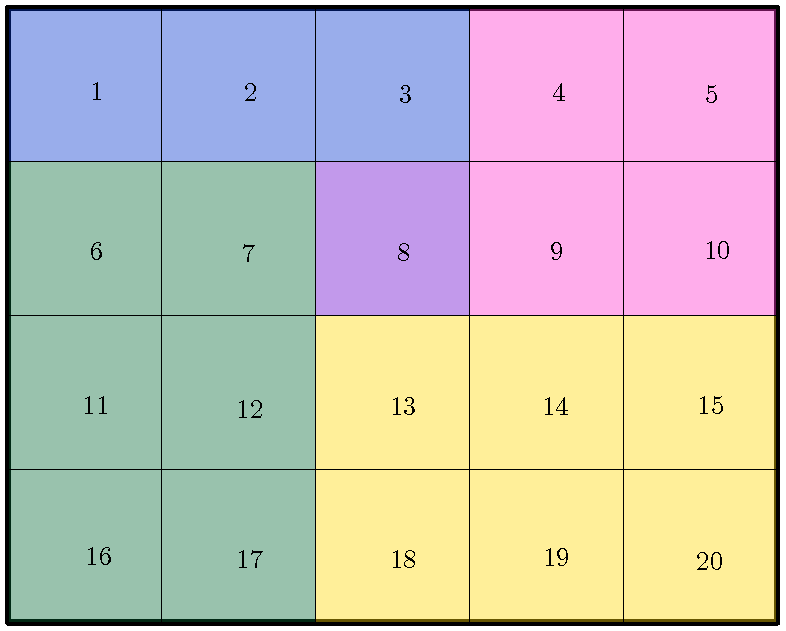
2. Problem Statement
- Input: A facility M divided into of samples (area units) of the soil, a parameter .
- Output: The facility divided into regions, with minimum and .
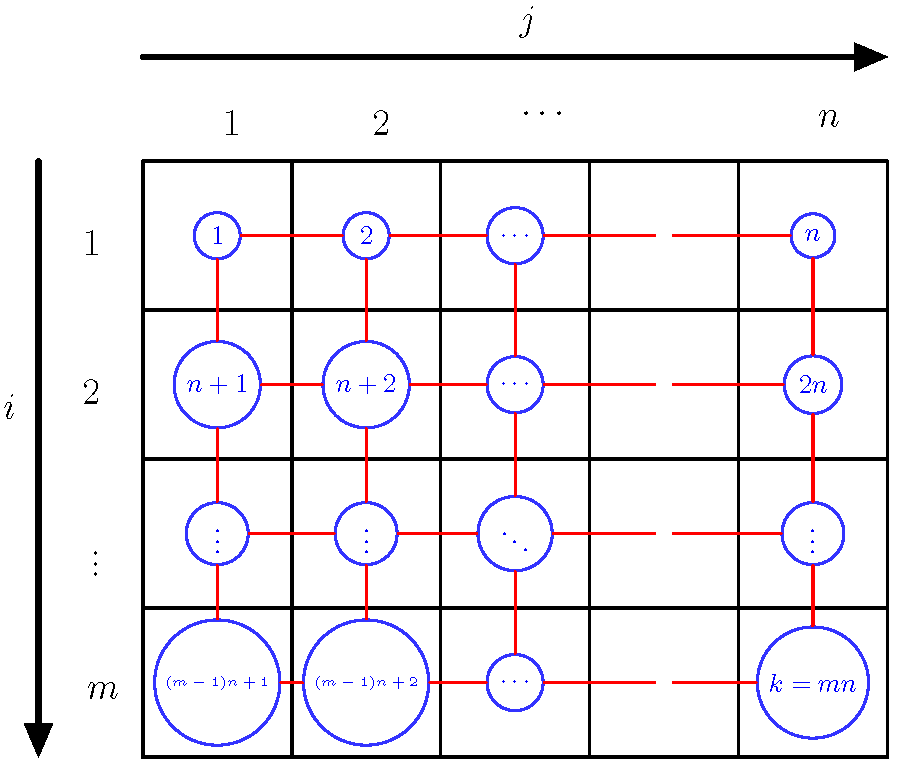
3. Methodology
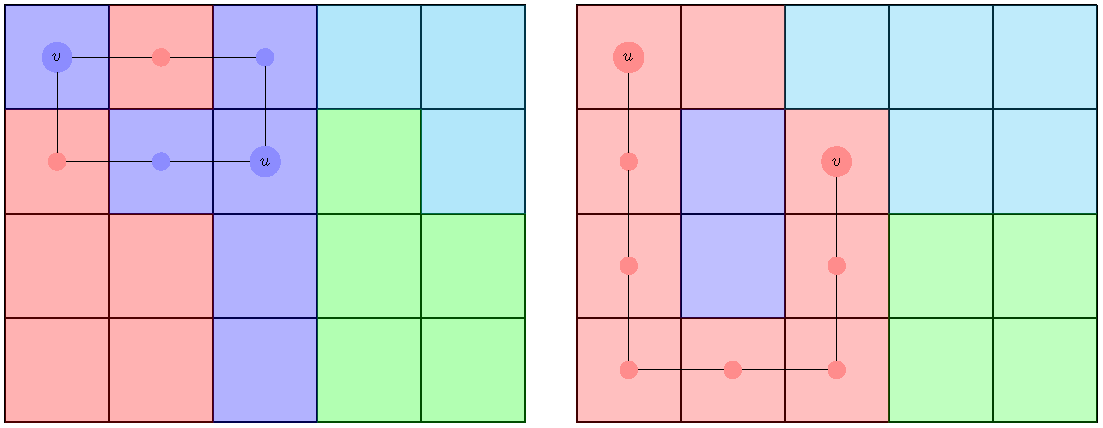
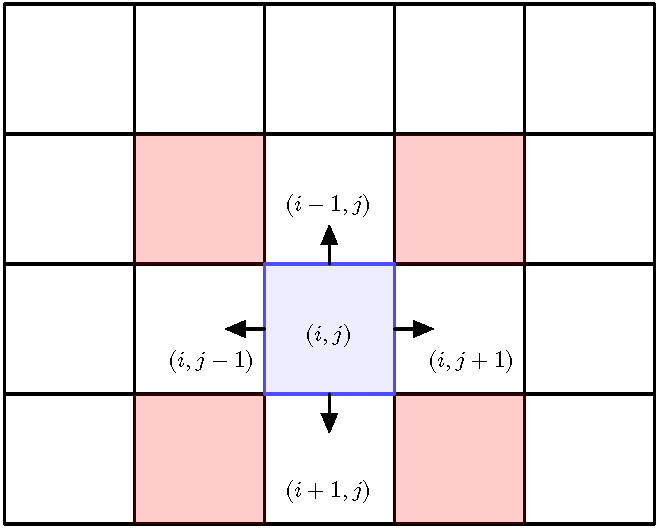
- Only consider the neighbors to merge with an area unit ;
- We can consider the set of neighbors to merge with an area unit .
- If a valid area unit is merged with , then area units and are added to if they are valid.
- If a valid area unit is merged with , then area units and are added to if they are valid.
- If a valid area unit is merged with , then area units and are added to if they are valid.
- If a valid area unit is merged with , then area units and are added to if they are valid.
- : New is the first nonvisited neighbor in lexicographical order from N;
- : New is a random nonvisited neighbor from N;
- : New is a nonvisited neighbor that produces a minimal decrease in H from N.
| Algorithm 1 A simple greedy heuristic for the SSMZ problem. |
|
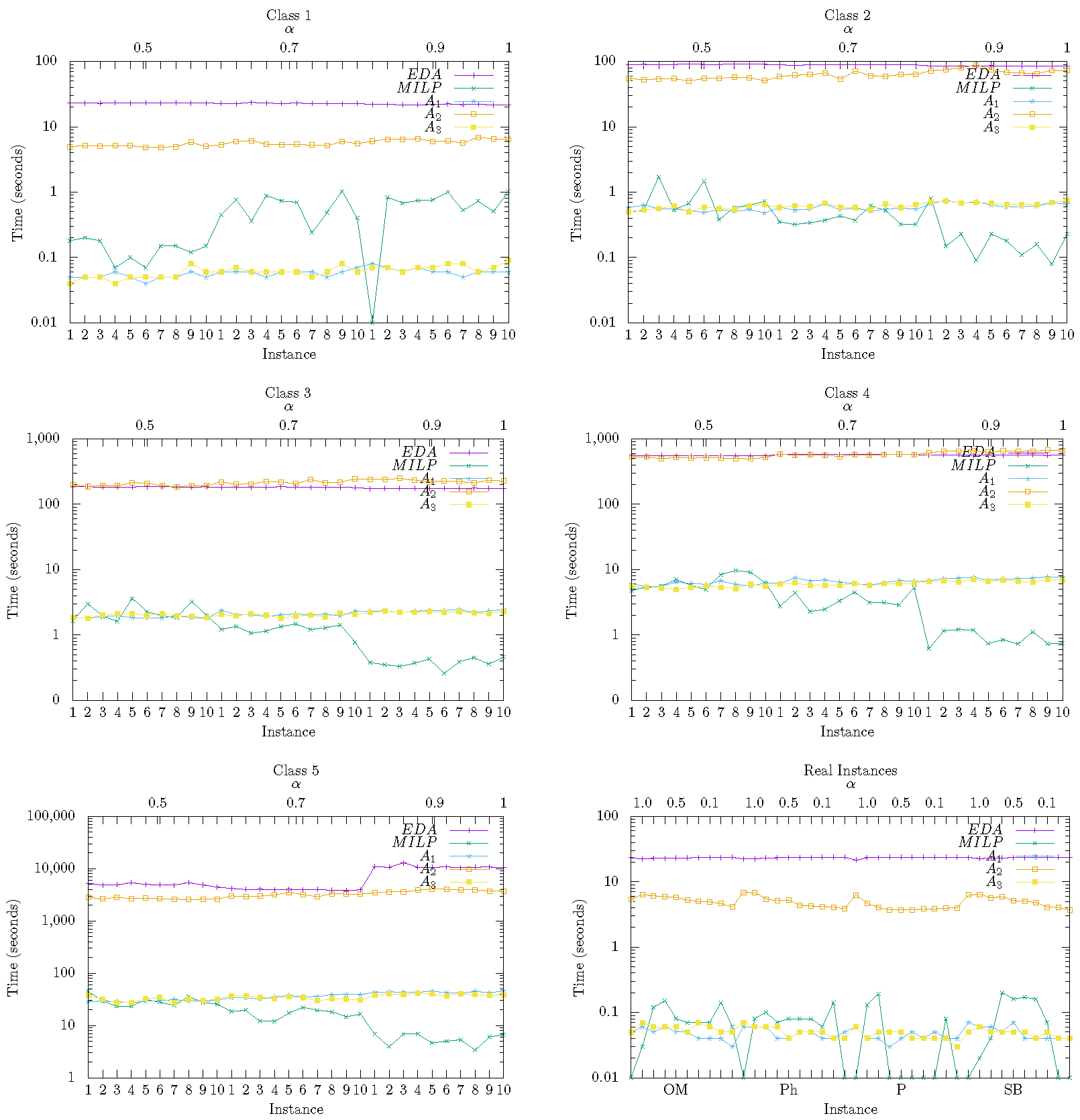
4. Experimental Results
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kamath, N. Application of Operation Research Techniques in Agriculture. Int. J. Res. Appl. Sci. Eng. Technol. 2020, 8, 734–742. [Google Scholar] [CrossRef]
- Zhao, Q.; Wang, C.; Zhang, Z.; Zhang, Y.; Wang, C. The application of operations research in the optimization of agricultural production. Oper. Res. 1991, 39, 194–205. [Google Scholar]
- Ortega, R.; Flores, L.; Inia, C.Q.; de Recursos Naturales, D.; Ambiente, M. Agricultura de Precisión: Introducción al Manejo Sitio-Específico; Ministerio de Agricultura, Instituto de Investigaciones Agropecuarias, CRI Quilamapu: Chillán, Chile, 1999; pp. 13–46. [Google Scholar]
- Corwin, D.L. Site-specific management and delineating management zones. In Precision Agriculture for Sustainability and Environmental Protection; Routledge: London, UK, 2013; pp. 135–157. [Google Scholar]
- Ortega, R.A.; Santibáñez, O.A. Determination of management zones in corn (Zea mays L.) based on soil fertility. Comput. Electron. Agric. 2007, 58, 49–59. [Google Scholar] [CrossRef]
- Ortega, J.; Foster, W.; Ortega, R. Definición de sub-rodales para una silvicultura de precisión: Una aplicación del método Fuzzy K-Means. Cienc. Investig. Agrar. 2002, 29, 35–44. [Google Scholar] [CrossRef]
- Li, X.; Pan, Y.; Zhang, C.; Liu, L.; Wang, J. A new algorithm on delineation of management zone. In Proceedings of the 2005 IEEE International Geoscience and Remote Sensing Symposium (IGARSS’05), Seoul, Korea, 29 July 2005; Volume 1, p. 4. [Google Scholar]
- Jiang, Q.; Fu, Q.; Wang, Z. Study on delineation of irrigation management zones based on management zone analyst software. In Proceedings of the International Conference on Computer and Computing Technologies in Agriculture, Nanchang, China, 22–25 October 2010; pp. 419–427. [Google Scholar]
- Cid-Garcia, N.M.; Albornoz, V.; Rios-Solis, Y.A.; Ortega, R. Rectangular shape management zone delineation using integer linear programming. Comput. Electron. Agric. 2013, 93, 1–9. [Google Scholar] [CrossRef]
- Velasco, J.; Vicencio, S.; Lozano, J.A.; Cid-Garcia, N.M. Delineation of site-specific management zones using estimation of distribution algorithms. Int. Trans. Oper. Res. 2021. [Google Scholar] [CrossRef]
- Schepers, A.R.; Shanahan, J.F.; Liebig, M.A.; Schepers, J.S.; Johnson, S.H.; Luchiari, A., Jr. Appropriateness of management zones for characterizing spatial variability of soil properties and irrigated corn yields across years. Agron. J. 2004, 96, 195–203. [Google Scholar] [CrossRef] [Green Version]
- Fraisse, C.; Sudduth, K.; Kitchen, N. Delineation of site-specific management zones by unsupervised classification of topographic attributes and soil electrical conductivity. Trans. ASAE 2001, 44, 155–166. [Google Scholar] [CrossRef] [Green Version]


| Instance | ||||||
|---|---|---|---|---|---|---|
| MILP | EDA | MILP | EDA | MILP | EDA | |
| Class 1 | 93.33% | 10.00% | 96.67% | 70.00% | 90.00% | 16.67% |
| Class 2 | 93.33% | 3.33% | 100.00% | 30.00% | 83.33% | 6.67% |
| Class 3 | 96.67% | 0.00% | 100.00% | 16.67% | 100.00% | 3.33% |
| Class 4 | 100.00% | 0.00% | 100.00% | 0.00% | 100.00% | 0.00% |
| Class 5 | 100.00% | 6.67% | 100.00% | 26.67% | 100.00% | 6.67% |
| OM | 80.00% | 10.00% | 100.00% | 20.00% | 70.00% | 10.00% |
| Ph | 60.00% | 30.00% | 100.00% | 70.00% | 40.00% | 10.00% |
| P | 100.00% | 100.00% | 100.00% | 100.00% | 100.00% | 100.00% |
| SB | 70.00% | 20.00% | 90.00% | 30.00% | 50.00% | 10.00% |
| Instance | Alpha | Time (s) | Time (s) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Z | Time (s) | Z | Time (s) | s | Z | Time (s) | |||||||
| OM | 1 | 40 | 23.28 | 40 | 0.01 | 40 | 0.05 | 40 | 5.38 | 40.00 | 0.00 | 40 | 0.05 |
| 0.9 | 17 | 22.33 | 20 | 0.03 | 19 | 0.06 | 18 | 6.34 | 19.53 | 1.09 | 19 | 0.07 | |
| 0.8 | 11 | 22.73 | 17 | 0.12 | 17 | 0.05 | 14 | 6.09 | 15.95 | 0.91 | 17 | 0.06 | |
| 0.7 | 9 | 22.94 | 14 | 0.15 | 12 | 0.06 | 10 | 5.91 | 11.40 | 0.90 | 11 | 0.06 | |
| 0.6 | 6 | 23.17 | 11 | 0.08 | 9 | 0.05 | 7 | 5.74 | 9.59 | 1.43 | 10 | 0.06 | |
| 0.5 | 5 | 23.26 | 9 | 0.07 | 7 | 0.05 | 5 | 5.22 | 7.58 | 0.99 | 9 | 0.05 | |
| 0.4 | 4 | 23.33 | 7 | 0.07 | 7 | 0.04 | 5 | 4.98 | 6.66 | 1.30 | 9 | 0.07 | |
| 0.3 | 2 | 23.43 | 6 | 0.07 | 7 | 0.04 | 4 | 4.92 | 5.48 | 0.82 | 6 | 0.06 | |
| 0.2 | 2 | 23.47 | 5 | 0.14 | 4 | 0.04 | 3 | 4.63 | 4.80 | 0.89 | 6 | 0.05 | |
| 0.1 | 2 | 23.63 | 3 | 0.06 | 4 | 0.03 | 3 | 4.16 | 3.76 | 0.77 | 5 | 0.05 | |
| Ph | 1 | 19 | 22.30 | 24 | 0.01 | 19 | 0.06 | 19 | 6.83 | 19.00 | 0.00 | 19 | 0.07 |
| 0.9 | 13 | 22.33 | 17 | 0.08 | 16 | 0.06 | 15 | 6.80 | 16.46 | 0.54 | 17 | 0.06 | |
| 0.8 | 8 | 23.15 | 10 | 0.10 | 10 | 0.06 | 9 | 5.42 | 10.60 | 0.79 | 10 | 0.06 | |
| 0.7 | 6 | 23.28 | 7 | 0.07 | 8 | 0.04 | 6 | 5.13 | 8.55 | 1.14 | 10 | 0.06 | |
| 0.6 | 5 | 23.39 | 5 | 0.08 | 5 | 0.04 | 5 | 5.25 | 6.61 | 1.09 | 6 | 0.04 | |
| 0.5 | 4 | 23.45 | 4 | 0.08 | 4 | 0.05 | 4 | 4.38 | 5.37 | 0.63 | 5 | 0.05 | |
| 0.4 | 3 | 23.52 | 4 | 0.08 | 5 | 0.05 | 3 | 4.25 | 4.76 | 0.73 | 5 | 0.05 | |
| 0.3 | 3 | 23.62 | 3 | 0.06 | 4 | 0.04 | 3 | 4.18 | 4.19 | 0.72 | 4 | 0.05 | |
| 0.2 | 2 | 23.60 | 3 | 0.14 | 3 | 0.04 | 3 | 4.09 | 3.61 | 0.58 | 3 | 0.04 | |
| 0.1 | 2 | 23.64 | 2 | 0.01 | 3 | 0.05 | 2 | 3.86 | 2.87 | 0.44 | 3 | 0.04 | |
| P | 1 | 32 | 21.46 | 33 | 0.01 | 32 | 0.06 | 32 | 6.23 | 32.00 | 0.00 | 32 | 0.06 |
| 0.9 | 7 | 23.28 | 9 | 0.13 | 6 | 0.04 | 5 | 4.63 | 5.69 | 0.81 | 7 | 0.04 | |
| 0.8 | 4 | 23.46 | 5 | 0.19 | 3 | 0.04 | 3 | 4.06 | 3.02 | 0.14 | 3 | 0.05 | |
| 0.7 | 3 | 23.54 | 3 | 0.01 | 2 | 0.03 | 2 | 3.70 | 2.00 | 0.00 | 2 | 0.05 | |
| 0.6 | 2 | 23.64 | 3 | 0.01 | 2 | 0.04 | 2 | 3.71 | 2.00 | 0.00 | 2 | 0.05 | |
| 0.5 | 2 | 23.67 | 3 | 0.01 | 2 | 0.05 | 2 | 3.71 | 2.00 | 0.00 | 2 | 0.04 | |
| 0.4 | 2 | 23.67 | 3 | 0.01 | 2 | 0.04 | 2 | 3.84 | 2.02 | 0.14 | 2 | 0.04 | |
| 0.3 | 2 | 23.66 | 3 | 0.01 | 2 | 0.05 | 2 | 3.84 | 2.18 | 0.39 | 2 | 0.04 | |
| 0.2 | 2 | 23.64 | 3 | 0.08 | 2 | 0.04 | 2 | 3.94 | 2.17 | 0.38 | 2 | 0.04 | |
| 0.1 | 2 | 23.61 | 2 | 0.01 | 2 | 0.04 | 2 | 3.98 | 2.11 | 0.31 | 2 | 0.03 | |
| SB | 1 | 40 | 23.51 | 40 | 0.01 | 40 | 0.07 | 40 | 6.27 | 40.00 | 0.00 | 40 | 0.05 |
| 0.9 | 14 | 22.60 | 20 | 0.02 | 15 | 0.06 | 14 | 6.40 | 14.94 | 0.91 | 15 | 0.06 | |
| 0.8 | 9 | 22.94 | 16 | 0.04 | 13 | 0.06 | 12 | 5.68 | 13.46 | 0.77 | 13 | 0.05 | |
| 0.7 | 5 | 23.16 | 12 | 0.20 | 11 | 0.05 | 10 | 5.87 | 12.33 | 1.01 | 13 | 0.05 | |
| 0.6 | 3 | 23.35 | 9 | 0.16 | 9 | 0.07 | 6 | 5.14 | 9.05 | 1.35 | 8 | 0.05 | |
| 0.5 | 3 | 23.43 | 7 | 0.17 | 6 | 0.04 | 5 | 5.06 | 7.42 | 1.65 | 6 | 0.05 | |
| 0.4 | 2 | 23.54 | 5 | 0.16 | 6 | 0.04 | 5 | 4.77 | 6.49 | 1.16 | 6 | 0.04 | |
| 0.3 | 2 | 23.50 | 4 | 0.07 | 5 | 0.04 | 3 | 4.09 | 4.90 | 1.14 | 6 | 0.05 | |
| 0.2 | 2 | 23.57 | 2 | 0.01 | 5 | 0.04 | 3 | 4.05 | 4.72 | 1.31 | 6 | 0.04 | |
| 0.1 | 2 | 23.51 | 2 | 0.01 | 2 | 0.04 | 2 | 3.65 | 2.73 | 0.69 | 4 | 0.04 | |
| Class | k | Time (s) | Time (s) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Z | Time (s) | Z | Time (s) | s | Z | Time (s) | ||||||||
| 1 | 1 | 0.5 | 6 | 23.03 | 11 | 0.18 | 7 | 0.05 | 5 | 4.96 | 8.11 | 1.34 | 8 | 0.04 |
| 2 | 5 | 23.01 | 10 | 0.20 | 7 | 0.05 | 5 | 5.15 | 7.58 | 0.99 | 9 | 0.05 | ||
| 3 | 6 | 22.87 | 8 | 0.18 | 7 | 0.05 | 6 | 5.08 | 9.58 | 1.99 | 11 | 0.05 | ||
| 4 | 4 | 23.32 | 10 | 0.07 | 8 | 0.06 | 4 | 5.11 | 7.23 | 1.56 | 7 | 0.04 | ||
| 5 | 8 | 23.08 | 11 | 0.10 | 12 | 0.05 | 7 | 5.12 | 9.82 | 1.45 | 10 | 0.05 | ||
| 6 | 3 | 23.23 | 9 | 0.07 | 7 | 0.04 | 5 | 4.86 | 7.92 | 1.69 | 5 | 0.05 | ||
| 7 | 8 | 22.94 | 13 | 0.15 | 7 | 0.05 | 8 | 4.85 | 10.55 | 0.98 | 10 | 0.05 | ||
| 8 | 4 | 23.19 | 10 | 0.15 | 7 | 0.05 | 4 | 4.98 | 6.42 | 1.16 | 8 | 0.05 | ||
| 9 | 7 | 22.96 | 13 | 0.12 | 8 | 0.06 | 8 | 5.79 | 10.63 | 1.60 | 8 | 0.08 | ||
| 10 | 5 | 23.02 | 11 | 0.15 | 7 | 0.05 | 6 | 4.99 | 7.02 | 0.77 | 7 | 0.06 | ||
| 1 | 0.7 | 10 | 22.76 | 16 | 0.45 | 11 | 0.06 | 9 | 5.34 | 12.18 | 1.45 | 12 | 0.06 | |
| 2 | 10 | 22.54 | 18 | 0.76 | 12 | 0.06 | 10 | 5.96 | 11.40 | 0.90 | 11 | 0.07 | ||
| 3 | 9 | 23.63 | 14 | 0.36 | 15 | 0.06 | 13 | 6.14 | 15.44 | 0.67 | 16 | 0.06 | ||
| 4 | 6 | 23.00 | 13 | 0.88 | 7 | 0.05 | 6 | 5.41 | 7.86 | 0.97 | 9 | 0.06 | ||
| 5 | 10 | 22.72 | 16 | 0.73 | 11 | 0.06 | 10 | 5.33 | 11.76 | 0.75 | 11 | 0.06 | ||
| 6 | 8 | 23.00 | 14 | 0.70 | 9 | 0.06 | 8 | 5.37 | 10.86 | 1.22 | 11 | 0.06 | ||
| 7 | 13 | 22.68 | 18 | 0.24 | 17 | 0.06 | 12 | 5.23 | 14.35 | 1.33 | 17 | 0.05 | ||
| 8 | 6 | 22.88 | 14 | 0.49 | 9 | 0.05 | 5 | 5.15 | 8.38 | 1.39 | 7 | 0.06 | ||
| 9 | 12 | 22.38 | 19 | 1.02 | 13 | 0.06 | 12 | 5.98 | 12.82 | 0.83 | 12 | 0.08 | ||
| 10 | 8 | 22.66 | 15 | 0.40 | 10 | 0.07 | 7 | 5.53 | 9.60 | 0.84 | 9 | 0.06 | ||
| 1 | 0.9 | 19 | 22.02 | 24 | 0.00 | 20 | 0.08 | 19 | 6.02 | 19.53 | 0.50 | 20 | 0.07 | |
| 2 | 21 | 21.84 | 26 | 0.83 | 18 | 0.07 | 17 | 6.44 | 18.60 | 1.06 | 18 | 0.07 | ||
| 3 | 22 | 21.81 | 25 | 0.68 | 21 | 0.06 | 18 | 6.41 | 19.98 | 1.12 | 19 | 0.06 | ||
| 4 | 22 | 21.81 | 24 | 0.74 | 24 | 0.07 | 22 | 6.58 | 23.00 | 1.01 | 22 | 0.07 | ||
| 5 | 21 | 21.86 | 25 | 0.76 | 24 | 0.06 | 23 | 6.00 | 23.95 | 0.22 | 24 | 0.07 | ||
| 6 | 16 | 22.40 | 21 | 0.99 | 18 | 0.06 | 17 | 6.08 | 17.84 | 0.99 | 17 | 0.08 | ||
| 7 | 23 | 21.77 | 26 | 0.53 | 25 | 0.05 | 23 | 5.66 | 23.98 | 1.00 | 23 | 0.08 | ||
| 8 | 16 | 22.15 | 21 | 0.73 | 18 | 0.06 | 17 | 6.93 | 17.68 | 0.47 | 18 | 0.06 | ||
| 9 | 25 | 21.54 | 29 | 0.51 | 26 | 0.06 | 26 | 6.48 | 26.00 | 0.00 | 26 | 0.07 | ||
| 10 | 16 | 21.66 | 22 | 1.03 | 27 | 0.06 | 27 | 6.42 | 27.00 | 0.00 | 27 | 0.09 | ||
| 2 | 1 | 0.5 | 8 | 89.83 | 24 | 0.50 | 19 | 0.58 | 12 | 54.84 | 17.03 | 2.25 | 18 | 0.50 |
| 2 | 8 | 90.11 | 22 | 0.52 | 17 | 0.63 | 13 | 52.59 | 17.78 | 2.39 | 23 | 0.53 | ||
| 3 | 10 | 89.80 | 22 | 1.70 | 20 | 0.56 | 13 | 54.05 | 17.83 | 2.43 | 23 | 0.56 | ||
| 4 | 10 | 89.86 | 24 | 0.53 | 17 | 0.55 | 15 | 54.54 | 20.16 | 2.35 | 21 | 0.61 | ||
| 5 | 5 | 90.90 | 14 | 0.67 | 12 | 0.52 | 8 | 50.47 | 11.49 | 1.76 | 12 | 0.50 | ||
| 6 | 10 | 90.01 | 25 | 1.46 | 19 | 0.49 | 14 | 54.77 | 19.05 | 2.40 | 16 | 0.59 | ||
| 7 | 9 | 90.01 | 19 | 0.38 | 23 | 0.54 | 15 | 55.39 | 19.95 | 2.01 | 22 | 0.56 | ||
| 8 | 8 | 90.51 | 17 | 0.58 | 17 | 0.51 | 12 | 57.62 | 16.33 | 1.58 | 18 | 0.54 | ||
| 9 | 8 | 90.10 | 22 | 0.63 | 17 | 0.54 | 11 | 56.33 | 16.31 | 2.71 | 13 | 0.62 | ||
| 10 | 8 | 90.16 | 14 | 0.72 | 11 | 0.48 | 8 | 50.83 | 13.96 | 2.14 | 15 | 0.64 | ||
| 1 | 0.7 | 16 | 88.23 | 36 | 0.35 | 29 | 0.59 | 17 | 58.92 | 22.05 | 2.43 | 22 | 0.58 | |
| 2 | 18 | 87.75 | 35 | 0.32 | 27 | 0.53 | 19 | 61.32 | 23.95 | 2.67 | 25 | 0.62 | ||
| 3 | 16 | 88.21 | 34 | 0.34 | 20 | 0.55 | 17 | 62.58 | 20.83 | 2.17 | 20 | 0.60 | ||
| 4 | 20 | 88.17 | 36 | 0.37 | 32 | 0.66 | 24 | 66.49 | 29.04 | 2.00 | 29 | 0.68 | ||
| 5 | 11 | 89.37 | 25 | 0.43 | 18 | 0.54 | 13 | 54.19 | 16.08 | 1.69 | 17 | 0.59 | ||
| 6 | 18 | 88.07 | 35 | 0.37 | 28 | 0.57 | 21 | 71.00 | 26.57 | 2.39 | 27 | 0.58 | ||
| 7 | 18 | 88.68 | 32 | 0.62 | 25 | 0.51 | 23 | 60.60 | 26.23 | 1.61 | 27 | 0.54 | ||
| 8 | 15 | 88.79 | 30 | 0.52 | 23 | 0.55 | 19 | 59.35 | 23.21 | 1.86 | 23 | 0.66 | ||
| 9 | 15 | 88.71 | 31 | 0.32 | 25 | 0.57 | 19 | 63.00 | 22.20 | 1.86 | 22 | 0.58 | ||
| 10 | 13 | 88.45 | 25 | 0.32 | 22 | 0.55 | 16 | 63.36 | 21.07 | 1.77 | 20 | 0.65 | ||
| 1 | 0.9 | 41 | 85.22 | 50 | 0.80 | 47 | 0.66 | 39 | 71.90 | 42.87 | 1.59 | 45 | 0.71 | |
| 2 | 44 | 84.77 | 57 | 0.15 | 48 | 0.75 | 43 | 74.92 | 48.08 | 2.20 | 48 | 0.73 | ||
| 3 | 39 | 85.49 | 52 | 0.23 | 38 | 0.67 | 34 | 79.70 | 37.89 | 2.38 | 38 | 0.68 | ||
| 4 | 41 | 85.08 | 55 | 0.09 | 46 | 0.71 | 40 | 88.49 | 44.51 | 1.42 | 43 | 0.69 | ||
| 5 | 32 | 86.03 | 49 | 0.23 | 37 | 0.63 | 32 | 74.92 | 36.42 | 1.17 | 36 | 0.68 | ||
| 6 | 40 | 85.23 | 51 | 0.18 | 42 | 0.59 | 40 | 67.97 | 41.07 | 0.69 | 42 | 0.64 | ||
| 7 | 39 | 84.71 | 50 | 0.11 | 46 | 0.60 | 40 | 66.51 | 44.02 | 1.56 | 44 | 0.65 | ||
| 8 | 42 | 84.71 | 51 | 0.16 | 43 | 0.61 | 41 | 65.44 | 45.97 | 2.98 | 41 | 0.64 | ||
| 9 | 42 | 84.94 | 52 | 0.08 | 48 | 0.69 | 45 | 72.95 | 47.39 | 1.59 | 48 | 0.70 | ||
| 10 | 37 | 85.30 | 44 | 0.23 | 39 | 0.65 | 37 | 72.16 | 40.45 | 1.53 | 41 | 0.74 | ||
| Class | k | Time (s) | Time (s) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Z | Time (s) | Z | Time (s) | s | Z | Time (s) | ||||||||
| 3 | 1 | 0.5 | 10 | 184.61 | 30 | 1.63 | 28 | 1.84 | 19 | 198.73 | 25.11 | 2.92 | 27 | 1.83 |
| 2 | 12 | 184.51 | 29 | 2.98 | 26 | 1.81 | 19 | 186.48 | 24.26 | 2.57 | 26 | 1.81 | ||
| 3 | 9 | 184.11 | 32 | 1.94 | 29 | 1.91 | 21 | 193.94 | 26.73 | 2.69 | 27 | 2.03 | ||
| 4 | 9 | 184.19 | 27 | 1.60 | 26 | 1.96 | 14 | 191.36 | 21.82 | 2.73 | 25 | 2.13 | ||
| 5 | 8 | 184.11 | 24 | 3.59 | 21 | 1.84 | 15 | 214.47 | 21.34 | 2.52 | 20 | 2.12 | ||
| 6 | 8 | 185.65 | 30 | 2.25 | 26 | 1.82 | 19 | 209.62 | 25.56 | 3.12 | 28 | 1.99 | ||
| 7 | 12 | 185.01 | 32 | 1.96 | 28 | 1.83 | 20 | 192.35 | 26.22 | 2.90 | 30 | 2.13 | ||
| 8 | 10 | 184.04 | 27 | 1.84 | 24 | 1.97 | 18 | 185.46 | 23.53 | 2.42 | 25 | 1.98 | ||
| 9 | 11 | 184.09 | 28 | 3.22 | 27 | 1.85 | 18 | 193.38 | 24.68 | 2.99 | 26 | 1.92 | ||
| 10 | 9 | 184.53 | 31 | 1.99 | 33 | 1.81 | 20 | 192.32 | 29.32 | 3.31 | 30 | 1.84 | ||
| 1 | 0.7 | 23 | 181.06 | 53 | 1.21 | 43 | 2.36 | 33 | 219.43 | 39.13 | 2.65 | 39 | 2.06 | |
| 2 | 23 | 181.86 | 46 | 1.35 | 36 | 2.04 | 26 | 201.93 | 34.22 | 2.90 | 39 | 1.96 | ||
| 3 | 20 | 180.93 | 49 | 1.06 | 33 | 2.04 | 27 | 204.07 | 34.37 | 3.30 | 36 | 2.10 | ||
| 4 | 21 | 181.65 | 42 | 1.14 | 34 | 1.93 | 26 | 221.53 | 32.03 | 2.75 | 31 | 2.03 | ||
| 5 | 16 | 185.36 | 38 | 1.34 | 28 | 2.02 | 20 | 217.91 | 26.19 | 2.62 | 27 | 1.81 | ||
| 6 | 18 | 182.68 | 46 | 1.47 | 36 | 2.10 | 27 | 205.88 | 33.82 | 3.27 | 31 | 1.95 | ||
| 7 | 25 | 180.52 | 51 | 1.21 | 39 | 2.01 | 33 | 237.16 | 38.61 | 2.82 | 34 | 2.00 | ||
| 8 | 19 | 181.85 | 43 | 1.29 | 33 | 2.07 | 23 | 212.60 | 30.44 | 3.06 | 34 | 1.90 | ||
| 9 | 19 | 181.34 | 44 | 1.41 | 32 | 1.96 | 28 | 217.31 | 34.03 | 2.85 | 34 | 2.15 | ||
| 10 | 28 | 179.75 | 51 | 0.77 | 41 | 2.31 | 32 | 244.44 | 41.44 | 3.67 | 45 | 2.07 | ||
| 1 | 0.9 | 76 | 173.18 | 84 | 0.38 | 77 | 2.30 | 75 | 240.86 | 79.46 | 2.09 | 80 | 2.20 | |
| 2 | 58 | 175.08 | 77 | 0.35 | 69 | 2.34 | 62 | 238.80 | 66.55 | 2.52 | 69 | 2.31 | ||
| 3 | 59 | 175.10 | 82 | 0.33 | 65 | 2.21 | 62 | 248.14 | 65.22 | 1.80 | 68 | 2.23 | ||
| 4 | 61 | 174.78 | 75 | 0.37 | 66 | 2.30 | 60 | 233.73 | 66.22 | 2.30 | 68 | 2.22 | ||
| 5 | 60 | 174.90 | 73 | 0.43 | 69 | 2.38 | 68 | 219.14 | 69.9 | 1.87 | 69 | 2.29 | ||
| 6 | 60 | 175.35 | 72 | 0.26 | 63 | 2.37 | 58 | 227.88 | 64.25 | 2.69 | 64 | 2.22 | ||
| 7 | 64 | 174.87 | 77 | 0.39 | 66 | 2.46 | 60 | 222.60 | 64.48 | 1.83 | 62 | 2.27 | ||
| 8 | 53 | 176.12 | 69 | 0.45 | 61 | 2.21 | 57 | 211.76 | 61.6 | 1.97 | 59 | 2.19 | ||
| 9 | 56 | 175.21 | 73 | 0.36 | 62 | 2.32 | 55 | 233.39 | 58.2 | 1.40 | 61 | 2.14 | ||
| 10 | 71 | 173.64 | 82 | 0.46 | 76 | 2.44 | 74 | 225.69 | 75.57 | 0.81 | 75 | 2.28 | ||
| 4 | 1 | 0.5 | 11 | 549.32 | 39 | 4.77 | 33 | 6.06 | 22 | 533.58 | 31.98 | 3.60 | 37 | 5.60 |
| 2 | 18 | 550.24 | 47 | 5.40 | 46 | 5.52 | 30 | 528.36 | 37.58 | 3.57 | 43 | 5.27 | ||
| 3 | 10 | 553.42 | 41 | 5.57 | 35 | 5.58 | 27 | 496.85 | 33.92 | 3.55 | 33 | 5.23 | ||
| 4 | 14 | 549.75 | 45 | 7.03 | 38 | 6.43 | 28 | 520.63 | 35.24 | 3.77 | 30 | 5.00 | ||
| 5 | 13 | 550.75 | 43 | 5.69 | 38 | 6.09 | 31 | 506.77 | 38.74 | 3.56 | 41 | 5.32 | ||
| 6 | 7 | 552.61 | 37 | 4.95 | 25 | 5.95 | 22 | 513.77 | 29.53 | 3.31 | 37 | 5.63 | ||
| 7 | 18 | 551.79 | 47 | 8.36 | 36 | 6.69 | 27 | 508.59 | 37 | 3.82 | 41 | 5.34 | ||
| 8 | 10 | 552.06 | 34 | 9.65 | 33 | 5.92 | 25 | 500.65 | 30.42 | 3.07 | 28 | 5.14 | ||
| 9 | 12 | 550.08 | 42 | 9.08 | 38 | 5.63 | 29 | 495.64 | 34.83 | 3.22 | 34 | 5.93 | ||
| 10 | 11 | 551.20 | 38 | 6.18 | 37 | 6.24 | 23 | 517.97 | 31.44 | 3.72 | 31 | 5.58 | ||
| 1 | 0.7 | 24 | 579.22 | 64 | 2.75 | 51 | 6.17 | 40 | 586.60 | 47.48 | 3.29 | 43 | 5.96 | |
| 2 | 36 | 574.92 | 69 | 4.38 | 57 | 7.46 | 43 | 559.33 | 54 | 3.47 | 58 | 6.23 | ||
| 3 | 25 | 584.00 | 66 | 2.27 | 45 | 6.70 | 40 | 574.14 | 47.33 | 3.54 | 46 | 5.76 | ||
| 4 | 25 | 574.06 | 71 | 2.46 | 56 | 6.94 | 39 | 563.77 | 45.62 | 3.17 | 44 | 5.72 | ||
| 5 | 28 | 579.34 | 68 | 3.31 | 54 | 6.41 | 43 | 538.85 | 51.54 | 3.26 | 56 | 5.77 | ||
| 6 | 21 | 583.24 | 63 | 4.49 | 43 | 6.08 | 31 | 570.12 | 38.35 | 3.79 | 35 | 6.10 | ||
| 7 | 30 | 584.97 | 73 | 3.11 | 51 | 5.81 | 40 | 564.40 | 48.15 | 3.51 | 45 | 5.67 | ||
| 8 | 24 | 583.46 | 62 | 3.13 | 50 | 6.33 | 37 | 575.43 | 44.51 | 3.47 | 46 | 6.09 | ||
| 9 | 29 | 574.14 | 64 | 2.86 | 52 | 6.78 | 43 | 583.33 | 50.66 | 3.50 | 50 | 6.11 | ||
| 10 | 28 | 577.07 | 63 | 5.27 | 47 | 6.67 | 42 | 572.92 | 49.34 | 3.72 | 50 | 6.27 | ||
| 1 | 0.9 | 72 | 565.32 | 108 | 0.62 | 88 | 6.75 | 81 | 614.80 | 86.19 | 2.71 | 88 | 6.53 | |
| 2 | 84 | 570.64 | 115 | 1.16 | 101 | 7.29 | 93 | 646.93 | 98.91 | 2.55 | 99 | 6.79 | ||
| 3 | 82 | 569.74 | 112 | 1.21 | 107 | 7.37 | 94 | 649.69 | 101.49 | 2.48 | 100 | 6.45 | ||
| 4 | 76 | 560.41 | 105 | 1.18 | 96 | 7.60 | 82 | 661.03 | 89.82 | 2.83 | 91 | 7.06 | ||
| 5 | 80 | 565.92 | 114 | 0.74 | 95 | 6.93 | 83 | 624.30 | 91.74 | 3.57 | 91 | 6.54 | ||
| 6 | 74 | 562.85 | 106 | 0.85 | 88 | 7.16 | 78 | 654.74 | 86.35 | 3.22 | 91 | 6.93 | ||
| 7 | 75 | 568.91 | 111 | 0.73 | 92 | 7.26 | 81 | 642.09 | 88.37 | 2.93 | 88 | 6.65 | ||
| 8 | 82 | 567.64 | 114 | 1.11 | 95 | 7.41 | 89 | 650.47 | 96.7 | 3.52 | 98 | 6.40 | ||
| 9 | 87 | 557.68 | 116 | 0.73 | 111 | 7.73 | 95 | 669.86 | 104.6 | 3.89 | 107 | 7.02 | ||
| 10 | 79 | 572.69 | 113 | 0.74 | 89 | 7.69 | 81 | 656.42 | 87.59 | 2.19 | 93 | 6.90 | ||
| Class | k | Time (s) | Time (s) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Z | Time (s) | Z | Time (s) | s | Z | Time (s) | ||||||||
| 5 | 1 | 0.5 | 17 | 5253.77 | 69 | 44.95 | 56 | 28.76 | 42 | 2814.74 | 51.35 | 4.63 | 59 | 37.47 |
| 2 | 25 | 4864.24 | 77 | 29.77 | 69 | 29.20 | 49 | 2648.76 | 61.00 | 4.94 | 58 | 31.95 | ||
| 3 | 19 | 4911.34 | 70 | 23.29 | 63 | 28.74 | 45 | 2829.82 | 55.18 | 5.17 | 60 | 27.17 | ||
| 4 | 19 | 5395.65 | 70 | 23.28 | 63 | 27.17 | 45 | 2684.11 | 55.18 | 5.17 | 60 | 27.66 | ||
| 5 | 22 | 4974.36 | 67 | 31.68 | 62 | 29.05 | 51 | 2730.93 | 61.78 | 5.12 | 56 | 32.80 | ||
| 6 | 18 | 4923.22 | 64 | 27.89 | 59 | 29.74 | 50 | 2655.97 | 58.50 | 4.07 | 55 | 34.32 | ||
| 7 | 12 | 4861.87 | 60 | 24.29 | 60 | 31.45 | 37 | 2608.92 | 48.31 | 4.34 | 60 | 27.00 | ||
| 8 | 20 | 5402.27 | 66 | 35.56 | 59 | 29.13 | 40 | 2558.70 | 52.57 | 4.54 | 60 | 31.49 | ||
| 9 | 24 | 4885.62 | 73 | 27.62 | 63 | 29.04 | 44 | 2599.34 | 60.84 | 5.15 | 55 | 29.92 | ||
| 10 | 24 | 4419.26 | 78 | 25.60 | 65 | 30.67 | 51 | 2609.56 | 64.40 | 4.55 | 67 | 31.94 | ||
| 1 | 0.7 | 38 | 4201.84 | 114 | 18.51 | 73 | 33.97 | 65 | 3017.16 | 75.20 | 4.22 | 78 | 36.74 | |
| 2 | 50 | 3991.92 | 130 | 19.61 | 86 | 33.79 | 73 | 2913.28 | 86.04 | 4.68 | 90 | 37.23 | ||
| 3 | 43 | 4041.12 | 113 | 12.01 | 86 | 32.15 | 71 | 2999.65 | 79.42 | 4.66 | 76 | 34.48 | ||
| 4 | 42 | 3957.44 | 113 | 12.03 | 86 | 35.29 | 71 | 3145.89 | 79.42 | 4.66 | 76 | 33.11 | ||
| 5 | 52 | 4047.37 | 116 | 17.34 | 93 | 37.33 | 75 | 3507.80 | 87.25 | 4.63 | 93 | 35.64 | ||
| 6 | 38 | 3927.64 | 104 | 22.18 | 70 | 35.53 | 63 | 3184.77 | 75.36 | 4.88 | 70 | 34.16 | ||
| 7 | 34 | 4011.76 | 103 | 19.59 | 66 | 35.75 | 55 | 2914.08 | 64.86 | 4.73 | 60 | 29.64 | ||
| 8 | 43 | 3857.57 | 106 | 18.26 | 72 | 38.73 | 60 | 3320.67 | 74.16 | 5.43 | 66 | 32.35 | ||
| 9 | 49 | 3800.13 | 118 | 14.67 | 86 | 39.38 | 72 | 3272.55 | 84.98 | 4.80 | 86 | 31.98 | ||
| 10 | 50 | 3950.53 | 124 | 16.40 | 101 | 38.93 | 82 | 3253.40 | 94.82 | 4.77 | 95 | 31.07 | ||
| 1 | 0.9 | 146 | 10,977.90 | 189 | 6.92 | 149 | 42.97 | 143 | 3448.07 | 151.84 | 4.03 | 155 | 37.93 | |
| 2 | 178 | 10,537.90 | 221 | 3.97 | 180 | 44.10 | 167 | 3615.78 | 178.19 | 5.42 | 179 | 40.37 | ||
| 3 | 157 | 12,930.10 | 198 | 6.87 | 163 | 43.49 | 154 | 3596.70 | 163.57 | 4.05 | 164 | 39.40 | ||
| 4 | 158 | 10,631.30 | 198 | 6.88 | 163 | 43.19 | 154 | 3861.99 | 163.57 | 4.05 | 164 | 41.24 | ||
| 5 | 164 | 10,579.00 | 196 | 4.63 | 172 | 45.08 | 158 | 4092.14 | 167.92 | 4.32 | 171 | 39.66 | ||
| 6 | 151 | 10,777.20 | 185 | 5.01 | 147 | 42.58 | 139 | 4020.81 | 147.77 | 3.73 | 157 | 36.80 | ||
| 7 | 145 | 10,424.40 | 174 | 5.34 | 145 | 41.28 | 139 | 3908.27 | 148.16 | 4.24 | 151 | 40.67 | ||
| 8 | 149 | 10,667.60 | 183 | 3.42 | 162 | 45.03 | 150 | 3948.83 | 158.85 | 3.77 | 153 | 39.06 | ||
| 9 | 156 | 10,715.10 | 200 | 6.03 | 167 | 42.30 | 154 | 3716.99 | 164.78 | 4.07 | 171 | 37.46 | ||
| 10 | 160 | 10,486.20 | 201 | 6.72 | 171 | 46.17 | 162 | 3679.30 | 172.11 | 4.45 | 177 | 38.39 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Urbán Rivero, L.E.; Velasco, J.; Ramírez Rodríguez, J. A Simple Greedy Heuristic for Site Specific Management Zone Problem. Axioms 2022, 11, 318. https://doi.org/10.3390/axioms11070318
Urbán Rivero LE, Velasco J, Ramírez Rodríguez J. A Simple Greedy Heuristic for Site Specific Management Zone Problem. Axioms. 2022; 11(7):318. https://doi.org/10.3390/axioms11070318
Chicago/Turabian StyleUrbán Rivero, Luis Eduardo, Jonás Velasco, and Javier Ramírez Rodríguez. 2022. "A Simple Greedy Heuristic for Site Specific Management Zone Problem" Axioms 11, no. 7: 318. https://doi.org/10.3390/axioms11070318
APA StyleUrbán Rivero, L. E., Velasco, J., & Ramírez Rodríguez, J. (2022). A Simple Greedy Heuristic for Site Specific Management Zone Problem. Axioms, 11(7), 318. https://doi.org/10.3390/axioms11070318







