On r-Ideals and m-k-Ideals in BN-Algebras

Abstract

A BN-algebra is a non-empty set $X$ with a binary operation “$\ast$” and a constant 0 that satisfies the following axioms: $\left(B1\right) x\ast x=0,$ $\left(B2\right) x\ast 0=x,$ and $\left(BN\right) \left(x\ast y\right)\ast z=\left(0\ast z\right)\ast \left(y\ast x\right)$ for all $x, y, z \in X$. A non-empty subset $I$ of $X$ is called an ideal in BN-algebra X if it satisfies $0\in X$ and if $y\in I$ and $x\ast y\in I$, then $x\in I$ for all $x,y\in X$. In this paper, we define several new ideal types in BN-algebras, namely, r-ideal, k-ideal, and m-k-ideal. Furthermore, some of their properties are constructed. Then, the relationships between ideals in BN-algebra with r-ideal, k-ideal, and m-k-ideal properties are investigated. Finally, the concept of r-ideal homomorphisms is discussed in BN-algebra.

1. Introduction

J. Neggers and H.S. Kim introduced the B-algebra, which is a non-empty set $X$ with a binary operation $\ast$ and a constant 0, denoted by $\left(X; \ast , 0\right)$, that fulfills the axioms (B1) $x\ast x=0$, (B2) $x\ast 0=x$, and (B3) $\left(x\ast y\right)\ast z=x\ast \left(z\ast \left(0\ast y\right)\right)$ for all $x,y,z\in X$ (see [1]). H.S. Kim and H.G. Park discuss a special form of B-algebra, called 0-commutative B-algebra, which also satisfies a further axiom, namely, $x\ast \left(0\ast y\right)=y\ast \left(0\ast x\right)$ for all $x,y\in X$ (see [2]). Furthermore, C. B. Kim constructed the related BN-algebra, which is an algebra $\left(X; \ast , 0\right)$ that satisfies axioms (B1) and (B2), as well as (BN) $\left(x\ast y\right)\ast z=\left(0\ast z\right)\ast \left(y\ast x\right)$ for all $x,y,z\in X$ (see [3]). For example, let $X=\left\{0, 1, 2\right\}$ be a set with a binary operation “$\ast$” on $X$ as shown in Table 1.

Table 1. Cayley’s table for $\left(X; \ast ,0\right)$.

*	0	$1$	$2$
0	0	$1$	$2$
$1$	$1$	0	$1$
$2$	$2$	$1$	0

Then, $\left(X; \ast ,0\right)$ is a BN-algebra.

A BN-algebra $\left(X; \ast ,0\right)$ that satisfies $\left(x\ast y\right)\ast z=x\ast \left(z\ast y\right)$ for all $x, y,z \in X$ is said to be a BN-algebra with condition D. A. Walendziak introduced another special form of BN-algebra, namely, a BN₁-algebra, which is a BN-algebra $\left(X; \ast ,0\right)$ that satisfies $x=\left(x\ast y\right)\ast y$ for all $x, y \in X$ (see [4]). Furthermore, the new QM-BZ-algebras were proposed by Y. Du and X. Zhang (see [5]). The relationship between B-algebra and BN-algebra is that every 0-commutative B-algebra is a BN-algebra, and a BN-algebra with condition D is a B-algebra. The relationship between a BN-algebra and other algebras can be seen in Figure 1.

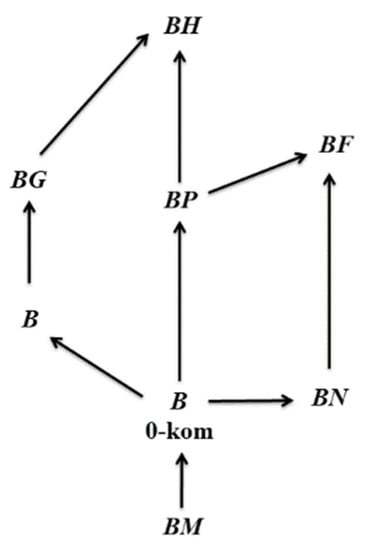
Figure 1. The relationship of BN-algebra with other algebras.

In 2017, E. Fitria et al. discussed the concept of prime ideals in B-algebras, which produces a definition and various prime ideals and their properties in B-algebras, including that a non-empty subset I is said to be ideal in a B-algebra X if it satisfies $0\in X$ and if $y\in I,$ $x\ast y\in I$ applies to $x\in I$ for all $x,y\in X$ (see [6]). Moreover, $I$ is called a prime ideal of $X$ if it satisfies $A{\displaystyle \cap }B\subseteq I$; then, $A\subseteq I$ or $B\subseteq I$ for all $A$ and $B$ are two ideals in $X$. The concept of the ideal was also discussed in BN-algebras by G. Dymek and A. Walendziak, and the resulting definition of an ideal in BN-algebras is the same as in B-algebras, but their properties differ (see [7]).

In [3], the definition of a homomorphism in BN-algebras was given: for two BN-algebras $\left(X; \ast , 0\right)$ and $\left(Y; \ast , 0\right)$, a mapping $\phi :X \to Y$ is called a homomorphism of $X$ to $Y$ if it satisfies $\phi \left(x\ast y\right)=\phi \left(x\right)\ast \phi \left(y\right)$ for all $x,y\in X$. In [7], G. Dymek and A. Walendziak stated that the kernel of $\phi$ is an ideal of $X$. In addition, G. Dymek and A. Walendziak also investigated the kernel by letting $X$ and $Y$ be a BN-algebra and a BM-algebra, respectively, such that the kernel $\phi$ is a normal ideal. The concepts of ideals are also discussed in [8].

In 2020, S. Gemawati et al. discussed the concept of a complete ideal (briefly, c-ideal) of BN-algebra and introduced the concept of an n-ideal in BN-algebra (see [9]). From this research, several interesting properties were obtained that showed the relationship between an ideal, c-ideal, and n-ideal, as well as the relationship between a subalgebra and a normal with a c-ideal and n-ideal in BN-algebras. The research also discussed the concepts of a c-ideal and n-ideal in a homomorphism of BN-algebra and BM-algebra. In 2016, M. A. Erbay et al. defined the concept of an r-ideal in commutative semigroups (see [10]). Furthermore, M. M. K. Rao defined the concept of an r-ideal and m-k-ideal in an incline (see [11]). An incline is a non-empty set $M$ with two binary operations, addition (+) and multiplication ($·)$, satisfying certain axioms. For example, let $M=\left[0,1\right]$ be subject to a binary operation “+” defined by $a+b=\max \left\{a,b\right\}$ for all $a,b\in M$, and multiplication defined by $xy=\min \left\{x,y\right\}$ for all $x,y\in M$. Then, $M$ is an incline. However, interesting properties were obtained from the concepts of an r-ideal and m-k-ideal in an incline, such as a relationship between an ideal, r-ideal, and m-k-ideal in an incline, as well as properties of these ideals in a homomorphism of incline.

Based on this description, the concepts of an r-ideal, a k-ideal, and a m-k-ideal in BN-algebras are discussed and their properties determined, followed by the properties of homomorphism in BN-algebras.

2. Preliminaries

In this section, some definitions that are needed to construct the main results of the study are given. We start with some definitions and theories about B-algebra and BN-algebra. Then, we give the concepts of an r-ideal in a semigroup, and a k-ideal and m-k-ideal in an incline, as discussed in [1,2,3,4,6,10,11].

Definition 1

([1]). A B-algebra is a non-empty set $X$ with a constant0 and a binary operation “$\ast$” that satisfies the following axioms for all x, y, z ∈ X:

(B1) 

x ∗ x = 0;

(B2) 

x ∗ 0 = x;

(B3) 

(x ∗ y) ∗ z = x ∗ (z ∗ (0 ∗ y)).

Definition 2

([3]). A BN-algebra is a non-empty set $X$ with a constant0 and a binary operation “$\ast$” that satisfies axioms (B1) and (B2), as well as (BN) $\left(x\ast y\right)\ast z=\left(0\ast z\right)\ast \left(y\ast x\right)$, for all x, y, z ∈ X.

Theorem 1

([3]). Let $\left(X; \ast , 0\right)$ be a BN-algebra, then for all x, y, z ∈ X:

(i) 

0 ∗ (0 ∗ x) = x;

(ii) 

$y\ast x=\left(0\ast x\right)\ast \left(0\ast y\right)$

(iii) 

$\left(0\ast x\right)\ast y=\left(0\ast y\right)\ast x$;

(iv) 

If $x\ast y=0$, then $y\ast x=0$;

(v) 

If $0\ast x=0\ast y$, then $x=y$;

(vi) 

$\left(x\ast z\right)\ast \left(y\ast z\right)=\left(z\ast y\right)\ast \left(z\ast x\right)$.

Let $\left(X; \ast , 0\right)$ be an algebra. A non-empty set S is called a subalgebra or BN-subalgebra of $X$ if it satisfies $x\ast y \in S$ for all x, y ∈ S, and a non-empty set $N$ of $X$ is called normal in $X$ if it satisfies $\left(x\ast a\right)\ast \left(y\ast b\right)\in N$ for all $x\ast y, a\ast b\in N.$ Let $\left(X; \ast , 0\right)$ and $\left(Y; \ast ,0\right)$ be BN-algebras. A map $\phi :X \to Y$ is called a homomorphism of $X$ to $Y$ if it satisfies $\phi \left(x\ast y\right)=\phi \left(x\right)\ast \phi \left(y\right)$ for all $x,y\in X$. A homomorphism of $X$ to itself is called an endomorphism.

Definition 3

([7]). A non-empty subset I of BN-algebra X is called an ideal of X if satisfies

(i) 

$0\in I$;

(ii) 

$x\ast y\in I$ and $y\in I$ implies $x\in I,$ for all $x,y\in X.$

An ideal I of a BN-algebra X is called a closed ideal if $a\ast b\in I$ for all $a,b\in I$. In the following, some properties of ideals in BN-algebra are as given in [7].

Proposition 1.

If I isa normalidealinBN-algebra $A$, then I isasubalgebraof $A$.

Proposition 2.

Let $A$ be a BN-algebra and $S\subseteq A$. $S$ is a normal subalgebra of $A$ if and only if $S$ isa normal ideal.

Definition 4

([3]). An algebra $\left(X; \ast ,0\right)$ is called 0-commutative if, for all $x, y\in X$,

x ∗ (0 ∗ y) = y ∗ (0 ∗ x).

A semigroup is a non-empty set G, together with an associative binary operation, we can write $\left(x\cdot y\right)\cdot z=x\cdot \left(y\cdot z\right)$ for all x, y, z ∈ $G$. An ideal of semigroup $G$ is a subset $A$ of $G$ such that $A\cdot G$ and $G\cdot A$ is contained in $G$. Any element $x$ of $G$ is a zero divisor if $ann\left(x\right)=\left\{g\in G:g\cdot x=0\right\}\ne 0$.

Definition 5

([10]). Let $G$ be a semigroup. A proper ideal $A$ of $G$ is said to be an r-ideal of $G$ if when $x\cdot y\in A$ with $ann\left(x\right)=0$, then $y\in A$ for all$x, y\in G$.

Definition 6

([11]). An incline is a non-empty set $M$ with two binary operations, namely, addition (+) and multiplication ($·$), satisfying the following axioms for all x, y, z ∈ X:

(i) 

$x+y=y+x$;

(ii) 

$x+x=x$;

(iii) 

$x+xy=x$;

(iv) 

$y+xy=y$;

(v) 

$x+\left(y+z\right)=\left(x+y\right)+z$;

(vi) 

$x\left(yz\right)=\left(xy\right)z$;

(vii) 

$x\left(y+z\right)=xy+xz$;

(viii) 

$\left(x+y\right)z=xz+yz$;

(ix) 

$x1=1x=x$;

(x) 

$x+0=0+x=x$.

A subincline of an incline M is a non-empty subset I of M that is closed under addition and multiplication. Note that $x\le y$ iff $x+y=y$ for all $x,y\in M.$

Definition 7

([11]). Let $M$ be an incline and $I$ a subincline of M. I is called an ideal of M if when $x\in I$, $y\in M$, and $y\le x$, then $y\in I.$

Definition 8

([11]). Let $M$ be an incline and $I$ a subincline of M. I is said to be a left r-ideal of M if $MI\subseteq I$ and I is said to be a right r-ideal of M if $IM\subseteq I$. If I is a left and right r-ideal of M, then I is called an r-ideal of M.

Definition 9

([11]). Let $M$ be an incline and $I$ be a subincline of M. I is said to be a k-ideal of M if when $x+y\in I$ and $y\in I$, then $x\in I.$

Definition 10

([11]). Let $M$ be an incline and $I$ be an ideal of M. I is said to be an m-k-ideal of M if $xy\in I,$ $x\in I,$ and $1\ne y\in M,$ then $y\in I.$

3. r-Ideal in BN-Algebra

In this section, the main results of the study are given. Starting from the definition of an r-ideal in BN-algebras, which was constructed based on the concept of r-ideal in a semigroup. Then, some properties of r-ideals in BN-algebras are investigated.

Definition 11.

Let $\left(X; \ast , 0\right)$ be a BN-algebraand $I$ be a proper ideal of $X$. $I$ is called an r-ideal of $X$ if when $x\ast y\in I$ and $0\ast x=0$, then $y\in I$ for all $x,y\in X$.

Example 1.

Let $A=\left\{0, 1, 2, 3\right\}$ be a set. Define a binary operation “ $\ast$” with theTable 2.

Table 2. Cayley’s table for $\left(A; \ast ,0\right)$.

*	0	1	2	3
0	0	1	2	3
1	1	0	1	1
2	2	1	0	1
3	3	1	1	0

Then, $\left(A; \ast ,0\right)$ is a BN-algebra. We obtain that $I_1=\left\{0,2\right\}$, $I_2=\left\{0,3\right\}$, and $I_3=\left\{0, 2, 3\right\}$ are r-ideals in A.

In the following, the properties of an r-ideal in BN-algebras are given.

Theorem 2.

Let $\left(X; \ast , 0\right)$ be a BN-algebra. If $I$ is a closed ideal of X, then I is an r-ideal of X.

Proof. 

Since I is an ideal of X, then $0\in I$; furthermore, if $y\in I$ and $x\ast y\in I$, then $x\in I$ for all $x,y\in X$. Let $x\ast y\in I$ and $0\ast x=0$ for all $x, y\in X$. Since $I$ is closed, if we can prove that $x\in I$, then it shows that $y\in I$. By Theorem 1 (ii) and Axiom B2, we obtain

$$x\ast y=\left(0\ast y\right)\ast \left(0\ast x\right)=\left(0\ast y\right)\ast 0=0\ast y$$

(1)

Furthermore, by (1), Theorem 1 (i), and by all axioms of BN-algebra, we obtain

$$y\ast x=\left(y\ast x\right)\ast 0=\left(0\ast 0\right)\ast \left(x\ast y\right)=0\ast \left(0\ast y\right)=y$$

(2)

By (1) and (2), we obtain $x=0\in I$. Thus, we obtain $y\in I$. Therefore, I is an r-ideal of X. □

The converse of Theorem 2 does not hold in general. In Example 1, $I_1$ and $I_2$ are two closed ideals in A, and thus, $I_1$ and $I_2$ are clearly r-ideals. Meanwhile, $I_3=\left\{0, 2, 3\right\}$ is an ideal in A, but it is not a closed ideal. However, $I_3$ is an r-ideal in A. It should be noted that not all ideals are r-ideals. To be clear, consider the following example.

Example 2.

Let $X=\left(\mathbb{Z};-, 0\right)$ be a set of integers $\mathbb{Z}$ with a subtraction operation. Then, $X$ is a BN-algebra. Let subset ${\mathbb{Z}}^{+}$ of $X$ be positive integers, then $I={\mathbb{Z}}^{+}{\displaystyle \cup }\left\{0\right\}$ is an ideal of $X$, but $I$ is not a closed ideal and it is not an r-ideal of $X$.

Theorem 3.

Let $\left(X; \ast , 0\right)$ be a BN-algebra. If $I$ is a normal ideal of X, then I is a normal r-ideal of X.

Proof. 

Since I is a normal ideal of X, then, by Proposition 1, we have that $I$ is a BN-subalgebra of $X$, which for all $x, y\in I$, $x\ast y\in I$ implies that $I$ is closed. Furthermore, by Theorem 2, we obtain that $I$ is an r-ideal of $X$. Since $I$ is normal, then I is a normal r-ideal of X. □

Theorem 4.

Let $\left(X; \ast , 0\right)$ be a BN-algebra and $f$ be an endomorphism of X. If $I$ is an r-ideal of X, then $f\left(I\right)$ is an r-ideal of X.

Proof. 

Let I be an r-ideal of X, then clearly $I\subset X$ and I is a proper ideal of X such that $0\in I$ and $f\left(I\right)\subset X$. Since $f$ is an endomorphism of X and by Axiom B1, for all $x\in I$, we obtain

$$f\left(0\right)=f\left(x\ast x\right)=f\left(x\right)\ast f\left(x\right)=0\in I.$$

Let $f\left(y\right)\in f\left(I\right)$ and $f\left(x\ast y\right)\in f\left(I\right)$. Since I is an ideal of X, then $x\in I$; consequently, $f\left(x\right)\in f\left(I\right)$. Thus, $f\left(I\right)$ is an ideal of X. Let $f\left(x\ast y\right)\in f\left(I\right)$ and $0\ast f\left(x\right)=0$. Since I is an r-ideal of X, then $y\in I$ implies $f\left(y\right)\in f\left(I\right)$. Therefore, $f\left(I\right)$ is an r-ideal of X. □

The converse of Theorem 4 does hold in general.

Corollary 1.

Let $\left(X; \ast , 0\right)$ be a BN-algebra and$f$ be an endomorphism of X. If $I$ is a closed r-ideal of X, then $f\left(I\right)$ is a closed r-ideal of X.

Proof. 

Follows directly from Theorem 4. □

Example 3.

Let $A=\left\{0, 1, 2, 3\right\}$ be aBN-algebra in Example 1. Define a map $f:A\to A$ by

$$f\left(x\right)=\{\begin{array}{c}\begin{array}{c}0 \mathrm{if} x=0\\ 1 \mathrm{if} x=1\end{array}\\ \begin{array}{c}3 \mathrm{if} x=2\\ 2 \mathrm{if} x=3\end{array}\end{array}$$

Then, $f$ is an endomorphism. By Example 1, we obtain that $I_1=\left\{0,2\right\}$, $I_2=\left\{0,3\right\}$, and $I_3=\left\{0, 2, 3\right\}$ are r-ideals in A. It easy to check that $f(I_1)=\left\{0,3\right\}$ and $f(I_2)=\left\{0,2\right\}$ are two closed r-ideals of A. However, $f(I_3)=\left\{0,2,3\right\}$ is an r-ideal of A, but it is not closed.

4. m-k-Ideals in BN-Algebras

This section gives the main results of the study. We start by defining the concepts of k-ideal and m-k-ideal in a BN-algebra, which is constructed based on the concept of a k-ideal and m-k-ideal in an incline. The properties of k-ideals and m-k-ideals in a BN-algebra are given.

Definition 12.

Let $\left(X; \ast , 0\right)$be aBN-algebraand $I$ be a BN-subalgebra of $X$. $I$ is called a k-ideal in $X$ if when $y\in I, x\in X,$ and $x\ast y\in I,$ then $x\in I.$

Example 4.

Let $B=\left\{0, 1, 2, 3, 4, 5, 6, 7\right\}$ be a set. Define a binary operation “ $\ast$” with theTable 3.

Table 3. Cayley’s table for $\left(B; \ast ,0\right)$.

*	0	1	2	3	4	5	6	7
0	0	1	2	3	4	5	6	7
1	1	0	3	2	5	4	7	6
2	2	3	0	1	6	7	4	5
3	3	2	1	0	7	6	5	4
4	4	5	6	7	0	1	2	3
5	5	4	7	6	1	0	3	2
6	6	7	4	5	2	3	0	1
7	7	6	5	4	3	2	1	0

Then $\left(B; \ast ,0\right)$ is a BN-algebra. It is easy to check that $I_1=\left\{0,1\right\}$, $I_2=\left\{0,2\right\}$, $I_3=\left\{0,3\right\}$, $I_4=\left\{0,4\right\}$, $I_5=\left\{0,5\right\}$, $I_6=\left\{0,6\right\}$, $I_7=\left\{0,7\right\}$, and $I_8=\left\{0, 1, 2, 3\right\}$ are closed ideals in B and also BN-subalgebras in B. Thus, we can prove that they are k-ideals in B.

Some properties of a k-ideal in BN-algebras are given.

Theorem 5.

Let $\left(X; \ast , 0\right)$ be a BN-algebra.If $I$ is a closed ideal of$X$, then $I$ is a k-ideal of $X$.

Proof. 

Let $\left(X; \ast , 0\right)$ be a BN-algebra. Let I be a closed ideal of $X$. Then, I is a BN-subalgebra of $X$, and if $y\in I$, $x\in X$, and $x\ast y\in I$, then $x\in I$. Therefore, $I$ is a k-ideal of $X$. □

Theorem 6.

Let $\left(X; \ast , 0\right)$ be a BN-algebra.If $I$ is a k-ideal of $X$, then I is a closed ideal of $X$.

Proof. 

Let $\left(X; \ast , 0\right)$ be a BN-algebra. Since $I$ is a k-ideal of $X$, then I is a BN-subalgebra of $X$. Consequently, $I$ is closed and for all $x\in I$, $x\ast x=0\in I$. Moreover, since $I$ is a k-ideal of $X$ that is obtained when $y\in I, x\in X,$ and $x\ast y\in I,$ then $x\in I$. Thus, I is a closed ideal of $X$. □

Corollary 2.

Let $\left(X; \ast , 0\right)$ be a BN-algebra. $I$ is a closed ideal of $X$ if and only if $I$ is a k-ideal of $X$.

Proof. 

Follows directly from Theorems 5 and 6. □

Theorem 7.

Let $\left(X; \ast , 0\right)$ be a BN-algebra. If $N$ is a normal BN-subalgebra of $X$, then $N$ is a normal k-ideal of $X$.

Proof. 

Since $N$ is a normal BN-subalgebra of $X,$ then, by Proposition 2, it is obtained that $N$ is a normal ideal of $X$. We know that $N$ is a BN-subalgebra such that it is a closed ideal of $X$. Consequently, by Theorem 5, it is obtained that $N$ is a k-ideal of $X$. Since $N$ is normal, then $N$ is a normal k-ideal of $X$. □

Definition 13.

Let $\left(X; \ast , 0\right)$ be aBN-algebraand $I$ be an ideal of $X$. I is called an m-k-ideal of $X$ if when $x\in I, 0\ne y\in X,$ and $x\ast y\in I,$ then $y\in I.$

Theorem 8.

Let $\left(X; \ast , 0\right)$ be a BN-algebra.If $I$ is a k-ideal of $X$, then $I$ is an m-k-ideal.

Proof. 

Let $\left(X; \ast , 0\right)$ be a BN-algebra. Since $I$ is a k-ideal of $X$, then by Theorem 6, $I$ is a closed ideal of $X$ such that if $y\in I$, $x\in X,$ and $x\ast y\in I,$ then $x\in I$. Furthermore, since $I$ is closed, it must be the case that if $x\in I, 0\ne y\in X,$ and $x\ast y\in I,$ then $y\in I$. Hence, we prove that $I$ is an m-k-ideal of $X.$ □

The converse of Theorem 8 does not hold in general. Let $A=\left\{0, 1, 2, 3\right\}$ be a BN-algebra in Example 1. It is easy to check that $I_1=\left\{0,2\right\}$ and $I_2=\left\{0,3\right\}$ are k-ideals and m-k-ideals of A. Meanwhile, $I_3=\left\{0, 2, 3\right\}$ is an m-k-ideal in A, but $I_3$ is not k-ideal because it is not a BN-subalgebra of A.

Theorem 9.

Let $\left(X; \ast , 0\right)$ be a BN-algebra.If $I$ is a closed ideal of $X$, then $I$ is an m-k-ideal.

Proof. 

Follows directly from Theorems 5 and 8. □

Theorem 10.

Let $\left(X; \ast , 0\right)$ be a BN-algebra.If $I$ is a k-ideal of $X$, then $I$ is an r-ideal.

Proof. 

Since $I$ is a k-ideal of $X$, by Theorem 6, we obtain that $I$ is a closed ideal of $X$ such that by Theorem 2, we obtain that $I$ is an r-ideal of $X$. □

The converse of Theorem 10 does not hold in general since, in Example 1, we have $I_3$ as an r-ideal in $A$, but it is not a k-ideal.

Theorem 11.

Let $\left(X; \ast , 0\right)$ be a BN-algebra.If $I$ is a closed r-ideal of $X$, then $I$ is a k-ideal.

Proof. 

Since $I$ is an r-ideal of $X$, clearly $I$ is a proper ideal of $X$. Since $I$ is closed, then by Theorem 5, we obtain that $I$ is a k-ideal of $X$. □

By Theorem 10, we know that the converse of Theorem 11 does hold in general. In Example 1, $I_1$ and $I_2$ are two closed r-ideals in $A$ and also k-ideals.

Proposition 3.

Let $\left(X; \ast , 0\right)$ be a BN-algebra and $f$ be an endomorphism of X. If $I$ is a k-ideal of X, then $f\left(I\right)$ is an r-ideal of X.

Proof. 

Follows directly from Theorems 4 and 10. □

The converse of Proposition 3 does not hold in general.

Proposition 4.

Let $\left(X; \ast , 0\right)$ be a BN-algebra and $f$ be an endomorphism of X. If $f\left(I\right)$ is a closed r-ideal of X, then $I$ is a k-ideal of X.

Proof. 

Follows directly from Corollary 1 and Theorem 11. □

5. Conclusions and Future Work

In this paper, we defined the concepts of an r-ideal, k-ideal, and m-k-ideal in BN-algebras and investigated several properties. We obtained the relationships between a closed ideal, r-ideal, k-ideal, and m-k-ideal in a BN-algebra. Some of its properties are every closed ideal in BN-algebras is an r-ideal, a k-ideal, and an m-k-ideal. Every k-ideal is an r-ideal and an m-k-ideal of BN-algebras. Moreover, if $I$ is an r-ideal or k-ideal of a BN-algebra, then $f\left(I\right)$ is an r-ideal, where $f$ is an endomorphism of the BN-algebra.

We did this research to build complete concepts of an r-ideal, k-ideal, and m-k-ideal in BN-algebras. These results can be used by researchers in the field of abstract algebra to discuss more deeply about types of ideals in BN-algebras.

In future work, we will consider the concept of an r-ideal and m-k-ideal in QM-BZ-algebra and quasi-hyper BZ-algebra, investigating several properties and the relationship between an r-ideal and m-k-ideal in a QM-BZ-algebra and quasi-hyper BZ-algebra.