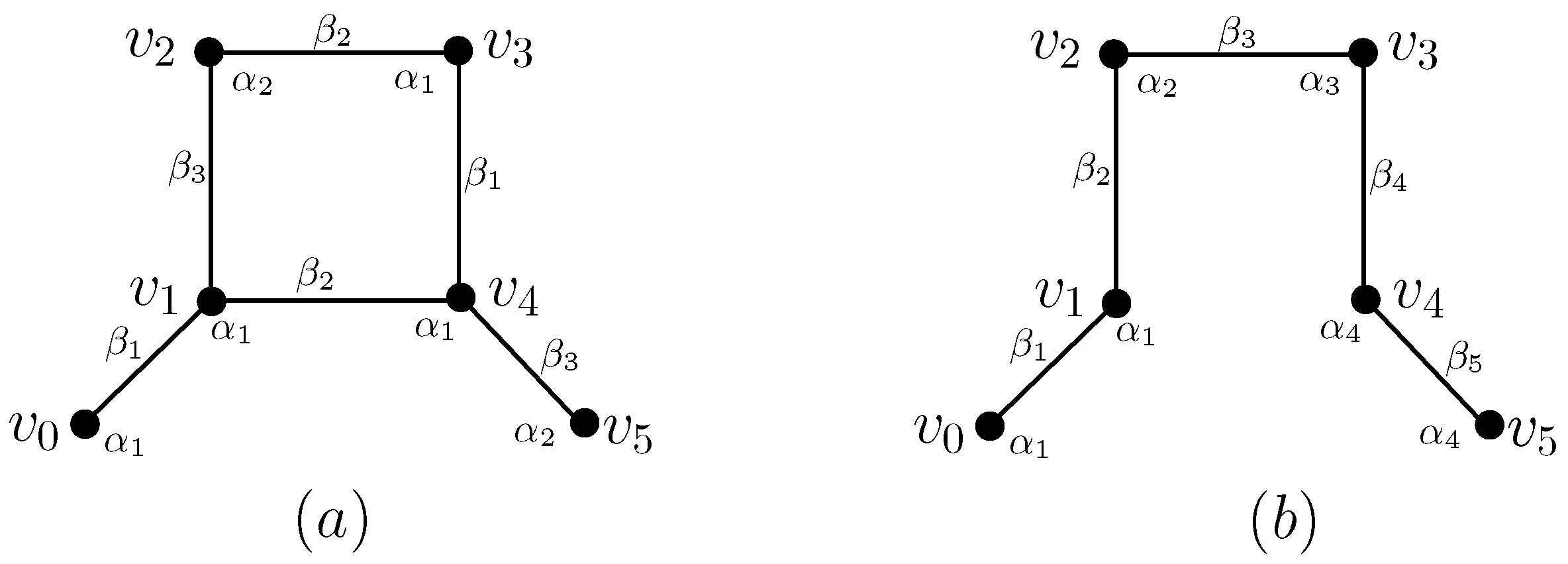Total Rainbow Connection Number of Some Graph Operations

Abstract

In a graph H with a total coloring, a path Q is a total rainbow if all elements in $V\left(Q\right)\cup E\left(Q\right)$, except for its end vertices, are assigned different colors. The total coloring of a graph H is a total rainbow connected coloring if, for any $x,y\in V\left(H\right)$, there is a total rainbow path joining them. The total rainbow connection number $trc\left(H\right)$ of H is the minimum integer r such that there is a total rainbow-connected coloring of H using r colors. In this paper, we study the total rainbow connection number of several graph operations (specifically, adding an edge, deleting an edge, and the Cartesian product) for which the total rainbow connection number is upper-bounded by a linear function of its radius.

1. Introduction

Each graph is simple, undirected, and finite in this paper. Let H be a graph.

The $distance$$d_H(x,y)$ from x to y in H is the number of edges of a shortest path joining x and y. The $eccentricity$ $ec{c}_H\left(x\right)$ of a vertex x is $ma{x}_{y\in V\left(H\right)}{d}_H(x,y)$. The $radius$ $rad\left(H\right)$ and $diameter$ $diam\left(H\right)$ of H are, respectively, $mi{n}_{u\in V\left(G\right)}ec{c}_G\left(u\right)$ and $ma{x}_{u\in V\left(G\right)}ec{c}_G\left(u\right)$. A vertex x is a $center$ of H if $ec{c}_H\left(x\right)=rad\left(H\right)$.

An edge coloring of a graph H is a mapping $c:E\left(H\right)\to A$, where A is a set of colors. A graph H with an edge coloring c is an edge-colored graph, and denoted by $(H,c)$. A total coloring of a graph H is a mapping $c:V\left(H\right)\cup E\left(H\right)\to A$, where A is a set of colors. A graph H with a total coloring c is a total-colored graph, and denoted by $(H,c)$. In an edge-colored graph $(H,c)$, a path Q is $rainbow$ if $c\left(f_1\right)\ne c\left(f_2\right)$ for $f_1,f_2\in E\left(Q\right)$ with $f_1\ne f_2$. An edge coloring is a rainbow-connected edge coloring for H if H has a rainbow path joining x and y for $x,y\in V\left(H\right)$. Such a graph H is called rainbow connected. The rainbow connection number $rc\left(H\right)$ of H is the minimum value r for which H has a rainbow-connected edge coloring using r colors.

McKeon and Zhang in [1] introduced and studied the rainbow connection number, which has applications in transferring high-security information in multicomputer networks [2,3]. We refer the readers to [4,5,6] for more results.

As one can see, the above involves the edge coloring of a graph. A natural idea is to generalize it to a concept that involves total coloring.

In a graph H with a total coloring, a path Q is total rainbow if all elements in $V\left(Q\right)\cup E\left(Q\right)$, except for its end vertices, are assigned different colors. A total coloring of a graph H is a total rainbow-connected coloring if for any $x,y\in V\left(H\right)$, there is a total rainbow path joining them. The total rainbow connection number $trc\left(H\right)$ of H is the minimum integer r such that there is a total rainbow connected coloring of H using r colors.

Uchizawa et al. introduced total rainbow connected coloring in [7]. For a total-colored graph $(H,c)$, the rainbow total-connectivity problem is designed to determine whether H is total rainbow connected. Uchizawa et al. [7] showed that the rainbow total-connectivity problem is strongly NP-complete even for outerplanar graphs. Chen et al. [8] showed that deciding whether a total-colored graph H is total rainbow connected is NP-complete. Jiang et al. [9] studied the upper bound of the total rainbow connection number of a graph with respect to its order and minimum degree. Liu et al. [10] studied the minimum number of colors required to color G, such that each pair of distinct vertices of G are connected by r internally vertex-disjoint total rainbow paths. Ma [11] studied the total rainbow connection number of a graph by some property of its complementary graph. Ma et al. [12] determined the total rainbow connection number of circular ladders and Möbius ladders. Sun [13] determined the rainbow total-connection numbers of complete graphs, trees, cycles and wheels. Sun [14] studied the upper bound of the total rainbow connection number of a graph with respect to its size.

We will study the total rainbow connection number of several graph operations. In Section 2, we how the total rainbow connection number of a graph G will change if we add (or delete) an edge in G. In Section 3, we study the total rainbow connection number of Cartesian product graphs.

2. Adding an Edge or Deleting an Edge

In this section, we shall investigate how the rainbow vertex connection number of a graph G will change if we add (or delete) an edge in G.

First, we need some new notations. A path with n vertices is denoted by $P_n$. A path Q is called an a-b path, denoted by $P_{ab}$, if a and b are its endpoints. Let H be a graph. For an integer $r\ge 1$ and subset $A\subseteq V\left(H\right)$, the r-step open neighborhood $N_H^r\left(A\right)$ is $\{y\in V\left(H\right):d_H(A,y)=r\}$. We simply write $N_H\left(A\right)$ for $N_H^1\left(A\right)$ and $N_A^r\left(x\right)$ for $N_H^r\left(\left\{x\right\}\right)$. Similarly, the r-step closed neighborhood $N_H^r\left[A\right]$ is $\{y\in V(H):d(A,y)\le r\}$. We simply write $N_H\left[A\right]$ for $N_H^1\left[A\right]$ and $N_H^r\left[x\right]$ for $N_H^r\left[\left\{x\right\}\right]$. For $A,B\subseteq V\left(H\right)$, let $E_H[A,B]$ denote $\{ab:a\in A,b\in B,ab\in E(H\left)\right\}$. For a graph H and an edge $ab\in E\left(G\right)$, we use $G-ab$ to denote the graph obtained from G by delating $ab$. For a graph H and two vertices $a,b\in V\left(H\right)$ such that $ab\notin E\left(H\right)$, we use $H+ab$ to denote the graph obtained from H by adding $xy$. We refer to the book [15] for notation and terminology not described here.

Let $Q_{v_0{v}_k}=v_0{v}_1\cdots v_k$ be a total coloring path in $(G,c)$. We define four sets of colors as follows.

$$\begin{array}{cc}\hfill & c\left(Q_{v_0{v}_k}\right)=\{c\left(f\right):f\in E\left(Q_{v_0{v}_k}\right)\}\cup \{c\left(w\right):w\in V\left(Q_{v_0{v}_k}\right)\setminus \{v_0,v_k\}\},\hfill \\ \hfill & c\left[Q_{v_0{v}_k}\right)=\{c\left(f\right):f\in E\left(Q_{v_0{v}_k}\right)\}\cup \{c\left(w\right):w\in V\left(Q_{v_0{v}_k}\right)\setminus \left\{v_k\right\}\},\hfill \\ \hfill & c\left(Q_{v_0{v}_k}\right]=\{c\left(f\right):f\in E\left(Q_{v_0{v}_k}\right)\}\cup \{c\left(w\right):w\in V\left(Q_{v_0{v}_k}\right)\setminus \left\{v_0\right\}\},\hfill \\ \hfill & c\left[Q_{v_0{v}_k}\right]=\{c\left(f\right):f\in E\left(Q_{v_0{v}_k}\right)\}\cup \{c\left(w\right):w\in V\left(Q_{v_0{v}_k}\right)\}.\hfill \end{array}$$

We can see that the following observations hold.

Observation 1.

For any connected graph H, $trc\left(H\right)=1$ if and only if H is complete, and otherwise, $trc\left(H\right)\ge 3$.

Observation 2.

For any connected graph H,

$$trc\left(H\right)\ge 2diam\left(H\right)-1.$$

Observation 3.

Let H and $H^{\prime }$ be two connected graphs. If $H^{\prime }$ is a spanning subgraph of H, then

$$trc\left(H\right)\le trc\left(H^{\prime }\right).$$

Theorem 1.

Let H be a connected graph, and let $ab$ be an edge of H for which $H-ab$ is connected. Then

$$trc\left(H\right)\le trc(H-ab)\le trc\left(H\right)+2d_{H-ab}(a,b)-1.$$

Proof. 

Since $H-ab$ is a connected spanning subgraph of H, we show that $trc\left(H\right)\le trc(H-ab)$ by Observation 3.

Next, we only need to show that $trc(H-ab)\le trc\left(H\right)+2d_{H-ab}(a,b)-1$. We fixed a total rainbow-connected coloring c of H using $trc\left(H\right)$ colors, and set $d_{H-ab}(a,b)=k$ for simplicity. We picked two sets of colors $\alpha =\{{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_{k-1}\}$ and $\beta =\{{\beta }_1,{\beta }_2,\dots ,{\beta }_k\}$ such that $\alpha \cap \beta =\varnothing$ and $(\alpha \cup \beta )\cap c\left(H\right)=\varnothing$, and let $P_{ab}=x_0{x}_1\dots x_k$ be a shortest path between a and b in $H-ab$, where $x_0=a$ and $x_k=b$. For $H-ab$, we define a $\left(trc\right(H)+2k-1)$-total coloring $c^{\prime }$ of $H-ab$ as follows:

For each $v\in V\left(H\right)$,

$$c^{\prime }\left(v\right)=\left\{\begin{array}{cc}{\alpha }_i,\hfill & ifv=x_i,1\le i\le k-1;\hfill \\ c\left(v\right),\hfill & otherwise.\hfill \end{array}\right.$$

and for each $e\in E\left(H\right)$,

$$c^{\prime }\left(e\right)=\left\{\begin{array}{cc}{\beta }_i,\hfill & ife=x_{i-1}{x}_i,1\le i\le k;\hfill \\ c\left(e\right),\hfill & otherwise.\hfill \end{array}\right.$$

Now, we will prove that $c^{\prime }$ is a total rainbow connected coloring of $H-ab$. For $u,v\in V(H-ab)$, there is a total rainbow u-v path $Q_{uv}$ in $(H,c)$ since c is a total rainbow connected coloring of H. We divide three cases.

Case 1. $V\left(Q_{uv}\right)\cap V\left(P\right)=\varnothing$.

In this case, the path $Q_{uv}$ is also a total rainbow u-v path in $(H-ab,c^{\prime })$ by definition of total coloring $c^{\prime }$,

Case 2. $|V\left(Q_{uv}\right)\cap V\left(P_{ab}\right)|=1$.

In this case, we assume that $V\left(Q_{uv}\right)\cap V\left(P_{ab}\right)=\left\{z\right\}$. If $z=a$ or $z=b$, then $Q_{uv}$ is also a total rainbow u-v path in $(H-ab,c^{\prime })$. Otherwise, the path $Q_{uv}$ is also a total rainbow u-v path in $(H-ab,c^{\prime })$ since $c^{\prime }\left(z\right)\notin c\left(Q_{uv}\right)$.

Case 3. $|V\left(Q_{uv}\right)\cap V\left(P_{ab}\right)|\ge 2$.

In this case, let $u^{\prime }$ be the first vertex on $Q_{uv}$ from u to v so that $u^{\prime }\in V\left(P_{ab}\right)\cap V\left(Q_{uv}\right)$, and $v^{\prime }$ is the last vertex on $Q_{uv}$ from u to v so that $v^{\prime }\in V\left(P_{ab}\right)\cap V\left(Q_{uv}\right)$. Let $Q_{u{u}^{\prime }}$ denote the subpath connecting u and $u^{\prime }$ on $Q_{uv}$, and let $Q_{v^{\prime }v}$ denote the subpath connecting $v^{\prime }$ and v on $Q_{uv}$.

Because $Q_{uv}$ is a total rainbow, we know that $c\left(Q_{u{u}^{\prime }}\right)\cap c\left(Q_{v^{\prime }v}\right)=\varnothing$. It follows the definition of $c^{\prime }$ that $Q_{u{u}^{\prime }}$ and $Q_{v^{\prime }v}$ are also a total rainbow in $(H-ab,c^{\prime })$ such that $c^{\prime }\left(Q_{u{u}^{\prime }}\right)\cap c^{\prime }\left(Q_{v^{\prime }v}\right)=\varnothing$ and $c^{\prime }\left(Q_{u{u}^{\prime }}\right)\cup c^{\prime }\left(Q_{v^{\prime }v}\right)\subseteq c\left(H\right)$. Pick the subpath $P_{u^{\prime }{v}^{\prime }}$ joining $u^{\prime }$ and $v^{\prime }$ on $P_{ab}$ with total coloring $c^{\prime }$. Thus, $c^{\prime }\left[P_{u^{\prime }{v}^{\prime }}\right]\subseteq \alpha \cup \beta$ and $P_{u^{\prime }{v}^{\prime }}$ is a total rainbow. Since $c\left(H\right)\cap (\alpha \cup \beta )=\varnothing$, the path $Q_{u{u}^{\prime }}\cup P_{u^{\prime }{v}^{\prime }}\cup Q_{v^{\prime }v}$ is a total rainbow in $(H-ab,c^{\prime })$.

Following the above three cases shows that $c^{\prime }$ is a total rainbow connected coloring of $H-ab$. Thus, $trc(H-ab)\le trc\left(H\right)+2d_{H-ab}(a,b)-1$. □

Remark 1.

Pick a complete graph $K_4$ with vertex set $\{v_0,v_1,v_2,v_3\}$, and let H be the graph obtained from $K_4$ by deleting edge $v_0{v}_2$. On one hand, since $diam\left(H\right)=diam(H-v_1{v}_3)=2$, by Observation 2, $trc\left(H\right)\ge 3$ and $trc(H-v_1{v}_3)\ge 3$. On the other hand, the graphs H and $H-v_1{v}_3$ have a total rainbow connected coloring using 3 colors as Figure 1a,b, respectively. Thus, $trc\left(H\right)=trc(H-v_1{v}_3)=3$, and the lower bound in Theorem 1 is sharp.

Remark 2.

Let $P_6=v_0{v}_1\cdots v_5$ be a path of length 5, and let H be the graph obtained from $P_6$ by adding edge $v_1{v}_4$. See Figure 2a for details. Since $diam\left(H\right)=3$, we know that $trc\left(H\right)\ge 2diam\left(H\right)-1=5$ from Observation 2. Moreover, the graph H has a total rainbow connected coloring using 5 colors as Figure 2a. So $trc\left(H\right)=5$. Since $diam(H-v_1{v}_4)=5$, we know that $trc(H-v_1{v}_4)\ge 2diam(H-v_1{v}_4)-1=9$ from Observation 2. Moreover, the graph $H-v_1{v}_4$ has a total rainbow connected coloring using 9 colors as shown in Figure 2b. So $trc(H-v_1{v}_4)=9$. Thus, $trc(H-v_1{v}_4)=9=trc\left(H\right)+2d_{H-v_1{v}_4}(v_1,v_4)-2$, and the upper bound in Theorem 1 is almost sharp.

Corollary 1.

Let H be a connected graph. Pick $xy\in E\left(H\right)$ such that $H-xy$ is connected. Then

$$trc\left(H\right)\le trc(H-xy)\le trc\left(H\right)+2diam(H-xy)-1.$$

Theorem 2.

Let H be a connected graph. Pick $x,y\in V\left(H\right)$ such that $xy\notin E\left(H\right)$. Then

$$trc\left(H\right)-2d_H(x,y)+1\le trc(H+xy)\le trc\left(H\right).$$

Proof. 

Since H is an induced subgraph of $H+xy$, we have that $trc(H+xy)\le trc\left(H\right)$ by Observation 3.

Next, we only need to prove that $trc\left(H\right)-2d_H(x,y)+1\le trc(H+xy)$. Let $H^{\prime }=H+xy$. Then $H^{\prime }-xy=H$. By Theorem 1, we know that $trc(H^{\prime }-xy)\le trc\left(H^{\prime }\right)+2d_{H^{\prime }-xy}(x,y)-1$, i.e., $trc\left(H\right)\le trc(H+xy)+2d_H(x,y)-1$. Thus, $trc(H+xy)\ge trc\left(H\right)-2d_H(x,y)+1$. □

Remark 3.

Let H be the graph in Remark 1. Then $H^{\prime }=H-v_1{v}_3$ and $e=v_1{v}_3$ is a sharp example of the upper bound in Theorem 2. Let H be the graph in Remark 2. Then $H^{\prime }=H-v_1{v}_4$ and $e=v_1{v}_4$ is an almost sharp example of the lower bound in Theorem 2.

Corollary 2.

Let H be a connected graph. Pick $x,y\in V\left(H\right)$ such that $xy\notin E\left(H\right)$. Then

$$trc\left(H\right)-2diam\left(H\right)+1\le trc(H+xy)\le trc\left(H\right).$$

3. Cartesian Product

Let I and J be two graphs. Their Cartesian product$I\square J$ is the graph with vertex set $V\left(I\right)\times V\left(J\right)$, and $(i,i)$ and $(i^{\prime },i^{\prime })$ are adjacent if and only if $i=i^{\prime }$ and $j{j}^{\prime }\in E\left(J\right)$, or $j=j^{\prime }$ and $i{i}^{\prime }\in E\left(I\right)$. It is easy to check that $rad(I\square J)=rad\left(I\right)+rad\left(J\right)$ and $diam(I\square J)=diam\left(I\right)+diam\left(J\right)$.

Let I and J be two graphs. Assume that $V\left(I\right)$ = $\{x_1,x_2,\dots ,$$x_n\}$ and $V\left(J\right)=\{y_1,y_2,\dots ,y_m\}$. Define serval mappings as follows.

For a $y_a\in V\left(J\right)$, define

$$\begin{array}{cc}\hfill & x^{y_a}:=(x,y_a)\mathrm{for}\mathrm{each}\mathrm{vertex}x\in V\left(I\right),\hfill \\ \hfill & I_1^{y_a}:=(V\left(I_1^{y_a}\right),E\left(I_1^{y_a}\right))\mathrm{for}\mathrm{each}\mathrm{subgraph}{I}_1\subseteq I,\hfill \end{array}$$

where $V\left(I_1^{y_a}\right)=\{(x,y_a):u\in V\left(I_1\right)\}$ and $E\left(I_1^{y_a}\right)=\{(x,y_a)(x^{\prime },v_a):x{x}^{\prime }\in E\left(I_1\right)\}$.

For a $y_b\in V\left(J\right)$, define

$$\begin{array}{cc}\hfill & {(x,y_a)}^{y_b}:=(x,y_b)\mathrm{for}\mathrm{each}\mathrm{vertex}(x,y_a)\in V\left(I^{y_a}\right),\hfill \\ \hfill & I_1^{y_b}:=(V\left(I_1^{y_b}\right),E\left(I_1^{y_b}\right))\mathrm{for}\mathrm{each}\mathrm{subgraph}{I}_1\subseteq I^{y_a},\hfill \end{array}$$

where $V\left(I_1^{y_b}\right)=\{(x,y_b):(x,y_a)\in V\left(I_1^{y_a}\right)\}$ and $E\left(I_1^{y_b}\right)=\{(x,y_b)(x^{\prime },y_b):(x,v_a)(x^{\prime },y_a)\in E\left(I_1^{y_a}\right)\}$.

Similarly, for $u_a\in V\left(I\right)$, define mappings $v^{u_a}$ for each $v\in V\left(J\right)$, $J_1^{u_a}$ for subgraph $J_1\subseteq J$; for $u_b\in V\left(I\right)$, define mappings ${(u_a,v)}^{u_b}$ for $(u_a,v)\in V\left(J^{u_a}\right)$, and $J_1^{u_b}$ for $J_1\subseteq J^{u_a}$.

An r-tree is a tree with a root r. For a r-tree R, $rTv$ is the only path connecting r and v in R. The level${\ell }_R\left(v\right)$ of a vertex v in R is the length of the path $rTv$. The depth of an r-tree is $dep\left(R\right)=max\{{\ell }_R\left(v\right):v\in V\left(R\right)\}$.

If $x\in rRy$, then x is an ancestor of y, and y is a descendant of x. In R, both vertices are related if one is a descendant of the other.

Given an r-tree R and two sets of colors $\alpha =\{{\alpha }_i:0\le i\le dep\left(R\right)\}$ and $\gamma =\{{\gamma }_i:1\le i\le dep\left(R\right)\}$, we define a $(\alpha ,\gamma )$-total coloringc of R as follows:

$$c\left(v\right)={\alpha }_{{\ell }_R\left(v\right)}foranyv\in V\left(R\right)$$

and

$$c\left(e\right)={\gamma }_{k}foranye=xy\in E\left(R\right),$$

where $k=max\{{\ell }_R\left(x\right),{\ell }_R\left(y\right)\}$.

Now, we are ready to show the following result.

Theorem 3.

Let I and J be two connected, non-trivial graphs. Then

$$2rad(I\square J)-1\le trc(I\square J)\le 4rad(I\square J).$$

Proof. 

Since $trc(I\square J)\ge 2diam(I\square J)-1\ge 2rad(I\square J)-1$, we have $trc(I\square J)\ge 2rad(I\square J)-1$. Thus, the lower bound holds.

Next, we prove that the upper bound is true. Pick a breadth-first search tree (or BFS-tree) R in I rooted at some center $u_0$, and pick a breadth-first search tree (or BFS-tree) Q in J rooted at some center $v_0$. To prove that $trc(I\square J)\le 4rad(I\square J)$, it is sufficient to prove that $trc(R\square Q)\le 4rad(I\square J)$ from Observation 3.

Let $V\left(I\right)=V\left(R\right)=\{u_0,u_1,\cdots ,u_n\}$, $V\left(J\right)=V\left(Q\right)=\{v_0,v_1,\cdots ,v_m\}$, $dep\left(R\right)=a$ and $dep\left(Q\right)=b$. It is easy to see that $dep\left(R\right)=rad\left(R\right)=rad\left(I\right)=a$ and $dep\left(Q\right)=rad\left(Q\right)=rad\left(J\right)=b$. Let $\alpha =\{{\alpha }_0,{\alpha }_1,\cdots ,{\alpha }_a\}$, ${\alpha }^{\prime }=\{{\alpha }_0^{\prime },{\alpha }_1^{\prime },\cdots ,{\alpha }_a^{\prime }\}$, $\beta =\{{\beta }_0,{\beta }_1,\cdots ,{\beta }_b\}$, ${\beta }^{\prime }=\{{\beta }_0^{\prime },{\beta }_1^{\prime },\cdots ,{\beta }_b^{\prime }\}$, $\gamma =\{{\gamma }_1,{\gamma }_2,\cdots ,{\gamma }_a\}$, ${\gamma }^{\prime }=\{{\gamma }_1^{\prime },{\gamma }_2^{\prime },\cdots ,{\gamma }_a^{\prime }\}$, $\epsilon =\{{\epsilon }_1,{\epsilon }_2,\cdots ,{\epsilon }_b\}$, and ${\epsilon }^{\prime }=\{{\epsilon }_1^{\prime },{\epsilon }_2^{\prime },\cdots ,{\epsilon }_b^{\prime }\}$ be eight sets of colors such that they are pairwise disjoints. We color $R\square Q$ by two steps.

Step 1: We give $R^{v_0}$ a $(\alpha ,\gamma )$-total coloring, and give $R^{v_i}$ a $({\alpha }^{\prime },{\gamma }^{\prime })$-total coloring, where $i\ge 1$. Denoted by $c_1$, this total coloring of $R\square Q$.

Step 2: We must change the colors at this step for some vertices. For $Q^{u_0}$, give it a $(\beta ,\epsilon )$-total coloring, and $Q^{u_j}$ so that $u_j$ is a leaf in R, give it a $({\beta }^{\prime },{\epsilon }^{\prime })$-total coloring. Moreover, we assign the other edges not colored by color ${\alpha }_1$ (it does matter). Denote by $c_2$ this modified total coloring of $R\square Q$.

Please note that colors ${\alpha }_0,{\alpha }_0^{\prime },{\alpha }_a$, and ${\alpha }_a^{\prime }$ do not arise in $(R\square Q,c_2)$. Therefore, we use $4a+4b$ colors in $(R\square Q,c_2)$.

Now, we will prove that $c_2$ is our desired coloring. First, we have the following two claims. □

Claim 1.

Let $v_i$ be any vertex in Q. In each $R^{v_i}$ with $0\le i\le m$, if x and y are related, then the path $x{R}^{v_i}y$ joining x and y is total rainbow.

Proof of Claim 1.

Since x and y are related in $R^{v_i}$, there exists the path $x{R}^{v_i}y$ in $R^{v_i}$ joining x and y. In Step 1, since different vertices on $x{R}^{v_i}y$ have different levels in $R^{v_i}$, the path $x{R}^{v_i}y$ is total rainbow in $(R^{v_i},c_1)$. Moreover, since the internal vertices of $x{R}^{v_i}y$ are not leaves in $R^{v_i}$, the colors of the internal vertices of $x{R}^{v_i}y$ are not changed in Step 2. Therefore, $x{R}^{v_i}y$ is also the total rainbow in $(R^{v_i},c_2)$, and Claim 1 holds. □

Claim 2.

Let $u_i$ be a vertex in R such that $u_i$ is a leaf in R or the root of R. In $Q^{u_i}$, if x and y are related, then the path $x{Q}^{u_i}y$ joining x and y is total rainbow.

Proof of Claim 2.

Since x and y are related in $Q^{u_i}$, there exists the path $x{Q}^{u_i}y$ in $Q^{u_i}$ joining x and y. Since different vertices on $x{Q}^{u_i}y$ have different levels in $Q^{u_i}$, the path $x{Q}^{u_i}y$ is total rainbow in Step 2, and Claim 2 holds. □

For any two vertices $x=(u_i,v_j),y=(u_s,v_t)\in V(R\square Q)$, it is sufficient to prove that $(R\square Q,c_2)$ has a total rainbow path joining them. By symmetry, suppose that ${\ell }_R\left(u_i\right)\le {\ell }_R\left(u_s\right)$. Consider three cases.

Case 1. $v_j\ne v_0$ and $v_t\ne v_0$.

Pick a leaf $u_k$ in R so that $u_k$ is a descendant of $u_s$. Then the path $x{R}^{v_j}(u_0,v_j)Q^{u_0}(u_0,v_0)$$R^{v_0}(u_k,v_0)Q^{u_k}(u_k,v_t)R^{v_t}y$ is our desired total rainbow x-y path in $R\square Q$.

Case 2. $v_j=v_t=v_0$.

Pick a leaf $u_k$ in R so that $u_k$ is a descendant of $u_s$, and a leaf $v_r$ in Q. Then the path $x{R}^{v_0}(u_0,v_0)Q^{u_0}(u_0,v_r)\left[2\right]R^{v_r}(u_k,v_r)Q^{u_k}(u_k,v_0)R^{v_0}y$ is our desired total rainbow x-y path in $R\square Q$.

Case 3. Exactly one of $v_j$ and $v_t$ is $v_0$.

Assume that $v_j=v_0$. Pick a leaf $u_k$ in R such that $u_k$ is a descendant of $u_s$, and a leaf $v_r$ in Q such that $u_r$ is a descendant of $u_t$. Then the path $x{R}^{v_0}(u_0,v_0)Q^{u_0}(u_0,v_r)R^{v_r}(u_k,v_r)$$Q^{u_k}(u_k,v_t)R^{v_t}y$ is our desired total rainbow x-y path in $R\square Q$.

Thus, $c_2$ is our desired coloring, and we are done. □

Remark 4.

$K_2\square K_2$ is a sharp example for the lower bound of Theorem 3. Pick two graphs I and J such that $diam\left(I\right)=2rad\left(I\right)$ and $diam\left(J\right)=2rad\left(J\right)$, then $trc(I\square J)\ge 2diam(I\square J)-1=2diam\left(I\right)+2diam\left(J\right)-1=4rad\left(I\right)+4rad\left(J\right)-1$. Therefore, the upper bound of Theorem 3 is sharp up to an additive constant 1.

4. Conclusions

In our paper, we obtain the upper bound of the total rainbow connection number of several graph operations (specifically, adding or deleting an edge, and the Cartesian product). It is interesting to study the total rainbow connection number of some other graph operations, such as lexicographic product, strong product and directed product.