A Two-Stage Multi-Criteria Supplier Selection Model for Sustainable Automotive Supply Chain under Uncertainty
Abstract
:1. Introduction
- In practice, this is the first research in Vietnam to perform a comprehensive sustainable supplier selection (SSS) inside the automotive sector. A major feature of the COVID-19 pandemic’s impact is evaluated, as are general sustainability requirements based on three pillars (economic, environmental, and social); this is a significant benefit of the proposed work.
- To the best of our knowledge, this work is the first to design an integrated SF-AHP and G-COPRAS methodology in the existing supplier selection literature. The MCDM method is implemented with the aid of experts’ inputs.
- For managerial implications, our suggested method and results can help enterprises achieve supply chain sustainability in the post-pandemic period, respond to risks/threats from future pandemics, identify opportunities, and preserve competitiveness by reconfiguring resources. The approach can be applied not just to SSS, but also to other comparable industries in Asian developing markets and even industrialized ones.
2. Literature Review
2.1. Literature Review on SSS and Criteria
2.2. Literature Review on Proposed Methodology
3. Materials and Methods
3.1. Spherical Fuzzy Analytical Hierarchy Process (SF-AHP)
- Union operation
- Intersection operation
- Addition operation
- Multiplication operation
- Multiplication by a scalar;
- Power of
3.2. Grey Complex Proportional Assessment (G-COPRAS)
4. Empirical Analysis
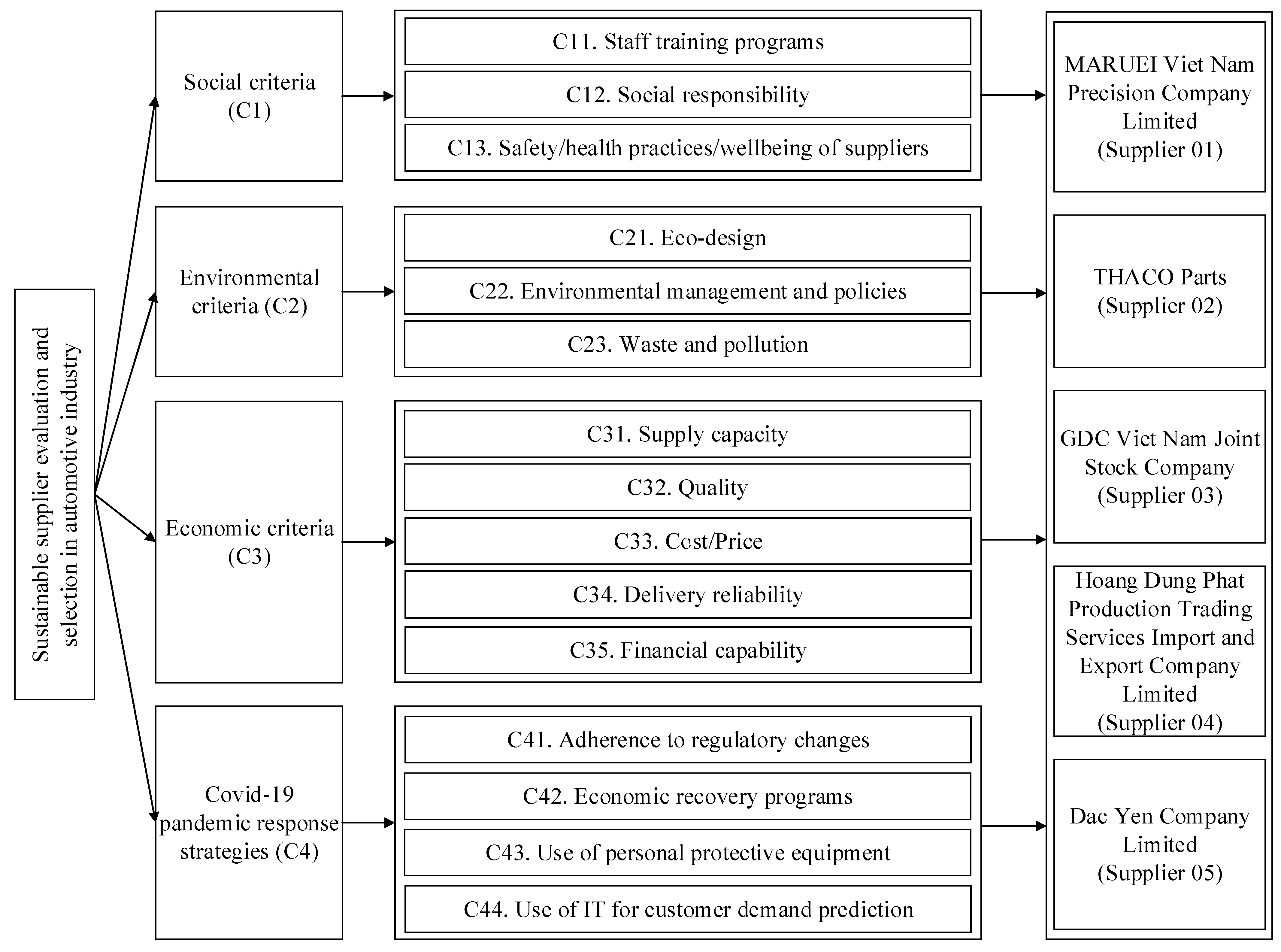
4.1. A Case Study of the Automotive Industry in Vietnam
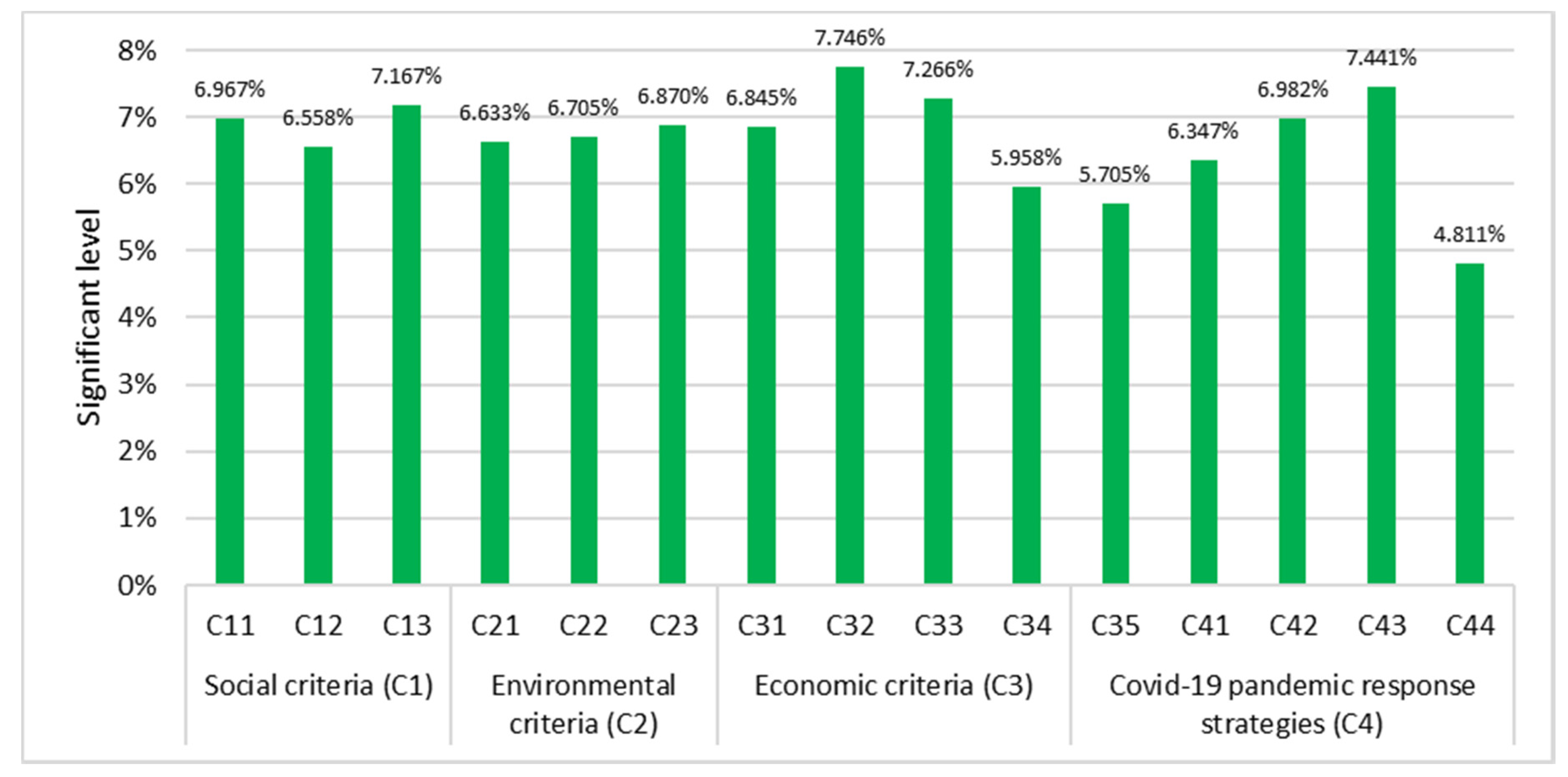
4.2. SF-AHP for Determination Criteria Weights
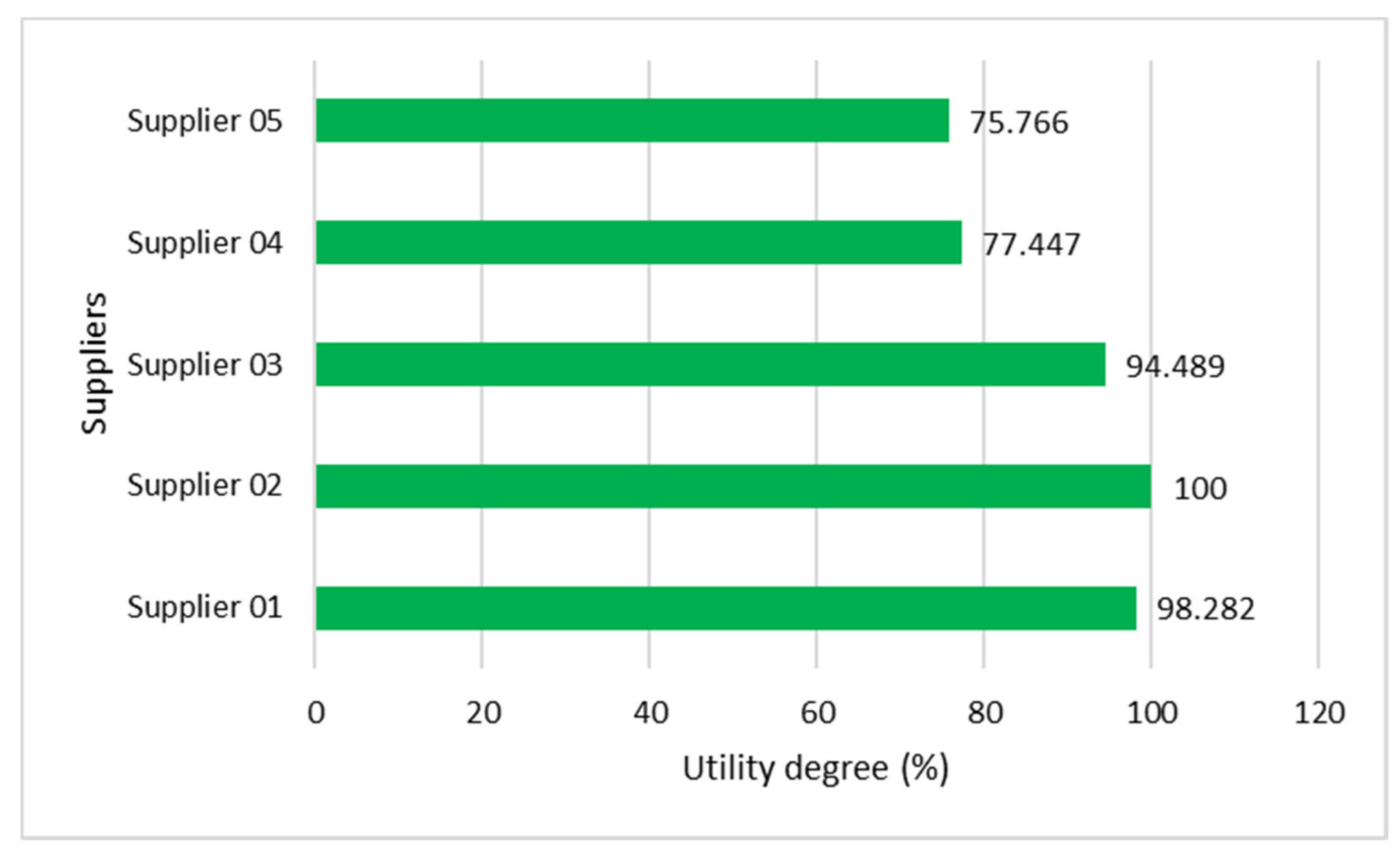
4.3. G-COPRAS for Ranking Suppliers
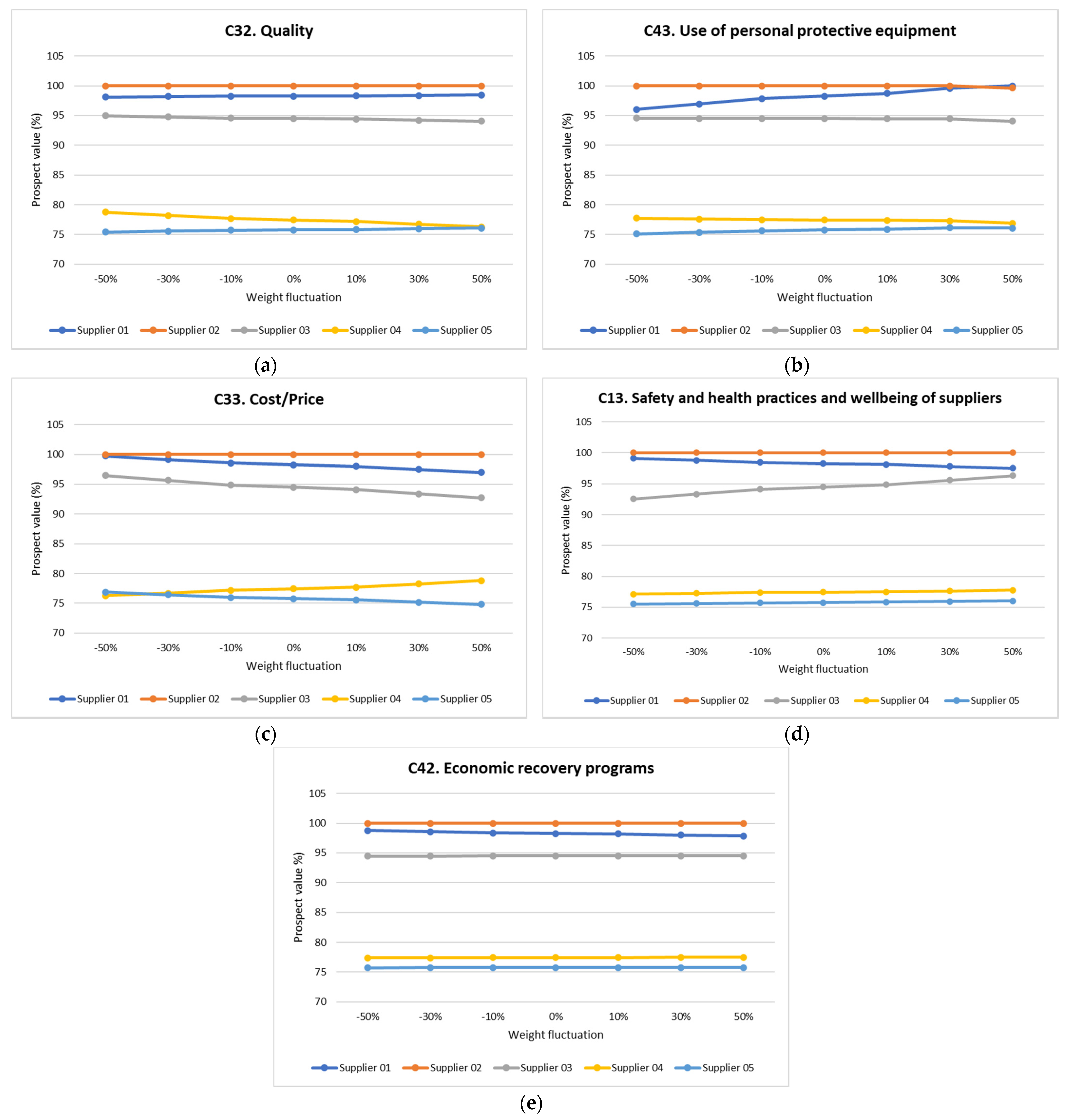
5. Sensitivity Analysis
6. Managerial Implications
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Criteria | C11 | C12 | C13 | C21 | C22 | ||||||||||
| C11 | 0.500 | 0.400 | 0.400 | 0.485 | 0.498 | 0.314 | 0.517 | 0.464 | 0.315 | 0.507 | 0.471 | 0.321 | 0.493 | 0.482 | 0.336 |
| C12 | 0.450 | 0.525 | 0.318 | 0.500 | 0.400 | 0.400 | 0.455 | 0.531 | 0.314 | 0.449 | 0.549 | 0.285 | 0.519 | 0.467 | 0.310 |
| C13 | 0.414 | 0.565 | 0.307 | 0.493 | 0.484 | 0.413 | 0.500 | 0.400 | 0.400 | 0.608 | 0.373 | 0.297 | 0.470 | 0.532 | 0.279 |
| C21 | 0.433 | 0.541 | 0.321 | 0.484 | 0.508 | 0.146 | 0.338 | 0.649 | 0.269 | 0.500 | 0.400 | 0.400 | 0.493 | 0.482 | 0.336 |
| C22 | 0.458 | 0.511 | 0.338 | 0.425 | 0.557 | 0.170 | 0.395 | 0.593 | 0.286 | 0.458 | 0.511 | 0.338 | 0.500 | 0.400 | 0.400 |
| C23 | 0.512 | 0.464 | 0.321 | 0.517 | 0.467 | 0.358 | 0.410 | 0.571 | 0.310 | 0.493 | 0.475 | 0.332 | 0.508 | 0.473 | 0.310 |
| C31 | 0.517 | 0.452 | 0.327 | 0.367 | 0.620 | 0.142 | 0.488 | 0.479 | 0.336 | 0.512 | 0.470 | 0.308 | 0.493 | 0.475 | 0.332 |
| C32 | 0.512 | 0.470 | 0.308 | 0.517 | 0.452 | 0.327 | 0.475 | 0.494 | 0.336 | 0.556 | 0.417 | 0.315 | 0.583 | 0.409 | 0.287 |
| C33 | 0.406 | 0.580 | 0.293 | 0.508 | 0.481 | 0.480 | 0.578 | 0.405 | 0.297 | 0.527 | 0.462 | 0.297 | 0.475 | 0.514 | 0.303 |
| C34 | 0.425 | 0.550 | 0.314 | 0.454 | 0.522 | 0.197 | 0.354 | 0.631 | 0.282 | 0.354 | 0.626 | 0.289 | 0.354 | 0.626 | 0.289 |
| C35 | 0.323 | 0.676 | 0.248 | 0.450 | 0.547 | 0.154 | 0.347 | 0.650 | 0.255 | 0.320 | 0.659 | 0.281 | 0.302 | 0.688 | 0.243 |
| C41 | 0.425 | 0.557 | 0.306 | 0.421 | 0.572 | 0.212 | 0.458 | 0.534 | 0.291 | 0.458 | 0.511 | 0.338 | 0.476 | 0.505 | 0.314 |
| C42 | 0.552 | 0.432 | 0.304 | 0.458 | 0.511 | 0.342 | 0.373 | 0.613 | 0.283 | 0.531 | 0.446 | 0.319 | 0.437 | 0.563 | 0.272 |
| C43 | 0.551 | 0.420 | 0.317 | 0.532 | 0.453 | 0.449 | 0.542 | 0.445 | 0.302 | 0.541 | 0.447 | 0.305 | 0.556 | 0.427 | 0.306 |
| C44 | 0.296 | 0.706 | 0.215 | 0.433 | 0.534 | 0.301 | 0.316 | 0.684 | 0.235 | 0.338 | 0.647 | 0.276 | 0.308 | 0.676 | 0.262 |
| Criteria | C23 | C31 | C32 | C33 | C34 | ||||||||||
| C11 | 0.435 | 0.553 | 0.307 | 0.418 | 0.567 | 0.306 | 0.419 | 0.573 | 0.289 | 0.529 | 0.459 | 0.304 | 0.513 | 0.467 | 0.317 |
| C12 | 0.408 | 0.586 | 0.282 | 0.569 | 0.418 | 0.296 | 0.418 | 0.567 | 0.306 | 0.436 | 0.559 | 0.290 | 0.472 | 0.515 | 0.306 |
| C13 | 0.544 | 0.438 | 0.318 | 0.458 | 0.521 | 0.327 | 0.471 | 0.508 | 0.328 | 0.373 | 0.621 | 0.273 | 0.596 | 0.383 | 0.304 |
| C21 | 0.450 | 0.531 | 0.321 | 0.419 | 0.573 | 0.289 | 0.354 | 0.639 | 0.271 | 0.416 | 0.579 | 0.283 | 0.589 | 0.383 | 0.312 |
| C22 | 0.431 | 0.559 | 0.296 | 0.450 | 0.531 | 0.321 | 0.340 | 0.661 | 0.246 | 0.470 | 0.524 | 0.300 | 0.589 | 0.383 | 0.312 |
| C23 | 0.500 | 0.400 | 0.400 | 0.479 | 0.518 | 0.288 | 0.396 | 0.595 | 0.286 | 0.469 | 0.517 | 0.318 | 0.589 | 0.383 | 0.312 |
| C31 | 0.458 | 0.534 | 0.291 | 0.500 | 0.400 | 0.400 | 0.407 | 0.582 | 0.293 | 0.503 | 0.479 | 0.310 | 0.619 | 0.356 | 0.298 |
| C32 | 0.542 | 0.436 | 0.311 | 0.537 | 0.439 | 0.313 | 0.500 | 0.400 | 0.400 | 0.632 | 0.360 | 0.279 | 0.643 | 0.360 | 0.257 |
| C33 | 0.479 | 0.499 | 0.321 | 0.429 | 0.547 | 0.310 | 0.308 | 0.687 | 0.242 | 0.500 | 0.400 | 0.400 | 0.580 | 0.403 | 0.304 |
| C34 | 0.354 | 0.626 | 0.289 | 0.338 | 0.647 | 0.276 | 0.325 | 0.675 | 0.235 | 0.363 | 0.622 | 0.283 | 0.500 | 0.400 | 0.400 |
| C35 | 0.347 | 0.645 | 0.262 | 0.512 | 0.446 | 0.337 | 0.294 | 0.701 | 0.230 | 0.288 | 0.712 | 0.216 | 0.410 | 0.571 | 0.310 |
| C41 | 0.458 | 0.534 | 0.291 | 0.458 | 0.511 | 0.338 | 0.425 | 0.550 | 0.314 | 0.381 | 0.594 | 0.309 | 0.414 | 0.568 | 0.306 |
| C42 | 0.507 | 0.483 | 0.304 | 0.446 | 0.532 | 0.307 | 0.373 | 0.611 | 0.289 | 0.458 | 0.511 | 0.338 | 0.532 | 0.444 | 0.317 |
| C43 | 0.578 | 0.411 | 0.288 | 0.532 | 0.444 | 0.317 | 0.551 | 0.440 | 0.300 | 0.493 | 0.475 | 0.332 | 0.517 | 0.452 | 0.327 |
| C44 | 0.357 | 0.640 | 0.262 | 0.338 | 0.647 | 0.276 | 0.328 | 0.670 | 0.238 | 0.302 | 0.700 | 0.222 | 0.360 | 0.632 | 0.265 |
| Criteria | C35 | C41 | C42 | C43 | C44 | ||||||||||
| C11 | 0.628 | 0.371 | 0.278 | 0.519 | 0.467 | 0.310 | 0.401 | 0.592 | 0.287 | 0.364 | 0.628 | 0.278 | 0.661 | 0.347 | 0.246 |
| C12 | 0.470 | 0.532 | 0.279 | 0.511 | 0.487 | 0.289 | 0.493 | 0.482 | 0.336 | 0.420 | 0.573 | 0.293 | 0.501 | 0.471 | 0.328 |
| C13 | 0.606 | 0.393 | 0.280 | 0.479 | 0.518 | 0.288 | 0.565 | 0.421 | 0.305 | 0.401 | 0.595 | 0.280 | 0.623 | 0.381 | 0.271 |
| C21 | 0.608 | 0.355 | 0.317 | 0.493 | 0.482 | 0.336 | 0.412 | 0.578 | 0.300 | 0.398 | 0.599 | 0.280 | 0.619 | 0.356 | 0.298 |
| C22 | 0.631 | 0.353 | 0.283 | 0.464 | 0.526 | 0.304 | 0.476 | 0.528 | 0.280 | 0.358 | 0.639 | 0.265 | 0.628 | 0.342 | 0.299 |
| C23 | 0.599 | 0.393 | 0.289 | 0.479 | 0.518 | 0.288 | 0.433 | 0.564 | 0.290 | 0.356 | 0.642 | 0.253 | 0.601 | 0.397 | 0.283 |
| C31 | 0.424 | 0.553 | 0.319 | 0.493 | 0.482 | 0.336 | 0.480 | 0.505 | 0.303 | 0.415 | 0.573 | 0.300 | 0.619 | 0.356 | 0.298 |
| C32 | 0.644 | 0.349 | 0.270 | 0.513 | 0.467 | 0.317 | 0.575 | 0.406 | 0.307 | 0.373 | 0.628 | 0.265 | 0.587 | 0.416 | 0.273 |
| C33 | 0.679 | 0.323 | 0.244 | 0.573 | 0.397 | 0.321 | 0.493 | 0.482 | 0.336 | 0.450 | 0.531 | 0.321 | 0.654 | 0.353 | 0.253 |
| C34 | 0.544 | 0.438 | 0.318 | 0.533 | 0.451 | 0.310 | 0.415 | 0.573 | 0.300 | 0.418 | 0.567 | 0.306 | 0.582 | 0.413 | 0.283 |
| C35 | 0.500 | 0.400 | 0.400 | 0.410 | 0.573 | 0.306 | 0.476 | 0.504 | 0.324 | 0.419 | 0.570 | 0.296 | 0.593 | 0.397 | 0.291 |
| C41 | 0.532 | 0.434 | 0.325 | 0.500 | 0.400 | 0.400 | 0.431 | 0.558 | 0.307 | 0.407 | 0.582 | 0.293 | 0.602 | 0.377 | 0.299 |
| C42 | 0.466 | 0.505 | 0.329 | 0.511 | 0.466 | 0.323 | 0.500 | 0.400 | 0.400 | 0.571 | 0.393 | 0.326 | 0.659 | 0.342 | 0.254 |
| C43 | 0.521 | 0.457 | 0.310 | 0.537 | 0.439 | 0.313 | 0.370 | 0.601 | 0.309 | 0.500 | 0.400 | 0.400 | 0.623 | 0.371 | 0.276 |
| C44 | 0.357 | 0.635 | 0.269 | 0.347 | 0.638 | 0.276 | 0.288 | 0.710 | 0.216 | 0.340 | 0.655 | 0.255 | 0.500 | 0.400 | 0.400 |
| Criteria | C11 | C12 | C13 | C21 | C22 | |||||
| Suppliers | ||||||||||
| Supplier 01 | 0.160 | 0.217 | 0.122 | 0.184 | 0.111 | 0.187 | 0.181 | 0.263 | 0.241 | 0.305 |
| Supplier 02 | 0.169 | 0.230 | 0.181 | 0.233 | 0.160 | 0.240 | 0.111 | 0.198 | 0.229 | 0.299 |
| Supplier 03 | 0.208 | 0.268 | 0.220 | 0.289 | 0.263 | 0.351 | 0.222 | 0.288 | 0.192 | 0.268 |
| Supplier 04 | 0.208 | 0.272 | 0.207 | 0.256 | 0.134 | 0.218 | 0.169 | 0.251 | 0.076 | 0.134 |
| Supplier 05 | 0.102 | 0.166 | 0.125 | 0.184 | 0.134 | 0.202 | 0.119 | 0.198 | 0.101 | 0.155 |
| Suppliers | C23 | C31 | C32 | C33 | C34 | |||||
| Supplier 01 | 0.150 | 0.204 | 0.212 | 0.274 | 0.218 | 0.272 | 0.185 | 0.244 | 0.189 | 0.247 |
| Supplier 02 | 0.159 | 0.213 | 0.259 | 0.322 | 0.210 | 0.269 | 0.118 | 0.168 | 0.196 | 0.254 |
| Supplier 03 | 0.142 | 0.193 | 0.167 | 0.224 | 0.174 | 0.228 | 0.238 | 0.297 | 0.199 | 0.252 |
| Supplier 04 | 0.255 | 0.326 | 0.113 | 0.167 | 0.091 | 0.137 | 0.081 | 0.134 | 0.083 | 0.128 |
| Supplier 05 | 0.153 | 0.204 | 0.104 | 0.158 | 0.174 | 0.228 | 0.238 | 0.297 | 0.199 | 0.252 |
| Suppliers | C35 | C41 | C42 | C43 | C44 | |||||
| Supplier 01 | 0.200 | 0.259 | 0.225 | 0.293 | 0.168 | 0.225 | 0.284 | 0.354 | 0.171 | 0.224 |
| Supplier 02 | 0.203 | 0.263 | 0.216 | 0.283 | 0.196 | 0.262 | 0.166 | 0.216 | 0.158 | 0.221 |
| Supplier 03 | 0.131 | 0.181 | 0.155 | 0.209 | 0.182 | 0.253 | 0.151 | 0.203 | 0.133 | 0.179 |
| Supplier 04 | 0.209 | 0.278 | 0.126 | 0.187 | 0.156 | 0.208 | 0.102 | 0.160 | 0.156 | 0.211 |
| Supplier 05 | 0.113 | 0.163 | 0.122 | 0.184 | 0.151 | 0.199 | 0.154 | 0.210 | 0.244 | 0.302 |
| Criteria | C11 | C12 | C13 | C21 | C22 | |||||
| Suppliers | ||||||||||
| Supplier 01 | 0.011 | 0.015 | 0.008 | 0.012 | 0.008 | 0.013 | 0.012 | 0.017 | 0.016 | 0.020 |
| Supplier 02 | 0.012 | 0.016 | 0.012 | 0.015 | 0.011 | 0.017 | 0.007 | 0.013 | 0.015 | 0.020 |
| Supplier 03 | 0.014 | 0.019 | 0.014 | 0.019 | 0.019 | 0.025 | 0.015 | 0.019 | 0.013 | 0.018 |
| Supplier 04 | 0.014 | 0.019 | 0.014 | 0.017 | 0.010 | 0.016 | 0.011 | 0.017 | 0.005 | 0.009 |
| Supplier 05 | 0.007 | 0.012 | 0.008 | 0.012 | 0.010 | 0.014 | 0.008 | 0.013 | 0.007 | 0.010 |
| Suppliers | C23 | C31 | C32 | C33 | C34 | |||||
| Supplier 01 | 0.010 | 0.014 | 0.014 | 0.019 | 0.017 | 0.021 | 0.013 | 0.018 | 0.011 | 0.015 |
| Supplier 02 | 0.011 | 0.015 | 0.018 | 0.022 | 0.016 | 0.021 | 0.009 | 0.012 | 0.012 | 0.015 |
| Supplier 03 | 0.010 | 0.013 | 0.011 | 0.015 | 0.013 | 0.018 | 0.017 | 0.022 | 0.012 | 0.015 |
| Supplier 04 | 0.018 | 0.022 | 0.008 | 0.011 | 0.007 | 0.011 | 0.006 | 0.010 | 0.005 | 0.008 |
| Supplier 05 | 0.011 | 0.014 | 0.007 | 0.011 | 0.013 | 0.018 | 0.017 | 0.022 | 0.012 | 0.015 |
| Suppliers | C35 | C41 | C42 | C43 | C44 | |||||
| Supplier 01 | 0.011 | 0.015 | 0.014 | 0.019 | 0.012 | 0.016 | 0.021 | 0.026 | 0.008 | 0.011 |
| Supplier 02 | 0.012 | 0.015 | 0.014 | 0.018 | 0.014 | 0.018 | 0.012 | 0.016 | 0.008 | 0.011 |
| Supplier 03 | 0.007 | 0.010 | 0.010 | 0.013 | 0.013 | 0.018 | 0.011 | 0.015 | 0.006 | 0.009 |
| Supplier 04 | 0.012 | 0.016 | 0.008 | 0.012 | 0.011 | 0.015 | 0.008 | 0.012 | 0.008 | 0.010 |
| Supplier 05 | 0.006 | 0.009 | 0.008 | 0.012 | 0.011 | 0.014 | 0.011 | 0.016 | 0.012 | 0.015 |
References
- Chowdhury, P.; Paul, S.K.; Kaisar, S.; Moktadir, M.A. COVID-19 Pandemic Related Supply Chain Studies: A Systematic Review. Transp. Res. Part E Logist. Transp. Rev. 2021, 148, 102271. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, D.; Dolgui, A. OR-Methods for Coping with the Ripple Effect in Supply Chains during COVID-19 Pandemic: Managerial Insights and Research Implications. Int. J. Prod. Econ. 2021, 232, 107921. [Google Scholar] [CrossRef] [PubMed]
- Orji, I.J.; Ojadi, F. Investigating the COVID-19 Pandemic’s Impact on Sustainable Supplier Selection in the Nigerian Manufacturing Sector. Comput. Ind. Eng. 2021, 160, 107588. [Google Scholar] [CrossRef] [PubMed]
- Belhadi, A.; Kamble, S.; Jabbour, C.J.C.; Gunasekaran, A.; Ndubisi, N.O.; Venkatesh, M. Manufacturing and Service Supply Chain Resilience to the COVID-19 Outbreak: Lessons Learned from the Automobile and Airline Industries. Technol. Forecast. Soc. Change 2021, 163, 120447. [Google Scholar] [CrossRef] [PubMed]
- Impact of the COVID-19 Pandemic on the Global Supply Chain and Opportunities for Vietnam. Available online: https://tapchicongthuong.vn/bai-viet/tac-dong-cua-dai-dich-covid-19-den-chuoi-cung-ung-toan-cau-va-co-hoi-cho-viet-nam-86331.htm (accessed on 3 March 2022).
- Orji, I.J.; Liu, S. A Dynamic Perspective on the Key Drivers of Innovation-Led Lean Approaches to Achieve Sustainability in Manufacturing Supply Chain. Int. J. Prod. Econ. 2020, 219, 480–496. [Google Scholar] [CrossRef]
- Ranjbari, M.; Shams Esfandabadi, Z.; Zanetti, M.C.; Scagnelli, S.D.; Siebers, P.O.; Aghbashlo, M.; Peng, W.; Quatraro, F.; Tabatabaei, M. Three Pillars of Sustainability in the Wake of COVID-19: A Systematic Review and Future Research Agenda for Sustainable Development. J. Clean. Prod. 2021, 297, 126660. [Google Scholar] [CrossRef]
- Sarkis, J. Supply Chain Sustainability: Learning from the COVID-19 Pandemic. Int. J. Oper. Prod. Manag. 2020, 41, 63–73. [Google Scholar] [CrossRef]
- The Auto Industry Is Hit Hardest by Supply Chain Disruptions during the COVID Pandemic. Available online: https://moit.gov.vn/tin-tuc/doanh-nghiep/nganh-cong-nghiep-o-to-bi-anh-huong-nang-ne-nhat-boi-su-gian-doan-chuoi-cung-ung-trong-dai-dich-covid.html (accessed on 3 March 2022).
- Jain, N.; Singh, A.R. Sustainable Supplier Selection under Must-Be Criteria through Fuzzy Inference System. J. Clean. Prod. 2020, 248, 119275. [Google Scholar] [CrossRef]
- Hendiani, S.; Mahmoudi, A.; Liao, H. A Multi-Stage Multi-Criteria Hierarchical Decision-Making Approach for Sustainable Supplier Selection. Appl. Soft Comput. 2020, 94, 106456. [Google Scholar] [CrossRef]
- Orji, I.J.; Wei, S. An Innovative Integration of Fuzzy-Logic and Systems Dynamics in Sustainable Supplier Selection: A Case on Manufacturing Industry. Comput. Ind. Eng. 2015, 88, 1–12. [Google Scholar] [CrossRef]
- Stević, Ž.; Pamučar, D.; Puška, A.; Chatterjee, P. Sustainable Supplier Selection in Healthcare Industries Using a New MCDM Method: Measurement of Alternatives and Ranking According to COmpromise Solution (MARCOS). Comput. Ind. Eng. 2020, 140, 106231. [Google Scholar] [CrossRef]
- Tayyab, M.; Sarkar, B. An Interactive Fuzzy Programming Approach for a Sustainable Supplier Selection under Textile Supply Chain Management. Comput. Ind. Eng. 2021, 155, 107164. [Google Scholar] [CrossRef]
- Bringing Green Supply Chains to Adapt to the Post-COVID-19 Context. Available online: https://moit.gov.vn/phat-trien-ben-vung/ung-dung-chuoi-cung-ung-xanh-tich-ung-voi-boi-canh-hau-covid-19.html (accessed on 3 March 2022).
- Goodarzian, F.; Taleizadeh, A.A.; Ghasemi, P.; Abraham, A. An Integrated Sustainable Medical Supply Chain Network during COVID-19. Eng. Appl. Artif. Intell. 2021, 100, 104188. [Google Scholar] [CrossRef]
- Karmaker, C.L.; Ahmed, T.; Ahmed, S.; Ali, S.M.; Moktadir, M.A.; Kabir, G. Improving Supply Chain Sustainability in the Context of COVID-19 Pandemic in an Emerging Economy: Exploring Drivers Using an Integrated Model. Sustain. Prod. Consum. 2021, 26, 411–427. [Google Scholar] [CrossRef]
- Kumar, A.; Mangla, S.K.; Kumar, P.; Song, M. Mitigate Risks in Perishable Food Supply Chains: Learning from COVID-19. Technol. Forecast. Soc. Change 2021, 166, 120643. [Google Scholar] [CrossRef]
- Majumdar, A.; Shaw, M.; Sinha, S.K. COVID-19 Debunks the Myth of Socially Sustainable Supply Chain: A Case of the Clothing Industry in South Asian Countries. Sustain. Prod. Consum. 2020, 24, 150–155. [Google Scholar] [CrossRef]
- Nagurney, A. Supply Chain Game Theory Network Modeling under Labor Constraints: Applications to the COVID-19 Pandemic. Eur. J. Oper. Res. 2021, 293, 880–891. [Google Scholar] [CrossRef]
- Severo, E.A.; de Guimarães, J.C.F.; Dellarmelin, M.L. Impact of the COVID-19 Pandemic on Environmental Awareness, Sustainable Consumption and Social Responsibility: Evidence from Generations in Brazil and Portugal. J. Clean. Prod. 2021, 286, 124947. [Google Scholar] [CrossRef]
- Schramm, V.B.; Cabral, L.P.B.; Schramm, F. Approaches for Supporting Sustainable Supplier Selection—A Literature Review. J. Clean. Prod. 2020, 273, 123089. [Google Scholar] [CrossRef]
- Tseng, M.L. A Causal and Effect Decision Making Model of Service Quality Expectation Using Grey-Fuzzy DEMATEL Approach. Expert Syst. Appl. 2009, 36, 7738–7748. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Deng, J. Control Problems of Grey Systems. Syst. Control. Lett. 1982, 1, 288–294. [Google Scholar]
- Luthra, S.; Govindan, K.; Kannan, D.; Mangla, S.K.; Garg, C.P. An Integrated Framework for Sustainable Supplier Selection and Evaluation in Supply Chains. J. Clean. Prod. 2017, 140, 1686–1698. [Google Scholar] [CrossRef]
- Awasthi, A.; Govindan, K.; Gold, S. Multi-Tier Sustainable Global Supplier Selection Using a Fuzzy AHP-VIKOR Based Approach. Int. J. Prod. Econ. 2018, 195, 106–117. [Google Scholar] [CrossRef] [Green Version]
- Jain, V.; Sangaiah, A.K.; Sakhuja, S.; Thoduka, N.; Aggarwal, R. Supplier Selection Using Fuzzy AHP and TOPSIS: A Case Study in the Indian Automotive Industry. Neural Comput. Appl. 2018, 29, 555–564. [Google Scholar] [CrossRef]
- Gupta, S.; Soni, U.; Kumar, G. Green Supplier Selection Using Multi-Criterion Decision Making under Fuzzy Environment: A Case Study in Automotive Industry. Comput. Ind. Eng. 2019, 136, 663–680. [Google Scholar] [CrossRef]
- Memari, A.; Dargi, A.; Akbari Jokar, M.R.; Ahmad, R.; Abdul Rahim, A.R. Sustainable Supplier Selection: A Multi-Criteria Intuitionistic Fuzzy TOPSIS Method. J. Manuf. Syst. 2019, 50, 9–24. [Google Scholar] [CrossRef]
- Wang, Y.-C.; Chen, T. A Bi-Objective AHP-MINLP-GA Approach for Flexible Alternative Supplier Selection amid the COVID-19 Pandemic. Soft Comput. Lett. 2021, 3, 100016. [Google Scholar] [CrossRef]
- Petrudi, S.H.H.; Ahmadi, H.B.; Rehman, A.; Liou, J.J.H. Assessing Suppliers Considering Social Sustainability Innovation Factors during COVID-19 Disaster. Sustain. Prod. Consum. 2021, 27, 1869–1881. [Google Scholar] [CrossRef]
- Veličkovska, I. Implementation of a SWOT-AHP Methodology for Strategic Development of a District Heating Plant in Fuzzy Environment. Strateg. Manag. 2022, 27, 43–56. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, M.; Smarandache, F. A Hybrid Neutrosophic Group ANP-TOPSIS Framework for Supplier Selection Problems. Symmetry 2018, 10, 226. [Google Scholar] [CrossRef] [Green Version]
- Keshavarz Ghorabaee, M.; Zavadskas, E.K.; Olfat, L.; Turskis, Z. Multi-Criteria Inventory Classification Using a New Method of Evaluation Based on Distance from Average Solution (EDAS). Informatica 2015, 26, 435–451. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, D.; Li, Q.; Lev, B.; Ma, Y. Research on Sustainable Supplier Selection Based on the Rough DEMATEL and FVIKOR Methods. Sustainability 2020, 13, 88. [Google Scholar] [CrossRef]
- Thanh, N.V.; Lan, N.T.K. A New Hybrid Triple Bottom Line Metrics and Fuzzy MCDM Model: Sustainable Supplier Selection in the Food-Processing Industry. Axioms 2022, 11, 57. [Google Scholar] [CrossRef]
- Popović, M. An Mcdm Approach for Personnel Selection using the Cocoso Method. J. Process Manag. New Technol. 2021, 9, 78–88. [Google Scholar] [CrossRef]
- Karamaşa, Ç. Ranking service quality using multi-criteria decision-making methods: Example of erzurum province. J. Process Manag. New Technol. 2021, 9, 1–12. [Google Scholar] [CrossRef]
- Salimian, S.; Mousavi, S.M.; Antucheviciene, J. An Interval-Valued Intuitionistic Fuzzy Model Based on Extended VIKOR and MARCOS for Sustainable Supplier Selection in Organ Transplantation Networks for Healthcare Devices. Sustainability 2022, 14, 3795. [Google Scholar] [CrossRef]
- Ulutaş, A.; Stanujkić, D.; Karabašević, D.; Popović, G.; Novaković, S. Pallet Truck Selection with MEREC and WISP-S Methods. Strateg. Manag. 2022. [Google Scholar] [CrossRef]
- Keshavarz-Ghorabaee, M.; Amiri, M.; Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. Simultaneous Evaluation of Criteria and Alternatives (SECA) for Multi-Criteria Decision-Making. Informatica 2018, 29, 265–280. [Google Scholar] [CrossRef] [Green Version]
- Azimifard, A.; Moosavirad, S.H.; Ariafar, S. Selecting Sustainable Supplier Countries for Iran’s Steel Industry at Three Levels by Using AHP and TOPSIS Methods. Resour. Policy 2018, 57, 30–44. [Google Scholar] [CrossRef]
- Mohammed, A.; Harris, I.; Govindan, K. A Hybrid MCDM-FMOO Approach for Sustainable Supplier Selection and Order Allocation. Int. J. Prod. Econ. 2019, 217, 171–184. [Google Scholar] [CrossRef]
- Wong, J.T. Dynamic Procurement Risk Management with Supplier Portfolio Selection and Order Allocation under Green Market Segmentation. J. Clean. Prod. 2020, 253, 119835. [Google Scholar] [CrossRef]
- Çalık, A. A Novel Pythagorean Fuzzy AHP and Fuzzy TOPSIS Methodology for Green Supplier Selection in the Industry 4.0 Era. Soft Comput. 2021, 25, 2253–2265. [Google Scholar] [CrossRef]
- Nguyen, N.B.T.; Lin, G.-H.; Dang, T.-T. A Two Phase Integrated Fuzzy Decision-Making Framework for Green Supplier Selection in the Coffee Bean Supply Chain. Mathematics 2021, 9, 1923. [Google Scholar] [CrossRef]
- Saaty, T.L. How to Make a Decision: The Analytic Hierarchy Process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Mohammady, P.; Amid, A. Integrated Fuzzy AHP and Fuzzy VIKOR Model for Supplier Selection in an Agile and Modular Virtual Enterprise. Fuzzy Inf. Eng. 2011, 3, 411–431. [Google Scholar] [CrossRef]
- Ecer, F. Multi-Criteria Decision Making for Green Supplier Selection Using Interval Type-2 Fuzzy AHP: A Case Study of a Home Appliance Manufacturer. Oper. Res. 2022, 22, 199–233. [Google Scholar] [CrossRef]
- Wu, L.; Qian, F.; Wang, L.; Ma, X. An improved type-reduction algorithm for general type-2 fuzzy sets. Info. Sci. 2022, 593, 99–120. [Google Scholar] [CrossRef]
- Kahraman, C.; Öztayşi, B.; Uçal Sari, I.; Turanoǧlu, E. Fuzzy Analytic Hierarchy Process with Interval Type-2 Fuzzy Sets. Knowl. Based Syst. 2014, 59, 48–57. [Google Scholar] [CrossRef]
- Tooranloo, H.S.; Iranpour, A. Supplier Selection and Evaluation Using Interval-Valued Intuitionistic Fuzzy AHP Method. Int. J. Procure. Manag. 2017, 10, 539. [Google Scholar] [CrossRef]
- Pamucar, D.; Yazdani, M.; Obradovic, R.; Kumar, A.; Torres-Jiménez, M. A Novel Fuzzy Hybrid Neutrosophic Decision-making Approach for the Resilient Supplier Selection Problem. Int. J. Intell. Syst. 2020, 35, 1934–1986. [Google Scholar] [CrossRef]
- Sharaf, I.M. Global Supplier Selection with Spherical Fuzzy Analytic Hierarchy Process. In Decision Making with Spherical Fuzzy Sets; Springer: Cham, Switzerland, 2021; pp. 323–348. [Google Scholar]
- Unal, Y.; Temur, G.T. Sustainable Supplier Selection by Using Spherical Fuzzy AHP. J. Intell. Fuzzy Syst. 2021, 42, 593–603. [Google Scholar] [CrossRef]
- Unal, Y.; Temur, G.T. Using Spherical Fuzzy AHP Based Approach for Prioritization of Criteria Affecting Sustainable Supplier Selection. In Intelligent and Fuzzy Techniques: Smart and Innovative Solutions, Proceedings of the INFUS 2020 Conference, Istanbul, Turkey, 21–23 July 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 160–168. [Google Scholar]
- Kutlu Gündoğdu, F.; Kahraman, C. A Novel VIKOR Method Using Spherical Fuzzy Sets and Its Application to Warehouse Site Selection. J. Intell. Fuzzy Syst. 2019, 37, 1197–1211. [Google Scholar] [CrossRef]
- Kutlu Gundogdu, F.; Kahraman, C. Extension of WASPAS with Spherical Fuzzy Sets. Informatica 2019, 30, 269–292. [Google Scholar] [CrossRef] [Green Version]
- Kutlu Gündoğdu, F.; Kahraman, C. Spherical Fuzzy Sets and Spherical Fuzzy TOPSIS Method. J. Intell. Fuzzy Syst. 2019, 36, 337–352. [Google Scholar] [CrossRef]
- Gündoğdu, F.K.; Kahraman, C. A novel fuzzy TOPSIS method using emerging interval-valued spherical fuzzy sets. Eng. Appl. Artif. Intell. 2019, 85, 307–323. [Google Scholar] [CrossRef]
- Kayapinar Kaya, S.; Aycin, E. An Integrated Interval Type 2 Fuzzy AHP and COPRAS-G Methodologies for Supplier Selection in the Era of Industry 4.0. Neural Comput. Appl. 2021, 33, 10515–10535. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Hasan Aghdaie, M.; Hashemkhani Zolfani, S. Decision Making in Machine Tool Selection: An Integrated Approach with SWARA and COPRAS-G Methods. Eng. Econ. 2013, 24, 5–17. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Krishankumar, R.; Mardani, A.; Cavallaro, F.; Soundarapandian Ravichandran, K.; Balasubramanian, K. Hesitant Fuzzy SWARA-Complex Proportional Assessment Approach for Sustainable Supplier Selection (HF-SWARA-COPRAS). Symmetry 2020, 12, 1152. [Google Scholar] [CrossRef]
- Masoomi, B.; Sahebi, I.G.; Fathi, M.; Yıldırım, F.; Ghorbani, S. Strategic Supplier Selection for Renewable Energy Supply Chain under Green Capabilities (Fuzzy BWM-WASPAS-COPRAS Approach). Energy Strategy Rev. 2022, 40, 100815. [Google Scholar] [CrossRef]
- Kumari, R.; Mishra, A.R. Multi-Criteria COPRAS Method Based on Parametric Measures for Intuitionistic Fuzzy Sets: Application of Green Supplier Selection. Iran. J. Sci. Technol. Trans. Electr. Eng. 2020, 44, 1645–1662. [Google Scholar] [CrossRef]
- Kannan, D. Role of Multiple Stakeholders and the Critical Success Factor Theory for the Sustainable Supplier Selection Process. Int. J. Prod. Econ. 2018, 195, 391–418. [Google Scholar] [CrossRef]
- Rajesh, G.; Malliga, P. Selection of Suppliers Using Swara and Copras-G. Int. J. Enterp. Netw. Manag. 2018, 9, 169. [Google Scholar] [CrossRef]
- Malaga, A.; Vinodh, S. Benchmarking Smart Manufacturing Drivers Using Grey TOPSIS and COPRAS-G Approaches. Benchmarking Int. J. 2021, 28, 2916–2951. [Google Scholar] [CrossRef]
- Kutlu Gündoğdu, F.; Kahraman, C. A Novel Spherical Fuzzy Analytic Hierarchy Process and Its Renewable Energy Application. Soft Comput. 2020, 24, 4607–4621. [Google Scholar] [CrossRef]
- Wang, C.N.; Chou, C.C.; Dang, T.T.; Nguyen, H.P.; Nguyen, N.A.T. Integrating Triple Bottom Line in Sustainable Chemical Supplier Selection: A Compromise Decision-Making-Based Spherical Fuzzy Approach. Processes 2022, 10, 889. [Google Scholar] [CrossRef]
- Dogan, O. Process Mining Technology Selection with Spherical Fuzzy AHP and Sensitivity Analysis. Expert Syst. Appl. 2021, 178, 114999. [Google Scholar] [CrossRef]
- Julong, D. Introduction to Grey System Theory. J. Grey Syst. 1989, 1, 1–24. [Google Scholar]
- Li, G.D.; Yamaguchi, D.; Nagai, M. A Grey-Based Decision-Making Approach to the Supplier Selection Problem. Math. Comput. Model. 2007, 46, 573–581. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Kaklauskas, A.; Turskis, Z.; Tamošaitienė, J. Multi-Attribute Decision-Making Model by Applying Grey Numbers. Informatica 2009, 20, 305–320. [Google Scholar] [CrossRef]
- Turanoglu Bekar, E.; Cakmakci, M.; Kahraman, C. Fuzzy COPRAS Method for Performance Measurement in Total Productive Maintenance: A Comparative Analysis. J. Bus. Econ. Manag. 2016, 17, 663–684. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.; Xu, Z. An Integrated Sustainable Supplier Selection Approach Based on Hybrid Information Aggregation. Sustainability 2018, 10, 2543. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.-N.; Nguyen, N.-A.-T.; Dang, T.-T.; Lu, C.-M. A Compromised Decision-Making Approach to Third-Party Logistics Selection in Sustainable Supply Chain Using Fuzzy AHP and Fuzzy VIKOR Methods. Mathematics 2021, 9, 886. [Google Scholar] [CrossRef]
- Donthu, N.; Gustafsson, A. Effects of COVID-19 on Business and Research. J. Bus. Res. 2020, 117, 284–289. [Google Scholar] [CrossRef]
- Pantano, E.; Pizzi, G.; Scarpi, D.; Dennis, C. Competing during a Pandemic? Retailers’ Ups and Downs during the COVID-19 Outbreak. J. Bus. Res. 2020, 116, 209–213. [Google Scholar] [CrossRef]
- Govindan, K.; Mina, H.; Alavi, B. A Decision Support System for Demand Management in Healthcare Supply Chains Considering the Epidemic Outbreaks: A Case Study of Coronavirus Disease 2019 (COVID-19). Transp. Res. Part E Logist. Transp. Rev. 2020, 138, 101967. [Google Scholar] [CrossRef]
- Jäntschi, L.; Bolboacă, S.-D. Results from the Use of Molecular Descriptors Family on Structure Property/Activity Relationships. Int. J. Mol. Sci. 2007, 8, 189–203. [Google Scholar] [CrossRef]
- Liu, J.; Xu, F.; Lin, S. Site Selection of Photovoltaic Power Plants in a Value Chain Based on Grey Cumulative Prospect Theory for Sustainability: A Case Study in Northwest China. J. Clean. Prod. 2017, 148, 386–397. [Google Scholar] [CrossRef]
- Wang, C.-N.; Nguyen, N.-A.-T.; Dang, T.-T.; Hsu, H.-P. Evaluating Sustainable Last-Mile Delivery (LMD) in B2C E-Commerce Using Two-Stage Fuzzy MCDM Approach: A Case Study From Vietnam. IEEE Access 2021, 9, 146050–146067. [Google Scholar] [CrossRef]
- Wang, C.-N.; Dang, T.-T.; Nguyen, N.-A.-T. Location Optimization of Wind Plants Using DEA and Fuzzy Multi-Criteria Decision Making: A Case Study in Vietnam. IEEE Access 2021, 9, 116265–116285. [Google Scholar] [CrossRef]

| Authors | Approaches | Issues Addressed |
|---|---|---|
| Luthra et al. [26] | AHP and VIKOR | SSS for the Indian automobile industry |
| Azimifard et al. [43] | AHP and TOPSIS | SSS for Iran’s Steel Industry |
| Awasthi et al. [27] | Fuzzy AHP and Fuzzy VIKOR | Multi-tier SSS for electronic goods manufacturing |
| Jain et al. [28] | AHP and TOPSIS | SSS in the Indian automotive industry |
| Abdel-Basset et al. [34] | Neutrosophic Group ANP and TOPSIS | SSS in a dairy company in Egypt |
| Mohammed et al. [44] | MCDM-FMOO | SSS in a metal factory in Saudi Arabia |
| Gupta et al. [29] | Fuzzy AHP, TOPSIS, MABAC and WASPAS | Green supplier selection in the automotive industry in India |
| Memari et al. [30] | Intuitionistic fuzzy TOPSIS | SSS for the manufacturer of catalytic converters |
| Wong [45] | Fuzzy goal programming | Green supplier selection with risk management |
| Hendiani et al. [11] | Fuzzy BWM | SSS for refineries in Iran |
| Zhang et al. [36] | DEMATEL and fuzzy VIKOR | Numerical analysis |
| Thanh and Lan [37] | Fuzzy AHP and CoCoSo | SSS in the food processing industry |
| Çalık [46] | Pythagorean fuzzy AHP and fuzzy TOPSIS | Green supplier selection in the industry 4.0 era |
| Orji and Ojadi [3] | AHP and MULTIMOORA | SSS in the Nigerian manufacturing sector with COVID-19 impacts |
| Wang and Chen [31] | AHP-MINLP-GA | SSS with COVID-19 impacts |
| Nguyen et al. [47] | Fuzzy AHP and VIKOR | Supplier selection in coffee bean supply chain with COVID-19 impacts |
| Petrudi et al. [32] | BWM and GRA | SSS with COVID-19 impacts in Iran |
| Salimian et al. [40] | VIKOR and MARCOS | SSS in the healthcare sector |
| Linguistics Scale | Score Index (SI) | |
|---|---|---|
| Absolutely high importance (AMI) | (0.9, 0.1, 0.0) | 9 |
| Very high importance (VHI) | (0.8, 0.2, 0.1) | 7 |
| High importance (HI) | (0.7, 0.3, 0.2) | 5 |
| Slightly high importance (SMI) | (0.6, 0.4, 0.3) | 3 |
| Equal importance (EI) | (0.5, 0.4, 0.4) | 1 |
| Slightly low importance (SLI) | (0.4, 0.6, 0.3) | 1/3 |
| Low importance (LI) | (0.3, 0.7, 0.2) | 1/5 |
| Very low importance (VLI) | (0.2, 0.8, 0.1) | 1/7 |
| Absolutely low importance (ALI) | (0.1, 0.9, 0.0) | 1/9 |
| Linguistics Scale | |
|---|---|
| Very Poor (VP) | [0, 1] |
| Poor (P) | [1, 3] |
| Medium Poor (MP) | [3, 4] |
| Fair (F) | [4, 5] |
| Medium Good (MG) | [5, 6] |
| Good (G) | [6, 9] |
| Very Good (VG) | [9, 10] |
| No | Suppliers | Name of Suppliers | Website (accessed on 30 March 2022) |
|---|---|---|---|
| 1 | Supplier 01 | MARUEI Viet Nam Precision Company Limited | http://www.marueikogyo.jp/english/group/vietnam/ |
| 2 | Supplier 02 | THACO Parts | https://thacoparts.vn/en/home/ |
| 3 | Supplier 03 | GDC Viet Nam Joint Stock Company | http://gdcvietnam.vn/ |
| 4 | Supplier 04 | Hoang Dung Phat Production Trading Services Import and Export Company Limited | http://cokhihoangdungphat.com/ |
| 5 | Supplier 05 | Dac Yen Company Limited | https://phutungotovietnam.com.vn/en/ |
| Dimension | Criteria | Objective | References |
|---|---|---|---|
| Social (C1) | C11. Staff training programs | Maximum | [11,29,30,67,77] |
| C12. Social responsibility | Maximum | [3,26] | |
| C13. Safety and health practices and wellbeing of suppliers | Maximum | [3,11,26,27,30,32] | |
| Environmental (C2) | C21. Eco-design | Maximum | [3,26,29,30] |
| C22. Environmental management and policies | Maximum | [3,26,29,30] | |
| C23. Waste and pollution | Minimum | [3,11,26,29,30] | |
| Economic (C3) | C31. Supply capacity | Maximum | [11,29,78] |
| C32. Quality | Maximum | [3,11,26,27,29,30,47] | |
| C33. Cost/Price | Minimum | [3,11,26,27,29,30,47] | |
| C34. Delivery reliability | Maximum | [11,26,27,29,30,47] | |
| C35. Financial capability | Maximum | [3,26] | |
| COVID-19 pandemic response strategies (C4) | C41. Adherence to regulatory changes | Maximum | [3,11,27,30,79] |
| C42. Economic recovery programs | Maximum | [1,3,4,80] | |
| C43. Use of personal protective equipment | Maximum | [3,81] | |
| C44. Use of IT for customer demand prediction | Maximum | [12,80] |
| Dimension | Left Criteria Is Greater | Right Criteria Is Greater | Dimension | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| AMI | VHI | HI | SMI | EI | SLI | LI | VLI | ALI | ||
| C1 | 1 | 3 | 3 | 2 | 1 | 3 | 1 | 1 | C2 | |
| C1 | 3 | 2 | 2 | 6 | 2 | C3 | ||||
| C1 | 2 | 1 | 2 | 1 | 2 | 4 | 3 | C4 | ||
| C2 | 3 | 3 | 3 | 2 | 1 | 3 | C3 | |||
| C2 | 1 | 2 | 3 | 1 | 2 | 2 | 4 | C4 | ||
| C3 | 1 | 4 | 3 | 1 | 1 | 3 | 2 | C4 | ||
| Dimension | C1 | C2 | C3 | C4 |
|---|---|---|---|---|
| C1 | 1.000 | 1.000 | 0.436 | 0.637 |
| C2 | 1.000 | 1.000 | 0.904 | 0.729 |
| C3 | 2.293 | 1.107 | 1.000 | 1.132 |
| C4 | 1.571 | 1.372 | 0.883 | 1.000 |
| SUM | 5.864 | 4.478 | 3.223 | 3.498 |
| Dimension | C1 | C2 | C3 | C4 | MEAN | WSV | CV |
|---|---|---|---|---|---|---|---|
| C1 | 0.171 | 0.223 | 0.135 | 0.182 | 0.178 | 0.718 | 4.036 |
| C2 | 0.171 | 0.223 | 0.280 | 0.208 | 0.221 | 0.893 | 4.045 |
| C3 | 0.391 | 0.247 | 0.310 | 0.324 | 0.318 | 1.291 | 4.059 |
| C4 | 0.268 | 0.306 | 0.274 | 0.286 | 0.284 | 1.146 | 4.043 |
| Dimension | C1 | C2 | C3 | C4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C1 | 0.500 | 0.400 | 0.400 | 0.430 | 0.587 | 0.236 | 0.363 | 0.638 | 0.246 | 0.393 | 0.622 | 0.219 |
| C2 | 0.458 | 0.553 | 0.254 | 0.500 | 0.400 | 0.400 | 0.433 | 0.573 | 0.259 | 0.397 | 0.619 | 0.220 |
| C3 | 0.579 | 0.420 | 0.276 | 0.475 | 0.523 | 0.281 | 0.500 | 0.400 | 0.400 | 0.461 | 0.559 | 0.229 |
| C4 | 0.504 | 0.521 | 0.229 | 0.503 | 0.518 | 0.241 | 0.446 | 0.569 | 0.238 | 0.500 | 0.400 | 0.400 |
| Dimension | SF-AHP Weight | Crisp Weight | ||
|---|---|---|---|---|
| C1 | 0.426 | 0.553 | 0.292 | 0.226 |
| C2 | 0.450 | 0.529 | 0.298 | 0.239 |
| C3 | 0.507 | 0.471 | 0.306 | 0.272 |
| C4 | 0.489 | 0.498 | 0.290 | 0.263 |
| Criteria | Geometric Mean | Spherical Fuzzy Weights | Crisp Weights | ||||
|---|---|---|---|---|---|---|---|
| C11. Staff training programs | 0.747 | 0.494 | 0.108 | 0.503 | 0.494 | 0.328 | 0.070 |
| C12. Social responsibility | 0.775 | 0.511 | 0.100 | 0.475 | 0.511 | 0.317 | 0.066 |
| C13. Safety and health practices and wellbeing of suppliers | 0.733 | 0.476 | 0.110 | 0.517 | 0.476 | 0.331 | 0.072 |
| C21. Eco-design | 0.770 | 0.513 | 0.100 | 0.479 | 0.513 | 0.315 | 0.066 |
| C22. Environmental management and policies | 0.766 | 0.512 | 0.100 | 0.484 | 0.512 | 0.316 | 0.067 |
| C23. Waste and pollution | 0.753 | 0.493 | 0.109 | 0.497 | 0.493 | 0.331 | 0.069 |
| C31. Supply capacity | 0.756 | 0.492 | 0.104 | 0.494 | 0.492 | 0.322 | 0.068 |
| C32. Quality | 0.693 | 0.430 | 0.107 | 0.554 | 0.430 | 0.328 | 0.077 |
| C33. Cost/Price | 0.726 | 0.471 | 0.111 | 0.524 | 0.471 | 0.334 | 0.073 |
| C34. Delivery reliability | 0.813 | 0.562 | 0.089 | 0.432 | 0.562 | 0.298 | 0.060 |
| C35. Financial capability | 0.829 | 0.588 | 0.080 | 0.414 | 0.588 | 0.284 | 0.057 |
| C41. Adherence to regulatory changes | 0.787 | 0.526 | 0.103 | 0.462 | 0.526 | 0.320 | 0.063 |
| C42. Economic recovery programs | 0.749 | 0.489 | 0.095 | 0.501 | 0.489 | 0.309 | 0.070 |
| C43. Use of personal protective equipment | 0.715 | 0.449 | 0.107 | 0.534 | 0.449 | 0.328 | 0.074 |
| C44. Use of IT for customer demand prediction | 0.876 | 0.654 | 0.066 | 0.353 | 0.654 | 0.257 | 0.048 |
| Suppliers | Ranking | ||||
|---|---|---|---|---|---|
| Supplier 01 | 0.192 | 0.028 | 0.220 | 98.28 | 2 |
| Supplier 02 | 0.190 | 0.023 | 0.224 | 100 | 1 |
| Supplier 03 | 0.186 | 0.031 | 0.212 | 94.49 | 3 |
| Supplier 04 | 0.145 | 0.028 | 0.174 | 77.45 | 4 |
| Supplier 05 | 0.145 | 0.032 | 0.170 | 75.77 | 5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dang, T.-T.; Nguyen, N.-A.-T.; Nguyen, V.-T.-T.; Dang, L.-T.-H. A Two-Stage Multi-Criteria Supplier Selection Model for Sustainable Automotive Supply Chain under Uncertainty. Axioms 2022, 11, 228. https://doi.org/10.3390/axioms11050228
Dang T-T, Nguyen N-A-T, Nguyen V-T-T, Dang L-T-H. A Two-Stage Multi-Criteria Supplier Selection Model for Sustainable Automotive Supply Chain under Uncertainty. Axioms. 2022; 11(5):228. https://doi.org/10.3390/axioms11050228
Chicago/Turabian StyleDang, Thanh-Tuan, Ngoc-Ai-Thy Nguyen, Van-Thanh-Tien Nguyen, and Le-Thanh-Hieu Dang. 2022. "A Two-Stage Multi-Criteria Supplier Selection Model for Sustainable Automotive Supply Chain under Uncertainty" Axioms 11, no. 5: 228. https://doi.org/10.3390/axioms11050228
APA StyleDang, T.-T., Nguyen, N.-A.-T., Nguyen, V.-T.-T., & Dang, L.-T.-H. (2022). A Two-Stage Multi-Criteria Supplier Selection Model for Sustainable Automotive Supply Chain under Uncertainty. Axioms, 11(5), 228. https://doi.org/10.3390/axioms11050228









