Quadratic Equation in Split Quaternions

Abstract

Split quaternions are noncommutative and contain nontrivial zero divisors. Generally speaking, it is difficult to solve equations in such an algebra. In this paper, by using the roots of any split quaternions and two real nonlinear systems, we derive explicit formulas for computing the roots of $x^2+bx+c=0$ in split quaternion algebra.

1. Introduction

1.1. Split Quaternions

Let $\mathbb{R}$ and $\mathbb{C}$ be the field of real and complex numbers, respectively. The split quaternion algebra is a non-commutative extension of the complex numbers. Such an algebra is a 4-dimensional associative algebra original introduced by James Cockle in 1849. Split quaternions can be represented as

$${\mathbb{H}}_s=\{x=x_0+x_1\mathbf{i}+x_2\mathbf{j}+x_3\mathbf{k},x_i\in \mathbb{R},i=0,1,2,3\},$$

where $1,\mathbf{i},\mathbf{j},\mathbf{k}$ are the basis of ${\mathbb{H}}_s$ satisfying the following equalities:

$${\mathbf{i}}^2=-{\mathbf{j}}^2=-{\mathbf{k}}^2=-1,\mathbf{i}\mathbf{j}=\mathbf{k}=-\mathbf{j}\mathbf{i},\mathbf{j}\mathbf{k}=-\mathbf{i}=-\mathbf{k}\mathbf{j},\mathbf{k}\mathbf{i}=\mathbf{j}=-\mathbf{i}\mathbf{k}.$$

(1)

Let $\overline{x}=x_0-x_1\mathbf{i}-x_2\mathbf{j}-x_3\mathbf{k}$ be the conjugate of x and

$$I_x=\overline{x}x=x\overline{x}=x_0^2+x_1^2-x_2^2-x_3^2.$$

(2)

Let

$$\Re \left(x\right)=(x+\overline{x})/2=x_0,\Im \left(x\right)=(x-\overline{x})/2=x_1\mathbf{i}+x_2\mathbf{j}+x_3\mathbf{k}$$

be the real part and imaginary part of x and

$$K_x=\Im {\left(x\right)}^2=-x_1^2+x_2^2+x_3^2.$$

(3)

It can be easily verified that

$$\overline{xy}=\overline{y}\overline{x},I_{yx}=I_y{I}_x,\forall x,y\in {\mathbb{H}}_s.$$

Obviously, $\mathbb{C}=\mathbb{R}\oplus \mathbb{R}\mathbf{i}$; likewise, ${\mathbb{H}}_s=\mathbb{C}\oplus \mathbb{C}\mathbf{j}$ and $\mathbf{j}z=\overline{z}\mathbf{j}$ for $z\in \mathbb{C}$. That is, a split quaternion can be expressed as

$$x=(x_0+x_1\mathbf{i})+(x_2+x_3\mathbf{i})\mathbf{j}=z_1+z_2\mathbf{j}=z_1+\mathbf{j}\overline{z_2},z_1,z_2\in \mathbb{C}.$$

Unlike the Hamilton quaternion algebra, the split quaternion algebra contains nontrivial zero divisors, nilpotent elements, and idempotents. For example, $\frac{1+\mathbf{j}}{2}$ is an idempotent zero divisor, and $\mathbf{i}-\mathbf{j}$ is nilpotent. The set of zero divisors is denoted by

$$Z\left({\mathbb{H}}_s\right)=\{x\in {\mathbb{H}}_s:I_x=0\}.$$

(4)

If $I_x\ne 0$, then x is invertible and its inverse is

$$x^{-1}=\frac{\overline{x}}{I_x}.$$

(5)

If $I_x=0$, then x is not invertible. Cao and Chang [1] defined its Moore–Penrose inverse $x^{+}$ and used it to solve some simple linear equations.

The split quaternion algebra is closely related to these spaces ${\mathbb{R}}^{2,1}$, ${\mathbb{R}}^{3,1}$, and ${\mathbb{R}}^{2,2}$ and plays an important role in modern physics [2,3,4,5,6,7].

1.2. Quadratic Equations in $\mathbb{R},\mathbb{C},\mathbb{H}$

In algebra, a quadratic equation is any equation having the form

$$a{x}^2+bx+c=0,$$

(6)

where x represents an unknown, and $a,b$ and c represent known numbers and $a\ne 0$.

In real number setting, Equation (6) is solvable if and only if its discriminant $b^2-4ac\ge 0$. In complex number setting, by the fundamental theorem of algebra, Equation (6) is always solvable, and its roots are expressed by the quadratic formula

$$x_{1,2}=\frac{-b\pm \sqrt{b^2-4ac}}{2a}.$$

(7)

The quadratic equation has been investigated in Hamilton quaternion setting in [8,9]. Huang and So [8] considered $x^2+bx+c=0$ and obtained explicit formulas of its roots. These formulas had been used in the classification of quaternionic Möbius transformations [10,11].

1.3. Quadratic Equation in ${\mathbb{H}}_s$

In Hamilton quaternions, any nonzero element is invertible, while there are nonzero noninvertible split quaternions. Thus, it is interesting and novel to consider the quadratic Equation (6) in split quaternions ${\mathbb{H}}_s$. In an algebra system, finding the roots of the quadratic equation always connects with the factorizability of quadratic polynomial [12]. In $\mathbb{R}$ and $\mathbb{C}$, the two problems are identical. In noncommutative algebra, the two problems are relevant. Scharler et al. [13] have considered the factorizability of a quadratic split quaternion polynomial. The result reveals some information of the roots of a split quaternion quadratic equation.

In this paper, we will focus on deriving explicit formulas of the roots of the quadratic equation

$$x^2+bx+c=0,b,c\in {\mathbb{H}}_s.$$

However, this is a great challenge because of the noncommutativity of split quaternions and noninvertibility of split quaternions in $Z\left({\mathbb{H}}_s\right)$. We will use the following strategies to overcome these difficulties and find the roots of $x^2+bx+c=0$.

For equation $x^2+bx+c=0$ with $b\notin \mathbb{R}$, we have the following proposition.

Proposition 1.

The quadratic equation

$$y^2+dy+f=0,d=d_0+d_1\mathbf{i}+d_2\mathbf{j}+d_3\mathbf{j}\notin \mathbb{R}$$

is solvable if and only if the quadratic equation

$$x^2+bx+c=0,b=\Im \left(d\right)\ne 0,c=f-\frac{d_0}{2}(d-\frac{d_0}{2})$$

is solvable.

If the quadratic equation $x^2+bx+c=0$ is solvable and x is a solution, then $y=x-\frac{d_0}{2}$ is a solution of $y^2+dy+f=0$.

Proof. 

Rewriting $y^2+dy+f=0$ as

$${(y+\frac{d_0}{2})}^2+\Im \left(d\right)(y+\frac{d_0}{2})+f-\frac{d_0}{2}(d-\frac{d_0}{2})=0$$

and letting $x=y+\frac{d_0}{2}$, $b=\Im \left(d\right)$ and $c=f-\frac{d_0}{2}(d-\frac{d_0}{2})$, we conclude the proof of this proposition. □

Hence, we only need to solve the following equations:

• Equation I:

  $$x^2+bx+c=0,b\in \mathbb{R};$$

  (8)
• Equation II:

  $$x^2+bx+c=0,b=b_1\mathbf{i}+b_2\mathbf{j}+b_3\mathbf{k}\ne 0.$$

  (9)

Equation I can be reformulated as

$${\left(x+\frac{b}{2}\right)}^2=\frac{b^2-4c}{4}.$$

(10)

By the roots of any split quaternions obtained in [1,14], we will solve Equations I in Section 2 (Theorem 1).

Any solutions $x=x_0+x_1\mathbf{i}+x_2\mathbf{j}+x_3\mathbf{k}$ of Equation II fall into two categories:

$$\mathrm{SI}=\{x\in {\mathbb{H}}_s:x^2+bx+c=0 \mathrm{and} 2x_0+b\in {\mathbb{H}}_s-Z\left({\mathbb{H}}_s\right)\},$$

(11)

$$\mathrm{SZ}=\{x\in {\mathbb{H}}_s:x^2+bx+c=0 \mathrm{and} 2x_0+b\in Z\left({\mathbb{H}}_s\right)\}.$$

(12)

The following example shows that Equation II may have solutions in both $\mathrm{SI}$ and $\mathrm{SZ}$.

Example 1.

The quadratic equation

$$x^2+(\mathbf{i}+\mathbf{j})x-1+\mathbf{i}+\mathbf{j}=0$$

has solutions $\{-1,1-\mathbf{i}-\mathbf{j}\}\subset \mathrm{SI}$ and solutions $\{x_1\mathbf{i}+x_1\mathbf{j}+\mathbf{k},\forall x_1\in \mathbb{R}\}\subset \mathrm{SZ}.$

In order to solve Equation II, for technical reasons, we divide Equation II into the following two equations:

• Equation II for SI,
• Equation II for SZ.

We first consider Equation II for SI. The assumption that $2x_0+b$ is invertible enables us to use the method employed by Huang and So [8].

Observe that

$$x^2=x(2x_0-\overline{x})=2x_{0}x-I_x.$$

(13)

Therefore, $x^2+bx+c=0$ becomes

$$(2x_0+b)x=I_x-c.$$

(14)

Let

$$\begin{array}{ccc}\hfill N& =& I_x=\overline{x}x,\hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill T& =& \overline{x}+x=2x_0.\hfill \end{array}$$

(16)

If Equation II has a solution $x\in \mathrm{SI}$, i.e., $2x_0+b\in {\mathbb{H}}_s-Z\left({\mathbb{H}}_s\right)$; then, by (14), we have

$$x={(2x_0+b)}^{-1}(I_x-c)={(T+b)}^{-1}(N-c)=\frac{(T+\overline{b})(N-c)}{T^2+I_b}$$

(17)

and

$$\overline{x}=\frac{(N-\overline{c})(T+b)}{T^2+I_b}.$$

(18)

Substituting the above formulas of x and $\overline{x}$ in (15) and (16), we obtain that $(T,N)$ satisfies our first real nonlinear system:

$$\left\{\begin{array}{c}\hfill N^2-(B+T^2)N+E=0,\\ \hfill T^3+(B-2N)T+D=0,\end{array}\right.$$

(19)

where $B=2c_0+I_b,E=I_c,D=2\Re \left(\overline{b}c\right)$.

Since we do not know $x_0$ beforehand, it is an embarrassing situation to assume that

$$2x_0+b=T+b\in {\mathbb{H}}_s-Z\left({\mathbb{H}}_s\right).$$

This embarrassing situation can be remedied afterward. We can solve the real nonlinear system (19) to obtain the pair $(T,N)$ and then test whether or not $T+b\in {\mathbb{H}}_s-Z\left({\mathbb{H}}_s\right)$. Only for the pair $(T,N)$ such that $T+b\in {\mathbb{H}}_s-Z\left({\mathbb{H}}_s\right)$ do we obtain the corresponding solution $x={(T+b)}^{-1}(N-c)$ (Theorem 2).

However, Equation II for SZ can not use the real nonlinear system (19). This may be the big difference between split quaternions and Hamilton quaternions in solving quadratic equations. We will use a different technical route.

Let $b=b_0+b_1\mathbf{i}+b_2\mathbf{j}+b_3\mathbf{k}$, $c=c_0+c_1\mathbf{i}+c_2\mathbf{j}+c_3\mathbf{k}\in {\mathbb{H}}_s$. By the rule of multiplication (1), $x^2+bx+c=0$ can be reformulated as our second real nonlinear system:

$$\left\{\begin{array}{cc}\hfill x_0^2-x_1^2+x_2^2+x_3^2+b_0{x}_0-b_1{x}_1+b_2{x}_2+b_3{x}_3+c_0=0,& \\ \hfill 2x_0{x}_1+b_0{x}_1+b_1{x}_0-b_2{x}_3+b_3{x}_2+c_1=0,& \\ \hfill 2x_0{x}_2+b_0{x}_2-b_1{x}_3+b_2{x}_0+b_3{x}_1+c_2=0,& \\ \hfill 2x_0{x}_3+b_0{x}_3+b_1{x}_2-b_2{x}_1+b_3{x}_0+c_3=0.\end{array}\right.$$

(20)

Generally speaking, Equation (20) is very complicated and hard to solve. However, if $x=x_0+x_1\mathbf{i}+x_2\mathbf{j}+x_3\mathbf{k}\in SZ$, then $x_0$ can be determined by $2x_0+b\in Z\left({\mathbb{H}}_s\right)$ in advance. We only need to find $x_1,x_2,x_3$ in Equation (20). We can deduce the linear relations expressed by Equations (49)–(51) of $x_1,x_2$ and $x_3$ form Equation (20). By the linear relations, we can solve Equation (20) (Theorem 3).

This strategy of using the roots of any split quaternions and the above two real nonlinear systems help us to overcome the difficulty caused by the noncommutativity of split quaternions and noninvertibility of split quaternions in $Z\left({\mathbb{H}}_s\right)$. Consequently, we obtain explicit formulas for commuting the roots of $x^2+bx+c=0$. We will give examples to illustrate the use of our formulas obtained in Section 2, Section 3 and Section 4 and find all solutions of these examples.

After we have finished our paper, one of the referees kindly informed the author that Kwun et al. [15,16] also considered a quadratic equation in split quaternions. In fact, the main results in [15] overlap with Theorem 2, although there is a slight difference in proving this result. Theorems 3 of this paper answer the open question left by Kwun, etc. (see Theorem 2 Open Question and Discussion of [15]). Munir et al. [16] considered the quadratic equation in the finite ring ${\mathbb{H}}_s/{\mathbb{Z}}_p$, which is a different algebra setting from ${\mathbb{H}}_s$. I would like to express my appreciation to the referees for pointing this out and for several other suggestions that lead to improvement of the quality of this paper.

2. Equation ${\mathit{x}}^{\mathbf{2}}+\mathit{bx}+\mathit{c}=\mathbf{0}$ with $\mathit{b}\in \mathbb{R}$

In this section, we will find the possible solutions of the equation $x^2+bx+c=0$ with $b\in \mathbb{R}$. For convenience, we begin with a definition:

Definition 1.

Let $w=w_0+w_1\mathbf{i}+w_2\mathbf{j}+w_3\mathbf{k}\in {\mathbb{H}}_s$. We define that $\sqrt[s]{w}=\{x\in {\mathbb{H}}_s:x^2=w\}.$

By this definition, $\sqrt[s]{w}$ means the square root of w in split quaternions. We will follow the conventional sign $\sqrt{z}$ for $z\in \mathbb{R}$ or $\mathbb{C}$.

Since $b\in \mathbb{R}$, we can rewrite $x^2+bx+c=0$ as

$${(x+\frac{b}{2})}^2=\frac{b^2-4c}{4}.$$

(21)

If $w=\frac{b^2-4c}{4}\in {\mathbb{H}}_s$ has square root $\sqrt[s]{w}$, then $x^2+bx+c=0$ has solutions of the form

$$x=-\frac{b}{2}+\sqrt[s]{w}.$$

Thus, we need to consider the square root of elements in split quaternions. Fortunately, Ozdemir [14] obtained the root of any invertible split quaternions and Cao and Chang [1] obtained the root of any noninvertible split quaternions. For our purpose, we rewrite these formulas of the square of split quaternions as the following lemma:

Lemma 1

([1,14]). Let $w=w_0+w_1\mathbf{i}+w_2\mathbf{j}+w_3\mathbf{k}\in {\mathbb{H}}_s$.

(1) 

If $w\in \mathbb{R}$, that is, $w=w_0$, then

$$\sqrt[s]{w_0}=\{x_1\mathbf{i}+x_2\mathbf{j}+x_3\mathbf{k}:-x_1^2+x_2^2+x_3^2=w_0\}provided{w}_0\le 0;$$

(22)

$$\sqrt[s]{w_0}=\{x_1\mathbf{i}+x_2\mathbf{j}+x_3\mathbf{k}:-x_1^2+x_2^2+x_3^2=w_0\}\cup \{\pm \sqrt{w_0}\}provided{w}_0>0.$$

(23)

(2) 

If $w\notin \mathbb{R}$, then $\sqrt[s]{w}\ne \varnothing$ if and only if $I_w\ge 0$ and $w_0+\sqrt{I_w}>0$.

(i) 

If $w_0-\sqrt{I_w}>0$, then

$$\sqrt[s]{w}=\{\pm \frac{w+\sqrt{I_w}}{\sqrt{2(w_0+\sqrt{I_w})}}\}\cup \{\pm \frac{w-\sqrt{I_w}}{\sqrt{2(w_0-\sqrt{I_w})}}\}.$$

(24)

(ii) 

If $w_0+\sqrt{I_w}>0\ge w_0-\sqrt{I_w}$, then

$$\sqrt[s]{w}=\{\pm \frac{\sqrt{I_w}+w}{\sqrt{2(w_0+\sqrt{I_w})}}\}.$$

(25)

Proof. 

Note that $x^2=x(2x_0-\overline{x})=x_0^2-x_1^2+x_2^2+x_3^2+2x_0(x_1\mathbf{i}+x_2\mathbf{j}+x_3\mathbf{k})$. If $x\in \sqrt[s]{w}$, then

$$2x_0{x}_1=w_1,2x_0{x}_2=w_2,2x_0{x}_3=w_3,x_0^2-x_1^2+x_2^2+x_3^2=w_0.$$

(26)

Observe that $w\in \mathbb{R}$ implies that $x_0=0$ or $x_1^2+x_2^2+x_3^2=0$. This observation proves Equations (22) and (23). By (26), if $w\notin \mathbb{R}$, then $x_0\ne 0$. Consequently,

$$x_1=\frac{w_1}{2x_0},x_2=\frac{w_2}{2x_0},x_3=\frac{w_3}{2x_0}$$

and

$$4x_0^4-4x_0^2{w}_0-w_1^2+w_2^2+w_3^2=0.$$

(27)

Viewing Equation (27) as a real quadratic equation with unknown $x_0^2$, we obtain its discriminant $16I_w$. If $I_w\ge 0$ and $w_0+\sqrt{I_w}>0$, then Equation (27) is solvable. If $w_0-\sqrt{I_w}>0$, then

$$x_0^2=\frac{w_0-\sqrt{I_w}}{2},\mathrm{or}{x}_0^2=\frac{w_0+\sqrt{I_w}}{2}.$$

If $w_0+\sqrt{I_w}>0\ge w_0-\sqrt{I_w}$, then

$$x_0^2=\frac{w_0+\sqrt{I_w}}{2}.$$

In each case, we have $x=\frac{1}{2x_0}(2x_0^2+w_1\mathbf{i}+w_2\mathbf{j}+w_3\mathbf{k})$. This observation concludes the proof. □

Our main theorem of this section is the following theorem.

Theorem 1.

([15]). Equation I is solvable if and only if

$$\sqrt[s]{\frac{b^2-4c}{4}}\ne \varnothing .$$

If Equation I is solvable, its solution(s) can be given by

$$x=\frac{-b}{2}+\sqrt[s]{\frac{b^2-4c}{4}}.$$

(28)

In other words, the solutions of Equation I can be obtained by formulas according to the following cases:

(1) 

If $b,c\in \mathbb{R}$ and $b^2<4c$, then

$$x=\frac{-b}{2}+x_1\mathbf{i}+x_2\mathbf{j}+x_3\mathbf{k},$$

where $-x_1^2+x_2^2+x_3^2=\frac{b^2-4c}{4}$ and $x_1,x_2,x_3\in \mathbb{R}$.

(2) 

If $b,c\in \mathbb{R}$ and $b^2\ge 4c$, then the set of solutions is

$$\{x=\frac{-b\pm \sqrt{b^2-4c}}{2}\}\cup \{x\in {\mathbb{H}}_s:x=\frac{-b}{2}+x_1\mathbf{i}+x_2\mathbf{j}+x_3\mathbf{k}\},$$

where $-x_1^2+x_2^2+x_3^2=\frac{b^2-4c}{4}$ and $x_1,x_2,x_3\in \mathbb{R}$.

(3) 

If $b\in \mathbb{R}$, $c=c_0+c_1\mathbf{i}+c_2\mathbf{j}+c_3\mathbf{k}\notin \mathbb{R}$, ${(b^2-4c_0)}^2-16K_c\ge 0$ and $\frac{b^2-4c_0+\sqrt{{(b^2-4c_0)}^2-16K_c}}{2}>0$, then the solutions are as follows:

(i) 

If $\frac{b^2-4c_0-\sqrt{{(b^2-4c_0)}^2-16K_c}}{2}>0$, then

$$x=\frac{1}{2}(-b\pm {\rho }_i)\mp \frac{1}{{\rho }_i}(c_1\mathbf{i}+c_2\mathbf{j}+c_3\mathbf{k}),i=1,2,$$

where ${\rho }_{1,2}=\sqrt{\frac{b^2-4c_0\pm \sqrt{{(b^2-4c_0)}^2-16K_c}}{2}}$.

(ii) 

If $\frac{b^2-4c_0+\sqrt{{(b^2-4c_0)}^2-16K_c}}{2}>0\ge \frac{b^2-4c_0-\sqrt{{(b^2-4c_0)}^2-16K_c}}{2}$, then

$$x=\frac{1}{2}(-b\pm \rho )\mp \frac{1}{\rho }(c_1\mathbf{i}+c_2\mathbf{j}+c_3\mathbf{k}),$$

where $\rho =\sqrt{\frac{b^2-4c_0+\sqrt{{(b^2-4c_0)}^2-16K_c}}{2}}$.

Proof. 

Expanding the part $\sqrt[s]{\frac{b^2-4c}{4}}$ by Lemma 1 concludes the proof. □

Example 2.

Consider the quadratic equation $x^2+3+\mathbf{i}+\mathbf{j}+\mathbf{k}=0$. Since $\sqrt[s]{-c}=\sqrt[s]{-3-\mathbf{i}-\mathbf{j}-\mathbf{k}}=\varnothing$, this quadratic equation is unsolvable.

Some examples of Theorem 1 are given in Table 1.

Table 1. Some examples in Theorem 1.

	$(\mathit{b},\mathit{c})$	The Solution(s) of ${\mathit{x}}^2+\mathit{bx}+\mathit{c}=0$
(1)	$(0,c_0)$,$(c_0>0)$	$x=x_1\mathbf{i}+x_2\mathbf{j}+x_3\mathbf{k}$ with $-x_1^2+x_2^2+x_3^2=-c_0$
(1)	$(0,c_0),(c_0<0)$	$x=\pm \sqrt{-c_0}$
		$x=x_1\mathbf{i}+x_2\mathbf{j}+x_3\mathbf{k}$ with $-x_1^2+x_2^2+x_3^2=-c_0$
(2)	$(2,-3)$	$x=1,x=-3$
		$x=-1+x_1\mathbf{i}+x_2\mathbf{j}+x_3\mathbf{k}$ with $-x_1^2+x_2^2+x_3^2=4$
(3) (i)	$(4,\mathbf{i}+2\mathbf{j}+3\mathbf{k})$	$x=-2+\sqrt{3}-\frac{\sqrt{3}}{6}\mathbf{i}-\frac{\sqrt{3}}{3}\mathbf{j}-\frac{\sqrt{3}}{2}\mathbf{k}$
		$x=-2-\sqrt{3}+\frac{\sqrt{3}}{6}\mathbf{i}+\frac{\sqrt{3}}{3}\mathbf{j}+\frac{\sqrt{3}}{2}\mathbf{k}$
		$x=-1-\frac{1}{2}\mathbf{i}-\mathbf{j}-\frac{3}{2}\mathbf{k}$
		$x=-3+\frac{1}{2}\mathbf{i}+\mathbf{j}+\frac{3}{2}\mathbf{k}$
(3) (ii)	$(2,\frac{7}{2}\mathbf{i}+\mathbf{j})$	$x=\frac{1}{2}-\frac{7}{6}\mathbf{i}-\frac{1}{3}\mathbf{j}$ and $x=-\frac{5}{2}+\frac{7}{6}\mathbf{i}+\frac{1}{3}\mathbf{j}$

3. $\mathbf{2}{\mathit{x}}_{\mathbf{0}}+\mathit{b}$ Being Invertible

In this section, we assume that x is a solution of Equation II and $2x_0+b$ is invertible. To find such a solution, we need to solve the following real nonlinear system:

$$\begin{array}{cc}\hfill N^2-(B+T^2)N+E=0,& \end{array}$$

(29)

$$\begin{array}{c}\hfill T^3+(B-2N)T+D=0,\end{array}$$

(30)

where $B=2c_0+I_b,E=I_c,D=2\Re \left(\overline{b}c\right)$.

If $D\ne 0$, then, by Equation (30), we have $T\ne 0$. It follows from (30) that

$$N=\frac{T^3+BT+D}{2T}.$$

(31)

Substituting the above in (29), we obtain

$$\frac{{(T^3+BT+D)}^2}{4T^2}-\frac{(T^3+BT+D)\left[2T(B+T^2)\right]}{4T^2}+\frac{4T^{2}E}{4T^2}=0.$$

Hence, we have

$$T^2{(T^2+B)}^2-4E{T}^2{D}^2=0.$$

Let $T^2=z$. Then,

$$z^3+2B{z}^2+(B^2-4E)z-D^2=0.$$

(32)

In order to find the pairs $(T,N)$ of Equations (29) and (30), we need to know all the positive solutions of Equation (32) when $D\ne 0$ . The following lemma provides our required information of positive solutions of Equation (32):

Lemma 2.

Let $B,E,D\in \mathbb{R}$ such that $D\ne 0$,

$$F_1=\frac{-2B^3+2{(B^2+12E)}^{\frac{3}{2}}}{27}+\frac{8EB}{3}-D^2$$

and

$$F_2=\frac{-2B^3-2{(B^2+12E)}^{\frac{3}{2}}}{27}+\frac{8EB}{3}-D^2.$$

Then, the cubic equation

$$z^3+2B{z}^2+(B^2-4E)z-D^2=0$$

(33)

has solutions in the interval $(0,\infty )$ as follows.

Case 1. If one of the following conditions holds, then Equation (33) has exactly one positive solution z:

(i) 

$B^2+12E\le 0$;

(ii) 

$B^2+12E>0,B\ge 0$;

(iii) 

$B<0,B^2-4E<0$;

(iv) 

$B^2+12E>0,B<0,B^2-4E>0,F_1<0$;

(v) 

$B^2+12E>0,B<0,B^2-4E>0,F_2>0$.

Case 2. If one of the following conditions holds, then Equation (33) has exactly two positive solutions $z_1$ and $z_2$:

(vi) 

$B^2+12E>0,B<0,B^2-4E>0,F_1=0$;

(vii) 

$B^2+12E>0,B<0,B^2-4E>0,F_2=0$.

Case 3. If $B^2+12E>0,B<0,B^2-4E>0,F_1>0>F_2$, then Equation (33) has exactly three positive solutions $z_i,i=1,2,3$.

Proof. 

Let $f\left(z\right)=z^3+2B{z}^2+(B^2-4E)z-D^2.$ We focus our attention on the interval $(0,\infty )$. It is obvious that

$$f\left(0\right)=-D^2<0,\underset{z\to +\infty }{lim}f\left(z\right)=+\infty .$$

Note that

$$f^{\prime }\left(z\right)=3z^2+4Bz+B^2-4E=3\left({(z+\frac{2B}{3})}^2-\frac{B^2+12E}{9}\right).$$

(34)

The discriminant of $f^{\prime }\left(z\right)=0$ is

$${\Delta }_{f^{\prime }}=4(B^2+12E).$$

If ${\Delta }_{f^{\prime }}\le 0$, then $f^{\prime }\left(z\right)\ge 0$. Hence, Equation (33) has exactly one positive solution z. This proves Case 1 (i).

We now consider the case ${\Delta }_{f^{\prime }}=4(B^2+12E)>0$. Note that the solutions of $f^{\prime }\left(z\right)=0$ are

$$z_1=\frac{-2B-\sqrt{B^2+12E}}{3},z_2=\frac{-2B+\sqrt{B^2+12E}}{3},$$

and it can be verified that $F_1=f\left(z_1\right),F_2=f\left(z_2\right)$.

If $B\ge 0$, then $z=-\frac{2B}{3}\le 0$. This means that $f^{\prime }\left(z\right)$ is increasing in $(-\frac{2B}{3},\infty )$. If $z_2\le 0$, then $f^{\prime }\left(z\right)>0$ in $(0,\infty )$ and therefore $f\left(z\right)$ is increasing in $(0,\infty )$. If $z_2>0$, then $f^{\prime }\left(z\right)<0$ in $(0,z_2)$ and $f^{\prime }\left(z\right)>0$ in $(z_2,\infty )$. Therefore, $f\left(z\right)$ is decreasing in $(0,z_2)$ and then increasing in the interval $(z_2,\infty )$. Note that $f\left(0\right)=-D^2<0$. In both cases, Equation (33) has exactly one positive solution z in $(0,\infty )$. This proves Case 1 (ii).

If $B<0$, then $z=-\frac{2B}{3}>0$. If $f^{\prime }\left(0\right)=B^2-4E<0$, then $z_1<0$ and $f\left(z\right)$ decrease at first in the interval $(0,z_2)$ and increases in the interval $(z_2,+\infty )$. Hence, $f\left(z\right)$ has exactly one positive solution z. This proves Case 1 (iii).

We now consider the case $B<0$ and $f^{\prime }\left(0\right)=B^2-4E>0$. In this case, $f^{\prime }\left(z\right)$ is positive in $(0,z_1)\cup (z_2,\infty )$ and negative in $(z_1,z_2)$.

If $f\left(z_1\right)<0$, then $f\left(z\right)$ is increasing in $(0,z_1)$, decreasing in $(z_1,z_2)$ and then increasing in $(z_2,+\infty )$. Hence, Equation (33) has exactly one positive solution in $(z_2,+\infty )$. This proves Case 1 (iv).

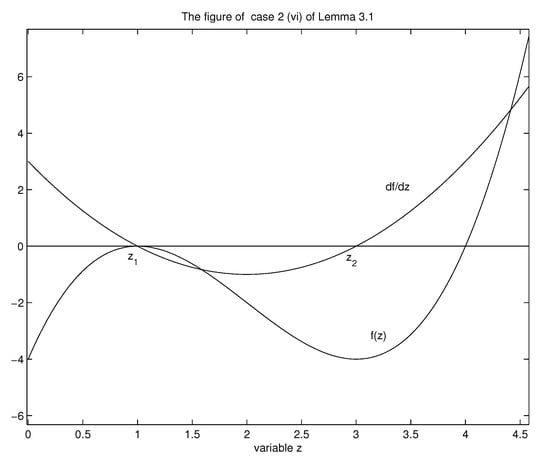
If $f\left(z_1\right)=0$, then it is obvious that Equation (33) has exactly two positive solutions, and the other one is in $(z_2,+\infty )$. This proves Case 2 (vi). For the sake of readability, we present the following Figure 1 for Case 2 (vi).

Figure 1. The figure of case 2 (vi).

If $f\left(z_1\right)>f\left(z_2\right)>0$, then Equation (33) has exactly one positive solution in $[0,z_1]$. This proves Case 1 (v).

If $f\left(z_1\right)>0=f\left(z_2\right)$, then Equation (33) has exactly two positive solutions, and the other one is in $[0,z_1]$. This proves Case 2 (vii). If $f\left(z_1\right)>0>f\left(z_2\right)$, then Equation (33) has exactly three positive solutions which lie in

$$(0,z_1)\cup (z_1,z_2)\cup (z_2,+\infty ).$$

This proves Case 3. □

We are ready to find the pairs $(T,N)$ of Equations (29) and (30).

Lemma 3.

Let $B,E,D\in \mathbb{R}$. Then, the real system

$$\begin{array}{cc}\hfill N^2-(B+T^2)N+E=0,& \end{array}$$

(35)

$$\begin{array}{c}\hfill T^3+(B-2N)T+D=0\end{array}$$

(36)

has solutions $(T,N)\in {\mathbb{R}}^2$ as follows:

(1) 

$T=0,N=\frac{B\pm \sqrt{B^2-4E}}{2}$ provided $D=0,B^2-4E\ge 0$;

(2) 

$T=\pm \sqrt{-2\sqrt{E}-B},N=-\sqrt{E}$; and $T=\pm \sqrt{2\sqrt{E}-B},N=\sqrt{E}$ provided $D=0,E\ge 0,-2\sqrt{E}-B\ge 0$;

(3) 

$T=\pm \sqrt{2\sqrt{E}-B},N=\sqrt{E}$ provided $D=0,E\ge 0,2\sqrt{E}-B\ge 0>-2\sqrt{E}-B$;

(4) 

$T=\pm \sqrt{z},N=\frac{T^3+BT+D}{2T}$ provided $D\ne 0$, Case 1 of Lemma 2 holds, and z is the unique positive root of real polynomial $z^3+2B{z}^2+(B^2-4E)z-D^2$;

(5) 

$T=\pm \sqrt{z_i},N=\frac{T^3+BT+D}{2T},i=1,2$ provided $D\ne 0$, Case 2 of Lemma 2 hold and $z_1,z_2$ are two positive roots of real polynomial $z^3+2B{z}^2+(B^2-4E)z-D^2$;

(6) 

$T=\pm \sqrt{z_i},N=\frac{T^3+BT+D}{2T},i=1,2,3$ provided $D\ne 0$, Case 3 of Lemma 2 hold and $z_1,z_2,z_3$ are the three positive roots of real polynomial $z^3+2B{z}^2+(B^2-4E)z-D^2$.

Proof. 

We divide our consideration into two subcases $D=0$ and $D\ne 0$.

We begin with the subcase $D=0$. In this case, Equation (36) becomes

$$T(T^2+B-2N)=0.$$

Hence, $T=0$ or $T^2+B-2N=0$. If $T=0$, then Equation (35) becomes $N^2-BN+E=0$ and therefore $N_{1,2}=\frac{B\pm \sqrt{B^2-4E}}{2}$ provided $B^2-4E\ge 0$. This proves (1).

If $T^2+B-2N=0$, then $T^2+B=2N$ and therefore Equation (35) becomes $N^2=E$. Thus, $N_{1,2}=\pm \sqrt{E}$ provided $E\ge 0$. Hence, $T^2=2N-B=\pm 2\sqrt{E}-B$. Take $N=-\sqrt{E},T^2=-2\sqrt{E}-B$ provided $E\ge 0,-2\sqrt{E}-B\ge 0$. In this case, we also can take $N=\sqrt{E},T^2=2\sqrt{E}-B$ because of $2\sqrt{E}-B\ge -2\sqrt{E}-B\ge 0$. This proves (2).

If $E\ge 0,2\sqrt{E}-B\ge 0>-2\sqrt{E}-B$, then we can take $N=\sqrt{E},T^2=2\sqrt{E}-B$. This proves (3).

For the second case $D\ne 0$, such a system can be solved by Lemma 2 as claimed. These prove (4), (5), and (6). □

Theorem 2.

For the coefficients $b,c$ in Equation II, we define

$$B=2c_0+I_b,E=I_c,D=2\Re \left(\overline{b}c\right).$$

(37)

If Equation II is solvable and has solution $x=x_0+x_1\mathbf{i}+x_2\mathbf{j}+x_3\mathbf{k}$ with $x_0^2\ne \frac{K_b}{4}$, then

$$x={(T+b)}^{-1}(N-c),$$

(38)

where $(T,N)$ is chosen as follows:

(1) 

$T=0,N=\frac{B\pm \sqrt{B^2-4E}}{2}$ provided $D=0,B^2-4E\ge 0$;

(2) 

$T=\pm \sqrt{-2\sqrt{E}-B},N=-\sqrt{E}$, and $T=\pm \sqrt{2\sqrt{E}-B},N=\sqrt{E}$ provided $D=0,E\ge 0,-2\sqrt{E}-B\ge 0$;

(3) 

$T=\pm \sqrt{2\sqrt{E}-B},N=\sqrt{E}$ provided $D=0,E>0,2\sqrt{E}-B\ge 0>-2\sqrt{E}-B$;

(4) 

$T=\pm \sqrt{z},N=\frac{T^3+BT+D}{2T}$ provided $D\ne 0$, Case 1 of Lemma 2 holds and z is the unique positive root of real polynomial $z^3+2B{z}^2+(B^2-4E)z-D^2$;

(5) 

$T=\pm \sqrt{z_i},N=\frac{T^3+BT+D}{2T},i=1,2$ provided $D\ne 0$, Case 2 of Lemma 2 holds and $z_1,z_2$ are two positive roots of real polynomial $z^3+2B{z}^2+(B^2-4E)z-D^2$;

(6) 

$T=\pm \sqrt{z_i},N=\frac{T^3+BT+D}{2T},i=1,2,3$ provided $D\ne 0$, Case 3 of Lemma 2 holds and $z_1,z_2,z_3$ are the three positive roots of real polynomial $z^3+2B{z}^2+(B^2-4E)z-D^2$.

Proof. 

By Lemma 3, we obtain the pairs $(T,N)$ of Equations (35) and (36). For each pair $(T,N)$, if $T+b$ is invertible, then we obtain a solution $x={(T+b)}^{-1}(N-c)$. □

Some examples of Theorem 2 are given in Table 2 and Table 3. In Table 3, “C1(i)L3.1” is an abbreviation of Case 1 (i) of Lemma 2.

Table 2. Some examples in Theorem 2 with $D=0$.

	$(\mathit{b},\mathit{c})$	$(\mathit{T},\mathit{N})$	The Solution(s) of ${\mathit{x}}^2+\mathit{bx}+\mathit{c}=0$
(1)	$(2\mathbf{j},2\mathbf{i}+3\mathbf{k})$	$(0,1)$	$x=\frac{3}{2}\mathbf{i}+\frac{1}{2}\mathbf{j}+\mathbf{k}$
		$(0,-5)$	$x=\frac{3}{2}\mathbf{i}-\frac{5}{2}\mathbf{j}+\mathbf{k}$
(2)I	$(\mathbf{i}+\mathbf{j},-1+\mathbf{i}+\mathbf{j})$	$(0,0),(0,-1),(0,-2)$	no solution
		$(-2,1)$	$x=-1$
		$(2,1)$	$x=1-\mathbf{i}-\mathbf{j}$
(2)II	$(2\mathbf{j}+\mathbf{k},2\mathbf{i})$	$(1,-2)$	$x=\frac{1}{2}+\frac{1}{2}\mathbf{i}-\frac{3}{2}\mathbf{j}+\frac{1}{2}\mathbf{k}$
		$(-1,-2)$	$x=-\frac{1}{2}-\frac{1}{2}\mathbf{i}-\frac{3}{2}\mathbf{j}+\frac{1}{2}\mathbf{k}$
		$(3,2)$	$x=\frac{3}{2}-\frac{3}{2}\mathbf{i}-\frac{1}{2}\mathbf{j}-\frac{3}{2}\mathbf{k}$
		$(-3,2)$	$x=-\frac{3}{2}+\frac{3}{2}\mathbf{i}-\frac{1}{2}\mathbf{j}-\frac{3}{2}\mathbf{k}$
(3)	$(\mathbf{k},5\mathbf{i}+3\mathbf{j})$	$(3,4)$	$x=\frac{3}{2}-\frac{3}{2}\mathbf{i}-\frac{1}{2}\mathbf{j}-\frac{1}{2}\mathbf{k}$
		$(-3,4)$	$x=-\frac{3}{2}+\frac{9}{4}\mathbf{i}+\frac{7}{4}\mathbf{j}-\frac{1}{2}\mathbf{k}$

Table 3. Some examples in Theorem 2 with $D\ne 0$.

	$(\mathit{b},\mathit{c})$	$(\mathit{z},\mathit{T},\mathit{N})$	Solution(s) of ${\mathit{x}}^2+\mathit{bx}+\mathit{c}=0$
(4) & C1(i)L3.1		$(\frac{1}{2},\frac{\sqrt{2}}{2},\frac{1-\sqrt{2}}{4})$	$x=\frac{\sqrt{2}}{4}+\frac{\sqrt{2}-1}{2}\mathbf{i}+\frac{\sqrt{2}-2}{4}\mathbf{j}+\frac{1}{2}\mathbf{k}$
	$(\mathbf{i}+\mathbf{j},\frac{\mathbf{j}}{4})$	$(\frac{1}{2},-\frac{\sqrt{2}}{2},\frac{1+\sqrt{2}}{4})$	$x=-\frac{\sqrt{2}}{4}-\frac{\sqrt{2}+1}{2}\mathbf{i}-\frac{\sqrt{2}+2}{4}\mathbf{j}+\frac{1}{2}\mathbf{k}$
(4) & C1(ii)L3.1		$(4,2,4)$	$x=1-2\mathbf{i}-\frac{4}{5}\mathbf{j}-\frac{3}{5}\mathbf{k}$
	$(\mathbf{i},3\mathbf{i}+\mathbf{j}+2\mathbf{k})$	$(4,-2,1)$	$x=-1+\mathbf{i}+\mathbf{k}$
(4) & C1(iii)L3.1		$(4,2,2)$	$x=1-3\mathbf{i}+2\mathbf{j}-2\mathbf{k}$
	$(\mathbf{i}+2\mathbf{k},1+\mathbf{i})$	$(4,-2,1)$	$x=-1+2\mathbf{i}+2\mathbf{j}$
(4) & C1(iv)L3.1		$(4,2,2)$	$x=1-\frac{9}{4}\mathbf{i}-\frac{1}{4}\mathbf{j}-2\mathbf{k}$
	$(\frac{11}{4}\mathbf{i}+\frac{3}{4}\mathbf{j}+3\mathbf{k},\mathbf{i}+\mathbf{j})$	$(4,-2,0)$	$x=-1+\frac{5}{2}\mathbf{i}+\frac{5}{2}\mathbf{j}+\mathbf{k}$
(4) & C1(v)L3.1		$(1,1,-\sqrt{11}-3)$	$x=\frac{1}{2}-\frac{2+\sqrt{11}}{2}\mathbf{i}+\frac{1}{2}\mathbf{j}-\frac{\sqrt{11}+4}{2}\mathbf{k}$
	$(2\mathbf{i}+\sqrt{11}\mathbf{k},\mathbf{j}+\mathbf{k})$	$(1,1,\sqrt{11}-3)$	$x=-\frac{1}{2}+\frac{\sqrt{11}-6}{6}\mathbf{i}+\frac{1}{6}\mathbf{j}+\frac{8-3\sqrt{11}}{6}\mathbf{k}$
(5) & C2(vi)L3.1	$(-\mathbf{i}+2\mathbf{k},-\mathbf{i}+\mathbf{j})$	$(1,1,0)$	$x=\frac{1}{2}-\frac{3}{2}\mathbf{i}+\frac{3}{2}\mathbf{j}+\frac{1}{2}\mathbf{k}$
		$(1,-1,-2)$	$x=-\frac{1}{2}+\frac{1}{2}\mathbf{i}+\frac{1}{2}\mathbf{j}-\frac{3}{2}\mathbf{k}$
		$(4,2,1)$	$x=1+5\mathbf{i}-4\mathbf{j}-3\mathbf{k}$
		$(4,-2,0)$	$x=-1-\mathbf{k}$
(5) & C2(vii)L3.1	$(2\mathbf{j}+2\mathbf{k},2\mathbf{j}+\mathbf{k})$	$(4,2,-5)$	$x=1-\frac{1}{2}\mathbf{i}-\frac{3}{2}\mathbf{j}-2\mathbf{k}$
		$(4,-2,1)$	$x=-1-\frac{1}{2}\mathbf{i}-\frac{1}{2}\mathbf{j}$
		$(6,\sqrt{6},-1-\sqrt{6})$	$x=\frac{\sqrt{6}}{2}-\mathbf{i}-\mathbf{j}-(\frac{\sqrt{6}}{2}+1)\mathbf{k}$
		$(6,-\sqrt{6},\sqrt{6}-1)$	$x=-\frac{\sqrt{6}}{2}-\mathbf{i}-\mathbf{j}+(\frac{\sqrt{6}}{2}-1)\mathbf{k}$
(6) & C3L3.1	$(2\mathbf{j}+3\mathbf{k},3+\mathbf{i}+3\mathbf{j}-\mathbf{k})$	$(1,1,-6)$	$x=\frac{1}{2}-\frac{5}{6}\mathbf{i}-\frac{3}{2}\mathbf{j}-\frac{13}{6}\mathbf{k}$
		$(1,-1,0)$	$x=-\frac{1}{2}-\mathbf{i}-\mathbf{j}-\frac{1}{2}\mathbf{k}$
		$(4,2,-3)$	$x=1-\mathbf{i}-\mathbf{j}-2\mathbf{k}$
		$(4,-2,0)$	$x=-1-\frac{13}{9}\mathbf{i}-\frac{15}{9}\mathbf{j}-\frac{5}{9}\mathbf{k}$
		$(9,3,0)$	$x=\frac{3}{2}-2\mathbf{i}-\frac{5}{2}\mathbf{k}$
		$(9,-3,2)$	$x=-\frac{3}{2}-\frac{7}{2}\mathbf{i}-\frac{7}{2}\mathbf{j}+\frac{1}{2}\mathbf{k}$

4. $\mathbf{2}{\mathit{x}}_{\mathbf{0}}+\mathit{b}$ Being Noninvertible

In this section, we will find the necessary and sufficient conditions of Equation II having a solution $x\in 2x_0+b\in Z\left({\mathbb{H}}_s\right)$.

Suppose that $x^2+bx+c=0$ has a solution of $2x_0+b\in Z\left({\mathbb{H}}_s\right)$. Then, we have

$$x_0^2=\frac{K_b}{4}.$$

(39)

Since $(2x_0+b)x=I_x-c$, we have $I_x-c=I_x-c_0-c_1\mathbf{i}-c_2\mathbf{j}-c_3\mathbf{k}\in Z\left({\mathbb{H}}_s\right)$ and therefore

$$I_x^2-2c_0{I}_x+I_c=0.$$

(40)

The existence of $I_x$ leads to the discriminate

$$4c_0^2-4I_c=4K_c\ge 0.$$

(41)

Therefore, we at first need that

$$K_b,K_c\ge 0.$$

Let $x=x_0+x_1\mathbf{i}+x_2\mathbf{j}+x_3\mathbf{k}$ with $x_0^2=\frac{K_b}{4}$. For Equation II, the real system (20) can be reformulated as

$$\begin{array}{ccc}\hfill -x_1^2+x_2^2+x_3^2-b_1{x}_1+b_2{x}_2+b_3{x}_3+x_0^2+c_0& =& 0,\hfill \end{array}$$

(42)

$$\begin{array}{ccc}\hfill 2x_0{x}_1+b_3{x}_2-b_2{x}_3& =& -b_1{x}_0-c_1,\hfill \end{array}$$

(43)

$$\begin{array}{ccc}\hfill b_3{x}_1+2x_0{x}_2-b_1{x}_3& =& -b_2{x}_0-c_2,\hfill \end{array}$$

(44)

$$\begin{array}{ccc}\hfill -b_2{x}_1+b_1{x}_2+2x_0{x}_3& =& -b_3{x}_0-c_3.\hfill \end{array}$$

(45)

Let $y={(x_1,x_2,x_3)}^T$. Equations (43)–(45) can be expressed as

$$Ay=u,$$

(46)

where

$$A=\left(\begin{array}{ccc}2x_0& b_3& -b_2\\ b_3& 2x_0& -b_1\\ -b_2& b_1& 2x_0\end{array}\right),u=\left(\begin{array}{c}-b_1{x}_0-c_1\\ -b_2{x}_0-c_2\\ -b_3{x}_0-c_3\end{array}\right).$$

(47)

Note that

$$det\left(A\right)=8x_0^3+2x_0(b_1^2-b_2^2-b_3^2)=2x_0(4x_0^2-K_b)=0.$$

Let

$$M=\left(\begin{array}{cc}2x_0& -b_1\\ b_1& 2x_0\end{array}\right).$$

Since $b=b_1\mathbf{i}+b_2\mathbf{j}+b_3\mathbf{k}\ne 0$ and $K_b=-b_1^2+b_2^2+b_3^2\ge 0$, the subdeterminant

$$det\left(M\right)=4x_0^2+b_1^2=b_2^2+b_3^2>0.$$

This means that $rank\left(A\right)=2$. We reformulate () and () as

$$\left\{\begin{array}{ccc}\hfill 2x_0{x}_2-b_1{x}_3& =\hfill & \hfill -b_3{x}_1-b_2{x}_0-c_2,\\ \hfill b_1{x}_2+2x_0{x}_3& =\hfill & \hfill b_2{x}_1-b_3{x}_0-c_3.\end{array}\right.$$

(48)

Since

$$M^{-1}=\frac{1}{b_2^2+b_3^2}\left(\begin{array}{cc}2x_0& b_1\\ -b_1& 2x_0\end{array}\right),$$

by Equation (48), we have

$$x_2=a_{21}+a_{22}{x}_1,x_3=a_{31}+a_{32}{x}_1,$$

(49)

where

$$a_{21}=\frac{-2x_0^2{b}_2-(b_1{b}_3+2c_2)x_0-b_1{c}_3}{b_2^2+b_3^2},a_{22}=\frac{b_1{b}_2-2b_3{x}_0}{b_2^2+b_3^2},$$

(50)

$$a_{31}=\frac{-2x_0^2{b}_3+(b_1{b}_2-2c_3)x_0+b_1{c}_2}{b_2^2+b_3^2},a_{32}=\frac{b_1{b}_3+2b_2{x}_0}{b_2^2+b_3^2}.$$

(51)

Let

$$F_1=\frac{(b_2{c}_3-b_3{c}_2)x_0-b_1(b_2{c}_2+b_3{c}_3)+c_1(b_2^2+b_3^2)}{b_2^2+b_3^2}.$$

(52)

Substituting $x_2,x_3$ of Equation (49) in Equation (43), we must have

$$F_1=0.$$

(53)

In fact, the condition $F_1=0$ is just a restatement of the condition $rank\left(A\right)=rank(A,u)=2$.

Let

$$F_2=c_0(b_2^2+b_3^2)+b_1(b_3{c}_2-b_2{c}_3)+c_2^2+c_3^2.$$

(54)

Substituting $x_2,x_3$ of Equation (49) in Equation (42), we have

$$2(b_3{c}_2-b_2{c}_3)x_1+F_2=0.$$

(55)

If $b_3{c}_2-b_2{c}_3=0$, we should have $F_2=0$ and, in this case, $x_1$ is arbitrary. If $b_3{c}_2-b_2{c}_3\ne 0$, then

$$x_1=-\frac{F_2}{2(b_3{c}_2-b_2{c}_3)}.$$

Summarizing our reasoning process, we figure out the following conditions.

Definition 2.

For the coefficients $b,c$ in Equation II with $K_b,K_c\ge 0$, letting $r\in \mathbb{R}$ such that

$$r^2=\frac{K_b}{4},$$

(56)

we say that $(b,c)$ satisfiesCondition Aif the following two conditions hold:

(1) 

There exists an r of (56) satisfying

$$(b_2{c}_3-b_3{c}_2)r-b_1(b_2{c}_2+b_3{c}_3)+c_1(b_2^2+b_3^2)=0;$$

(2) 

If $b_3{c}_2=b_2{c}_3$, then $c_0(b_2^2+b_3^2)+c_2^2+c_3^2=0$.

Note that, if $b_3{c}_2-b_2{c}_3\ne 0$ and the coefficients $b,c$ in Equation II satisfy Condition A, then we have

$$r=\frac{b_1(b_2{c}_2+b_3{c}_3)-c_1(b_2^2+b_3^2)}{b_2{c}_3-b_3{c}_2}.$$

Summarizing the previous results, we obtain the following theorem.

Theorem 3.

Equation II has a solution $x\in \mathrm{SZ}$ if and only if Condition A holds. If Condition A is held by r, then we have the following cases:

(1) 

If $b_3{c}_2-b_2{c}_3\ne 0$, then Equation II has solutions

$$x=r+x_1\mathbf{i}+x_2\mathbf{j}+x_3\mathbf{k},$$

where

$$r=\frac{b_1(b_2{c}_2+b_3{c}_3)-c_1(b_2^2+b_3^2)}{b_2{c}_3-b_3{c}_2},$$

$$x_1=\frac{c_0(b_2^2+b_3^2)+b_1(b_3{c}_2-b_2{c}_3)+c_2^2+c_3^2}{2(b_2{c}_3-b_3{c}_2)}$$

and

$$x_2=a_{21}+a_{22}{x}_1,x_3=a_{31}+a_{32}{x}_1,$$

where

$$a_{21}=\frac{-K_b{b}_2-(b_1{b}_3+2c_2)r-b_1{c}_3}{b_2^2+b_3^2},a_{22}=\frac{b_1{b}_2-2b_{3}r}{b_2^2+b_3^2};$$

(57)

$$a_{31}=\frac{-K_b{b}_3+(b_1{b}_2-2c_3)r+b_1{c}_2}{b_2^2+b_3^2},a_{32}=\frac{b_1{b}_3+2b_{2}r}{b_2^2+b_3^2}.$$

(58)

(2) 

If $b_3{c}_2-b_2{c}_3=0$, then Equation II has solutions

$$x=r+x_1\mathbf{i}+(a_{21}+a_{22}{x}_1)\mathbf{j}+(a_{31}+a_{32}{x}_1)\mathbf{k},\forall x_1\in \mathbb{R},$$

where $a_{21},a_{22},a_{31},a_{32}$ are given by (57) and (58) with $r=\frac{\sqrt{K_b}}{2}$ or $r=-\frac{\sqrt{K_b}}{2}$.

Some examples of Theorem 3 are given in Table 4.

Table 4. Some examples in Theorem 3.

	$(\mathit{b},\mathit{c})$	r	The Solution(s) of ${\mathit{x}}^2+\mathit{bx}+\mathit{c}=0$
(1)	$(\mathbf{i}+\mathbf{j},2+\mathbf{k})$	0	$x=\mathbf{i}$
(2)I	$(\mathbf{i}+\mathbf{j},-1+\mathbf{i}+\mathbf{j})$	0	$x=x_1\mathbf{i}+x_1\mathbf{j}+\mathbf{k},\forall x_1\in \mathbb{R}$
(2)II	$(2\mathbf{i}+2\mathbf{j}+4\mathbf{k},-4+4\mathbf{i}+4\mathbf{j}+8\mathbf{k})$	−2	$x=-2+x_1\mathbf{i}+x_1\mathbf{j},\forall x_1\in \mathbb{R}$
		2	$x=2+x_1\mathbf{i}-(\frac{16}{5}+\frac{3x_1}{5})\mathbf{j}+(\frac{-12}{5}+\frac{4x_1}{5})\mathbf{k},\forall x_1\in \mathbb{R}$