On the Generalized Bilal Distribution: Some Properties and Estimation under Ranked Set Sampling
Abstract
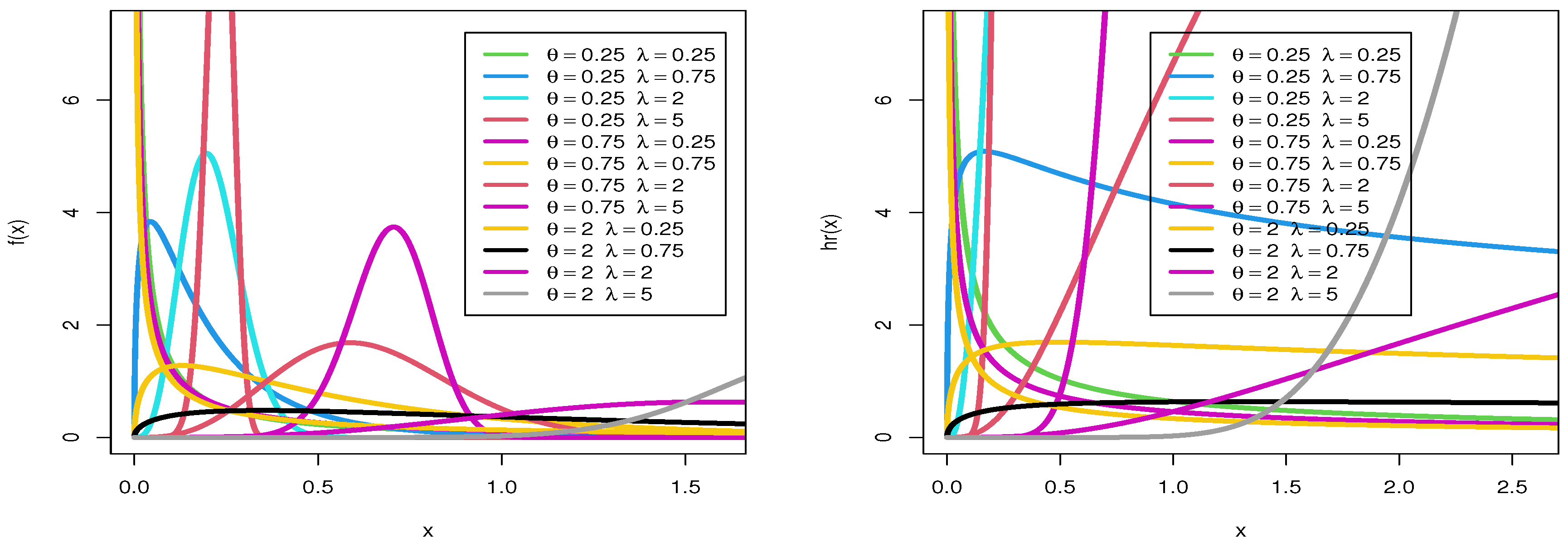
1. Introduction
2. Moments of Order Statistics
2.1. Preliminaries on Order Statistics
2.2. Single Moments
2.3. Product Moments
2.4. L-Moments
3. Estimation of the Parameters
3.1. Estimation of Parameters under the SRS Scheme
3.2. Estimation of Parameters under the RSS Scheme
- Randomly select units from the population and allocate these units randomly into r sets of size r.
- Assign ranks to the units in each set based on some accessible and non-expensive ordering criterion.
- To obtain a sample based on the RSS scheme, select the unit ranked at ith position from the ith set, .
- To obtain a final sample of size , repeat steps 1 to 3 c times.
3.3. Asymptotic Confidence Interval
3.4. Simulation Study
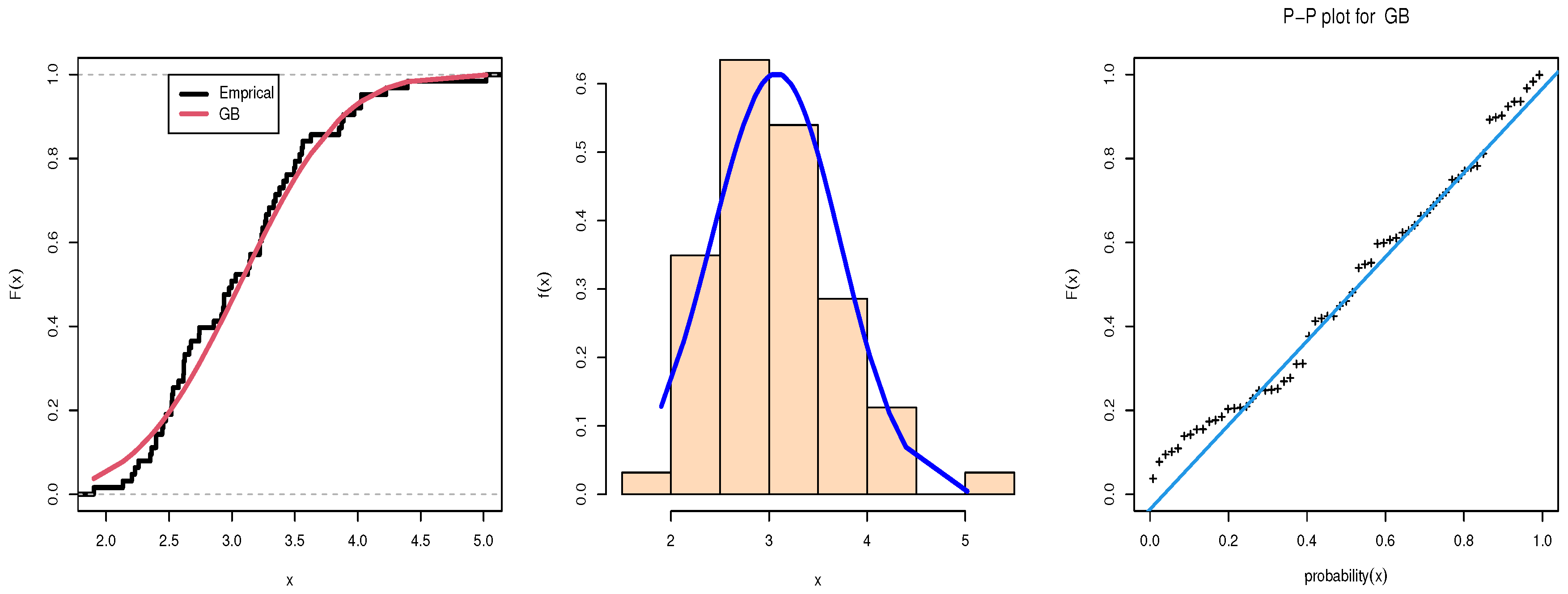
4. Application to Real Data
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abd-Elrahman, A.M. Utilizing ordered statistics in lifetime distributions production: A new lifetime distribution and applications. J. Probab. Stat. Sci. 2013, 11, 153–164. [Google Scholar]
- Abd-Elrahman, A.M. A new two-parameter lifetime distribution with decreasing, increasing or upside-down bathtub-shaped failure rate. Comm. Statist. Theory Methods 2017, 46, 8865–8880. [Google Scholar] [CrossRef]
- Abd-Elrahman, A.M. Reliability estimation under type-II censored data from the generalized Bilal distribution. J. Egypt. Math. Soc. 2019, 27, 1. [Google Scholar] [CrossRef]
- Chaturvedi, A.; Kumari, T.; Pandey, V.K. On the estimation of parameters and reliability functions of a new-parameter lifetime distribution based on type ii censoring. Statistica 2020, 80, 201–232. [Google Scholar]
- Shi, X.; Shi, Y.; Zhou, K. Estimation for entropy and parameters of generalized Bilal distribution under adaptive type ii progressive hybrid censoring scheme. Entropy 2021, 23, 206. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Cohen, A.C. Order Statistics and Inference: Estimation Methods; Academic Press: San Diego, CA, USA, 1991. [Google Scholar]
- McIntyre, G.A. A method for unbiased selective sampling using ranked sets. Aust. J. Agric. Res. 1952, 3, 385–390. [Google Scholar] [CrossRef]
- Dell, T.R.; Clutter, J.L. Ranked set sampling theory with order statistics background. Biometrics 1972, 28, 545–555. [Google Scholar] [CrossRef]
- Takahasi, K.; Wakimoto, K. On unbiased estimates of the population mean based on the sample stratified by means of ordering. Ann. Inst. Statist. Math. 1968, 20, 1–31. [Google Scholar] [CrossRef]
- Chen, Z.; Bai, Z.; Sinha, B.K. Ranked Set Sampling, Theory and Applications: Lecture Notes in Statistics; Springer: New York, NY, USA, 2004. [Google Scholar]
- Abu-Dayyeh, W.; Assrhani, A.; Ibrahim, K. Estimation of the shape and scale parameters of pareto distribution using ranked set sampling. Statist. Pap. 2013, 54, 207–225. [Google Scholar] [CrossRef]
- Aljohani, H.M.; Almetwally, E.M.; Alghamdi, A.S.; Hafez, E.H. Ranked set sampling with application of modified Kies exponential distribution. Alex. Eng. J. 2021, 60, 4041–4046. [Google Scholar] [CrossRef]
- Bantan, R.; Elsehetry, M.; Hassan, A.S.; Elgarhy, M.; Sharma, D.; Chesneau, C.; Jamal, F. A Two-Parameter Model: Properties and Estimation under Ranked Sampling. Mathematics 2021, 9, 1214. [Google Scholar] [CrossRef]
- Chen, W.; Yang, R.; Yao, D.; Long, C. Pareto parameters estimation using moving extremes ranked set sampling. Statist. Pap. 2021, 6, 1195–1211. [Google Scholar] [CrossRef]
- Esemen, M.; Selma, G. Parameter estimation of generalized Rayleigh distribution based on ranked set sample. J. Stat. Comput. Simul. 2017, 88, 615–628. [Google Scholar] [CrossRef]
- He, X.; Chen, W.; Qian, W. Maximum likelihood estimators of the parameters of the log-logistic distribution. Statist. Pap. 2020, 61, 1875–1892. [Google Scholar] [CrossRef]
- Sabry, M.H.; Almetwally, E.M. Estimation of the exponential Pareto distribution’s Parameters under ranked and double ranked set sampling designs. Pak. J. Stat. Oper. Res. 2021, 17, 169–184. [Google Scholar] [CrossRef]
- Sabry, M.A.; Almetwally, E.M.; Almongy, H.M.; Ibrahim, G.M. Assessing the Performance of Some Ranked Set Sampling Designs Using Hybrid Approach. Cmc-Comput. Mater. Contin. 2021, 68, 3737–3753. [Google Scholar] [CrossRef]
- Singh, H.P.; Mehta, V. Improved estimation of the scale parameter for log-logistic distribution using balanced ranked set sampling. Stat. Transit. New Ser. Pol. Stat. Assoc. 2017, 18, 53–74. [Google Scholar] [CrossRef][Green Version]
- Taconeli, C.A.; Giolo, S.R. Maximum likelihood estimation based on ranked set sampling designs for two extensions of the Lindley distribution with uncensored and right-censored data. Comput. Statist. 2020, 35, 1827–1851. [Google Scholar] [CrossRef]
- Pedroso, V.C.; Taconeli, C.A.; Giolo, S.R. Estimation based on ranked set sampling for the two-parameter Birnbaum Saunders distribution. J. Stat. Comput. Simul. 2021, 91, 316–333. [Google Scholar] [CrossRef]
- Taconeli, C.A.; Bonat, W.H. On the performance of estimation methods under ranked set sampling. Comput. Statist. 2020, 35, 1805–1826. [Google Scholar] [CrossRef]
- Zamanzade, E.; Parvardeh, A.; Asadi, M. Estimation of mean residual life based on ranked set sampling. Comput. Stat. Data Anal. 2019, 135, 35–55. [Google Scholar] [CrossRef]
- Zamanzade, E.; Mahdizadeh, M. Using ranked set sampling with extreme ranks in estimating the population proportion. Stat. Methods Med. Res. 2020, 29, 165–177. [Google Scholar] [CrossRef] [PubMed]
- Al-Omari, A.I.; Bouza, C.N. Review of ranked set sampling: Modifications and applications. Rev. Investig. Oper. 2014, 35, 215–235. [Google Scholar]
- Bouza-Herrera, C.N.; Al-Omari, A.I.F. Ranked Set Sampling: 65 Years Improving the Accuracy in Data Gathering; Academic Press: San Diego, CA, USA, 2018. [Google Scholar]
- Arnold, B.C.; Balakrishnan, N.; Nagaraja, H.N. A First Course in Order Statistics; SIAM Publishers: Philadelphia, PA, USA, 2008. [Google Scholar]
- David, H.A.; Nagaraja, H.N. Order Statistics, 3rd ed.; John Wiley: New York, NY, USA, 2003. [Google Scholar]
- Gradshteyn, I.S.L.; Ryzhik, I.M. Tables of Integrals, Series and Products, 7th ed.; Jeffrey, A., Zwillinger, D., Eds.; Academic Press: San Diego, CA, USA, 2007. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020; Available online: https://www.R-project.org/ (accessed on 14 March 2021).
- Hosking, J. L-Moments: Analysis and Estimation of Distributions Using Linear Combinations of Order Statistics. J. R. Stat. Soc. Ser. B Stat. Methodol. 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Casella, G.; Berger, R.L. Statistical Inference; Brooks/Cole Publishing Company: Bel Air, CA, USA, 1990. [Google Scholar]
- Bolker, B.; R Development Core Team. 2021 Bbmle: Tools for General Maximum Likelihood Estimation [Computer Software Manual]. (R Package Version 1.0.24). Available online: https://CRAN.R-project.org/package=bbmle (accessed on 11 April 2021).
- Badar, M.G.; Priest, A.M. Statistical aspects of fiber and bundle strength in hybrid composites. In Progress in Science and Engineering of Composites; Hayashi, T., Kawata, K., Umekawa, S., Eds.; ICCM-IV: Tokyo, Japan, 1982; pp. 1129–1136. [Google Scholar]
- Kaur, A.; Patil, G.P.; Taillie, C. Unequal allocation models for ranked set sampling with skew distributions. Biometrics 1997, 53, 123–130. [Google Scholar] [CrossRef]
- Latpate, R.; Kshirsagar, J.; Gupta, V.K.; Chandra, G. Balanced and Unbalanced Ranked Set Sampling. In Advanced Sampling Methods; Springer: Singapore, 2021; pp. 257–274. [Google Scholar]
- Bhoj, D.; Chandra, G. Simple unequal allocation procedure for ranked set sampling with skew distributions. J. Mod. Appl. Stat. Methods 2020, 18, 22. [Google Scholar] [CrossRef]
- Ahsanullah, M.; Alzaatreh, A. Parameter estimation for the Log-logistic distribution based on order statistics. REVSTAT Stat. J. 2018, 16, 429–443. [Google Scholar]
- Akhter, Z.; Saran, J.; Verma, K.; Pushkarna, N. Moments of order statistics from length-biased exponential distribution and associated inference. Ann. Data. Sci. 2020. [Google Scholar] [CrossRef]
- Akhter, Z.; MirMostafaee, S.M.T.K.; Ormoz, E. On the order statistics of exponentiated moment exponential distribution and associated inference. J. Stat. Comput. Simul. 2022, 92, 1322–1346. [Google Scholar] [CrossRef]
| n | r | ||||
|---|---|---|---|---|---|
| 1 | 1 | ||||
| 2 | 1 | ||||
| 2 | |||||
| 3 | 1 | ||||
| 2 | |||||
| 3 | |||||
| 4 | 1 | ||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | 1 | ||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 |
| n | s | r | ||||
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | ||||
| 2 | 1 | 1 | ||||
| 2 | 1 | |||||
| 2 | ||||||
| 3 | 1 | 1 | ||||
| 2 | 1 | |||||
| 2 | ||||||
| 3 | 1 | |||||
| 2 | ||||||
| 3 | ||||||
| 4 | 1 | 1 | ||||
| 2 | 1 | |||||
| 2 | ||||||
| 3 | 1 | |||||
| 2 | ||||||
| 3 | ||||||
| 4 | 1 | |||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 | 1 | 1 | ||||
| 2 | 1 | |||||
| 2 | ||||||
| 3 | 1 | |||||
| 2 | ||||||
| 3 | ||||||
| 4 | 1 | |||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 | 1 | |||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 |
| SRS | RSS | RSS 2 | RE | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bias | MSE | Bias | MSE | Bias | MSE | RE1 | RE2 | |||
| 0.25 | 4 | 0.10056 | 0.19554 | 0.04653 | 0.09963 | 0.05762 | 0.10295 | 1.96256 | 1.89933 | |
| 0.03811 | 0.01460 | 0.03585 | 0.01342 | 0.03046 | 0.01260 | 1.08814 | 1.15898 | |||
| 7 | 0.04526 | 0.06025 | 0.04343 | 0.04234 | 0.03655 | 0.02608 | 1.42310 | 2.31015 | ||
| 0.00617 | 0.00628 | 0.00537 | 0.00586 | 0.00429 | 0.00404 | 1.07321 | 1.55582 | |||
| 10 | 0.03514 | 0.04235 | 0.03019 | 0.01631 | 0.02174 | 0.01193 | 2.59593 | 3.54922 | ||
| −0.00135 | 0.00470 | −0.00115 | 0.00329 | −0.00229 | 0.00202 | 1.42844 | 2.32197 | |||
| 15 | 0.03794 | 0.02684 | 0.01839 | 0.00747 | 0.01457 | 0.00466 | 3.59388 | 5.76114 | ||
| −0.01308 | 0.00312 | −0.00693 | 0.00165 | −0.00683 | 0.00082 | 1.89221 | 3.82938 | |||
| 20 | 0.00602 | 0.01483 | 0.00839 | 0.00388 | 0.00975 | 0.00278 | 3.81807 | 5.33176 | ||
| −0.01749 | 0.00238 | −0.00571 | 0.00091 | −0.00662 | 0.00056 | 2.62979 | 4.25989 | |||
| 0.75 | 4 | −0.00148 | 0.00797 | −0.00902 | 0.00602 | −0.00505 | 0.00490 | 1.32291 | 1.62674 | |
| 0.16129 | 0.11055 | 0.15845 | 0.10940 | 0.14741 | 0.10162 | 1.01053 | 1.08788 | |||
| 7 | 0.00018 | 0.00362 | −0.00291 | 0.00261 | −0.00024 | 0.00187 | 1.38868 | 1.93722 | ||
| 0.07838 | 0.03593 | 0.07204 | 0.03047 | 0.06240 | 0.02506 | 1.17942 | 1.43385 | |||
| 10 | 0.00004 | 0.00283 | −0.00037 | 0.00121 | −0.00156 | 0.00096 | 2.34942 | 2.94128 | ||
| 0.06572 | 0.02829 | 0.03900 | 0.01787 | 0.03878 | 0.01176 | 1.58334 | 2.40503 | |||
| 15 | 0.00481 | 0.00198 | −0.00057 | 0.00058 | 0.00003 | 0.00042 | 3.41952 | 4.76559 | ||
| 0.03679 | 0.01388 | 0.01443 | 0.00835 | 0.01137 | 0.00461 | 1.66195 | 3.01034 | |||
| 20 | −0.00319 | 0.00142 | −0.00187 | 0.00036 | −0.00054 | 0.00026 | 3.99485 | 5.51584 | ||
| 0.02324 | 0.00967 | 0.01398 | 0.00453 | 0.00824 | 0.00278 | 2.13618 | 3.47364 | |||
| 2 | 4 | −0.00413 | 0.00108 | −0.00633 | 0.00090 | −0.00417 | 0.00069 | 1.19711 | 1.55925 | |
| 0.43000 | 0.78595 | 0.42519 | 0.70556 | 0.40729 | 0.68976 | 1.11394 | 1.13945 | |||
| 7 | −0.00159 | 0.00050 | −0.00232 | 0.00037 | −0.00095 | 0.00026 | 1.33903 | 1.92014 | ||
| 0.20894 | 0.25550 | 0.20453 | 0.23090 | 0.16635 | 0.17815 | 1.10651 | 1.43412 | |||
| 10 | −0.00129 | 0.00039 | −0.00070 | 0.00017 | −0.00104 | 0.00014 | 2.28691 | 2.82881 | ||
| 0.17525 | 0.20105 | 0.10394 | 0.12702 | 0.10336 | 0.08357 | 1.58286 | 2.40573 | |||
| 15 | 0.00091 | 0.00027 | −0.00048 | 0.00008 | −0.00018 | 0.00006 | 3.27836 | 4.60162 | ||
| 0.09805 | 0.09871 | 0.03842 | 0.05939 | 0.03026 | 0.03278 | 1.66195 | 3.01088 | |||
| 20 | −0.00187 | 0.00020 | −0.00087 | 0.00005 | −0.00033 | 0.00004 | 4.07494 | 5.68931 | ||
| 0.06191 | 0.06878 | 0.03722 | 0.03219 | 0.02233 | 0.01962 | 2.13688 | 3.50477 | |||
| 5 | 4 | −0.00218 | 0.00018 | −0.00299 | 0.00015 | −0.00201 | 0.00011 | 1.16128 | 1.55214 | |
| 1.07516 | 4.91362 | 0.98564 | 3.97810 | 0.91822 | 3.60870 | 1.23517 | 1.36160 | |||
| 7 | −0.00088 | 0.00008 | −0.00111 | 0.00006 | −0.00051 | 0.00004 | 1.33101 | 1.93414 | ||
| 0.52233 | 1.59683 | 0.46129 | 1.29293 | 0.41596 | 1.11371 | 1.23505 | 1.43380 | |||
| 10 | −0.00070 | 0.00006 | −0.00037 | 0.00003 | −0.00049 | 0.00002 | 2.29067 | 2.82201 | ||
| 0.43809 | 1.25650 | 0.25983 | 0.79392 | 0.25845 | 0.52244 | 1.58265 | 2.40508 | |||
| 15 | 0.00024 | 0.00004 | −0.00023 | 0.00001 | −0.00010 | 0.00001 | 3.25695 | 4.58442 | ||
| 0.24511 | 0.61696 | 0.09605 | 0.37123 | 0.07566 | 0.20492 | 1.66193 | 3.01072 | |||
| 20 | −0.00085 | 0.00003 | −0.00037 | 0.00001 | −0.00015 | 0.00001 | 4.13097 | 5.79048 | ||
| 0.15479 | 0.42981 | 0.09311 | 0.20117 | 0.05585 | 0.12269 | 2.13652 | 3.50330 | |||
| SRS | RSS | RSS 2 | RE | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bias | MSE | Bias | MSE | Bias | MSE | RE1 | RE2 | |||
| 0.25 | 4 | 0.30376 | 1.75665 | 0.14183 | 0.89516 | 0.16588 | 0.91976 | 1.96239 | 1.90991 | |
| 0.04386 | 0.01386 | 0.04187 | 0.01241 | 0.03951 | 0.01154 | 1.11652 | 1.20094 | |||
| 7 | 0.13942 | 0.54164 | 0.10677 | 0.34636 | 0.09188 | 0.21885 | 1.56380 | 2.47498 | ||
| 0.01350 | 0.00537 | 0.01220 | 0.00516 | 0.01101 | 0.00353 | 1.04165 | 1.52141 | |||
| 10 | 0.10729 | 0.38085 | 0.07435 | 0.13360 | 0.04799 | 0.09963 | 2.85074 | 3.82246 | ||
| 0.00867 | 0.00418 | 0.00348 | 0.00287 | 0.00337 | 0.00172 | 1.45452 | 2.43040 | |||
| 15 | 0.11653 | 0.24241 | 0.03638 | 0.05589 | 0.03276 | 0.04017 | 4.33748 | 6.03468 | ||
| −0.00320 | 0.00255 | −0.00190 | 0.00128 | −0.00273 | 0.00068 | 1.98744 | 3.73125 | |||
| 20 | 0.01993 | 0.13383 | 0.01430 | 0.03291 | 0.01834 | 0.02333 | 4.06679 | 5.73621 | ||
| −0.00930 | 0.00189 | −0.00197 | 0.00075 | −0.00271 | 0.00041 | 2.52980 | 4.57054 | |||
| 0.75 | 4 | −0.00445 | 0.07169 | −0.02706 | 0.05419 | −0.01508 | 0.04417 | 1.32302 | 1.62323 | |
| 0.16127 | 0.11055 | 0.15785 | 0.10593 | 0.14774 | 0.10263 | 1.04356 | 1.07720 | |||
| 7 | 0.00055 | 0.03258 | −0.00874 | 0.02346 | −0.00072 | 0.01682 | 1.38868 | 1.93727 | ||
| 0.07837 | 0.03593 | 0.06920 | 0.03435 | 0.06240 | 0.02506 | 1.04619 | 1.43400 | |||
| 10 | 0.00011 | 0.02549 | −0.00111 | 0.01085 | −0.00469 | 0.00867 | 2.34942 | 2.94100 | ||
| 0.06574 | 0.02828 | 0.03900 | 0.01787 | 0.03879 | 0.01176 | 1.58315 | 2.40603 | |||
| 15 | 0.01444 | 0.01784 | −0.00170 | 0.00522 | 0.00009 | 0.00374 | 3.41971 | 4.76631 | ||
| 0.03679 | 0.01388 | 0.01443 | 0.00835 | 0.01137 | 0.00461 | 1.66210 | 3.01049 | |||
| 20 | −0.00957 | 0.01277 | −0.00562 | 0.00320 | −0.00168 | 0.00231 | 3.99416 | 5.52372 | ||
| 0.02324 | 0.00967 | 0.01398 | 0.00453 | 0.00840 | 0.00276 | 2.13670 | 3.50372 | |||
| 2 | 4 | −0.01240 | 0.00968 | −0.01900 | 0.00808 | −0.01252 | 0.00621 | 1.19715 | 1.55920 | |
| 0.43006 | 0.78611 | 0.42497 | 0.75545 | 0.40730 | 0.69773 | 1.04058 | 1.12666 | |||
| 7 | −0.00477 | 0.00448 | −0.00698 | 0.00335 | −0.00286 | 0.00233 | 1.33894 | 1.92012 | ||
| 0.20896 | 0.25551 | 0.20454 | 0.23091 | 0.16639 | 0.17817 | 1.10656 | 1.43408 | |||
| 10 | −0.00386 | 0.00352 | −0.00212 | 0.00154 | −0.00314 | 0.00125 | 2.28712 | 2.82879 | ||
| 0.17530 | 0.20112 | 0.10398 | 0.12704 | 0.10340 | 0.08359 | 1.58314 | 2.40600 | |||
| 15 | 0.00273 | 0.00241 | −0.00145 | 0.00073 | −0.00055 | 0.00052 | 3.27776 | 4.60100 | ||
| 0.09808 | 0.09873 | 0.03846 | 0.05940 | 0.03030 | 0.03279 | 1.66208 | 3.01051 | |||
| 20 | −0.00562 | 0.00184 | −0.00261 | 0.00045 | −0.00099 | 0.00032 | 4.07439 | 5.68943 | ||
| 0.06194 | 0.06879 | 0.03727 | 0.03219 | 0.02238 | 0.01963 | 2.13683 | 3.50405 | |||
| 5 | 4 | −0.00654 | 0.00158 | −0.00896 | 0.00136 | −0.00602 | 0.00102 | 1.16131 | 1.55209 | |
| 1.07517 | 4.91318 | 0.98564 | 3.97022 | 0.95824 | 3.61076 | 1.23751 | 1.36071 | |||
| 7 | −0.00263 | 0.00073 | −0.00334 | 0.00055 | −0.00152 | 0.00038 | 1.33073 | 1.93409 | ||
| 0.52247 | 1.59708 | 0.50614 | 1.29317 | 0.41603 | 1.11366 | 1.23502 | 1.43409 | |||
| 10 | −0.00212 | 0.00057 | −0.00110 | 0.00025 | −0.00146 | 0.00020 | 2.29033 | 2.82176 | ||
| 0.43832 | 1.25708 | 0.25998 | 0.79417 | 0.25853 | 0.52250 | 1.58288 | 2.40587 | |||
| 15 | 0.00071 | 0.00038 | −0.00070 | 0.00012 | −0.00030 | 0.00008 | 3.25697 | 4.58461 | ||
| 0.24522 | 0.61708 | 0.09621 | 0.37126 | 0.07578 | 0.20499 | 1.66212 | 3.01034 | |||
| 20 | −0.00255 | 0.00030 | −0.00112 | 0.00007 | −0.00045 | 0.00005 | 4.13039 | 5.79047 | ||
| 0.15488 | 0.42991 | 0.09320 | 0.20122 | 0.05598 | 0.12269 | 2.13655 | 3.50408 | |||
| SRS | RSS | RSS 2 | RE | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Bias | MSE | Bias | MSE | Bias | MSE | RE1 | RE2 | |||
| 0.25 | 4 | 0.8079 | 12.4217 | 0.3810 | 6.3619 | 0.4305 | 6.5093 | 1.95251 | 1.90830 | |
| 0.0484 | 0.0133 | 0.0469 | 0.0124 | 0.0452 | 0.0121 | 1.07373 | 1.10571 | |||
| 7 | 0.3730 | 3.8194 | 0.2483 | 2.3011 | 0.2187 | 1.5370 | 1.65980 | 2.48498 | ||
| 0.0180 | 0.0049 | 0.0153 | 0.0046 | 0.0147 | 0.0032 | 1.08368 | 1.55359 | |||
| 10 | 0.2857 | 2.7101 | 0.1711 | 0.9086 | 0.1042 | 0.6708 | 2.98255 | 4.04022 | ||
| 0.0127 | 0.0040 | 0.0064 | 0.0026 | 0.0063 | 0.0016 | 1.51814 | 2.53252 | |||
| 15 | 0.3138 | 1.7279 | 0.0798 | 0.3914 | 0.0723 | 0.2732 | 4.41495 | 6.32470 | ||
| 0.0020 | 0.0022 | 0.0003 | 0.0012 | −0.0007 | 0.0006 | 1.88979 | 3.48829 | |||
| 20 | 0.0573 | 0.9540 | 0.0187 | 0.2261 | 0.0350 | 0.1620 | 4.22029 | 5.88760 | ||
| −0.0038 | 0.0016 | 0.0007 | 0.0006 | −0.0007 | 0.0004 | 2.42153 | 4.27447 | |||
| 0.75 | 4 | −0.0119 | 0.5098 | −0.0722 | 0.3853 | −0.0403 | 0.3139 | 1.32291 | 1.62396 | |
| 0.1613 | 0.1105 | 0.1528 | 0.1036 | 0.1577 | 0.1013 | 1.06711 | 1.09168 | |||
| 7 | 0.0015 | 0.2317 | −0.0233 | 0.1668 | −0.0019 | 0.1196 | 1.38867 | 1.93715 | ||
| 0.0784 | 0.0359 | 0.0692 | 0.0324 | 0.0624 | 0.0251 | 1.10792 | 1.43413 | |||
| 10 | 0.0003 | 0.1813 | −0.0030 | 0.0772 | −0.0125 | 0.0616 | 2.34955 | 2.94090 | ||
| 0.0657 | 0.0283 | 0.0390 | 0.0179 | 0.0388 | 0.0118 | 1.58301 | 2.40576 | |||
| 15 | 0.0385 | 0.1269 | −0.0045 | 0.0371 | 0.0002 | 0.0266 | 3.41983 | 4.76643 | ||
| 0.0368 | 0.0139 | 0.0144 | 0.0084 | 0.0114 | 0.0046 | 1.66198 | 3.01044 | |||
| 20 | −0.0255 | 0.0908 | −0.0150 | 0.0227 | −0.0045 | 0.0164 | 3.99464 | 5.52447 | ||
| 0.0232 | 0.0097 | 0.0140 | 0.0045 | 0.0084 | 0.0028 | 2.13696 | 3.50413 | |||
| 2 | 4 | −0.0331 | 0.0688 | −0.0507 | 0.0575 | −0.0334 | 0.0441 | 1.19713 | 1.55923 | |
| 0.4301 | 0.7861 | 0.7404 | 0.7056 | 0.4730 | 0.8978 | 1.11418 | 0.87563 | |||
| 7 | −0.0127 | 0.0319 | −0.0186 | 0.0238 | −0.0076 | 0.0166 | 1.33895 | 1.92011 | ||
| 0.2090 | 0.2555 | 0.2015 | 0.2309 | 0.1664 | 0.1782 | 1.10659 | 1.43404 | |||
| 10 | −0.0103 | 0.0250 | −0.0057 | 0.0110 | −0.0084 | 0.0089 | 2.28706 | 2.82882 | ||
| 0.1753 | 0.2011 | 0.1040 | 0.1270 | 0.1034 | 0.0836 | 1.58315 | 2.40591 | |||
| 15 | 0.0073 | 0.0171 | −0.0039 | 0.0052 | −0.0015 | 0.0037 | 3.27793 | 4.60098 | ||
| 0.0981 | 0.0987 | 0.0385 | 0.0594 | 0.0303 | 0.0328 | 1.66209 | 3.01057 | |||
| 20 | −0.0150 | 0.0131 | −0.0070 | 0.0032 | −0.0026 | 0.0023 | 4.07422 | 5.68928 | ||
| 0.0619 | 0.0688 | 0.0373 | 0.0322 | 0.0224 | 0.0196 | 2.13657 | 3.50378 | |||
| 5 | 4 | −0.0174 | 0.0113 | −0.0239 | 0.0097 | −0.0161 | 0.0073 | 1.16128 | 1.55213 | |
| 1.0752 | 4.9135 | 0.9856 | 1.9712 | 0.7824 | 1.2961 | 2.49261 | 3.79094 | |||
| 7 | −0.0070 | 0.0052 | −0.0089 | 0.0039 | −0.0041 | 0.0027 | 1.33069 | 1.93407 | ||
| 0.5224 | 1.5970 | 0.4614 | 1.2932 | 0.4160 | 1.1136 | 1.23495 | 1.43408 | |||
| 10 | −0.0056 | 0.0040 | −0.0029 | 0.0018 | −0.0039 | 0.0014 | 2.29036 | 2.82161 | ||
| 0.4383 | 1.2571 | 0.2600 | 0.7940 | 0.2585 | 0.5225 | 1.58319 | 2.40588 | |||
| 15 | 0.0019 | 0.0027 | −0.0019 | 0.0008 | −0.0008 | 0.0006 | 3.25638 | 4.58419 | ||
| 0.2452 | 0.6171 | 0.0962 | 0.3713 | 0.0758 | 0.2050 | 1.66202 | 3.01055 | |||
| 20 | −0.0068 | 0.0021 | −0.0030 | 0.0005 | −0.0012 | 0.0004 | 4.13039 | 5.79057 | ||
| 0.1549 | 0.4299 | 0.0932 | 0.2012 | 0.0560 | 0.1227 | 2.13672 | 3.50395 | |||
| SRS | RSS | RSS | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Lower | Upper | CP | Lower | Upper | CP | Lower | Upper | CP | |||
| 0.25 | 4 | 0.4934 | 1.1946 | 27.178% | 0.3154 | 0.9084 | 39.959% | 0.3110 | 0.9263 | 40.726% | |
| 0.0633 | 0.5129 | 93.726% | 0.0699 | 0.5018 | 93.779% | 0.0687 | 0.4922 | 94.085% | |||
| 7 | 0.1776 | 0.7681 | 60.209% | 0.1008 | 0.6876 | 75.615% | 0.0218 | 0.5949 | 91.241% | ||
| 0.1013 | 0.4111 | 94.931% | 0.1057 | 0.4050 | 94.944% | 0.1300 | 0.3786 | 94.948% | |||
| 10 | 0.1123 | 0.6826 | 73.501% | 0.0369 | 0.5234 | 94.320% | 0.0619 | 0.4816 | 94.527% | ||
| 0.1143 | 0.3829 | 94.996% | 0.1365 | 0.3612 | 94.996% | 0.1597 | 0.3357 | 94.971% | |||
| 15 | 0.0244 | 0.6003 | 90.757% | 0.1029 | 0.4339 | 94.455% | 0.1339 | 0.3953 | 94.452% | ||
| 0.1304 | 0.3434 | 94.334% | 0.1646 | 0.3215 | 94.657% | 0.1888 | 0.2975 | 94.302% | |||
| 20 | 0.0177 | 0.4944 | 94.972% | 0.1374 | 0.3794 | 94.789% | 0.1582 | 0.3613 | 94.594% | ||
| 0.1432 | 0.3218 | 93.296% | 0.1864 | 0.3022 | 94.571% | 0.1989 | 0.2879 | 94.020% | |||
| 0.75 | 4 | 0.0736 | 0.4234 | 94.997% | 0.0899 | 0.3920 | 94.843% | 0.1082 | 0.3817 | 94.941% | |
| 0.3414 | 1.4812 | 91.407% | 0.3394 | 1.4775 | 91.525% | 0.3434 | 1.4514 | 91.831% | |||
| 7 | 0.1323 | 0.3681 | 95.000% | 0.1472 | 0.3470 | 94.963% | 0.1650 | 0.3345 | 95.000% | ||
| 0.4901 | 1.1667 | 92.607% | 0.5104 | 1.1337 | 92.617% | 0.5273 | 1.0976 | 92.868% | |||
| 10 | 0.1457 | 0.3544 | 95.000% | 0.1816 | 0.3177 | 94.999% | 0.1877 | 0.3092 | 94.971% | ||
| 0.5123 | 1.1192 | 92.912% | 0.5384 | 1.0396 | 93.928% | 0.5903 | 0.9873 | 93.305% | |||
| 15 | 0.1681 | 0.3416 | 94.865% | 0.2023 | 0.2966 | 94.994% | 0.2101 | 0.2900 | 95.000% | ||
| 0.5674 | 1.0062 | 93.754% | 0.5875 | 0.9413 | 94.707% | 0.6301 | 0.8926 | 94.670% | |||
| 20 | 0.1732 | 0.3204 | 94.918% | 0.2114 | 0.2849 | 94.886% | 0.2180 | 0.2809 | 94.987% | ||
| 0.5859 | 0.9605 | 94.320% | 0.6350 | 0.8930 | 94.482% | 0.6561 | 0.8604 | 94.714% | |||
| 2 | 4 | 0.1821 | 0.3096 | 94.815% | 0.1862 | 0.3011 | 94.464% | 0.1950 | 0.2966 | 94.704% | |
| 0.9105 | 3.9495 | 91.409% | 1.0053 | 3.8450 | 90.970% | 0.9887 | 3.8259 | 91.301% | |||
| 7 | 0.2048 | 0.2920 | 94.942% | 0.2102 | 0.2852 | 94.832% | 0.2175 | 0.2806 | 94.960% | ||
| 1.3068 | 3.1111 | 92.608% | 1.3523 | 3.0568 | 92.430% | 1.4060 | 2.9267 | 92.869% | |||
| 10 | 0.2100 | 0.2874 | 94.952% | 0.2237 | 0.2749 | 94.967% | 0.2260 | 0.2719 | 94.910% | ||
| 1.3663 | 2.9842 | 92.911% | 1.4358 | 2.7721 | 93.929% | 1.5742 | 2.6325 | 93.305% | |||
| 15 | 0.2189 | 0.2829 | 94.965% | 0.2318 | 0.2672 | 94.968% | 0.2349 | 0.2648 | 94.994% | ||
| 1.5130 | 2.6831 | 93.755% | 1.5667 | 2.5101 | 94.708% | 1.6804 | 2.3802 | 94.671% | |||
| 20 | 0.2203 | 0.2759 | 94.800% | 0.2353 | 0.2629 | 94.826% | 0.2379 | 0.2614 | 94.966% | ||
| 1.5624 | 2.5614 | 94.322% | 1.6932 | 2.3812 | 94.484% | 1.7513 | 2.2934 | 94.701% | |||
| 5 | 4 | 0.2222 | 0.2735 | 94.682% | 0.2236 | 0.2704 | 94.282% | 0.2275 | 0.2685 | 94.577% | |
| 2.2758 | 9.8746 | 91.408% | 2.5871 | 9.3842 | 91.224% | 2.6587 | 9.1777 | 91.441% | |||
| 7 | 0.2316 | 0.2666 | 94.890% | 0.2338 | 0.2640 | 94.762% | 0.2369 | 0.2621 | 94.930% | ||
| 3.2670 | 7.7776 | 92.608% | 3.4243 | 7.4983 | 92.715% | 3.5150 | 7.3169 | 92.868% | |||
| 10 | 0.2338 | 0.2648 | 94.910% | 0.2394 | 0.2599 | 94.945% | 0.2403 | 0.2587 | 94.879% | ||
| 3.4158 | 7.4604 | 92.911% | 3.5893 | 6.9303 | 93.929% | 3.9354 | 6.5815 | 93.305% | |||
| 15 | 0.2374 | 0.2630 | 94.985% | 0.2427 | 0.2568 | 94.953% | 0.2439 | 0.2559 | 94.988% | ||
| 3.7825 | 6.7077 | 93.756% | 3.9168 | 6.2753 | 94.708% | 4.2009 | 5.9504 | 94.671% | |||
| 20 | 0.2380 | 0.2603 | 94.746% | 0.2441 | 0.2551 | 94.800% | 0.2452 | 0.2545 | 94.956% | ||
| 3.9062 | 6.4034 | 94.321% | 4.2332 | 5.9531 | 94.483% | 4.3781 | 5.7336 | 94.701% | |||
| SRS | RSS | RSS | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Lower | Upper | CP | Lower | Upper | CP | Lower | Upper | CP | |||
| 0.25 | 4 | 1.4748 | 3.5824 | 27.304% | 0.9416 | 2.7253 | 40.149% | 0.9355 | 2.7673 | 40.580% | |
| 0.0797 | 0.5080 | 93.135% | 0.0895 | 0.4942 | 93.096% | 0.0937 | 0.4853 | 93.190% | |||
| 7 | 0.5269 | 2.3058 | 60.555% | 0.2776 | 1.9911 | 77.682% | 0.0572 | 1.7409 | 91.916% | ||
| 0.1223 | 0.4047 | 94.597% | 0.1234 | 0.4009 | 94.660% | 0.1465 | 0.3755 | 94.592% | |||
| 10 | 0.3339 | 2.0484 | 73.693% | 0.1229 | 1.5258 | 94.505% | 0.1865 | 1.4095 | 94.729% | ||
| 0.1331 | 0.3843 | 94.790% | 0.1486 | 0.3583 | 94.952% | 0.1724 | 0.3344 | 94.924% | |||
| 15 | 0.0711 | 1.8041 | 90.832% | 0.3286 | 1.2442 | 94.722% | 0.3952 | 1.1703 | 94.685% | ||
| 0.1480 | 0.3456 | 94.954% | 0.1780 | 0.3183 | 94.968% | 0.1963 | 0.2983 | 94.874% | |||
| 20 | 0.0540 | 1.4859 | 94.966% | 0.4099 | 1.1187 | 94.929% | 0.4711 | 1.0655 | 94.833% | ||
| 0.1574 | 0.3240 | 94.449% | 0.1946 | 0.3015 | 94.940% | 0.2078 | 0.2868 | 94.794% | |||
| 0.75 | 4 | 0.2208 | 1.2703 | 94.997% | 0.2698 | 1.1761 | 94.843% | 0.3241 | 1.1458 | 94.941% | |
| 0.3414 | 1.4812 | 91.408% | 0.3500 | 1.4657 | 91.410% | 0.3406 | 1.4549 | 91.853% | |||
| 7 | 0.3968 | 1.1043 | 95.000% | 0.4415 | 1.0410 | 94.963% | 0.4951 | 1.0035 | 95.000% | ||
| 0.4901 | 1.1667 | 92.607% | 0.4822 | 1.1562 | 93.125% | 0.5273 | 1.0975 | 92.867% | |||
| 10 | 0.4372 | 1.0631 | 95.000% | 0.5447 | 0.9531 | 94.999% | 0.5631 | 0.9276 | 94.971% | ||
| 0.5123 | 1.1191 | 92.910% | 0.5384 | 1.0396 | 93.928% | 0.5903 | 0.9872 | 93.303% | |||
| 15 | 0.5042 | 1.0247 | 94.865% | 0.6068 | 0.8898 | 94.994% | 0.6302 | 0.8700 | 95.000% | ||
| 0.5674 | 1.0062 | 93.754% | 0.5875 | 0.9413 | 94.707% | 0.6301 | 0.8926 | 94.670% | |||
| 20 | 0.5197 | 0.9612 | 94.918% | 0.6341 | 0.8547 | 94.886% | 0.6541 | 0.8425 | 94.986% | ||
| 0.5859 | 0.9606 | 94.321% | 0.6350 | 0.8930 | 94.482% | 0.6567 | 0.8601 | 94.700% | |||
| 2 | 4 | 0.5463 | 0.9289 | 94.815% | 0.5587 | 0.9033 | 94.463% | 0.5850 | 0.8899 | 94.703% | |
| 0.9104 | 3.9497 | 91.408% | 0.9389 | 3.9110 | 91.331% | 0.9779 | 3.8367 | 91.358% | |||
| 7 | 0.6144 | 0.8761 | 94.942% | 0.6305 | 0.8556 | 94.831% | 0.6526 | 0.8417 | 94.960% | ||
| 1.3068 | 3.1111 | 92.608% | 1.3523 | 3.0568 | 92.429% | 1.4061 | 2.9267 | 92.868% | |||
| 10 | 0.6301 | 0.8622 | 94.952% | 0.6711 | 0.8247 | 94.967% | 0.6780 | 0.8158 | 94.909% | ||
| 1.3663 | 2.9843 | 92.910% | 1.4358 | 2.7722 | 93.928% | 1.5742 | 2.6326 | 93.304% | |||
| 15 | 0.6567 | 0.8487 | 94.965% | 0.6955 | 0.8016 | 94.967% | 0.7046 | 0.7943 | 94.994% | ||
| 1.5130 | 2.6832 | 93.755% | 1.5667 | 2.5102 | 94.707% | 1.6804 | 2.3802 | 94.670% | |||
| 20 | 0.6610 | 0.8278 | 94.800% | 0.7060 | 0.7888 | 94.825% | 0.7138 | 0.7842 | 94.966% | ||
| 1.5624 | 2.5615 | 94.321% | 1.6933 | 2.3813 | 94.482% | 1.7513 | 2.2935 | 94.700% | |||
| 5 | 4 | 0.6665 | 0.8204 | 94.682% | 0.6708 | 0.8113 | 94.282% | 0.6825 | 0.8055 | 94.577% | |
| 2.2760 | 9.8743 | 91.408% | 2.5915 | 9.3797 | 91.214% | 2.7421 | 9.1744 | 91.011% | |||
| 7 | 0.6948 | 0.7999 | 94.890% | 0.7014 | 0.7920 | 94.761% | 0.7106 | 0.7863 | 94.929% | ||
| 3.2671 | 7.7778 | 92.607% | 3.5102 | 7.5021 | 92.126% | 3.5152 | 7.3169 | 92.867% | |||
| 10 | 0.7013 | 0.7945 | 94.910% | 0.7181 | 0.7797 | 94.945% | 0.7208 | 0.7762 | 94.879% | ||
| 3.4157 | 7.4610 | 92.909% | 3.5893 | 6.9307 | 93.928% | 3.9355 | 6.5816 | 93.304% | |||
| 15 | 0.7123 | 0.7891 | 94.985% | 0.7281 | 0.7705 | 94.953% | 0.7318 | 0.7676 | 94.988% | ||
| 3.7825 | 6.7080 | 93.755% | 3.9169 | 6.2755 | 94.707% | 4.2009 | 5.9507 | 94.670% | |||
| 20 | 0.7139 | 0.7810 | 94.746% | 0.7323 | 0.7654 | 94.800% | 0.7355 | 0.7636 | 94.956% | ||
| 3.9061 | 6.4036 | 94.321% | 4.2332 | 5.9532 | 94.482% | 4.3783 | 5.7337 | 94.700% | |||
| SRS | RSS | RSS | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Lower | Upper | CP | Lower | Upper | CP | Lower | Upper | CP | |||
| 0.25 | 4 | 3.9161 | 9.5319 | 27.418% | 2.5059 | 7.2680 | 40.229% | 2.4984 | 7.3594 | 40.491% | |
| 0.0929 | 0.5038 | 92.529% | 0.0988 | 0.4949 | 92.499% | 0.0992 | 0.4913 | 92.625% | |||
| 7 | 1.3871 | 6.1330 | 60.972% | 0.6849 | 5.1814 | 79.350% | 0.1731 | 4.6105 | 91.661% | ||
| 0.1348 | 0.4011 | 94.194% | 0.1365 | 0.3942 | 94.376% | 0.1581 | 0.3714 | 94.155% | |||
| 10 | 0.8919 | 5.4634 | 73.651% | 0.3332 | 4.0091 | 94.618% | 0.5120 | 3.6964 | 94.812% | ||
| 0.1417 | 0.3836 | 94.516% | 0.1570 | 0.3559 | 94.817% | 0.1797 | 0.3329 | 94.703% | |||
| 15 | 0.1881 | 4.8157 | 90.841% | 0.8636 | 3.2960 | 94.811% | 1.0577 | 3.0869 | 94.777% | ||
| 0.1601 | 0.3439 | 94.980% | 0.1834 | 0.3172 | 94.999% | 0.2001 | 0.2985 | 94.991% | |||
| 20 | 0.1462 | 3.9684 | 94.961% | 1.0875 | 2.9498 | 94.983% | 1.2490 | 2.8210 | 94.913% | ||
| 0.1694 | 0.3231 | 94.895% | 0.2011 | 0.3003 | 94.992% | 0.2120 | 0.2866 | 94.984% | |||
| 0.75 | 4 | 0.5889 | 3.3874 | 94.997% | 0.7194 | 3.1363 | 94.843% | 0.8644 | 3.0550 | 94.941% | |
| 0.3414 | 1.4811 | 91.408% | 0.3475 | 1.4580 | 91.607% | 0.3660 | 1.4494 | 91.193% | |||
| 7 | 1.0581 | 2.9448 | 95.000% | 1.1774 | 2.7759 | 94.963% | 1.3203 | 2.6759 | 95.000% | ||
| 0.4901 | 1.1667 | 92.607% | 0.4933 | 1.1451 | 92.993% | 0.5273 | 1.0975 | 92.867% | |||
| 10 | 1.1658 | 2.8349 | 95.000% | 1.4526 | 2.5415 | 94.999% | 1.5015 | 2.4735 | 94.971% | ||
| 0.5123 | 1.1191 | 92.910% | 0.5384 | 1.0396 | 93.928% | 0.5903 | 0.9872 | 93.303% | |||
| 15 | 1.3444 | 2.7326 | 94.865% | 1.6180 | 2.3729 | 94.994% | 1.6805 | 2.3200 | 95.000% | ||
| 0.5674 | 1.0062 | 93.755% | 0.5875 | 0.9413 | 94.707% | 0.6301 | 0.8926 | 94.670% | |||
| 20 | 1.3858 | 2.5631 | 94.918% | 1.6909 | 2.2791 | 94.886% | 1.7443 | 2.2467 | 94.986% | ||
| 0.5859 | 0.9606 | 94.321% | 0.6350 | 0.8930 | 94.482% | 0.6567 | 0.8601 | 94.700% | |||
| 2 | 4 | 1.4568 | 2.4770 | 94.815% | 1.4900 | 2.4087 | 94.463% | 1.5601 | 2.3732 | 94.703% | |
| 0.9104 | 3.9497 | 91.408% | 1.9630 | 3.5178 | 53.708% | 0.8638 | 4.0822 | 91.120% | |||
| 7 | 1.6383 | 2.3363 | 94.942% | 1.6812 | 2.2815 | 94.831% | 1.7403 | 2.2444 | 94.960% | ||
| 1.3068 | 3.1111 | 92.608% | 1.3464 | 3.0565 | 92.524% | 1.4061 | 2.9268 | 92.867% | |||
| 10 | 1.6802 | 2.2992 | 94.952% | 1.7895 | 2.1992 | 94.967% | 1.8079 | 2.1753 | 94.909% | ||
| 1.3662 | 2.9844 | 92.910% | 1.4358 | 2.7722 | 93.928% | 1.5742 | 2.6326 | 93.303% | |||
| 15 | 1.7512 | 2.2633 | 94.965% | 1.8547 | 2.1376 | 94.967% | 1.8790 | 2.1181 | 94.994% | ||
| 1.5130 | 2.6832 | 93.755% | 1.5668 | 2.5102 | 94.707% | 1.6804 | 2.3802 | 94.670% | |||
| 20 | 1.7626 | 2.2074 | 94.800% | 1.8828 | 2.1033 | 94.825% | 1.9035 | 2.0913 | 94.966% | ||
| 1.5624 | 2.5615 | 94.321% | 1.6933 | 2.3813 | 94.482% | 1.7513 | 2.2935 | 94.700% | |||
| 5 | 4 | 1.7773 | 2.1878 | 94.682% | 1.7888 | 2.1634 | 94.282% | 1.8199 | 2.1479 | 94.577% | |
| 2.2759 | 9.8745 | 91.408% | 4.0259 | 7.9454 | 83.342% | 4.1616 | 7.4033 | 84.284% | |||
| 7 | 1.8528 | 2.1331 | 94.890% | 1.8703 | 2.1119 | 94.762% | 1.8950 | 2.0969 | 94.929% | ||
| 3.2671 | 7.7778 | 92.607% | 3.4242 | 7.4985 | 92.715% | 3.5152 | 7.3168 | 92.867% | |||
| 10 | 1.8701 | 2.1186 | 94.910% | 1.9149 | 2.0793 | 94.945% | 1.9223 | 2.0700 | 94.879% | ||
| 3.4156 | 7.4609 | 92.910% | 3.5895 | 6.9305 | 93.928% | 3.9355 | 6.5816 | 93.304% | |||
| 15 | 1.8996 | 2.1042 | 94.985% | 1.9415 | 2.0548 | 94.953% | 1.9514 | 2.0470 | 94.988% | ||
| 3.7825 | 6.7079 | 93.755% | 3.9169 | 6.2755 | 94.707% | 4.2009 | 5.9506 | 94.670% | |||
| 20 | 1.9037 | 2.0827 | 94.746% | 1.9529 | 2.0412 | 94.800% | 1.9613 | 2.0363 | 94.956% | ||
| 3.9061 | 6.4037 | 94.321% | 4.2332 | 5.9532 | 94.482% | 4.3782 | 5.7337 | 94.700% | |||
| One Cycle | ||||
|---|---|---|---|---|
| 2.518 | 2.659 | 2.856 | 3.22 | 4.395 |
| 2.132 | 2.257 | 3.332 | 3.628 | 4.027 |
| 2.396 | 2.397 | 3.971 | 4.024 | 5.02 |
| 2.228 | 2.937 | 3.223 | 3.562 | 3.871 |
| 2.532 | 2.74 | 2.937 | 3.493 | 3.886 |
| Cycle 1 | ||||
| 2.856 | 2.996 | 3.537 | ||
| 2.977 | 3.125 | 3.377 | ||
| 2.396 | 2.616 | 4.395 | ||
| Cycle 2 | ||||
| 2.203 | 2.616 | |||
| 3.139 | 5.02 | |||
| SRS | RSS | RSS | ||||
|---|---|---|---|---|---|---|
| MLEs | 3.6561 | 3.6561 | 3.6591 | 3.1871 | 4.1497 | 1.8640 |
| SEs | 0.7766 | 0.7766 | 0.2211 | 0.8621 | 0.4384 | 0.5353 |
| Lower | 2.1340 | 2.1340 | 3.2257 | 1.4974 | 3.2905 | 0.8148 |
| Upper | 5.1783 | 5.1783 | 4.0925 | 4.8768 | 5.0090 | 2.9132 |
| K-S (Stat) | 0.3577 | 0.2489 | 0.1817 | |||
| K-S (p-value) | 0.4417 | 0.8479 | 0.9861 | |||
| One Cycle | |||||
|---|---|---|---|---|---|
| 2.856 | 2.977 | 2.996 | 3.125 | 3.377 | 3.537 |
| 2.203 | 2.396 | 2.616 | 3.139 | 3.852 | 4.395 |
| 2.624 | 3.408 | 3.501 | 3.554 | 3.628 | 3.971 |
| 2.35 | 2.474 | 2.518 | 2.738 | 3.294 | 3.493 |
| 2.132 | 2.257 | 2.659 | 3.264 | 3.346 | 5.02 |
| 2.397 | 2.618 | 3.03 | 3.145 | 3.223 | 4.024 |
| Cycle 1 | |||||
| 2.917 | 2.977 | 3.294 | |||
| 3.125 | 3.223 | 3.886 | |||
| 2.522 | 2.74 | 3.408 | |||
| Cycle 2 | |||||
| 2.624 | 2.937 | 3.886 | |||
| 2.522 | 2.977 | 3.22 | |||
| 2.532 | 3.125 | 3.852 | |||
| SRS | RSS | RSS | ||||
|---|---|---|---|---|---|---|
| MLEs | 2.3347 | 2.3347 | 3.4455 | 3.8604 | 3.4364 | 4.2626 |
| SEs | 0.5644 | 0.5644 | 0.1500 | 0.5498 | 0.1372 | 1.1060 |
| Lower | 1.2285 | 1.2285 | 3.1516 | 2.7829 | 3.1675 | 2.0948 |
| Upper | 3.4409 | 3.4409 | 3.7394 | 4.9380 | 3.7053 | 6.4305 |
| K-S (Stat) | 0.8198 | 0.1708 | 0.1811 | |||
| K-S (p-value) | 0.0001 | 0.9805 | 0.9674 | |||
| One Cycle | ||||||
|---|---|---|---|---|---|---|
| 2.856 | 2.977 | 2.996 | 3.125 | 3.377 | 3.537 | 4.395 |
| 2.203 | 2.396 | 2.616 | 3.139 | 3.554 | 3.628 | 3.852 |
| 2.474 | 2.518 | 2.624 | 2.738 | 3.408 | 3.501 | 3.971 |
| 2.35 | 2.659 | 3.264 | 3.294 | 3.346 | 3.493 | 5.02 |
| 2.132 | 2.257 | 2.397 | 3.03 | 3.145 | 3.223 | 4.024 |
| 2.228 | 2.575 | 2.618 | 3.235 | 3.332 | 3.871 | 4.225 |
| 2.454 | 2.522 | 2.532 | 2.917 | 3.22 | 3.272 | 4.027 |
| Cycle 1 | ||||||
| 2.257 | 2.35 | 3.272 | ||||
| 2.397 | 2.618 | 2.659 | ||||
| 3.125 | 3.294 | 3.562 | ||||
| Cycle 2 | ||||||
| 2.618 | 3.332 | 4.027 | 4.225 | |||
| 2.614 | 3.125 | 3.272 | 3.554 | |||
| 2.474 | 3.145 | 3.346 | 3.628 | |||
| 2.454 | 2.532 | 2.977 | 3.852 | |||
| SRS | RSS | RSS | ||||
|---|---|---|---|---|---|---|
| MLEs | 2.2814 | 2.2814 | 3.4602 | 4.0823 | 3.3762 | 3.8009 |
| SEs | 0.6290 | 0.6290 | 0.1252 | 0.5895 | 0.1175 | 0.4895 |
| Lower | 1.0485 | 1.0485 | 3.2147 | 2.9269 | 3.1458 | 2.8415 |
| Upper | 3.5143 | 3.5143 | 3.7056 | 5.2377 | 3.6065 | 4.7603 |
| K-S (Stat) | 0.8388 | 0.1761 | 0.1716 | |||
| K-S (p-value) | 0.0000 | 0.9556 | 0.9593 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akhter, Z.; Almetwally, E.M.; Chesneau, C. On the Generalized Bilal Distribution: Some Properties and Estimation under Ranked Set Sampling. Axioms 2022, 11, 173. https://doi.org/10.3390/axioms11040173
Akhter Z, Almetwally EM, Chesneau C. On the Generalized Bilal Distribution: Some Properties and Estimation under Ranked Set Sampling. Axioms. 2022; 11(4):173. https://doi.org/10.3390/axioms11040173
Chicago/Turabian StyleAkhter, Zuber, Ehab M. Almetwally, and Christophe Chesneau. 2022. "On the Generalized Bilal Distribution: Some Properties and Estimation under Ranked Set Sampling" Axioms 11, no. 4: 173. https://doi.org/10.3390/axioms11040173
APA StyleAkhter, Z., Almetwally, E. M., & Chesneau, C. (2022). On the Generalized Bilal Distribution: Some Properties and Estimation under Ranked Set Sampling. Axioms, 11(4), 173. https://doi.org/10.3390/axioms11040173








