Deterministic and Stochastic Prey–Predator Model for Three Predators and a Single Prey
Abstract
1. Introduction
2. Mathematical Model
3. Some Preliminary Results
3.1. Existence and Uniqueness
3.2. Non-Negativity and Boundedness
4. Equilibria and Stability
- The trivial equilibrium point , which always exists;
- The predator free equilibrium point , which always exists;
- The equilibrium point exists if
- The equilibrium point exists if
- The equilibrium point exists if ;
- The equilibrium point , where:where . exists if
- The coexistence equilibrium point , where:exists if , and .
- ;
- ;
- ;
- .
5. Stochastic Models
5.1. Stochastic Perturbations
5.2. Random Harvesting
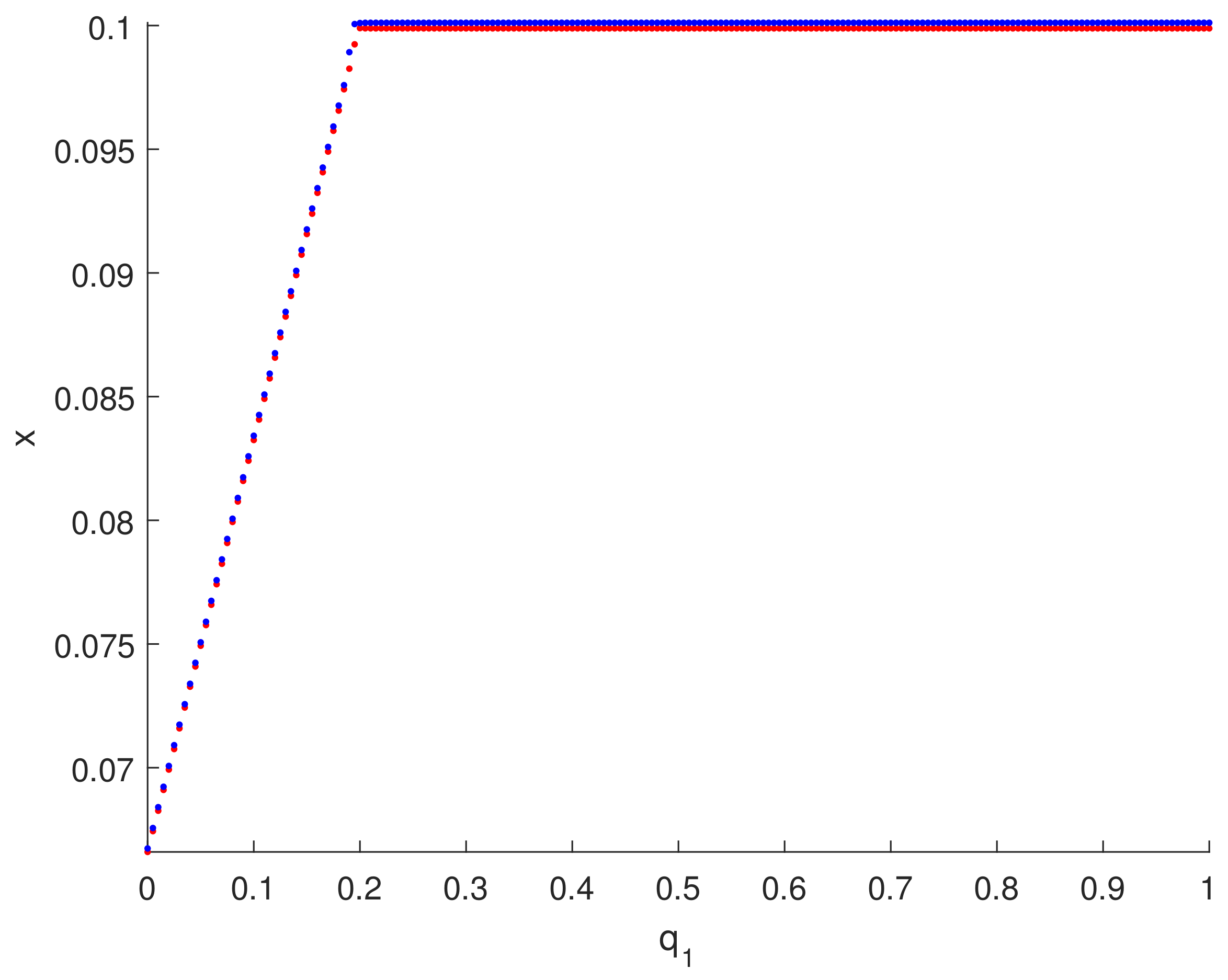
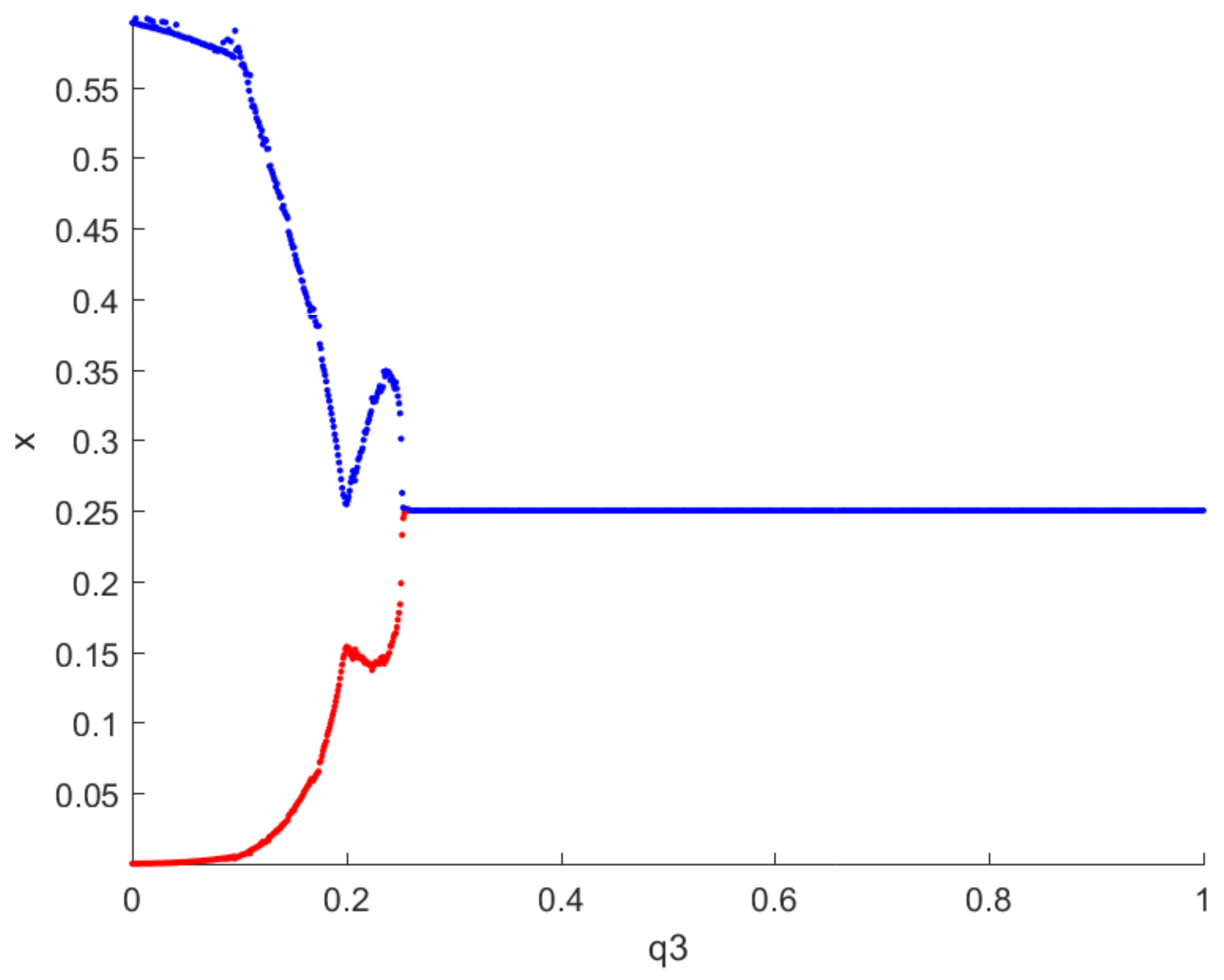
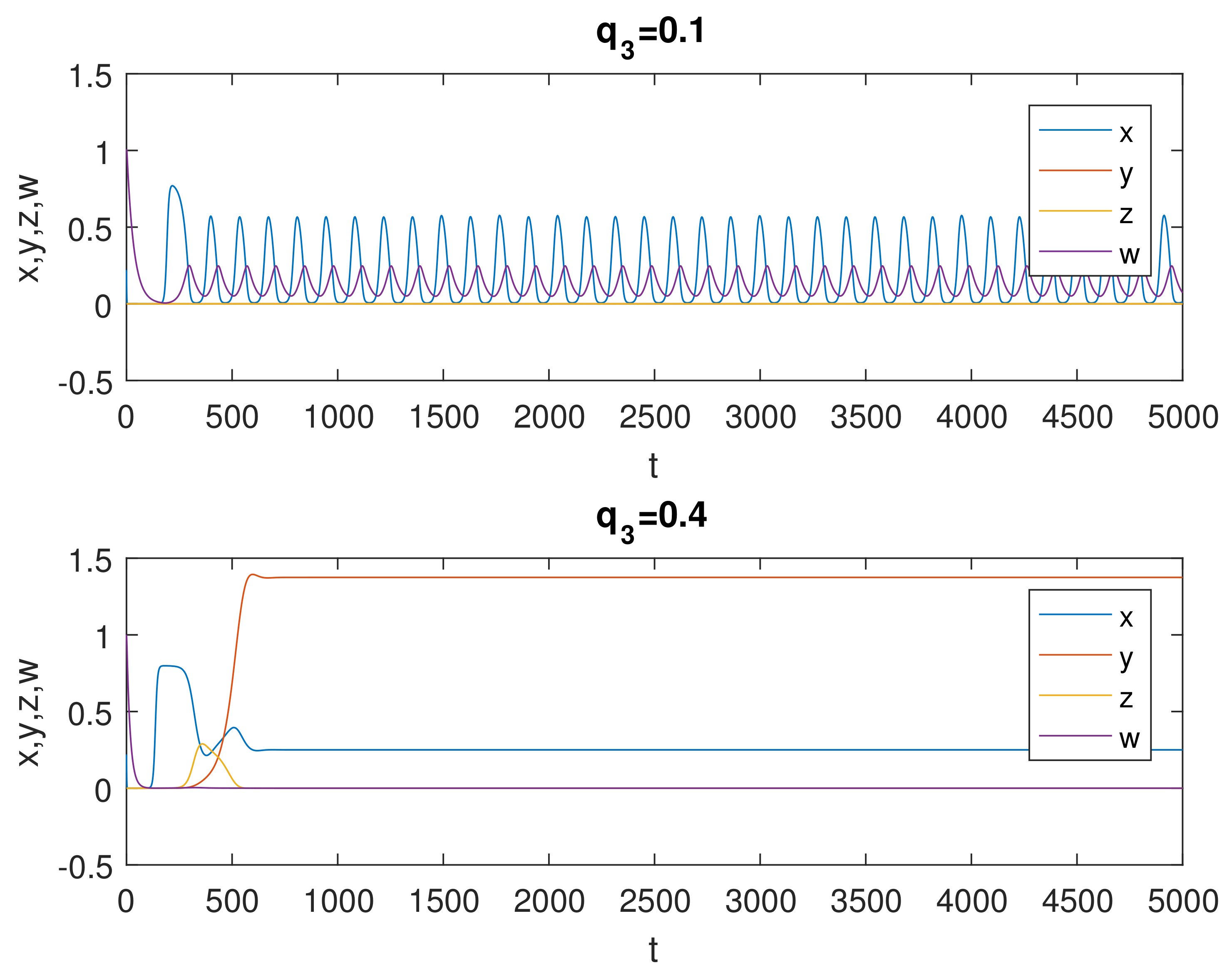
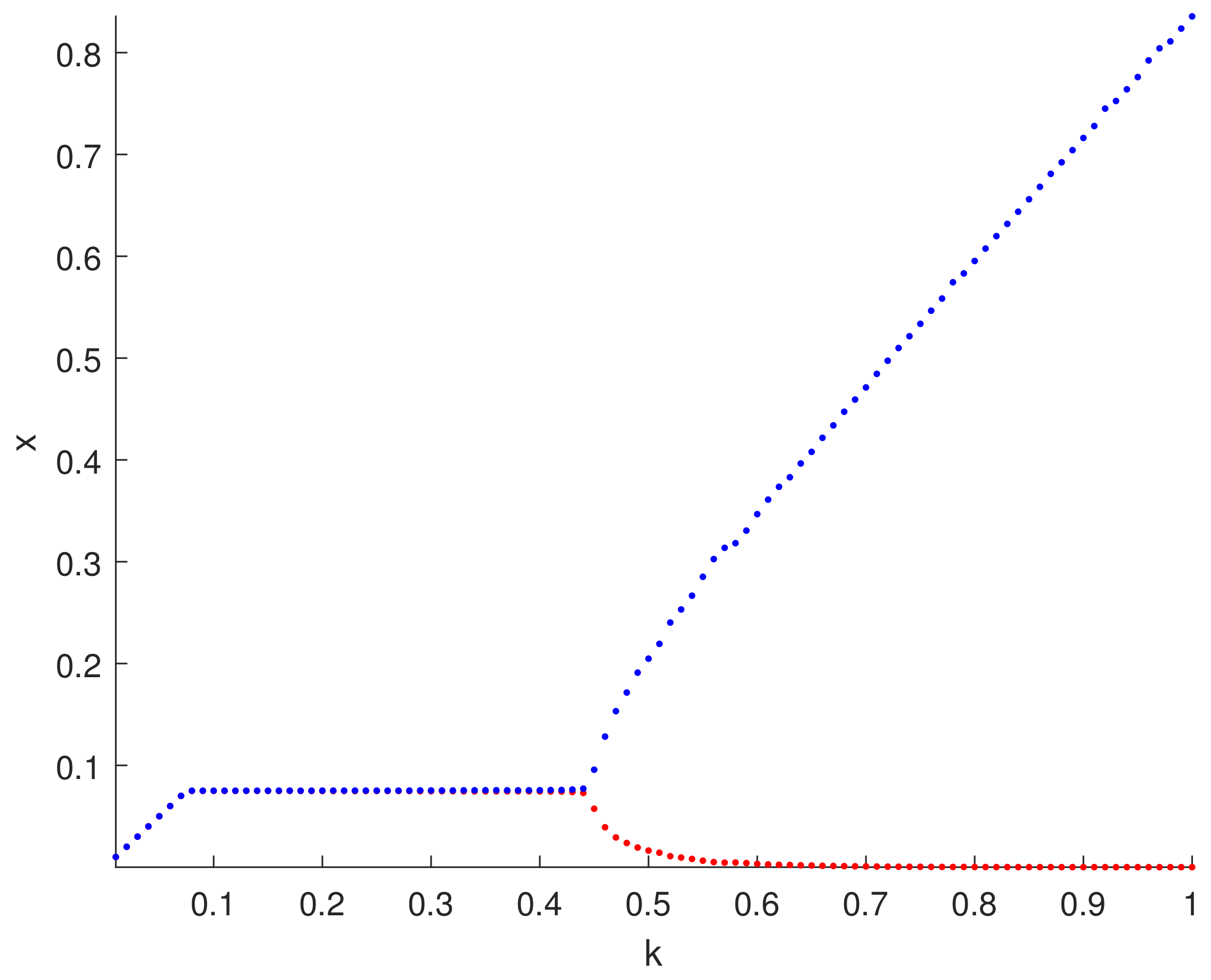
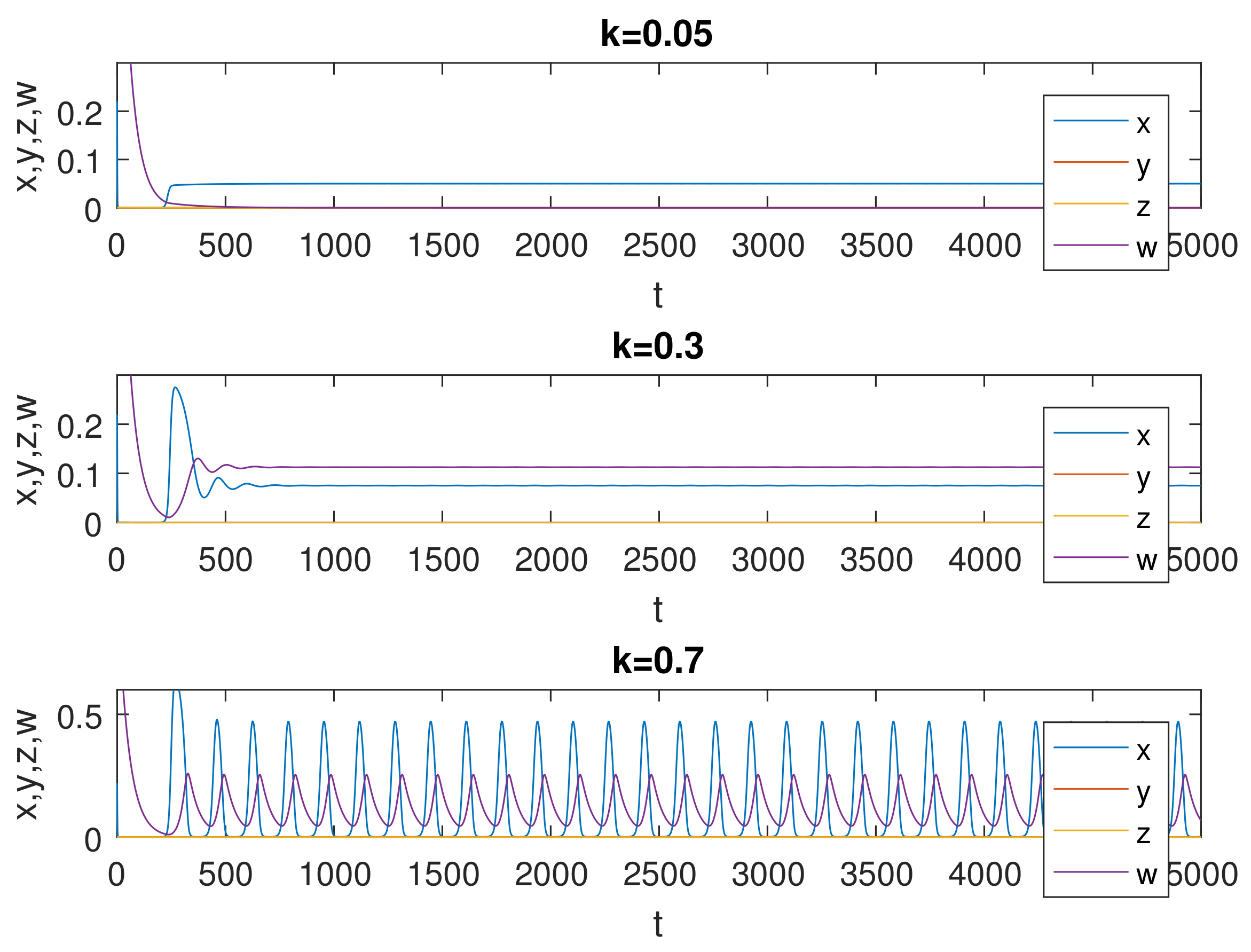
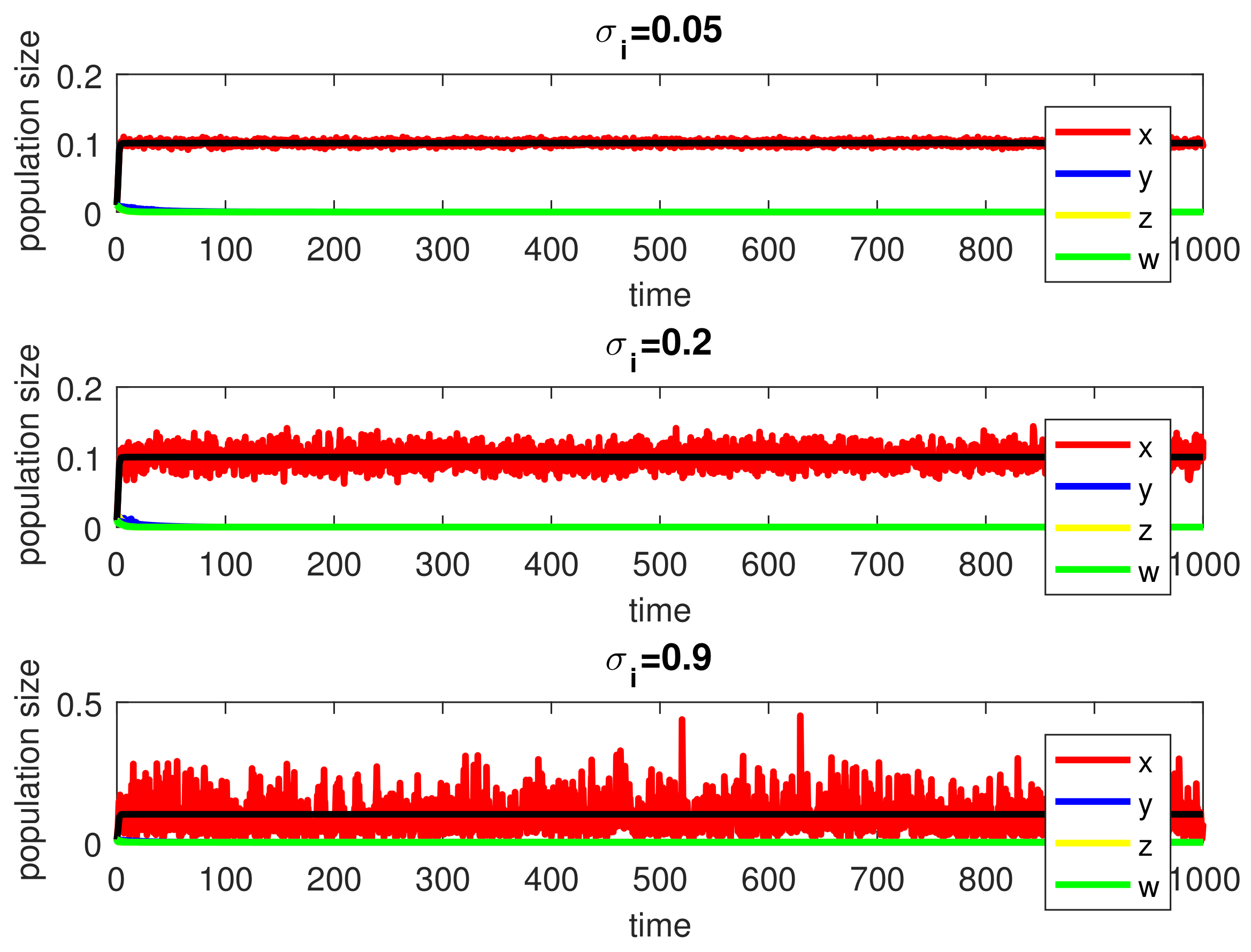
6. Numerical Simulations
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wikan, A.; Kristensen, Ø. Prey–predator interactions in two and three species population models. Discret. Dyn. Nat. Soc. 2019, 2019, 9543139. [Google Scholar] [CrossRef]
- Sayekti, I.; Malik, M.; Aldila, D. One–prey two–predator model with prey harvesting in a food chain interaction. In Proceedings of the International Symposium on Current Progress in Mathematics and Sciences 2016 (ISCPMS 2016), AIP Conference Proceedings, Depok, Indonesia, 1–2 November 2016; AIP Publishing LLC: College Park, MD, USA, 2017; Volume 1862, p. 030124. [Google Scholar]
- Ghosh, U.; Sarkar, S.; Mondal, B. Study of Stability and Bifurcation of Three Species Food Chain Model with Non–monotone Functional Response. Int. J. Appl. Comput. Math. 2021, 7, 63. [Google Scholar] [CrossRef]
- Pal, D.; Kar, T.K.; Yamauchi, A.; Ghosh, B. Balancing maximum sustainable yield and ecological resilience in an exploited two–predator one–prey system. Biosystems 2020, 187, 104064. [Google Scholar] [CrossRef] [PubMed]
- Kaviya, R.; Muthukumar, P. Dynamical analysis and optimal harvesting of conformable fractional prey–predator system with predator immigration. Eur. Phys. J. Plus 2021, 136, 136. [Google Scholar]
- Fattahpour, H.; Zangeneh, H.R.; Nagata, W. Dynamics of Rodent Population With Two Predators. Bull. Iran. Math. Soc. 2019, 45, 965–996. [Google Scholar] [CrossRef]
- Li, H.; Zhang, L.; Hu, C.; Jiang, Y.; Teng, Z. Dynamical analysis of a fractional-order predator-prey model incorporating a prey refuge. J. Appl. Math. Comput. 2016, 54, 435–449. [Google Scholar] [CrossRef]
- Sambath, M.; Ramesh, P.; Balachandran, K. Asymptotic Behavior of the Fractional Order three Species Prey–Predator Model. Int. J. Nonlinear Sci. Numer. Simul. 2018, 19, 721–733. [Google Scholar] [CrossRef]
- Das, D.K.; Das, K.; Kar, T. Dynamical Behaviour of Infected Predator–Prey Eco–epidemics with Harvesting Effort. Int. J. Appl. Comput. Math. 2021, 7, 66. [Google Scholar] [CrossRef]
- Mondal, S.; Samanta, G. Impact of fear on a predator–prey system with prey-dependent search rate in deterministic and stochastic environment. Nonlinear Dyn. 2021, 104, 2931–2959. [Google Scholar] [CrossRef]
- Zhang, Y.; Tian, B.; Chen, X.; Li, J. A stochastic diseased predator system with modified LG–Holling type II functional response. Ecol. Complex. 2021, 45, 100881. [Google Scholar] [CrossRef]
- Mukhopadhyay, B.; Bhattacharyya, R. Effects of harvesting and predator interference in a model of two–predators competing for a single prey. Appl. Math. Model. 2016, 40, 3264–3274. [Google Scholar] [CrossRef]
- Garneau, D.E.; Post, E.; Boudreau, T.; Keech, M.; Valkenburg, P. Spatio–temporal patterns of predation among three sympatric predators in a single–prey system. Wildl. Biol. 2007, 13, 186–194. [Google Scholar] [CrossRef]
- Cresson, J.; Szafrańska, A. Discrete and continuous fractional persistence problems—The positivity property and applications. Commun. Nonlinear Sci. Numer. Simul. 2017, 44, 424–448. [Google Scholar] [CrossRef]
- Perko, L. Differential Equations and Dynamical Systems; Springer Science & Business Media: New York, NY, USA, 2013; Volume 7. [Google Scholar]
- Wiggins, S.; Golubitsky, M. Introduction to Applied Nonlinear Dynamical Systems and Chaos; Springer: New York, NY, USA, 2003; Volume 2. [Google Scholar]
- Maji, C.; Mukherjee, D.; Kesh, D. Deterministic and stochastic analysis of an eco–epidemiological model. J. Biol. Phys. 2018, 44, 17–36. [Google Scholar] [CrossRef]
- Cresson, J.; Puig, B.; Sonner, S. Stochastic models in biology and the invariance problem. Discret. Contin. Dyn. Syst. B 2016, 21, 2145. [Google Scholar] [CrossRef][Green Version]
- Cresson, J.; Sonner, S. A note on a derivation method for SDE models: Applications in biology and viability criteria. Stoch. Anal. Appl. 2018, 36, 224–239. [Google Scholar] [CrossRef]
- Phan, T.A.; Tian, J.P.; Wang, B. Dynamics of cholera epidemic models in fluctuating environments. Stoch. Dyn. 2021, 21, 2150011. [Google Scholar] [CrossRef]
- Mao, X. Stochastic Differential Equations and Applications; Woodhead Publishing: Cambridge, UK, 2007. [Google Scholar]
- Cai, Y.; Mao, X. Stochastic prey–predator system with foraging arena scheme. Appl. Math. Model. 2018, 64, 357–371. [Google Scholar] [CrossRef]
- Wei, C.; Liu, J.; Zhang, S. Analysis of a stochastic eco–epidemiological model with modified Leslie–Gower functional response. Adv. Differ. Equ. 2018, 2018, 119. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, D.; Hayat, T.; Alsaedi, A.; Ahmad, B. A stochastic SIRS epidemic model with logistic growth and general nonlinear incidence rate. Phys. A Stat. Mech. Appl. 2020, 551, 124152. [Google Scholar] [CrossRef]
- Li, Q.; Cong, F.; Liu, T.; Zhou, Y. Stationary distribution of a stochastic HIV model with two infective stages. Phys. A Stat. Mech. Appl. 2020, 554, 124686. [Google Scholar] [CrossRef]
- Afanasiev, V.N.; Kolmanovskii, V.; Nosov, V. Mathematical Theory of Control Systems Design; Springer Science & Business Media: Dordrecht, The Netherlands, 2013; Volume 341. [Google Scholar]
- Mukhopadhyay, B.; Bhattacharyya, R. A nonlinear mathematical model of virus–tumor–immune system interaction: Deterministic and stochastic analysis. Stoch. Anal. Appl. 2009, 27, 409–429. [Google Scholar] [CrossRef]
- Mukhopadhyay, B.; Bhattacharyya, R. On a three–tier ecological food chain model with deterministic and random harvesting: A mathematical study. Nonlinear Anal. Model. Control. 2011, 16, 77–88. [Google Scholar] [CrossRef]
- Mukhopadhyay, B.; Bhattacharyya, R. Effects of deterministic and random refuge in a prey–predator model with parasite infection. Math. Biosci. 2012, 239, 124–130. [Google Scholar] [CrossRef]
- Ghosh, P.; Das, P.; Mukherjee, D. Persistence and stability of a seasonally perturbed three species stochastic model of salmonoid aquaculture. Differ. Equ. Dyn. Syst. 2019, 27, 449–465. [Google Scholar] [CrossRef]
- Higham, D.J. An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev. 2001, 43, 525–546. [Google Scholar] [CrossRef]
- Alnafisah, Y. The implementation of Milstein scheme in two–dimensional SDEs using the Fourier method. Abstr. Appl. Anal. 2018, 2018, 3805042. [Google Scholar] [CrossRef]
- Cao, Y.; Denu, D. Analysis of stochastic vector–host epidemic model with direct transmission. Discret. Contin. Dyn. Syst. B 2016, 21, 2109–2127. [Google Scholar] [CrossRef][Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alnafisah, Y.; El-Shahed, M. Deterministic and Stochastic Prey–Predator Model for Three Predators and a Single Prey. Axioms 2022, 11, 156. https://doi.org/10.3390/axioms11040156
Alnafisah Y, El-Shahed M. Deterministic and Stochastic Prey–Predator Model for Three Predators and a Single Prey. Axioms. 2022; 11(4):156. https://doi.org/10.3390/axioms11040156
Chicago/Turabian StyleAlnafisah, Yousef, and Moustafa El-Shahed. 2022. "Deterministic and Stochastic Prey–Predator Model for Three Predators and a Single Prey" Axioms 11, no. 4: 156. https://doi.org/10.3390/axioms11040156
APA StyleAlnafisah, Y., & El-Shahed, M. (2022). Deterministic and Stochastic Prey–Predator Model for Three Predators and a Single Prey. Axioms, 11(4), 156. https://doi.org/10.3390/axioms11040156




