1. Introduction and Preliminaries
Let
E be a subset of a normed vector space
X. The operator
is called a contraction if:
where
. Banach [
1] was the first to introduce these mappings and proved that such mappings in a closed subset of Banach space always posses a unique fixed point, that is,
for some
q. Note that when the real constant
is equal to 1 in (
1), then
is called nonexpansive. When the space
X is restricted to the case of uniformly convex Banach space (UCBS), and
E is closed bounded and convex in
X, then each nonexpansive map
has a fixed point (e.g., see Browder [
2] and Gohde [
3]).
Note that it is sometimes possible that a given equation (functional, differential, integral, etc.) has a solution, but its value cannot be found by applying available analytical methods. In such cases, one needs the approximate value of such solutions. The natural question of how to obtain such approximate solutions arises, which is one of the difficult tasks. One of the successful methods are iterative techniques, which are the best choice for computing such approximate solutions. To achieve the objective, we first try to express the original given equation in the form of a fixed point equation, in a way that the fixed point set of this equation coincides with the solution set of the original equation. We then use an iterative method, which converges in the fixed point set of the fixed point equation, and hence in the solution set of the original equation as well.
It is normally easy to iterate a single-valued function, but for a multi-valued map, it is a difficult task. The fixed point theory connected to multi-valued maps has played a significant role in many areas of science and technology (e.g., see [
4] and others). Thus, once any result for a single-valued map is available in the literature, it is always desirable to obtain its multi-valued version. Now, we can set the concepts of fixed points for multi-valued maps: a point
is called a fixed point for a multi-valued map
if
q is an element of the set
, that is,
, where
. If
for every fixed point
q of
, then such a multi-valued map is said to be endowed with the endpoint condition (e.g., see Jung [
5]). All throughout,
will denote the fixed point set of
.
To establish the fixed point and the related results on multi-valued maps, one often requires the following concept of metric. Suppose that
and set the real-valued function
with the following formula:
Here, the function H essentially holds all requirements of the metric, which is called a Hausdorff metric on the set .
Using the function H, we thus mention the following notions of multi-valued maps.
Definition 1. If E is any nonempty subset of Banach space, and and . Then is known as:
- (i)
nonexpansive if ;
- (ii)
quasi-nonexpansive if ;
- (iii)
proximally nonexpansive if ;
- (iv)
proximally quasi-nonexpansive if .
Remark 1. Note that a nonexpansive multi-valued map is always continuous. Moreover, every multi-valued nonexpansive map with a nonempty fixed point set is always a multi-valued quasi-nonexpansive, but the converse is not valid in general because there exists discontinuous, multi-valued maps which are multi-valued quasi-nonexpansive (e.g., see [6] and others). When a result on the existence of a fixed point for a given operator is proved, then calculating such a fixed point by using an appropriate fixed point iteration method is essentially an active research area on its own. To compute the value of contractions, the well-known result of Banach [
1] essentially suggests the simplest Picard iteration method. However, the drawback of this method is that it fails to converge in the fixed point set of nonexpansive operators; for example,
is a nonexpansive mapping on the set
and admits a unique fixed point
, but the Picard iteration method suggests a divergent sequence for every selection of
. In order to find the fixed points of nonexpansive mappings and to gain a relatively better rate of convergence, there are many iterative processes in the literature (cf. Mann [
7], Ishikawa [
8], Picard-Ishikawa [
9], Noor [
10], Agarwal [
11], Abbas [
12], Picard-S [
13], and so on). The fixed point theory of multi-valued mappings finds its roots in the papers of Nadler [
14], who studied the Banach result [
1] in the setting of multi-valued mappings. In [
15], Lim proved a fixed point theorem for a multi-valued nonexpansive, which is in fact the multi-valued version of the Browder–Göhde fixed point theorem. In 2005, Sastry and Babu [
16] essentially constructed multi-valued versions of the Mann and Ishikawa iteration schemes, respectively, for multi-valued nonexpansive mappings and proved their convergence results in a Hilbert space setting. Panyanak [
17] studied these schemes in the general context of a UCBS setting. Soon, Song, and Wang [
18] improved the main outcome of Panyanak [
17] by introducing the Mann and Ishikawa iterative schemes in a new sense. However, the Song and Wang [
18] iterative schemes use too much time consumer estimates; these schemes also require the endpoint condition to establish their convergence. After this, Shahzad and Zegeye [
6] constructed new modified Mann and Ishikawa iterative schemes and proved their convergence for proximally nonexpansive mappings without an endpoint condition. Song and Cho [
19] extended their results to the setting of proximally quasi-nonexpansive mappings. Using the idea of Shahzad and Zegeye [
6], Khan and Yilirim [
20] used the S iteration for approximating fixed points of proximally nonexpansive mappings. Khan et al. [
21] used the Abbas iteration for approximating fixed points of proximally quasi-nonexpansive nonexpansive mappings. Okeke et al. [
9] used the Picard–Ishikawa iterative scheme to approximate fixed points of proximally quasi-nonexpansive mappings. The aim of this paper is to propose new efficient algorithms for the class of proximally quasi-nonexpansive mappings and a class of BVPs on a Banach space setting.
Now we list the following single-valued iterative schemes along with their multi-valued versions in
Table 1. Set
,
,
, and
.
Now we set and study the following
F iterative scheme, the single-valued version of which was introduced and studied by Ali and Ali [
22] for multi-valued mappings:
where
,
,
,
, and
. In this research paper, we approximate fixed points for the class of proximally quasi-nonexpansive mappings (which contains the class of proximally nonexpansive mappings as a special case) using the multi-valued version of the
F iterative scheme (
2). We establish several weak and strong convergence results for proximally quasi-nonexpansive operators regarding the iteration method (
2). To validate the theoretical outcome, we suggest some numerical examples and perform a comparative experiment.
As usual, some of the following concepts will be used.
Definition 2 ([
23])
. A normed vector space X is said to be with Opial’s property if any converges in the weak sense to , then the following equation:essentially holds for any element . Definition 3 ([
20])
. A multi-valued operator, namely , is said to be demiclosed at point if any admitting a weak limit, namely w, and admitting a strong limit, namely s, then one has . Definition 4 ([
24])
. A multi-valued operator, namely , is said to satisfy a condition if there is a continuous and non-decreasing function, namely , with the following properties , for every such that for each choice of . Song and Cho [
19] noted the following facts.
Lemma 1. The following conditions for any multi-valued mapping are equivalent.
- ()
;
- ()
;
- ()
.
Furthermore, .
Every UCBS X enjoys the following property.
Lemma 2 ([
25])
. Suppose and for . If X denotes a UCBS, , and , where is some real constant, then . 2. Main Results
Lemma 3. If the operator is proximally quasi-nonexpansive on a convex nonempty closed subset E of a UCBS X and the set , then the sequence of iterates (2) has the property that exists for each fixed point q of . Proof. For any
and
, consider the following:
Hence, we obtain
. Using this, we have the following:
Consequently, we obtain the inequality for all fixed points q of and . It follows that exists for each fixed point q of . □
Using the established lemma above, we provide another key lemma, which will help us in establishing the main outcome of the sequel.
Lemma 4. If the operator is proximally quasi-nonexpansive on a convex nonempty closed subset E of a UCBS X and the set , then the sequence of iterates (2) has the property . Proof. We proved in Lemma 3 that
exists if one selects any
. This strong limit establishes that
, where
denotes any real constant. Without loss of generality, we assume that
. Then, since
is proximally quasi-nonexpansive and
, it follows that:
Looking deeply into the proof of Lemma 3, it can be seen that:
Once again, we can observe the proof of Lemma 3 to note the following:
We can now combine inequalities (
4) and (
5) to get the following equality:
Using (
6), we get the following equation:
Now, all the requirements for Lemma 2 are fulfilled, and hence:
Since
, we get the equation below:
□
We now suggest the weak convergence result.
Theorem 1. If the operator is proximally quasi-nonexpansive on a convex nonempty closed subset E of a UCBS X and the set , then the sequence of iterates (2) converges weakly in the set whenever is assumed to be demiclosed at zero and X is endowed with the Opial’s property. Proof. Suppose
, it follows that
. By Lemma 3,
exists. To obtain the weak convergence of
in the set
, we take two points
such that the subsequences
and
of
respectively converge weakly to them. According to (
7),
exists such that
. According to the demicloseness of
at zero, the element
. Similarly, one can prove that
. It now remains to be proven that
. If
. Now, using Opial’s property of space, one has the following:
Hence, we have reached . This strict inequality suggests a contradiction. Thus, the proof is established. □
After the weak convergence, we are now interested in providing the strong convergence result.
Theorem 2. If the operator is proximally quasi-nonexpansive on a convex nonempty compact subset E of a UCBS X, and the set , then the sequence of iterates (2) converges strongly in the set . Proof. The set
E is convex and compact, so the sequence
is contained in
E and has a convergent subsequence, namely
. Suppose
for some
. The target is to prove that
p is a fixed point of
and a strong limit of
. Now,
is proximally nonexpansive and
. Additionally, according to Lemma 4,
. Accordingly, we have the following:
If we apply , we obtain . Thus, , so by Lemma 1, ; that is, p is also a fixed point of . By Lemma 3, exists. Hence, p is the strong limit of . □
The last result is established under the compactness of the set E. For the next results, the compactness of E is not essential; however, the condition of must be assumed.
Theorem 3. If the operator is proximally quasi-nonexpansive on a convex nonempty closed subset E of a UCBS X and the set , then the sequence of iterates (2) converges strongly in the set whenever is assumed to be endowed with the condition . Proof. By Lemma 3,
exists for every choice of
. When
, then one has nothing to show. Hence, we consider the only case
. We have observed in Lemma 3 that
. This gives
. Hence, we get the following equation:
Accordingly, we notice that
exists. The next purpose is to show
. Set
for some real constant
. Thus, for every choice of
, set the following:
It can be observed that
and
because
. Thus, using condition
of
, one has:
Next, since
and
(see the proof of Lemma 4). Using these two, one has the following:
Now, by Lemma 2, we get
, which is clearly a contradiction to
. Thus, we conclude that
. Therefore:
Hence, the sequence converges strongly to some fixed point q of . □
Now we compare the speed of convergence of our iterative process with many other processes. To do this, we consider the following example.
Example 1. If and is defined as for each , then the following holds:
- (i)
;
- (ii)
satisfies condition I;
- (iii)
is proximally nonexpansive.
Proof. For (i), we see that , that is, . For (ii), we set a nondeacreasing function such that for each . Now,
Case (I). When
, then
. Hence,
Case (II). When
. Then,
Consequently, for each . This proves (ii). Finally, we prove (iii). Notice that whenever , and if otherwise. There are two cases to prove the proximally quasi-nonexpansiveness of as provided below.
Case (I). When
. Then, for any fixed point q of
, we have the following equation:
Case (II). When
. Then, for any fixed point q of
, we have the following equation:
Consequently,
for each
and
. This proves (iii). Hence, all the requirements of our main results now hold. Thus,
generated by (
2) converges to a point of
. This convergence can be seen in the
Table 2. □
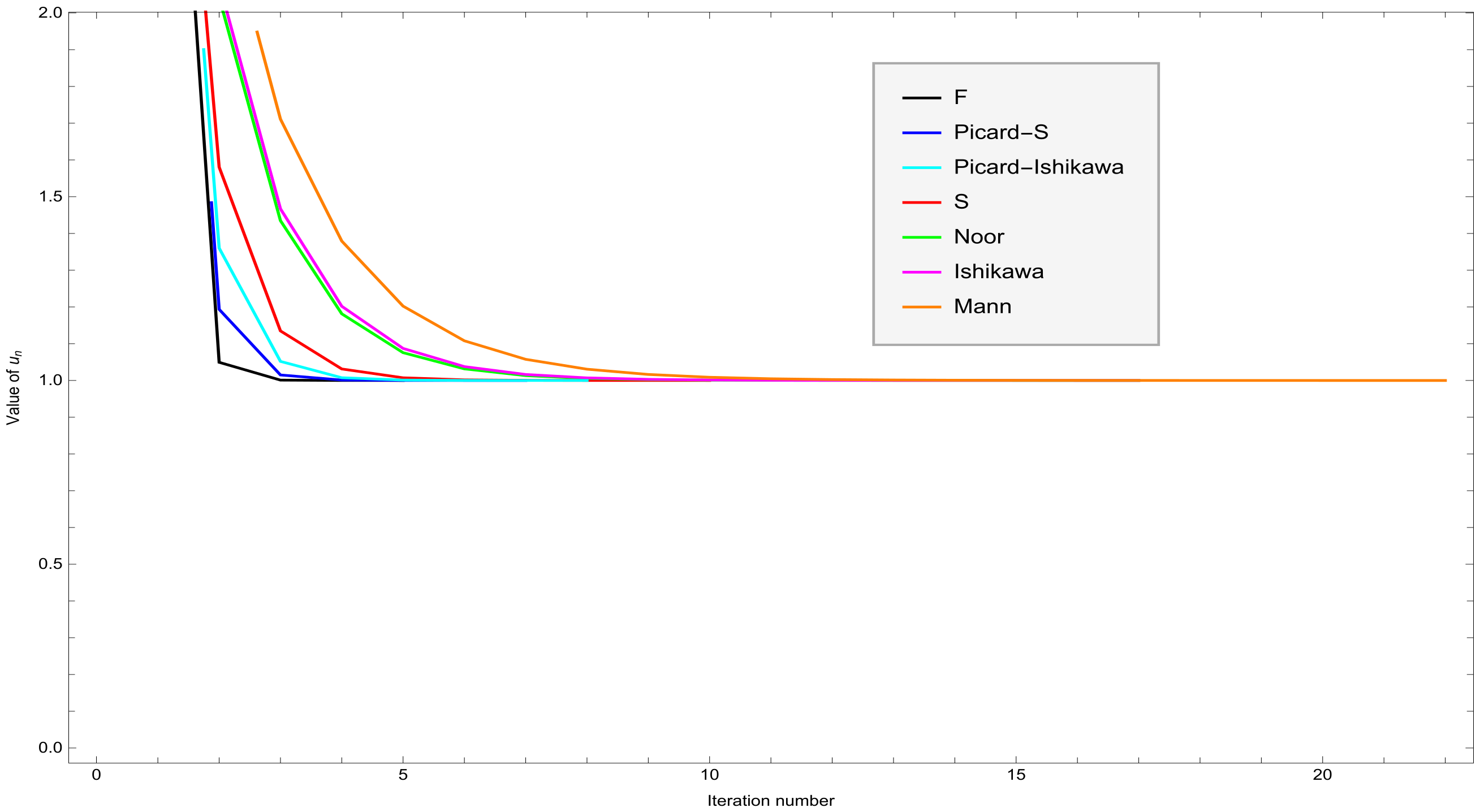
Assume that
and
and
, we compare the high accuracy of the proposed F iterative method with the Picard–S [
13], Picard–Ishikawa [
9], S [
11], Noor [
10], Ishikawa [
8], and Mann [
7] iterative methods using
of Example 1. The iterative values are provided in
Table 2, and the convergence behaviors can be observed in
Figure 1.
Remark 2. Table 2 and Figure 1 suggest that the F iterative method is better than all of the Picard–S, Picard–Ishikawa, S, Noor, Ishikawa, and Mann iterative processes. Every proximally nonexpansive mapping is proximally quasi-nonexpansive; thus, our results are also valid for proximally nonexpansive mappings. The presented results in this section therefore improve and extend many well-known single and multi-valued results from the current literature, especially Shahzad and Zegeye [6], Khan and Yilirim [20], Okeke [26], Gursoy and Karakaya [13], Ali and Ali [22], and many others. 3. An Application to a Class of BVPs
BVPs of various orders played a very significant role, especially in mathematical modelings, physics, and engineering problems. Finding approximate solutions for different classes of BVPs with various orders is also an active and difficult field of mathematics. In the present article, we propose and study a new approach for solving a two-point BVP (second order) by applying the
F iterative method of Ali and Ali [
22]. We now take a real Banach space
X and select any
. Then, the
F iterates suggest a sequence
, which is generated in the following way:
Notice that the sequence
involved in method (
8) essentially holds the restriction
.
Now, the well-known Green’s function is given as follows. For each
, assume that
is a continuous map on the interval
, then functions which satisfy
can be written as follows:
Thus, the unique solution of the following given BVP:
is in the form of (
9), provided that
and
have appropriate values. If the values of both of the
and
are known, then the solution of (
10) can be expressed in the following form:
where the notation
is known as Green’s function of the BVP:
and it is defined in the following way:
In the same way, the solution of BVP:
can be easily stated in the following way:
where
is the solution for the equation
, with
and
. Suppose the function
is continuous on the set
. Then (
11) suggests that whenever
is the solution of
with
and
, then the function
is the solution for the BVP:
if and only if
is the element of
, and it is always the solution of the following given integral equation:
Now assume that
is given by the following equation:
for every choice of
such that
, then each fixed point of the mapping
is the solution of (
13), as well as of (
12).
Recently, Bello et al. [
27] suggested the following two-point BVP:
where both the
,
,
and
are any real numbers satisfying
and
and so on.
Now to solve (
14) and (
15) with process (
8), we must first transform the underlying problem in the following way:
where
and
.
Keep in mind that
solves (
14) as well as (
15) if and only if it essentially solves the following:
and the notation
represents Green’s function associated with the following BVP:
and
is the solution of (
17).
We now assume that
is set as follows:
where the mapping
is such that every solution
of (
14) and (
15) is the fixed point of
[
28].
Next, we take the derivative of our proposed iteration process defined by (
8) in order to solve the suggested BVP. For this purpose, we assume
E to be any nonempty convex subset of real Banach space
X and
to be a multi-valued mapping. Suppose the sequence
is generated by (
8) such that
with
.
Now we are in the position to compare our procedure (
16) with (
8) to establish their equivalence. First, we differentiate (
18) as follows:
Second, twice differentiating (
8), we have the following equation:
Now, the third step is to differentiate (
19), as follows:
Lastly, by substituting (
21) in (
20), one has the following:
Now (
22) can be expressed as follows, which is our proposed fixed point method:
We now provide the main outcome of this section.
Theorem 4. Suppose is a contraction operator (
18)
, with a contraction constant . If f is any affine function, and is a sequence of iterates (8) with and the boundary condition in (
15)
with in such that , then the sequence converges to the solution of (
14)
and (
15)
Proof. The Banach result [
1] suggests the uniqueness and existence of
. We show that the sequence
converges strongly to this
q. Using (
8), one has the following:
Inductively, we obtain the following:
Since
and
for
, therefore
. Now using the well-known inequality
for
together with
and then applying
, we get from (
24),
. It follows that
. Accordingly,
converges to a solution
of (
14) and (
15). □