An Effective Approximation Algorithm for Second-Order Singular Functional Differential Equations
Abstract
1. Introduction
2. The Bessel Matrix Technique
| Algorithm 1: The computation of s-derivative of the vector . |
|
Initial Conditions in the Matrix Form
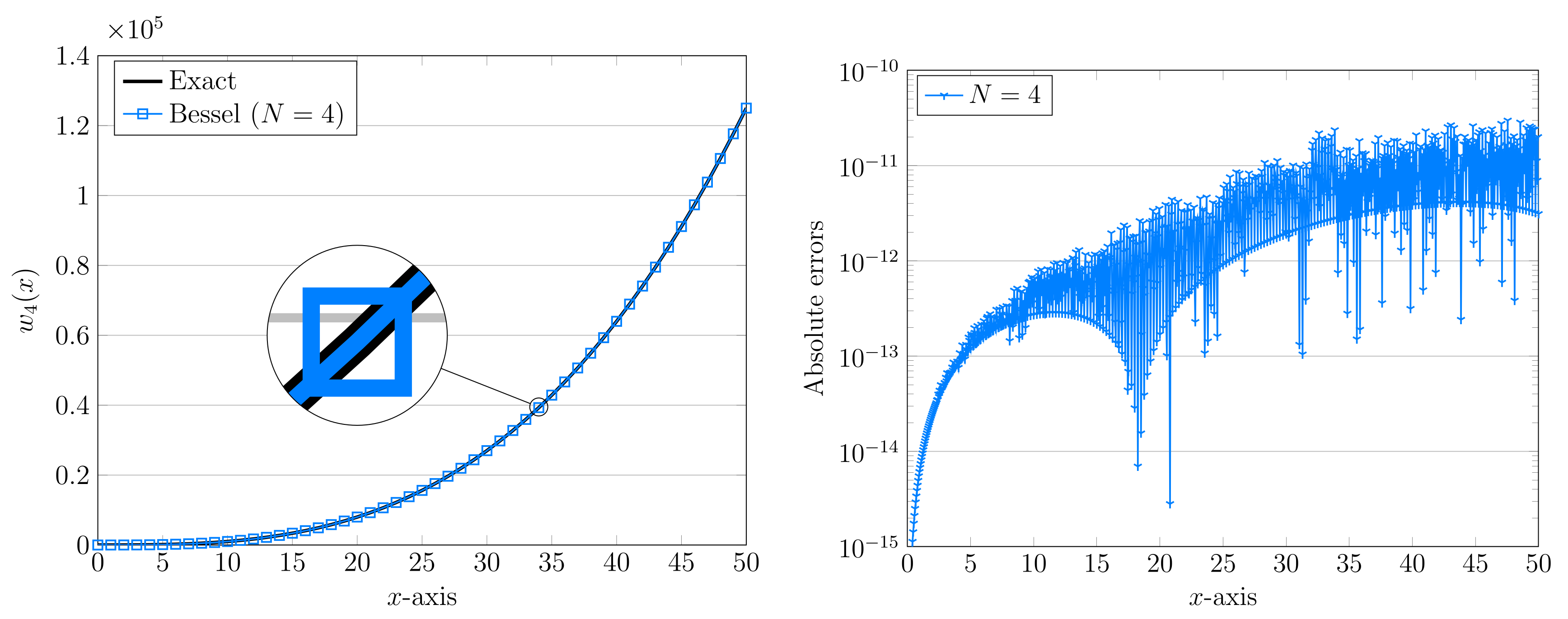
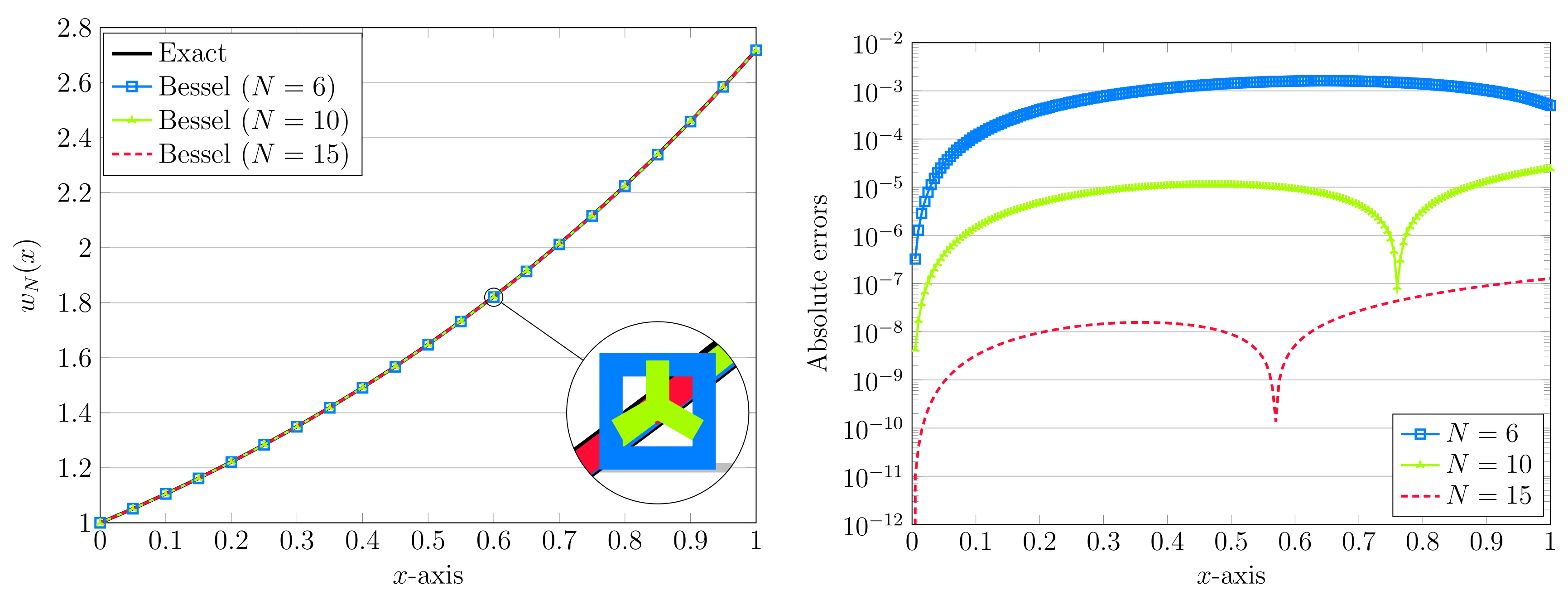
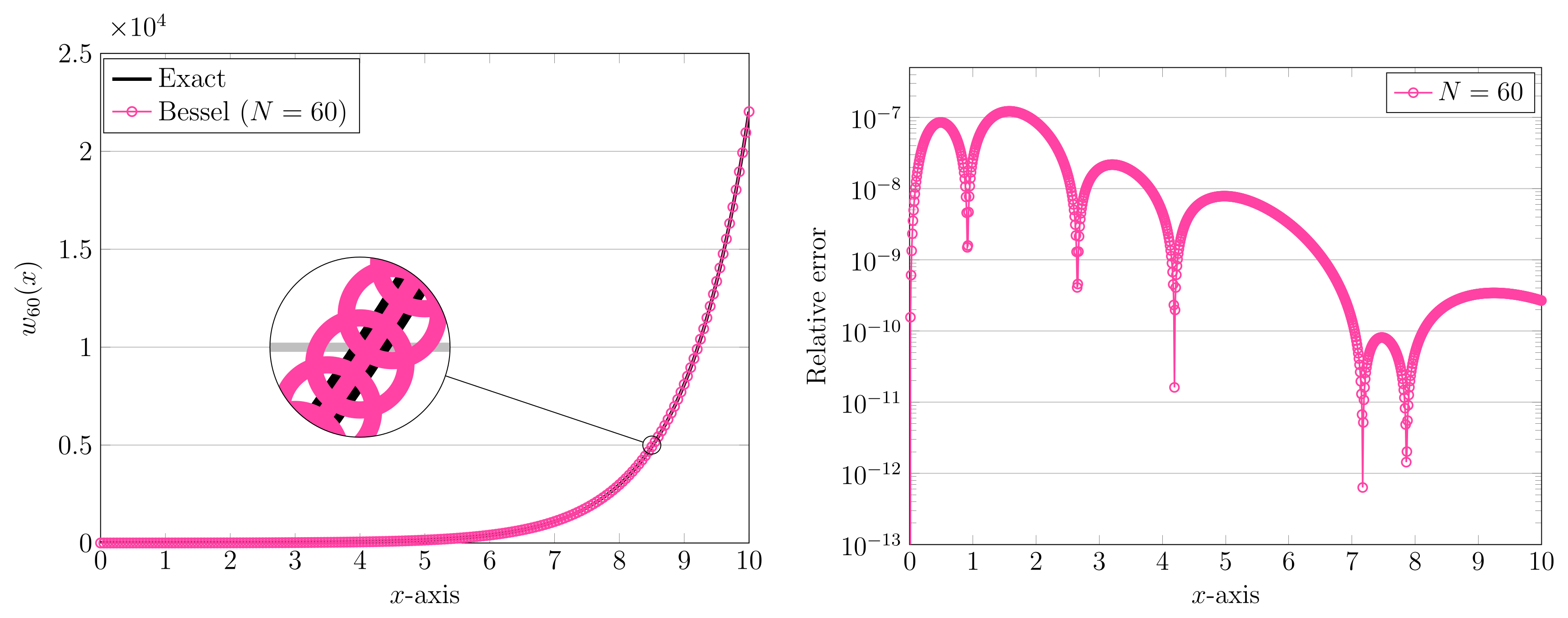
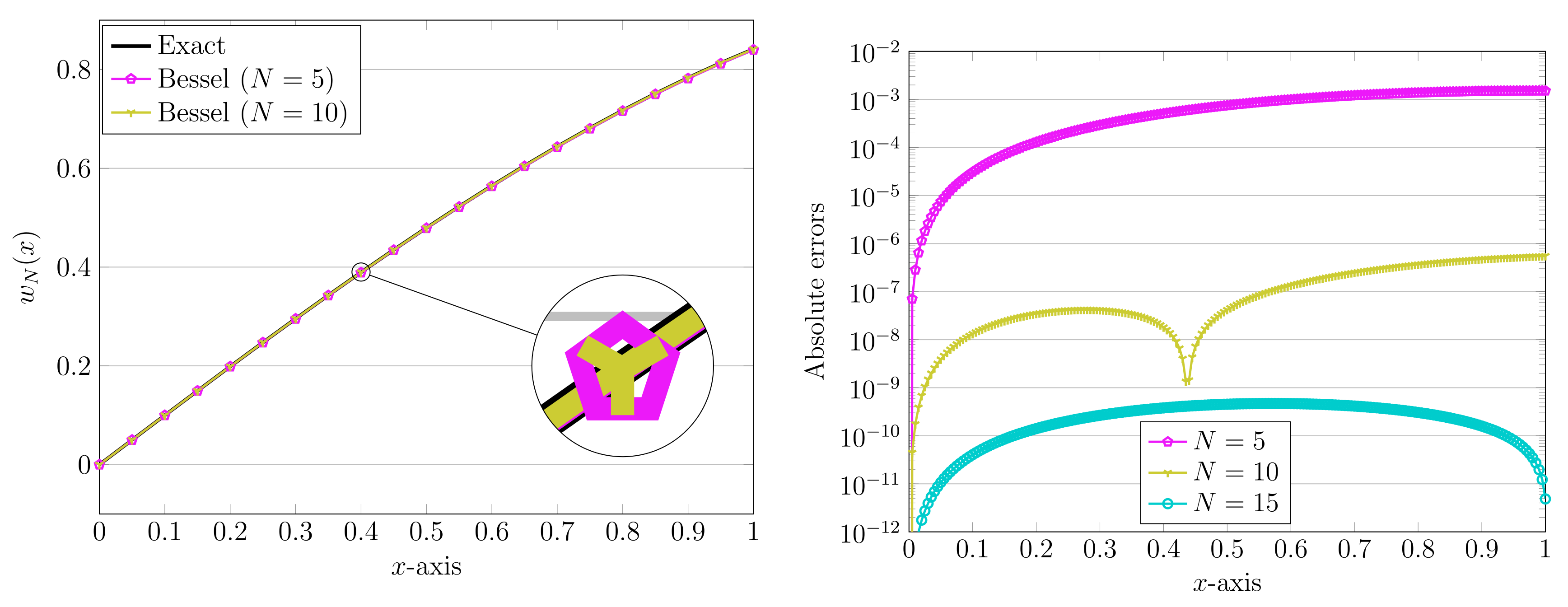
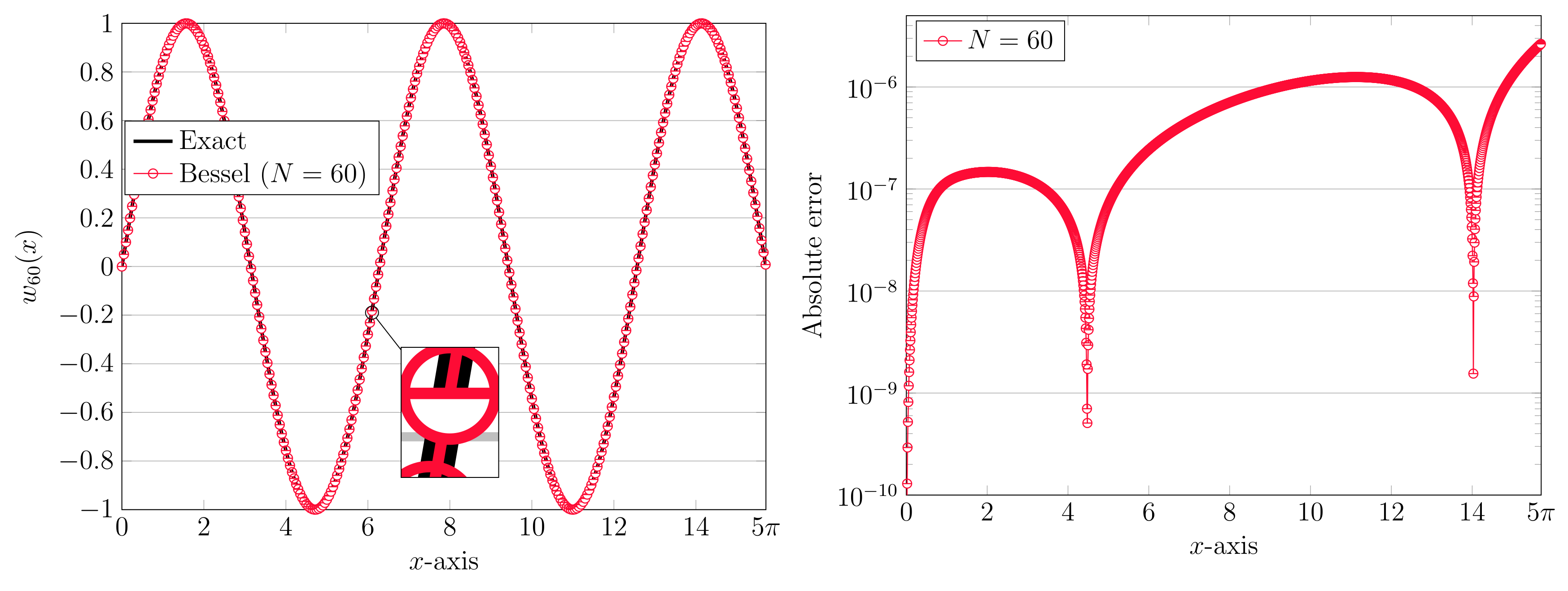
3. Computational Simulations
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dehghan, M.; Shakeri, F. The use of the decomposition procedure of Adomian for solving a delay differential equation arising in electrodynamics. Phys. Scr. 2008, 78, 065004. [Google Scholar] [CrossRef]
- Nelson, P.W.; Perelson, A.S. Mathematical analysis of delay differential equation models of HIV-1 infection. Math. Biosci. 2002, 179, 73–94. [Google Scholar] [CrossRef]
- Liu, X.; Ballinger, G. Boundedness for impulsive delay differential equations and applications to population growth models. Nonlinear Anal. 2003, 53, 1041–1062. [Google Scholar] [CrossRef]
- Villasana, M.; Radunskaya, A. A delay differential equation model for tumor growth. J. Math. Biol. 2003, 47, 270–294. [Google Scholar] [CrossRef] [PubMed]
- Roussel, M.R. The use of delay differential equations in chemical kinetics. J. Phys. Chem. 1996, 100, 8323–8330. [Google Scholar] [CrossRef]
- Bratsun, D.; Volfson, D.; Tsimring, L.S.; Hasty, J. Delay-induced stochastic oscillations in gene regulation. Proc. Natl. Acad. Sci. USA 2005, 102, 14593–14598. [Google Scholar] [CrossRef]
- Huang, G.; Takeuchi, Y.; Ma, W. Lyapunov functional for delay differential equations model of viral infections. SIAM J. Appl. Math. 2010, 70, 2693–2708. [Google Scholar] [CrossRef]
- Chambre, P.L. On the solution of the Poisson-Boltzmann equation with application to the theory of thermal explosions. J. Chem. Phys. 1952, 20, 1795–1797. [Google Scholar] [CrossRef]
- Boubaker, K.; Van Gorder, R.A. Application of the BPES to Lane–Emden equations governing polytropic and isothermal gas spheres. New Astron. 2012, 17, 565–569. [Google Scholar] [CrossRef]
- Wazwaz, A.M. A new method for solving singular initial value problems in the second-order ordinary differential equations. Appl. Math. Comput. 2002, 128, 45–57. [Google Scholar] [CrossRef]
- Mirzaee, F.; Hoseini, S.F. Solving singularly perturbed differential-difference equations arising in science and engineering with Fibonacci polynomials. Results Phys. 2013, 3, 134–141. [Google Scholar] [CrossRef]
- Kadalbajoo, M.K.; Sharma, K.K. Numerical analysis of boundary-value problems for singularly perturbed differential-difference equations with small shifts of mixed type. J. Optim. Theory Appl. 2002, 115, 145–163. [Google Scholar] [CrossRef]
- Xu, H.; Jin, Y. The asymptotic solutions for a class of nonlinear singular perturbed differential systems with time delays. Sci. World J. 2014, 2014, 965376. [Google Scholar] [CrossRef]
- Sabir, Z.; Raja, M.A.; Umar, M.; Shoaib, M. Neuro-swarm intelligent computing to solve the second-order singular functional differential model. Eur. Phys. J. Plus 2020, 135, 474. [Google Scholar] [CrossRef]
- Adel, W.; Sabir, Z. Solving a new design of nonlinear second-order Lane–Emden pantograph delay differential model via Bernoulli collocation method. Eur. Phys. J. Plus 2020, 135, 427. [Google Scholar] [CrossRef]
- Izadi, M.; Srivastava, H.M. An efficient approximation technique applied to a non-linear Lane–Emden pantograph delay differential model. Appl. Math. Comput. 2021, 401, 126123. [Google Scholar] [CrossRef]
- Sabir, Z.; Abdul Wahab, H.; Umar, M.; Erdŏgan, F. Stochastic numerical approach for solving second order nonlinear singular functional differential equation. Appl. Math. Comput. 2019, 363, 124605. [Google Scholar] [CrossRef]
- Singh, H.; Srivastava, H.M.; Kumar, D. A reliable algorithm for the approximate solution of the nonlinear Lane–Emden type equations arising in astrophysics. Numer. Methods Partial Differ. Equ. 2018, 34, 1524–1555. [Google Scholar] [CrossRef]
- Izadi, M. A discontinuous finite element approximation to singular Lane–Emden type equations. Appl. Math. Comput. 2021, 401, 126115. [Google Scholar] [CrossRef]
- Krall, H.L.; Frink, O. A new class of orthogonal polynomials: The Bessel polynomials. Trans. Am. Math. Soc. 1949, 65, 100–115. [Google Scholar] [CrossRef]
- Grosswald, E. Bessel Polynomials, Lecture Notes in Math; Springer: Berlin, Germany, 1978; Volume 698. [Google Scholar]
- Srivastava, H.M. A note on the Bessel polynomials. Riv. Mat. Univ. Parma (Ser. 4) 1983, 9, 207–212. [Google Scholar]
- Srivastava, H.M. Orthogonality relations and generating functions for the generalized Bessel polynomials. Appl. Math. Comput. 1994, 61, 99–134. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Manocha, H.L. A Treatise on Generating Functions; Ellis Horwood Limited: Chichester, UK; John Wiley and Sons: New York, NY, USA; Chichester, UK; Brisbane, Australia; Toronto, ON, Canada, 1984. [Google Scholar]
- Yang, S.; Srivastava, H.M. Some families of generating functions for the Bessel polynomials. J. Math. Anal. Appl. 1997, 211, 314–325. [Google Scholar] [CrossRef][Green Version]
- Lin, S.-D.; Chen, I.-C.; Srivastava, H.M. Certain classes of finite-series relationships and generating functions involving the generalized Bessel polynomials. Appl. Math. Comput. 2003, 137, 261–275. [Google Scholar] [CrossRef]
- Izadi, M.; Cattani, C. Generalized Bessel polynomial for multi-order fractional differential equations. Symmetry 2020, 12, 1260. [Google Scholar] [CrossRef]
- Izadi, M.; Yüzbaşı, Ş.; Cattani, C. Approximating solutions to fractional-order Bagley-Torvik equation via generalized Bessel polynomial on large domains. Ric. Mat. 2021, 1–27. [Google Scholar] [CrossRef]
- Izadi, M.; Yüzbaşı, Ş.; Adel, W. Two novel Bessel matrix techniques to solve the squeezing flow problem between infinite parallel plates. Comput. Math. Math. Phys. 2021, 61, 2034–2053. [Google Scholar] [CrossRef]
- Izadi, M.; Srivastava, H.M. Numerical approximations to the nonlinear fractional-order Logistic population model with fractional-order Bessel and Legendre bases. Chaos Solitons Fractals 2021, 145, 110779. [Google Scholar] [CrossRef]
- Torabi, M.; Hosseini, M.M. A new efficient method for the numerical solution of linear time-dependent partial differential equations. Axioms 2018, 7, 70. [Google Scholar] [CrossRef]
- Izadi, M. Fractional polynomial approximations to the solution of fractional Riccati equation. Punjab Univ. J. Math. 2019, 51, 123–141. [Google Scholar]
- Srivastava, H.M.; Abdel-Gawad, H.I.; Saad, K.M. Stability of traveling waves based upon the Evans function and Legendre polynomials. Appl. Sci. 2020, 10, 846. [Google Scholar] [CrossRef]
- Roul, P.; Prasad Goura, V.M. A Bessel collocation method for solving Bratu’s problem. J. Math. Chem. 2020, 58, 1601–1614. [Google Scholar] [CrossRef]
- Izadi, M.; Srivastava, H.M. A novel matrix technique for multi-order pantograph differential equations of fractional order. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2021, 477, 2021031. [Google Scholar] [CrossRef]
- Khader, M.M.; Saad, K. A numerical approach for solving the fractional Fisher equation using Chebyshev spectral collocation method. Chaos Solitons Fractals 2018, 110, 169–177. [Google Scholar] [CrossRef]
- Izadi, M.; Srivastava, H.M. A discretization approach for the nonlinear fractional logistic equation. Entropy 2020, 22, 1328. [Google Scholar] [CrossRef]
- Abdalla, M.; Hidan, M. Analytical properties of the two-variables Jacobi matrix polynomials with applications. Demonstr. Math. 2020, 54, 178–188. [Google Scholar] [CrossRef]
- Zaeri, S.; Saeedi, H.; Izadi, M. Fractional integration operator for numerical solution of the integro-partial time fractional diffusion heat equation with weakly singular kernel. Asian-Eur. J. Math. 2017, 10, 1750071. [Google Scholar] [CrossRef]
- Deniz, S.; Sezer, M. Rational Chebyshev collocation method for solving nonlinear heat transfer equations. Int. Commun. Heat Mass Transf. 2020, 114, 104595. [Google Scholar] [CrossRef]
| Bessel () | ANNs () [17] | |||||
|---|---|---|---|---|---|---|
| x | Min | Mean | S.D | |||
| Bessel | ANNs () [17] | |||||
|---|---|---|---|---|---|---|
| x | Min | Mean | S.D | |||
| Bessel | ANNs () [17] | |||||
|---|---|---|---|---|---|---|
| x | Min | Mean | S.D | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Izadi, M.; Srivastava, H.M.; Adel, W. An Effective Approximation Algorithm for Second-Order Singular Functional Differential Equations. Axioms 2022, 11, 133. https://doi.org/10.3390/axioms11030133
Izadi M, Srivastava HM, Adel W. An Effective Approximation Algorithm for Second-Order Singular Functional Differential Equations. Axioms. 2022; 11(3):133. https://doi.org/10.3390/axioms11030133
Chicago/Turabian StyleIzadi, Mohammad, Hari M. Srivastava, and Waleed Adel. 2022. "An Effective Approximation Algorithm for Second-Order Singular Functional Differential Equations" Axioms 11, no. 3: 133. https://doi.org/10.3390/axioms11030133
APA StyleIzadi, M., Srivastava, H. M., & Adel, W. (2022). An Effective Approximation Algorithm for Second-Order Singular Functional Differential Equations. Axioms, 11(3), 133. https://doi.org/10.3390/axioms11030133








