Abstract
The exploration of the dependency structure of the Chinese and EU carbon trading markets is crucial to the construction of a globally harmonized carbon market. In this paper, we studied the characteristics of structural interdependency between China’s major carbon markets and the European Union (EU) carbon market before and after the launch of the national carbon emissions trading scheme (ETS) and the occurrence of the new coronavirus (COVID-19) by applying the C-vine copula method, with the carbon trading prices of the EU, Beijing, Shanghai, Guangdong, Shenzhen and Hubei as the research objects. The study shows that there exists a statistically significant dependence between the EU and the major carbon markets in China and their extremal dependences and dependence structures are different at different stages. After the launch of the national carbon ETS, China has become more independent in terms of interdependency with the EU carbon market, and is more relevant between domestic carbon markets. Most importantly, we found that the dependence between the EU and Chinese carbon markets has increased following the outbreak of COVID-19, and tail dependency structures existed before the launch of the national carbon ETS and during the outbreak of the COVID-19. The results of this study provide a basis for the understanding of the linkage characteristics of carbon trading prices between China and the EU at different stages, which in turn can help market regulators and investors to formulate investment decisions and policies.
1. Introduction
It now has become a global consensus to reduce greenhouse gas emissions and actively respond to climate change. As an energy consumption, carbon emissions are closely related to the economic development of countries [1]. Following the rapid growth of the national economies and the acceleration of globalization, the huge demand for energy consumption in the world has led to the emission of large amounts of greenhouse gases and caused abnormal climate and ecological changes [2]. To combat climate change at low cost, carbon trading is gradually becoming an effective market instrument to control greenhouse gas emissions [3,4,5]. With the entry into force of the “Kyoto Protocol”, carbon emission rights have become an international commodity, which undoubtedly has a huge driving effect on the global carbon trading market. The EUA is the first carbon emissions trading market established worldwide, and as the world’s largest carbon trading market by the end of 2017, it is closely related to global carbon emission reduction. As the world’s largest developing country and the world’s second largest emitter of greenhouse gases, China has also actively responded to the call for global greenhouse gas emission reduction. Since the Kyoto Protocol came into force in 2005, China has actively participated in international carbon emissions trading, providing support to the global goal of achieving low-carbon economic development [6]. Subsequently, China established eight carbon emissions trading pilots in 2013, including Beijing, Shanghai, Guangdong and Shenzhen, and commenced the construction of a national carbon emissions trading scheme (ETS) at the end of 2017, to achieve an effective docking between different carbon trading markets. At the same time, the launch of the national ETS means that China’s carbon market is becoming the largest carbon market in the world. Since the launch of the carbon pilots, the carbon trading scheme in China has been continuously improved and the national carbon market is actively converging with the international carbon market. However, the carbon price has experienced large fluctuations in the course of operation and there are still significant risks in the operation of the market. Meanwhile, the sudden outbreak and spread of the novel coronavirus (COVID-19) in 2020 had a severe impact on financial markets across the world, leading to dramatic fluctuations in global financial markets [7,8]. In order to prevent the spread of COVID-19, many countries have adopted lockdown rules, during which the greenhouse gases contributing to global warming have continued to decrease [9]. Therefore, the dependence structure between important international carbon markets may change.
The purpose of this paper is to identify changes in the dependence structure between the EU and China carbon trading markets during the period from April 2014 to July 2021. Our aim is to explore whether the dependency structure and extreme dependency between the China and EU carbon markets will be affected by the launch of a national ETS in China and the global COVID-19 outbreak. Given the consensus on building a global carbon market, it is crucial to study the changes in the interdependency of the EU and the major carbon markets in China. On the one hand, an accurate portrayal of the dependency structure and extreme dependency between the Chinese and EU carbon markets will help market regulators and investors in their risk supervision and investment decisions, thus ensuring the healthy operation of the carbon trading market. On the other hand, the exploration of the dependency of carbon prices in various markets in the EU and China before and after the launch of the national ETS will help us to understand the linkage characteristics of the carbon markets in China with the EU carbon market at different stages and provide a valuable reference for China to actively converge with the international carbon market. In addition, the Chinese financial market is the centre of the financial contagion of COVID-19 [10], and it would be helpful to explore the interdependency of the EU and Chinese carbon markets before and after the outbreak of COVID-19 to understand the impact of the shock of COVID-19 on the linkages between the various carbon markets.
With the expansion of the international carbon market and the frequent trading in recent years, there has been a growing interest in carbon trading, and many developments have been achieved in related researches. Many scholars have conducted extensive and in-depth researches on the correlation between carbon trading markets and related asset markets, as well as on correlation-based risk measurements. As carbon markets continue to develop and become more closely related to other financial markets [11,12,13], more and more attention has been paid and focused on studying the linkages between carbon trading markets and energy and financial markets. For example, Hanif et al. [14] explored the non-linear dependency between EU carbon emission allocation (EUA) prices and clean/renewable energy indices with the help of a copula model. Chang et al. [15] studied the dynamic correlation between emission allocations and fossil energy markets in China by using a DCC GARCH model. Meanwhile, there are also studies on the non-linear correlation and spillover effects between carbon trading markets and oil markets [16], electricity markets [17], and stock markets [18]. Oestreich and Tsiakas [19] studied the impact of EUA on stock returns, and conducted a comprehensive empirical evaluation on whether the enterprises that obtained carbon emission quotas were significantly better than those that did not. In addition, many scholars have studied the dependency between carbon markets and the associated asset markets, but mostly focused on the EU market. For example, Hu et al. [20] explored the dependency characteristics of the EU carbon market using the R-vine copula model. Zeng et al. [2] investigated the dependency of the EUA and certified emissions reduction (CER) markets by applying a modified BEKK-GARCH model. Arouri et al. [21] examined the dynamic relationship between EUA cash and futures prices by using a vector auto regression (VAR) model and a switching transition regression–exponential GARCH model (STR-EGARCH). Other scholars have also studied the interdependency among Chinese carbon pilot markets and risk measures based on interdependency. For example, Zhao et al. [22] studied non-linear Granger causality and time-varying effects in the carbon markets in China and found that there were significant non-linear interactions between the carbon markets in Guangdong, Hubei and Shenzhen. Zhu et al. [23] explored the associated risk spillover effects among the pilot carbon markets in China with the help of the R-Vine Copula-CoES method. Mai et al. [24] examined the impact of COVID-19 on risk correlations between national and regional carbon markets using a diagonal BEKK model, and found that the magnitude of volatility spill-over effects during COVID-19 was very large. However, there have been few studies that focus on the interdependency between the EU and carbon markets in China. Fang and Cao [25] modelled the extreme risks of carbon emission allocations (CEA) and EUA in China by using the value at risk (VaR) and expected returns and losses (ES) methods and found that the relationship between EUA and CEA varied across time and between VaR and ES. Sun et al. [6] conducted a comparative study of EU and Chinese carbon emissions permit trading market fluctuations by applying the extended MFDFA method and found that the Chinese carbon market is less efficient than the EU carbon market.
Regarding research methods, vector autoregressive (VAR) models, generalized autoregressive conditional heteroskedasticity (GARCH) models and other related methods have been widely used in the studies of interdependencies among financial markets [21,26]. However, these methods suffer from limitations regarding the handling of non-normal data and the portrayal of non-linear correlations [27]. As research continues, the copula model has been proposed and has become an important method for the study of non-linear interdependencies in financial markets. Copula describes the correlation between variables and is used to connect joint distribution functions to their respective marginal distribution functions [28,29]. Embrechts et al. [30] first proposed the use of copula as a tool to measure non-linear correlations between financial time series. However, in the high-dimensional case, the standard binary and multivariate copula functions do not allow for different dependency structures between different variables, which makes it difficult to capture the complex dependencies between variables accurately [31]. To study the dependency between high-dimensional financial markets, Bedford and Cooke [32,33] proposed a vine copula-based method that can provide a flexible and dynamic description of the non-linear dependency structure between multivariate variables. The more commonly used vine copula decomposition methods are C-vine copula and D-vine copula. The former is more suitable for modelling economic series where there are key variables or variables in a certain order of precedences [34], while the latter does not require key variables [31].
While the above studies have analyzed the relationship between different carbon markets from a range of different perspectives, there is very limited knowledge on the interdependency of the EU and Chinese carbon markets at different times. In addition, the vine copula model has been widely used to study the interdependencies between multiple financial assets [35,36,37]. However, the existing literature has mostly relied on binary or multivariate copula to study the interdependency structure between carbon markets, while vine copula is rarely used, let alone the application research on the interdependence of different carbon trading markets. Therefore, this study aims to investigate changes in the interdependency between the EU and carbon markets in China during the period from April 2014 to July 2021 by using the C-vine copula and tail-dependence measures. We first examine whether the dependency structure of each pilot carbon market in China and the EU carbon market changed before and after the launch of the national ETS and the outbreak of COVID-19 by using the C-vine copula model, and this method enables us to identify a key market and investigate the interdependencies between this key market and each of the other markets. Then, we measured the extreme dependency between the carbon markets in China and the EU through a tail dependency measure to obtain an understanding of the co-movement between the markets under extreme risk at different stages.
The main contributions of this paper are threefold. Firstly, compared with previous studies with a similar research focus, such as Fang and Cao [25] and Sun et al. [6], this study further measured the interdependency between the five carbon trading markets in China and the EU carbon trading market on the basis of fluctuations analysis, which filled the academic gap in the dependence of carbon markets. Secondly, although Hu et al. [20] and Zhao et al. [22] have discussed the relationship between carbon trading markets, there is a lack of discussion on the heterogeneity of different important stages. Considering the possible heterogeneity of the dependence structure at different stages, this paper further compares and analyzes the changes in the dependence of the carbon trading market between China and the EU before and after the launch of national ETS and the outbreak of COVID-19. We find that the launch of a national ETS in China and the global COVID-19 outbreak have significantly changed the interdependent structure and extreme dependency of the carbon trading markets in China and the EU. After the launch of national ETS, the correlation between the carbon trading markets of China and the European Union weakens in general, and the carbon return pairs with tail dependence change from two to three. However, the outbreak of COVID-19 increased the linkage between China and the EU carbon trading market, and triggered the tail dependence between the EU and Shenzhen carbon markets. Finally, in terms of research methods, we applied the C-vine copula method to the study of the dependence of the carbon trading market, and further investigated the carbon return relationship between China’s carbon markets with the EU carbon market as the condition. The study found that, compared with the EU carbon trading market, the linkage between domestic carbon trading markets may be stronger after the launch of national ETS.
2. Methods
In this paper, we used the C-vine copula model to estimate the dependency structure of the carbon trading markets between China and the EU. The modelling process of the C-vine copula involves a number of steps, and the inference function on margins (IFM) is the dominant method for the estimation of copula models, and the estimates under this method usually provide good efficiency [38]. Therefore, we used IFM to estimate the copula model. The IFM method involves two steps: firstly, determine the marginal distribution of the random variables with the marginal model; secondly, bring the established marginal distribution into a suitable binary copula to estimate the corresponding parameters. Based on the characteristics of the model applied, we added the relevant technical treatment to the two steps above. This section presents the basic theory of the C-vine copula correlation model.
2.1. GARCH Model
Financial time series generally have the characteristics of autocorrelation and conditional heteroskedasticity, which can be fully described by the GARCH model [39]. The autoregressive moving average (ARMA) model can eliminate series correlation, but this model assumes that the variance of interference term is constant, which does not conform to the fluctuation aggregation characteristics of time series [40]. It needs to further apply generalized autoregressive conditional heteroskedasticity (GARCH) model to describe the conditional heteroskedasticity problem [39]. Therefore, GARCH family models are considered to be the best models to describe the fluctuation of financial time series.
In this paper, the ARMA(p, q)-GARCH(1, 1) model is used to characterize the marginal distribution of each carbon price return series, and the student t-distribution is used to fit the residual of the model. Finally, an independent isodistributed residual series without sequence autocorrelation and conditional heteroskedasticity is obtained. Let the carbon return sequence be given by . Combined with copula theory, the form of ARMA(p, q)-GARCH(1, 1)-copula model can be expressed as:
where is the EU carbon price return series, are carbon price return series of Shenzhen, Shanghai, Beijing, Guangdong and Hubei, respectively; , and , , , , , are the parameters to be estimated. Equation (1) is a mean equation, is the series of returns of the carbon trading price, is the residual, and are the orders of the AR and MA, respectively. is the standardized residual, is the conditional variances of the fluctuations. Equation (3) is the variance equation, where the parameters and are the coefficients of ARCH and GARCH. is any copula function; is the information set from the initial time to the time ; is the normalized student t-distribution function with the parameter as the degree of freedom. We use the variable to obtain the conditional marginal distribution [41], defined as follows:
In addition, a new series with a (0, 1) uniform distribution was obtained by probabilistic integration transformation before performing copula modelling to derive a marginally distributed series that satisfies copula modelling. Then, a suitable binary copula function was used to connect the new series to estimate the correlation between the carbon price returns of China and the EU.
2.2. Copula Model
2.2.1. Basic Copula Theory
The copula describes the dependency between variables and is used to connect the joint distribution functions with their corresponding marginal distribution functions. To build a multivariate model, we first use ARMA-GARCH model to model the edge, and then use copula to model their dependence structure. According to Sklar’s theorem [42], we assume that are n-dimensional random vectors of with marginal distribution whose joint distribution function is , then a copula function can be obtained as follows.
Assuming that the marginal distribution function is uniformly continuous, the density function of the n-dimensional distribution function can be expressed as follows.
where is the density function of the copula and is the marginal density function of the marginal distribution .
2.2.2. Copula Families
After the series of marginal distributions of the variables were obtained, the next step was to insert the marginal distributions into the copula model. The main copula models covered in this paper include the following seven forms: t [43], Normal [44], Frank [45], Joe [46], Gumbel [47], Clayton [48] and BB7 [49]. Of these, t, Normal and Frank copula have symmetry and the latter two have no tail dependency. Joe, Gumbel, Clayton and BB7 copula have an asymmetric tail dependence, with the former two having upper tail dependency and the Clayton copula having lower tail dependency. BB7 copula reflects different tail dependencies between upper and lower tails. For a more detailed description of copula functions, see Sriboonchitta et al. [50], and we will present several copula forms below.
t copula [51] has the following forms:
where is the student t-distribution, is the degree of freedom and is the Pearson correlation coefficient.
The form of Normal copula is defined as:
where and are cumulative distribution functions of standardized residuals, subjected to a uniform distribution between 0 and 1; is the Pearson linear correlation coefficient, ; is the inverse cumulative distribution function of a standard normal distribution. The Normal copula has no tail dependence, i.e., .
The form of Frank copula can be expressed as follows.
where . Frank copula has a tailed distribution symmetry; when , it has positive correlation; when , it has independency; and when , it has negative correlation. The Kendall rank formula derived by Frank copula is as follows.
The form of Joe copula [46] can be expressed as follows
where . It can be used to capture upper tail dependency, with .
The form of Clayton copula can be expressed as follows:
where the Kendall rank of the Clayton copula is ; it can be used to capture the lower tail dependency, with .
The form of Gumbel copula can be expressed as follows:
where . The Kendall rank of Gumbel copula is , with the upper tail dependency being , and the lower tail dependency being .
The form of BB7 copula can be expressed as follows:
where and ; The upper tail dependence coefficient is and the low tail dependence coefficient is .
In addition, different forms of copula will result in different correlation structures, and in copula modelling we need to select the optimal copula model for each pair of carbon price return series. The method used in this study was the Akaike Information Criterion (AIC) [52]. Brechmann et al. [53] found that the AIC was relatively robust in terms of copula selection.
2.2.3. Canonical Vine (C-Vine) Copulas
Bedford and Cooke [32,33] proposed the Vine copula method, which sets up a n-dimensional copula through a pair-copula decomposition to construct a dependency structure between n-dimensional variable distributions, hence the name pair-copula construction (PCC). Compared with the multivariate copula functions, vine copula allows different dependency structures between different variables and can flexibly depict the nonlinear dependency structures between multivariate variables, so it is widely used to study the interdependence between multiple financial assets [31,35]. Common vine copula models include C-vine copula and D-vine copula. Figure 1 illustrates the four-dimensional structural decomposition of the C-vine copula. As can be seen from Figure 1, the C-vine tree is formed by nodes and edges, and a root node in each tree is connected to other nodes in the tree, indicating that the variables of the root node are more dominant than other variables [54]. Therefore, the C-vine copula is more suitable for modelling economic series where there are key variables or variables in a certain order of precedence [55]. In reality, EUA, as the world’s largest carbon trading market by the end of 2017, plays an important role in the international carbon market. However, China’s carbon trading market started late and has relatively little influence in the international carbon market. Therefore, we hope to explore the role and power of the EU in China’s carbon market, so that we can use the C-vine copula to study the dependency between the EU and the five carbon markets in China. In addition, we can further study the carbon return linkages between the Chinese carbon market conditioned on the EU carbon return. In general, the C-vine copula model is more suitable for our research.
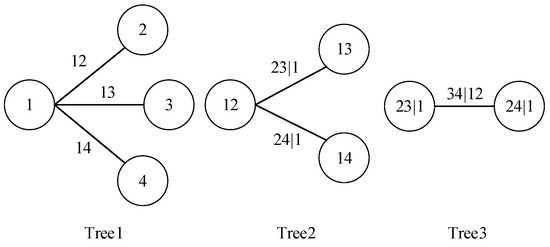
Figure 1.
Example of three-dimensional canonical vine (C-vine) trees.
For a copula density function with an n-dimensional random variable, it can be factored into the product of pair copula density functions. In particular, a n-dimensional vine structure can be represented by trees, i.e., tree , tree has nodes and edges, each of which corresponds to a pair copula function. Figure 1 illustrates the four-dimensional structural decomposition of the C-vine copula, so based on Equation (7), the C-vine copula density function of Figure 1 can be factored out as follows.
where the copula functions are all in binary forms, is the joint copula density function for Market 1 and Market 2, and is the copula density function for Market 2 and Market 3 under the conditions of Market 1. Two of the parameters are expressed as follows.
Similarly, the corresponding joint density functional factorization form for a n-dimensional C-vine copula model can be expressed as follows.
where refers to the density function of the unconditional or conditional copula function and is the marginal conditional distribution function.
The log likelihood function of Equation (17) is then expressed as follows.
where denotes a parameter vector estimated from the marginal models, and is a parameter vector estimated from three bivariate copulas [56]. We estimated the parameters of the marginal model and copula model by IFM. First, the parameters in the edge model are estimated. Secondly, the normalized residuals after probabilistic integration transformation are used as the copula pseudo sample observations to estimate the parameters of the unconditional binary copula in the first tree of the vine copula. In addition, for other trees, we obtain new pseudo-sample observation values through Equation (18), so as to estimate the parameters of conditional binary copula in other trees. The choice of binary copula model is determined by AIC criterion.
It is notable that during the construction of the C-vine copula model, there is a problem with the sequential selection of variables, i.e., the determination of the root node of each tree. Therefore, we need to determine the order of the variables prior to the construction of the copula model. In this paper, we selected the EU carbon price return series as the root node of the first C-vine tree to investigate the dependency between the carbon trading prices in the EU and China, thereby exploring the role and impact of the EU carbon price in the carbon market in China. Then, for the sequence of the other five variables, we ranked the selection based on the sum of the absolute values of the maximized serial rank correlation coefficients for each pair.
2.2.4. Non-Linear Correlation and Tail Correlation Metrics
In this paper, we measured the non-linear correlation between the carbon price return series using the Kendall rank correlation coefficient, which is a common measure of the overall correlation between variables and can be defined as the probability of consistency minus the probability of inconsistency [57]. Let and be independent and identically distributed random vectors and the Kendall rank can be defined as follows.
By Equation (21) it follows that
The Kendall rank correlation coefficient can also be expressed by the copula [54]:
where is a copula function, and are edge distribution functions, with , .
Tail correlation is a term used to describe the correlation in the tails of a binary joint distribution, that is, the probability that when one variable is extreme, the other variable will also be extreme. The upper tail correlation coefficient and the lower tail correlation coefficient are as follows.
where . If (or ) exists and or , then the random variable is correlated with the upper tail (or lower tail) of . If (or ), then can be considered asymptotically independent from .
3. Empirical Models and Data
This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation, as well as the experimental conclusions that can be drawn.
3.1. Data Description
In this paper, we investigated the dependency structure of the EU and carbon trading markets in China by selecting the daily returns rates of the EUA futures price and the daily closing prices of the five domestic carbon trading pilot markets in Beijing (BJ), Shanghai (SH), Guangdong (GD), Shenzhen (SZ) and Hubei (HB) as the study sample, with the sample time period ranging from 2 April 2014 to 16 July 2021. As different markets have different trading start times, for comparability of the study, we selected the Hubei carbon trading market, which has the latest trading start time among the five major markets, as the starting point, and removed the data where the trading days do not overlap. Data were sourced from the Wind database. The data scope includes the launch of the national ETS in China on 19 December 2017, the global COVID-19 outbreak in January 2020 and the completion of the harmonisation of the national carbon emission market in China on 16 July 2021.
Figure 2 shows the movement of trading prices in the various carbon markets since 2014. It can be seen that the EU carbon trading price reached its lowest point at the end of 2017 and began to show a fluctuate increase, while the carbon prices in the various markets in China also showed varying degrees of movement after reaching their extreme points around the beginning of 2018. After the global shock of COVID-19, the similarity in price trends across carbon markets became more apparent. In early 2020, carbon prices in China and the EU experienced a brief decline before returning to an upward or more stable trend. However, another outbreak of COVID-19 in late 2020 led to another drop in carbon prices. The sudden outbreak of COVID-19 increased the uncertainty of carbon price movements. We obtained the return series of carbon trading prices by applying the natural logarithm to the carbon trading price data of each carbon market. The calculation formula is as follows.
where represents the return at time and represents the price of carbon trading at time .
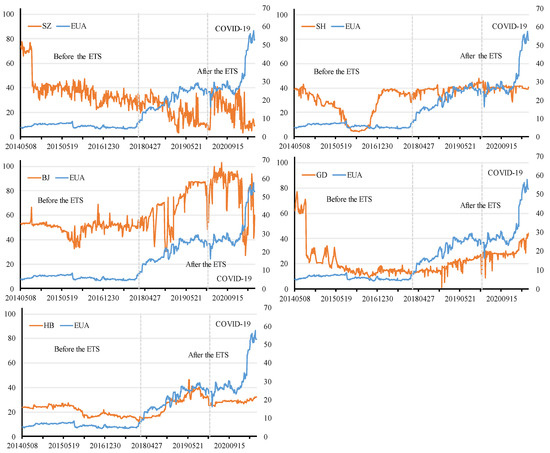
Figure 2.
Daily closing price of carbon trading market, April 2014 to June 2021. Notes: The dividing point of the first vertical line is 16 December 2017, the official launch date of the national ETS in China; The dividing point of the second vertical line is 1 January 2020, the date of the global COVID-19 outbreak; The same below.
The movement of the carbon price return series for each carbon market is shown in Figure 3. As can be seen from Figure 3, the fluctuations of the log return series increases when the market is under stress, that is, in the periods of 2018 to 2019 and 2020 to 2021. We also find that there are varying degrees of co-movement across carbon markets in extreme regions. Hence, in this paper, we divided the entire sample into two time periods, namely using 19 December 2017 as the node to capture the differences before and after the launch of the National ETS. Then, we explored the correlation between China and EU carbon price return series before and after the global COVID-19 outbreak, with 2018 as the starting point and January 2020 as the node.
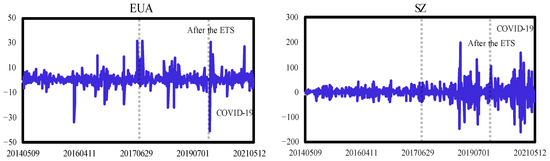
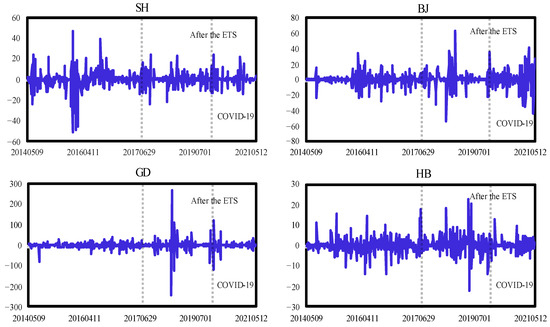
Figure 3.
Carbon return rate of carbon trading market, April 2014 to June 2021.
3.2. Statistical Characteristics of the Carbon Price Return Series
Table 1 and Table 2 list the basic statistical characteristics of the carbon price return series for the five carbon trading markets in the EU and China. Based on the mean and standard deviation of returns in the Chinese and EU carbon markets, the EU carbon market features higher returns and a smaller standard deviation, indicating a higher profitability and lower market risk. According to the results of the Jarque–Bera test, all return series fail to follow a normal distribution in the national ETS as well as in the four time periods before and after the outbreak of the COVID-19, indicating the presence of significant spikes and thick tails in the return series. The results of the unit root test suggest that all return series are smooth at the significance level of 1%. The series were tested for autocorrelation and the LB-Q statistic indicates that the majority of the market carbon price return series are autocorrelated. The results of the heteroskedasticity test statistic, ARCH-LM, indicate that the majority of the return time series are characterized by heteroskedasticity at the level of 1% and that there is an ARCH effect. Therefore, to describe these characteristics, we will fit the data in this paper by using an ARMA-GARCH model and assuming that the residuals obey the distribution of the student-t.

Table 1.
Basic statistics (before and after the ETS).

Table 2.
Basic statistics (before and after COVID-19).
3.3. Estimation Results of the Marginal Distribution
To construct the copula analysis framework, we first fitted the data using an ARMA-GARCH model and assumed that the residuals obeyed the distribution of the student-t. Table 3 and Table 4 report the parameter estimation results for the ARMA(1, 1)-GARCH(1, 1) model. The results indicate that most of the parameters in the GARCH model are statistically significant.

Table 3.
Estimation results for the marginal models of carbon trading price (before and after the ETS).

Table 4.
Estimation results for the marginal models of carbon trading price (before and after COVID-19).
In the GARCH model, is the effect of the external environment on the carbon price returns of the market and represents the effect of carbon price return fluctuations on its own market [58]. For both before and after the launch of the national ETS, the GARCH coefficient is significant at the significance level of 1%, suggesting that the fluctuations of carbon returns in the current period in each carbon market is positively influenced by the fluctuations of the previous period. With the estimation of the ARMA(1, 1)-GARCH(1, 1)-t model, is greater than in most cases before the launch of the national ETS, or the difference is smaller, suggesting that more internal factors of the carbon market have a greater impact on the fluctuations of carbon returns than the external environment. After the launch of the national ETS, is much larger than in Shanghai and Guangdong, where carbon return fluctuations in this market are more influenced by the external environment, which is more evident after the onset of COVID-19. It can be observed that is much larger than in the EU at any stage, reaching a maximum of 0.999, which suggests that 99.9% of the fluctuations in the current period carry over to the next period, respectively, and that fluctuations have a long-term memory. When there are large fluctuations in the various carbon markets, it is possible to analyse whether the fluctuations are due to own factors or the influence of the external environment.
3.4. Estimation Results of C-Vine-Copula
After modelling the edge distribution, we extracted the standardized residuals and obtained a residual sequence with (0, 1) uniform distribution by probabilistic integration transformation to obtain an edge distribution sequence satisfying copula modelling. Then, we determined the choice of variable order to fit the vine structure. In this paper, we took the EU carbon price return series as the root node of the first C-vine tree, and the other variables were selected in order based on maximizing the sum of the absolute values of the rank correlation coefficients for each pair of series.
Figure 4 shows the fitted vine structures before the the launch of national ETS (row 1 left), after the launch of national ETS (row 1 right), before the outbreak of COVID-19 (row 2 left) and after the outbreak of COVID-19 (row 2 right), with the four matrices containing the entire vine structure for the six indices for the four time periods. Where 1, 2, 3, 4, 5 and 6 correspond to the EU, Shenzhen, Shanghai, Beijing, Guangdong and Hubei carbon markets, respectively. Tree 1 is an unconditional binary copula function, while Tree 2, 3, 4 and 5 are all conditional binary copulas. Without considering the EU order, according to the ranking order of market correlations, Guangdong is the most correlated with other carbon markets before the launch of the national ETS, followed by Beijing, Shenzhen, Shanghai and Hubei in descending order. After the launch of the national ETS, the correlation between Beijing and other carbon markets leaps to the first highest, followed by Hubei, Shanghai, Guangdong and Shenzhen in descending order. It can be observed that the correlation between the Shanghai and Hubei carbon markets and other carbon markets has increased significantly after the launch of the national ETS. This may be due to the fact that the launch of the national carbon market further established a registration system and a trading system for the national carbon market led by Hubei and Shanghai, respectively, which to some extent facilitated the inter-connectivity between that market and other carbon markets. In addition, the interdependency structure between the carbon markets changed significantly around the occurrence of COVID-19. Therefore, it is reasonable to analyse the interdependencies between carbon markets by dividing them into national ETS and before and after the outbreak of the COVID-19.

Figure 4.
Fitted vine structure matrix for four periods.
The estimation results of the static C-vine copula are shown in Table 5 and Table 6. The results have presented the optimal copula form chosen for each pair of markets in each tree according to the AIC, the estimation of the parameters (parameter 1, parameter 2), the standard error, Kendall’s rank correlation coefficient T and the tail correlation coefficient tail dependence. The degree of dependence between carbon markets can be understood more clearly based on the Kendall rank correlation coefficient. Based on the C-vine copula property, a conditional copula function was used to inscribe the dependency structure between each of the two carbon markets in the Tree 2, 3, 4 and 5 respectively.

Table 5.
Static vine estimation results (before and after the ETS).

Table 6.
Static vine estimation results (before and after COVID-19).
3.4.1. Analysis of the Dependency between the Carbon Markets before and after the Launch of National ETS
Tree 1 shows the dependency structure of the carbon price return series for the EU carbon market and the five carbon markets in China before and after the launch of national ETS. Table 5 suggests that the parameter estimates in Tree 1 are basically significant, which means that there is a dependency relationship between the EU and China’s major carbon markets. Before the launch of the national ETS, the Kendall rank correlation coefficients for the EU and Shenzhen and Guangdong in Tree 1 are negative, while the Kendall rank coefficients for the EU and Hubei, Beijing and Shanghai are positive. This suggests that the EU carbon price return was negatively correlated with the Shenzhen and Guangdong carbon price returns and positively correlated with changes in the Hubei, Beijing and Shanghai carbon price returns during this period, and provides evidence of co-movement between the carbon price in China and the EU carbon price. When the Chinese carbon market was first established, the main source of participation in the international carbon market was through the CMD project, and the EU was the main demand side of this project, which led to the Chinese carbon market being influenced to a certain extent by the EU carbon market. Compared to other carbon markets, the Hubei carbon market was established in the middle of 2014. Due to the relatively short period of establishment and the fact that it was still in the exploratory stage, it was difficult for the Hubei carbon market to establish strong linkages with the EU carbon market in a relatively short period of time.
Following the launch of the national ETS, the Kendall rank correlation coefficient in Tree 1 is almost negative, with the exception of the EU and Guangdong. This suggests an overall negative correlation between the changes in carbon price returns in the carbon trading markets in China and the EU during this period. The launch of national ETS has significantly changed the dependency structure between carbon markets. From the perspective of the interdependence between the EU and China’s five carbon markets, the volatility of the gap between them has slowed down. Among them, the EU and the Shanghai carbon market are most closely related. It is notable that the overall Kendall rank correlation coefficient in Tree 1 is slightly lower after the launch of the national ETS than before the launch of the national ETS. This suggests that the overall dependency between the EU and the carbon markets in China decreases after the launch of the national ETS. It is reasonable to expect this result. At the beginning of the establishment of the various carbon pilots, the carbon trading market in China was in its infancy and the maturity of the market was not high, leading to the carbon trading markets in China being more susceptible to the influence of the important global carbon market, the EU carbon market, to a certain extent. With the launch of the national carbon emissions trading scheme, however, China’s carbon trading market has gradually developed and matured into the world’s largest carbon emission trading market, becoming more independent in its interdependency with the international carbon market. In 2017, China and the EU further launched a brand new cooperation project on carbon emission trading based on the project in 2014, which facilitated the empirical cooperation between the two sides. In January 2018, the cross-border settlement of carbon emission trading in RMB was officially launched, and this initiative has promoted the internationalization of the carbon emissions market in China.
Considering the copula forms, the optimal copula functions fitted by Tree 1 include three forms, namely, t, Frank and Normal. Of these, the Frank, Normal and t-connected functions are all symmetric, but the Frank and Normal-connected functions have no tail dependency. This suggests that in Tree 1, there is symmetric tail dependency between all carbon markets, i.e., the probability of simultaneous extreme returns and simultaneous extreme losses is equal between the returns of the two carbon markets, i.e., the level of risk under extreme scenarios (returns/losses) is comparable between the two carbon markets. From the perspective of tail correlations, the EU and Hubei and the EU and Shanghai are more connected in extreme scenarios, but the tail correlation coefficient decreases after the launch of the national ETS, with less connectedness when extreme scenarios occur. As the construction of the two systems advances, the ability of the Shanghai and Hubei carbon markets to withstand external extreme risks is significantly strengthened. The EU and Shenzhen carbon markets, on the other hand, experience tail dependency after the launch of the national ETS and need to pay close attention to preventive controls in the event of extreme risks. Furthermore, for the EU–Guangdong and EU–Beijing carbon benefit pairs, there is no tail dependency before the launch of the national ETS, and no findings are favoured after the launch of the national ETS, as the copula parameter is not significant. In summary, although the tail dependence of EU and Hubei, EU and Shanghai has weakened, the carbon revenue pairs with extreme dependence have changed from two pairs to three pairs after the national ETS was launched. Therefore, the extreme risk between the China and EU carbon markets is still of concern.
In Tree 2, the correlation structure changes with the inclusion of a conditional market, making the correlation level between the two time periods carbon markets incomparable. However, it can be observed that the Kendall rank correlation coefficient for Tree 2 is generally larger than that of Tree 1, suggesting that the movement of carbon price returns in Beijing is more linked to the domestic context than in the EU, and plays an important role in the stability of the domestic carbon market. With the inclusion of a conditional market, asymmetric lower-tail dependence emerges between carbon markets, suggesting that these pairs of carbon returns with lower-tail dependency are more likely to occur in the event of simultaneous extreme declines. For example, the lower tail correlation coefficient between Shanghai and Beijing is 0.02, suggesting that the correlation between these two carbon price declines is generally higher in Shanghai and Beijing, and that changes between the two markets are more sensitive to bad news than good news. This may be another source of systematic risk in regional carbon markets, and there would be some risk in investing in these binary portfolios at this time. The results of Tree 3, Tree 4 and Tree 5 show that the lower tail correlation coefficients of the conditional dependency structure are generally lower or the lower tails are progressively independent after the inclusion of more conditional markets, and even more so after the launch of the national ETS. It is evident that the inclusion of more conditional markets has a certain degree of risk diversification in extreme loss scenarios. Investors may consider the inclusion of conditional markets when making investments for the purpose of risk avoidance. Due to the length of this article, the results of Tree 3–Tree 5 are not presented for the time being. Please refer to Appendix A for details.
3.4.2. Analysis of Dependencies between Carbon Markets before and after COVID-19
Tree 1 shows the dependency between the main carbon markets in the EU and China before and after the outbreak of COVID-19. It is noticeable that the Kendall rank correlation coefficient becomes generally larger after the outbreak of COVID-19, which suggests that the outbreak of COVID-19 increased the inter-connectivity between the EU and the carbon markets in China. The sudden outbreak of COVID-19 during 2020 causes a rapid decline in global carbon emissions, while changes in the demand for carbon credits lead to changes in the carbon trading prices, which increase the correlation between the various carbon markets. So, it is evident that the sudden outbreak of COVID-19 significantly increases the uncertainty of carbon price movements. In terms of structural features, the COVID-19 outbreak has significantly increased the dependency of the EU and Shanghai, Beijing and Guangdong, especially the EU and Shanghai. This may be strongly related to Shanghai’s positioning as an international financial center, where the shock of the global crisis bore the brunt of intensifying the EU–Shanghai linkage. Furthermore, the value of the Kendall rank correlation coefficient in Tree 2 is relatively larger than that in Tree 1, both before and after the outbreak of COVID-19. This suggests that the linkages between domestic carbon markets are stronger than those between EU carbon markets.
The shock of COVID-19 changed the formal structure of the copula. Before COVID-19 occurred, Tree 1 contains three copula forms, t, Clayton and Gumbel. Clayton and Gumbel connection functions have a lower tail dependency and upper tail dependency, and the t connection function has a symmetric dependency structure. After COVID-19 occurred, the carbon returns changed their dependency on the overall from an asymmetric tail dependency to a symmetric tail dependency, which may be associated with the similarity of the recovery cycle. In addition, due to the different timing, degree and length of exposure to COVID-19 shocks across carbon markets, the linkages between carbon markets are not greater when extreme scenarios occur. The outbreak of COVID-19 significantly increased the tail dependence of the EU and Shenzhen carbon markets, and significantly reduced the tail dependence of the EU and Shanghai and Hubei carbon markets. However, there is an upward trend in tail dependency between the EU and Shenzhen, and this trend movement ought to encourage investors and policymakers to remain cautious about the risk of carbon price return linkages. It is also notable that the inclusion of more conditional markets has led to an overall increase in the correlation coefficients between markets and greater linkages between carbon markets after the onset of COVID-19. However, the inclusion of more conditional markets reduces the tail dependency between carbon return pairs, both before and after the outbreak of COVID-19.
4. Conclusions and Discussion
In this paper, we investigated the structural dependency characteristics between the main carbon markets in China and the EU carbon market between 2 April 2014 to 16 July 2021 by using the C-vine copula method with the EU, Beijing, Shanghai, Guangdong, Shenzhen and Hubei carbon trading prices as the research objects, and compared the correlation degree of the relevant structures between the carbon markets in China and the EU before and after the launch of the national ETS, and before and after the outbreak of COVID-19.
Our research results show that there is a dependency relationship between the EU and China’s major carbon markets, and that the launch of a national ETS in China and the global COVID-19 outbreak have significantly changed the interdependent structure and extreme interdependence of the carbon trading markets in China and the EU. Firstly, the overall correlation between the EU and the carbon markets in China has weakened after the launch of the national ETS. This shows that with the launch of the national ETS, the carbon trading market in China is becoming increasingly mature and more independent in its dependency with the EU carbon market. Specifically, the relationship between the EU and Shanghai carbon market is closer than that between the EU and the other four carbon markets. Secondly, after joining a conditional market, it can be found that the movement of carbon returns in Beijing is more linked to the domestic market than in the EU after the launch of the national ETS, and plays an important role in the stability of the domestic carbon market. Therefore, special attention should be paid to the stability of the Beijing carbon market to avoid creating linkage risks with other domestic markets. Thirdly, after the launch of the national ETS, the tail dependence between the EU and Hubei, the EU and Shanghai was weakened, but the tail dependence between the EU and Shenzhen carbon market was triggered. This means that the carbon revenue pairs with tail dependence have changed from two pairs to three pairs after the national ETS was launched. However, whether before or after the launch of national ETS, carbon revenue has a symmetrical tail dependence. The extreme risk between the EU and the carbon market in China is a concern. Fourthly, the interdependency between the EU and the main carbon markets in China has generally increased following the outbreak of COVID-19. Specifically, the outbreak of COVID-19 has increased the dependence of the EU on Shanghai, Beijing and Guangdong, especially with Shanghai. The sudden outbreak of COVID-19 led to a rapid decline in global carbon emissions and changes in demand led to changes in carbon trading prices, increasing the correlation between the various carbon markets. It can be found that, whether after the launch of national ETS or the outbreak of COVID-19, the EU has always had the strongest dependence on Shanghai’s carbon market, which may have a lot to do with Shanghai’s positioning as an international financial center. Fifthly, from the perspective of tail dependence structure, although the outbreak of COVID-19 has reduced the tail dependence of the EU and Shanghai, Hubei carbon markets, the tail dependence of the EU and Shenzhen is on the rise. This trend change should encourage investors and policymakers to be cautious about the risk of carbon price return linkages.
Our findings have important implications for investors and policymakers. First of all, China should further accelerate the construction and improvement of a unified national carbon trading market, improve the price management system of the carbon trading market, and enhance the international voice of China’s carbon trading market. Secondly, in order to prevent and control the risk linkage between China and the EU carbon trading market, an effective carbon trading market risk early warning system can be established between China and the EU to prevent the possibility of increasing extreme risks and ensure the healthy operation of the carbon trading market. The domestic carbon trading market should introduce a reasonable regulatory mechanism, especially the Shanghai carbon trading market, which can prevent the risk linkage between domestic and foreign carbon trading markets to a certain extent. Thirdly, for investors, when investing in the products of a carbon market, they should comprehensively consider the risks caused by the interaction between the market and other markets, rather than just focusing on the price of a carbon market. Finally, the government should improve the risk management system of carbon emission trading to enhance the ability of domestic carbon trading market to withstand unexpected risks. Moreover, in the face of the ongoing impact of COVID-19, it is important to seek long-term development mechanisms for carbon trading markets.
Our results provide evidence for the understanding of the linkage characteristics of the carbon market in China with the EU at different stages and the effectiveness of a unified national carbon market. The results provide a useful reference for risk regulation and investment decisions by market regulators and investors, to ensure the healthy operation of the carbon trading market, accurately address the market risks posed by COVID-19, as well as to promote the active convergence to international carbon markets for China. However, there are certain limitations to this paper. Firstly, our results are a static linkage analysis of the correlation between the carbon markets in China and the EU. Future research could concentrate on examining the dynamic linkage characteristics between carbon markets in order to capture more clearly the co-movement between markets. Secondly, we have only investigated the structural characteristics of interdependencies between the carbon markets in China and the EU, but have not examined the main influencing factors that determine the interdependencies. In future studies, this could be further investigated by using the influencing factors as an extension point. From the perspective of methodology, the C-vine copula model has been widely used, but the scope of application is limited. In the future, better or improved model methods can be further used to depict the interdependence between carbon trading markets.
Author Contributions
Conceptualization, M.Z. and J.L.; methodology, M.Z. and Z.L.; software, M.Z. and H.L.; validation, M.Z. and H.L.; investigation, M.Z.; resources, M.Z.; writing—original draft preparation, M.Z.; funding acquisition, M.Z.; formal analysis, H.L. and C.C.; writing—review and editing, J.L. and C.C.; supervision, S.S. and Z.L.; data curation, B.W.; visualization, Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the “Study on the evolution mechanism and optimization strategy of population distribution structure under the “flow space” effect of high-speed rail network” (Grant No. ZR2022QG005); “Effect of high-speed rail network on urban population distribution pat-tern in Shandong province” (Grant No. 20DRKJ02); “Theoretical and economic research-oriented innovation team” of the youth innovation talent introduction and education plan of colleges and universities in Shandong Province (Grant No. 201901); Taishan Scholars Program (Grant No. tsqn201909135); “Employment polarization effect of low-carbon development constraint from the perspective of unequal opportunities” (Grant No. ZR2020QG040).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data were sourced from the Wind database.
Acknowledgments
The authors thank the “Theoretical Economics Research Innovation Team” of the Youth Innovation Talent Introduction and Education Plan of Colleges and Universities in Shandong Province, the China–ASEAN High-Quality Development Research Center in Shandong University of Finance and Economics, and the Shandong Digital Yellow River Industrial Chain System Construction Innovation Team of Youth Innovation Team of Shandong Colleges and Universities for financial support. In addition, this work was supported by the Faculty of Economics and the Centre of Excellence in Econometrics at Chiang Mai University.
Conflicts of Interest
We declare that there are no conflict of interest.
Appendix A

Table A1.
Static vine estimation results (before and after the ETS).
Table A1.
Static vine estimation results (before and after the ETS).
| Paris | Copula | Parameter 1 (SE) | Parameter 2 (SE) | Tau | Tail Dep | |
|---|---|---|---|---|---|---|
| Before the ETS | ||||||
| Tree 1 | EUA-HB | t | 0.01 (0.07) | 5.46 *** (1.99) | 0.00 | 0.04 |
| EUA-SH | t | 0.03 (0.06) | 5.09 *** (1.60) | 0.02 | 0.05 | |
| EUA-SZ | t | −0.13 ** (0.06) | 11.51 (9.02) | −0.08 | 0.00 | |
| EUA-BJ | N | 0.12 ** (0.06) | - | 0.07 | - | |
| EUA-GD | t | −0.17 *** (0.06) | 9.13 (5.81) | −0.11 | 0.00 | |
| Tree 2 | GD-HB|EUA | t | −0.04 (0.06) | 6.00 *** (2.20) | −0.02 | 0.03 |
| GD-SH|EUA | N | 0.08 (0.05) | - | 0.05 | - | |
| GD-SZ|EUA | C | 0.16 ** (0.07) | - | 0.07 | 0.01 L | |
| GD-BJ|EUA | C | 0.18 ** (0.07) | - | 0.08 | 0.02 L | |
| Tree 3 | BJ-HB|GD, EUA | J | 1.07 *** (0.05) | - | 0.04 | 0.09 U |
| BJ-SH|GD, EUA | BB7 | 1.00 *** (0.06) | 0.11 * (0.06) | 0.05 | 0.00 | |
| BJ-SZ|GD, EUA | N | −0.07 (0.06) | - | −0.04 | - | |
| Tree 4 | SZ-HB|BJ, GD, EUA | C | 0.13 ** (0.06) | - | 0.06 | 0.00 L |
| SZ-SH|BJ, GD, EUA | F | 0.24 (0.35) | - | 0.03 | - | |
| Tree 5 | SH-HB|SZ, BJ, GD, EUA | J | 1.06 *** (0.04) | - | 0.04 | 0.08 U |
| After the ETS | ||||||
| Tree 1 | EUA-HB | t | −0.04 (0.06) | 7.11 *** (2,75) | −0.02 | 0.02 |
| EUA-SH | t | −0.07 (0.06) | 6.41 *** (2.32) | −0.04 | 0.02 | |
| EUA-SZ | t | −0.02 (0.06) | 7.45 ** (3.36) | −0.02 | 0.02 | |
| EUA-BJ | F | −0.29 (0.43) | - | −0.03 | - | |
| EUA-GD | N | 0.04 (0.06) | - | 0.02 | - | |
| Tree 2 | BJ-SZ|EUA | F | 0.07 (0.51) | - | 0.01 | - |
| BJ-GD|EUA | t | −0.09 (0.15) | 5.11 ** (2.56) | −0.05 | 0.04 | |
| BJ-SH|EUA | C | 0.18 ** (0.07) | - | 0.08 | 0.02 L | |
| BJ-HB|EUA | N | 0.05 (0.09) | - | 0.03 | - | |
| Tree 3 | HB-SZ|BJ, EUA | F | −0.40 (0.08) | - | −0.04 | - |
| HB-GD|BJ, EUA | N | −0.05 (0.07) | - | −0.03 | - | |
| HB-SH|BJ, EUA | F | −0.78 * (0.42) | - | −0.09 | - | |
| Tree 4 | SH-SZ|HB, BJ, EUA | N | −0.03 (0.06) | - | −0.02 | - |
| SH-GD|HB, BJ, EUA | BB7 | 1.18 *** (0.12) | 0.02 (0.05) | 0.10 | 0.20 U | |
| Tree 5 | GD-SZ|SH, HB, BJ, EUA | C | 0.06 (0.05) | - | 0.03 | 0.00 L |
Note: Significance at the 0.01, 0.05, and 0.10 levels indicated by ***, **, and *; Standard errors in parentheses; The symbol “U” represents upper tail dependence, “L” represents lower tail dependence.

Table A2.
Static vine estimation results (before and after COVID-19).
Table A2.
Static vine estimation results (before and after COVID-19).
| Paris | Copula | Parameter 1 (SD) | Parameter 2 (SD) | Tau | Tail Dep | |
|---|---|---|---|---|---|---|
| Before COVID-19 | ||||||
| Tree 1 | EUA-SZ | C | 0.04 (0.07) | - | 0.02 | 0.00 L |
| EUA-GD | C | 0.07 (0.08) | - | 0.04 | 0.00 L | |
| EUA-SH | t | 0.05 (0.09) | 4.00 *** (1.27) | 0.03 | 0.09 | |
| EUA-HB | t | −0.09 (0.08) | 4.54 *** (1.68) | −0.05 | 0.05 | |
| EUA-BJ | G | 1.01 *** (0.06) | - | 0.01 | 0.01 U | |
| Tree 2 | BJ-SZ|EUA | F | −0.23 (0.66) | - | −0.03 | - |
| BJ-GD|EUA | t | 0.05 (0.02) | 4.51 * (2.39) | 0.03 | 0.07 | |
| BJ-SH|EUA | C | 0.25 ** (0.01) | - | 0.11 | 0.06 L | |
| BJ-HB|EUA | F | 0.64 (0.62) | - | 0.07 | - | |
| Tree 3 | HB-SZ|BJ, EUA | J | 1.03 *** (0.06) | - | 0.02 | 0.04 U |
| HB-GD|BJ, EUA | C | 0.00 (0.08) | - | 0.00 | - | |
| HB-SH|BJ, EUA | N | −0.12 (0.08) | - | −0.08 | - | |
| Tree 4 | SH-SZ|HB, BJ, EUA | N | −0.01 (0.08) | - | −0.01 | - |
| SH-GD|HB, BJ, EUA | J | 1.25 *** (0.13) | - | 0.12 | 0.26 U | |
| Tree 5 | GD-SZ|SH, HB, BJ, EUA | C | 0.11 (0.07) | - | 0.05 | 0.00 L |
| After COVID-19 | ||||||
| Tree 1 | EUA-SZ | t | −0.06 (0.10) | 5.46 * (3.06) | −0.04 | 0.03 |
| EUA-GD | C | 0.00 (0.10) | - | 0.00 | - | |
| EUA-SH | t | −0.20 * (0.10) | 10.43 (9.42) | −0.13 | 0.00 | |
| EUA-HB | t | 0.02 (0.11) | - | 0.01 | 0.01 | |
| EUA-BJ | t | −0.09 (0.09) | - | −0.06 | 0.00 | |
| Tree 2 | SH-GD|EUA | t | −0.09 (0.14) | - | −0.06 | 0.00 |
| SH-SZ|EUA | J | 1.26 *** (0.16) | - | 0.13 | 0.27 | |
| SH-BJ|EUA | F | 0.81 (0.66) | - | 0.09 | - | |
| SH-HB|EUA | F | −1.18 (0.75) | - | −0.13 | - | |
| Tree 3 | HB-GD|SH, EUA | G | 1.06 *** (0.10) | - | 0.06 | 0.08 U |
| HB-SZ|SH, EUA | F | −1.27 (0.61) | - | −0.14 | - | |
| HB-BJ|SH, EUA | F | −0.21 (0.63) | - | −0.02 | - | |
| Tree 4 | BJ-GD|HB, SH, EUA | F | −0.66 (0.64) | - | −0.07 | - |
| BJ-SZ|HB, SH, EUA | t | −0.01 (0.10) | - | −0.01 | 0.00 U | |
| Tree 5 | SZ-GD|BJ, HB, SH, EUA | F | 0.63 (0.63) | - | 0.07 | - |
Note: Significance at the 0.01, 0.05, and 0.10 levels indicated by ***, **, and *; Standard errors in parentheses; The symbol “U” represents upper tail dependence, “L” represents lower tail dependence.
References
- Rajalingam, M.; Srivastava, A. Rational hybrid analytical model for steel pipe rack quantification in oil & gas industries. Civ. Eng. J. 2020, 6, 649–658. [Google Scholar] [CrossRef]
- Zeng, S.H.; Jia, J.M.; Su, B.; Jiang, C.X.; Zeng, G.W. The volatility spillover effect of the European Union (EU) carbon financial market. J. Clean. Prod. 2021, 282, 124394. [Google Scholar] [CrossRef]
- Lin, B.; Chen, Y. Dynamic linkages and spillover effects between CET market, coal market and stock market of new energy companies: A case of Beijing CET market in China. Energy 2019, 172, 1198–1210. [Google Scholar] [CrossRef]
- Stoerk, T.; Dudek, D.J.; Yang, J. China’s national carbon emissions trading scheme: Lessons from the pilot emission trading schemes, academic literature, and known policy details. Clim. Policy 2019, 19, 472–486. [Google Scholar] [CrossRef]
- Wen, F.; Wu, N.; Gong, X. China’s carbon emissions trading and stock returns. Energy Econ. 2020, 86, 104627. [Google Scholar] [CrossRef]
- Sun, L.M.; Xiang, M.Q.; Shen, Q. A comparative study on the volatility of EU and China’s carbon emission permits trading markets. Phys. A 2020, 560, 125037. [Google Scholar] [CrossRef]
- Benkraiem, R.; Garfatta, R.; Lakhal, F.; Zorgati, I. Financial contagion intensity during the COVID-19 outbreak: A copula approach. Int. Rev. Financ. Anal. 2022, 81, 102136. [Google Scholar] [CrossRef]
- Liu, J.X.; Cheng, Y.N.; Li, X.Q.; Sriboonchitta, S. The role of risk forecast and risk tolerance in portfolio management: A case study of the Chinese financial sector. Axioms 2022, 11, 134. [Google Scholar] [CrossRef]
- Rupani, P.F.; Nilashi, M.; Abumalloh, R.A.; Asadi, S.; Samad, S.; Wang, S. Coronavirus pandemic (COVID-19) and its natural environmental impacts. Int. J. Environ. Sci. Technol. 2020, 17, 4655–4666. [Google Scholar] [CrossRef]
- Corbet, S.; Hou, Y.; Hu, Y.; Lucey, B.; Oxley, L. Aye Corona! The contagion effects of being named Corona during the COVID-19 pandemic. Financ. Res. Lett. 2021, 38, 101591. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, Y. The dynamic volatility spillover between European carbon trading market and fossil energy market. J. Clean. Prod. 2016, 112, 2654–2663. [Google Scholar] [CrossRef]
- Dhamija, A.K.; Yadav, S.S.; Jain, P.K. Volatility spillover of energy markets into EUA markets under EU ETS: A multi-phase study. Environ. Econ. Policy Stud. 2017, 20, 561–591. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, M.; Tian, L. The market-linkage of the volatility spillover between traditional energy price and carbon price on the realization of carbon value of emission reduction behavior. J. Clean. Prod. 2020, 245, 118682. [Google Scholar] [CrossRef]
- Hanif, W.; Hernandez, J.A.; Mensi, W.; Kang, S.H.; Uddin, G.S.; Yoon, S.M. Nonlinear dependence and connectedness between clean/renewable energy sector equity and European emission allowance prices. Energy Econ. 2021, 101, 105409. [Google Scholar] [CrossRef]
- Chang, K.; Ye, Z.F.; Wang, W.H. Volatility spillover effect and dynamic correlation between regional emissions allowances and fossil energy markets: New evidence from China’s emissions trading scheme pilots. Energy 2019, 185, 1314–1324. [Google Scholar] [CrossRef]
- Reboredo, J.C. Volatility spillovers between the oil market and the European Union carbon emission market. Econ. Model 2014, 36, 229–234. [Google Scholar] [CrossRef]
- Zhu, B.Z.; Huang, L.Q.; Yuan, L.L.; Ye, S.X.; Wang, P. Exploring the risk spillover effects between carbon market and electricity market: A bidimensional empirical mode decomposition based conditional value at risk approach. Int. Rev. Econ. Financ. 2020, 67, 163–175. [Google Scholar] [CrossRef]
- Xu, L.; Wu, C.Y.; Qin, Q.D.; Lin, X.Y. Spillover effects and nonlinear correlations between carbon emissions and stock markets: An empirical analysis of China’s carbon-intensive industries. Energy Econ. 2022, 111, 106071. [Google Scholar] [CrossRef]
- Oestreich, A.M.; Tsiakas, I. Carbon emissions and stock returns: Evidence from the EU emissions trading scheme. J. Bank. Financ. 2015, 58, 294–308. [Google Scholar] [CrossRef]
- Hu, G.H.; Wu, H.Y.; Qiu, J.X. Dependence structure of carbon emission markets: Regular Vine approach. Chin. J. Popul. Resour. 2015, 25, 44–52. [Google Scholar]
- Arouri, M.E.H.; Jawadi, F.; Nguyen, D.K. Nonlinearities in carbon spot-futures price relationships during Phase II of the EU ETS. Econ. Model. 2012, 29, 884–892. [Google Scholar] [CrossRef]
- Zhao, L.L.; Wen, F.H.; Wang, X. Interaction among China carbon emission trading markets: Nonlinear Granger causality and time-varying effect. Energy Econ. 2020, 91, 104901. [Google Scholar] [CrossRef]
- Zhu, B.Z.; Zhou, X.X.; Liu, X.F.; Wang, H.F.; He, K.J.; Wang, P. Exploring the risk spillover effects among China’s pilot carbon markets: A regular vine copula-CoES approach. J. Clean. Prod. 2020, 242, 118455. [Google Scholar] [CrossRef]
- Mai, T.K.; Foley, A.M.; McAleer, M.; Chang, C.L. Impact of COVID-19 on returns-volatility spillovers in national and regional carbon markets in China. Renew. Sustain. Energy Rev. 2022, 169, 112861. [Google Scholar] [CrossRef]
- Fang, S.; Cao, G.X. Modelling extreme risks for carbon emission allowances—Evidence from European and Chinese carbon markets. J. Clean. Prod. 2021, 316, 128023. [Google Scholar] [CrossRef]
- Du, J.Z. Examining the Inter-relationship between RMB Markets. Procedia Comput. Sci. 2018, 139, 313–320. [Google Scholar] [CrossRef]
- Wu, C.C.; Chung, H.; Chang, Y.H. The economic value of co-movement between oil price and exchange rate using copula-based GARCH models. Energy Econ. 2012, 34, 270–282. [Google Scholar] [CrossRef]
- Benlagha, N. Dependence structure between nominal and index-linked bond returns: A bivariate copula and DCC-GARCH approach. Appl. Econ. 2014, 46, 3849–3860. [Google Scholar] [CrossRef]
- Min, A.; Czado, C. Bayesian inference for multivariate copulas using pair-copula constructions. J. Financ. Econom. 2010, 8, 511–546. [Google Scholar] [CrossRef]
- Embrechts, P.; McNeil, A.; Straumann, D. Correlation and Dependence in Risk Management: Properties and Pitfalls. Risk Manag. Value Risk Beyond 2002, 1, 176–223. [Google Scholar]
- So, M.K.; Yeung, C.Y. Vine-copula GARCH model with dynamic conditional dependence. Comput. Stat. Data Anal. 2014, 76, 655–671. [Google Scholar] [CrossRef]
- Bedford, T.; Cooke, R.M. Probability Density Decomposition for Conditionally Dependent Random Variables Modeled by Vines. Ann. Math. Artif. Intel. 2001, 32, 245–268. [Google Scholar] [CrossRef]
- Bedford, T.; Cooke, R.M. Vines: A New Graphical Model for Dependent Random Variables. Ann. Stat. 2002, 30, 1031–1068. [Google Scholar] [CrossRef]
- Brechmann, E.C.; Czado, C. Risk management with high-dimensional vine copulas: An analysis of the Euro Stoxx 50. Statist. Risk. Model 2013, 30, 307–342. [Google Scholar] [CrossRef]
- Song, Q.; Liu, J.X.; Sriboonchitta, S. Risk Measurement of Stock Markets in BRICS, G7, and G20: Vine Copulas versus Factor Copulas. Mathematics 2019, 7, 274. [Google Scholar] [CrossRef]
- Zhang, X.M.; Zhang, T.; Lee, C.C. The path of financial risk spillover in the stock market based on the R-vine-Copula model. Phys. A 2022, 600, 127470. [Google Scholar] [CrossRef]
- Jiang, C.X.; Li, Y.Q.; Xu, Q.F.; Liu, Y.Z. Measuring risk spillovers from multiple developed stock markets to China: A vine-copula-GARCH-MIDAS model. Int. Rev. Econ. Financ. 2021, 75, 386–398. [Google Scholar] [CrossRef]
- Joe, H. Asymptotic efficiency of the two-stage estimation method for copula-based models. J. Multivariate. Anal. 2005, 94, 401–419. [Google Scholar] [CrossRef]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Bentes, S.R. On the stylized facts of precious metals’ volatility: A comparative analysis of pre-and during COVID-19 crisis. Phys. A Stat. Mech. Appl. 2022, 600, 127528. [Google Scholar] [CrossRef]
- Huang, J.J.; Lee, K.J.; Liang, H.M.; Lin, W.F. Estimating value at risk of portfolio by conditional copula-GARCH method. Insur. Math. Econ. 2009, 45, 315–324. [Google Scholar] [CrossRef]
- Sklar, A. Fonctions de Répartition à n Dimensions et Leurs Marges. Publ. Inst. Statist. Univ. Paris. 1959, 8, 229–231. [Google Scholar]
- Embrechts, P.; Lindskog, F.; McNeil, A. Modelling dependence with copulas and applications to risk management. In Handbook of Heavy Tailed Distributions in Finance; Rachev, S., Ed., Elsevier: Amsterdam, The Netherlands, 2003; pp. 25–26. [Google Scholar] [CrossRef]
- Patton, A.J. Modelling asymmetric exchange rate dependence. Int. Econ. Rev. 2006, 47, 527–556. [Google Scholar] [CrossRef]
- Frank, M.J. On the simultaneous associativity of F(x,y) and x+y−F(x,y). Aequ. Math. 1979, 19, 194–226. [Google Scholar] [CrossRef]
- Joe, H. Parametric families of multivariate distributions with given margins. J. Multivar. Anal. 1993, 46, 262–282. [Google Scholar] [CrossRef]
- Gumbel, E.J. Bivariate exponential distributions. J. Am. Stat. Assoc. 1960, 55, 698–707. [Google Scholar] [CrossRef]
- Clayton, D.G. A model for association in bivariate life tables and its application in epidemiological studies of familial tendency in chronic disease incidence. Biometrika 1978, 65, 141–152. [Google Scholar] [CrossRef]
- Ly, L.; Sriboonchitta, S.; Tang, J.C.; Wong, W.K. Exploring dependence structures among European electricity markets: Static and dynamic copula-GARCH and dynamic state-space approaches. Energy Rep. 2022, 8, 3827–3846. [Google Scholar] [CrossRef]
- Sriboonchitta, S.; Nguyen, H.T.; Wiboonpongse, A.; Liu, J.X. Modeling volatility and dependency of agricultural price and production indices of Thailand: Static versus time-varying copulas. Int. J. Approx. Reason. 2013, 54, 793–808. [Google Scholar] [CrossRef]
- Viviana, F. Copula-based measures of dependence structure in assets returns. Phys. A 2008, 387, 3615–3628. [Google Scholar] [CrossRef]
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Selected Papers of Hirotugu Akaike; Parzen, E., Tanabe, K., Kitagawa, G., Eds.; Springer: New York, NY, USA, 1998; pp. 199–213. [Google Scholar]
- Brechmann, E.C. Truncated and simplified regular vines and their applications. Ph.D. Thesis, Technische Universitaet Muenchen, Munich, Germany, 2010. [Google Scholar]
- Emmanouil, K.N.; Nikos, N. Extreme Value Theory and Mixed Canonical Vine Copulas on Modelling Energy Price Risks; Working Paper; NTNU: Trondheim, Norway, 2012. [Google Scholar]
- Tachibana, M. Relationship between stock and currency markets conditional on the US stock returns: A vine copula approach. J. Multinatl. Financ. Manag. 2018, 46, 75–106. [Google Scholar] [CrossRef]
- Wei, Z.; Kim, S.Y.; Kim, D.Y. Multivariate Skew Normal Copula for non-exchangeable dependence. Procedia Comput. Sci. 2016, 91, 141–150. [Google Scholar] [CrossRef]
- Schweizer, B.; Wolff, E. On nonparametric measures of dependence for random variables. Ann. Stat. 1981, 9, 879–885. [Google Scholar] [CrossRef]
- Qiu, Q.; Guo, S.Q. Analysis of regional trading market risks in carbon finance. Resour. Dev. Market. 2017, 2, 188–193. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).