Abstract
In this work, we analyzed the nonlinear fractional dynamics in the equations of motion of a bar coupled to support under the effect of a potential described by two equally spaced magnetic poles. We also considered Bouc–Wen damping in the equations of motion. For external force vibrations, we considered an equation of a non-ideal motor based on the parameters that related the interaction between the oscillation and the excitation source. With such considerations, we explored the influence of the fractional derivative operator parameter on the average power generated by the device and the dynamic behavior to determine the chaotic and periodic regions. We use Bifurcation Diagrams, Test 0–1, Phase Portrait, and Poincaré Maps. As a conclusion, we established a set of parameters for the fractional differential equations to obtain higher average powers and the periodicity windows that corroborate the establishment of energetic orbits for energy harvesting.
MSC:
37N30; 26A33; 65P20
1. Introduction
In recent decades, researchers from the most diverse areas have sought new technologies to produce clean and sustainable energy from the kinetic movements of the environment. An example is the capture of energy produced by the movement of the winds. Another example widely explored by researchers is a structure excited by environmental vibrations with piezoelectric materials (PZT) to produce clean energy. A kinetic energy collection device with piezoelectric materials is of the portal frame type. Portal frame structures are applied in different ways, such as in houses, buildings, bridges, etc. [,,].
Another widely explored example is the oscillator, as such devices can be applied both in the micro and the macro scale. One oscillator that has attracted considerable attention is the Duffing oscillator, as it has a rich dynamic behavior and several modalities in applications in mechanics, chemistry, and engineering systems. It can be described by a mathematical model that is based on the transverse deflection of a bent beam. Works such as Holmes [] analyzed the chaotic dynamics of a bistable oscillator using a ferromagnetic beam deviated from the central position with attractive magnetic fields symmetrically arranged. This oscillator will often include harmonic external force excitation of the type f(t) = Asin(ωt), where A is the external force amplitude and ω is the frequency applied to the oscillator. The excitation of the applied force can also be stochastic [].
This structure has been widely explored both experimentally and theoretically in various applications. However, the application that has gained prominence is in energy production. Many authors couple pieces of piezoceramic material to the oscillator, which, when undergoing deformation, generate electrical charge movement and are collected by an electrical circuit. Analyses of the nonlinear dynamic behavior of this oscillator have determined the frequency bands for relatively high output powers because the analysis of the non-linear effects of the magnetic field guarantees an increase in the efficiency of energy capture under variable frequency and amplitude, and has a so-called frequency broadband effect [,,,,].
However, it is not only the magnetic fields that guarantee this efficiency in the production of energy. Another highly analyzed factor is the excitation force applied to the oscillator. As we mentioned earlier, such an excitation force can have several types, of which the most applied is a sinusoidal force. Several authors have explore the amplitude of the force and its frequency for the production of energy with the coupled piezoceramic material. In this line, many works explore the obtaining of control techniques to keep the oscillator in periodic orbits that optimize the energy production in a more efficient way, since there is the possibility of a chaotic regime being followed due to the non-linearities of the system.
Another aspect addressed is hysteresis, as it is a common phenomenon in ferromagnetic materials. Hysteresis modeling has been extensively investigated, however, it remains a challenging problem due to its non-linearity and memory effect [,,,,,]. Among the hysteresis models, the Bouc–Wen model shows good results to describe the hysteretic behavior of mechanical vibrations, such as positioning devices such as piezoceramic actuators. The memory effect of these materials can be analyzed using the fractional derivatives. According to [,,], the effect of memory on the system can be represented by fractional derivative operators. In this paper, we applied the Riemann–Liouville operator as its discretization for numerical analysis is more efficient, and one can consider the memory effect in a more simplified way. Another aspect is when the fractional derivative operator is close to 1 there is a loss of memory effect [,].
Therefore, our paper explores the application of an external force generated by a non-ideal motor that causes vibrations in a Duffing oscillator. Such an external force is based on the time-varying force from an eccentric mass that rotates due to a non-ideal motor torque [].
The motivation of this work is to explore with numerical simulations a structure for energy harvesting in a simple way, containing the piezoceramic material and under the action of a non-ideal motor. In [], the same symmetry-breaking device to energy harvesting was explored, considering the displacement of human walking. These results have experimental data on the power and frequency applied to the system.
Other works, such as [,,,,], experimentally explored the behavior of the system considering different types of external force (random, harmonic, and under human motion excitation). This study examines the voltage generated in these structures and thus shows the dynamic behavior of the basins of attraction. Basins of attraction describe the behavior of initial conditions that go asymptotically to attractors. The authors also established a range for the frequency of the applied external force for better energy harvesting in an experimental way.
Authors such as [] analyze a model of a higher-order nonlocal deformation gradient plate developed for vibrations of nanofilms of piezoelectric materials as mass sensors. The authors explore the behavior of nanoparticles transport to different locations, being subjected to thermoelectromechanical loads and thus proposing a mathematical model to describe the phenomenon and possible solutions to the equations. Other works in the literature [] explore the behavior of a model, using partial differential equations that describe the bending of nanotubes for energy harvesting.
However, our work explores the dynamics of the bar with a simple circuit model containing the piezoceramic material. The electrical circuit equation is well-explored in Refs. [,,,,,,,,,,,]. The proposal of a device theoretically is approached in several experiments, considering an external force with the vibration caused by a sinusoidal function. We propose analyzing the system considering a non-ideal motor described by an equation that considers only active interaction between the oscillating system and the excitation source. The time-varying frequency applied to the Duffing system in this manuscript depends on two essential parameters linked to the active interaction between the oscillator and the oscillation source. Such an external force applied by the non-ideal motor can lead to a better understanding of energy harvesting. Thus, our manuscript is based on the equations of motion of a cantilever containing piezoceramic material in which we adopted Bouc–Wen damping for our fractional numerical analyses. This work is entirely theoretical and numerical.
2. Magneto Piezo Oscillator Device
Piezo oscillator type collectors, composed of a ferromagnetic beam, are a recent addition to the stable of energy harvesting devices. It consists of a ferromagnetic beam fixed to a support (See Figure 1). Two magnets are located symmetrically at the base near the free end. The distance between the magnets determines the stable points.
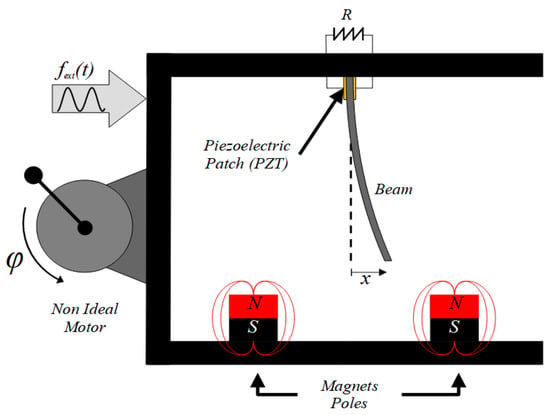
Figure 1.
Energy Harvesting model subjected to the kinematic excitation and magnetic poles symmetrically arranged. R is load resistance and is angular displacement.
We consider that the system has two unstable potentials and that the mechanical system has a double well potential. According to [,,,], the double well potential occasionally leads to a higher power generation when the beam displacement moves between the potential wells.
Piezo ceramic patches were made at the root of beam and thus we obtain a bimorphic generator, as the piezo ceramic patches are connected to a resistor and a maintenance output is through the load due to the kinematic excitations caused by the external force, as shown in Figure 1, being of primary interest for an energy harvest.
3. Mathematical Modeling
For description of the mathematical model, we consider Figure 1 of the previous section. The double well potential (DWP) is generated by the magnet field potential of two magnets arranged symmetrically. The DWP allows for near-optimal representative dynamic analysis and it is described in (1) [,,,,,,,,,,,,,,,,,,,,].
where x is beam displacement. This mathematical model considers the fractional calculation applied to Bouc–Wen () damping for the hysteresis caused by the piezo ceramic material coupled to the Duffing oscillator beam [,,,,,,,,,,,,,,,,,,,,,,]. The dimensionless equations is
The equation describing the voltage in the electrical circuit is defined by:
where is the beam displacement, is the dimensionless voltage across the load resistor, is damping coeficient of the beam, is the coupling term of the piezoelectric system in electrical equations, is the coupled constant of electrical circuit, is the reciprocal of the dimensionless time constant of the electrical circuit, is load resistance and is capacitance of piezoceramic patches material [,,,,].
The mathematical modeling analyzed numerically was systematically explored for energy harvesting in systems of small dimensions. Our manuscript numerically analyzes the dimensionless system containing an external force of a non-ideal motor proposed by [,,,,,,,] and containing the dimensionless Bouc–Wen damping.
The non-ideal motor coupled to the device, as shown in Figure 1, assumes that the non-ideal motor has time-varying frequency from an eccentric mass that rotates due to a torque actuator, defined as:
where. The parameters and are defined by the interaction between the oscillations and the non-ideal motor oscillation source. We consider a force external to the system described as follows:
where is the force amplitude of non-ideal motor. The parameters and are defined by the active interaction between the oscillating system and the excitation source. In addition, they are considered control parameters. If , then it corresponds to harmonic excitation [,,]. Note that for a0 = 0 we have no action of the non-ideal motor. Figure 2 depicts the first five of these functions, which aids in understanding the effect of the nonideal excitation.
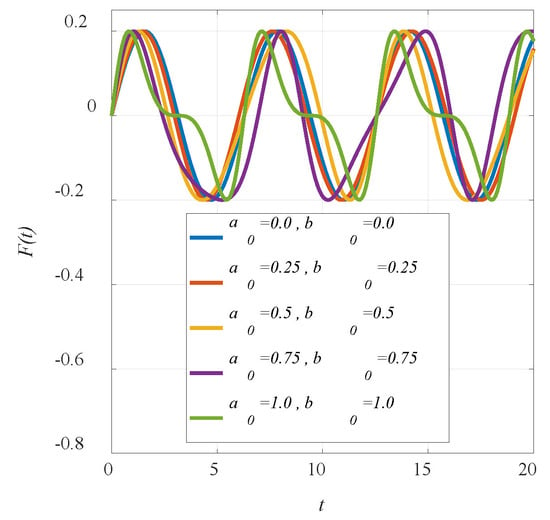
Figure 2.
External force behavior for different values for a0 and b0.
We considered the Bouc–Wen damping in the structure, i.e., the system has a hysteresis process in the beam containing the PZT patches material. The Bouc–Wen damping () is defined as:
where is derivative with respect to time, n ≥ 1 and 0 <<1. This model was originally developed in the context of mechanical systems. is a restoring force with the superposition of a linear component k1 > 0 and a purely hysteretic, D > 0 is the constant flow displacement and k1 ∈ (0,1) is the post/precedence stiffness ratio. A, β, γ, and n are parameters of shape and the size of the hysteresis loop [,,,,,,].
Using Equations (1)–(5), we have the equation of motion:
Rewriting these equations in state space notation:
where, and. When applied, the Riemann–Louville operator (RL) yields:
where . For our numerical analysis, we used the algorithm proposed by Petras in [,] for the discretization of a fractional derivative (Appendix A). By definition, the Riemman-Liouville (RL) operator is [,,,,]:
where is RL operator parameter.
4. Numerical Results
The results obtained in this analyses are numerical, due to the non-linearities involved in the process, and the initial condition adopted for our analyses is. The numerical analyses were obtained with time of integration of the fractional differential equations [s] and transient time and with an . The parameter is available in Table 1, and the numerical algorithm for the integration and discretization of the fractional operator was proposed by Petrás [,].

Table 1.
Parameters used for numerical analysis of fractional differential equations described in Equation (6). Adapted from [].
Here, the analyses for the fractional model consider the parameters of the fractional derivative operator we analyzed the which makes the hysteresis equation Bouc–Wen fractional to represent asymmetry of piezoelectric hysteresis. We also considered a range for the parameters connected to the external force, that is, and According to [,,],, the average power () was:
We analyzed the behavior of the average power obtained by Equation (10) in the following parameter spaces and , that is, the parameters that are linked to the external force of the system and the parameter of the fractional derivative operator that is related to BW damping.
Figure 2, Figure 3 and Figure 4 show computational simulations to obtain the Pavg considering the parameters of Table 1 to observe the behavior of the parameter related to non-ideal motor rotation and the parameter of the fractional derivative. The values a0 close to zero with b0 = 0.5 and values of q4 close to 0.85 have a low average power value (Figure 2a). However, for values of b0 with values between 0 and 1 and q4 close to 0.85, there is a decrease in average power with a0 = 0.5.
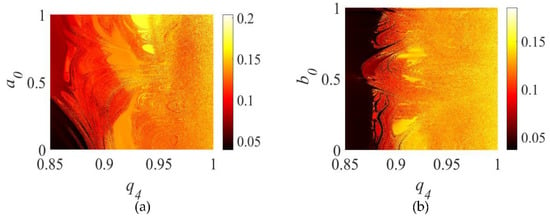
Figure 3.
behavior. (a) and (b).
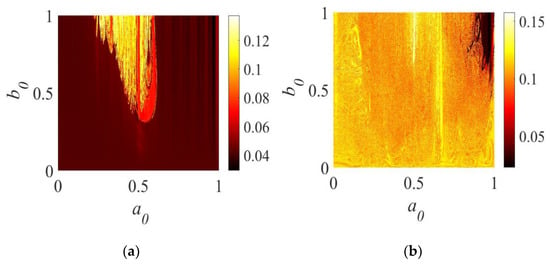
Figure 4.
behavior. (a) with and (b) with .
Figure 3a shows the behavior of for the parameter space of and Figure 3b shows for the parameter space . In both figures, dark red represents the minimum power and yellow represents the maximum power. We can determine the regions where the power is at the maximum value or minimum values for the parameters and related to the parameter , referring to the Bouc–Wen damping.
As we can see in Figure 3 and Figure 4, there is the appearance of minimum and maximum Pavg regions with the variation of the parameters (a0, b0, and q4), and changes in the behavior in the hysteresis of the piezoceramic materials caused by the system of Equation (8) reaches orbits with larger beam displacement amplitudes. This larger displacement causes vibrations in the piezoceramic material, allowing for a higher average power, considering the parameters adopted (See Table 1). Another aspect associated with the piezoceramic material is defined by [,,,,,,,,,,,,,], which establishes that changes observed in the hysteresis curves can characterize hard-type piezoceramic materials, which have a piezoelectric constant with low values, or soft-type piezoceramic materials with high piezoelectric constants.
However, an analysis considering the motor parameters is not ideal, considering some values of q4. For values of q4 = 0.8586 and q4 = 0.9495, we can observe the results in Figure 4a,b obtained by numerical simulations using the algorithm described in Appendix A and Equations (8) and (10), where it can be seen that there is a maximum of Pavg with maximum values close to a0 = 0.5 and values above b0 = 0.5 (Figure 3a). For the case of q4 = 0.9495, we will have a minimum region for the values of a a0 = 1.0 and b0 = 1.0, as seen in Figure 3b.
However, as we observed a significant change in the behavior, as shown in the Figure 4a,b, we analyzed the behavior of the parameter space for and and Figure 4a,b show the.
However, for values of q4→1.0 there is a larger region for Pavg values, as we can see in Figure 5a,b.
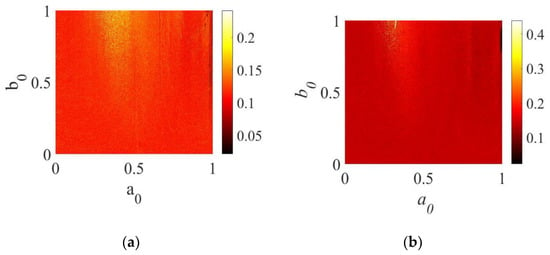
Figure 5.
(a) with and (b) with.
We observed a significant change in the power of the system with the change in the exponent of the fractional derivative, because, for the application of the fractional operator in the system of Equation (7) the non-linearity of hysteresis depends on the rate and asymmetry of the piezoelectric actuators. According to [,], it states that the model with the classic Bouc–Wen damping is only efficient for the description of symmetric and rate independent hysteresis, and the model containing the fractional operator is dedicated to characterizing the asymmetric and rate-dependent behavior hysteresis. Therefore, we analyzed the dynamic behavior on the fractional parameter of the operator applied in this damping.
For the fractional dynamical analysis, we used the parameters described in Table 1, with the values of and . Figure 5a and Figure 6a represent the bifurcation diagram for the system described by the Equation (6), however, with the scanning of the parameters of the fractional RL operator. However, the periodic ranges in the structure are observed, that is, for the values of in approximately in the intervals [0.9272, 0.9439], [0.945, 0.9459], [0.9538,0.9548], [0.9606,0.9619], and [0.9801, 0.9833] has periodic behavior for displacement (x1) and velocity (x2).
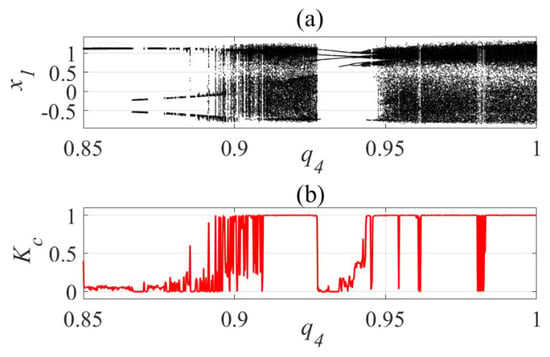
Figure 6.
(a) Bifurcation diagram for displacement and (b) of displacement (x1).
Thus, we used the 0–1 test, which consisted of statistically estimating the parameter Kc, considering the time series described by the integration of the system of fractional differential equations. For a better description of the 0–1 test see Refs. [,,]. Thus, if Kc is close to 0, the system has a periodic behavior, however, if Kc is close to 1 the behavior will be chaotic. The parameter Kc confirms these intervals obtained from the bifurcation diagrams. For the other intervals, the behavior was chaotic according to the bifurcation diagrams and the Kc. In Figure 5a we show the bifurcation diagram of displacement and Figure 6b shows () referring to the is displacement of cantiliver. This diagram makes it possible to observe the dynamic behavior of the displacement of the bar containing the piezoceramic patches, thus observing the intervals in which the system has a periodic and chaotic regime when considering the parameter of the fractional derivative operator.
Figure 7a shows the bifurcation diagram of displacement and Figure 6b shows (), referring to being the velocity of cantiliver. Analogously, the bifurcation diagram considering the speed of the beam containing the piezoceramic patches, in this way, observes the intervals in which the system has a periodic and chaotic regime when considering the parameter of the fractional derivative operator.
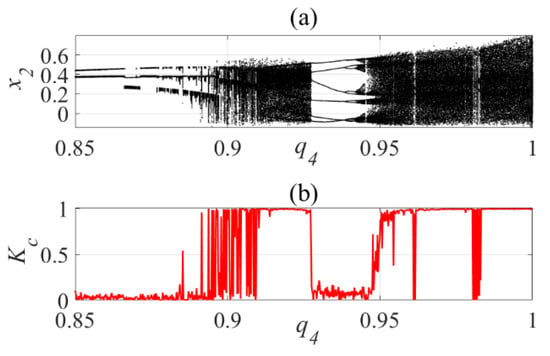
Figure 7.
(a) Bifurcation diagram for velocity and (b) of velocity x2.
Figure 8a,b represent the phase portraits for values of and , which lie in the periodic and chaotic regions as detected in Figure 6 and Figure 7. The black line describes the phase portrait and the red dots the Poincaré map (which describes an estimate of the chaotic attractor defined by the system of fractional dynamic equations).
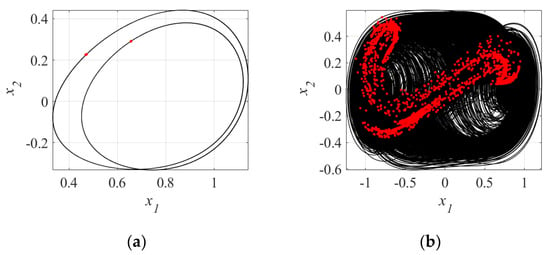
Figure 8.
Representation of systems of the Equation (8), the black line is portrait phase and the red dot is the Poincaré Map. (a) and (b) .
Figure 9a,b show the behavior of the phase portraits (black line) and Poincaré maps (red dots), for the values from and , respectively.
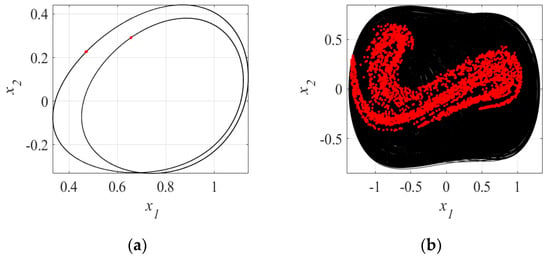
Figure 9.
Representation of systems of the Equation (8), the black line is the portrait phase and the red dot is the Poincaré Map. (a) and (b).
Figure 10a–d represent the behavior of the hysteresis curves of Equation (8) considering (a) and (b), (c) and (d).
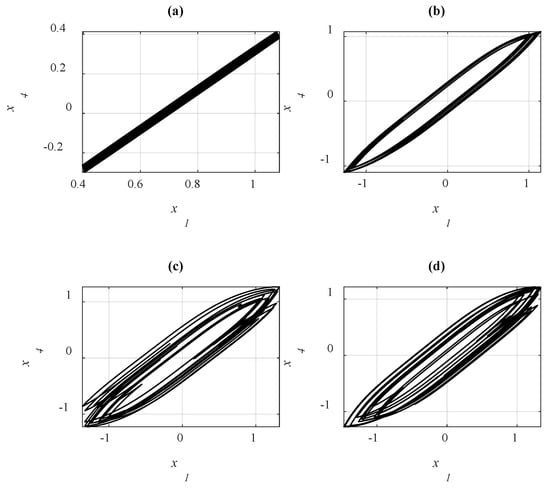
Figure 10.
Representation of is displacement x of the beam and represents z for the Bouc–Wen damping. The hysteresis curves of the Equation (8). (a) and (b) , (c) and (d) .
5. Conclusions
Our work analyzed the behavior of the fractional model with an external force described in Equation (2) and the fractional BW damping. We established the dependance of the power generated by the system based on the parameters of the external force 𝑎0 and 𝑏0 according to the order of the RL derivative operator (𝑞4). We show that in the limit 𝑞4 → 1.0, the system tends to the high-power region.
Furthermore, we also indicate the regions with low and medium power. Namely, we observe the changes in the power of system with the fractional parameter, and this is because the trajectories of the systems are influenced by the parameter. Therefore, we observed some values of 𝑞4 = 0.8486, 0.9495, 0.9999, and 1.0 with the parameters of the external force 𝑎0 and 𝑏0, and we observed that the power goes through the significant changes in its regions. In the next step, we analyzed the behavior of the fractional system dynamics based on 𝑞4 for the values of 𝑎0 = 0.2 and 𝑏0 = 0.5. Therefore, we noted that values of 𝑞4 in the intervals and in the intervals , [0.9272, 0.9439], [0.945, 0.9459], [0.9538,0.9548], [0.9606,0.9619], and [0.9801, 0.9833] have periodic behavior for displacement (x1) and velocity (x2). Thus, we used Kc to confirm these intervals obtained from the bifurcation diagrams. For other intervals, the behavior of the equations of motion was chaotic. The intervals were confirmed with the 0–1 Test and with the phase maps and the Poincaré maps with values of 𝑞4 pertaining to those intervals.
We attributed the fractional Bouc–Wen hysterical damping and observed that it dissipates mechanical energy in the oscillator that cannot be harvested. On the other hand, it flatters the resonance of the oscillator (mechanical resonator) by amplifying the frequency bandwidth effect. It can additionally influence the resonance curve, causing its frequency-dependent deformation which can be useful for energy capture. However, to talk more about practical aspects, more systematic studies should be done with frequency sweeps. The Bouc–Wen fractional hysterical damping enriches the dynamics by changing the way it dissipates mechanical energy in the oscillator. On one hand, it flatters the resonance of the oscillator (mechanical resonator) by amplifying the frequency bandwidth effect. On the other hand, it can influence the resonance curve, causing its frequency-dependent deformation, which is useful for energy capture. The fractional Bouc–Wen damping changed the beam vibration and, therefore, the displacements in the piezoceramic material, allowing a higher average power, which establishes that the changes observed in the fractional hysteresis can characterize the piezoelectricity of the material.
Author Contributions
Conceptualization, methodology, validation, formal analysis, resources, data curation, writing—original draft preparation and writing—review and editing M.A.R.; J.M.B.; W.B.L.; J.L.P.F. and G.L.; software, M.A.R. and W.B.L.; visualization, supervision, project administration and funding acquisition A.M.T., G.L. and J.M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Brazilian agencies CAPES and the authors also acknowledge the financial support by the Brazilian Council for Scientific and Technological Development, CNPq, grants 306525/2015-1 and 307371/2017-4, respectively and support of the program of the Ministry of Science and Higher Education in project DIALOG 0019/DLG/2019/10 in the years 2019–2021.Poland DIALOG 0019/DLG/2019/10 in the years 2019–2021.
Data Availability Statement
Not applicable.
Acknowledgments
The authors acknowledge the support from the Brazilian agencies CAPES and the authors also acknowledge the financial support by the Brazilian Council for Scientific and Technological Development, CNPq, grants 306525/2015-1 and 307371/2017-4, respectively and support of the program of the Ministry of Science and Higher Education in project DIALOG 0019/DLG/2019/10 in the years 2019–2021.Poland DIALOG 0019/DLG/2019/10 in the years 2019–2021.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The numerical calculus for the fractional derivative operator the fractional derivative operator assumes that the fact that for a wide class of functions the three definitions—Grunwald Letnikov, Riemman-Liouville, and Caputo—are equivalent if f(a) = 0. The relation for the explicit numerical approximation of q-th derivative at the points kh, (k = 1, 2, …) has the following form:
where is the memory length, tk = kh, h is the time step for the calculation and are binomial coefficients. For the calculation of the following expressions are considered:
The Binomial coefficients can be expressed using the gamma function. We will describe how to express the previous equation in the form of gamma functions, however, in the discretization of our work, there is no use. Therefore, if we consider f(t) ≤ M, an estimate for the memory length , providing the required accuracy ϵ, is easily established:
Some examples of algorithms are described in [] to clarify the algorithms used.
References
- Ribeiro, M.A.; Tusset, A.M.; Lenz, W.B.; Felix, J.L.P.; Litak, G.; Balthazar, J.M. On non-ideal and fractional dynamics of a magneto piezo elastic oscillator with Bouc-Wen damping to harvesting energy. In DSTA-2021 Conference Books—Abstracts, Proceedings of the 16th International Conference of Dynamical Systems—Theory and Applications, Łódź, Poland, 6–9 December 2021; Awrejcewicz, J., Kaźmierczak, M., Mrozowski, J., Olejnik, P., Eds.; Marek Kaźmierczak Editor: Łódź, Poland; pp. 103–104. [CrossRef]
- Rocha, R.T.; Tusset, A.M.; Ribeiro, M.A.; Lenz, W.B.; Junior, R.H.; Jarzebowska, E.; Balthazar, J.M. On the positioning of a piezoelectric material in the energy harvesting from a nonideally excited portal frame. J. Comput. Nonlinear Dyn. 2020, 15, 121002-12. [Google Scholar] [CrossRef]
- Wang, J.; Gu, S.; Zhang, C.; Hu, G.; Chen, G.; Yang, K.; Li, H.; Lai, Y.; Litak, G.; Yurchenko, D. Hybrid wind energy scavenging by coupling vortex-induced vibrations and galloping. Energy Convers. Manag. 2020, 213, 112835. [Google Scholar] [CrossRef]
- Holmes, P. A nonlinear oscillator with a strange attractor. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Sci. 1979, 292, 419–448. [Google Scholar]
- Wu, Z.; Harne, R.L.; Wang, K.W. Excitation-induced stability in a bistable Duffing oscillator: Analysis and experiments. J. Comput. Nonlinear Dyn. 2015, 10, 011016-7. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Piezoelectric Energy Harvesting; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Erturk, A.; Hoffmann, J.; Inman, D.J. A piezomagnetoelastic structure for broadband vibration energy harvesting. Appl. Phys. Lett. 2009, 94, 254102. [Google Scholar] [CrossRef]
- Litak, G.; Friswell, M.I.; Adhikari, S. Magnetopiezoelastic energy harvesting driven by random excitations. Appl. Phys. Lett. 2010, 96, 214103-3. [Google Scholar] [CrossRef]
- Kononenko, V.O. Vibrating Systems with A Limited Power Supply; Iliffe: Cambridge, London, UK, 1969. [Google Scholar]
- Felix, J.L.P.; Bianchin, R.P.; Almeida, A.; Balthazar, J.M.; Rocha, R.T.; Brasil, R.M. On energy transfer between vibration modes under frequency-varying excitations for energy harvesting. Appl. Mech. Mater. 2016, 849, 65–75. [Google Scholar] [CrossRef]
- Wang, L.X.; Willatzen, M. Nonlinear dynamical model for hysteresis based on nonconvex potential energy. J. Eng. Mech. 2007, 133, 506–513. [Google Scholar] [CrossRef]
- Noll, M.U.; Lentz, L.; Wagner, U.V. Comparison of the dynamics of a Duffing equation model and experimental results for a bistable beam beam in magnetoelastic energy harvesting. Tech. Mech. 2020, 40, 111–119. [Google Scholar]
- Wang, L.; Lu, Z.R. Identification of Bouc-Wen hysteretic parameters based on enhanced response sensitivity approach. J. Phys. 2017, 842, 012021. [Google Scholar] [CrossRef]
- Kumar, J.A.; Sundar, D.S. A numerical study on vibration control of a nonlinear Jeffcott rotor via Bouc-Wen model. FME Trans. 2019, 47, 190–194. [Google Scholar] [CrossRef]
- Kang, S.; Wu, H.; Li, Y.; Yang, X.; Yao, J. A Fractional-Order Normalized Bouc–Wen Model for Piezoelectric Hysteresis Nonlinearity. IEEE/ASME Trans. Mechatron. 2022, 27, 126–136. [Google Scholar] [CrossRef]
- Lu, Y.; Shan, J.; Gabbert, U.; Qi, N. Hysteresis and creep modeling and compensation for a piezoelectric actuator using a fractional-order Maxwell resistive capacitor approach. Smart Mater. Struct. 2013, 22, 115020. [Google Scholar] [CrossRef]
- Barba-Franco, J.J.; Gallegos, A.; Jaimes-Reátegui, R.; Pisarchik, A.N. Dynamics of a ring of three fractional-order Duffing oscillators. Chaos Solitons Fractals 2022, 155, 111747. [Google Scholar] [CrossRef]
- Erturk, A.; Inman, D.J. Broadband piezoelectric power generation on high-energy orbits of the bistable Duffing oscillator with electromechanical coupling. J. Sound Vib. 2011, 330, 2339–2353. [Google Scholar] [CrossRef]
- Elvin, N.; Erturk, A. Advances in Energy Harvesting Methods; Springer Science: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Wang, W.; Cao, J.; Bowen, C.R.; Inman, D.J.; Lin, J. Performance enhancement of nonlinear asymmetric bistable energy harvesting from harmonic, random and human motion excitations. Appl. Phys. Lett. 2018, 112, 213903. [Google Scholar] [CrossRef]
- Triplett, A.; Quinn, D.D. The effect of non-linear piezoelectric coupling on vibration-based energy harvesting. J. Intell. Mater. Syst. Struct. 2009, 20, 1959–1967. [Google Scholar] [CrossRef]
- Norenberg, J.P.; Cunha, A.; da Silva, S.; Varoto, P.S. Global sensitivity analysis of asymmetric energy harvesters. Nonlinear Dyn. 2022, 109, 443–458. [Google Scholar] [CrossRef]
- Litak, G.; Friswell, M.I.; Kwuimy, C.A.K.; Adhikari, S.; Borowiec, M. Energy harvesting by two magnetopiezoelastic oscillators with mistuning. Theor. Appl. Mech. Lett. 2012, 2, 043009. [Google Scholar] [CrossRef]
- Amin Karami, M.; Inman, D.J. Powering pacemakers from heartbeat vibrations using linear and nonlinear energy harvesters. Appl. Phys. Lett. 2012, 100, 042901. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Alanazi, R.; Sedighi, H.M. Thermal plane waves in unbounded non-local medium exposed to a moving heat source with a non-singular kernel and higher order time derivatives. Eng. Anal. Bound. Elem. 2022, 140, 464–475. [Google Scholar] [CrossRef]
- Hilal, M.I. Thermomechanical interactions of rotating thermoelastic magneto-microelongated medium heated by laser and initially stressed via non-local elasticity and GN III. Acta Mech. 2022, 233, 5183–5197. [Google Scholar] [CrossRef]
- Zhou, S.; Cao, J.; Inman, D.J.; Lin, J.; Li, D. Harmonic balance analysis of nonlinear tristable energy harvesters for performance enhancement. J. Sound Vib. 2016, 373, 223–235. [Google Scholar] [CrossRef]
- Lee, A.J.; Inman, D.J. Electromechanical modelling of a bistable plate with macro fiber composites under nonlinear vibrations. J. Sound Vib. 2019, 446, 326–342. [Google Scholar] [CrossRef]
- Fang, S.; Zhou, S.; Yurchenko, D.; Yang, T.; Liao, W.H. Multistability phenomenon in signal processing, energy harvesting, composite structures, and metamaterials: A review. Mech. Syst. Signal Process. 2022, 166, 108419. [Google Scholar] [CrossRef]
- Shahsavar, M.; Ashory, M.R.; Khatibi, M.M. Increasing the efficiency of a bistable beam beam energy harvester exploiting vibro-impact effects. J. Intell. Mater. Syst. Struct. 2022, 1045389X221115703. [Google Scholar] [CrossRef]
- Abedini, A.; Wang, F. Energy harvesting of a frequency up-conversion piezoelectric harvester with controlled impact. Eur. Phys. J. Spec. Top. 2019, 228, 1459–1474. [Google Scholar] [CrossRef]
- Ghouli, Z.; Litak, G. Effect of High-Frequency Excitation on a Bistable Energy Harvesting System. J. Vib. Eng. Technol. 2022, 1–8. [Google Scholar] [CrossRef]
- Harne, R.L.; Wang, K.W. A review of the recent research on vibration energy harvesting via bistable systems. Smart Mater. Struct. 2013, 22, 023001. [Google Scholar] [CrossRef]
- Syta, A.; Bowen, C.R.; Kim, H.A.; Rysak, A.; Litak, G. Experimental analysis of the dynamical response of energy harvesting devices based on bistable laminated plates. Meccanica 2015, 50, 1961–1970. [Google Scholar] [CrossRef]
- Wang, K.W.; Harne, R.L. Harnessing Bistable Structural Dynamics: For Vibration Control, Energy Harvesting and Sensing; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Safaei, M.; Sodano, H.A.; Anton, S.R. A review of energy harvesting using piezoelectric materials: State-of-the-art a decade later (2008–2018). Smart Mater. Struct. 2019, 28, 113001. [Google Scholar] [CrossRef]
- Daqaq, M.F.; Masana, R.; Erturk, A.; Quinn, D.D. On the role of nonlinearities in vibratory energy harvesting: A critical review and discussion. Appl. Mech. Rev. 2014, 66, 40801. [Google Scholar] [CrossRef]
- Huang, D.; Zhou, S.; Litak, G. Theoretical analysis of multistable energy harvesters with high-order stiffness terms. Commun. Nonlinear Sci. Numer. Simul. 2019, 69, 270–286. [Google Scholar] [CrossRef]
- Osinaga, S.; Febbo, M.; Machado, S. Effect of elastic restraints in the modeling of prestressed piezoelectric energy harvesters. Appl. Math. Model. 2022, 101, 573–585. [Google Scholar] [CrossRef]
- Kang, S.; Wu, H.; Yu, S.; Li, Y.; Yang, X.; Yao, J. Modeling and control of a six-axis parallel piezo-flexural micropositioning stage with cross-coupling hysteresis nonlinearities. In Proceedings of the 2020 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Boston, MA, USA, 6–9 July 2020; pp. 1350–1355. [Google Scholar]
- Spanos, P.D.; Di Matteo, A.; Pirrotta, A. Steady-state dynamic response of various hysteretic systems endowed with fractional derivative elements. Nonlinear Dyn. 2019, 98, 3113–3124. [Google Scholar] [CrossRef]
- Solovyov, A.M.; Semenov, M.E.; Meleshenko, P.A.; Barsukov, A.I. Bouc-Wen model of hysteretic damping. Procedia Eng. 2017, 201, 549–555. [Google Scholar] [CrossRef]
- Ismail, M.; Ikhouane, F.; Rodellar, J. The hysteresis Bouc-Wen model, a survey. Arch. Comput. Methods Eng. 2009, 16, 161–188. [Google Scholar] [CrossRef]
- Ikhouane, F.; Rodellar, J. On the hysteretic Bouc–Wen model. Nonlinear Dyn. 2005, 42, 63–78. [Google Scholar] [CrossRef]
- Petrás, I. Fractional Derivatives, Fractional Integrals, and Fractional Differential Equations in Matlab. In Engineering Education and Research Using MATLAB; Ali, H.A., Ed.; INTECH Open Access Publisher: Rijeka, Croatia, 2011; pp. 239–264. [Google Scholar]
- Petrás, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Baleanu, D.; Avkar, T. Lagrangians with linear velocities within riemann-liouville fractional derivatives. Il Nuovo Cim. B 2004, 119, 73–79. [Google Scholar]
- Atangana, A.; Gómez-Aguilar, J.F. Numerical approximation of riemann-liouville definition of fractional derivative: From riemann-liouville to atangana-baleanu. Numer. Methods Partial. Differ. Equ. 2018, 34, 1502–1523. [Google Scholar] [CrossRef]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific Singapore: Singapore, 2000; Volume 35. [Google Scholar]
- Iliuk, I.; Balthazar, J.M.; Tusset, A.M.; Piqueira, J.R.; de Pontes, B.R.; Felix, J.L.; Bueno, A.M. Application of passive control to energy harvester efficiency using a nonideal portal frame structural support system. J. Intell. Mater. Syst. Struct. 2014, 25, 417–429. [Google Scholar] [CrossRef]
- Priya, S.; Inman, D.J. (Eds.) Energy Harvesting Technologies; Springer: New York, NY, USA, 2009; Volume 21, p. 2. [Google Scholar]
- Stoleriu, L.; Ciomaga, C.; Fochi, F.; Ochoa, P.; Fernández, J.F.; Galassi, C.; Buscaglia, V.; Mitoseriu, L. Mechanically clamped PZT ceramics investigated by First-order reversal curves diagram. Process. Appl. Ceram. 2010, 4, 209–214. [Google Scholar] [CrossRef]
- Silva, L.L.; Savi, M.A.; Monteiro, P.C., Jr.; Netto, T.A. Effect of the piezoelectric hysteretic behavior on the vibration-based energy harvesting. J. Intell. Mater. Syst. Struct. 2013, 24, 1278–1285. [Google Scholar] [CrossRef]
- Gottwald, G.A.; Melbourne, I. A new test for chaos in deterministic systems. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2004, 460, 603–611. [Google Scholar] [CrossRef]
- Gottwald, G.; Melbourne, I. Testing for chaos in deterministic systems with noise. Phys. D Nonlinear Phenom. 2005, 212, 100–110. [Google Scholar] [CrossRef]
- Litak, G.; Syta, A.; Wiercigroch, M. Identification of chaos in a cutting process by the 0–1 test. Chaos Solitons Fractals 2009, 40, 2095–2101. [Google Scholar] [CrossRef]
- Fractional Order Chaotic Systems. Available online: https://www.mathworks.com/matlabcentral/fileexchange/27336-fractional-order-chaotic-systems (accessed on 21 November 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).