Towards Optimal Robustness of Network Controllability by Nested-Edge Rectification
Abstract
1. Introduction
- Due to the impossibility of theoretical analysis and exhaustive searching for large-sized networks, an exhaustive search was executed on feasible small-sized networks, and NRS was obtained. NRS satisfies ENC and has great controllability robustness.
- NER is proposed to improve the robustness of the network controllability against random attacks by constructing NRS in the network. Meanwhile, NER can be applied to networks with different scales. In addition, NER constructs a backbone ring through maximum matching, which rapidly improves the initial controllability of networks.
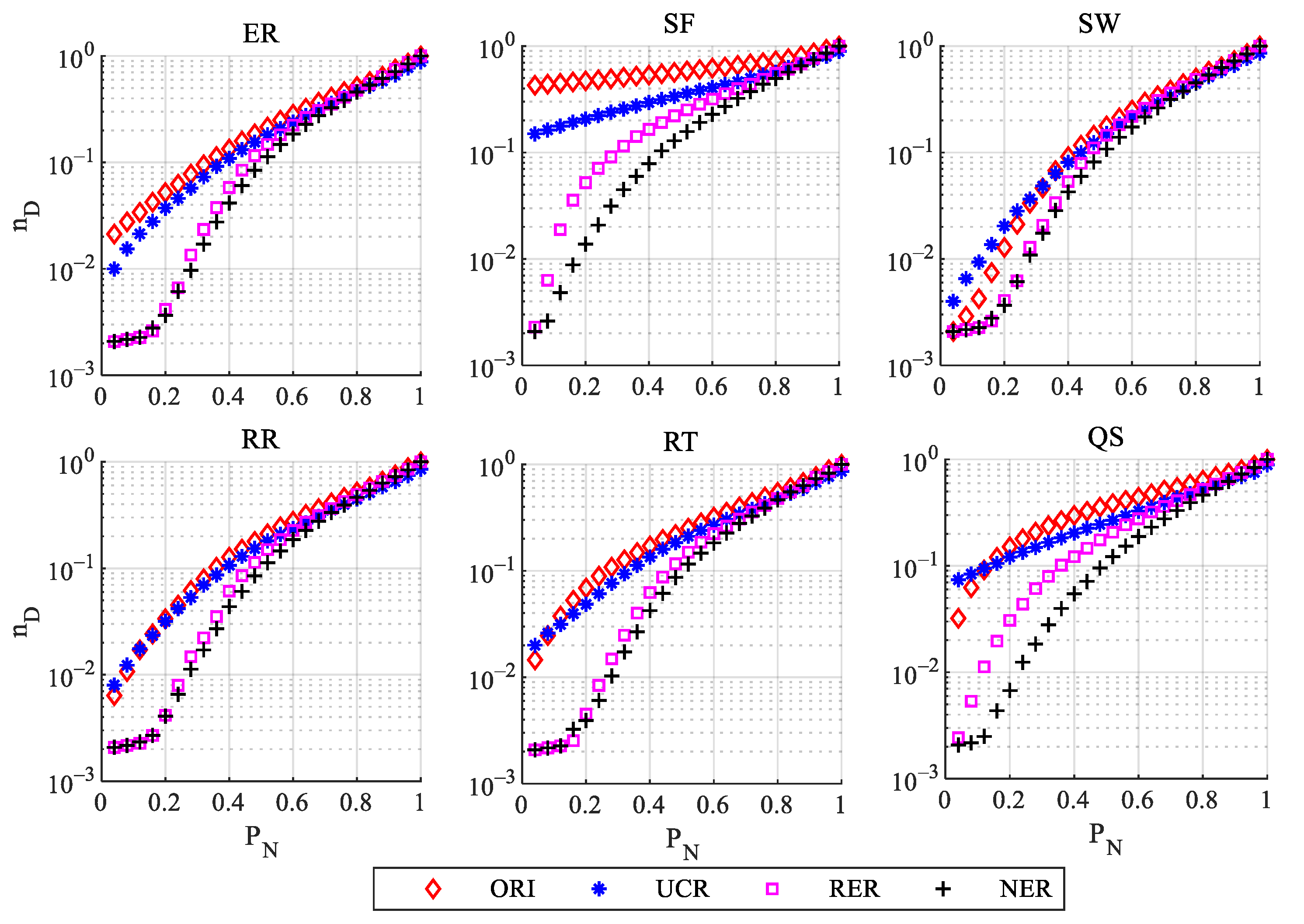
- The controllability robustness can be improved on six synthetic networks and real-world networks by NER, and NER is better than other methods of edge rectification. For networks with poor controllability robustness, such as the scale-free network, NER improves controllability robustness more obviously.
2. Network Controllability and Its Robustness
3. Nested Ring Structure and Optimization Strategy
3.1. Nested Ring Structure
3.2. Nested Edge Rectification
| Algorithm 1 Nested ring rectification strategy |
| input:The adjacency matrix of the network A; the number of network nodes N; the number of network edges M; Number of reconnected edges TIMES |
| Output: Adjacency matrix of the optimized network A |
| t ← 0; |
| if backbone does not exists on the network then |
| nodes that are only the started node of an edge in a maximum matching |
| nodes that are only the ended node of an edge in a maximum matching |
| for to do |
| node with the largest out-degree |
| node with the largest in-degree among the successors of node i |
| delete edge |
| add edge |
| end for |
| Number nodes as through backbone; |
| end if |
| for to do |
| for to N do |
| if do not exist edge then |
| node with the largest out-degree |
| The node with the largest outdegree among the successors of node i is except |
| delete edge |
| add edge |
| if then |
| return A |
| end if |
| end if |
| end for |
| end for |
| return A |
3.3. Computational Complexity
4. Simulation Results
4.1. Results on Synthetic Networks
4.2. Results of Real-World Networks
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

| Number of Edge Rectification | Strategy | ER | SF | RT | RR | SW | QS |
|---|---|---|---|---|---|---|---|
| 0 | 0.2957 | 0.6186 | 0.3135 | 0.2792 | 0.2593 | 0.3927 | |
| UCR | 0.2890 | 0.4891 | 0.3022 | 0.2801 | 0.2643 | 0.3783 | |
| 500 | RER | 0.2512 | 0.4162 | 0.2560 | 0.2477 | 0.2445 | 0.3190 |
| NER | 0.2442 | 0.3366 | 0.2478 | 0.2418 | 0.2368 | 0.2811 | |
| UCR | 0.2837 | 0.4490 | 0.2998 | 0.2799 | 0.2669 | 0.3621 | |
| 750 | RER | 0.2448 | 0.3542 | 0.2473 | 0.2435 | 0.2422 | 0.2913 |
| NER | 0.2352 | 0.2815 | 0.2368 | 0.2346 | 0.2295 | 0.2538 | |
| UCR | 0.2831 | 0.4176 | 0.2977 | 0.2798 | 0.2672 | 0.3487 | |
| 1000 | RER | 0.2417 | 0.3050 | 0.2436 | 0.2416 | 0.2406 | 0.2710 |
| NER | 0.2241 | 0.2549 | 0.2256 | 0.2243 | 0.2236 | 0.2303 |
| Number of Edge Rectification | Strategy | ER | SF | RT | RR | SW | QS |
|---|---|---|---|---|---|---|---|
| 0 | 0.2955 | 0.6709 | 0.3130 | 0.2796 | 0.2591 | 0.4284 | |
| UCR | 0.2895 | 0.5242 | 0.3028 | 0.2809 | 0.2640 | 0.4166 | |
| 1500 | RER | 0.2512 | 0.4524 | 0.2562 | 0.2476 | 0.2439 | 0.3566 |
| NER | 0.2437 | 0.3606 | 0.2482 | 0.2417 | 0.2354 | 0.2941 | |
| UCR | 0.2885 | 0.4798 | 0.3004 | 0.2796 | 0.2669 | 0.3989 | |
| 2250 | RER | 0.2439 | 0.3856 | 0.2465 | 0.2433 | 0.2419 | 0.3235 |
| NER | 0.2355 | 0.2926 | 0.2368 | 0.2339 | 0.2291 | 0.2618 | |
| UCR | 0.2871 | 0.4428 | 0.2971 | 0.2800 | 0.2687 | 0.3811 | |
| 3000 | RER | 0.2423 | 0.3301 | 0.2425 | 0.2412 | 0.2403 | 0.2951 |
| NER | 0.2238 | 0.2632 | 0.2249 | 0.2238 | 0.2231 | 0.2332 |
References
- Barabási, A.L. Network Science; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Newman, M.E. Networks: An Introduction; Oxford University Press: London, UK, 2010. [Google Scholar]
- Chen, G.R.; Wang, X.F.; Li, X. Fundamentals of Complex Networks: Models, Structures and Dynamics; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Chen, G.R.; Lou, Y. Naming Game:Models, Simulation and Analysis; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Yang, L.X.; Yang, X.F.; Liu, J.M. Epidemics of computer viruses: A complex-network approach. Appl. Math. Comput. 2013, 219, 8705–8717. [Google Scholar] [CrossRef]
- Xu, Z.W.; Harriss, R. Exploring the structure of the US intercity passenger air transportation network: A weighted complex network approach. GeoJournal 2008, 73, 87–102. [Google Scholar] [CrossRef]
- Buldyrev, S.V.; Parshani, R.; Paul, G. Catastrophic cascade of failures in interdependent networks. Nature 2010, 464, 1025–1028. [Google Scholar] [CrossRef] [PubMed]
- Cherifi, H.; Palla, G.; Szymanski, B.K.; Lu, X. On community structure in complex networks: Challenges and opportunities. Appl. Netw. Sci. 2019, 4, 117. [Google Scholar] [CrossRef]
- Liu, X.; Chen, T. Synchronization of complex networks via aperiodically intermittent pinning control. IEEE Trans. Autom. Control 2015, 60, 3316–3321. [Google Scholar] [CrossRef]
- Shi, D.H.; Lü, L.; Chen, G.R. Totally homogeneous networks. Natl. Sci. Rev. 2019, 6, 962–969. [Google Scholar] [CrossRef]
- Fan, T.; Lü, L.; Shi, D.H. Towards the cycle structures in complex network: A new perspective. arXiv 2019, arXiv:1903.01397. [Google Scholar]
- Zhao, P.; Han, J. On graph query optimization in large networks. Proc. VLDB Endow. 2010, 3, 340–351. [Google Scholar] [CrossRef]
- Lou, Y.; He, Y.D.; Wang, L. Knowledge-Based Prediction of Network Controllability Robustness. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 5739–5750. [Google Scholar] [CrossRef]
- Menichetti, G.; Dall’Asta, L.; Bianconi, G. Network controllability is determined by the density of low in-degree and out-degree nodes. Phys. Rev. Lett. 2014, 113, 078701. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, T. Controllability analysis for a networked dynamic system with autonomous subsystems. IEEE Trans. Autom. Control 2016, 62, 3408–3415. [Google Scholar] [CrossRef]
- Xiang, L.Y.; Chen, F.; Ren, W. Advances in network controllability. IEEE Circuits Syst. Mag. 2019, 19, 8–32. [Google Scholar] [CrossRef]
- Guang-Ren, D. High-order system approaches: II. Controllability and full-actuation. Acta Autom. Sin. 2020, 46, 1571–1581. [Google Scholar]
- Lou, Y.; He, Y.D.; Wang, L. Predicting Network Controllability Robustness: A Convolutional Neural Network Approach. IEEE Trans. Cybern. 2022, 52, 4052–4063. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.Y.; Slotine, J.J.; Barabási, A.L. Controllability of complex networks. Nature 2011, 473, 167–173. [Google Scholar] [CrossRef]
- Yuan, Z.; Zhao, C.; Di, Z.; Wang, W.X.; Lai, Y.C. Exact controllability of complex networks. Nat. Commun. 2013, 4, 2447. [Google Scholar] [CrossRef]
- Pósfai, M.; Liu, Y.Y.; Slotine, J.J. Effect of correlations on network controllability. Sci. Rep. 2013, 3, 1067. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Slotine, J.J.; Barabási, A.L. Control centrality and hierarchical structure in complex networks. PLoS ONE 2012, 7, e44459. [Google Scholar] [CrossRef]
- Xiao, Y.D.; Lao, S.Y.; Hou, L.L. Optimization of robustness of network controllability against malicious attacks. Chin. Phys. B 2014, 23, 118902. [Google Scholar] [CrossRef]
- Chan, H.; Akoglu, L. Optimizing network robustness by edge rewiring: A general framework. Data Min. Knowl. Discov. 2016, 30, 1395–1425. [Google Scholar] [CrossRef]
- Louzada, V.H.; Daolio, F.; Herrmann, H.J. Smart rewiring for network robustness. J. Complex Netw. 2013, 1, 150–159. [Google Scholar] [CrossRef]
- Herrmann, H.J.; Schneider, C.M.; Moreira, A.A. Onion-like network topology enhances robustness against malicious attacks. J. Stat. Mech. Theory Exp. 2011, 2011, P01027. [Google Scholar] [CrossRef]
- Wang, L.F.; Zhao, G.T.; Kong, Z. Controllability and Optimization of Complex Networks Based on Bridges. Complexity 2020, 2020, 6695026. [Google Scholar] [CrossRef] [PubMed]
- Lou, Y.; Wang, L.; Tsang, K.F. Towards optimal robustness of network controllability: An empirical necessary condition. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 3163–3174. [Google Scholar] [CrossRef]
- Lou, Y.; Wang, L.; Chen, G.R. Toward Stronger Robustness of Network Controllability: A Snapback Network Model. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 2983–2991. [Google Scholar] [CrossRef]
- Lou, Y.; Wang, L.; Chen, G.R. Enhancing Controllability Robustness of q-Snapback Networks through Redirecting Edges. Research 2019, 2019, 7857534. [Google Scholar] [CrossRef]
- Erdős, P.; Rényi, A. On the strength of connectedness of a random graph. Acta Math. Hung. 1961, 12, 261–267. [Google Scholar] [CrossRef]
- Pu, C.L.; Pei, W.J.; Michaelson, A. Robustness analysis of network controllability. Phys. A Stat. Mech. Its Appl. 2012, 391, 4420–4425. [Google Scholar] [CrossRef]
- Chen, G.R.; Lou, Y.; Wang, L. A comparative study on controllability robustness of complex networks. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 828–832. [Google Scholar] [CrossRef]
- Newman, M.E.J.; Watts, D.J. Renormalization group analysis of the small-world network model. Phys. Lett. A 1999, 263, 341–346. [Google Scholar] [CrossRef]
- Rossi, R.; Ahmed, N. The network data repository with interactive graph analytics and visualization. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015. [Google Scholar]











| Number of Edge Rectification | Strategy | ER | SF | RT | RR | SW | QS |
|---|---|---|---|---|---|---|---|
| 0 | 0.2963 | 0.6557 | 0.3124 | 0.2798 | 0.2605 | 0.4168 | |
| UCR | 0.2884 | 0.5147 | 0.2995 | 0.2796 | 0.2634 | 0.4012 | |
| 1000 | RER | 0.2510 | 0.4414 | 0.2564 | 0.2478 | 0.2437 | 0.3451 |
| NER | 0.2437 | 0.3527 | 0.2482 | 0.2419 | 0.2362 | 0.2900 | |
| UCR | 0.2852 | 0.4696 | 0.2962 | 0.2787 | 0.2657 | 0.3852 | |
| 1500 | RER | 0.2446 | 0.3745 | 0.2472 | 0.2433 | 0.2420 | 0.3121 |
| NER | 0.2353 | 0.2891 | 0.2368 | 0.2338 | 0.2301 | 0.2591 | |
| UCR | 0.2820 | 0.4348 | 0.2927 | 0.2786 | 0.2641 | 0.3682 | |
| 2000 | RER | 0.2419 | 0.3221 | 0.2435 | 0.2412 | 0.2402 | 0.2856 |
| NER | 0.2242 | 0.2603 | 0.2253 | 0.2233 | 0.2228 | 0.2322 |
| Strategy | ER | SF | RT | RR | SW | QS | |
|---|---|---|---|---|---|---|---|
| ORI | INF | INF | 4.8536 | 4.7131 | 5.1819 | 206.6615 | |
| UCR | INF | INF | INF | INF | INF | INF | |
| APL | RER | 4.8772 | 4.3943 | 4.9356 | 4.8762 | 4.9145 | 5.0733 |
| NER | 6.0785 | 5.8503 | 6.3936 | 6.0961 | 7.0076 | 65.9633 | |
| ORI | 3875 | 1351.8 | 4185.7 | 3709.4 | 3849.8 | 205460 | |
| UCR | 4002.3 | 2543.7 | 3867.0 | 3881.2 | 3912.7 | 4304.2 | |
| ABC | RER | 3873.4 | 3390.9 | 3931.7 | 3972.3 | 3910.6 | 4069.0 |
| NER | 5073.4 | 4845.4 | 5388.2 | 5091.0 | 6001.6 | 64898 | |
| ORI | 0.0024 | 0.0526 | 0.0014 | 0.0027 | 0.0020 | 0.0002 | |
| UCR | 0.0033 | 0.0185 | 0.003 | 0.0032 | 0.0019 | 0.0021 | |
| CC | RER | 0.0019 | 0.0072 | 0.0020 | 0.0020 | 0.0019 | 0.0016 |
| NER | 0.1540 | 0.1572 | 0.1616 | 0.1307 | 0.3329 | 0.4094 | |
| ORI | 1.2521 | 9.3584 | 1.3645 | 1.1989 | 1.1215 | 4.0503 | |
| UCR | 1.1291 | 4.0055 | 1.1868 | 1.1929 | 1.1211 | 2.2373 | |
| HO | RER | 1.0166 | 2.0102 | 1.0217 | 1.0144 | 1.0009 | 1.5408 |
| NER | 1.0115 | 1.1357 | 1.0366 | 1.0070 | 1.0001 | 1.2281 | |
| ORI | 1.2486 | 9.2805 | 1.4021 | 1.2171 | 1.1311 | 1.2288 | |
| UCR | 1.2401 | 4.2642 | 1.3044 | 1.2238 | 1.1298 | 1.2392 | |
| HI | RER | 1.0163 | 2.0038 | 1.0203 | 1.0137 | 1.0106 | 1.0132 |
| NER | 1.0280 | 3.3571 | 1.0371 | 1.0248 | 1.0233 | 1.0173 |
| Network | N | M |
|---|---|---|
| Roget | 1022 | 5075 |
| ia-email-univ | 1133 | 5451 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Z.; Nie, J.; Li, J. Towards Optimal Robustness of Network Controllability by Nested-Edge Rectification. Axioms 2022, 11, 639. https://doi.org/10.3390/axioms11110639
Yu Z, Nie J, Li J. Towards Optimal Robustness of Network Controllability by Nested-Edge Rectification. Axioms. 2022; 11(11):639. https://doi.org/10.3390/axioms11110639
Chicago/Turabian StyleYu, Zhuoran, Junfeng Nie, and Junli Li. 2022. "Towards Optimal Robustness of Network Controllability by Nested-Edge Rectification" Axioms 11, no. 11: 639. https://doi.org/10.3390/axioms11110639
APA StyleYu, Z., Nie, J., & Li, J. (2022). Towards Optimal Robustness of Network Controllability by Nested-Edge Rectification. Axioms, 11(11), 639. https://doi.org/10.3390/axioms11110639





