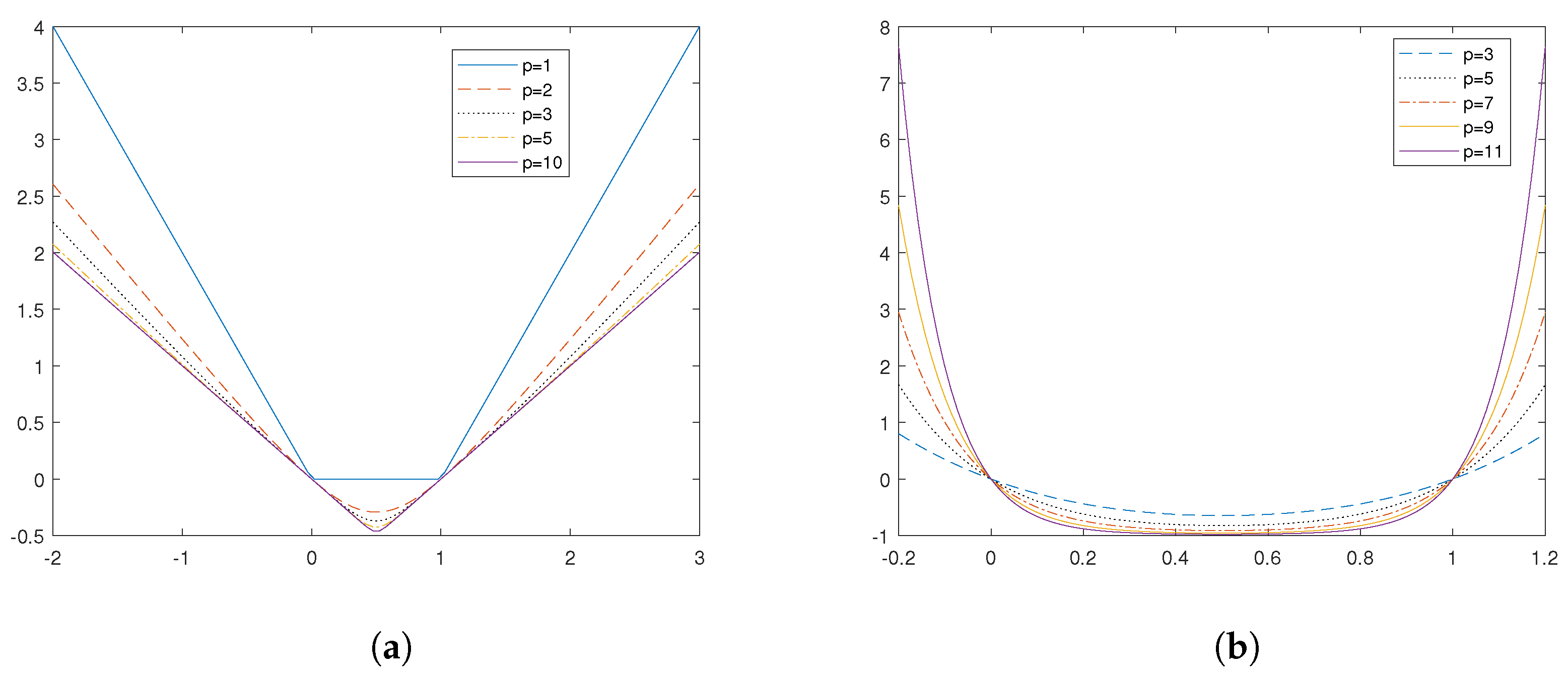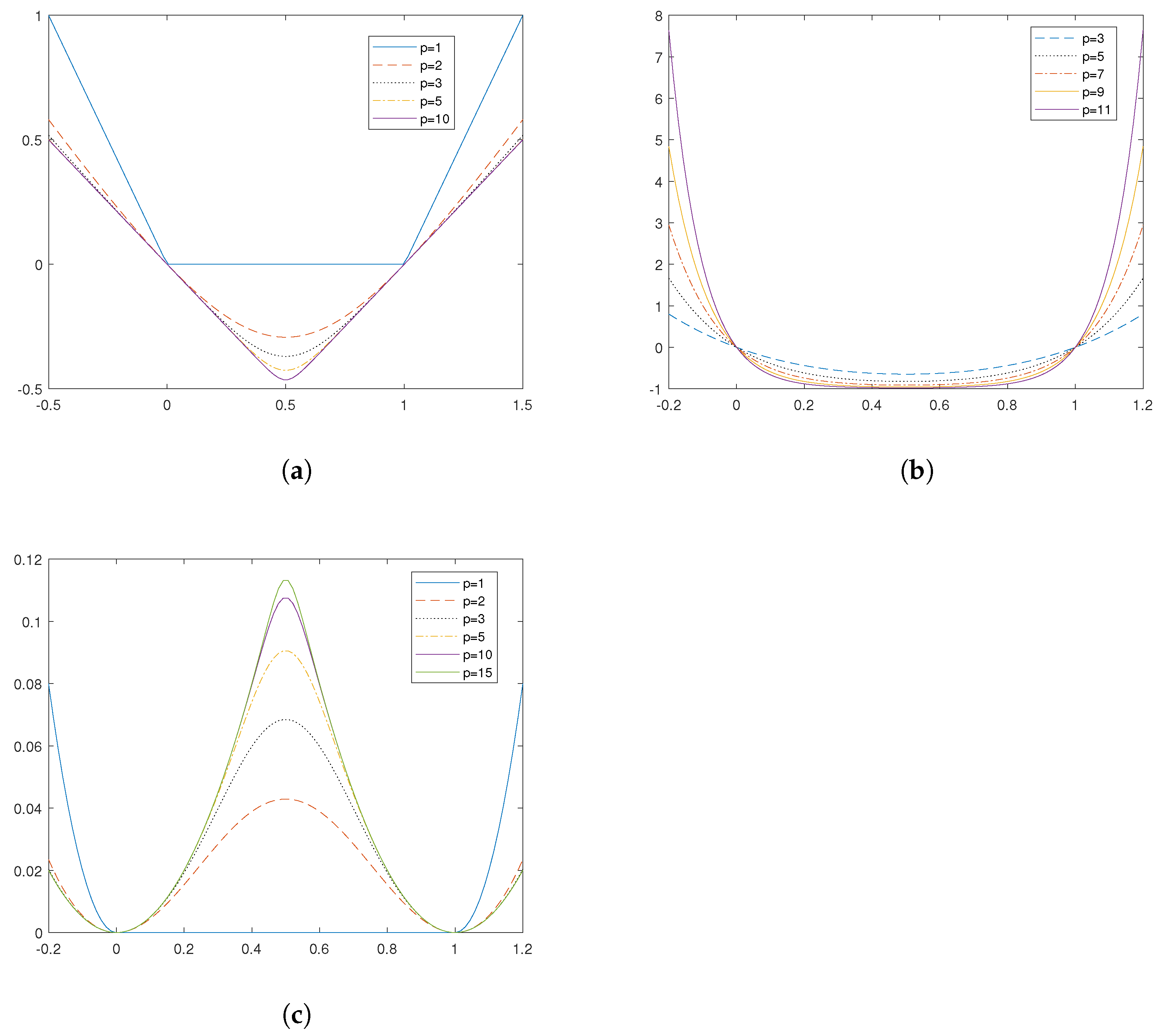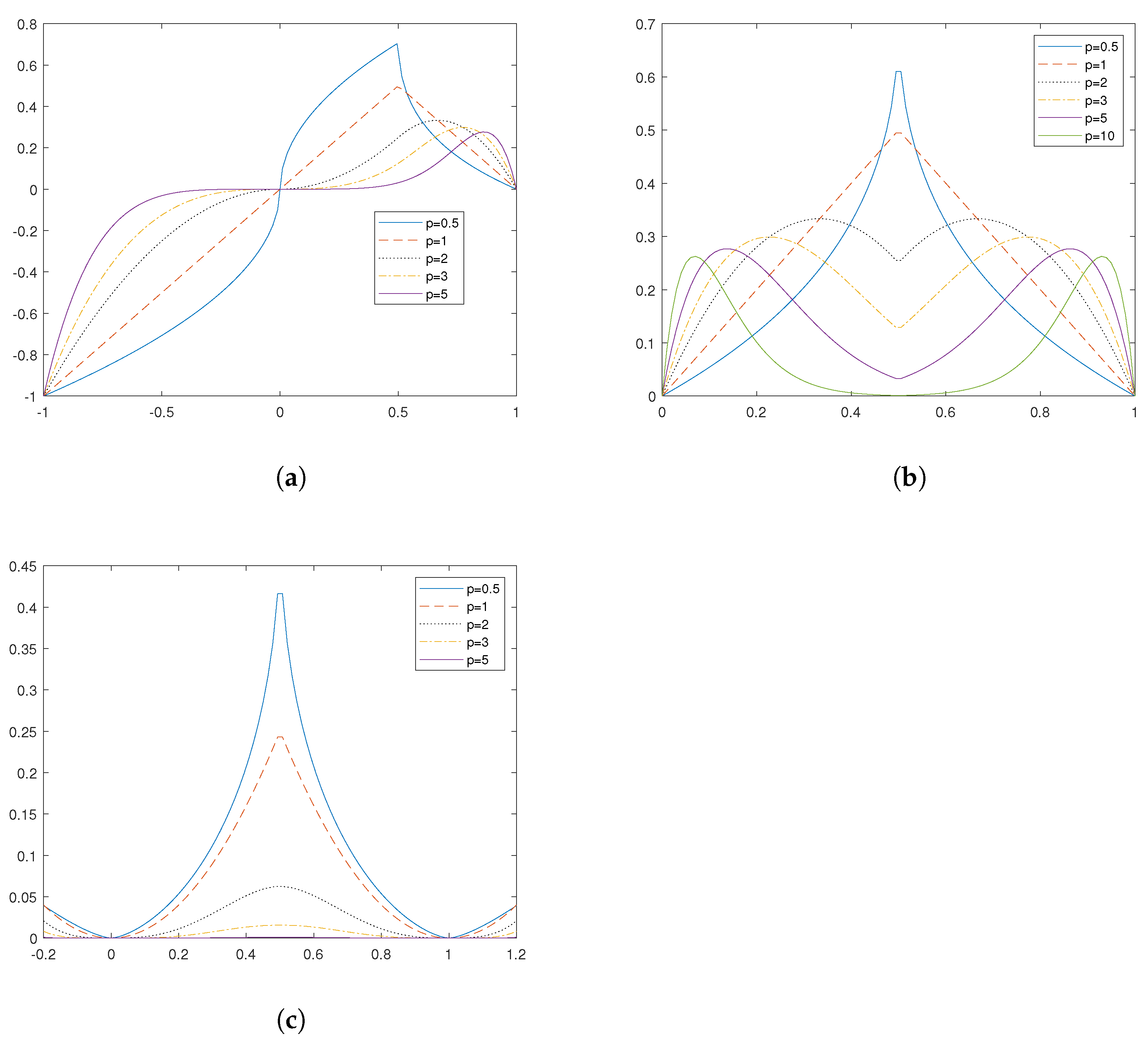1. Introduction
The nonlinear complementarity problem (NCP) is finding a vector
such that
where
is the Euclidean inner product and
F is a function from
to
. Since a few decades ago, the NCP has attracted significant attention due to its various applications in areas such as economics, engineering, and information engineering [
1]. There are many methods proposed for solving the NCP. One popular approach is to reformulate the NCP as a system of nonlinear equations, whereas the other approach is to recast the NCP as an unconstrained minimization problem. Both methods rely on the so-called NCP function. A function
is said to be an NCP function if it satisfies
In light of the NCP function, one can define the vector-valued function
by
where
is a mapping from
to
. Consequently, solving the NCP is equivalent to solving a system of equation
. In particular, it also induces a merit function of the NCP which is given by
It is clear that the global minimizer of
is the solution to the NCP. During the past few decades, several NCP functions have been discovered [
2,
3,
4,
5,
6,
7]. A well-known NCP function is the Fischer–Burmeister function [
8,
9]
, defined as
where
. In [
10], Tseng did an extension of the Fischer–Burmeister function, in which a 2-norm is relaxed to a general
p-norm. In other words, the so-called generalized FB function is defined by
where
and
. Similarly, it induces a merit function
given by
where
.
Another popular NCP function is the natural residual function [
4],
given by
Is there a similar extension for the natural residual NCP function? Wu, Ko and Chen answered this question in [
4]. The extension is kind of discrete generalization because they defined the function
by
where
and
p is an odd integer. Recently, the idea of discrete generalization of natural residual function has beei applied to construct discrete Fischer–Burmeister functions. More specifically,
is defined by
where
and
p is an odd integer. If
, then it is exactly the classical Fischer–Burmeister function (see [
4,
11]). The graph of
is not symmetric. Is it possible to construct a symmetric natural residual NCP function? Chang, Yang, and Chen answered this question in [
2]. Note that the function
can also be expressed as a piecewise function:
where
and
p is an odd integer. They use this expression of
to modify the part on
, and achieve symmetrization of
as below:
where
and
p is an odd integer. Surprisingly, it is still an NCP function.
How about the merit function induced by
? Observing that the merit function has squared terms, Chang, Yang, and Chen combined
and
together and constructed
as
where
and
p is an odd integer.
Recently, more and more NCP functions have been discovered. As mentioned, Wu et al. [
4] proposed a discrete type of natural residual function. Regarding this discrete counterpart, Alcantara and Chen [
1] consider a continuous type of natural residual function as below:
where
is a real number and
The main principle behind their work is described as follows. If
is a bijection mapping and
is a given NCP function, then
is also an NCP function. Hence, it can be verified that
is an NCP function by employing the bijective function
, see [
12]. Note that when
p is an positive odd integer, it reduces to the discrete type of a natural residual function, that is,
.
For further symmetrization, using the above idea in (
5) and (
6), one can obtain a continuous type of natural residual functions [
12]:
and its corresponding merit function
where
. Again, when
p is an odd integer, we see the beloe relations,
The NCP functions can also be constructed by certain invertible functions. What kind of inverse functions can be applied to construct the NCP functions? Lee, Chen, and Hu [
6] figured it out in ([
6], Proposition 3.8). In particular, let
be a continuous differentiable function and
with
. They chose functions of
and
satisfying the below conditions to construct new NCP functions:
- (i)
f is invertible on .
- (ii)
is a strictly monotonically increasing function.
- (iii)
, , and .
More specifically, it is shown that the function
is an NCP function. For example, taking
, we see that
is invertible on
and the inverse function is
. It is easy to see that
,
. Thus,
is strictly monotone increasing on
. For third condition, we take
, which gives
on
and
on
. We list some more examples of
f and
g as below. Examples of
are
and examples of
are
In summary, nine corresponding NCP functions are generated by using the above
and
.
In [
13], Tsai et al. discussed the geometry of curves on Fischer–Burmeister function surfaces, which are intersected by the plane
for
. They parametrized the curves by considering
and
and defined the vector valued function
and
as
and
, respectively. Tsai et al. also found the local maxima and minima and studied the convexity of curves.
In this paper, we follow a similar idea to the one in [
13] to investigate the curves, which are the intersection of a vertical plane
and surfaces based on NCP functions. We also have to point out that the study on these curves is very useful to binary quadratic programming. See [
14] for the details. We parametrize the curves by the vector functions
and
, where
and
. Then, we explore the behavior of the curves when the value
p is perturbed. In addition, we discuss the convexity and local minimum and maximum of curves. Although the inflection points cannot be exactly determined, we can still estimate the interval in which the curves are convex such as in ([
14], Proposition 2.1(b)). With the convexity or differentiability of a curve, we discuss the local minimum and maximum.
4. The Convexity of the Curves
In
Section 2, we discussed the convexity of NCP functions. It naturally leads to the convexity of the curves. Although we cannot find the inflection points one by one, we focus on estimating the interval where the curves are convex. In addition, with different
p, the geometric structure of the curves will be changed. The following lemma will be employed to check the convexity.
Lemma 4. (a) If and are convex on an interval, then is also convex on the interval.
- (b)
Let be a convex function and let be a nondecreasing convex function. Then is convex on .
Proof. These are very basic materials which are also well known, see [
16]. □
Proposition 6. Let and be defined as in (11) and (13), respectively. Then, the following hold. See Figure 1. - (a)
For , the function is convex on .
- (b)
When p is an odd integer, the function is convex on .
Proof. (a) First, as indicated in (
11),
Since the curve
is the section of a plane with the surface of the function
, which is convex on
according to Lemma 1(a).
is convex on
.
(b) As shown in (
13),
where
p is an odd integer. Let
and
. It is clear that
is nondecreasing and convex; moreover,
is positive and convex. Then, according to Lemma 4(b),
is convex on
. □
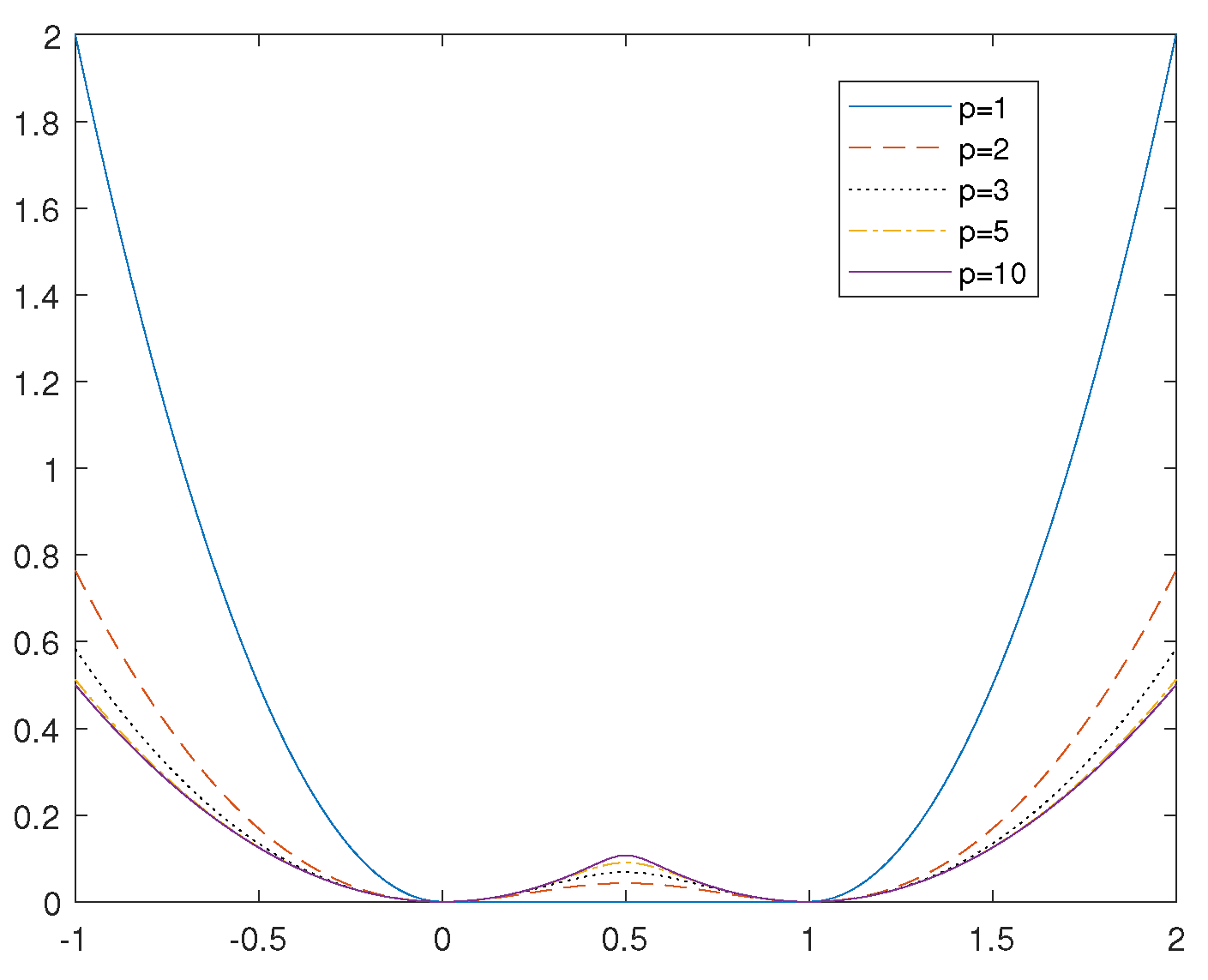
Proposition 7. Let be defined as in (12). Then, for any , the function is convex on and See Figure 2. Proof. As given in (
12),
Let
and
. It is clear that
is nondecreasing and convex on
. Furthermore,
is convex and positive on
. Hence, according to Lemma 4(b),
is convex on
. In addition, due to symmetry,
is also convex on
. □
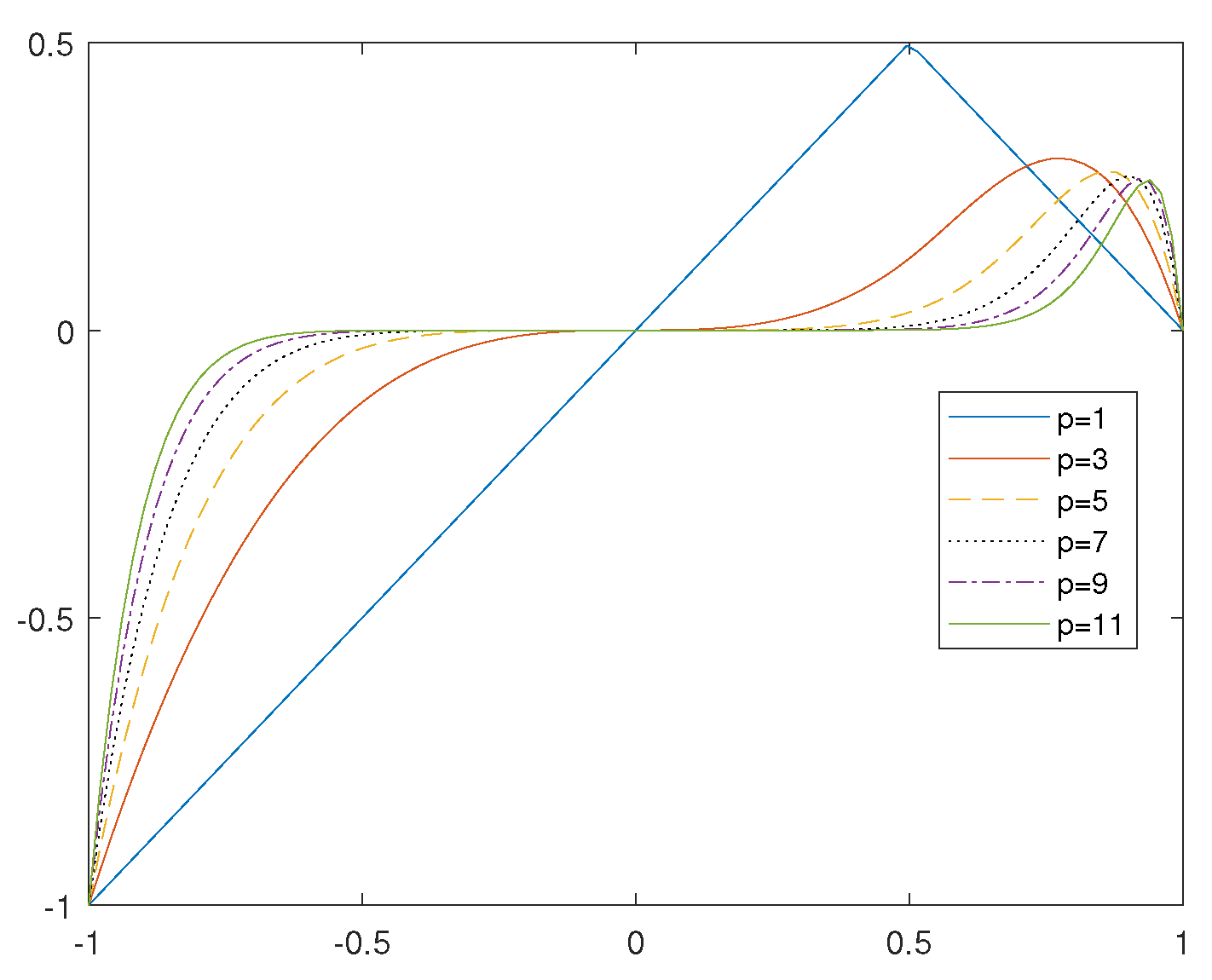
Remark 1. (i)
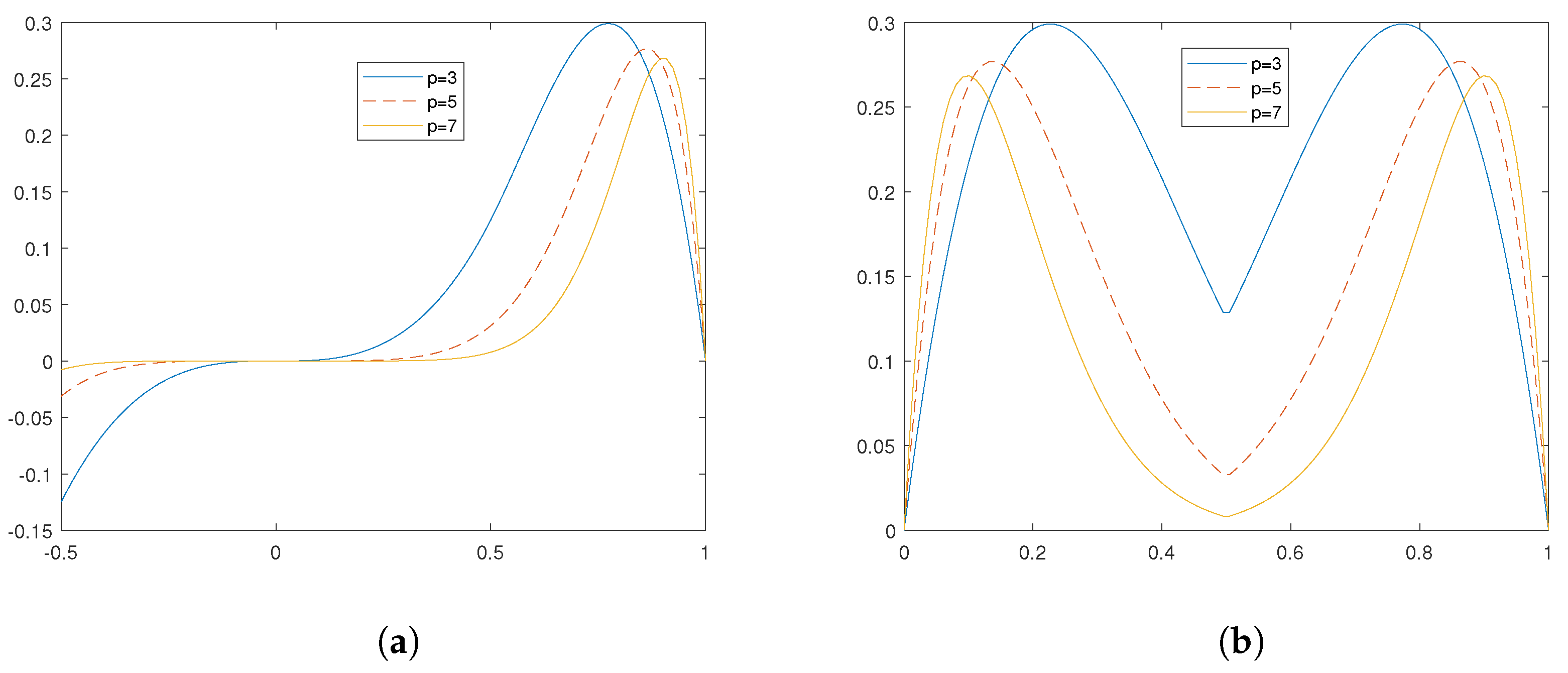
Set . The second derivative of givesFrom this, we know that are two inflection points of the function . Hence, the function is convex on the intervals and . For a general , we have difficulty in determining their infection points. However, let us study their behavior when p goes to ∞ on the interval . When , we have . Hence, the function approaches as p goes to ∞. Similarly, provided , the function approaches as p goes to ∞. Note also that approaches as p goes to ∞.- (ii)
We also examine the behavior of the second derivative of the function at the point which is near . We present the numerical results in Figure 3. Observe that their inflection points approaches , and also that approaches 1 as p goes to ∞.
According to Remark 1 and
Figure 3, we make a conjecture here.
Conjecture 1. Let be defined as in (12). Then, for any , the function has two inflection points , and both approach as p goes to ∞.
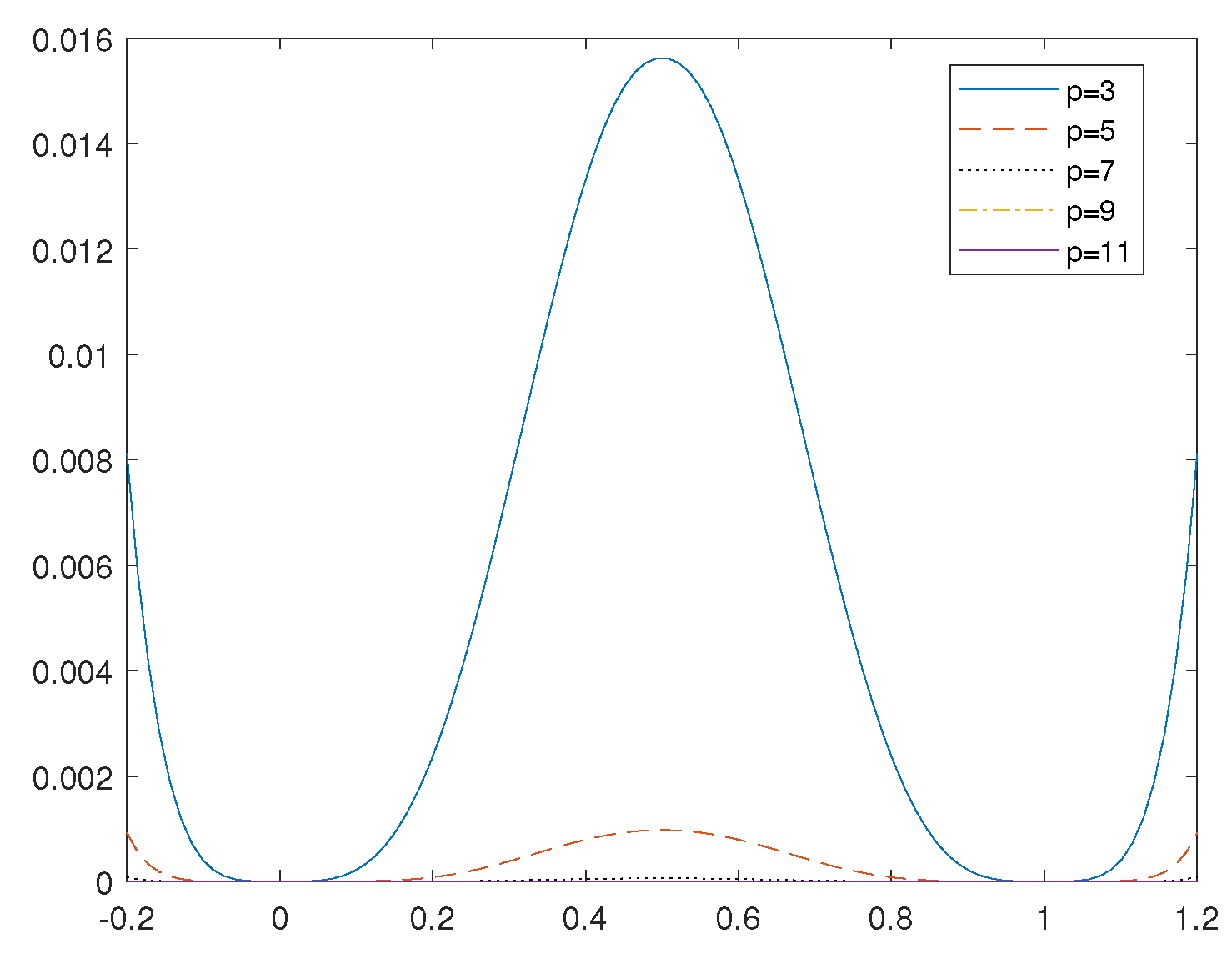
Proposition 8. Let and be defined as in (14) and (15), respectively. Then, when p is an odd integer, the following hold. See Figure 4. - (a)
The function is convex on .
- (b)
The function is convex on .
Proof. (a) As given in (
14),
which says
To proceed, we discuss three subcases:
Case (i): On the interval , we have , which says .
Case (ii): At the points , we have as well.
Case (iii): On the interval
, we need to show that
over
for all
. Indeed, on the interval
, we have
and
. Define
. Then, our goal is to show
for all
on the interval
. When
, we have
on
. In addition, note that
on the same interval. For other
with
, we have
Let
. Then, the term
in
is expressed as
Since, on the interval a and b are positive, we conclude that .
To summarize, on the interval , the second derivative , which means that is convex on this interval.
(b) As stated in (
15),
For
, similar to part (a), it can be verified that
is convex. Therefore,
is convex on
. For
, due to symmetry,
is convex on
.
Additionally, note that is continuous on , and increasing (decreasing) on the right (left) hand side of the point , since , on the interval as well as , on the interval . Hence, the point is the only minimizer on the interval . In summary, we can conclude that is convex on the interval . □
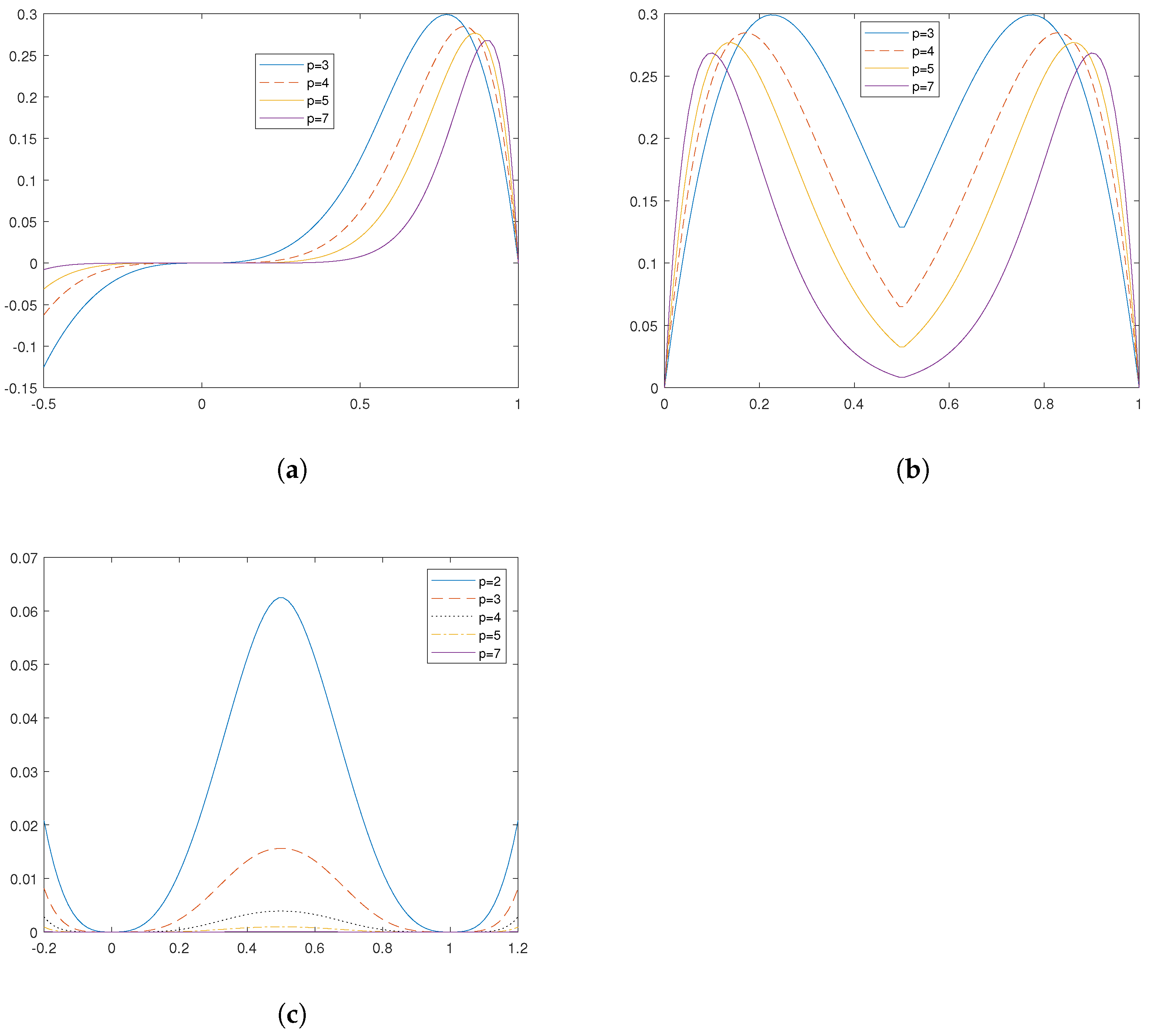
Proposition 9. Let be defined as in (16). Then, when and p is an odd integer, the function is convex on and . See Figure 5. Proof. As indicated in (
16),
where
p is an odd integer and
. Since
is symmetric about
, we divide it into two cases:
Cases (i): Suppose
, the first and second derivative of this function are
where
Note that , we want to show that is positive for .
Because , we have , which implies . Moreover, as we have and , then . Similarly, because , we have . Hence, . Moreover, as we have and , then . Finally, because we have , which gives . Moreover, we have and . Then, it says .
To summarize, we have shown for , which says for . In other words, is convex on .
Cases (ii): Suppose , since is symmetric about . In this case, it is clear that is convex on .
By cases (i) and (ii), we prove that is convex on and . □
Because , and are the continuous types of , and , similar to Propositions 8 and 9, we establish the next proposition.
Proposition 10. Let , and be defined as in (17), (18), and (19), respectively. Then, the following hold. See Figure 6. - (a)
If , then the function is convex on .
- (b)
If , then the function is convex on .
- (c)
If , then the function is convex on and .
The following proposition is simple but tedious. We list it here for the readers’ convenience.
Proposition 11. Let where and be defined from (20)–(28). Then, the following hold. - (a)
The function for and is convex on .
- (b)
The function for is convex on intervals , and .
- (c)
The function for has inflection points, and thus is neither convex nor concave on entire .
Proof. (a) As stated in (
20),
Let
and
. Because
is convex on
according to Proposition 6(b), it suffices to show that
is convex. Taking the first and second derivatives of this function give
In order to verify that , we divide it into three cases:
Cases (i): Suppose . We have , hence . Then, we obtain .
Cases (ii): Suppose . We have , hence . Then, we obtain .
Cases (iii): Suppose . We have , hence . Then, we obtain .
This shows that is always positive, which indicates that is convex on . Because and are convex on , according to Lemma 4(a), the function is convex on .
As indicated in(
21),
Let
and
. We need to verify that
is convex. Taking the second derivative of
gives
We want to show that that
. The main principle of this is to check whether the minimum of the second derivative is positive. Taking the third derivative gives
The critical numbers of are , and . Moreover, , and . The intervals where it is increasing are and , and the intervals where it is decreasing are and . Therefore, the local minimum is , and the local maximum is . Furthermore, we also find . This shows that the global minimum of is positive, hence on the entire . This implies that is convex on . As and are convex on according to Lemma 4(a), is convex on .
As shown in (
23),
As
and are convex on from previous discussions according to Lemma 4(a), is convex on .
As given in (
24),
As
and
are convex on
from previous work according to Lemma 4(a),
is convex on
.
(b) As shown in (
26),
Let
and
. As
is convex on
based on the proof of the case for
, the convexity of
is all that remains to determined. Note that
is not differentiable at
and
, and we need to discuss three cases:
Cases (i): Suppose
. Taking the first derivative and second derivative of
give
Since the denominator of is positive, we need to check whether the numerator is positive. The numerator is . For , we have and , which indicates that the numerator is positive. Therefore, we conclude , and hence is convex on the interval .
Cases (ii): Suppose
, taking the second derivative of
gives
We want to show that
for
. Taking the third derivative of
yields
For the first term of
, since
, the denominator is positive, and hence the first term is positive. For the second term of
, we have
As and when , it is also positive. Therefore, we obtain . This shows that is increasing. Note also that . Then, it follows that . is convex on the interval .
Cases (iii): Suppose . As is symmetric about the point according to case (ii), the function is convex on interval .
Let and . is convex on according to the proof of the case for and is convex on the intervals , and according to previous arguments. Therefore, is convex on the intervals , , and .
(c) As given in (
22),
Taking the second derivative of
gives
The inflection points are , , , and . Then, the intervals where the curve is convex are , and .
As indicated in (
25), we know
Similarly, we use the second derivative to find the inflection points. The inflection points are , , , and . Therefore, the intervals where the curve is convex are , , and .
As shown in (
28), we know
Similarly, we use the second derivative to find the inflection points. The inflection points are and . Because is not differentiable at the points 0 and 1, we can only assure that the interval where the curve is convex is . □
Recall that a function is called subdifferentiable at x if there exists at least one subgradient at x. Although is not differentiable at the points 0 and 1, with the help of Proposition 11(b), we can still show that it is subdifferentiable thereat.
Proposition 12. (a)
The function is subdifferentiable at the points 0 and 1 and the subdifferential is described by Moreover, is convex on .- (b)
The function is subdifferentiable at the points 0 and 1 and the subdifferential is described byMoreover, is convex on .
Proof. (a) Taking the first derivative of
gives
The right and left derivatives at the point 0 are
and
, respectively. Moreover, we have
. Based on the convexity of
on
from Proposition 11(b), we have
with small
and
. Note here the
is a continuous function. Let
. Thus, we have
for
. Similarly, according to the convexity of
on
from Proposition 11(b), we can obtain that
where
. Therefore, we show that
is subdifferentiable at 0, and
. Moreover based on Lemma 2.13 in [
17],
is convex on the interval
, especially at the point 0. Likewise,
and it is convex at the point 1. Hence,
is convex on entire
.
(b) Taking the first derivative of
yields
The right derivative at the point 0 is
and the left derivative at the point 0 is
. Therefore, we obtain
Similarly, □
5. The Local Minimum and Maximum of the Curves
After discussing the convexity and differentiability, we now work on finding the local minimum or maximum value of the curves. In addition, we shall investigate the convergent behavior of local minimum or maximum values when p becomes very large.
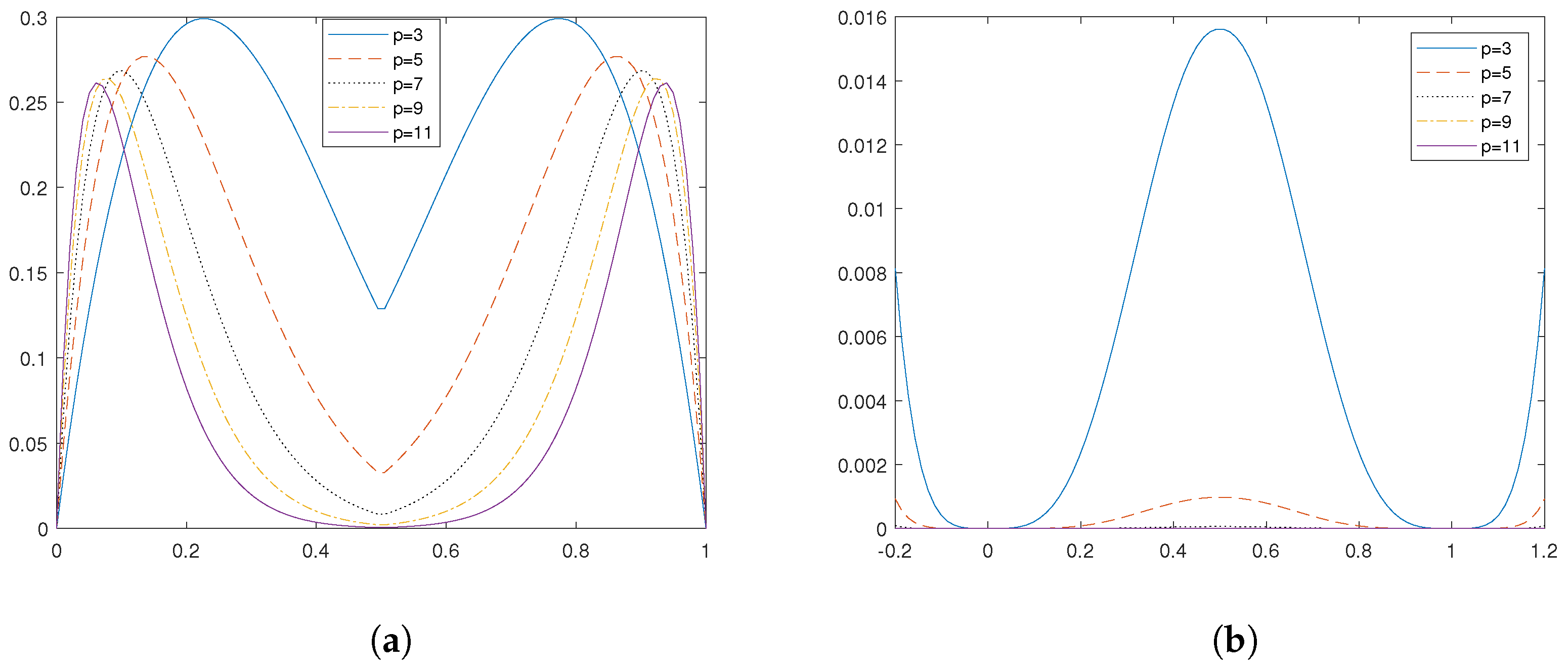
Proposition 13. Let , and be defined as in (11), (13), and (12) respectively. Then, the following hold. See Figure 7. - (a)
The function has a local minimum at and its local minimum value converges to .
- (b)
When p is an odd integer, the function has a local minimum at and its local minimum value converges to .
- (c)
The function has local minima at and 1. Furthermore, it has a local maximum value at and its local maximum value converges to .
Proof. (a) From (
11), we know that
where
. The first derivative of this function is
Note that the first term is positive. We then investigate the second term:
Case (i): If , then .
Case (ii): If , then .
Case (iii): When , we see that is the only root of . Moreover, is convex on , which indicates is the only local minimizer and the value is . Furthermore, we observe that the local minimum value converges to as .
(b) From (
13), we know that
where
and
p is an odd integer. Taking the first derivative of this function yields
It can be verified that is the singular critical point. Note that is convex on , hence is a local minimizer and the value is . In addition, the local minimum value converges to when .
(c) From (
12), we know that
where
. Taking the first derivative of this function gives
We want to solve , which implies or . If , we have and . If , we have . Thus, the critical numbers are . Note that 0 and 1 are the only two roots of and is non-negative. Therefore, we see that and are local minimizers, and the values are both 0.
On the other hand, we know that is decreasing (increasing) on the right (left) hand side of the point . Hence, the point is a local maximizer, and the value is . This further implies that when , the local maximum converges to . □
Proposition 14. Let be defined as in (14) with odd integer p. Then, the function has a local maximum at . Furthermore, its minimum value converges to . See Figure 8. Proof. From (
14), we know that
where
and
p is an odd integer. Computing the first derivative of this function gives
To proceed, we discuss two cases:
Cases (i): If , then . Hence, is increasing on , which indicates that it does not have local minimum or maximum value.
Cases (ii): If , then . It is verified that is the only root of for . Moreover, we have that is decreasing (increasing) on the right (left) hand side of the point a. Hence, a is a local maximizer and the local maximum value is Furthermore, the local maximum value converges to as . □
Proposition 15. Let and be defined as in (15) and (16), respectively. Then, for the odd integer p, the following hold. See Figure 9. - (a)
The function has a local maximum at and . Its local maximum value converges to . Furthermore, it has a local minimum at , which converges to 0.
- (b)
The function has a local maximum at and its maximum value converges to 0. In addition, it has a local minimum at and .
Proof. (a) From (
15), we know that
where
p is an odd integer. As
is symmetric at the point
, we consider the below two cases:
Cases (i): If , according to Proposition 14, the local maximum point is and the maximum value is , which converges to as .
Cases (ii): If , similar to Case (i), we obtain that is a local maximum point and the maximum value is which converges to as .
Furthermore, because the function is increasing (decreasing) on the right (left) hand side of the point , we can conclude is a local minimizer. Its the minimum value is , which converges to 0 when .
(b) From (
16), we know that
where
p is an odd integer. Since
is symmetric at the point
, we divide it into two cases:
Case (i): Suppose
, the first derivative is
Based on this, it is verified that is a critical point. Because is non-negative and , we can conclude that 1 is a local minimum point and the value is 0.
Case (ii): Suppose . Based on symmetry, the local minimum point is and the value is 0.
Case (iii): Suppose , we know that and is decreasing (increasing) on the right (left) side of the point . Hence, we obtain that is a local maximizer and the maximum value is for . It clearly converges to 0 when . □
Due to the fact that , , and are continuous counterparts of , and , analogous to Propositions 14 and 15, their local maximums and minimums can be obtained. We omit the proof here.
Proposition 16. Let , and be defined as in (17), (18), and (19), respectively. Then, for , the following hold. See Figure 10. - (a)
The function has a local maximum at . Furthermore its minimum value converges to .
- (b)
The function has a local maximum at and and its local maximum value converges to . Furthermore, it has a local minimum at and converges to 0.
- (c)
The function has a local maximum at and its local maximum value converges to 0. In addition, it has a local minimum at and .
The local minimum for other is simple.
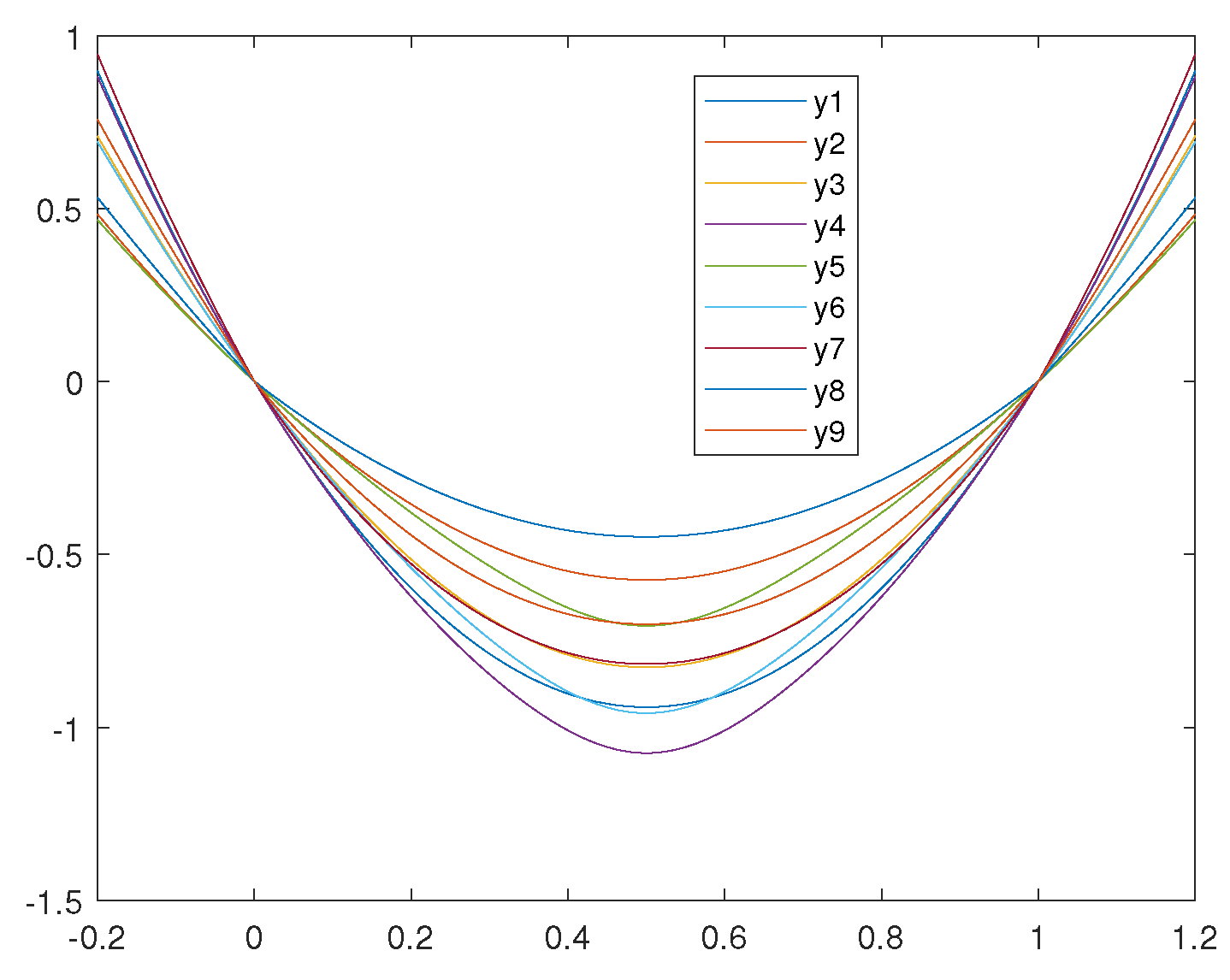
Proposition 17. Let with be defined as in (20)–(28). Then, the function has a local minimum at . See Figure 11. Proof. Because each
is nearly convex according to
and
has a critical number at
, the local minimum at
is confirmed and can be calculated easily. We only present the values here.
This completes the proof. □