Edge Degree Conditions for 2-Iterated Line Graphs to Be Traceable

Abstract

The line graph $L\left(G\right)$ of G has $E\left(G\right)$ as its vertex set, and two vertices are adjacent in $L\left(G\right)$ if and only if the corresponding edges share a common end vertex in G. Let ${\overline{\sigma }}_2\left(G\right)=min\{d_G\left(x\right)+d_G\left(y\right)|xy\in E\left(G\right)\}$. We show that, if ${\overline{\sigma }}_2\left(G\right)\ge 2(\lfloor \frac{n}{11}\rfloor -1)$ and n is sufficiently large, then either $L\left(L\right(G\left)\right)$ is traceable or the Veldman’s reduction $G^{\prime }$ is one of well-defined classes of exceptional graphs. Furthermore, if ${\overline{\sigma }}_2\left(G\right)\ge 2(\lfloor \frac{n}{7}\rfloor -1)$ and n is sufficiently large, then $L\left(L\right(G\left)\right)$ is traceable. The bound $2(\lfloor \frac{n}{7}\rfloor -1)$ is sharp. As a byproduct, we characterize the structure of a connected graph with a non-traceable 2-iterated line graph.

1. Introduction

For graph-theoretic notation not explained in this paper, we refer readers to [1]. We consider only simple graphs in this note. Let G be a connected graph and x be a vertex of G. We use $N_G\left(x\right)$ to denote the set of neighbours of x in G and $d_G\left(x\right)=\left|N_G\left(x\right)\right|$ is the degree of x in G. For any subgraph $G_1$ of G, we use $G\left[V\left(G_1\right)\right]$ to denote the subgraph of G induced by $V\left(G_1\right)$. For a graph G, we define $V_i\left(G\right)=\{y\in V\left(G\right):d_G\left(y\right)=i\}$, $V_{\ge i}\left(G\right)=\{y\in V\left(G\right):d_G\left(y\right)\ge i\}$ and ${\overline{\sigma }}_2\left(G\right)=min\{d_G\left(x\right)+d_G\left(y\right)|xy\in E\left(G\right)\}$.

The line graph $L\left(G\right)$ of $G=\left(V\right(G),E(G\left)\right)$ has $E\left(G\right)$ as its vertex set, and two vertices are adjacent in $L\left(G\right)$ if and only if the corresponding edges share a common end vertex in G. The k-iterated line graph$L^k\left(G\right)$ is defined recursively by $L^0\left(G\right)=G$, $L^1\left(G\right)=L\left(G\right)$ and $L^k\left(G\right)=L\left(L^{k-1}\left(G\right)\right)$.

1.1. Motivation

A graph G is hamiltonian if G has a Hamilton cycle (i.e., a spanning cycle). A graph G is almost bridgeless if every cut edge of G is incident with a vertex of degree one. Brualdi and Shanny [2] studied edge degree conditions of a simple graph G to ensure that its line graph $L\left(G\right)$ is hamiltonian, and Clark [3] improved this result with a large order. Chen [4] also used edge degree conditions to consider the hamiltonianicity of a claw-free graph, which was later extended slightly by Tian and Xiong [5] with more exceptional graphs. Recently, Liu et al. [6] gave a sharp bound of edge degree conditions of a graph G such that $L^2\left(G\right)$ is hamiltonian.

A graph G is traceable if G has a Hamilton path (i.e., a spanning path). In [6,7], Xiong et al. gave minimum edge degree conditions of a connected simple graph or a connected almost bridgeless simple graph guaranteeing its line graph and 2-iterated line graph to be traceable, respectively.

Besides hamiltonicity and traceability, there are many studies on the properties of graphs with edge degree conditions, including the characterization of Q-integral graphs with edge degree at most six [8], 3-uniform hypergraphs [9], up-embeddability [10], spanning closed trails [11], subpancyclicity [12], collapsibility [13,14,15] and supereulerianicity [16,17]. Edge degree can also be used as a powerful condition to study some practical problems, see [18]. Many researchers are concerned with the properties of iterated graphs. For example, the connectivity of 2-iterated line graphs was discussed in [19,20].

Motivated by the above results, it is natural to consider the following question about the traceability and hamiltonianicity of iterated line graphs.

Question. For sufficiently large integer $n\ge 3$ and $k\ge 0$, what is the minimum rational function $f_{trac}(n,k)$: ${\overline{\sigma }}_2\left(G\right)\ge f_{trac}(n,k)$ or $f_{hami}(n,k)$: ${\overline{\sigma }}_2\left(G\right)\ge f_{hami}(n,k)$ implying that $L^k\left(G\right)$ of a graph G with order n is traceable or hamiltonian, respectively?

Below are some of the answers to this Question.

(a)

Ref. [21] For $k=0$, $f_{trac}(n,0)=\frac{1}{2}(3n-3)$, $f_{hami}(n,0)=\frac{1}{2}(3n-2)$.

(b)

For $k=1$,

-

Ref. [7] $f_{trac}(n,1)=2(\lfloor \frac{n}{4}\rfloor -1)+ϵ$, where $ϵ$ is a sufficiently small positive rational number,

-

Ref. [3] $f_{hami}(n,1)=n-1$ when n is even and $f_{hami}(n,1)=n-2$ when n is odd.

(c)

Ref. [6] For $k=2$, $f_{hami}(n,2)=\lfloor \frac{n+3}{2}\rfloor +ϵ$, where $ϵ$ is a sufficiently small positive rational number.

(d)

For $k\ge 3$, $f_{trac}(n,k)=f_{hami}(n,k)=5$. Since ${\overline{\sigma }}_2\left(G\right)\ge 5$, $\delta \left(L\right(G\left)\right)\ge 3$, $L^2\left(G\right)$ is supereulerian and $L^k\left(G\right)$ is hamiltonian for $k\ge 3$.

The main focus of this paper is the unresolved problem of Question: determining the value of $f_{trac}(n,2)$. As an extension, we characterize the structure of a connected graph with a non-traceable 2-iterated line graph and give some well-defined classes of exceptional graphs when ${\overline{\sigma }}_2\left(G\right)>f_{trac}(n,2)$.

1.2. Reduction Methods and Main Results

Let G be a graph and $\Gamma$ be its connected subgraph. We use $G/\Gamma$ to denote the graph obtained from G by contracting edges in $\Gamma$ so that $\Gamma$ is contracted to a vertex $v_{\Gamma }$ in $G/\Gamma$. The subgraph $\Gamma$ is called the preimage of the vertex $v_{\Gamma }$ of $G/\Gamma$. The vertex $v_{{\Gamma }_i}$ is trivial if ${\Gamma }_i$ is a vertex and nontrivial otherwise.

Let $O\left(G\right)$ be the vertex set of odd degrees in G. A graph G is collapsible if for every even subset $F\subseteq V\left(G\right)$, there is a spanning connected subgraph $R_F$ of G with $O\left(R_F\right)=F$. $K_1$ is regarded as a collapsible graph. Catlin [22] showed that every graph G has a unique collection of maximal collapsible subgraphs ${\Gamma }_1,{\Gamma }_2,\dots ,{\Gamma }_k$ such that ${\cup }_{i=1}^{k}V\left({\Gamma }_i\right)=V\left(G\right)$. The reduction of G is the graph obtained from G by contracting ${\Gamma }_1,{\Gamma }_2,\dots ,{\Gamma }_k$.

In [23], Veldman refined Catlin’s reduction method. Let G be a simple graph and define $D\left(G\right)=V_1\left(G\right)\cup V_2\left(G\right)$. For an independent subset X of $D\left(G\right)$, define $I_X\left(G\right)$ as the graph obtained from G by deleting the vertices in X of degree one and replacing each path of length two whose internal vertex is a vertex in X of degree two by an edge. Note that $I_X\left(G\right)$ may not be simple. We call GX-collapsible if $I_X\left(G\right)$ is collapsible. A subgraph $\Gamma$ of G is an X-subgraph of G if $d_{\Gamma }\left(x\right)=d_G\left(x\right)$ for all $x\in X\cap V(\Gamma )$. An X-subgraph $\Gamma$ of G is called X-collapsible if $\Gamma$ is $(X\cap V(\Gamma \left)\right)$-collapsible. Let $R\left(X\right)$ be the set of vertices in X that are not contained in an X-collapsible X-subgraph of G. Since $I_X\left(G\right)$ has a unique collection of pairwise vertex-disjoint maximal collapsible subgraphs $L_1,L_2,\dots ,L_k$ such that ${\cup }_{i=1}^{k}V\left(L_i\right)=V\left(I_X\left(G\right)\right)$, the graph G has a unique collection of pairwise vertex-disjoint maximal X-collapsible X-subgraph ${\Gamma }_1,{\Gamma }_2,\dots ,{\Gamma }_k$ such that $\left({\cup }_{i=1}^{k}V\left({\Gamma }_i\right)\right)\cup R\left(X\right)=V\left(G\right)$. The X-reduction of G is the graph obtained from G by contracting ${\Gamma }_1,{\Gamma }_2,\dots ,{\Gamma }_k$, denoted by $G^{\prime }$. The trivial and the nontrivial vertex set of $G^{\prime }$ are denoted by $\mathbf{VT}\left(G^{\prime }\right)$ and $\mathbf{VNT}\left(G^{\prime }\right)$, respectively.

The above reduction methods are effective tools in research of hamiltonian properties of graphs, see [7,11,17]. Using Veldman’s reduction method, we give the following characterization of the 2-iterated line graph to be traceable involving the minimum edge degree condition, whose proof will be presented in Section 3.

Theorem 1.

Let G be a connected simple graph of order n and $p\ge 2$ be an integer such that ${\overline{\sigma }}_2\left(G\right)\ge 2(\lfloor \frac{n}{p}\rfloor -1).$ If n is sufficiently large, then either $L^2\left(G\right)$ is traceable or $G^{\prime }\in {\mathcal{F}}_p$, where $G^{\prime }$ is the Veldman’s $D\left(G\right)$-reduction of G.

• For $p\le 7$, ${\mathcal{F}}_p=\mathrm{Ø}$;
• For $8\le p\le 9$ , ${\mathcal{F}}_p=\left\{G_1^1\right\}$;
• For $p=10$, ${\mathcal{F}}_{10}={\mathcal{F}}_9\cup \{G_2^1,\cdots ,G_2^{11}\}$;
• For $p=11$, ${\mathcal{F}}_{11}={\mathcal{F}}_{10}\cup \{G_3^1,\cdots ,G_3^3\}$.

These graphs in ${\mathcal{F}}_p$ for $p=8,9,10$ and 11 are depicted in Figure 1 in which the hollow vertices are trivial vertices (2-vertices of G) and the solid vertices are nontrivial vertices.

2. Preliminaries and Auxiliary Results

An $xy$-path of a graph G is a path with ends x and y. A 2-vertex is a vertex of degree exactly two. A branchB of a graph G is a nontrivial path whose end vertices are not 2-vertices of G and whose internal vertices (if any) are 2-vertices of G. We denote by $\mathcal{B}\left(G\right)$ the set of branches of G. Define ${\mathcal{B}}_1\left(G\right)=\{B\in \mathcal{B}\left(G\right):V\left(B\right)\cap V_1\left(G\right)\ne \mathrm{Ø}\}$. We say $B\in \mathcal{B}\left(G\right)$ is an edge branch if B has a length of one.

A subset S of $\mathcal{B}\left(G\right)$ is called a branch-cut if the subgraph of G obtained from $G[E\left(G\right)\backslash {\cup }_{S\in \mathcal{B}\left(G\right)}E\left(S\right)]$ by deleting all internal vertices (if any) in each branch of S has more components than G. A minimal branch cut is called a branch-bond. We denote by $\mathcal{BB}\left(G\right)$ the set of branch bonds of G. The length of a branch-bond $BB\in \mathcal{BB}\left(G\right)$, denote by $l\left(BB\right)$, is the length of a shortest branch in it. Define ${\mathcal{BB}}_{\ge 2}\left(G\right)=\{BB\in \mathcal{BB}\left(G\right):l\left(BB\right)\ge 2\mathrm{and}\mathrm{each}\mathrm{end}\mathrm{of}\mathrm{branches}\mathrm{in}BB\mathrm{has}\mathrm{degree}\mathrm{at}\mathrm{least}\mathrm{three}\}$.

Let P be a path with $x,y\in V\left(P\right)$. We use $P[x,y]$ to denote the subpath from x to y in P, and $P[x,y)$, $P(x,y]$ and $P(x,y)$ are obtained from $P[x,y]$ by deleting y, x and $\{x,y\}$. For a graph G, we use $w\left(G\right)$ to denote the number of components of G. For any subgraph $G_1$ of G, define $G-G_1=G[V\left(G\right)\backslash V\left(G_1\right)]$ and $G\backslash G_1=G[E\left(G\right)\backslash E\left(G_1\right)]$. For any two subgraphs $G_1$ and $G_2$ of G, the distance $d_G(G_1,G_2)$ is defined to be min$\{d_G(x,y):x\in V\left(G_1\right),y\in V\left(G_2\right)\}$, where $d_G(x,y)$ denotes the length of a shortest path between x and y in G. We then will define some operations such that the resulting graphs have no isolated vertex. For any two subgraphs $G_1$ and $G_2$ of G, define $G_1\cup G_2=G[E\left(G_1\right)\cup E\left(G_2\right)]$, $G_1\cap G_2=G[E\left(G_1\right)\cap E\left(G_2\right)]$ and $G_1▵G_2=G[E\left(G_1\right)▵E\left(G_2\right)]=G[(E\left(G_1\right)\cup E\left(G_2\right))\backslash (E\left(G_1\right)\cap E\left(G_2\right))]$, respectively.

2.1. Traceable Iterated Line Graphs

For a positive integer k, Niu, Xiong, and Yang used ${\mathbf{EUP}}_k\left(G\right)$ to denote the set of subgraphs H of a graph G that satisfy the following conditions. Then they characterized the existence of those graphs G for which $L^k\left(G\right)$ is traceable and proved Theorem 2.

(I)

$\left|O\right(H\left)\right|\le 2$;

(II)

$V_0\left(H\right)\subseteq V_{\ge 3}\left(G\right)\subseteq V\left(H\right)$;

(III)

$d_G(H_1,H-H_1)\le k-1$ for any subgraph $H_1$ of H;

(IV)

$\left|E\right(B\left)\right|\le k+1$ for any branch $B\in \mathcal{B}\left(G\right)$ with $E\left(B\right)\cap E\left(H\right)=\mathrm{Ø}$;

(V)

$\left|E\right(B\left)\right|\le k$ for any branch $B\in {\mathcal{B}}_1\left(G\right)$ with $E\left(B\right)\cap E\left(H\right)=\mathrm{Ø}$.

Theorem 2

(Niu et al. [24]). Let G be a connected graph with $\left|E\right(G\left)\right|\ge 3$ and $k\ge 2$. Then $L^k\left(G\right)$ is traceable if and only if ${\mathbf{EUP}}_k\left(G\right)\ne \mathrm{Ø}$.

Remark 1.

If a connected graph G has an even subgraph H satisfying that $\left(II\right)-\left(V\right)$, then let $H^0$ be a subgraph of G by adding a path that connects any two vertices in $V_{\ge 3}\left(G\right)$ if $E\left(H\right)=\mathrm{Ø}$, and be a subgraph of G by deleting any edge from H otherwise. Obviously, $H^0$ has exactly two odd vertices. Moreover, $H^0$ is also a subgraph of G satisfying that $V_0\left(H^0\right)\subseteq V_{\ge 3}\left(G\right)\subseteq V\left(H^0\right)$, $d_G(H_1^0,H^0-H_1^0)\le k-1$ for every subgraph $H_1^0$ of $H^0$, $\left|E\right(B\left)\right|\le k+1$ for every branch $B\in \mathcal{B}\left(G\right)$ with $E\left(B\right)\cap E\left(H^0\right)=\mathrm{Ø}$, $\left|E\right(B\left)\right|\le k$ for every branch $B\in {\mathcal{B}}_1\left(G\right)$ with $E\left(B\right)\cap E\left(H^0\right)=\mathrm{Ø}$. Thus, we change the first condition to $“\left|O\right(H\left)\right|=2”$ in the following discussion.

2.2. The Veldman’s Reduction Method

Let X be an independent set of $D\left(G\right)$. Then, Veldman’s reduction method is the reduction method of Catlin when $X=\mathrm{Ø}$. In [23], Veldman obtained the following result.

Theorem 3

(Veldman [23]). Let G be a connected simple graph of order n and $p\ge 2$ an integer such that

$${\overline{\sigma }}_2\left(G\right)\ge 2(\lfloor \frac{n}{p}\rfloor -1).$$

(1)

If n is sufficiently large relative to p, then

$$|V\left(G^{\prime }\right)|\le max\{p,\frac{3}{2}p-4\},$$

(2)

where $G^{\prime }$ is the $D\left(G\right)$-reduction of G. Furthermore, Ineq. $\left(2\right)$ holds with equality only if Ineq. $\left(1\right)$ holds with equality for $p\le 7$.

A graph is triangle-free if it has no induced subgraph isomorphic to $K_3$. The following results are some observations about Veldman’s reduction method that will be used in our proofs.

Theorem 4.

Let G be a connected simple graph, X be an independent subset of $D\left(G\right)$ and $G^{\prime }$ be the X-reduction of G. Then each of the following holds:

(i) 

(Veldman [23]) $G^{\prime }$ is simple and triangle-free;

(ii) 

If $G^{\prime }$ has a subgraph $H^{\prime }$ satisfying that $\left|O\right(H^{\prime }\left)\right|=2$, $V_0\left(H^{\prime }\right)\subseteq (V_{\ge 3}\left(G^{\prime }\right)\cup \mathbf{VNT}\left(G^{\prime }\right))\subseteq V\left(H^{\prime }\right)$, $d_G(H_1^{\prime },H^{\prime }-H_1^{\prime })=1$ for every subgraph $H_1^{\prime }$ of $H^{\prime }$, $\left|E\right(B\left)\right|\le 3$ for every branch $B\in \mathcal{B}\left(G^{\prime }\right)$ with $E\left(B\right)\cap E\left(H^{\prime }\right)=\mathrm{Ø}$, $\left|E\right(B\left)\right|\le 2$ for every branch $B\in {\mathcal{B}}_1\left(G^{\prime }\right)$ with $E\left(B\right)\cap E\left(H^{\prime }\right)=\mathrm{Ø}$, then ${\mathbf{EUP}}_2\left(G\right)\ne \mathrm{Ø}$.

Proof. 

$\left(ii\right)$ Let ${\Gamma }_1,{\Gamma }_2,\dots ,{\Gamma }_k$ be a collection of maximal X-collapsible X-subgraph of G and $v_{{\Gamma }_1},v_{{\Gamma }_2},\dots ,v_{{\Gamma }_k}$ denote the vertex onto which ${\Gamma }_1,{\Gamma }_2,\dots ,{\Gamma }_k$ is contracted in $G^{\prime }$. Note that there must exist a vertex in $V\left({\Gamma }_i\right)$, say $v_i$, that incidents with odd number of edges in $H^{\prime }$ if $d_{H^{\prime }}\left(v_{{\Gamma }_i}\right)$ is odd. For each r with $1\le r\le k$, let $F_r=\{w\in V\left({\Gamma }_r\right):$w is incident with an odd number of edges in $H^{\prime }\}$ and

$$F_r^{\prime }=\left\{\begin{array}{ccc}\hfill F_r\backslash \{v_i,v_j\}& ,\hfill & \hfill \mathrm{if}O\left(H^{\prime }\right)=\{v_{{\Gamma }_i},v_{{\Gamma }_j}\}\mathrm{is}\mathrm{a}\mathrm{nontrivial}\mathrm{vertex}\mathrm{set};\\ \hfill F_r\backslash \left\{v_i\right\}& ,\hfill & \hfill \mathrm{if}\mathrm{exactly}\mathrm{one}\mathrm{vertex}{v}_{{\Gamma }_i}\mathrm{of}O\left(H^{\prime }\right)\mathrm{is}\mathrm{nontrivial}.\end{array}\right.$$

Then $|F_r^{\prime }|\equiv$ 0 (mod $2)$ for $1\le r\le k$. Since ${\Gamma }_r$ is X-collapsible, $I_X\left({\Gamma }_r\right)$ is collapsible. Let $R_{F_r^{\prime }}$ be the spanning connected subgraph in $I_X\left({\Gamma }_r\right)$ such that $O\left(R_{F_r^{\prime }}\right)=F_r^{\prime }$. Then ${\Gamma }_r$ has a connecting subgraph $R_{F_r^{\prime }}^{\prime }$ such that $O\left(R_{F_r^{\prime }}^{\prime }\right)=F_r^{\prime }$ and each edge of ${\Gamma }_r$ has an end contained in $V\left(R_{F_r^{\prime }}^{\prime }\right)$.

Hence $H=G[{\cup }_{1\le r\le k}E\left(R_{F_r^{\prime }}^{\prime }\right)\cup E\left(H^{\prime }\right)]$ is a subgraph of G satisfying that $\left|O\right(H\left)\right|=2$, $V_0\left(H\right)\subseteq V_{\ge 3}\left(G\right)\subseteq V\left(H\right)$ and $d_G(H_1,H-H_1)=1$ for every subgraph $H_1$ of H. Since $V\left(\mathcal{B}\left(G^{\prime }\right)\right)$ and $V\left({\mathcal{B}}_1\left(G^{\prime }\right)\right)$ may have nontrivial vertices, we have $\left|E\right(B\left)\right|\le 3$ for every branch $B\in \mathcal{B}\left(G\right)$ with $E\left(B\right)\cap E\left(H\right)=\mathrm{Ø}$, $\left|E\right(B\left)\right|\le 2$ for every branch $B\in {\mathcal{B}}_1\left(G\right)$ with $E\left(B\right)\cap E\left(H\right)=\mathrm{Ø}$. Hence G has a subgraph H satisfying Conditions $\left(I\right)$–$\left(V\right)$ of Theorem 2 of $n=2$ (i.e., ${\mathbf{EUP}}_2\left(G\right)\ne \mathrm{Ø}$). □

3. Proof of Main Results

To prove Theorem 1, we first give the structure of a connected graph with a non-traceable 2-iterated line graph and give the following auxiliary result. To contract an edge f of a graph G is to delete the edge f and then identify its ends. A graph G is contractible to a graph $G^{\prime }$ if, for an edge set $S\subseteq E\left(G\right)$, $G^{\prime }$ can be obtained from G by successively contracting edges in S.

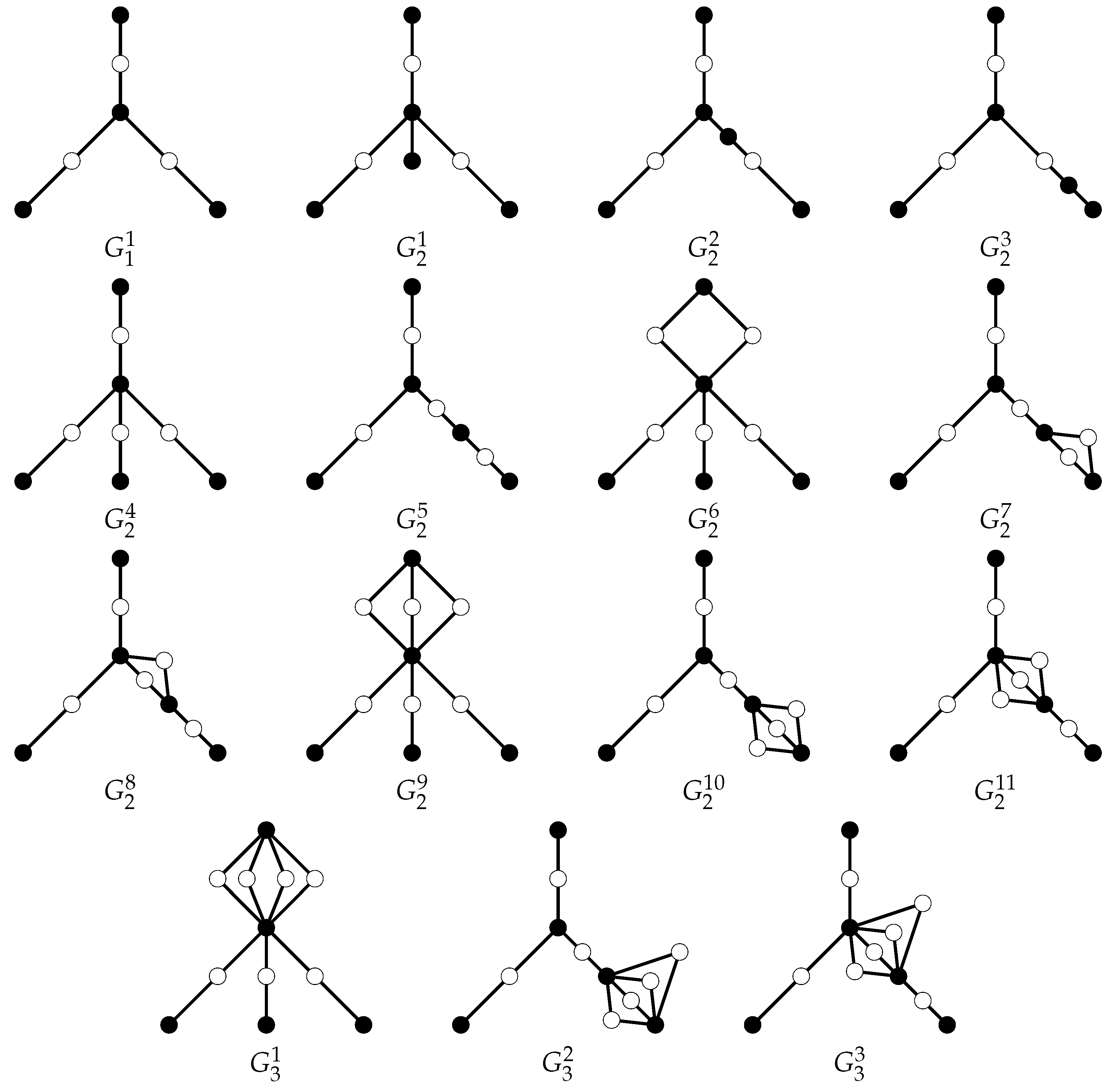
Lemma 1.

Let G be a connected simple graph. Then either $L^2\left(G\right)$ is traceable or G is contractible to a graph that contains an induced $S\left(K_{1,3}\right)$ (see Figure 2). Moreover, the induced $S\left(K_{1,3}\right)$ satisfies the following statements:

$(\ast )$

the vertices in subdivided vertices set $\{b_1,b_2,b_3\}$ are 2-vertices in G;

$(\ast \ast )$

any path of G terminating in $\{a_1,a_2,a_3,a_4\}$ has at least one 2-vertex of degree two in G.

Proof of Lemma 1. 

If ${\mathcal{B}}_1\left(G\right)$ has three branches of length at least two, then G could be contractible to a graph that contains an induced $S\left(K_{1,3}\right)$, and the induced $S\left(K_{1,3}\right)$ satisfies the conditions $(\ast )$ and $(\ast \ast )$ of Lemma. Hence we may assume that ${\mathcal{B}}_1\left(G\right)$ have at most two branches of length at least two. Now we choose a subgraph H of G satisfying that

(1)

$\left|O\right(H\left)\right|=2$ and H contains the branches of length at least two in ${\mathcal{B}}_1\left(G\right)$;

(2)

$V_0\left(H\right)\subseteq V_{\ge 3}\left(G\right)\subseteq V\left(H\right)$;

(3)

subject to $\left(1\right)$ and $\left(2\right)$, $w\left(G\right[V\left(H\right)\left]\right)$ is minimized;

(4)

subject to $\left(1\right)$, $\left(2\right)$ and $\left(3\right)$, H contains as many branches of length at least four in $\mathcal{B}\left(G\right)$ as possible.

By Theorem 2, $L^2\left(G\right)$ is traceable if $d_G(H_1,H-H_1)=1$ for any subgraph $H_1\subseteq H$ and $\left|E\right(B\left)\right|\le 3$ for any branch $B\in \mathcal{B}\left(G\right)$ with $E\left(B\right)\cap E\left(H\right)=\mathrm{Ø}$. Otherwise, we distinguish two cases:

Ca.

there exists a subgraph $H_1$ of H such that $d_G(H_1,H-H_1)\ge 2$ (i.e., there is a branch of length at least two connecting $H_1$ and $H-H_1$, say $B_1$);

Cb.

$d_G(H_1,H-H_1)=1$ for any subgraph $H_1\subseteq H$ (i.e., $G\left[V\right(H\left)\right]$ is connected) and there exists a branch $B_2\in \mathcal{B}\left(G\right)$ such that $\left|E\right(B_2\left)\right|\ge 4$ with $E\left(B_2\right)\cap E\left(H\right)=\mathrm{Ø}$.

Let $O\left(H\right)=\{x,y\}$. We assume without loss of generality that $O\left(H\right)\subseteq V\left(H_1\right)$ in Case Ca. Let $z_1=V\left(H_1\right)\cap V\left(B_1\right)$ and let $z_2\in V\left(H\right)\cap V\left(B_2\right)$. For $i\in \{1,2\}$, let $\mathcal{P}$ be the set of all $x{z}_i$-paths in G and $\mathcal{Q}$ be the set of all $y{z}_i$-paths in G.

We claim that, for any $P\in \mathcal{P}$ and any $Q\in \mathcal{Q}$, any branch of $\mathcal{B}\left(G\right)$ whose edges are in $P\cap Q$ must lie in a branch-bond that contains at least two branches whose edges are in H. Otherwise, let B be a branch of $\mathcal{B}\left(G\right)$ whose edges are in $P\cap Q$. And B is the only branch whose edges are in H of branch-bond it lies in. Then $H-B$ has a component that contains three odd vertices, a contradiction.

Then suppose, for any $P\in \mathcal{P}$ and any $Q\in \mathcal{Q}$, that there exist two branches in two different branch-bonds of ${\mathcal{BB}}_{\ge 2}\left(G\right)$ such that $B^1=B{B}^1\cap H$ and $B^2=B{B}^2\cap H$, and satisfying that $B^1\in P\backslash Q$ and $B^2\in Q\backslash P$. For $i\in \{1,2\}$, by contracting some edges in P, Q and $B_i$, we can obtain a graph containing an induced $S\left(K_{1,3}\right)$ in which the 2-vertices come from $B^1$, $B^2$ and $B_i$, respectively, and satisfying the condition $(\ast \ast )$ of Lemma.

Thus, there must exist at least one path in $\mathcal{P}$ or $\mathcal{Q}$ such that, for any branch-bond $BB$ passing through it, $l\left(BB\right)=1$ or $l\left(BB\right)\ge 2$ with at least two branches whose edges are in H. Denote all paths satisfying the above conditions by ${\mathcal{P}}^{\prime }$. For a branch-bond $BB$ of $\mathcal{BB}\left(G\right)$, a path $P\in {\mathcal{P}}^{\prime }$ and the subgraph H of G that we chose above, we say that P covers $BB$ of H if $BB\cap P=BB\cap H\ne \mathrm{Ø}$, i.e., P goes through all branches belonging to H in the branch-bond $BB$.

Claim 1.

For any path $P^{\prime }\in {\mathcal{P}}^{\prime }$, $P^{\prime }$ contains a branch of length at least four of $\mathcal{B}\left(G\right)$ whose edges are in H or covers a branch-bond of H in ${\mathcal{BB}}_{\ge 2}\left(G\right)$.

Proof. 

By contradiction. The length of branches of $\mathcal{B}\left(G\right)$ whose edges are in $H\cap P^{\prime }$ is at most three, and each branch-bond that $P^{\prime }$ passes through has either an edge-branch or a branch of length at least two belonging to $H\backslash P^{\prime }$ or belonging to $P^{\prime }\backslash H$. For $i\in \{1,2\}$, consider the subgraph $H^{\prime }$ of G obtained from $(P^{\prime }\cup B_i)▵H$ by adding all vertices of degree at least three of G in $(P^{\prime }\cup B_i)▵H$.

In Case Ca, $H^{\prime }$ is a subgraph of G satisfying the choice $\left(1\right)$ and $\left(2\right)$ of H. And, except for all deleted 2-vertices of G in $(P^{\prime }\cup B_1)▵H$, the vertices in $H_1$ and $H-H_1$ are connected by $B_1$. Then $w\left(G\left[V\left(H^{\prime }\right)\right]\right)=w\left(G\left[V\left(H\right)\right]\right)-1$, contrary to the choice $\left(3\right)$ of H. In Case Cb, note that $H^{\prime }$ is a subgraph of G satisfying the choice $\left(1\right)-\left(3\right)$ of H. Although $G\left[V\left(H^{\prime }\right)\right]$ is connected, $H^{\prime }$ contains more branches in $\mathcal{B}\left(G\right)$ of length at least four than H since $E\left(B_2\right)\subseteq E\left(H^{\prime }\right)$, contrary to the choice $\left(4\right)$ of H. This completes the proof of Claim 1. □

Now we choose one path $P^{\prime }\in {\mathcal{P}}^{\prime }$ satisfying that

(i)

$P^{\prime }$ contains as few branches of length at least four in $\mathcal{B}\left(G\right)\cap H$ as possible;

(ii)

subject to $\left(i\right)$, $P^{\prime }$ covers the least number of branch-bonds in ${\mathcal{BB}}_{\ge 2}\left(G\right)$.

Now, according to Claim 1, we consider two possibilities of $P^{\prime }$. Without loss of generality, assume that $P^{\prime }\in \mathcal{P}$. Consider the case that $P^{\prime }$ contains a branch of length at least four in $\mathcal{B}\left(G\right)\cap H$, denoted by $B^{\prime }$. Let $B{B}^{\prime }$ be the branch-bond of $\mathcal{BB}\left(G\right)$ that $B^{\prime }$ lies in. If $l\left(B{B}^{\prime }\right)\ge 2$ for any branch $B^{″}$ in $B{B}^{\prime }\backslash B^{\prime }$, by contracting the branches $B^{\prime }$, $B^{″}$ and $B_i$ for $i\in \{1,2\}$, then we obtain a graph containing an induced $S\left(K_{1,3}\right)$ in which 2-vertices come from $B^{\prime }$, $B^{″}$ and $B_i$, respectively. Thus, there exists an edge-branch in $B{B}^{\prime }\backslash B^{\prime }$, say $B^{″}$. Let $G_1$ and $G_2$ be the subgraphs of $G-B{B}^{\prime }$ and let $s_i=V\left(G_i\right)\cap V\left(B^{\prime }\right)$ and $t_i=V\left(G_i\right)\cap V\left(B^{\prime \prime }\right)$ for $i=1,2$. (Possibly $s_i=t_i$ for $i=1,2$).

Suppose that $B^{″}\subseteq P^{\prime }$. Without loss of generality, assume that $d_{P^{\prime }}(x,s_1)<d_{P^{\prime }}(x,s_2)\le d_{P^{\prime }}(z_i,t_2)<d_{P^{\prime }}(z_i,t_1)$. We claim that there exists another $s_1{t}_1$-path in $G_1$ which has a branch of length at least four whose edges are in H. Otherwise, for any path $R[s_1,t_1]$ connecting $s_1$ and $t_1$ in $G_1$, let $s_1^{\prime }$ be the vertex of $V\left(R[s_1,t_1]\right)\cap V\left(P^{\prime }[x,s_1]\right)$ such that $d_{P^{\prime }}(x,s_1^{\prime })$ is minimized and let $t_1^{\prime }$ be the vertex of $V\left(R[s_1,t_1]\right)\cap V\left(P^{\prime }[t_1,z_i]\right)$ for $i\in \{1,2\}$ such that $d_{P^{\prime }}(z_i,t_1^{\prime })$ is minimized. Replace $P^{\prime }[s_1^{\prime },t_1^{\prime }]$ with $R[s_1^{\prime },t_1^{\prime }]$ in $P^{\prime }$, we obtain a new $x{z}_i$-path which has fewer branches of length at least four whose edges are in H, contradicts the choose $\left(i\right)$ of $P^{\prime }$. Thus, let $R^{\prime }[s_1,t_1]$ be the path in $G_1$ such that $R^{\prime }[s_1,t_1]$ has a branch $B^{‴}$ of length at least four whose edges are in H. By contracting $P^{\prime }[s_1,t_1]$, $R^{\prime }[s_1,t_1]$ and $P^{\prime }[t_1,a_i]\cup B_i$ for $i\in \{1,2\}$, we get a subgraph containing an induced $S\left(K_{1,3}\right)$ in which the 2-vertices come from $B^{\prime }$, $B^{‴}$ and $B_i$, respectively.

Suppose that $B^{″}⊈P^{\prime }$. Without loss of generality, assume that $d_{P^{\prime }}(x,s_1)<d_{P^{\prime }}(x,s_2)$. We claim that there exists a path $s_1{t}_1$-path in $G_1$ or a $s_2{t}_2$-path in $G_2$ has a branch of length at least four whose edges are in H. Otherwise, for any path $M[s_1,t_1]$ connecting $s_1$ and $t_1$ in $G_1$ and for any path $N[s_1,t_1]$ connecting $s_2$ and $t_2$ in $G_2$, let $s_1^{\prime }$ be the vertex of $V\left(M[s_1,t_1]\right)\cap V\left(P^{\prime }[x,s_1]\right)$ such that $d_{P^{\prime }}(s_1^{\prime },x)$ is minimized and let $t_2^{\prime }$ be the vertex of $V\left(N[s_2,t_2]\right)\cap V\left(P^{\prime }[s_2,a_i]\right)$ for $i\in \{1,2\}$ such that $d_{P^{\prime }}(t_2^{\prime },z_i)$ is minimized. If $V\left(M[s_1,t_1]\right)\cap V\left(P^{\prime }[s_2,z_i]\right)\ne \mathrm{Ø}$, then let $t_1^{\prime }\in V\left(M[s_1,t_1]\right)\cap V\left(P^{\prime }[s_2,z_i]\right)$ such that $d_{P^{\prime }}(t_1^{\prime },z_i)$ is minimized. Substitute $M[s_1^{\prime },t_1^{\prime }]$ for $P^{\prime }[s_1^{\prime },t_1^{\prime }]$ in $P^{\prime }$, we obtain a new $x{z}_i$-path which has fewer branchs of length at least four in H, contradicts the choose $\left(i\right)$ of $P^{\prime }$. If $V(V\left(M[s_2,t_2]\right)\cap V\left(P^{\prime }[x,s_1]\right)\ne \mathrm{Ø}$, then let $s_2^{\prime }\in V\left(M[s_2,t_2]\right)\cap V\left(P^{\prime }[x,s_1]\right)$ such that $d_{P^{\prime }}(s_2^{\prime },x)$ is minimized. Substitute $M[s_2^{\prime },t_2^{\prime }]$ for $P^{\prime }[s_2^{\prime },t_2^{\prime }]$ in $P^{\prime }$, we obtain a new $x{z}_i$-path which has fewer branchs of length at least four in H, contradicts the choose $\left(i\right)$ of $P^{\prime }$. Hence we have $V\left(M[s_1,t_1]\right)\cap V\left(P^{\prime }[s_2,z_i]\right)=\mathrm{Ø}$ and $V\left(M[s_2,t_2]\right)\cap V\left(P^{\prime }[x,s_1]\right)=\mathrm{Ø}$. Then replace $P^{\prime }[s_1^{\prime },s_2^{\prime }]$ with $M[s_1^{\prime },t_1]\cup B^{″}\cup N[t_2,s_2^{\prime }]$ in $P^{\prime }$, we also get an $x{a}_i$-path which has fewer branchs of length at least four whose edges are in H, and derive a contradiction. Thus, let $M^{\prime }[s_1,t_1]$ be the path in $G_1$ or $N^{\prime }[s_2,t_2]$ be the path in $G_2$ which has a branch of length at least four in H. For $i\in \{1,2\}$, by contracting $P^{\prime }[s_1,s_2]$, $M^{\prime }[s_1,t_1]$ (or $N^{\prime }[s_2,t_2]$) and $B_i$, we get an induced $S\left(K_{1,3}\right)$ in which the 2-vertices come from $B^{\prime }$, $B_i$ and $M^{\prime }[s_1,t_1]$ (or $N^{\prime }[s_2,t_2]$), respectively.

It remains to consider that $P^{\prime }$ covers a branch-bond $B{B}^{\ast }$ of H in ${\mathcal{BB}}_{\ge 2}\left(G\right)$. Note that $B{B}^{\ast }$ has at least two branches in H. Then there exists at least one component of $G-B{B}^{\ast }$, say $G_1$, such that $\{u,v\}\subseteq V\left(P^{\prime }\right)\cap V\left(G_1\right)$, $V\left(P^{\prime }(u,v)\right)\cap V\left(G_1\right)=\mathrm{Ø}$ and $V\left(P^{\prime }(u,v)\right)\cap V\left(G_2\right)\ne \mathrm{Ø}$, where $G_2$ is the component of $G-B{B}^{\ast }$ other than $G_1$. Then we can claim that there exists another path $T^{\prime }[u,v]$ in $G_1$ such that $T^{\prime }[u,v]$ cover a branch-bond $B{B}^{\ast \ast }$ of H in ${\mathcal{BB}}_{\ge 2}\left(G\right)$. Otherwise, for any path $T[u,v]$ connecting u and v in $G_1$, let $u^{\prime }$ be the vertex of $V\left(T[u,v]\right)\cap V\left(P^{\prime }[x,u]\right)$ such that $d_{P^{\prime }}(u,u^{\prime })$ is maximized and let $v^{\prime }$ be the vertex of $V\left(T[u,v]\right)\cap V\left(P^{\prime }[v,z_i]\right)$ for $i\in \{1,2\}$ such that $d_{P^{\prime }}(v,v^{\prime })$ is maximized. Replace $P^{\prime }[u^{\prime },v^{\prime }]$ with $T[u^{\prime },v^{\prime }]$ in $P^{\prime }$, we can obtain a new $x{z}_i$-path which covers fewer branch-bonds of H in ${\mathcal{BB}}_{\ge 2}\left(G\right)$, contradicts the choose $\left(ii\right)$ of $P^{\prime }$. By contracting the three edge-disjoint paths $P^{\prime }[u,v]$, $T^{\prime }[u,v]$ and $P^{\prime }[v,z_i]\cup B_i$ for $i\in \{1,2\}$, we can obtain an induced $S\left(K_{1,3}\right)$ in which the 2-vertices come from $B{B}^{\ast }$, $B{B}^{\ast \ast }$ and $B_i$, respectively. This completes the proof of Lemma.

Now, we may present the proof of the main result.

Proof of Theorem 1. 

Let G be a connected simple graph of order n and $2\le p\le 11$ be an integer such that ${\overline{\sigma }}_2\left(G\right)\ge 2(\lfloor \frac{n}{p}\rfloor -1)$. Note that $D\left(G\right)$ is an independent set if n is sufficiently large relative to p. Let $G^{\prime }$ be the $D\left(G\right)$-reduction of G. If $G^{\prime }$ has a subgraph $H^{\prime }$ satisfying the condition of Theorem 4 (ii), then ${\mathbf{EUP}}_2\left(G\right)\ne \mathrm{Ø}$. By Theorem 2, $L^2\left(G\right)$ is traceable. Hence we may assume that $G^{\prime }$ has no subgraph $H^{\prime }$ satisfying the condition of Theorem 4 (ii) in the following discussion.

Let $V\left(G^{\prime }\right)=\{a_1,\dots ,a_t,b_1,\dots ,b_s\}$ with $s+t=\left|V\right(G^{\prime }\left)\right|$, where $a_1,\dots ,a_t\in \mathbf{VNT}\left(G^{\prime }\right)$ and $b_1,\dots ,b_s\in \mathbf{VT}\left(G^{\prime }\right)$, respectively. For $1\le i\le t$, let $\Gamma \left(a_i\right)$ be the preimage of $a_i$. Without loss of generality, we assume that $|V(\Gamma \left(a_1\right))|\le |V(\Gamma \left(a_2\right))|\le \cdots \le |V(\Gamma \left(a_t\right))|$. Since ${\sum }_{i=1}^t\left|V(\Gamma \left(a_i\right))\right|\le n$, we have $|V(\Gamma \left(a_1\right))|\le \frac{n}{t}$.

Let ${\mathcal{F}}_p$ denote the family of $G^{\prime }$ for $p\ge 2$. Since $D\left(G\right)$ is an independent set, it follows from Lemma that any graph $G^{\prime }$ in ${\mathcal{F}}_p$ (if ${\mathcal{F}}_p\ne \mathrm{Ø}$) could be contractible to a graph that contains an induced $S\left(K_{1,3}\right)$ (see Figure 2), which has the following properties.

(1)

The 2-vertices $\{b_1,b_2,b_3\}$ are trivial vertices of $G^{\prime }$ and $\{a_1,a_2,a_3,a_4\}$ are nontrivial vertices of $G^{\prime }$.

(2)

In $G^{\prime }$, any path connecting $a_1$ and $a_j$ (where $j\in \{2,3,4\})$ has at least one 2-vertex of G and any path connecting $a_i$ and $a_j$ (where $i\ne j$ and $i,j\in \{2,3,4\})$ has at least two 2-vertices of G.

(3)

$N_{G^{\prime }}\left(u\right)\subseteq \mathbf{VNT}\left(G^{\prime }\right)$ for any $u\in \mathbf{VT}\left(G^{\prime }\right)$.

(4)

${\mathcal{F}}_i\subseteq {\mathcal{F}}_j$ for $2\le i<j\le 11$.

Consider the case of $p=11$. We have $\left|V\right(G^{\prime }\left)\right|\le 12$ by Theorem 3. If $\left|\mathbf{VNT}\right(G^{\prime }\left)\right|=6$, then $|V(\Gamma \left(a_1\right))|\le \frac{n}{6}$ and ${\overline{\sigma }}_2\left(G\right)\le \frac{n}{6}+2$, contrary to the edge degree condition of G in Theorem 1. Hence $\left|\mathbf{VNT}\right(G^{\prime }\left)\right|\le 5$. If $\left|V\right(G^{\prime }\left)\right|\le 7$, then $G^{\prime }=S\left(K_{1,3}\right)=G_1^1$ by Lemma. Now we consider $8\le \left|V\right(G^{\prime }\left)\right|\le 12$ based on $S\left(K_{1,3}\right)$. The following two claims are some observations on the new nontrivial vertex.

Claim 2.

There exists exactly one nontrivial vertex in $V\left(G^{\prime }\right)\backslash V\left(S\left(K_{1,3}\right)\right)$.

Proof. 

Suppose, to the contrary, that all vertices in $V\left(G^{\prime }\right)\backslash V\left(S\left(K_{1,3}\right)\right)$ are trivial. Let $V\left(G^{\prime }\right)\backslash V\left(S\left(K_{1,3}\right)\right)=\{b_4,\dots ,b_l\}$ with $4\le l\le 8$. By Property $\left(3\right)$, $N_{G^{\prime }}\left(b_l\right)\subseteq \mathbf{VNT}\left(G^{\prime }\right)$. Assume that $\{a_1,a_2\}\subseteq N_{G^{\prime }}\left(b_4\right)$ by symmetry. Let $D^1=a_3{b}_2{a}_2{b}_1{a}_1{b}_4{a}_2{b}_3{a}_4$. And let $H^1$ be the union of $D^1$ and $b_l$$(5\le l\le 8)$ if $d_{G^{\prime }}\left(b_l\right)\ge 3$, and let $H^1=D^1$ otherwise. We can verify that $H^1$ is a subgraph of $G^{\prime }$ satisfying the condition of Theorem 4 (ii), a contradiction. This completes the proof of Claim 2. □

Let $V\left(G^{\prime }\right)\backslash V\left(S\left(K_{1,3}\right)\right)=\{a_5,b_4,\cdots ,b_l\}$ with $4\le l\le 7$.

Claim 3.

The nontrivial vertex $a_5$ cannot lie on the path, out of $S\left(K_{1,3}\right)$, connecting $a_i$ and $a_j$ for $1\le i<j\le 4$.

Proof. 

By contradiction. Suppose first that $a_5$ lies on the path $T_1$ out of $S\left(K_{1,3}\right)$ connecting $a_1$ and $a_2$. Let $D^2=a_3{b}_2{a}_1{b}_1{a}_2{T}_1{a}_1{b}_3{a}_4$. By Property (2), there is at least one trivial vertex in $V\left(T_1\right)$, say $b_4$. Let $H^2$ be the union of $D^2$ and $b_l$$(5\le l\le 7)$ if $d_{G^{\prime }}\left(b_l\right)\ge 3$ and $b_l\notin V\left(T_1\right)$, and let $H^2=D^2$ otherwise. Notice that $H^2$ is a subgraph of $G^{\prime }$ satisfying the condition of Theorem 4 (ii), a contradiction.

Then suppose that $a_5$ lies on the path $T_2$ out of $S\left(K_{1,3}\right)$ connecting $a_2$ and $a_3$. Let $D^3=a_4{b}_3{a}_1{b}_2{a}_3{T}_2{a}_2{b}_1{a}_1$. By Property (2), there are two trivial vertices in $V\left(T_2\right)$, denoted by $b_4$ and $b_5$. Clearly, $b_6,b_7\notin V\left(T_3\right)$. Then let $H^3=D^3\cup b_l$ if $d_{G^{\prime }}\left(b_l\right)\ge 3$ for $l\in \{4,5\}$, and let $H^3=D^3$ otherwise. We can also verify that $H^3$ is a subgraph of $G^{\prime }$ satisfying the condition of Theorem 4 (ii), a contradiction. This completes the proof of Claim 3. □

Case 1. $\left|V\right(G^{\prime }\left)\right|=8$.

By Claims 2 and 3, the nontrivial vertex $a_5$ is either a subdivided vertex of the edge in $E\left(S\left(K_{1,3}\right)\right)$ or a vertex of degree one in $G^{\prime }$. Suppose first that $d_{G^{\prime }}\left(a_5\right)=1$. Then $G^{\prime }=G_2^1$ or $G^{\prime }=G_2^3$ by symmetry.

Then suppose that $a_5$ is a subdivided vertex of the edge in $E\left(S\left(K_{1,3}\right)\right)$. If $\{a_1,b_1\}\subseteq N_{G^{\prime }}\left(a_5\right)$, since $G^{\prime }$ is contractible to a graph that contains an induced $S\left(K_{1,3}\right)$, then $a_5{a}_i\notin E\left(G^{\prime }\right)$ for $i\in \{2,3,4\}$. If $\{a_2,b_1\}\subseteq N_{G^{\prime }}\left(a_5\right)$, similarly, $a_5{a}_i\notin E\left(G^{\prime }\right)$ for $i\in \{1,3,4\}$. Hence $G^{\prime }=G_2^2$ or $G^{\prime }=G_2^3$ by symmetry.

Case 2. $\left|V\right(G^{\prime }\left)\right|=9$.

Suppose first that $N_{G^{\prime }}\left(a_5\right)=a_1$. If $\{a_2,a_1\}\subseteq b_4$, then let $H^4=a_3{b}_2{a}_1{b}_1{a}_2{b}_4{a}_1{b}_3{a}_4\cup a_5$. Note that $H^4$ is a subgraph of $G^{\prime }$ satisfying the condition of Theorem 4 (ii), a contradiction. So, $b_4$ is a subdivided vertex of $a_1{a}_5$. By Property $\left(2\right)$, $b_4{a}_i\notin E\left(G^{\prime }\right)$ for $i\in \{2,3,4\}$. Hence $G^{\prime }=G_2^4$. Then suppose $N_{G^{\prime }}\left(a_5\right)=a_2$. If $\{a_2,a_1\}\subseteq b_4$, then let $H^5=a_3{b}_2{a}_1{b}_1{a}_2{b}_4{a}_1{b}_3{a}_4\cup a_5$. If $\{a_5,a_1\}\subseteq b_4$, then let $H^6=a_3{b}_2{a}_1{b}_1{a}_2{a}_5{b}_4{a}_1{b}_3{a}_4$. If $\{a_3,a_1\}\subseteq b_4$, then let $H^7=a_4{b}_3{a}_1{b}_2{a}_3{b}_4{a}_1{b}_1{a}_2{a}_5$. Note that $H^5$, $H^6$ or $H^7$ is a subgraph of $G^{\prime }$ satisfying the condition of Theorem 4 (ii), a contradiction. So, $b_4$ is a subdivided vertex of $a_2{a}_5$. By Property $\left(2\right)$, $b_4{a}_i\notin E\left(G^{\prime }\right)$ for $i\in \{1,3,4\}$. Hence $G^{\prime }=G_2^5$.

Now suppose that $a_5$ is a subdivided vertex of $a_1{b}_1$. If $\{a_2,a_5\}\subseteq N_{G^{\prime }}\left(b_4\right)$, then $H^9=a_2{b}_1{a}_5{b}_4{a}_2\cup a_4{b}_3{a}_1{b}_2{a}_3$. If $\{a_2,a_1\}\subseteq N_{G^{\prime }}\left(b_4\right)$, then $H^{10}=a_4{b}_3{a}_1{a}_5{b}_1{a}_2{b}_4{a}_1{b}_2{a}_3$. If $\{a_1,a_3\}\subseteq N_{G^{\prime }}\left(b_4\right)$, then $H^{11}=a_4{b}_3{a}_1{b}_2{a}_3{b}_4{a}_1{a}_5{b}_1{a}_2$. Note that $H^9$, $H^{10}$ or $H^{11}$ is a subgraph of $G^{\prime }$ satisfying the condition of Theorem 4 (ii), a contradiction. Thus, $b_4$ is a subdivided vertex of $a_1{a}_5$. And $b_4{a}_i\notin E\left(G^{\prime }\right)$ for $i\in \{2,3,4\}$. Hence $G^{\prime }=G_2^5$.

Case 3. $\left|V\right(G^{\prime }\left)\right|=10$.

Suppose first that $N_{G^{\prime }}\left(a_5\right)=a_1$ and $b_4$ is a subdivided vertex of $a_1{a}_5$. If $\{a_2,a_5\}\subseteq N_{G^{\prime }}\left(b_5\right)$, then let $H^{12}=a_4{b}_3{a}_1{b}_4{a}_5{b}_5{a}_2{b}_1{a}_1{b}_2{a}_3$. Note that $H^{12}$ is a subgraph of $G^{\prime }$ satisfying the condition of Theorem 4 (ii), a contradiction. Thus, by symmetry, $\{a_1,a_3\}=N_{G^{\prime }}\left(b_5\right)$ and $G^{\prime }=G_2^6$.

By symmetry, then we only need to consider the case that $a_5$ is a subdivided vertex of $a_1{b}_1$ and $b_4$ is a subdivided vertex of $a_1{a}_5$. Let $H^{13}=a_4{b}_3{a}_1{b}_4{a}_5{b}_5{a}_2{b}_1{a}_1{b}_2{a}_3$ if $\{a_1,a_3\}\subseteq N_{G^{\prime }}\left(b_5\right)$ and let $H^{14}=a_4{b}_3{a}_1{b}_4{a}_5{b}_1{a}_2{b}_5{a}_1{b}_2{a}_3$ if $\{a_1,a_2\}\subseteq N_{G^{\prime }}\left(b_5\right)$. Then $H^{13}$ or $H^{14}$ is a subgraph of $G^{\prime }$ satisfying the condition of Theorem 4 (ii), a contradiction. Hence $G^{\prime }=G_2^7$ or $G^{\prime }=G_2^8$.

Case 4. $\left|V\right(G^{\prime }\left)\right|=11$.

We first consider this case based on $G_2^6$. Let $H^{15}=a_1{b}_2{a}_3{b}_5{a}_1{b}_1{a}_2{b}_6{a}_5{b}_4{a}_1{b}_3{a}_4$ if $\{a_2,a_5\}\subseteq N_{G^{\prime }}\left(b_6\right)$ and let $H^{16}=a_4{b}_3{a}_1{b}_2{a}_3{b}_5{a}_1{b}_1{a}_2{b}_6{a}_1{b}_4{a}_5$ if $\{a_2,a_1\}\subseteq N_{G^{\prime }}\left(b_6\right)$. Note that $H^{15}$ or $H^{16}$ is a subgraph of $G^{\prime }$ satisfying the condition of Theorem 4 (ii), a contradiction. Thus, by symmetry, $\{a_1,a_3\}=N_{G^{\prime }}\left(b_6\right)$ and $G^{\prime }=G_2^9$.

Then we consider this case based on $G_2^7$. Clearly, $\{a_1,a_2\}⊈N_{G^{\prime }}\left(b_6\right)$ and $\{a_1,a_3\}⊈N_{G^{\prime }}\left(b_6\right)$. If $\{a_1,a_5\}\subseteq N_{G^{\prime }}\left(b_6\right)$, then let $H^{17}=a_4{b}_3{a}_1{b}_4{a}_5{b}_1{a}_2{b}_5{a}_5{b}_6{a}_1{b}_2{a}_3$. If $\{a_3,a_5\}\subseteq N_{G^{\prime }}\left(b_6\right)$, then let $H^{18}=a_4{b}_3{a}_1{b}_2{a}_3{b}_6{a}_5{b}_1{a}_2$. Note that $H^{17}$ or $H^{18}$ is a subgraph of $G^{\prime }$ satisfying the condition of Theorem 4 (ii), a contradiction. Thus, $G^{\prime }=G_2^{10}$.

Finally, we consider this case based on $G_2^8$. Clearly, $\{a_1,a_2\}⊈N_{G^{\prime }}\left(b_6\right)$ and $\{a_1,a_3\}⊈N_{G^{\prime }}\left(b_6\right)$. If $\{a_2,a_5\}\subseteq N_{G^{\prime }}\left(b_6\right)$, then let $H^{19}=a_4{b}_3{a}_1{b}_4{a}_5{b}_1{a}_2{b}_6{a}_5{b}_5{a}_1{b}_2{a}_3$. If $\{a_3,a_5\}\subseteq N_{G^{\prime }}\left(b_6\right)$, then let $H^{20}=a_4{b}_3{a}_1{b}_2{a}_3{b}_6{a}_5{b}_1{a}_2$. Note that $H^{19}$ or $H^{20}$ is a subgraph of $G^{\prime }$ satisfying the condition of Theorem 4 (ii), a contradiction. Thus, $G^{\prime }=G_2^{11}$.

Case 5. $\left|V\right(G^{\prime }\left)\right|=12$.

We first consider this case based on $G_2^9$. By Property $\left(2\right)$, $\{a_i,b_j\}⊈N_{G^{\prime }}\left(b_7\right)$ for $i\in \{2,4,5\}$ and $j\in \{2,5,6\}$. If $\{a_1,a_2\}\subseteq N_{G^{\prime }}\left(b_7\right)$, then let $H^{21}=a_4{b}_3{a}_1{b}_2{a}_3{b}_5{a}_1{b}_1{a}_2{b}_7{a}_1{b}_4{a}_5$. If $\{a_2,a_5\}\subseteq N_{G^{\prime }}\left(b_7\right)$, then let $H^{22}=a_1{b}_2{a}_3{b}_5{a}_1{b}_1{a}_2{b}_7{a}_5{b}_4{a}_1{b}_3{a}_4$. Then $H^{21}$ or $H^{22}$ is a subgraph of $G^{\prime }$ satisfying the condition of Theorem 4 (ii), a contradiction. Thus, by symmetry, $\{a_1,a_3\}=N_{G^{\prime }}\left(b_7\right)$ and $G^{\prime }=G_3^1$.

Then we consider this case based on $G_2^{10}$. Let $H^{23}=a_4{b}_3{a}_1{b}_4{a}_5{b}_1{a}_2{b}_5{a}_5{b}_7{a}_1{b}_2{a}_3$ if $\{a_1,a_5\}\subseteq N_{G^{\prime }}\left(b_7\right)$ and let $H^{24}=a_4{b}_3{a}_1{b}_2{a}_3{b}_7{a}_5{b}_1{a}_2$ if $\{a_3,a_5\}\subseteq N_{G^{\prime }}\left(b_7\right)$. Then $H^{23}$ or $H^{24}$ is a subgraph of $G^{\prime }$ satisfying the condition of Theorem 4 (ii), a contradiction. Thus, $G^{\prime }=G_3^2$.

Finally, we consider this case based on $G_2^{11}$. Let $H^{25}=a_4{b}_3{a}_1{b}_4{a}_5{b}_1{a}_2{b}_7{a}_5{b}_5{a}_1{b}_2{a}_3$ if $\{a_2,a_5\}\subseteq N_{G^{\prime }}\left(b_7\right)$ and let $H^{26}=a_4{b}_3{a}_1{b}_2{a}_3{b}_7{a}_5{b}_1{a}_2$ if $\{a_3,a_5\}\subseteq N_{G^{\prime }}\left(b_7\right)$. Also, $H^{25}$ or $H^{26}$ is a subgraph of $G^{\prime }$ satisfying the condition of Theorem 4 (ii), a contradiction. Thus, $G^{\prime }=G_3^3$.

Therefore, ${\mathcal{F}}_{11}=\left\{G_1^1\right\}\cup \{G_2^1,\cdots ,G_2^{11}\}\cup \{G_3^1,\cdots ,G_3^3\}$. Note that ${\mathcal{F}}_i\subseteq {\mathcal{F}}_j$ for $2\le i<j\le 11$. Then we consider the cases of $2\le p\le 10$.

• For $p\le 7$, then $\left|V\right(G^{\prime }\left)\right|\le 7$ by Theorem 3. For each p with $2\le p\le 7,{\mathcal{F}}_p=\mathrm{Ø}$ follows from Lemma.
• For $p=8$, then $\left|V\right(G^{\prime }\left)\right|\le 8$ by Theorem 3. If $\left|\mathbf{VNT}\right(G^{\prime }\left)\right|=5$, then $|V(\Gamma \left(a_1\right))|\le \frac{n}{5}$ and ${\overline{\sigma }}_2\left(G\right)\le \frac{n}{5}+2<2(\lfloor \frac{n}{8}\rfloor -1)$, contrary to the condition of Theorem 1. Hence $\left|\mathbf{VNT}\right(G^{\prime }\left)\right|\le 4$. Then ${\mathcal{F}}_8=\left\{G_1^1\right\}$ by Property (4).
• For $p=9$, then $\left|V\right(G^{\prime }\left)\right|\le 9$ by Theorem 3. If $\left|\mathbf{VNT}\right(G^{\prime }\left)\right|=5$, then $|V(\Gamma \left(a_1\right))|\le \frac{n}{5}$ and ${\overline{\sigma }}_2\left(G\right)\le \frac{n}{5}+2<2(\lfloor \frac{n}{9}\rfloor -1)$, a contradiction. Hence $\left|\mathbf{VNT}\right(G^{\prime }\left)\right|\le 4$. Then ${\mathcal{F}}_9=\left\{G_1^1\right\}$ by Property (4).
• For $p=10$, then $\left|V\right(G^{\prime }\left)\right|\le 11$ by Theorem 3. If $\left|\mathbf{VNT}\right(G^{\prime }\left)\right|=5$, then $|V(\Gamma \left(a_1\right))|\le \frac{n}{6}$ and ${\overline{\sigma }}_2\left(G\right)\le \frac{n}{6}+2<2(\lfloor \frac{n}{10}\rfloor -1)$, a contradiction. Hence $\left|\mathbf{VNT}\right(G^{\prime }\left)\right|\le 4$. Then ${\mathcal{F}}_9=\left\{G_1^1\right\}\cup \{G_2^1,\cdots ,G_2^{11}\}$ by Property (4).

This completes the proof of Theorem 1.

4. Concluding Remarks

In this paper, we determine the value $f_{trac}(n,2)=2(\lfloor \frac{n}{7}\rfloor -1)$ and give some exceptional graphs of Veldman’s D(G)-reduction graph of G with nontraceable 2-iterated line graph $L^2\left(G\right)$ when ${\overline{\sigma }}_2\left(G\right)>2(\lfloor \frac{n}{7}\rfloor -1)$ ($8\le p\le 11$). To do this, we look at the structure of graphs without any traceable 2-iterated line graph in Lemma 1. The latter result may be interesting. We also think that a similar discussion using reduction methods may be applied to study more hamiltonian properties of graphs.

Note that the difference between the values of $f_{trac}(n,k)$ and $f_{hami}(n,k)$ are small when $k=0$. However, the difference becomes large when $k=1,2$ and tends to be unified to 5 when $k\ge 3$.

Although our results (Theorem 1) are similar to supereulerian line graphs by the first and the third authors [17], the proof idea may handle the general result (traceable 2-iterated line graphs), while we may also get more general result.