Three-Way Fuzzy Sets and Their Applications (II)

Abstract

Recently, the notion of a three-way fuzzy set is presented, inspired by the basic ideas of three-way decision and various generalized fuzzy sets, including lattice-valued fuzzy sets, partial fuzzy sets, intuitionistic fuzzy sets, etc. As the new theory of uncertainty, it has been used in attribute reduction and as a new control method for the water level. However, as an extension of a three-way decision, this new theory has not been used in multi-criteria decision making (MCDM for short). Based on the previous work, in this paper, we present rough set models based on three-way fuzzy sets, which extend the existing fuzzy rough set models in both complete and incomplete information systems. Furthermore, the new models are used to solve the issue of MCDM. Firstly, three-way fuzzy relation rough set and three-way fuzzy covering rough set models are presented for complete and incomplete information systems. Because almost all existing fuzzy rough set models are proposed under complete information, the new proposed models can be seen as a supplement to these existing models. Then, a relationship between the three-way fuzzy relation rough set and the three-way fuzzy covering rough set is presented. Finally, a novel method for the issue of MCDM is presented under the novel three-way fuzzy rough set models, which is used in paper defect diagnosis.

1. Introduction

To manage various kinds of data in data processing, Pawlak [1,2] proposed rough set theory as a mathematical tool in 1982. It has been used in many issues, such as rule extraction [3,4], feature selection [5,6], decision making [7,8], and knowledge discovery [9,10]. To generalize Pawlak’s rough set theory, it has been extended by various kinds of relations [11,12], coverings [13,14], and neighborhoods [15]. Furthermore, it has also been combined with many theories, including the lattice [16], matrix [17,18], and fuzzy set theories [19].

Zadeh’s fuzzy set theory [20] deals with the issue of how to manipulate and understand imperfect knowledge. It has been applied in many real-life problems [21,22,23]. Recently, there has been more attention attracted to combining rough set and fuzzy set theories, such as fuzzy covering rough sets [24] and fuzzy relation rough sets [25].

On the basis of the in-depth study of rough sets (especially decision rough sets), Y.Y. Yao has gradually established a new set of theories, called the three-way decision theory [26,27]. Originally, “three branches” originated from the concepts of the positive domain, negative domain, and boundary domain in the rough set theory, but now, the “three branches” in the three-way decision theory have a broader meaning, such as the three-way set [28] and three-way cluster [29]. Three-way decision making is a decision-making mode in line with human cognition. It holds that: in the real-life decision-making process, people can immediately make a quick judgment on the things they fully grasp to accept or reject. For those things that cannot be made immediately, the decision maker tends to delay the judgment of things, namely: delay the decision. The three-way decision theory has been widely and deeply studied, such as the three-way decision based on the notion of an SMV (Symbols-Meaning-Value) space [30] and a three-way density peak clustering method [31]. It is not only a decision method but also a philosophy of three-way thinking, a thinking paradigm of divide and conquer, and a new way of thinking and solving uncertain problems.

In 2021, Y.Y. Yao [28] explored the trisecting–acting–outcome (i.e., TAO) model in a set-theoretic setting, where the notion of a three-way set is presented. Inspired by the notion of the three-way set and various generalized fuzzy sets (including lattice-valued fuzzy sets, partial fuzzy sets, neutrosophic sets, intuitionistic fuzzy sets, etc.), the concept of a three-way fuzzy set (TFS for short) is presented in [32] (as the reference is written in Chinese, the link is Three-way fuzzy sets and their applications (I)). The contributions of [32] are listed as follows: (1) the notion of the TFS is presented which can be seen as an extension of a three-way decision, and several relations among the TFSs, generalized fuzzy sets, and three-way partitions are discussed; (2) the basic operations of the TFSs are proposed systematically, as well as a three-way fuzzy reasoning inference method; and (3) as a practical application of the TFSs, a new algorithm for attribute reduction in information systems is proposed, and a new control method for a water tank level is given based on the three-way fuzzy inference method. Based on the results in [32], in this paper, we further study the TFS theory from the view of a fuzzy rough set and apply it in multi-criteria decision making (MCDM for short). Firstly, we combine the TFS theory with the rough set theory for constructing three-way fuzzy rough set models. These models contain three-way fuzzy relation rough set and three-way fuzzy covering rough set models. Moreover, the relationship between them is presented. Finally, we propose a method to the issue of MCDM in paper defect diagnosis under the three-way fuzzy rough sets. So, the proposed MCDM method is compared with other methods which are proposed by Liu [33], Ye [34], Yang et al. [35], Wang et al. [36], and Wang et al. [37]. The significance and motivations of this paper are listed as follows:

• In [32], the notion of a TFS is presented to uniformly describe generalized fuzzy sets (including Zadeh’s fuzzy sets [20], intuitionistic fuzzy sets [38], L-fuzzy sets [39], interval-valued intuitionistic fuzzy sets [40], and so on [41]). Because there are many rough set models based on generalized fuzzy sets, it is important to establish a novel fuzzy rough set model by TFSs in this paper, which can be viewed as a unified description of these existing models. Moreover, these existing fuzzy rough set models are established in complete information systems, which can not deal with complete information. Because the notion of a TFS can well describe incomplete information, the new model presented in this paper can deal with incomplete information well.
• For the existing fuzzy rough set models and related decision-making approaches, they can only manage complete information. How to build a fuzzy rough set model to deal with incomplete information is an urgent issue to be solved. Therefore, three-way fuzzy rough sets are presented for dealing with complete and incomplete information in this paper, as well as the corresponding MCDM method.

The rest of this paper is organized as follows. Section 2 shows several basic definitions for the three-way set, lattice, and three-fuzzy fuzzy set. In Section 3, the concepts of the three-way fuzzy relation and three-way fuzzy $\beta$-covering are proposed. Then, the three-way fuzzy relation rough set and three-way fuzzy covering rough set models are constructed. Moreover, the relationship between them is presented. In Section 4, a method for the issue of MCDM in paper defect diagnosis is proposed under the three-way fuzzy rough set models. Moreover, this method is compared with other approaches. Section 5 summarizes the whole paper and gives the future work.

2. Fundamental Definitions

Several fundamental definitions about the three-way set, lattice, and three-fuzzy fuzzy set are shown in this section. Suppose U is a nonempty and finite set called universe.

Definition 1

([28]). Let U be a universe, $X,Y,Z\subseteq U$. A triple $\langle X,Y,Z\rangle$ is defined as a three-way set, if the following statements hold:

(1) $X\bigcup Y\bigcup Z=U$;

(2) $X\ne \varnothing$, $Y\ne \varnothing$, $Z\ne \varnothing$;

(3) $X\bigcap Y=\varnothing$, $X\bigcap Z=\varnothing$, $Y\bigcap Z=\varnothing$.

Suppose L is a nonempty set and ≤ is a binary relation on L. If ≤ satisfies reflexivity, antisymmetry, and transitivity, then $(L,\le )$ is called as a poset. For a poset $(L,\le )$, it is said to be a lattice if for any $a,b\in L$, both the upper bound $a\vee b$ and the lower bound $a\wedge b$ exist. A lattice is bounded if it has the minimum and maximum elements, usually denoted as $(L,\vee ,\wedge ,0,1)$, where the minimum and maximum elements are denoted as 0 and 1, respectively. A lattice in which any subset has upper and lower bounds is called complete. Obviously, a complete lattice must be a bounded lattice.

Definition 2

([42,43]). Suppose X and Y are two nonempty sets. If there is an empty subset $A\subseteq X$ such that a mapping is given by $f:A\to Y$, then f is called as a partial mapping from X to Y. In this case, if $x\in X-A$, then f is undefined at x.

Definition 3

([32]). Suppose U is a universe, $L,M,N$ are three lattices. For three partial mappings $f:U\to L$, $g:U\to M$ and $h:U\to N$, the $\langle f,g,h\rangle$ is called a three-way fuzzy set (TFS for short). Moreover, a three-way fuzzy set A is denoted as:

$$A=\{\langle a,f_A\left(a\right),g_A\left(a\right),h_A\left(a\right)\rangle :a\in U,f_A\left(a\right)\in L,g_A\left(a\right)\in M,h_A\left(a\right)\in N\}.$$

Remark 1. 

In the literature, fuzzy sets normally refer to fuzzy sets defined based on $[0,1]$, and L-fuzzy sets refer to fuzzy sets defined based on a lattice structure. To clearly note the difference in Definition 3, we list two main statements:

(1) There are partial mappings $(i.e.,f,g,h)$ in Definition 3, which can be used to describe incomplete information (such as missing value). For fuzzy sets and L-fuzzy sets, they can only describe complete information.

(2) The TFS is defined based on three different lattice structures $(i.e.,L,M,N)$ which means different evaluation systems or membership degrees. For fuzzy sets and L-fuzzy sets, they are based on only one evaluation system.

In Definition 3, we can also denote a TFS A as $A=\langle f_A,g_A,h_A\rangle$. It can be seen as the extension of Zadeh’s fuzzy sets [20], intuitionistic fuzzy sets [38], L-fuzzy sets [39], interval-valued intuitionistic fuzzy sets [40], and so on [41]. For example, in Definition 3:

(1) If $L=M=N$, then $\langle f,g,h\rangle$ is called a lattice-valued TFS, i.e., L-TFS;

(2) If $L=M=N=\{0,1\}$, $f,g,$ and h are mappings, and $f\left(a\right)+g\left(a\right)+h\left(a\right)=1$ for any $a\in U$, then the TFS $\langle f_A,g_A,h_A\rangle$ is a three-way set which is presented by Yao in [28];

(3) If $L=M=N$ and $f=g=h$, then the TFS $\langle f_A,g_A,h_A\rangle$ is a general fuzzy set which is more extensive than Zadeh’s fuzzy set [20] and L-fuzzy set [39];

(4) If $L=M=N$ and $g=h$, then the TFS $\langle f_A,g_A,h_A\rangle$ is a two-way fuzzy set which is more extensive than intuitionistic fuzzy set [38] and interval-valued intuitionistic fuzzy set [40].

Moreover, we use $TFS(U,L)$ to represent the distinct set formed by the L-TFS on U.

The following examples are presented for Definition 3.

Example 1. 

A student achievement sheet is shown in

Table 1. The table of student achievement.

U	Mathematics	Sports	English
$x_1$	$95.6$	$Good$	9
$x_2$	$80.5$	$Excellent$	8
$x_3$	$89.0$	$Pass$	8
$x_4$	$99.0$	$Good$	10

, where $U=\{x_1,x_2,x_3,x_4\}$ is the set of four students, the value range of “Mathematics” is from $(0,100]$, the value range of “English” is from $\{1,2,3,4,5,6,7,8,9,10\}$, the value range of “Sports” is from $\{Pass,Good,Excellent\}$ where the order is ${}^{“}Pass\le Good\le Excellen{t}^{”}$.

By Table 1, a TFS on U can be defined as $\{\langle x_1,95.6,Good,9\rangle ,\langle x_2,80.5,Excellent,8\rangle ,\langle x_3,89.0,Pass,8\rangle ,$$\langle x_4,99.0,Good,10\rangle \}$.

In Example 1, the TFS on U is presented on different mapping, i.e., “Mathematics” (f), “Sports” (g), and “English” $\left(h\right)$. They are independent of each other and taken from different lattices, where $L=(0,100]$, $M=\{Pass,Good,Excellent\}$ with $“Pass\le Good\le Excellen{t}^{”}$, and $N=\{1,2,3,4,5,6,7,8,9,10\}$.

Example 2. 

Let U be a set of pixels of a color image. For any $x\in U$, $f\left(x\right),g\left(x\right),h\left(x\right)$ denote the R, G, and B components corresponding to pixel x, respectively, then $\langle f,g,h\rangle$ is an L-TFS on lattice $L=[0,255]$. When the image is damaged, the R, G, and B components of some pixels cannot be determined, that is, the L-TFS $\langle f,g,h\rangle$ is undefined at these points.

Example 2 shows that the notion of TFS can be used to describe incomplete information.

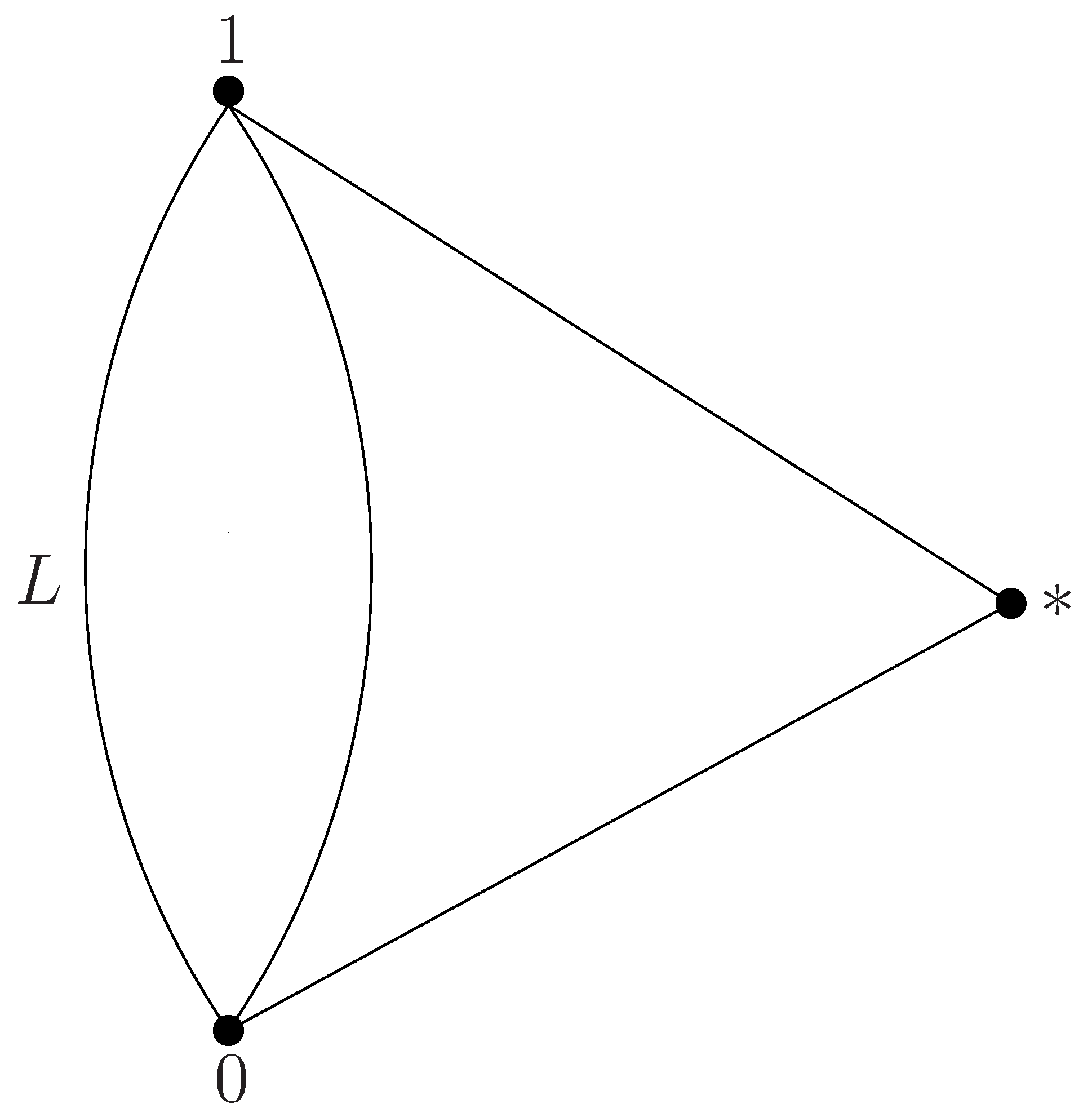
In [32], the undefined membership of the three fuzzy sets will be uniformly represented by the symbol “*”. Suppose $(L,\vee ,\wedge ,0,1)$ is a bounded lattice over which the order relation is ≤. Define a binary relation ${\le }_{*}$ on $L\bigcup \{*\}$ as follows:

$$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\forall x,y\in L,x{\le }_{*}y\iff x\le y;$$

$$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\forall z\in L-\{0,1\} \mathrm{and} *\left|\right|z.0{\le }_{*}*{\le }_{*}1.$$

where “$*\left|\right|z$” means that * and z are not comparable. Figure 1 visually expresses the binary relation ${\le }_{*}$ on $L\bigcup \{*\}$. Obviously, $L\bigcup \{*\}$ is still bounded with respect to ${\le }_{*}$.

Suppose $(L,\vee ,\wedge ,0,1)$ is a bounded lattice over which the order relation is ≤. Denote

$$\begin{gathered} \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}D\left(L\right)=\{(x_1,x_2,x_3):x_1,x_2,x_3\in L\}; \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{D}_{*}\left(L\right)=\{(x_1,x_2,x_3):x_1,x_2,x_3\in L\bigcup \{*\}\}. \end{gathered}$$

Definition 4

([32]). Suppose $(L,\vee ,\wedge ,0,1)$ is a bounded lattice over which the order relation is ≤. Denote a binary relation ${\le }_t$ on $D_{*}\left(L\right)$ as follows: for any $x,y\in D_{*}\left(L\right)$ with $x=(x_1,x_2,x_3)$ and $y=(y_1,y_2,y_3)$,

$$x{\le }_{t}y\iff (x_1{<}_{*}{y}_1,x_3{\ge }_{*}{y}_3) or (x_1=y_1,x_3{>}_{*}{y}_3) or (x_1=y_1,x_2{\le }_{*}{y}_2,x_3=y_3).$$

Theorem 1

([32]). Suppose $(L,\vee ,\wedge ,0,1)$ is a bounded lattice over which the order relation is ≤. Then, $(D_{*}\left(L\right),{\le }_t)$ is a bounded poset, where the minimum and maximum elements are $0_t=(0,0,1)$ and $1_t=(1,1,0)$. Moreover, $(D_{*}\left(L\right),{\vee }_t,{\wedge }_t,0_t,1_t)$ is a bounded lattice over which the order relation is ${\le }_{*}$, where for any $x,y\in D_{*}\left(L\right)$,

$$x{\vee }_{t}y=\left\{\begin{array}{cc}x,\hfill & y{\le }_{t}x;\hfill \\ y,\hfill & x{\le }_{t}y;\hfill \\ (x_1\vee y_1,0,x_3\wedge y_3),\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

$$x{\wedge }_{t}y=\left\{\begin{array}{cc}x,\hfill & x{\le }_{t}y;\hfill \\ y,\hfill & y{\le }_{t}x;\hfill \\ (x_1\wedge y_1,1,x_3\vee y_3),\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Definition 5

([32]). Let $(L,\vee ,\wedge ,0,1)$ be a bounded lattice over which the order relation is ≤, $TFS(U,L)$ be the distinct set formed by the L-TFS on U. For all $A,B\in TFS(U,L)$, we call A is contained in B, defined as $A{\subseteq }_{t}B$, if for any $a\in U$, $(f_A\left(a\right),g_A\left(a\right),h_A\left(a\right)){\le }_t(f_B\left(a\right),g_B\left(a\right),h_B\left(a\right))$.

Definition 6

([32]). Suppose $(L,\vee ,\wedge ,0,1)$ is a bounded lattice over which the order relation is ≤, $TFS(U,L)$ is the distinct set formed by the L-TFS on U. For any $A,B\in TFS(U,L)$, we define the intersection “${\bigcap }_t$” and union “${\bigcup }_t$” of them as follows: for any $a\in U$,

(1) if $(f_A\left(a\right),g_A\left(a\right),h_A\left(a\right)){\le }_t(f_B\left(a\right),g_B\left(a\right),h_B\left(a\right))$, then

$$\left(A{\bigcup }_{t}B\right)\left(a\right)=(f_B\left(a\right),g_B\left(a\right),h_B\left(a\right)), \left(A{\bigcap }_{t}B\right)\left(a\right)=(f_A\left(a\right),g_A\left(a\right),h_A\left(a\right)).$$

(2) if $(f_A\left(a\right),g_A\left(a\right),h_A\left(a\right))$ and $(f_B\left(a\right),g_B\left(a\right),h_B\left(a\right))$ are not comparable in the order relation ${\le }_t$, then

$$\begin{gathered} \left(A{\bigcup }_{t}B\right)\left(a\right)=(f_A\left(a\right)\vee f_B\left(a\right),0,h_A\left(a\right)\wedge h_B\left(a\right)), \left(A{\bigcap }_{t}B\right)\left(a\right)= \\ (f_A\left(a\right)\wedge f_B\left(a\right),1,h_A\left(a\right)\vee h_B\left(a\right)). \end{gathered}$$

Moreover, the complement of A is denoted as $A^{ct}\left(a\right)=1-A\left(a\right)=(h_A\left(a\right),1-g_A\left(a\right),f_A\left(a\right))$.

In Definition 6, if $g_A\left(a\right)=*$, then $1-g_A\left(a\right)=*$. For new inclusion relations and union/intersection operations, the corresponding algebraic structure is a generalized De Morgan algebra rather than a De Morgan algebra in [32].

3. Three-Way Fuzzy Rough Sets

In this section, we establish three-way fuzzy rough set models. These models contain three-way fuzzy relation rough set and three-way fuzzy covering rough set models. Moreover, the relationship between them is presented.

3.1. Three-Way Fuzzy Rough Sets Based on Three-Way Fuzzy Relations

Based on TFSs and fuzzy relations, we present the concept of three-way fuzzy relation. Moreover, a type of three-way fuzzy rough sets under three-way fuzzy relations is constructed in this subsection.

Definition 7. 

Suppose U is a universe, $L,M,N$ are three lattices. A TFS $\mathfrak{R}$ in $U\times U$ is defined as a three-way fuzzy relation on U, which is denoted by

$$\mathfrak{R}=\{\langle (a,b),f_{\mathfrak{R}}(a,b),g_{\mathfrak{R}}(a,b),h_{\mathfrak{R}}(a,b)\rangle :(a,b)\in U\times U,f_{\mathfrak{R}}(a,b)\in L,g_{\mathfrak{R}}(a,b)\in M,h_R(a,b)\in N\},$$

where $f_{\mathfrak{R}}:U\times U\to L$, $g_{\mathfrak{R}}:U\times U\to M$ and $h_{\mathfrak{R}}:U\times U\to N$ are three partial mappings.

In this paper, we establish the three-way fuzzy rough sets for all $TFS(U,L)$. Hence, we default the three-way fuzzy relation $\mathfrak{R}:U\times U\to D_{*}\left(L\right)$ in this paper.

For any three-way fuzzy relation $\mathfrak{R}$ on U, the pair $(U,\mathfrak{R})$ is named a three-way fuzzy relation approximation space (TFRAS for short). By Definition 6, for any $(a,b)\in U\times U$, $1-\mathfrak{R}(a,b)=(h_{\mathfrak{R}}(a,b),1-g_{\mathfrak{R}}(a,b),f_{\mathfrak{R}}(a,b))$.

Definition 8. 

Suppose $(L,\vee ,\wedge ,0,1)$ is a bounded lattice over which the order relation is ≤, $TFS(U,L)$ is the distinct set formed by the L-TFS on U, $(U,\mathfrak{R})$ is a TFRAS. For any $X\in TFS(U,L)$, then

$$\overline{\mathfrak{R}}\left(X\right)\left(a\right)=\underset{b\in U}{{\vee }_t}\left\{X\left(b\right){\wedge }_t\mathfrak{R}(a,b)\right\},\underline{\mathfrak{R}}\left(X\right)\left(a\right)=\underset{b\in U}{{\wedge }_t}\left\{X\left(b\right){\vee }_t(1-\mathfrak{R}(a,b))\right\}$$

are called the three-way fuzzy upper and lower approximations of X as to the three-way fuzzy relation $\mathfrak{R}$, respectively.

In Definition 8, we call X a three-way fuzzy rough set if $\overline{\mathfrak{R}}\left(X\right)\ne \underline{\mathfrak{R}}\left(X\right)$. In Definition 8, 0 and 1 are the minimum and maximum elements in the bounded lattice, respectively.

Example 3. 

Let $(U,\mathfrak{R})$ be a TFRAS, which is shown in

Table 2. The tabular representation of a three-way fuzzy relation $\mathfrak{R}$.

U	${\mathit{a}}_1$	${\mathit{a}}_2$	${\mathit{a}}_3$	${\mathit{a}}_4$	${\mathit{a}}_5$
$a_1$	$(3,6,5)$	$(4,5,7)$	$(9,6,5)$	$(4,9,10)$	$(8,10,7)$
$a_2$	$(5,5,6)$	$(2,7,3)$	$(10,7,8)$	$(9,2,8)$	$(4,3,10)$
$a_3$	$(4,10,7)$	$(10,6,2)$	$(2,3,10)$	$(2,8,9)$	$(9,10,8)$
$a_4$	$(10,0.6,0.2)$	$(3,8,9)$	$(7,5,10)$	$(7,5,10)$	$(10,9,7)$
$a_5$	$(5,7,8)$	$(9,6,5)$	$(4,2,7)$	$(9,8,6)$	$(6,2,4)$

, $L=[0,10]$. Suppose $X=\{\langle a_1,3,8,9\rangle ,\langle a_2,1,4,7\rangle ,\langle a_3,6,3,7\rangle ,\langle a_4,5,7,9\rangle ,\langle a_5,7,8,3\rangle \}$.

By Definition 8, we have:

$$\begin{array}{cc}& \overline{\mathfrak{R}}\left(X\right)=\{\langle a_1,7,10,7\rangle ,\langle a_2,6,0,7\rangle ,\langle a_3,7,0,7\rangle ,\langle a_4,7,10,7\rangle ,\langle a_5,6,2,4\rangle \},\hfill \\ & \underline{\mathfrak{R}}\left(X\right)=\{\langle a_1,5,10,7\rangle ,\langle a_2,3,10,9\rangle ,\langle a_3,2,0,7\rangle ,\langle a_4,3,8,9\rangle ,\langle a_5,5,10,9\rangle \},\hfill \end{array}$$

where “1” should be changed as “10” in $\underline{\mathfrak{R}}\left(X\right)\left(a\right)=\underset{b\in U}{{\wedge }_t}\left\{X\left(b\right){\vee }_t(1-\mathfrak{R}(a,b))\right\}$, because “10” is the maximum elements in the bounded lattice $L=[0,10]$.

Moreover, the bounded lattice $L=[0,10]$ can be normalized to $[0,1]$, which is shown in Example 4.

Example 4. 

Let $(U,\mathfrak{R})$ be a TFRAS, which is shown in

Table 3. The tabular representation of a three-way fuzzy relation $\mathfrak{R}$.

U	${\mathit{a}}_1$	${\mathit{a}}_2$	${\mathit{a}}_3$	${\mathit{a}}_4$	${\mathit{a}}_5$
$a_1$	$(0.3,0.6,0.5)$	$(0.4,0.5,0.7)$	$(0.9,0.6,0.5)$	$(0.4,0.9,1)$	$(0.8,1,0.7)$
$a_2$	$(0.5,0.5,0.6)$	$(0.2,0.7,0.3)$	$(1,0.7,0.8)$	$(0.9,0.2,0.8)$	$(0.4,0.3,1)$
$a_3$	$(0.4,1,0.7)$	$(1,0.6,0.2)$	$(0.2,0.3,1)$	$(0.2,0.8,0.9)$	$(0.9,1,0.8)$
$a_4$	$(1,0.6,0.2)$	$(0.3,0.8,0.9)$	$(0.7,0.5,1)$	$(0.7,0.5,1)$	$(1,0.9,0.7)$
$a_5$	$(0.5,0.7,0.8)$	$(0.9,0.6,0.5)$	$(0.4,0.2,0.7)$	$(0.9,0.8,0.6)$	$(0.6,0.2,0.4)$

. Suppose $X=\{\langle a_1,0.3,0.8,0.9\rangle ,\langle a_2,0.1,0.4,0.7\rangle ,\langle a_3,0.6,0.3,0.7\rangle ,\langle a_4,0.5,0.7,0.9\rangle ,\langle a_5,0.7,0.8,0.3\rangle \}$.

By Definition 8, we have:

$$\begin{array}{cc}& \overline{\mathfrak{R}}\left(X\right)=\{\langle a_1,0.7,1,0.7\rangle ,\langle a_2,0.6,0,0.7\rangle ,\langle a_3,0.7,0,0.7\rangle ,\langle a_4,0.7,1,0.7\rangle ,\langle a_5,0.6,0.2,0.4\rangle \},\hfill \\ & \underline{\mathfrak{R}}\left(X\right)=\{\langle a_1,0.5,1,0.7\rangle ,\langle a_2,0.3,1,0.9\rangle ,\langle a_3,0.2,0,0.7\rangle ,\langle a_4,0.3,0.8,0.9\rangle ,\langle a_5,0.5,1,0.9\rangle \}.\hfill \end{array}$$

Examples 3 and 4 show three-way fuzzy rough sets under complete information system, but a three-way fuzzy rough set model under incomplete information system is presented in Example 5.

Example 5. 

Let $(U,\mathfrak{R})$ be a TFRAS, which is shown in

Table 4. The tabular representation of a three-way fuzzy relation $\mathfrak{R}$.

U	${\mathit{a}}_1$	${\mathit{a}}_2$	${\mathit{a}}_3$	${\mathit{a}}_4$	${\mathit{a}}_5$
$a_1$	$(*,0.6,0.5)$	$(0.4,0.5,0.7)$	$(0.9,0.6,0.5)$	$(0.4,0.9,1)$	$(0.8,1,0.7)$
$a_2$	$(0.5,*,0.6)$	$(0.2,0.7,0.3)$	$(1,0.7,0.8)$	$(0.9,0.2,0.8)$	$(0.4,0.3,1)$
$a_3$	$(0.4,*,0.7)$	$(1,0.6,0.2)$	$(0.2,0.3,1)$	$(0.2,0.8,0.9)$	$(0.9,1,0.8)$
$a_4$	$(*,0.6,0.2)$	$(0.3,0.8,0.9)$	$(0.7,0.5,1)$	$(0.7,0.5,1)$	$(1,0.9,0.7)$
$a_5$	$(0.5,0.7,*)$	$(0.9,0.6,0.5)$	$(0.4,0.2,0.7)$	$(0.9,0.8,0.6)$	$(0.6,0.2,0.4)$

. Suppose $X=\{\langle a_1,0.3,0.8,0.9\rangle ,\langle a_2,0.1,0.4,0.7\rangle ,\langle a_3,0.6,0.3,0.7\rangle ,\langle a_4,0.5,0.7,0.9\rangle ,\langle a_5,0.7,0.8,0.3\rangle \}$.

By Definition 8, we have:

$$\begin{array}{cc}& \overline{\mathfrak{R}}\left(X\right)=\{\langle a_1,0.7,1,0.7\rangle ,\langle a_2,0.6,0,0.7\rangle ,\langle a_3,0.7,0,0.7\rangle ,\langle a_4,0.7,1,0.7\rangle ,\langle a_5,0.6,0.2,0.4\rangle \},\hfill \\ & \underline{\mathfrak{R}}\left(X\right)=\{\langle a_1,0.3,1,0.7\rangle ,\langle a_2,0.6,1,0.9\rangle ,\langle a_3,0.7,1,0.7\rangle ,\langle a_4,0.3,1,0.7\rangle ,\langle a_5,0.6,1,0.9\rangle \}.\hfill \end{array}$$

Let the three-way fuzzy universe set be $\mathfrak{U}=\{\langle a,1,1,0\rangle :a\in U\}$ and the three-way fuzzy empty set be $\Phi =\{\langle a,0,0,1\rangle :a\in U\}$. Several fundamental characteristics of the three-way fuzzy upper and lower approximation operators are presented as follows:

Proposition 1. 

Suppose $(L,\vee ,\wedge ,0,1)$ is a bounded lattice over which the order relation is ≤, $TFS(U,L)$ is the distinct set formed by the L-TFS on U, $(U,\mathfrak{R})$ is a TFRAS. Then, following properties hold: for all $X,Y\in TFS(U,L)$,

$\left(1\right)$$\underline{\mathfrak{R}}\left(\mathfrak{U}\right)=\mathfrak{U}$, $\overline{\mathfrak{R}}\left(\Phi \right)=\Phi$;

$\left(2\right)$$\overline{\mathfrak{R}}\left(X^{ct}\right)={\left(\underline{\mathfrak{R}}\left(X\right)\right)}^{ct}$, $\underline{\mathfrak{R}}\left(X^{ct}\right)={\left(\overline{\mathfrak{R}}\left(X\right)\right)}^{ct}$;

$\left(3\right)$ If $X{\subseteq }_{t}Y$, then $\underline{\mathfrak{R}}\left(X\right){\subseteq }_t\underline{\mathfrak{R}}\left(Y\right)$, $\overline{\mathfrak{R}}\left(X\right){\subseteq }_t\overline{\mathfrak{R}}\left(Y\right)$;

$\left(4\right)$$\underline{\mathfrak{R}}\left(X{\cap }_{t}Y\right)=\underline{\mathfrak{R}}\left(X\right){\cap }_t\underline{\mathfrak{R}}\left(Y\right)$, $\overline{\mathfrak{R}}\left(X{\cup }_{t}Y\right)=\overline{\mathfrak{R}}\left(X\right){\cup }_t\overline{\mathfrak{R}}\left(Y\right)$;

$\left(5\right)$$\underline{\mathfrak{R}}\left(X{\cup }_{t}Y\right){\supseteq }_t\underline{\mathfrak{R}}\left(X\right){\cup }_t\underline{\mathfrak{R}}\left(Y\right)$, $\underline{\mathfrak{R}}\left(X{\cap }_{t}Y\right){\subseteq }_t\underline{\mathfrak{R}}\left(X\right){\cap }_t\underline{\mathfrak{R}}\left(Y\right)$.

Proof. 

$\left(1\right)$ Based on Definition 8, for all $a\in U$, $\underline{\mathfrak{R}}\left(\mathfrak{U}\right)\left(a\right)=\underset{b\in U}{{\wedge }_t}\left\{\mathfrak{U}\left(b\right){\vee }_t(1-\mathfrak{R}(a,b))\right\}$. For any $\mathfrak{R}(a,b)\in D^{*}\left(L\right)$, $1-\mathfrak{R}(a,b){\le }_t\mathfrak{U}\left(b\right)$. Hence, $\mathfrak{U}\left(b\right){\vee }_t(1-\mathfrak{R}(a,b))=\mathfrak{U}\left(b\right)=(1,1,0)$, i.e., $\underline{\mathfrak{R}}\left(\mathfrak{U}\right)=\mathfrak{U}$.

By Definition 8, for any $a\in U$, $\overline{\mathfrak{R}}\left(\Phi \right)\left(a\right)=\underset{b\in U}{{\vee }_t}\left\{\Phi \left(b\right){\wedge }_t\mathfrak{R}(a,b)\right\}$. For any $\mathfrak{R}(a,b)\in D^{*}\left(L\right)$, $\Phi \left(b\right){\le }_t\mathfrak{R}(a,b)$. Hence, $\Phi \left(b\right){\wedge }_t\mathfrak{R}(a,b)=\Phi \left(b\right)=(0,0,1)$, i.e., $\overline{\mathfrak{R}}\left(\Phi \right)=\Phi$;

$\left(2\right)$ By Definition 8, for any $a\in U$,

$$\begin{array}{cc}\overline{\mathfrak{R}}\left(X^{ct}\right)\left(a\right)\hfill & =\underset{b\in U}{{\vee }_t}\left\{X^{ct}\left(b\right){\wedge }_t\mathfrak{R}(a,b)\right\}\hfill \\ & =1-\underset{b\in U}{{\wedge }_t}\left\{X\left(b\right){\vee }_t(1-\mathfrak{R}(a,b))\right\}\hfill \\ & =1-\underline{\mathfrak{R}}\left(X\right)\left(a\right)\hfill \\ & ={\left(\underline{\mathfrak{R}}\left(X\right)\right)}^{ct}\left(a\right).\hfill \end{array}$$

Hence, $\overline{\mathfrak{R}}\left(X^{ct}\right)={\left(\underline{\mathfrak{R}}\left(X\right)\right)}^{ct}$. By the similar way, we can prove $\underline{\mathfrak{R}}\left(X^{ct}\right)={\left(\overline{\mathfrak{R}}\left(X\right)\right)}^{ct}$;

$\left(3\right)$ Because $X{\subseteq }_{t}Y$, $X\left(a\right){\le }_{t}Y\left(a\right)$ for all $a\in U$. Therefore,

$$\begin{array}{cc}\underline{\mathfrak{R}}\left(X\right)\left(a\right)\hfill & =\underset{b\in U}{{\wedge }_t}\left\{X\left(b\right){\vee }_t(1-\mathfrak{R}(a,b))\right\}\hfill \\ & {\le }_t\underset{b\in U}{{\wedge }_t}\left\{Y\left(b\right){\vee }_t(1-\mathfrak{R}(a,b))\right\}\hfill \\ & =\underline{\mathfrak{R}}\left(Y\right)\left(a\right).\hfill \end{array}$$

Hence, $\underline{\mathfrak{R}}\left(X\right){\subseteq }_t\underline{\mathfrak{R}}\left(Y\right)$. By the similar way, there is $\overline{\mathfrak{R}}\left(X\right){\subseteq }_t\overline{\mathfrak{R}}\left(Y\right)$;

$\left(4\right)$ Because

$$\begin{array}{cc}\underline{\mathfrak{R}}\left(X\bigcap _{t}Y\right)\left(a\right)\hfill & =\underset{b\in U}{{\wedge }_t}\left\{\left(X\bigcap _{t}Y\right)\left(b\right){\vee }_t(1-\mathfrak{R}(a,b))\right\}\hfill \\ & =\underset{b\in U}{{\wedge }_t}\left\{\right[\left(X\left(b\right){\vee }_t(1-\mathfrak{R}(a,b))\right]{\wedge }_t\left[\left(Y\left(b\right){\vee }_t(1-\mathfrak{R}(a,b))\right]\right\}\hfill \\ & =\left(\underline{\mathfrak{R}}\left(X\right)\bigcap _t\underline{\mathfrak{R}}\left(Y\right)\right)\left(a\right).\hfill \end{array}$$

Hence, $\underline{\mathfrak{R}}\left(X{\cap }_{t}Y\right)=\underline{\mathfrak{R}}\left(X\right){\cap }_t\underline{\mathfrak{R}}\left(Y\right)$. Similarly, we can prove $\overline{\mathfrak{R}}\left(X{\cup }_{t}Y\right)=\overline{\mathfrak{R}}\left(X\right){\cup }_t\overline{\mathfrak{R}}\left(Y\right)$;

$\left(5\right)$ Inspired by the statement (3), because $X{\subseteq }_t\left(X{\cup }_{t}Y\right)$, $Y{\subseteq }_t\left(X{\cup }_{t}Y\right)$, $\left(X{\cap }_{t}Y\right){\subseteq }_{t}X$ and $\left(X{\cap }_{t}Y\right){\subseteq }_{t}Y$, we obtain

$\underline{\mathfrak{R}}\left(X\right){\subseteq }_t\underline{\mathfrak{R}}\left(X{\cup }_{t}Y\right)$, $\underline{\mathfrak{R}}\left(Y\right){\subseteq }_t\underline{\mathfrak{R}}\left(X{\cup }_{t}Y\right)$, $\overline{\mathfrak{R}}\left(X{\cap }_{t}Y\right){\subseteq }_t\overline{\mathfrak{R}}\left(X\right)$ and $\overline{\mathfrak{R}}\left(X{\cap }_{t}Y\right){\subseteq }_t\overline{\mathfrak{R}}\left(Y\right)$.

Hence, $\underline{\mathfrak{R}}\left(X{\cup }_{t}Y\right){\supseteq }_t\underline{\mathfrak{R}}\left(X\right){\cup }_t\underline{\mathfrak{R}}\left(Y\right)$, $\underline{\mathfrak{R}}\left(X{\cap }_{t}Y\right){\subseteq }_t\underline{\mathfrak{R}}\left(X\right){\cap }_t\underline{\mathfrak{R}}\left(Y\right)$.    □

3.2. Three-Way Fuzzy Rough Sets Based on Three-Way Fuzzy Covering

The concept of a three-way fuzzy $\beta$-covering approximation space is presented in this subsection. Moreover, a type of three-way fuzzy rough sets under a three-way fuzzy $\beta$-covering approximation is constructed.

Definition 9. 

Suppose $(L,\vee ,\wedge ,0,1)$ is a bounded lattice over which the order relation is ≤, $TFS(U,L)$ is the distinct set formed by the L-TFS on U. For $\beta =(a,b,c)$ and $\beta \in D\left(L\right)$, we define $\widehat{\mathbf{C}}=\{C_1,C_2,\cdots ,C_m\}$, with $C_i\in TFS(U,L)(i=1,2,$…$,m)$, as a three-way fuzzy β-covering of U, if for all $a\in U$, $C_i\in \widehat{\mathbf{C}}$ exists such that $C_i\left(a\right){\ge }_t\beta$. We also denote $(U,\widehat{\mathbf{C}})$ as a three-way fuzzy β-covering approximation space (β-TFAS for short).

In a $\beta$-TFAS $(U,\widehat{\mathbf{C}})$, the concept of three-way fuzzy $\beta$-neighborhood is presented as follows:

Definition 10. 

Suppose $(U,\widehat{\mathbf{C}})$ is a β-TFAS with $\widehat{\mathbf{C}}=\{C_1,C_2,\dots ,C_m\}$. For each $a\in U$, the three-way fuzzy β-neighborhood ${\mathfrak{N}}_x^{{\beta }^t}$ of x induced by $\widehat{\mathbf{C}}$ is denoted as:

$${\mathfrak{N}}_x^{{\beta }^t}={\cap }_t\{C_i\in \widehat{\mathbf{C}}:C_i\left(x\right){\ge }_t\beta \}.$$

(1)

Example 6. 

Suppose $U=\{a_1,a_2,a_3,a_4,a_5\}$, $\widehat{\mathbf{C}}=\{C_1,C_2,C_3,C_4\}$ and $\beta =(0.5,0.2,0.8)$. Then, $\widehat{\mathbf{C}}$ is a three-way fuzzy β-covering of U in

Table 5. A three-way fuzzy $\beta$-covering $\widehat{\mathbf{C}.}$.

U	${\mathit{C}}_1$	${\mathit{C}}_2$	${\mathit{C}}_3$	${\mathit{C}}_4$
$a_1$	$\langle 0.8,0.2,0.5\rangle$	$\langle 0.6,0.3,0.4\rangle$	$\langle 0.4,0.4,0.5\rangle$	$\langle 0.2,0.5,0.6\rangle$
$a_2$	$\langle 0.6,0.3,0.2\rangle$	$\langle 0.5,0.3,0.8\rangle$	$\langle 0.5,0.5,0.4\rangle$	$\langle 0.6,0.2,0.7\rangle$
$a_3$	$\langle 0.4,0.5,0.8\rangle$	$\langle 0.4,0.3,0.6\rangle$	$\langle 0.6,0.2,0.4\rangle$	$\langle 0.6,0.4,0.4\rangle$
$a_4$	$\langle 0.6,0.2,0.7\rangle$	$\langle 0.7,0.5,0.7\rangle$	$\langle 0.3,0.7,0.5\rangle$	$\langle 0.5,0.3,0.4\rangle$
$a_5$	$\langle 0.4,0.2,0.6\rangle$	$\langle 0.7,0.5,0.5\rangle$	$\langle 0.9,0.3,0.4\rangle$	$\langle 0.8,0.2,0.2\rangle$

.

Then,

$$\begin{array}{c}{\mathfrak{N}}_{a_1}^{{\beta }^t}=C_1{\cap }_t{C}_2,{\mathfrak{N}}_{a_2}^{{\beta }^t}=C_1{\cap }_t{C}_2{\cap }_t{C}_3{\cap }_t{C}_4,{\mathfrak{N}}_{a_3}^{{\beta }^t}=C_3{\cap }_t{C}_4,{\mathfrak{N}}_{a_4}^{{\beta }^t}=C_1{\cap }_t{C}_2{\cap }_t{C}_4,\hfill \\ {\mathfrak{N}}_{a_5}^{{\beta }^t}=C_2{\cap }_t{C}_3{\cap }_t{C}_4.\hfill \end{array}$$

Hence, all three-way fuzzy β-neighborhoods are shown in

Table 6. ${\mathfrak{N}}_{a_k}^{{\beta }^t}$ ($k=1,2,3,4,5$).

${\mathfrak{N}}_{{\mathit{a}}_{\mathit{k}}}^{{\mathit{\beta }}^{\mathit{t}}}$	${\mathit{a}}_1$	${\mathit{a}}_2$	${\mathit{a}}_3$	${\mathit{a}}_4$	${\mathit{a}}_5$
${\mathfrak{N}}_{a_1}^{{\beta }^t}$	$\langle 0.6,1,0.5\rangle$	$\langle 0.5,0.3,0.8\rangle$	$\langle 0.4,0.5,0.8\rangle$	$\langle 0.6,0.2,0.7\rangle$	$\langle 0.4,0.2,0.6\rangle$
${\mathfrak{N}}_{a_2}^{{\beta }^t}$	$\langle 0.2,0.5,0.6\rangle$	$\langle 0.5,0.3,0.8\rangle$	$\langle 0.4,0.5,0.8\rangle$	$\langle 0.3,1,0.7\rangle$	$\langle 0.4,0.2,0.6\rangle$
${\mathfrak{N}}_{a_3}^{{\beta }^t}$	$\langle 0.2,0.5,0.6\rangle$	$\langle 0.5,1,0.7\rangle$	$\langle 0.6,0.2,0.4\rangle$	$\langle 0.3,0.7,0.5\rangle$	$\langle 0.8,1,0.4\rangle$
${\mathfrak{N}}_{a_4}^{{\beta }^t}$	$\langle 0.2,0.5,0.6\rangle$	$\langle 0.5,0.3,0.8\rangle$	$\langle 0.4,0.5,0.8\rangle$	$\langle 0.5,1,0.7\rangle$	$\langle 0.4,0.2,0.6\rangle$
${\mathfrak{N}}_{a_5}^{{\beta }^t}$	$\langle 0.2,0.5,0.6\rangle$	$\langle 0.5,0.3,0.8\rangle$	$\langle 0.4,0.3,0.6\rangle$	$\langle 0.3,1,0.7\rangle$	$\langle 0.7,0.5,0.5\rangle$

:

Example 7. 

Suppose $U=\{a_1,a_2,a_3,a_4,a_5\}$, $\widehat{\mathbf{C}}=\{C_1,C_2,C_3,C_4\}$, and $\beta =(0.5,0.2,0.8)$. We know that $\widehat{\mathbf{C}}$ is a three-way fuzzy β-covering of U in

Table 7. A three-way fuzzy $\beta$-covering $\widehat{\mathbf{C}.}$.

U	${\mathit{C}}_1$	${\mathit{C}}_2$	${\mathit{C}}_3$	${\mathit{C}}_4$
$a_1$	$\langle *,0.2,0.5\rangle$	$\langle 0.6,0.3,0.4\rangle$	$\langle 0.4,0.4,0.5\rangle$	$\langle 0.2,0.5,0.6\rangle$
$a_2$	$\langle 0.6,0.3,0.2\rangle$	$\langle 0.5,0.3,0.8\rangle$	$\langle 0.5,0.5,0.4\rangle$	$\langle 0.6,0.2,0.7\rangle$
$a_3$	$\langle 0.4,*,0.8\rangle$	$\langle 0.4,0.3,0.6\rangle$	$\langle 0.6,0.2,0.4\rangle$	$\langle 0.6,0.4,0.4\rangle$
$a_4$	$\langle 0.6,0.2,0.7\rangle$	$\langle 0.7,0.5,0.7\rangle$	$\langle 0.3,0.7,0.5\rangle$	$\langle 0.5,0.3,0.4\rangle$
$a_5$	$\langle 0.4,0.2,*\rangle$	$\langle 0.7,0.5,0.5\rangle$	$\langle 0.9,0.3,0.4\rangle$	$\langle 0.8,0.2,0.2\rangle$

.

Then,

$$\begin{array}{c}{\mathfrak{N}}_{a_1}^{{\beta }^t}=C_2,{\mathfrak{N}}_{a_2}^{{\beta }^t}=C_1{\cap }_t{C}_2{\cap }_t{C}_3{\cap }_t{C}_4,{\mathfrak{N}}_{a_3}^{{\beta }^t}=C_3{\cap }_t{C}_4,{\mathfrak{N}}_{a_4}^{{\beta }^t}=C_1{\cap }_t{C}_2{\cap }_t{C}_4,\hfill \\ {\mathfrak{N}}_{a_5}^{{\beta }^t}=C_2{\cap }_t{C}_3{\cap }_t{C}_4.\hfill \end{array}$$

Hence, all three-way fuzzy β-neighborhoods are shown in

Table 8. ${\mathfrak{N}}_{a_k}^{{\beta }^2}$ ($k=1,2,3,4,5$).

${\mathfrak{N}}_{{\mathit{a}}_{\mathit{k}}}^{{\mathit{\beta }}^{\mathit{t}}}$	${\mathit{a}}_1$	${\mathit{a}}_2$	${\mathit{a}}_3$	${\mathit{a}}_4$	${\mathit{a}}_5$
${\mathfrak{N}}_{a_1}^{{\beta }^t}$	$\langle 0.6,0.3,0.4\rangle$	$\langle 0.5,0.3,0.8\rangle$	$\langle 0.4,0.3,0.6\rangle$	$\langle 0.7,0.5,0.7\rangle$	$\langle 0.7,0.5,0.5\rangle$
${\mathfrak{N}}_{a_2}^{{\beta }^t}$	$\langle 0,1,0.6\rangle$	$\langle 0.5,0.3,0.8\rangle$	$\langle 0.4,*,0.8\rangle$	$\langle 0.3,1,0.7\rangle$	$\langle 0.4,1,1\rangle$
${\mathfrak{N}}_{a_3}^{{\beta }^t}$	$\langle 0.2,0.5,0.6\rangle$	$\langle 0.5,1,0.7\rangle$	$\langle 0.6,0.2,0.4\rangle$	$\langle 0.3,0.7,0.5\rangle$	$\langle 0.8,1,0.4\rangle$
${\mathfrak{N}}_{a_4}^{{\beta }^t}$	$\langle 0,1,0.6\rangle$	$\langle 0.5,0.3,0.8\rangle$	$\langle 0.4,*,0.8\rangle$	$\langle 0.5,1,0.7\rangle$	$\langle 0.4,1,1\rangle$
${\mathfrak{N}}_{a_5}^{{\beta }^t}$	$\langle 0.2,0.5,0.6\rangle$	$\langle 0.5,0.3,0.8\rangle$	$\langle 0.4,0.3,0.6\rangle$	$\langle 0.3,1,0.7\rangle$	$\langle 0.7,0.5,0.5\rangle$

:

In a $\beta$-TFAS $(U,\widehat{\mathbf{C}})$, we propose the following characteristics of three-way fuzzy $\beta$-neighborhoods.

Proposition 2. 

Suppose $(U,\widehat{\mathbf{C}})$ is a β-TFAS with $\widehat{\mathbf{C}}=\{C_1,C_2,\dots ,C_m\}$. Then, ${\mathfrak{N}}_a^{{\beta }^t}\left(x\right){\ge }_t\beta$ for any $a\in U$.

Proof. 

For each $a\in U$, ${\mathfrak{N}}_a^{{\beta }^t}\left(a\right)=\left(\underset{C_i\left(a\right){\ge }_t\beta }{{\cap }_t}{C}_i\right)\left(a\right){\ge }_t\beta$.    □

Proposition 3. 

Suppose $(U,\widehat{\mathbf{C}})$ is a β-TFAS with $\widehat{\mathbf{C}}=\{C_1,C_2,\dots ,C_m\}$. For any $a,b,c\in U$, if ${\mathfrak{N}}_a^{{\beta }^t}\left(b\right){\ge }_t\beta$, ${\mathfrak{N}}_b^{{\beta }^t}\left(c\right){\ge }_t\beta$, then ${\mathfrak{N}}_a^{{\beta }^t}\left(c\right){\ge }_t\beta$.

Proof. 

Assume $I=\{1,2,\cdots ,m\}$. Because ${\mathfrak{N}}_a^{{\beta }^t}\left(b\right){\ge }_t\beta$, for each $i\in I$, if $C_i\left(a\right){\ge }_t\beta$, then $C_i\left(b\right){\ge }_t\beta$. Because ${\mathfrak{N}}_b^{{\beta }^t}\left(c\right){\ge }_t\beta$, for each $i\in I$, $C_i\left(c\right){\ge }_t\beta$ when $C_i\left(b\right){\ge }_t\beta$. Then, for each $i\in I$, $C_i\left(a\right){\ge }_t\beta$ implies $C_i\left(c\right){\ge }_t\beta$. Hence, ${\mathfrak{N}}_a^{{\beta }^t}\left(c\right){\ge }_t\beta$.    □

Then, we present a kind of three-way fuzzy covering rough set model on the basis of the three-way fuzzy $\beta$-neighborhoods. Moreover, several characteristics of the lower and upper three-way fuzzy covering approximation operators are proposed.

Definition 11. 

Suppose $(L,\vee ,\wedge ,0,1)$ is a bounded lattice over which the order relation is ≤, $TFS(U,L)$ is the distinct set formed by the L-TFS on U, $(U,\widehat{\mathbf{C}})$ is a β-TFAS. For each $X\in TFS(U,L)$, the three-way fuzzy covering upper approximation $\tilde{\mathfrak{C}}\left(X\right)$ and lower approximation $\underset{\sim }{\mathfrak{C}}\left(X\right)$ of X are denoted as

$$\tilde{\mathfrak{C}}\left(X\right)\left(a\right)=\underset{b\in U}{{\vee }_t}\left\{X\left(b\right){\wedge }_t{\mathfrak{N}}_a^{{\beta }^t}\left(b\right)\right\} \underset{\sim }{\mathfrak{C}}\left(X\right)\left(a\right)=\underset{b\in U}{{\wedge }_t}\left\{X\left(b\right){\vee }_t(1-{\mathfrak{N}}_a^{{\beta }^t}\left(b\right))\right\},$$

where $a\in U$.

Then, X is called the three-way fuzzy covering rough set, if $\tilde{\mathfrak{C}}\left(X\right)\ne \underset{\sim }{\mathfrak{C}}\left(X\right)$.

Example 8. 

Suppose $(U,\widehat{\mathbf{C}})$ is a β-TFAS in Example 6, $\beta =(0.5,0.2,0.8)$ and $X=\frac{(0.3,0.8,0.9)}{a_1}+\frac{(0.1,0.4,0.7)}{a_2}+\frac{(0.6,0.3,0.7)}{a_3}+\frac{(0.5,0.7,0.9)}{a_4}+\frac{(0.7,0.8,0.3)}{a_5}$. Then, all three-way fuzzy β-neighborhoods ${\mathfrak{N}}_{a_k}^{{\beta }^t}$ ($k=1,2,3,4,5$) are listed in Table 6. By Definition 11, we obtain:

$$\begin{array}{cc}& \tilde{\mathfrak{C}}\left(X\right)=\{\langle a_1,0.5,0,0.6\rangle ,\langle a_2,0.4,0.2,0.6\rangle ,\langle a_3,0.7,1,0.4\rangle ,\langle a_4,0.5,0,0.6\rangle ,\langle a_5,0.7,0.5,0.5\rangle \},\hfill \\ & \underset{\sim }{\mathfrak{C}}\left(X\right)=\{\langle a_1,0.5,0,0.6\rangle ,\langle a_2,0.6,1,0.5\rangle ,\langle a_3,0.5,1,0.6\rangle ,\langle a_4,0.6,1,0.5\rangle ,\langle a_5,0.6,1,0.5\rangle \}.\hfill \end{array}$$

Example 9. 

Suppose $(U,\widehat{\mathbf{C}})$ is a β-TFAS in Example 7, $\beta =(0.5,0.2,0.8)$ and $X=\frac{(0.3,0.8,0.9)}{a_1}+\frac{(0.1,0.4,0.7)}{a_2}+\frac{(0.6,0.3,0.7)}{a_3}+\frac{(0.5,0.7,0.9)}{a_4}+\frac{(0.7,0.8,0.3)}{a_5}$. Then, all three-way fuzzy β-neighborhoods ${\mathfrak{N}}_{a_k}^{{\beta }^t}$ ($k=1,2,3,4,5$) are listed in Table 8. By Definition 11, we obtain:

$$\begin{array}{cc}& \tilde{\mathfrak{C}}\left(X\right)=\{\langle a_1,0.7,0.5,0.5\rangle ,\langle a_2,0.4,*,0.8\rangle ,\langle a_3,0.7,1,0.4\rangle ,\langle a_4,0.5,0,0.8\rangle ,\langle a_5,0.7,0.5,0.5\rangle \},\hfill \\ & \underset{\sim }{\mathfrak{C}}\left(X\right)=\{\langle a_1,0.4,1,0.7\rangle ,\langle a_2,0.6,1,0.5\rangle ,\langle a_3,0.5,1,0.6\rangle ,\langle a_4,0.6,1,0.5\rangle ,\langle a_5,0.6,1,0.5\rangle \}.\hfill \end{array}$$

Let the three-way fuzzy universe set be $\mathfrak{U}=\{\langle a,1,1,0\rangle :a\in U\}$ and the three-way fuzzy empty set be $\Phi =\{\langle a,0,0,1\rangle :a\in U\}$. Several properties of the three-way fuzzy covering upper and lower approximation operators are shown as follows:

Proposition 4. 

Suppose $(L,\vee ,\wedge ,0,1)$ is a bounded lattice over which the order relation is ≤, $TFS(U,L)$ is the distinct set formed by the L-TFS on U, $(U,\widehat{\mathbf{C}})$ is a β-TFAS. Then, for any $X,Y\in TFS(U,L)$, the following statements hold:

$\left(1\right)$$\underset{\sim }{\mathfrak{C}}\left(\mathfrak{U}\right)=\mathfrak{U}$, $\tilde{\mathfrak{C}}\left(\Phi \right)=\Phi$;

$\left(2\right)$$\tilde{\mathfrak{C}}\left(X^{ct}\right)={\left(\underset{\sim }{\mathfrak{C}}\left(X\right)\right)}^{ct}$, $\underset{\sim }{\mathfrak{C}}\left(x^{ct}\right)={\left(\tilde{\mathfrak{C}}\left(X\right)\right)}^{ct}$;

$\left(3\right)$ If $X{\subseteq }_{t}Y$, then $\underset{\sim }{\mathfrak{C}}\left(X\right){\subseteq }_t\underset{\sim }{\mathfrak{C}}\left(Y\right)$, $\tilde{\mathfrak{C}}\left(X\right){\subseteq }_t\tilde{\mathfrak{C}}\left(Y\right)$;

$\left(4\right)$$\underset{\sim }{\mathfrak{C}}\left(X{\cap }_{t}Y\right)=\underset{\sim }{\mathfrak{C}}\left(X\right){\cap }_t\underset{\sim }{\mathfrak{C}}\left(Y\right)$, $\tilde{\mathfrak{C}}\left(X{\cup }_{t}Y\right)=\tilde{\mathfrak{C}}\left(X\right){\cup }_t\tilde{\mathfrak{C}}\left(Y\right)$;

$\left(5\right)$$\underset{\sim }{\mathfrak{C}}\left(X{\cup }_{t}Y\right){\supseteq }_t\underset{\sim }{\mathfrak{C}}\left(X\right){\cup }_t\underset{\sim }{\mathfrak{C}}\left(Y\right)$, $\tilde{\mathfrak{C}}\left(X{\cap }_{t}Y\right){\subseteq }_t\tilde{\mathfrak{C}}\left(X\right){\cap }_t\tilde{\mathfrak{C}}\left(Y\right)$.

Proof. 

$\left(1\right)$ By Definition 11, for each $a\in U$, $\underset{\sim }{\mathfrak{C}}\left(\mathfrak{U}\right)\left(a\right)=\underset{b\in U}{{\wedge }_t}\left\{\mathfrak{U}\left(b\right){\vee }_t(1-{\mathfrak{N}}_a^{{\beta }^t}\left(b\right))\right\}$. For any ${\mathfrak{N}}_a^{{\beta }^t}\left(b\right))\in D^{*}\left(L\right)$, $1-{\mathfrak{N}}_a^{{\beta }^t}\left(b\right)){\le }_t\mathfrak{U}\left(b\right)$. Hence, $\mathfrak{U}\left(b\right){\vee }_t(1-{\mathfrak{N}}_a^{{\beta }^t}\left(b\right)))=\mathfrak{U}\left(b\right)=(1,1,0)$, i.e., $\underset{\sim }{\mathfrak{C}}\left(\mathfrak{U}\right)=\mathfrak{U}$.

Based on Definition 11, for each $a\in U$, $\tilde{\mathfrak{C}}\left(\Phi \right)\left(a\right)=\underset{b\in U}{{\vee }_t}\left\{\Phi \left(b\right){\wedge }_t{\mathfrak{N}}_a^{{\beta }^t}\left(b\right)\right\}$. For any ${\mathfrak{N}}_a^{{\beta }^t}\left(b\right)\in D^{*}\left(L\right)$, $\Phi \left(b\right){\le }_t{\mathfrak{N}}_a^{{\beta }^t}\left(b\right)$. Hence, $\Phi \left(b\right){\wedge }_t{\mathfrak{N}}_a^{{\beta }^t}\left(b\right)=\Phi \left(b\right)=(0,0,1)$, i.e., $\tilde{\mathfrak{C}}\left(X\right)\left(\Phi \right)=\Phi$;

$\left(2\right)$ By Definition 11, for any $a\in U$,

$$\begin{array}{cc}\tilde{\mathfrak{C}}\left(X^{ct}\right)\left(a\right)\hfill & =\underset{b\in U}{{\vee }_t}\left\{X^{ct}\left(b\right){\wedge }_t{\mathfrak{N}}_a^{{\beta }^t}\left(b\right)\right\}\hfill \\ & =1-\underset{b\in U}{{\wedge }_t}\left\{X\left(b\right){\vee }_t(1-{\mathfrak{N}}_a^{{\beta }^t}\left(b\right))\right\}\hfill \\ & =1-\underset{\sim }{\mathfrak{C}}\left(X\right)\left(a\right)\hfill \\ & ={\left(\underset{\sim }{\mathfrak{C}}\left(X\right)\right)}^{ct}\left(a\right).\hfill \end{array}$$

Hence, $\tilde{\mathfrak{C}}\left(X^{ct}\right)={\left(\underset{\sim }{\mathfrak{C}}\left(X\right)\right)}^{ct}$. By the similar way, we have $\underset{\sim }{\mathfrak{C}}\left(X^{ct}\right)={\left(\tilde{\mathfrak{C}}\left(X\right)\right)}^{ct}$;

$\left(3\right)$ Because $X{\subseteq }_{t}Y$, $X\left(a\right){\le }_{t}Y\left(a\right)$ for all $a\in U$. Therefore,

$$\begin{array}{cc}\underset{\sim }{\mathfrak{C}}\left(X\right)\left(a\right)\hfill & =\underset{b\in U}{{\wedge }_t}\left\{X\left(b\right){\vee }_t(1-{\mathfrak{N}}_a^{{\beta }^t}\left(b\right))\right\}\hfill \\ & {\le }_t\underset{b\in U}{{\wedge }_t}\left\{Y\left(b\right){\vee }_t(1-{\mathfrak{N}}_a^{{\beta }^t}\left(b\right))\right\}\hfill \\ & =\underset{\sim }{\mathfrak{C}}\left(Y\right)\left(a\right).\hfill \end{array}$$

Hence, $\underset{\sim }{\mathfrak{C}}\left(X\right){\subseteq }_t\underset{\sim }{\mathfrak{C}}\left(Y\right)$. By the similar way, there is $\tilde{\mathfrak{C}}\left(X\right){\subseteq }_t\tilde{\mathfrak{C}}\left(Y\right)$;

$\left(4\right)$ Because

$$\begin{array}{cc}\underset{\sim }{\mathfrak{C}}\left(X\bigcap _{t}Y\right)\left(a\right)\hfill & =\underset{b\in U}{{\wedge }_t}\left\{\left(X\bigcap _{t}Y\right)\left(b\right){\vee }_t(1-{\mathfrak{N}}_a^{{\beta }^t}\left(b\right))\right\}\hfill \\ & =\underset{b\in U}{{\wedge }_t}\left\{\right[\left(X\left(b\right){\vee }_t(1-{\mathfrak{N}}_a^{{\beta }^t}\left(b\right))\right]{\wedge }_t\left[\left(Y\left(b\right){\vee }_t(1-{\mathfrak{N}}_a^{{\beta }^t}\left(b\right))\right]\right\}\hfill \\ & =\left(\underset{\sim }{\mathfrak{C}}\left(X\right)\bigcap _t\underset{\sim }{\mathfrak{C}}\left(Y\right)\right)\left(a\right).\hfill \end{array}$$

Hence, $\underset{\sim }{\mathfrak{C}}\left(X{\cap }_{t}Y\right)=\underset{\sim }{\mathfrak{C}}\left(X\right){\cap }_t\underset{\sim }{\mathfrak{C}}\left(Y\right)$. Similarly, we obtain $\tilde{\mathfrak{C}}\left(X{\cup }_{t}Y\right)=\tilde{\mathfrak{C}}\left(X\right){\cup }_t\tilde{\mathfrak{C}}\left(Y\right)$;

$\left(5\right)$ By the statement (3), because $X{\subseteq }_t\left(X{\cup }_{t}Y\right)$, $Y{\subseteq }_t\left(X{\cup }_{t}Y\right)$, $\left(X{\cap }_{t}Y\right){\subseteq }_{t}X$ and $\left(X{\cap }_{t}Y\right){\subseteq }_{t}Y$, we have

$\underset{\sim }{\mathfrak{C}}\left(X\right){\subseteq }_t\underset{\sim }{\mathfrak{C}}\left(X{\cup }_{t}Y\right)$, $\underset{\sim }{\mathfrak{C}}\left(Y\right){\subseteq }_t\underset{\sim }{\mathfrak{C}}\left(X{\cup }_{t}Y\right)$, $\tilde{\mathfrak{C}}\left(X{\cap }_{t}Y\right){\subseteq }_t\tilde{\mathfrak{C}}\left(X\right)$ and $\tilde{\mathfrak{C}}\left(X{\cap }_{t}Y\right){\subseteq }_t\tilde{\mathfrak{C}}\left(Y\right)$.

Hence, $\underset{\sim }{\mathfrak{C}}\left(X{\cup }_{t}Y\right){\supseteq }_t\underset{\sim }{\mathfrak{C}}\left(X\right){\cup }_t\underset{\sim }{\mathfrak{C}}\left(Y\right)$, $\tilde{\mathfrak{C}}\left(X{\cap }_{t}Y\right){\subseteq }_t\tilde{\mathfrak{C}}\left(X\right){\cap }_t\tilde{\mathfrak{C}}\left(Y\right)$.    □

3.3. Relationships between These Two Three-Way Fuzzy Rough Set Models

In this subsection, we investigate the relationship between the three-way fuzzy relation and covering rough set models.

In Definition 7, suppose U is a universe, $L,M,N$ are three lattices. A three-way fuzzy relation $\mathfrak{R}$ on U is denoted by

$$\mathfrak{R}=\{\langle (a,b),f_{\mathfrak{R}}(a,b),g_{\mathfrak{R}}(a,b),h_{\mathfrak{R}}(a,b)\rangle :(a,b)\in U\times U,f_{\mathfrak{R}}(a,b)\in L,g_{\mathfrak{R}}(a,b)\in M,h_R(a,b)\in N\}$$

where $f_{\mathfrak{R}}:U\times U\to L$, $g_{\mathfrak{R}}:U\times U\to M$ and $h_{\mathfrak{R}}:U\times U\to N$ are three partial mappings. If for each $x,y\in U$, $f_{\mathfrak{R}}(a,b)=f_{\mathfrak{R}}(b,a)$, $g_{\mathfrak{R}}(a,b)=g_{\mathfrak{R}}(b,a)$, and $h_{\mathfrak{R}}(a,b)=h_{\mathfrak{R}}(b,a)$, then $\mathfrak{R}$ is defined as a symmetric three-way fuzzy relation.

Proposition 5. 

Suppose $(U,\widehat{\mathbf{C}})$ is a β-TFAS. Then, $R_{\widehat{\mathbf{C}}}$ is a three-way fuzzy relation on U, which is denoted as

$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\mathfrak{R}}_{\widehat{\mathbf{C}}}(a,b)={\mathfrak{N}}_a^{{\beta }^t}\left(b\right)$, for each $a,b\in U$.

Proof. 

It is immediate by Definitions 7 and 10.    □

We call ${\mathfrak{R}}_{\widehat{\mathbf{C}}}$ the induced three-way fuzzy relation on U by $\widehat{\mathbf{C}}$. The following proposition gives a condition under which ${\mathfrak{R}}_{\widehat{\mathbf{C}}}$ is a symmetric three-way fuzzy relation.

Proposition 6. 

Suppose $(U,\widehat{\mathbf{C}})$ is a β-TFAS, and ${\mathfrak{R}}_{\widehat{\mathbf{C}}}$ is the induced three-way fuzzy relation on U by $\widehat{\mathbf{C}}$. If ${\mathfrak{N}}_a^{{\beta }^t}\left(b\right)={\mathfrak{N}}_b^{{\beta }^t}\left(a\right)$ for any $a,b\in U$, then ${\mathfrak{R}}_{\widehat{\mathbf{C}}}$ is a symmetric three-way fuzzy relation.

Proof. 

It is immediate by Proposition 5.    □

Proposition 7. 

Suppose $(U,\widehat{\mathbf{C}})$ is a β-TFAS, $R_{\widehat{\mathbf{C}}}$ is the induced three-way fuzzy relation on U by $\widehat{\mathbf{C}}$, and $C\in \widehat{\mathbf{C}}$. Then, ${\mathfrak{R}}_{\widehat{\mathbf{C}}}$ is a symmetric three-way fuzzy relation, if $|\widehat{\mathbf{C}}|=1$ and $C\left(x\right)=C\left(y\right)$ for any $x,y\in U$, where $|\widehat{\mathbf{C}}|$ means the cardinality of $\widehat{\mathbf{C}}$.

Proof. 

Because $|\widehat{\mathbf{C}}|=1$, there is only C in $\widehat{\mathbf{C}}$. Because $C\left(a\right)=C\left(a\right)$ for all $a,b\in U$, ${\mathfrak{N}}_a^{{\beta }^t}\left(b\right)={\mathfrak{N}}_b^{{\beta }^t}\left(a\right)$. Hence, ${\mathfrak{R}}_{\widehat{\mathbf{C}}}$ is a symmetric three-way fuzzy relation.    □

Finally, the three-way fuzzy covering rough set model in Definition 11 can be viewed as a three-way relation rough set model in Definition 8. Let $(U,\widehat{\mathbf{C}})$ be a $\beta$-TFAS, ${\mathfrak{R}}_{\widehat{\mathbf{C}}}$ be the induced three-way fuzzy relation on U by $\widehat{\mathbf{C}}$. By Definition 8, for any $X\in TFS(U,L)$, we obtain

$\overline{{\mathfrak{R}}_{\widehat{\mathbf{C}}}}\left(X\right)\left(a\right)=\underset{b\in U}{{\vee }_t}\left\{X\left(b\right){\wedge }_t{\mathfrak{R}}_{\widehat{\mathbf{C}}}(a,b)\right\}$, $\underline{{\mathfrak{R}}_{\widehat{\mathbf{C}}}}\left(X\right)\left(a\right)=\underset{b\in U}{{\wedge }_t}\left\{X\left(b\right){\vee }_t(1-{\mathfrak{R}}_{\widehat{\mathbf{C}}}(a,b))\right\}$.

Theorem 2. 

Suppose $(U,\widehat{\mathbf{C}})$ is a β-TFAS, ${\mathfrak{R}}_{\widehat{\mathbf{C}}}$ is the induced three-way fuzzy relation on U by $\widehat{\mathbf{C}}$. Then, for any $X\in TFS(U,L)$,

$$\begin{array}{cc}& \tilde{\mathfrak{C}}\left(X\right)=\overline{{\mathfrak{R}}_{\widehat{\mathbf{C}}}}\left(X\right),\hfill \\ & \underset{\sim }{\mathfrak{C}}\left(X\right)=\underline{{\underset{\sim }{R}}_{\widehat{\mathbf{C}}}}\left(X\right).\hfill \end{array}$$

Proof. 

It is immediate by Proposition 5, Definitions 11 and 8.    □

4. An Application of MCDM Issues in Paper Defect Diagnosis

In this section, based on the three-way fuzzy covering rough set model, we propose a novel method to MCDM issues in paper defect diagnosis, where the data can be incomplete.

4.1. The Issue of MCDM in Paper Defect Diagnosis

Suppose $U=\{a_k:k=1,2,\cdots ,n\}$ is the family of several types of papers and $V=\left\{y_i\right|i=1,2,\cdots ,m\}$ is the basic symptom for the paper defect B. Suppose that the decision maker evaluates any paper $a_k$ ($k=1,2,\cdots ,n$).

Suppose that the decision maker thinks that every paper $a_k\in U$ ($k=1,2,\cdots ,n$) has a symptom value $C_i$ ($i=1,2,\cdots ,m$), denoted by $C_i\left(a_k\right)=\langle f_{C_i}\left(a_k\right),g_{C_i}(a_k,h_{C_i}\left(a_k\right)\rangle$, where $f_{C_i}\left(a_k\right),g_{C_i}(a_k,h_{C_i}\left(a_k\right)\in [0,1]\bigcup \{*\}$ are three degrees that the decision maker diagnoses paper $a_k$ has symptom $y_i$, where * means the degree can not be given.

Let $\beta =\langle d_1,d_2,d_3\rangle$ be a critical value. If each paper $a_k\in U$, there exists $y_i\in V$ such that $C_i\left(a_k\right){\ge }_t\beta$, then $\widehat{\mathbf{C}}=\{C_1,C_2,\cdots ,C_m\}$ is a three-way fuzzy $\beta$-covering of U.

If $e_1$, $e_2$, $e_3$ are three degrees of the paper defect B of every paper $a_k\in U$ that is diagnosed by the decision maker, denoted by $A\left(a_k\right)=\langle e_1,e_2,e_3\rangle$, then the decision maker for the MCDM issue needs to evaluate whether the papers $a_k\in U$ have the paper defect B or not.

4.2. The MCDM Algorithm Based on Three-Way Fuzzy Covering Rough Set Model

In this subsection, we show a method for the issue of MCDM with the above characterizations using the three-way fuzzy covering rough set model. Based on the characterizations of the MCDM problem in Section 4.1, we establish the three-way fuzzy decision information system and propose Algorithm 1 of MCDM under the framework of the three-way fuzzy covering rough set model.

Algorithm 1 The MCDM algorithm under the three-way fuzzy covering rough set model

Input: A three-way fuzzy information table ($U,\widehat{\mathbf{C}},\beta ,A$). Output: The score ordering for all alternatives. Step 1: Calculate the three-way fuzzy $\beta$-neighborhood ${\mathfrak{N}}_a^{{\beta }^t}$ in ($U,\widehat{\mathbf{C}}$), for any $a\in U$; Step 2: Calculate the three-way fuzzy covering upper approximation $\tilde{\mathfrak{C}}\left(A\right)$ and lower approximation $\underset{\sim }{\mathfrak{C}}\left(A\right)$ of A; Step 3: Calculate ${\mathfrak{R}}_t\left(A\right)=\tilde{\mathfrak{C}}\left(A\right){\oplus }_t\underset{\sim }{\mathfrak{C}}\left(A\right)=\{\langle a,f_{\tilde{\mathfrak{C}}\left(A\right)}\left(a\right)+f_{\underset{\sim }{\mathfrak{C}}\left(A\right)}\left(a\right)-f_{\tilde{\mathfrak{C}}\left(A\right)}\left(a\right)·f_{\underset{\sim }{\mathfrak{C}}\left(A\right)}\left(a\right),g_{\tilde{\mathfrak{C}}\left(A\right)}\left(a\right)·g_{\underset{\sim }{\mathfrak{C}}\left(A\right)}\left(a\right),h_{\tilde{\mathfrak{C}}\left(A\right)}\left(a\right)·h_{\underset{\sim }{\mathfrak{C}}\left(A\right)}\left(a\right)\rangle :a\in U\}$; Step 4: Compute $$\begin{array}{c}s\left(a\right)=\frac{f_{{\mathfrak{R}}_t\left(A\right)}\left(a\right)}{\sqrt{{\left(f_{{\mathfrak{R}}_t\left(A\right)}\left(a\right)\right)}^2+{\left(g_{{\mathfrak{R}}_t\left(A\right)}\left(a\right)\right)}^2+{\left(h_{{\mathfrak{R}}_t\left(A\right)}\left(a\right)\right)}^2}};\hfill \end{array}$$ Step 5: Rank all the alternatives $s\left(a\right)$ and make a decision.

Based on the process above, we can make a decision according to the ranking in Algorithm 1. In Step 3, we use $b+*=b-*=b$, $b·*=0$ for any $b\in [0,1]$. Moreover, the three-way fuzzy covering rough set model is used to construct Algorithm 1, which can also be replaced by the three-way fuzzy relation rough set model.

4.3. A Real-Life Example

Example 10. 

Suppose $U=\{a_1,a_2,a_3,a_4,a_5\}$ is a set of papers. $V=\{y_1,y_2,y_3,y_4\}$ is the set of four main symptoms (including steak, spot, crater, and fracture) for a paper defect B. Suppose that the decision maker evaluates any paper $a_k$ ($k=1,2,\cdots ,5$) as listed in Table 7.

Assume $\beta =\langle 0.5,0.2,0.8\rangle$. Then, $\widehat{\mathbf{C}}=\{C_1,C_2,C_3,C_4\}$ is a three-way fuzzy β-coverings of U. Suppose that the decision maker diagnosed the value $A=\frac{(0.3,0.8,0.9)}{a_1}+\frac{(0.1,0.4,0.7)}{a_2}+\frac{(0.6,0.3,0.7)}{a_3}+\frac{(0.5,0.7,0.9)}{a_4}+\frac{(0.7,0.8,0.3)}{a_5}$ of the paper defect B of every paper.

Step 1: ${\mathfrak{N}}_{a_k}^{{\beta }^t}$ ($k=1,2,3,4,5$) are listed in Table 8.

Step 2:

$$\begin{array}{cc}& \tilde{\mathfrak{C}}\left(A\right)=\{\langle a_1,0.7,0.5,0.5\rangle ,\langle a_2,0.4,*,0.8\rangle ,\langle a_3,0.7,1,0.4\rangle ,\langle a_4,0.5,0,0.8\rangle ,\langle a_5,0.7,0.5,0.5\rangle \},\hfill \\ & \underset{\sim }{\mathfrak{C}}\left(A\right)=\{\langle a_1,0.4,1,0.7\rangle ,\langle a_2,0.6,1,0.5\rangle ,\langle a_3,0.5,1,0.6\rangle ,\langle a_4,0.6,1,0.5\rangle ,\langle a_5,0.6,1,0.5\rangle \}.\hfill \end{array}$$

Step 3:

$$\begin{array}{cc}& {\mathfrak{R}}_t\left(A\right)\hfill \\ =\hfill & \tilde{\mathfrak{C}}\left(A\right){\oplus }_t\underset{\sim }{\mathfrak{C}}\left(A\right)\hfill \\ =\hfill & \{\langle a_1,0.82,0.5,0.35\rangle ,\langle a_2,0.76,0,0.4\rangle ,\langle a_3,0.85,1,0.24\rangle ,\langle a_4,0.8,0,0.4\rangle ,\langle a_5,0.88,0.5,0.25\rangle \}.\hfill \end{array}$$

Step 4: We obtain $s\left(a_k\right)$ ($k=1,2,\cdots ,5$) in

Table 9. $s\left(a_k\right)$ ($k=1,2,\cdots ,5$).

U	${\mathit{a}}_1$	${\mathit{a}}_2$	${\mathit{a}}_3$	${\mathit{a}}_4$	${\mathit{a}}_5$
$s\left(a_{{}_k}\right)$	$0.8022$	$0.8849$	$0.6317$	$0.8944$	$0.8441$

.

Step 5: We have:

$a_3<a_1<a_5<a_2<a_4$.

Hence, the paper $x_4$ is more likely to be sick with the paper defect B.

4.4. The Comparison Analysis

To validate the feasibility of the presented MCDM approach, a comparison analysis is conducted with other methods. These approaches were proposed by Liu [33], Ye [34], Yang et al. [35], Wang et al. [36], and Wang et al. [37].

The results are shown in

Table 10. Different methods for three-way fuzzy information.

Methods	Complete Data	Incomplete Data
Liu [33]	√	×
Ye [34]	√	×
Yang et al. [35]	√	×
Wang et al. [36]	√	×
Wang et al. [37]	√	×
Our method in this paper	√	√

.

By Table 10, we find that the methods of Liu [33], Ye [34], Yang et al. [35], Wang et al. [36], and Wang et al. [37] can deal with three-way information if it is complete. For Example 10, because Table 7 is incomplete information, these methods can not be used to solve Example 10.

Because the existing methods can deal with complete information, we give a complete information table in [37] to show the effectiveness of our method. We list the complete information table in [37] as follows (

Table 11. The table in [37] which can be seen as a three-way fuzzy $(0.5,0.1,0.8)-$covering.

U	${\mathit{C}}_1$	${\mathit{C}}_2$	${\mathit{C}}_3$	${\mathit{C}}_4$
$a_1$	$\langle 0.7,0.2,0.5\rangle$	$\langle 0.6,0.2,0.4\rangle$	$\langle 0.4,0.1,0.5\rangle$	$\langle 0.1,0.5,0.6\rangle$
$a_2$	$\langle 0.5,0.3,0.2\rangle$	$\langle 0.5,0.2,0.8\rangle$	$\langle 0.4,0.5,0.4\rangle$	$\langle 0.6,0.1,0.7\rangle$
$a_3$	$\langle 0.4,0.5,0.2\rangle$	$\langle 0.2,0.3,0.6\rangle$	$\langle 0.5,0.2,0.4\rangle$	$\langle 0.6,0.3,0.4\rangle$
$a_4$	$\langle 0.6,0.1,0.7\rangle$	$\langle 0.4,0.5,0.7\rangle$	$\langle 0.3,0.6,0.5\rangle$	$\langle 0.5,0.3,0.2\rangle$
$a_5$	$\langle 0.3,0.2,0.6\rangle$	$\langle 0.7,0.3,0.5\rangle$	$\langle 0.6,0.3,0.5\rangle$	$\langle 0.8,0.1,0.2\rangle$

in this paper):

Then, we make a decision based on Table 11, and all the results are shown in

Table 12. The results utilizing the different methods of Table 11.

Methods	The Rank	The Decision Result
Liu [33]	$a_4<a_3<a_2<a_5<a_1$	$a_1$
Ye [34]	$a_4<a_3<a_2<a_5<a_1$	$a_1$
Yang et al. [35]	$a_4<a_3<a_5<a_2<a_1$	$a_1$
Wang et al. [36]	$a_4<a_3<a_2<a_1<a_5$	$a_5$
Wang et al. [37]	$a_3<a_4<a_2<a_1<a_5$	$a_5$
Our method in this paper	$a_3<a_5<a_4<a_1<a_2$	$a_2$

.

In Table 12, $a_1$ is the decision result for Liu [33], Ye [34], and Yang et al. [35]. Although $a_2$ is the decision result for our method which is different from those methods, $a_1$ and $a_2$ are very similar where $s\left(a_1\right)=0.9534$ and $s\left(a_2\right)=0.9536$. Hence, our method is effective.

In this paper, we present three-way fuzzy rough rough set models based on TFSs, which can well deal with complete and incomplete information. Under the three-way fuzzy rough set model, a novel approach for MCDM issues with three-way fuzzy information is proposed. The contributions of our method are listed as follows:

• Because TFSs can be seen as the extension of several generalized fuzzy sets (including lattice-valued fuzzy sets, partial fuzzy sets, intuitionistic fuzzy sets, and neutrosophic sets), our method based on three-way fuzzy rough sets is extended from those methods under generalized fuzzy rough sets.
• Our method can deal with both complete and incomplete information.

5. Conclusions

This paper constructs three-way fuzzy rough set models, which are a bridge linking fuzzy sets, three-way decision, and rough sets. Compared with the existing work, the contributions of this article are listed as follows:

(1)

A three-way fuzzy set is a very broad concept, which is closely related to many generalized fuzzy sets. Compared with the existing generalized fuzzy sets, the TFSs are more broader (for example, membership values can be missing; replacing maps with “partial maps”).

(2)

By introducing new definitions of the three-way fuzzy relation and $\beta$-TFAS, we propose two kinds of three-way fuzzy rough set models. These models contain three-way fuzzy relation rough set and three-way fuzzy covering rough set models. They can be seen as the extension of fuzzy rough sets and can deal with both complete and incomplete data. However, almost all existing fuzzy rough sets can deal with complete data only. Hence, our models are an extension of the existing models.

(3)

There are many MCDM methods presented by fuzzy rough set models. However, they can deal with complete decision information only. The MCDM method proposed in this paper can be used with incomplete decision information.

In this paper, we use the operators “${\wedge }_t$” and “${\vee }_t$” on TFSs. Based on t-norms [44,45] and overlap functions [46,47], “${\wedge }_t$” and “${\vee }_t$” will be extended to three-t-norms and three-overlap functions in the further study. Moreover, image processing [48] will be connected with the research content of this paper.