Abstract
A -cycle is a cycle of the form in the symmetric group . We study the subgroups of generated by several sets of -cycles. Our mathematical development is strongly supported by computational experiments and proofs based on do-it-yourself programming with the logic-based language Maude.
MSC:
20B05; 06F99; 68Q42
1. Introduction
Permutation group theory constitutes one of the origins of group theory, and is currently a very developed mathematical area. From the rather rich literature on the subject, we recommend the works [1,2,3,4,5].
Basic facts in this theory include that every permutation in the symmetric group decomposes as a product (composition) of disjoint cycles and that each cycle is a product of transpositions, with the immediate consequences that each permutation itself decomposes as a product of transpositions. Moreover, it is well known that the adjacent transpositions are in fact enough to generate the whole of . In computer science, this is represented by the rather famous bubble sort algorithm. Such adjacent transpositions are the simplest form of γ-cycles, which are cycles with consecutive entries. This terminology is introduced in this article by adopting the abbreviation of ‘consecutive’ by , as this is the Greek alphabet correspondent of ‘c’, which is the first letter of ‘consecutive’. Although general -cycles have a rather obscure presence in the literature on permutation group theory, their importance has been recognized for a long time. For instance, they are instrumental in the proof of the main results in Piccard’s work [6], namely, that for any non-identity permutation (except three permutations in the Klein group in the case of ) there is at least one permutation such that both permutations generate .
An important result concerning -cycles stated (though not proved) in the article [6] is P.4; we state it below in a slightly more particular form:
For any integers such that
distinct -cycles and generate when is even and otherwise.
Our paper develops new results on the generating power of -cycles that provide answers to questions left unanswered by P.4 of [6]. From the beginning, our endeavour was an experimental mathematical one, as we were crucially assisted by proper programming that contributed in various ways to the development of our results. By programming computational experiments, we discovered new mathematical truths, were able to check some of our guesses, and arrived at more elegant proofs. Several of our guesses were actually invalidated by such experiments, leading to a better understanding of the conditions underlying our results as well as to interesting new questions.
The programming part of this investigation was performed in a do-it-yourself style by using the general purpose logic-based programming language Maude, described in the book [7]. On the one hand, this allowed us to avoid the use of dedicated software programs that are now popular with mathematicians (Maple, Mathematica, Wolfram, MATLAB, GAP, etc.), which although powerful and useful in many ways lack transparency and provide little access on the computational side. On the other hand, Maude is very different from common programming languages such as C, Python, Java, etc., as it is very high-level (in the sense of being closer to human mathematical language and thinking rather to a machine). It is based upon a form of model theory, while its execution engine is based upon the advanced computational paradigm of algebraic term rewriting. There is a good analogy to make here; dedicated software is like climbing a mountain by cable car, while our method it is more like climbing by foot equipped with very good mountain gear. On the other hand, common programming is like going by foot with very poor gear. In terms of connection with the mountain and nature, in terms of freedom to go anywhere and explore anything, nothing compares to the second option.
The programming experience with Maude comes as close as possible to the common mathematical problem solving experience while maintaining an intimate connection to the computational aspects. By employing several of the uniquely powerful computational paradigms implemented by Maude, most notably non-deterministic programming, we were able to achieve programs that are both short and clear. In fact, the mix between programming and mathematical reasoning involved in our endeavour can be a truly unified and very satisfactory problem solving experience.
The contents of our paper are as follows:
- We provide a brief presentation of our method for computational experiments with permutations. Maude can be understood mathematically through a few elementary forms of model theory, which we present briefly.
- We develop a general formula for factoring any -cycle as a product of other -cycles of arbitrary fixed length. A corollary of this is a general result of the generating power of -cycles of fixed length. Although this can be derived from P.4 of [6], our formulas provide a very different proof route to this consequence.
- We establish the exact generating properties of the three exceptions from P.4 of Piccard’s article [6].
For all results, we make very explicit the role played by programming computational experiments and even provide the programs. Being highly declarative and logic-based, these programs are short and easy to read and understand, especially in light of the section introducing our programming method.
2. Preordered Algebra and Its Computational Side
Programming in Maude is a fundamentally mathematical activity, as it consists essentially of specifying logical theories in a form based on model theory. Maude is a complex and sophisticated environment which can be understood and used in a myriad of ways. In this project, we use it in a rather basic way, which can be understood in terms of preordered algebra (abbreviated POA), a model theory which we present briefly now. More about the POA model theory can be read in the monograph [8].
2.1. Preordered Algebra
The conceptual pillars of any model theory, including POA, are fourfold:
- Signatures, which are language symbols that are structured in a certain way and that vary across logical theories;
- Sentences, which are logical formulas built with the symbols provided by the respective signatures;
- Models, which are interpretations of the signatures in set theory and provide meaning to logical theories;
- A satisfaction relation between models (M) and sentences (), which denotes which axioms hold in which models.
Concretely, in POA these are as follows.
We let denote the set of all finite sequences of elements from S, with being the empty sequence. A (n S-sorted) signature is an -indexed family of sets of operation symbols. We call (sometimes denoted simply as ) a constant symbol of the sort s. That was about signatures.
An -term t of sort is a structure of the form , where and are -terms of sorts , where . An -equation is an equality between -terms t and of the same sort. An -rule is a sentence of the form , with t and being terms of the same sort. The POA atomic sentences are either such equations or rules. A POA sentence for a signature is of the form
where X is a finite set of variables and are atomic sentences for the signature that adjoins the variables X as new constants to F. That was about sentences.
Given a sort set S, an S-indexed (or sorted) set A is a family of sets indexed by the elements of S. Given an S-indexed set A and …, we let ; in particular, we let , i.e., some one point set. An -algebra (i.e., a model in POA) A consists of:
- an S-indexed set A (the set is called the carrier of A of sort s), and
- a function for each .
If , then determines a point in , which may be denoted . Any -term , where is an operation symbol and are -(sub)terms corresponding to the parity w, is interpreted as an element in an -algebra A by .
A model in POA for a signature , , called a preordered algebra, consists of an -algebra M and a family of preorders such that the interpretation of each operation in F is monotonic with respect to ≤. That was about models.
The satisfaction relation between preordered algebras and sentences is the Tarskian satisfaction defined inductively on the structure of sentences. Given a fixed arbitrary signature and a preordered -algebra ,
- if for equations,
- if for rules,
- if and , and similarly for ⇒, and
- for each -sentence , if for each expansion of M with interpretations of the variables of X as elements of M.
On the one hand, programming in Maude consists of writing down specifications of signatures and sentences according to syntactic rules that closely follow the mathematical definitions above. On the other hand, there is the semantic aspect, meaning that one has to make a permanent effort to ensure that what is written down accords with the intended class of models to be specified. In general, this may be a subtle issue where the mathematics of models and satisfaction play their role, however, trained mathematicians are in the best possible situation to cope with this.
2.2. Term Rewriting in Maude
The above dealt with the specification part of Maude. However, in addition Maude is a proper programming language with a powerful execution engine based on an advanced computational paradigm, namely, algebraic term rewriting. Its implementation in Maude consists of a complex software structure employing state of-the-art technologies. Computation by term rewriting follows the principle of computation as logical inference. POA admits an inference system that is sound and complete with respect to the model theory defined above. This inference system is just an extension of Birkhoff’s famous set of rules for equational deduction (presented in his work [9]) in a conditional form and with additional rules for atomic transitions (which are similar to the rules for the atomic equations minus the symmetry rule). Details of the POA inference system, including its soundness and completeness, can be found in the monograph [8]. In this way, term rewriting in Maude is an extension of the classical term rewriting paradigm from equational logic to POA, which means that it can be used in two different ways corresponding to the two types of atomic sentences.
- In order to compute equalities between elements of models using equations, terms are reduced to normal forms; for this, it is important that the set of equations enjoy the properties known as confluence and termination. The former means that when several equations can be used in rewriting, the choice does not matter. The latter means that the rewriting of any terms eventually comes to an end, and does not run indefinitely.
- In order to compute elements along preorder relations in models. In a more computing science-oriented terminology, elements of the models are states and the preorder relations are transitions. This approach concerns which statesare reached from which other states, and uses rules rather than equations. Here, neither the confluence nor the termination property is required. Lack of confluence means an open door to non-deterministic programming, a crucial distinctive computational paradigm that we use in the present project.
2.3. Implications
To summarise, POA has three strongly interconnected levels. At the top, there is model theory. At the bottom, there is term rewriting. In the middle, there is the sound and complete inference system of POA that bridges the model theory and the computational side.
The ultimate effect of this conceptual structure is a highly declarative, compact, computationally powerful and transparent programming and experimentation method. Transparency has at least two positive consequences: higher confidence in the correctness of the experiment and a great enhancement of understanding. These are two aspects that, in general, the dedicated mathematical software systems lack. Thus, we think that, when possible, it is worth avoiding opaque experimentation and instead aiming for transparent alternatives even at the cost of greater programming effort. However, when complex and sophisticated algorithms are unavoidable, i.e., for programming tasks that are too large or even impossible due to lack of knowledge, dedicated pre-built software can represent an alternative. What is most important when seeking transparency is to strike a right balance between the two.
The computation as logical inference principle underlying Maude programming implies that proofs that consist of a combination of mathematical reasoning and run on Maude programs are in fact 100% mathematical proofs, as the parts relying on programming can be considered simply as formal proofs. In this way,
“such a combination is just a mathematical proof consisting of more informal parts (i.e., the mathematical arguments in a conventional style) and of purely formal parts, and nothing else.”
Then, the transparency aspect additionally implies rather easy access to the formal parts of such proofs.
3. -Cycles Generated by -Cycles of Fixed Length
Let us recall a few basic notations and techniques from permutation group theory. We denote the product of permutations in the same order as functional compositions; in other words, if and are permutations and , then . An easy corollary of the decomposition
of a cycle as a product of transpositions is the decomposition
of a cycle as a product of subcycles. If , then .
In any group G, if , then denotes the subgroup of Ggenerated by S, which is the smallest subgroup of G that contains S. In any group G, the notation means or the conjugation of by . A few helpful properties of conjugations are (as, in addition, conjugation is bijective, meaning that it is automorphism) and . The conjugacy class of an element is . For the particular case of permutation groups, there is a helpful property for the cycles:
Definition 1
(-cycles). In , a -cycleis a cycle of the form
where . We may denote these cycles simply as An m--cycleis a γ-cycle of length m. The γ-cycles are called initial while the are called final γ-cycles.
For instance, the 2--cycle is just the adjacent transposition .
The following results are established in the literature and are used in what follows. While the former is better known, the latter is much less known (it can be found in Conrad’s work [10]).
Proposition 1.
is generated by the set of all adjacent transpositions. is generated by the set of all 3-γ-cycles.
In the literature on group theory, these properties often receive unnecessarily difficult proofs, especially the result for 3--cycles. However, both of them can be shown easily through algorithmic reasoning by sorting the permutations () as follows. In the former case, at each step we simply select any pair of adjacent elements that are not in order, i.e., , and swap them. This algorithm terminates because at each step the number of inversions is decreased. Moreover, it can only terminate when the permutation is sorted. In the latter case, by successively applying 3--cycles we first bring 1 to its place (i.e., such that ), then we bring 2, 3, etc., until 1, 2, …, are all sorted. Now, if and the permutation is sorted; otherwise, it means that the starting permutation was odd.
3.1. Computational Experiments with Fixed Length -Cycles
The origin of our endeavour was not Piccard’s work [6] (in fact, we learned about it at a rather late stage), but rather a misinterpreted version (perhaps due to poor translation) of a problem proposed in 1994 to the participants at the Russian Mathematical Olympiad. In the end, the misinterpreted variant proved to be much more interesting and challenging than the true version. In higher algebra terminology, this was equivalent to the following question:
What is the subgroup of generated by all m--cycles?
In order to obtain an answer to this question, in the beginning we wrote a program that generated all permutations in from m--cycles. By embedding h of into , now used in the proof of Theorem 1 below, and in the light of Proposition 1, we were able to reduce the problem to the case . By running the program and by inspecting the cardinality of the generated group, we noticed quickly that is generated when m is even, while is generated when m is odd. With this understanding, we approached larger values for m in order to check this truth more thoroughly. For this, we had to abandon the generation of all permutation and instead rely on Proposition 1 to focus only on the adjacent transpositions when m is even and on the 3--cycles when m is odd. This has carried out with two rules, as follows:
- We represented permutations as lists of numbers in the obvious way. For example, the list represents the permutation . This choice of representation is motivated by the fact that Maude provides unparalleled computational support for lists through rewriting modulo associativity.
- One rule (denoted ) generates non-deterministically the inverses of all k--cycles. Its corresponding logical formula iswhere are variables ranging over lists of naturals, b is a variable ranging over the naturals, and is the length of .
- The other rule (denoted ) applies m--cycles non-deterministically, its corresponding logical formula being
We use a “flag” (i.e., a variable that takes either 0 or 1 as its values) to ensure that the former rule is applied exactly once at the beginning of the computation, while the latter can be applied any number of times. In this way, we can generate all compositions between an inverse of a k--cycle and any sequence of m--cycles. When this yields the identity, we can find the respective k--cycle is a product of m--cycles. In the light of Proposition 1, for our immediate purpose it is enough to run the program only for , although the program built in this way can be run more generally as well. For and , this process can be represented by the diagram below:
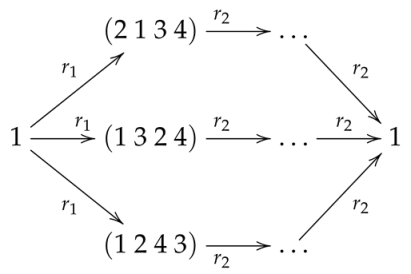 |
This diagram can be interpreted in two ways. On the one hand, it is a fragment of any model satisfying the two logical formulas above. On the other hand, the computational angle shows the relevant fragment of the computation process. With Maude, these are the two sides of the same coin.
The actual Maude programs can be found in Appendix A.
3.2. The Mathematical Results
After assuring confidence with respect to the generation of and through experimentation with the programs discussed above, we assessed how k--cycles for are generated, and noticed immediately that this was always carried out in steps. Then, we looked into the actual decomposition of those k--cycles as products of m--cycles, and by inspecting patterns we arrived at the following formulas:
- (i)
- If m is even, then
- (ii)
- If m is odd, then
where and are the m--cycles of .
While working to prove these formulas, we came to understand that they hold more generally as well, and thus arrived at the results of Proposition 2 and its consequences, Corollary 1 and Theorem 1.
Proposition 2.
In , let , , . Then, for each i and ℓ
Proof.
We begin with the proof of the first equality by induction on ℓ. For , we have:
For the inductive step, we have:
The second equality is proven as follows:
□
Corollary 1.
Under the notations used in Proposition 2, if is even, then . Moreover,
Proof.
The key to the derivation of this consequence is the equation , which can be checked easily. In order to use this, we have to see when the two exponents of involved in one of the two equations in the statement of Proposition 2 are even. Indeed,
- when ℓ is even, then either both i and are even or else both and are even, and
- when ℓ is odd, then m is even, which implies that either both i and are even or else both and are even; in this case, in order to invoke the results of Proposition 2, we use .
□
Note that while the formulas of Corollary 1 are new, its first conclusion can be derived from P.4 of [6].
The theorem below shows that all m--cycles generate either or depending on the parity of m, thereby generalizing the results of Proposition 1.
Theorem 1.
Fix integers , with . Then,
Proof.
For , , we consider . By applying Corollary 1 through homomorphic embedding h of into defined by
the -cycle is generated by and . This conclusion follows from the results of Proposition 1. □
4. The Three Exceptions
P.4 of [6] is a general result for the subgroups of generated by an initial and final -cycle that have a non-empty intersection. Three exceptions are stated therein where the result does not hold. The aim of this section is to establish the nature of the actual subgroups of generated by these exceptions.
We establish the following result through a combination of mathematical reasoning with programming and with classification theory know-how. This exception from P.4 of article [6] was actually discovered by us through programming independently before we were made aware of the above publication.
Proposition 3.
The subgroup of is isomorphic to .
Proof.
was suggested to us by the cardinality of G, which we noticed when generating its elements by programming. However, according to the database [11] there are 47 groups with cardinality 120.
In order to establish the isomorphism to , we implemented the following steps:
- We computed the orders of all elements of G as follows. The program that computes the subgroup of generated by and implements the logical formulasandwhere range over naturals and over lists of naturals. Of course, the parts of the POA models considered refer only to the case in which the terms of the equations are permutations in . To these, we added another sentence used for specifying powers of permutations:where P and L are lists of naturals (which are used only as permutations) and is their composition as permutations. We implemented these three POA sentences as a Maude program, which is explained in detail in Appendix B. By running it for and , we obtained the list of all elements of G together with their respective orders.
- We noticed that the set of the orders of the elements of G is . We ran the program again in order to partition G into six order classes (the order class of , denoted , consists of all elements of G of the same order with ).
- Then, with a simple Maude program implementing the logical formulaswe pick one element from each of the six order classes and compute its conjugacy class. For the orders 1, 3, 4, 5, 6, we have , which implies , because it is always the case that . This consumed five short computations. For the second order, we used a random permutation from the respective order class and obtained . Then, we tried randomly with another permutation, , and obtained . It follows that the set of the permutations in G of the second order is partitioned into two conjugacy classes. To summarise, with seven short computations we were able to establish that G has seven conjugacy classes of sizes 1(1), 10(2), 15(2), 20(3), 30(4), 24(5), and 20(6), where means that the conjugacy class has size a and elements of order b.
- Finally, we relied on established knowledge about groups of order 120 as follows. According to the database [11], is the only group with order 120 and seven conjugacy classes, which means that G is isomorphic to .
□
In the proof of Proposition 3, programming is involved at two points, once explicitly and another time implicitly. On the one hand, we use highly transparent logic-based Maude programming to establish the conjugacy classes of G. On the other hand, at the end of the argument we rely on the result provided by the database in [11], namely, that is the only group with order 120 and seven conjugacy classes, which to our understanding has been obtained through the GAP system [12]. We can say that this is an implicit involvement of programming.
For the other two exceptions, we have two options: either to replicate the proof procedure of Proposition 3 or else to approach them by conventional mathematical reasoning, eventually by relying on the result of Proposition 3. The former option is straightforward, while the latter requires mathematical effort, the result being uncertain. However, for the case of the third exception there is no such dilemma, as we may note immediately a symmetry with the case in Proposition 3, meaning that we can rely on that result.
Corollary 2.
The subgroup of is isomorphic to
Proof.
Let . Then, and , hence, is isomorphic to through an automorphism of . □
The remaining exception is less straightforward mathematically, and in this case it makes a lot of sense to approach it in the style of Proposition 3. However, that would not bring anything new to our exposition; therefore, in order to contrast the two approaches, we approach it in a conventional way. However, this does not mean we start from scratch; we rely on the result of Proposition 3, which is the most important result in this section and a base for deriving the other results.
Corollary 3.
The subgroup of is isomorphic to .
Proof.
Let , and . Because
it follows that
Because and , we obtain that is isomorphic to through an automorphism of . □
4.1. Grasping Concrete Isomorphisms
Proposition 3 tells us that there are isomorphisms . Now, we establish them concretely.
On the basis of Proposition 3, let us consider an isomorphism . Note that, as an isomorphism, preserves orders. In particular, it follows that the order of is 5, becuase in all permutations of order 5 form a single conjugacy class (see the third stage in the proof of Proposition 3) and there exists such that . Let be the composition between and the automorphism defined by the conjugation with . All we have to do now is establish the value of .
By programming, we non-deterministically generate all permutations P of as candidates for , and again by programming we check for each of them whether permutations generated by P and have the same order as the corresponding permutations generated in by and .
We try this gradually with permutations generated in 1, 2, and 3 steps. Upon inspecting the results, it can be seen that all of them share five solutions, while in certain cases (for example when ) these five are all solutions. Then, we note that these are , which is expected, as for any solution P, because , we automatically have for as solutions as well. This means that up to a conjugation by we have found only one possibility for ; hence, we can formulate the following consequence of Proposition 3:
Corollary 4.
and define an isomorphism . Moreover, this is the unique such isomorphism up to a conjugation by a permutation in .
Similar results may be established for the other two exceptions. This can be done either directly, as for Corollary 4, or else as a consequence of Corollary 4 through the isomorphisms of Corollaries 2 and 3, respectively. The program that establishes the value of is presented in Appendix C.
5. Conclusions
We have introduced a new experimental mathematics method that combines conventional mathematical development with preordered algebra based computation with Maude programming language. The computation-as-logical-inference foundation of the programming parts means that, as a whole, our proofs are merely mathematical proofs that may contain a few formal parts. Moreover, the programming parts are highly transparent thanks to the strong declarative character of Maude and because we use general purpose programming rather than dedicated software.
In this way, we were able to discover formulas for generating any -cycles from arbitrary fixed length -cycles, then applied this to show that all -cycles of arbitrary fixed length generate either or depending upon the parity of their length. Then, we turned to the exceptions of an old general result on the generating power of two -cycles. By our method, we able to first discover and then prove that the subgroups generated within the context of all three exceptions correspond to certain uncommon embeddings of into .
Funding
This research received no external funding.
Acknowledgments
We thank Stefan Catoiu for enlightening discussions and advice related to permutation group theory. He suggested a preliminary version of the proof of Corollary 3. We thank Radu Simion for providing us with reference [6].
Conflicts of Interest
The author declares no conflict of interest.
Appendix A. Programs for Proposition 2 and Theorem 1
The program follows closely from the explanation in Section 3.1. However, there are additional details that have to do with managing information rather than the computation process. During the computation process, we maintain the following data:
- The current value of the permutation that suffers the computation process. When this becomes the identity permutation, the computation process stops
- The value of m
- The value of k
- The value of the flag that ensures that the k- cycles are first generated in parallel, then starts the non-deterministic sorting process that applies successive m- cycles
- The inverse of the k- cycle that is currently sorted.
These five pieces of information are stored as the data Config, which is built through a 5-ary operation. The two Maude rules are the obvious Maude writing of the logical formulas and from Section 3.1 using the data in Config.
mod G-CYCLES is
protecting LIST{Nat} .
sort Config .
op <_|_|_|_|_> : List{Nat} Nat Nat Nat List{Nat} -> Config .
vars L L’ l l’ : List{Nat} .
vars k b m : Nat .
crl < l (b L’) l’ | m | k | 0 | L > =>
< l (L’ b) l’ | m | k | 1 | l (L’ b) l’ >
if size(b L’) == k .
crl < l (L’ b ) l’ | m | k | 1 | L > =>
< l (b L’) l’ | m | k | 1 | L >
if size(L’ b) == m .
endm
Next is an example of how to use the program. For instance, the result of Theorem 1 is obtained for and by launching the following command:
search [6] in G-CYCLES :
< 1 2 3 4 5 6 7 | 6 | 2 | 0 | nil > =>*
< L’ | 6 | 2 | 1 | 1 2 4 5 6 7 > .
This triggers the computation of the relevant part of the POA models defined by G-CYCLES and then a search for the states (i.e., elements of the POA models) that match the constraint specified in the target of the search, namely, that the result is the identity permutation. The parameter [6] means that we are interested in ensuring that all six adjacent transpositions are sorted, meaning that after reaching six solutions the computation stops. Otherwise, the system may unnecessarily continue to build more of the POA model. However, even them it eventually stops because, in this case, the model is finite. However, this would take more time unnecessarily.
The slightly abbreviated form of the result of the run is:
Solution 1 (state 792)
states: 793 rewrites: 116631
L --> 2 1 3 4 5 6 7
Solution 2 (state 896)
states: 897 rewrites: 134101
L --> 1 3 2 4 5 6 7
Solution 3 (state 1006)
states: 1007 rewrites: 152447
L --> 1 2 4 3 5 6 7
Solution 4 (state 1104)
states: 1105 rewrites: 169041
L --> 1 2 3 5 4 6 7
Solution 5 (state 1226)
states: 1227 rewrites: 189139
L --> 1 2 3 4 6 5 7
Solution 6 (state 1300)
states: 1301 rewrites: 202229
L --> 1 2 3 4 5 7 6
From this output, it is easy to learn that all the adjacent transpositions have been sorted. We can investigate further and inspect how they have been sorted, which in group theoretical terminology means how they are generated. For instance, for the transposition we pick the indicated state (which is an element of the POA model) and run:
show path 1006 .
This yields an output that, in abbreviated form, looks like this:
state 0, Config: < 1 2 3 4 5 6 7 | 6 | 2 | 0 | nil >
state 3, Config: < 1 2 4 3 5 6 7 | 6 | 2 | 1 | 1 2 4 3 5 6 7 >
state 11, Config: < 6 1 2 4 3 5 7 | 6 | 2 | 1 | 1 2 4 3 5 6 7 >
state 28, Config: < 6 7 1 2 4 3 5 | 6 | 2 | 1 | 1 2 4 3 5 6 7 >
state 61, Config: < 3 6 7 1 2 4 5 | 6 | 2 | 1 | 1 2 4 3 5 6 7 >
state 128, Config: < 3 5 6 7 1 2 4 | 6 | 2 | 1 | 1 2 4 3 5 6 7 >
state 262, Config: < 3 4 5 6 7 1 2 | 6 | 2 | 1 | 1 2 4 3 5 6 7 >
state 524, Config: < 1 3 4 5 6 7 2 | 6 | 2 | 1 | 1 2 4 3 5 6 7 >
state 1006, Config: < 1 2 3 4 5 6 7 | 6 | 2 | 1 | 1 2 4 3 5 6 7 >
Upon inspecting the progress of the computation, we arrive at the formula (the notations are those from Section 3.2). In order to reach to the pattern of the formulas from Section 3.2, we run several such examples.
Appendix B. Programs for Proposition 3
The first two modules contain simple recursive definitions of a couple of auxiliary operations; computes the k-th element of the list L, while computes the compositions of the permutations P and L represented as lists. These work only for values that make sense.
mod LIST-AS-ARRAY is
protecting LIST{Nat} .
protecting INT .
op _[_] : List{Nat} Nat -> Nat .
vars x k : Nat .
var L : List{Nat} .
eq (x L)[1] = x .
ceq (x L)[k] = L[k + -1] if k > 1 .
endm
mod PERM-L-COMP is
protecting LIST-AS-ARRAY .
op _o_ : List{Nat} List{Nat} -> List{Nat} .
vars L P : List{Nat} .
var x : Nat .
eq P o nil = nil .
eq P o (L x) = (P o L) (P[x]) .
endm
The next program implements the three logical formulas in the proof of Proposition 3 for computing the elements of generated by and together with their orders. The program is developed to work in general for any values of m and n. In order to happen in two stages, the computation is controlled by a flag (on the fourth position of the configurations). First, we have the non-deterministic application of the first two formulas from the proof of Proposition 3; then, for each permutation thus obtained, its powers are computed until the identity permutation is obtained. In the first two fields of the configurations, we store the values of the permutation computed in these two stages, respectively. When the first stage stops, the value in the first field is frozen and then duplicated in the second field in order to start the second stage of computation. The third field stores the value of m. The fourth field has two roles: on the one hand, it acts as a flag that keeps the computation inside the first stage (the value is 0), and on the other hand it computes the actual order of the respective permutation in the second stage. The moment the computation is switched from the first to the second stage, this value change from 0 to 1. Note that while the computation in the first stage is non-deterministic, the computation in the second stage is deterministic.
mod ORDERS-PERM is
protecting PERM-L-COMP .
protecting SORTING .
protecting LIST-OF-NUMBERS-FROM-TILL .
sort Config .
op <_|_|_|_> : List{Nat} List{Nat} Nat Nat -> Config .
vars x y m k : Nat .
vars L L’ P : List{Nat} .
rl < x (y L) | nil | m | 0 > =>
< x (L y) | nil | m | 0 > .
crl < (x L) L’ | nil | m | 0 > =>
< (L x) L’ | nil | m | 0 >
if size(x L) == m .
rl < L | nil | m | 0 > =>
< L | L | m | 1 > .
crl < L | P | m | k > =>
< L | P o L | m | k + 1 >
if not sorted(P) .
endm
The elements of subgroup G and their orders are obtained by running a search for the terminal elements of the generated POA model, hence, =>!.
search in ORDERS-PERM :
< from 1 till 6 | nil | 4 | 0 > =>! < L | P | 4 | k > .
Then, we obtain the order classes by running six different searches, one for each of the six orders obtained from the previous run. For instance, the following search provides all permutations of order 4 in G:
search in ORDERS-PERM :
< from 1 till 6 | nil | 4 | 0 > =>! < L | P | 4 | 4 > .
The following program just computes the conjugacy class of a permutation P in G by conjugating non-deterministically with the two generators and . It is used in the third stage in the proof of Proposition 3.
mod CONJUGACY-CLASS is
protecting PERM-L-COMP .
sort Config .
op <_> : List{Nat} -> Config .
var P : List{Nat} .
rl < P > => < (2 3 4 1 5 6) o P o (4 1 2 3 5 6) > .
rl < P > => < (1 3 4 5 6 2) o P o (1 6 2 3 4 5) > .
endm
The program is run seven times, as explained in the proof of Proposition 3. For instance, when establishing that the order class 4 consists of only one conjugacy class, we perform the following search (the input permutation is chosen arbitrarily from the order class 4 computed with ORDERS-PERM):
search in CONJUGACY-CLASS : < 2 3 4 1 5 6 > =>* < P > .
The result consists of 30 permutations, which shows that the conjugacy class coincides with the order class.
Appendix C. Programs for Section 4.1
The program implements computation in three stages:
- Generate all permutations P of non-deterministically.
- For each , we inductively generate the pairs of elements , , such that . This is achieved non-deterministically by two rules, one for each of the two generators (on the one hand P and , on the other hand and ), and by relying on the basic fact that the generated group is just the generated monoid. Moreover, during the generation process we keep trace of the current corresponding element in the free monoid (with two generators, 1 for P and and 2 for and ).
- For each pair , by one rule we establish whether they have the same order by successively computing their powers and . If they have different orders, then the whole computation branch for P halts; otherwise, we continue by going back to stage 2 and generating a new pair .
We structure the values of these variables as follows:
where S is the pool set of numbers from that is used to generate permutations P.
mod ISO-TO-S5 is
protecting SET{Nat} .
protecting PERM-L-COMP .
protecting SORTING .
sort Config .
op <_|_|_|_|_|_|_> : Set{Nat} List{Nat} List{Nat}
List{Nat} List{Nat} List{Nat} List{Nat} -> Config .
var i : Nat .
var S : Set{Nat} .
vars p P P5 P6 L5 L6 : List{Nat} .
The following is the rule that generates permutations P. It non-deterministically moves elements from the pool set S to the list P.
rl < (i, S) | P | nil | nil | nil | nil | nil > =>
< S | (i P) | nil | nil | nil | nil | nil > .
The following two rules initiate the computation of and ; this is the base step of the inductive generation process. The system applies them non-deterministically.
rl < empty | P | nil | nil | nil | nil | nil > =>
< empty | P | P | P | (2 3 4 1 5 6) | (2 3 4 1 5 6) | 1 > .
rl < empty | P | nil | nil | nil | nil | nil > =>
< empty | P | (2 3 4 5 1) | (2 3 4 5 1) |
(1 3 4 5 6 2) | (1 3 4 5 6 2) | 2 > .
The inductive step in the generation of and is specified by the following two rules, each corresponding to one corresponding pair of generators in and in . We set an arbitrary bound to the size of the preordered algebra by constraining the size of the elements in the free monoid.
crl < empty | P | P5 | L5 | P6 | L6 | p > =>
< empty | P | P5 o P | P5 o P |
P6 o (2 3 4 1 5 6) | P6 o (2 3 4 1 5 6) | (p 1) >
if sorted(L5) and sorted(L6) and size(p) < 5 .
crl < empty | P | P5 | L5 | P6 | L6 | p > =>
< empty | P | P5 o (2 3 4 5 1) | P5 o (2 3 4 5 1) |
P6 o (1 3 4 5 6 2) | P6 o (1 3 4 5 6 2) | (p 2) >
if sorted(L5) and sorted(L6) and size(p) < 5 .
At the third stage of the computation, we simultaneously compute powers and , while the minimum of the orders of and is not yet reached. When the first is reached, the computation process is shifted to the stage 2 rules.
crl < empty | P | P5 | L5 | P6 | L6 | p > =>
< empty | P | P5 | L5 o P5 | P6 | L6 o P6 | p >
if (not sorted(L5)) and (not sorted(L6)) .
endm
By running this program for different pairs , we obtain the values of P for which and have the same order. For instance, for and we run the following search:
search in ISO-TO-S5 :
< (1,2,3,4,5) | nil | nil | nil | nil | nil | nil > =>*
< empty | P | P5 | L5 | P6 | L6 | 1 2 2 >
such that sorted(L5) and sorted(L6) .
Then, we obtain five solutions (the output is presented in an abbreviated form):
Solution 1 (state 3402)
states: 3403 rewrites: 550058
P --> 4 5 3 2 1
Solution 2 (state 3592)
states: 3593 rewrites: 588338
P --> 1 5 4 2 3
Solution 3 (state 3609)
states: 3610 rewrites: 591790
P --> 2 5 1 4 3
Solution 4 (state 3633)
states: 3634 rewrites: 596516
P --> 4 2 1 5 3
Solution 5 (state 3751)
states: 3752 rewrites: 620438
P --> 4 3 1 2 5
As mentioned in Section 4.1, these are just for .
References
- Cameron, P. Permutation Groups; LMS Student Textbook; Cambridge University Press: Cambridge, UK, 1999; Volume 45. [Google Scholar]
- Hall, M. The Theory of Groups; Macmillan: New York, NY, USA, 1959. [Google Scholar]
- Isaacs, I.M. Finite Group Theory; American Mathematical Society: Providence, RI, USA, 2008. [Google Scholar]
- Passman, D.S. Permutation Groups; Benjamin: New York, NY, USA, 1968. [Google Scholar]
- Wielandt, H. Finite Permutation Groups; Academic Press: New York, NY, USA, 1964. [Google Scholar]
- Piccard, S. Sur les bases du groupe symétrique et du groupe alternant. Math. Ann. 1939, 116, 752–767. [Google Scholar] [CrossRef]
- Clavel, M.; Durán, F.; Eker, S.; Lincoln, P.; Martí-Oliet, N.; Meseguer, J.; Talcott, C. All about Maude—A High-Performance Logical Framework, Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4350. [Google Scholar]
- Diaconescu, R. Institution-Independent Model Theory; Birkhäuser: Basel, Switzerland, 2008. [Google Scholar]
- Birkhoff, G. On the Structure of Abstract Algebras. Proc. Camb. Philos. Soc. 1935, 31, 433–454. [Google Scholar] [CrossRef]
- Conrad, K. Generating Sets. Available online: http://kconrad.math.uconn.edu/blurbs/grouptheory/genset.pdf (accessed on 1 July 2021).
- Naik, V. The Group Properties Wiki. Available online: http://groupprops.subwiki.org (accessed on 1 July 2021).
- GAP. Groups, Algorithms, Programming—A System for Computational Discrete Algebra. Available online: https://www.gap-system.org (accessed on 1 July 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).