Almost Periodic Solution for Forced Perturbed Non-Instantaneous Impulsive Model
Abstract
1. Introduction
2. Preliminaries
3. Existence and Uniqueness of Almost Periodic Solution
4. Exponential Stability
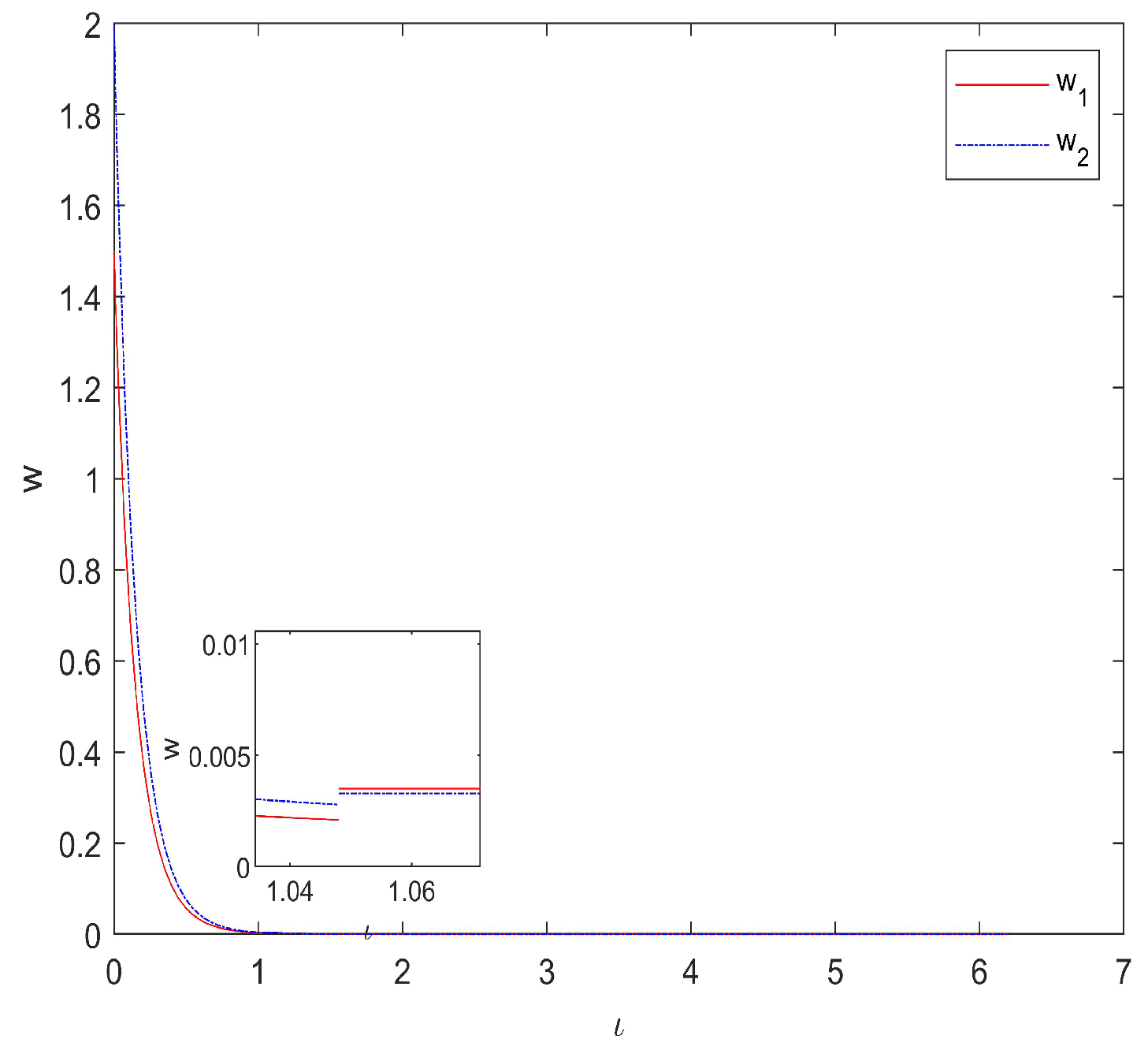
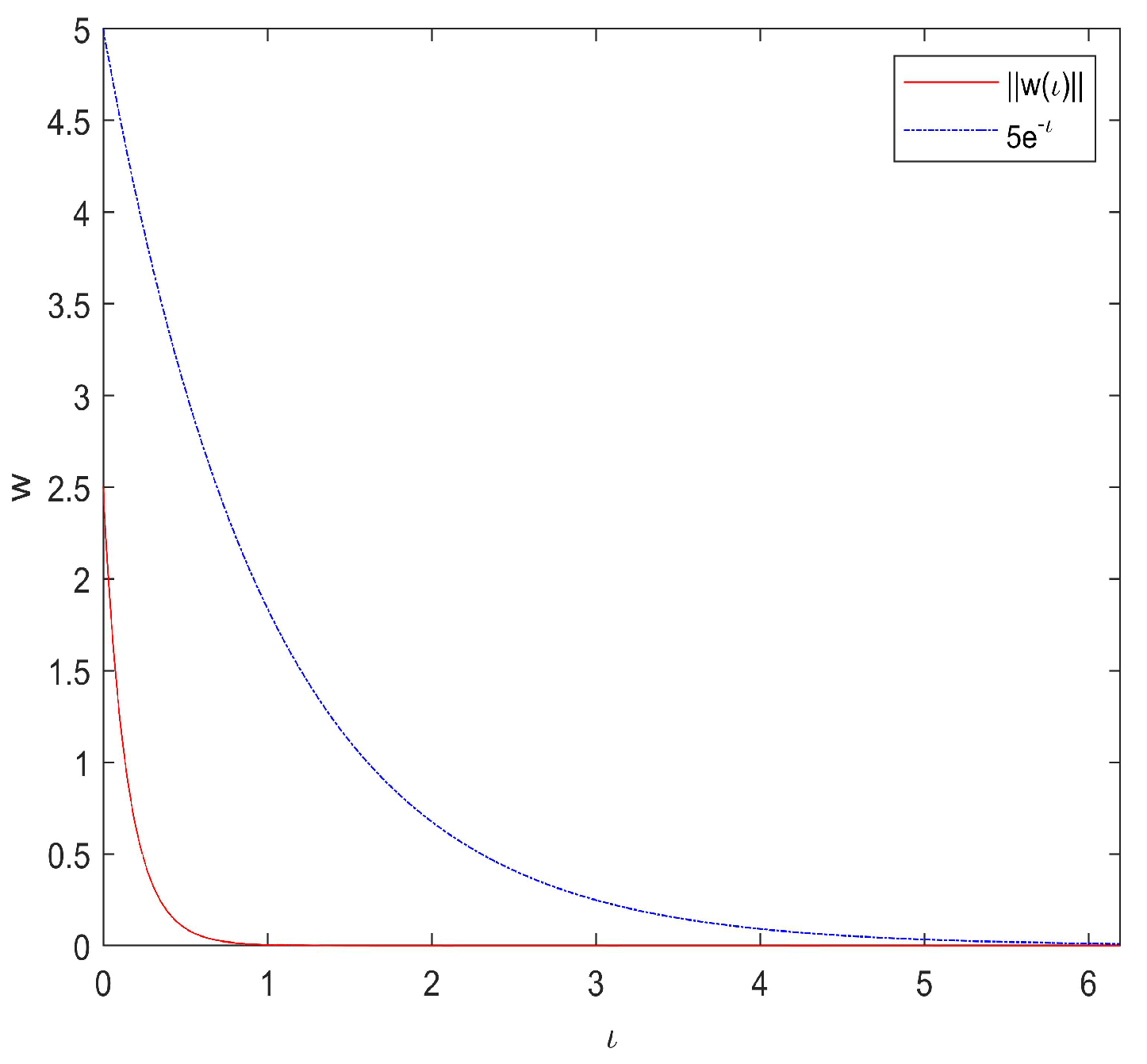
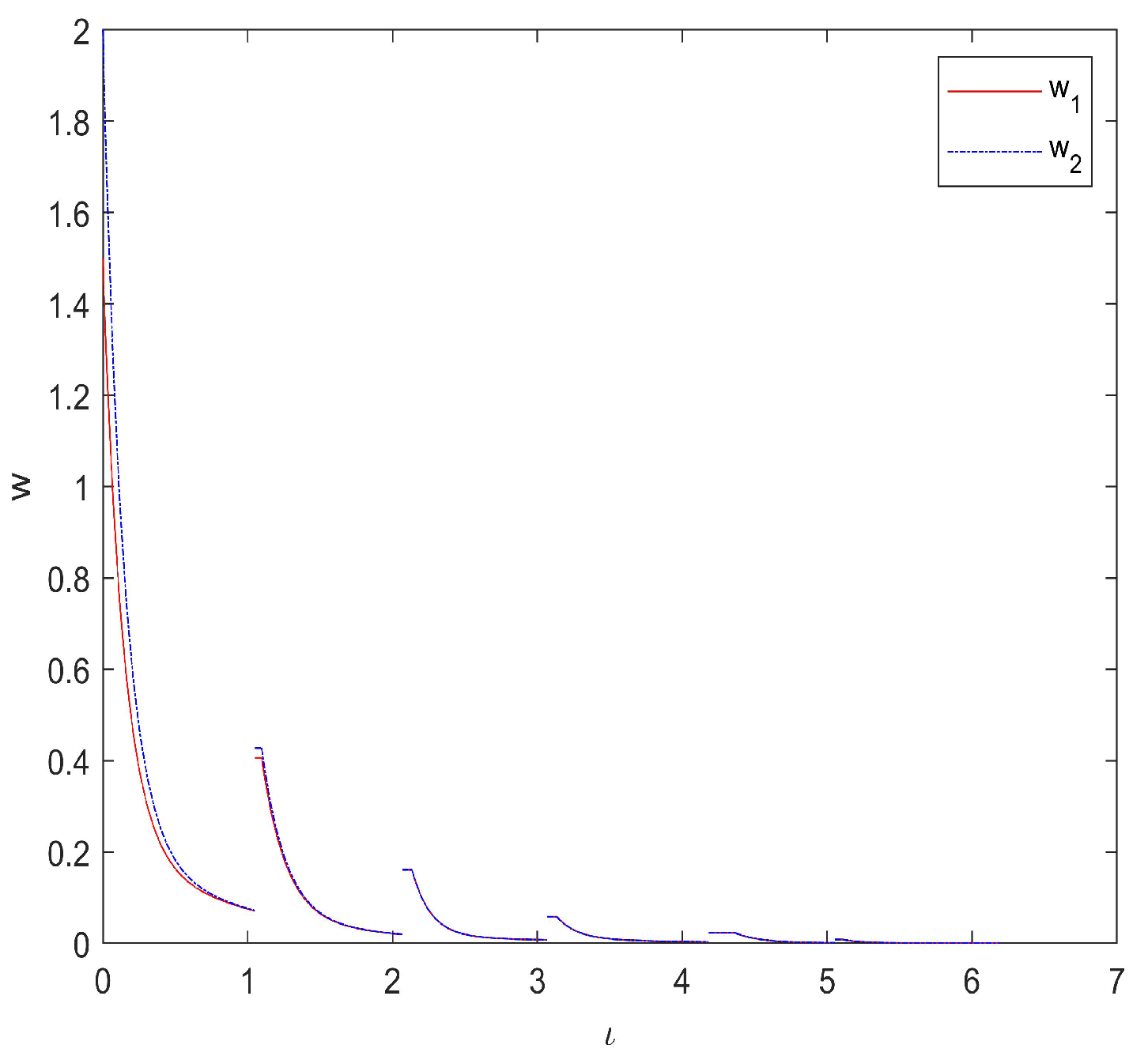
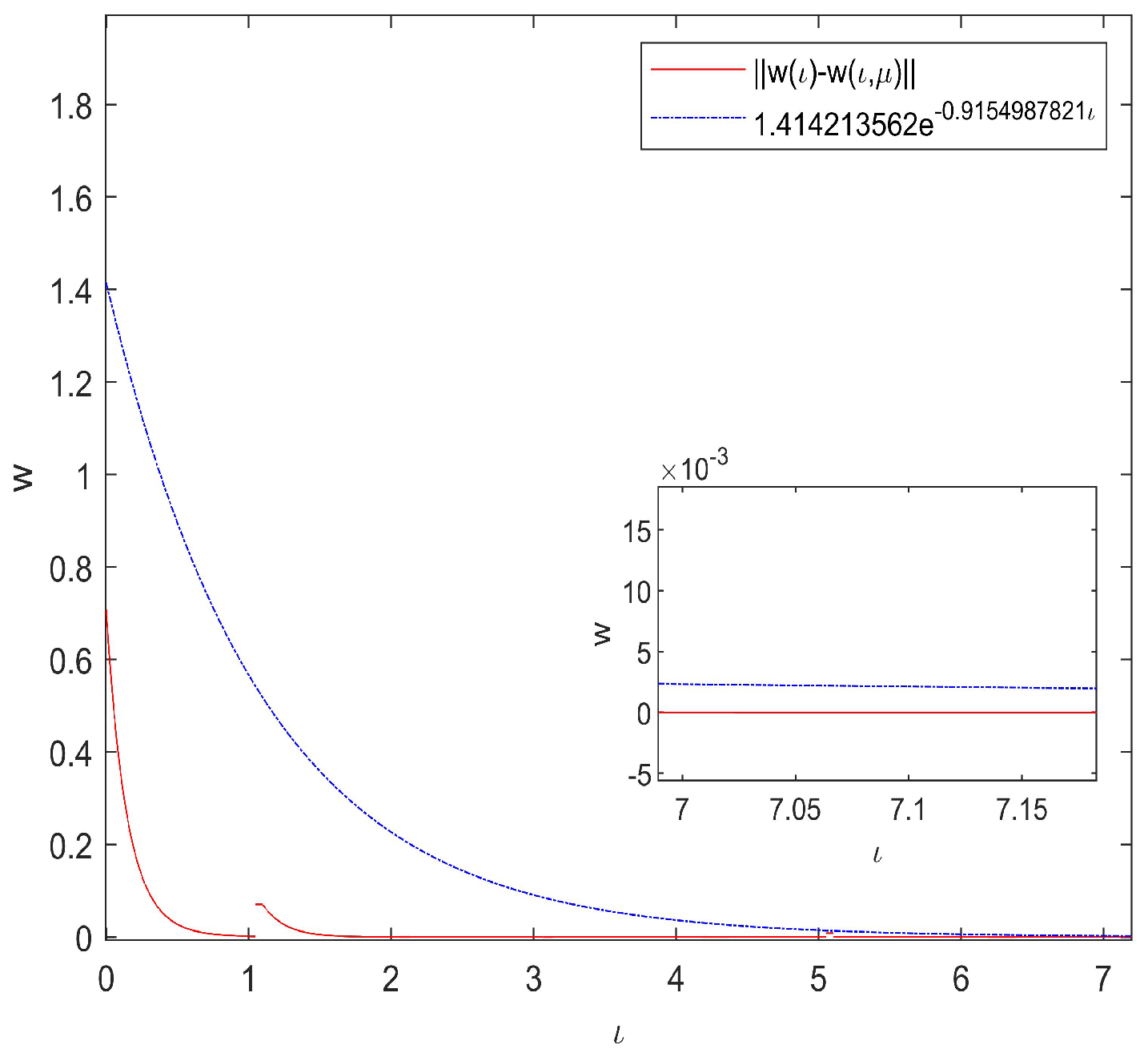
5. Numerical Simulations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cushing, J.M. Integrodifferential Equations and Delay Models in Population Dynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Feng, X.M.; Liu, L.L.; Zhang, F.Q. Dynamical behavior of SEIR-SVS epidemic models with nonlinear incidence and vaccination. Acta Math. Appl. Sin. Engl. Ser. 2022, 38, 282–303. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, X.F. A linear uncertain pharmacokinetic model driven by Liu process. Appl. Math. Model. 2021, 89, 1881–1899. [Google Scholar] [CrossRef]
- Wang, J.R.; Fečkan, M.; Zhang, W.L. On the nonlocal boundary value problem of geophysical fluid flows. Z. Angew. Math. Phys. 2021, 72, 27. [Google Scholar] [CrossRef]
- Wang, C.; Agarwal, R.P.; O’Regan, D. Matrix measure on time scales and almost periodic analysis of the impulsive Lasota-Wazewska model with patch structure and forced perturbations. Math. Methods Appl. Sci. 2016, 39, 5651–5669. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, K.H.; Gui, Z.J. Periodic solution of impulsive predator-prey model with stage structure for the prey undercrowding effect. J. Phys. Conf. Ser. 2021, 1903, 012032. [Google Scholar] [CrossRef]
- Cardinali, T.; Rubbioni, P. The controllability of an impulsive integro-differential process with nonlocal feedback controls. Appl. Math. Comput. 2019, 347, 29–39. [Google Scholar] [CrossRef]
- Stamova, I.; Stamov, G. Applied Impulsive Mathematical Models; Springer International Publishing: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Hernández, E.; O’Regan, D.; Bená, M.A. On a new class of abstract integral equations and applications. Appl. Math. Comput. 2012, 219, 2271–2277. [Google Scholar] [CrossRef]
- Wang, J.R.; Fečkan, M. A general class of impulsive evolution equations. Topol. Methods Nonlinear Anal. 2015, 46, 915–933. [Google Scholar] [CrossRef]
- Wang, J.R.; Zhou, Y.; Lin, Z. On a new class of impulsive fractional differential equations. Appl. Math. Comput. 2014, 242, 649–657. [Google Scholar] [CrossRef]
- Wang, J.R.; Fečkan, M. Non-Instantaneous Impulsive Differential Equations; IOP: London, UK, 2018. [Google Scholar]
- Guan, Y.; Fečkan, M.; Wang, J.R. Periodic solutions and Hyers-Ulam stability of atmospheric Ekman flows. Discret. Contin. Dyn. Syst. 2021, 41, 1157–1176. [Google Scholar] [CrossRef]
- Li, M.M.; Wang, J.R.; O’Regan, D. Positive almost periodic solution for a noninstantaneous impulsive Lasota-Wazewska model. Bull. Iran. Math. Soc. 2019, 46, 851–864. [Google Scholar] [CrossRef]
- Chen, X.X. Almost periodic solutions of nonlinear delay population equation with feedback control. Nonlinear Anal. Real World Appl. 2007, 8, 62–72. [Google Scholar]
- Chen, X.X.; Chen, F.D. Almost-periodic solutions of a delay population equation with feedback control. Nonlinear Anal. Real World Appl. 2006, 7, 559–571. [Google Scholar]
- Huang, P.; Li, X.; Liu, B. Almost periodic solutions for an asymmetric oscillation. J. Differ. Equ. 2017, 263, 8916–8946. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, W.; Yang, L. Stage-structured hematopoiesis model with delays in an almost periodic environment. Appl. Math. Lett. 2021, 120, 107336. [Google Scholar] [CrossRef]
- Samoilenko, A.M.; Perestyuk, N.A. Impulsive Differential Equations; World Scientific: Singapore, 1995. [Google Scholar]
- Stamova, I. Stability Analysis of Impulsive Functional Differential Equations; Walter de Gruyter: Berlin, Germany, 2009. [Google Scholar]
- Ma, R.; Wang, J.R.; Li, M.M. Almost periodic solutions for two non-instantaneous impulsive biological models. Qual. Theory Dyn. Syst. 2022, 21, 84. [Google Scholar] [CrossRef]
- Qin, Y. Integral and Discrete Inequalities and Their Applications; Birkhäuser: Berlin, Germany, 2016. [Google Scholar]
- Jiao, J.J.; Cai, S.H.; Li, L.M.; Zhang, Y.J. Dynamics of a predator-prey model with impulsive biological control and unilaterally impulsive diffusion. Adv. Differ. Equ. 2016, 2016, 1–19. [Google Scholar] [CrossRef][Green Version]
- He, Z.L.; Li, C.D.; Chen, L.; Cao, Z.G. Dynamic behaviors of the FitzHugh-Nagumo neuron model with state-dependent impulsive effects. Neural Netw. 2020, 121, 497–511. [Google Scholar] [CrossRef]
- Xiang, J.; Zhang, J.S.; Zheng, R.Q.; Li, X.Y.; Li, M. NIDM: Network impulsive dynamics on multiplex biological network for disease-gene prediction. Brief. Bioinform. 2021, 22, bbab080. [Google Scholar] [CrossRef]
- Shao, Y.F. Dynamics of an impulsive stochastic predator-prey system with the Beddington-DeAngelis functional response. Axioms 2021, 10, 323. [Google Scholar] [CrossRef]
- Ji, X.R.; Lu, J.Q.; Jiang, B.X.; Shi, K.B. Distributed synchronization of delayed neural networks: Delay-Dependent hybrid impulsive control. IEEE Trans. Netw. Sci. Eng. 2021, 9, 634–647. [Google Scholar] [CrossRef]
- You, Z.L.; Fečkan, M.; Wang, J.R. Relative controllability of fractional delay differential equations via delayed perturbation of Mittag-Leffler functions. J. Comput. Appl. Math. 2020, 378, 112939. [Google Scholar] [CrossRef]
- Sathiyaraj, T.; Wang, J.R.; O’Regan, D. Controllability of stochastic nonlinear oscillating delay systems driven by the Rosenblatt distribution. Proc. R. Soc. Edinb. Sect. A Math. 2021, 151, 217–239. [Google Scholar] [CrossRef]
- Kim, S.Y.; Ji, W.Q.; Deng, S.L.; Ma, Y.B.; Rackauckas, C. Stiff neural ordinary differential equations, Chaos: An Interdisciplinary. J. Nonlinear Sci. 2021, 31, 093122. [Google Scholar]
- Ramos, H.; Rufai, M.A. An adaptive one-point second-derivative Lobatto-type hybrid method for solving efficiently differential systems. Int. J. Comput. Math. 2022, 99, 1687–1705. [Google Scholar] [CrossRef]
- Jódar, L.; Villanueva, R.J.; Arenas, A.J.; González, G.C. Nonstandard numerical methods for a mathematical model for influenza disease. Math. Comput. Simul. 2008, 79, 622–633. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, R.; Li, M. Almost Periodic Solution for Forced Perturbed Non-Instantaneous Impulsive Model. Axioms 2022, 11, 496. https://doi.org/10.3390/axioms11100496
Ma R, Li M. Almost Periodic Solution for Forced Perturbed Non-Instantaneous Impulsive Model. Axioms. 2022; 11(10):496. https://doi.org/10.3390/axioms11100496
Chicago/Turabian StyleMa, Rui, and Mengmeng Li. 2022. "Almost Periodic Solution for Forced Perturbed Non-Instantaneous Impulsive Model" Axioms 11, no. 10: 496. https://doi.org/10.3390/axioms11100496
APA StyleMa, R., & Li, M. (2022). Almost Periodic Solution for Forced Perturbed Non-Instantaneous Impulsive Model. Axioms, 11(10), 496. https://doi.org/10.3390/axioms11100496





