Abstract
D numbers theory is an extension of Dempster–Shafer evidence theory. It eliminates the constraints of mutual exclusion and completeness under the frame of discernment of Dempster–Shafer evidence theory, so it has been widely used to deal with uncertainty modelling, but if it cannot effectively deal with the problem of missing information, sometimes unreasonable conclusions will be drawn. This paper proposes a new type of integration representation of D numbers, which compares the data of multiple evaluation items horizontally, and can reasonably fill in missing information. We apply this method to the user experience evaluation problem of online live course platform to verify the effectiveness of this method.
1. Introduction
The theory of multiple criteria decision making (MCDM) originated from the Pareto optimal concept, and was introduced into the field of decision science as a standardized decision-making method in the 1960s. In 1981, Hwang and Yoon [1] divided MCDM into two types: multiple objective decision making (MODM) and multiple attribute decision making (MADM) based on different decision spaces. The decision space of MODM is continuous, and the goal of decision-making is to plan and design the optimal plan; MADM corresponds to the discrete decision space, and the goal of decision-making is to use the evaluation information of multiple attributes, and through certain calculation or processing, several attribute values are converted into the comprehensive evaluation value of the scheme, so as to reasonably rank the limited alternatives. In the actual decision-making process of MADM problem, due to the complexity of the actual decision-making problem, the evaluation information of the project attributes often needs to be obtained with the cognition of domain experts, and the cognition of the experts participating in the evaluation is often difficult to accurately describe the problem, which brings great uncertainty. On the one hand, this uncertainty comes from the vagueness of the expert’s own cognition, and on the other hand, it comes from the inherent uncertainty of realistic decision-making problems. Moreover, for complex decision-making problems, a single expert has insufficient ability to deal with it. Therefore, uncertain multi-attribute group decision-making has become a research hotspot in decision theory in recent years. The main research methods include: grey correlation analysis [2], Dempster–Shafer evidence theory (D–S evidence theory) [3,4,5], fuzzy set theory [6,7,8], and rough sets theory [9,10,11], etc., among them, D–S evidence theory can well describe the uncertainty and incompleteness of evaluation information without prior probability. At the same time, the Dempster combination rule can effectively integrate data from multiple information sources, which makes it widely used in fields such as information fusion [12], fault diagnosis [13], reliability evaluation [14], human reliability analysis [15], etc.
An important extension of the D–S evidence theory is the D numbers theory [16]. The D number theory is mainly used for the representation and processing of uncertain information. It can be regarded as a special form of random set. It relaxes the assumptions of mutual independence between elements in the frame of discernment of D–S evidence theory, and relaxes the constraints of the completeness of the BPA function. Compared with fuzzy theories such as intuitionistic fuzzy sets and hesitation fuzzy sets and their extended forms, D numbers theory can directly express uncertainty by assigning probabilities to multiple subsets, which greatly improves the ability to represent and process uncertain information. However, the D numbers theory also has its own limitations. It is essentially a method of gathering multi-attribute information, which does not solve the shortcomings of the D–S evidence theory [16]. Therefore, scholars continue to improve the D numbers theory. For example, for multi-level and multi-attribute evaluation data, Deng et al. [17,18] combined the D numbers theory with analytic hierarchy process (AHP) and proposed the D-AHP method. Aiming at the problem that the combination rule cannot satisfy the associative law, Wang et al. [19] developed an improved multiple D numbers combination method, and Guan X et al. [20] proposed a new combination rule. In view of the problem that both qualitative and quantitative data exist at the same time, through the conversion model, all quantitative and qualitative data are transformed into the same qualitative description level, forming a D numbers decision matrix of the evaluation criteria, and using the D numbers integration method to integrate information under different criteria [21]. When the elements in the frame of discernment are not mutually exclusive, the distance between two D numbers is defined according to the definition form of the distance between two BPA in D–S evidence theory, so that the distance between two D numbers is smaller than the distance between D–S evidence theory under the same identification framework [22]. For data with incomplete information, Wang et al. [23] defined an improved D numbers integrated representation method to solve the MADM problem and so on. The D numbers approach is widely applied in different fields, including human reliability analysis [24], green supply chain management [25], and emergency management [26], university scientific research evaluation [27], failure model and effects analysis [28,29], renewable energy resources evaluation [30], and health-care waste treatment technology assessment [31]. Despite there are the above advantages for D numbers theory in dealing with uncertain information issues, some disadvantages still exist when transforming D numbers into the real value of D numbers’ integration rules. In this paper, improvements on the disadvantages of D numbers’ integration rules in incomplete information will be made, etc.
In the previous integrated representation of the D numbers, if the information is incomplete, the missing part of the assessment is directly ignored, and the result may violate common sense. In order to overcome this shortcoming, Wang et al. [23] proposed an improved D numbers integrated representation method, which proportionally distributes the missing information to the decision according to the original value of D numbers. However, this method does not consider the evaluation object globally, and the results may be counterintuitive. For instance, ten experts make an assessment of program A and program B. For program A, seven experts give eight points, and the other three experts make no assessment as they are unfamiliar with A, and this part is regarded as missing information, and the result can be expressed by . Based on the integrated method from the literature [16], it can be transformed into the real number , that is to say, when D numbers are integrated, 0 is given as the three experts do not make an assessment. According to the literature [23], when the D numbers are integrated, the missing part of information should be allocated to the given results of assessment in a certain proportion. There is only eight points for the given results, so the missing part should be assigned eight points, and the integration result is expressed by . The different ways the two integration results treat missing information leads to vastly different integration results. When it comes to the integration of , we should also consider the assessment on program B made by the experts, and the integration results obtained can be more comparable. Based on [16,23], this paper proposes a new type of D numbers integrated representation, which can deal with the lack of information more reasonably. Then the proposed method is applied to the user experience evaluation problem of the online live course platform to verify the effectiveness of the method.
The rest of this paper is organized as follows. Section 2 first briefly introduces the basic concepts. Section 3 introduces our D numbers integration method (stepwise comparison and replacement integration (SCRI) method). Section 4 studies the implementation of our proposed method on the user experience evaluation problem of the online live course platform. Section 5 discusses and summarizes.
2. Preliminaries
2.1. Dempster–Shafer Theory
Aiming at the uncertainty and incompleteness of information, how to use expert group experience and collected relevant data as decision-making information to reduce the uncertainty of decision-making and improve the credibility of the results is the key content in the research of multi-attribute group decision-making methods. D–S evidence theory [3,4,5] provides a general framework for constructing uncertain reasoning models, which can satisfy an axiom system that is weaker than probability, can describe the uncertainty and incompleteness of evaluation information well. It also has a synthesis rule for synthesizing the opinions of multiple experts, so it is an important and effective group decision-making method.
Definition 1
[3,4]. (basic probability assignment, BPA) Let be a nonempty finite set of hypotheses or propositions, which is called the frame of discernment. A basic probability assignment (BPA) is a function , which is called a mass function, satisfying:
where is an empty set and is the power set of .
Definition 2
[3,4]. (Dempster’s combination rule) Suppose and are two independent BPAs from different sources, the Dempster combination rule, denoted by ,is defined as follows:
with
where is a normalization constant, called conflict coefficient of two BPAs. When, it means that and completely conflict, and they cannot be combined by Dempster’s combination rule.
2.2. D Numbers Theory
D numbers theory [16] is an extension of Dempster–Shafer evidence theory. It eliminates the constraints of mutual exclusion and completeness under the frame of discernment. The general definition and combination rules of D numbers are given below.
Definition 3
[16]. Let be a finite nonempty set, D number is a mapping , such that
where is an empty set and is a subset of . Note that different from the concept of frame of discernment in Dempster–Shafer theory, in set the elements don’t require mutually exclusive.
There is a special situation of D numbers.
Definition 4
[16]. For a discrete set , where (), and if , a special form of D numbers can be expressed by
Simple notes for, whereand. If,the information is said to be complete; If, the information is said to be incomplete.
Definition 5
[16]. (D numbers theory combination rule) Suppose and are two D numbers, denoted by
The combination ofand, indicated by, is defined by
with
where
We can treat D numbers as “special” discrete random variables. Takingfor example,() is the value for it, and() stands for the corresponding probability. It is a “special” discrete random variable as it requires the sum of probabilities to be less than or equal to 1, that is,. It is stated by the definition that two D numbers, namelyand, can be integrated into a new D number, that is,. Its value isand the corresponding probability is, of whichcan be regarded as a regulation constant, and the value ofis determined by (10). In this case, it is guaranteed that the sum of all probabilities in new D numbers is still less than or equal to 1.
Definition 6
[16]. (D numbers’ Integration) Let be a D number, the integration representation of D is defined as
where is real number.
3. Limitations and Proposed Method
3.1. Limitations
According to Deng [16], the integration representation of D numbers is defined as . If the information given by experts is incomplete, namely , then the missing part of evaluation is directly excluded. Wang et al. [23] argued that this may lead to unreasonable outcomes of decision-making.
Example 1
(Wang et al. [23]). According to Wang et al. [23], it is assumed that 10 experts are invited to evaluate the automobile performance of A and B, and the evaluation system is set , in which “9” means “very good” and “1” means “very bad”. When the 10 experts give an evaluation on the performance of car A, six of them choose “7”, two choose “8”, and the other two do not give an evaluation as they are not familiar with the car. The evaluation result can be expressed as . When the same 10 experts evaluate the performance of car B, they all choose “6”. The expression of D numbers is . Based on the D integrated representation of D numbers, the final evaluation results of the two cars are respectively calculated as:
In terms of the integrated results, car B gets a better score than car A, as two experts are uncertain about the score when evaluating A and do not give an evaluation, and incomplete information is abandoned in integration of D numbers. That is to say, if the experts give no evaluation, 0 is applied to deal with it, thus making the final result of car A relatively low.
Wang et al. [23] put forward a method to improve the integration of D numbers. They argued that for experts with incomplete cognition, they could refer to the evaluation results given by experts familiar with the evaluation results, and the incomplete part of incomplete information should be assigned to the evaluation results given in line with certain rules. For the given numbers, , , () is the evaluation level given by experts, , () is the credibility of corresponding evaluation level , and stands for the percentage of credibility of evaluation level . Wang et al. [23] believed that the incomplete part of incomplete information should be assigned to the known evaluation level () according to the percentage of credibility.
Definition 7
(Wang et al. [23]). For . The overall assessment is denoted by,
Obviously, if the information is complete, that is, when, the proposed method is degenerated as the traditional D numbers’ integration.
The improved integration representation of D numbers is adopted to reevaluate the performance of car A and car B in Example 1. For car B, the information is complete, thus:
For car A, is incomplete, and the incomplete part of 0.2 should be assigned to the known evaluation level based on the percentage of credibility, thereby:
Obviously, when the improved integration representation of D numbers is adopted, car A gets a higher total score than car B, which is contrary to the traditional integrated results of D numbers.
Nevertheless, we also see that the improved integration representation of D numbers can also bring about some counterintuitive results, as shown in the following example:
Example 2.
It is still assumed that 10 experts are invited to evaluate the automobile performance of A and B, and the evaluation system is set . When the 10 experts evaluate the performance of car A, seven of them choose “8” and three of them do not evaluate as they are not familiar with the car. Thu, the evaluation of car A is expressed as . When the same 10 experts evaluate the performance of car B, eight of them choose “8” and the rest two choose “7”. Thus, the expression is . For car A, is incomplete. The incomplete part of 0.3 should be assigned to the known evaluation level in line with the percentage of credibility, while the known evaluation level is only “8”. Thereby:
For car B, the information is complete, thus:
Obviously, the evaluation result obtained through this method is that car A is in the ascendant, but from the original evaluation result, the number of experts who give a score of “8” to car B is more than that of experts who give score of “8” to car A, and complete information is obtained for the evaluation result of car B. The reason for this lies in the fact that in certain information of , the score of “8” accounts for 100%, and when the improved integration representation of D numbers is adopted, the incomplete information remained, namely opinions from the three experts who do not give and evaluation, are replaced with “8”. If the above operation is conducted when the evaluation results of car B are not fully considered, the final score of car A might be made too high. In this case, a more effective integration representation of D numbers needs to be proposed.
3.2. Proposed Method (Stepwise Comparison and Replacement Integration (SCRI) Method)
In this section, a new method of D numbers integration is proposed, which not only considers the assessment results of a single program, but also horizontally compares with the assessment results of other programs. It can fill in the missing information in a more reasonable way. Compared with existing methods, it is more effective.
It assumes that there are N objects ,to be evaluated, and experts in total who participate in the evaluation. The stepwise representation of the proposed method is given as follows. The flowchart of the proposed method is shown in Figure 1.
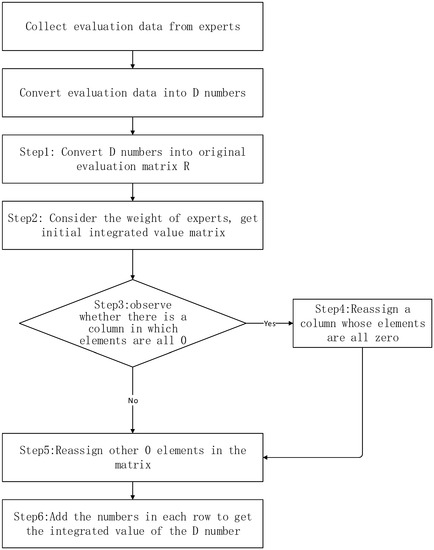
Figure 1.
The flowchart of the proposed SCRI method.
Step 1 for the object , the evaluation grade from each expert is arranged in descending order, and if there is no evaluation, the temporary record is 0. That is to say, the evaluation result from experts on the object arranged in descending order is viewed as a row vector, thus forming the original evaluation matrix of .
Step 2 there is a total of experts participating in the evaluation, and the corresponding credibility from each expert is considered as . Each element in the original evaluation matrix is multiplied by , and it is concluded that the initial integrated value matrix is .
Step 3 observe whether there is a column in which elements are all 0. If so, enter step 4; otherwise, go directly to step 5.
Step 4 check each column from the first column to see whether there exists element 0. It assumes that 0 appears in the column for the first time, that is to say, the corresponding elements for the first columns are initial integrated value obtained based on the definite evaluation and calculation from experts. Add up each element of each row in the first columns and then take the average of their sum, that is to divide the sum of each row by , which is called reference value for basic evaluation. As for the columns where all the column elements are 0, replace the element 0 in this column with the reference value for basic evaluation of the corresponding row, that is to assign this part of incomplete information to the evaluation results clearly given in the previous columns in proportion. Then it comes to the matrix .
Step 5 check whether there is element 0 in each column. If so, make a comparison of the non-zero elements in this column, and substitute the minimum value for the element 0. That is to say, the incomplete information is replaced with the minimum evaluation value corresponding to the evaluation object through horizontal comparison, until all elements in the matrix are nonzero, which is called the modified integrated value matrix .
Step 6 add up elements of each row in the matrix, and then it comes to the value, which is the integrated value of D numbers corresponding to the evaluation objects .
Let us use this method to operate Example 2.
Step 1 set up an original evaluation matrix .
Step 2 multiply each element by , here , and then it comes to the initial integrated value matrix. The weights of experts are the same .
Step 3 no column with all 0 elements, then go to step 5.
Step 5 checking whether element 0 appears in each column. If so, make a comparison of the non-zero elements in this column and replace element 0 with the minimum value.
Step 6 add up elements of each row in the matrix, and then it comes to the integrated value of D numbers corresponding to evaluation objects A and B, which are all 7. The integration results of the two cars are the same, which is more in line with our intuition.
Example 3.
It still assumes that 10 experts are invited to evaluate three objects A, B, and C, and set is adopted as the evaluation system. When these 10 experts make evaluation of A, 4 choose “9”, 2 choose “8”, and 3 choose “7”, and as the other one expert is not familiar with A, no evaluation is given. Thus, evaluation for A is expressed as . Similarly, when the 10 experts evaluate the automobile performance of B, 3 choose “9”, 5 choose “8”, and the other 2 experts do not give evaluation as they are not familiar with B. Thus, the expression is . When the 10 experts evaluate the automobile performance of C, 4 choose “9”, 3 choose “8”, and the other 3 do not give evaluation as they are not familiar with C. The expression for D numbers is .
Step 1 set up an original evaluation matrix
Step 2 multiply each element by , here , and then it comes to the initial integrated value matrix
Step 3 observe whether there exists a column in which all column elements are 0. Herein, the elements are all 0 in the last column, then go to step 4.
Step 4 0 appears in the 8th column for the first time, that is, the elements corresponding to the first seven columns are interval integrated values obtained based on the definite evaluation given by the experts. The elements in each row of the first seven columns are added up and then averaged, and ,, are obtained respectively. Replace these values with the elements in the last column of the initial integrated value matrix, and then it comes to the matrix .
Step 5 check whether element 0 appears in each column. If so, make a comparison of the non-zero elements in this column and replace element 0 with the minimum value. As for in the 8th column, replace 0 with , and in the 9th column, replace 0 with to obtain the modified integrated value matrix :
Step 6 add up elements of each row in the matrix, and then it comes to the integrated value of D numbers corresponding to evaluation objects A, B and C, which are 8.143, 8.243 and 8.257 respectively. Thereby, we consider that object , in which the symbol means ‘superior’.
4. Applications in MADM
In this section, we will put forward the method of D numbers integration that is adopted to make an assessment of user experience of the online live course platform, and account for the rationality of the proposed method by data collection based on the evaluation index system in the literature [32].
During the rapid transmission of the COVID-19 pandemic, online learning has become an effective way to implement “suspended class, ongoing learning”, and carried out all over the world. Since there are reasons such as technology and network bandwidth, etc., some telecommuting and conferencing software has undertaken the role of online live course platforms. However, due to the original design purpose and the characteristics of the software, the software cannot fully meet the needs of schools in online live courses. In this case, it is prominently significant to optimize the user experience of the online live course platforms [32].
In Wang et al. [32], qualitative and quantitative methods were combined to establish evaluation indicators by integrating data obtained through the literature research, interviews and network research from the perspective of user experience. Delphi method and analytic hierarchy process were utilized to establish the weight of each indicator and set the scoring grade. T-test method was adopted to establish the comparative analysis method of model application, and the standard procedure of model application was designed to build a complete evaluation system.
However, there is an important issue that has not been well resolved in [32]: when evaluating different platforms, some experts may not give definite scores as they are not familiar with the scoring items. In this case, the scores made reluctantly may greatly affect the final evaluation results. The SCRI method proposed by us can solve this in a good way, and it can deal with possible uncertainty, ignorance and missing information in a simple and effective way.
In Wang et al. [32], the main factors affecting the user experience of the online live course platforms are divided into four primary indicators, which are respectively Ease of Operation, Functional Completeness, Interface Rationality, Technical Reliability. Each primary indicator is divided into several secondary indicators. The hierarchical structure and corresponding weights of user experience evaluation of the online live course platforms are shown in the Figure 2. below.
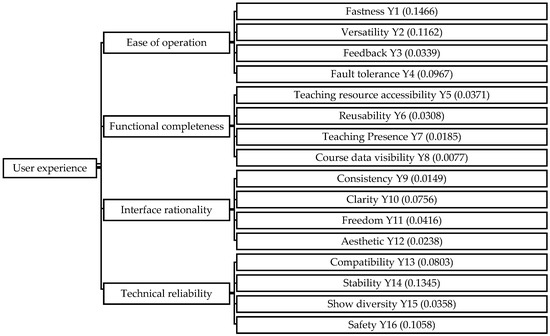
Figure 2.
Evaluation index system of live online courses [32].
In the hierarchical structure, a total of 16 secondary indicators are included. Experts are invited to evaluate all the influencing factors. To keep consistent with the requirements of the scale, the evaluation results are divided into 9 grades, , in which “9” means “very good” and “1” means “very bad”. If the experts do not have a good understanding of some factors, they do not need to score, and finally we obtain evaluation data with missing information.
All the results are expressed in the form of D numbers herein. For instance, 10 experts are invited to evaluate the user experience of the platform. When evaluating a certain influencing factor, 4 experts give 8 scores, 3 experts give 7 scores, 2 experts give 5 scores, and the other one expert does not score as he or she is unfamiliar with the factor. Hence, the evaluation result can be expressed as , which is not a complete D number. Ding Talk, Tencent Classroom and Tencent QQ are adopted in this paper, and the evaluation results are shown in the following Table 1:

Table 1.
Assessment data for Ding Talk, Tencent Classroom and Tencent QQ are represented by D numbers.
Then we adopted the SCRI method to transform the evaluation results from all experts into a clear form of real numbers. For instance, in the Table 2, the evaluation results on Y2 made by the ten experts are as follows:

Table 2.
Assessment data for Y2 of the three platforms are represented by D numbers.
Step 1, establish the original evaluation matrix ;
Step 2, multiply each element by to obtain the initial integrated value matrix
Step 3, elements in the last column are all 0, then go to step 4;
Step 4, 0 appears in the 8th column for the first time, that is, the elements corresponding to the first 7 columns are initial integrated values obtained based on the definite evaluation and calculation given by the experts. Add up the elements in each row of the first 7 columns and calculate the arithmetic mean, and ,, are obtained respectively. Replace these with the elements of the last column in the matrix , and it is concluded that:
Step 5, check whether element 0 appears in each column. If so, make a comparison of the non-zero elements in this column and replace element 0 with the minimum value. As for in the 8th column, replace 0 with , and in the 9th column, replace 0 with to obtain the modified integrated value matrix :
Step 6, add up the elements of each row in the matrix and convert the evaluation results from all experts into a clear form of real numbers, as follows:
7.8286, 6.4714 and 6.5857.
The evaluation results of all secondary indicators are converted into real numbers as shown in Table 3:

Table 3.
Integration of the assessment results.
Finally, multiply these numbers by the corresponding weights and total them up to obtain the comprehensive evaluation value of user experience from the three platforms, as well as the scores of each primary indicator in Table 4:

Table 4.
The overall assessments and the ranking of the three platforms.
5. Conclusions and Future Work
As an extension of D–S evidence theory, D numbers theory has recently attracted the attention from scholars, but it is not quite satisfactory while dealing with incomplete information. In this paper, a new integration method SCRI is proposed, of which the advantages are as follows: reasonably filling the missing information by comparing the data of several assessment programs in a horizontal way, to a certain extent, makes up for the decision-making mistakes which may be led by missing information for the D numbers theory in integrated data. The possible limitation of this method is that the information filled in is only the inference of the missing part, which is not guaranteed to be completely accurate. This method can be combined with other MADM classical methods to deal with decision-making issues in uncertain environments such as fuzziness and incompleteness, which is also the direction of subsequent efforts.
Author Contributions
Conceptualization, H.H. and C.Z.; methodology, H.H. and C.Z.; formal analysis, H.H. and C.Z.; data curation, H.H. and C.Z.; writing—original draft preparation, H.H.; writing—review and editing, C.Z.; project administration, C.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Key projects of soft science of Zhejiang Province (No. 2021C25035) and Humanities and Social Science Research Special Task Project of the Ministry of Education (Engineering Science and Technology Talent Training Research) (No.18JDGC036).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making—Methods and Applications: A State-of-the-Art Survey; Springer: New York, NY, USA, 1981. [Google Scholar]
- Deng, J.L. The control problem of gray systems. Syst. Control. Lett. 1982, 1, 288–294. [Google Scholar]
- Dempster, A.P. Upper and lower probabilities induced by a multivalued mapping. Ann. Math. Stat. 1967, 38, 325–339. [Google Scholar] [CrossRef]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976. [Google Scholar]
- Yager, R.R. Generalized dempster—Shafer structures. IEEE Trans. Fuzzy Syst. 2019, 27, 428–435. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Yager, R.R.; Reformat, M.; To, N.D. Drawing on the ipad to input fuzzy sets with an application to linguistic data science. Inf. Sci. 2019, 479, 277–291. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough sets. Int. J. Inf. Comput. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Xiong, W.; Su, Q.; Li, J. The group decision-making rules based on rough sets on large scale engineering emergency. Syst. Eng. Procedia 2012, 4, 331–337. [Google Scholar] [CrossRef] [Green Version]
- Eisa, M. Improving group decision support systems using rough set. Int. J. Comput. Appl. 2013, 69, 9–13. [Google Scholar] [CrossRef]
- Xiao, F.Y. A new divergence measure for belief functions in D—S evidence theory for multisensor data fusion. Inf. Sci. 2020, 514, 462–483. [Google Scholar] [CrossRef]
- Zhang, H.; Deng, Y. Engine fault diagnosis based on sensor data fusion considering information quality and evidence theory. Adv. Mech. Eng. 2018, 10, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Song, Y.; Wang, X.; Zhu, J.; Lei, L. Sensor dynamic reliability evaluation based on evidence theory and intuitionistic fuzzy sets. Appl. Intell. 2018, 48, 3950–3962. [Google Scholar] [CrossRef]
- Su, X.Y.; Mahadevan, S.; Xu, P.D.; Deng, Y. Dependence Assessment in Human Reliability Analysis Using Evidence Theory and AHP. Risk Anal. 2015, 35, 1296–1316. [Google Scholar] [CrossRef] [PubMed]
- Deng, Y. D numbers: Theory and applications. J. Inf. Comput. Sci. 2012, 9, 2421–2428. [Google Scholar]
- Deng, X.Y.; Hu, Y.; Deng, Y.; Mahadevan, S. Environmental impact assessment based on D numbers. Expert Syst. Appl. 2014, 41, 635–643. [Google Scholar] [CrossRef]
- Deng, X.Y.; Hu, Y.; Deng, Y.; Mahadevan, S. Supplier selection using AHP methodology extended by D numbers. Expert Syst. Appl. 2014, 41, 156–167. [Google Scholar] [CrossRef]
- Wang, N.K.; Liu, F.Y.; Wei, D.J. A modified combination rule for D numbers theory. Math. Probl. Eng. 2016, 2016, 1–10. [Google Scholar] [CrossRef]
- Guan, X.; Liu, H.Q.; Yi, X.; Zhao, J. The improved combination rule of D numbers and its application in radiation source identification. Math. Probl. Eng. 2018, 2018, 6025680. [Google Scholar] [CrossRef] [Green Version]
- Mo, H.M.; Deng, Y. A new MADA methodology based on D numbers. Int. J. Fuzzy Syst. 2018, 20, 2458–2469. [Google Scholar] [CrossRef]
- Li, M.Z.; Hu, Y.; Zhang, Q.; Deng, Y. A novel distance function of D numbers and its application in product engineering. Eng. Appl. Artif. Intell. 2016, 47, 61–67. [Google Scholar] [CrossRef]
- Wang, N.K.; Liu, X.M.; Wei, D.J. A modified D numbers’ integration for multiple attributes decision making. Int. J. Fuzzy Syst. 2018, 20, 104–115. [Google Scholar] [CrossRef]
- Zhou, X.Y.; Deng, X.Y.; Deng, Y.; Mahadevan, S. Dependence assessment in human reliability analysis based on D numbers and AHP. Nucl. Eng. Des. 2017, 313, 243–252. [Google Scholar] [CrossRef]
- Deng, X.Y.; Jiang, W. Evaluating Green Supply Chain Management Practices Under Fuzzy Environment: A Novel Method Based on D Number Theory. Int. J. Fuzzy Syst. 2019, 21, 1389–1402. [Google Scholar] [CrossRef]
- Zhou, X.Y.; Shi, Y.; Deng, X.Y.; Deng, Y. D-DEMATEL: A new method to identify critical success factors in emergency management. Saf. Sci. 2017, 91, 93–104. [Google Scholar] [CrossRef]
- Zong, F.; Wang, L. Evaluation of university scientific research ability based on the output of sci-tech papers: A D-AHP approach. PLoS ONE 2017, 12, e0171437. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bian, T.; Zheng, H.; Yin, L.; Deng, Y. Failure mode and effects analysis based on D numbers and topsis. Qual. Reliab. Eng. Int. 2018, 34, 501–515. [Google Scholar] [CrossRef]
- Seiti, H.; Hafezalkotob, A.; Herrera-Viedma, E. A novel linguistic approach for multi-granular information fusion and decision-making using risk-based linguistic D numbers. Inf. Sci. 2020, 530, 43–65. [Google Scholar] [CrossRef]
- Mousavi-Nasab, S.H.; Sotoudeh-Anvari, A. An extension of best-worst method with D numbers: Application in evaluation of renewable energy resources. Sustain. Energy Technol. Assess. 2020, 40, 100771. [Google Scholar] [CrossRef]
- Xiao, F. A novel multi-criteria decision making method for assessing health-care waste treatment technologies based on D numbers. Eng. Appl. Artif. Intell. 2018, 71, 216–225. [Google Scholar] [CrossRef]
- Wang, S.R.; Liu, Y.; Song, F.H.; Xie, X.J.; Yu, D. Research on evaluation system of user experience with online live course platform. IEEE Access 2021, 9, 23863–23875. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).