Hybrid Method for Simulation of a Fractional COVID-19 Model with Real Case Application
Abstract
:1. Introduction
2. Model Formulation
- .
- All the variables and parameters of the system are non-negative.
- .
- The susceptible people transfer to the infectious compartment with a constant susceptible inflow into population.
- .
- Originally infectious or susceptible persons transfer to the quarantined class while reported cases return to the infected class from quarantined classes.
3. Preliminary Results
- (1)
- ,
- (2)
- is a contraction, and
- (3)
- is compact and continuous.
4. Qualitative Analysis of the Proposed Model
- (H1)
- there is and such that
- (H2)
- there is such that ∀ one has
5. Construction of an Algorithm for Deriving the Solution of the Model
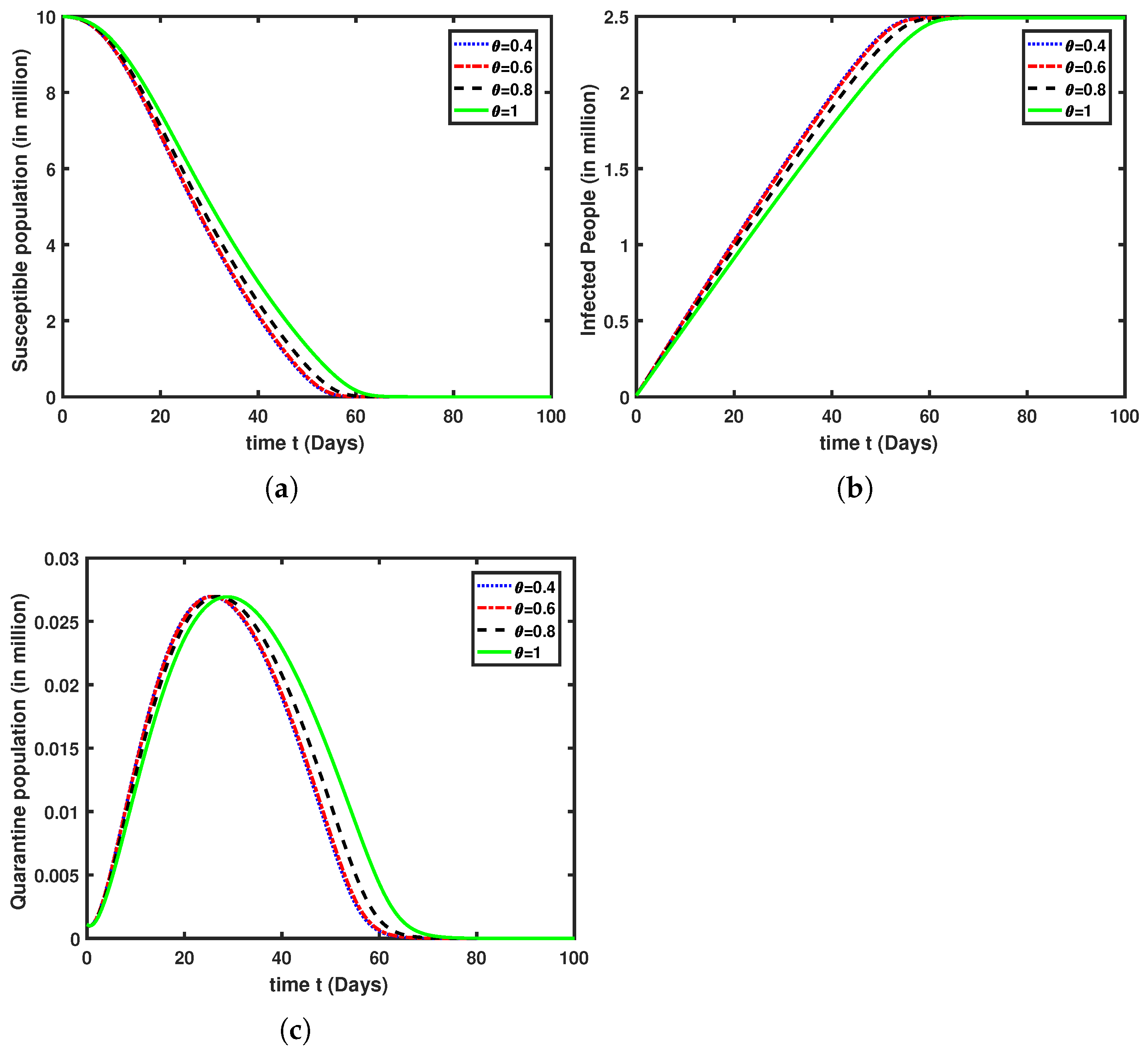
6. Numerical Interpretation and Discussion
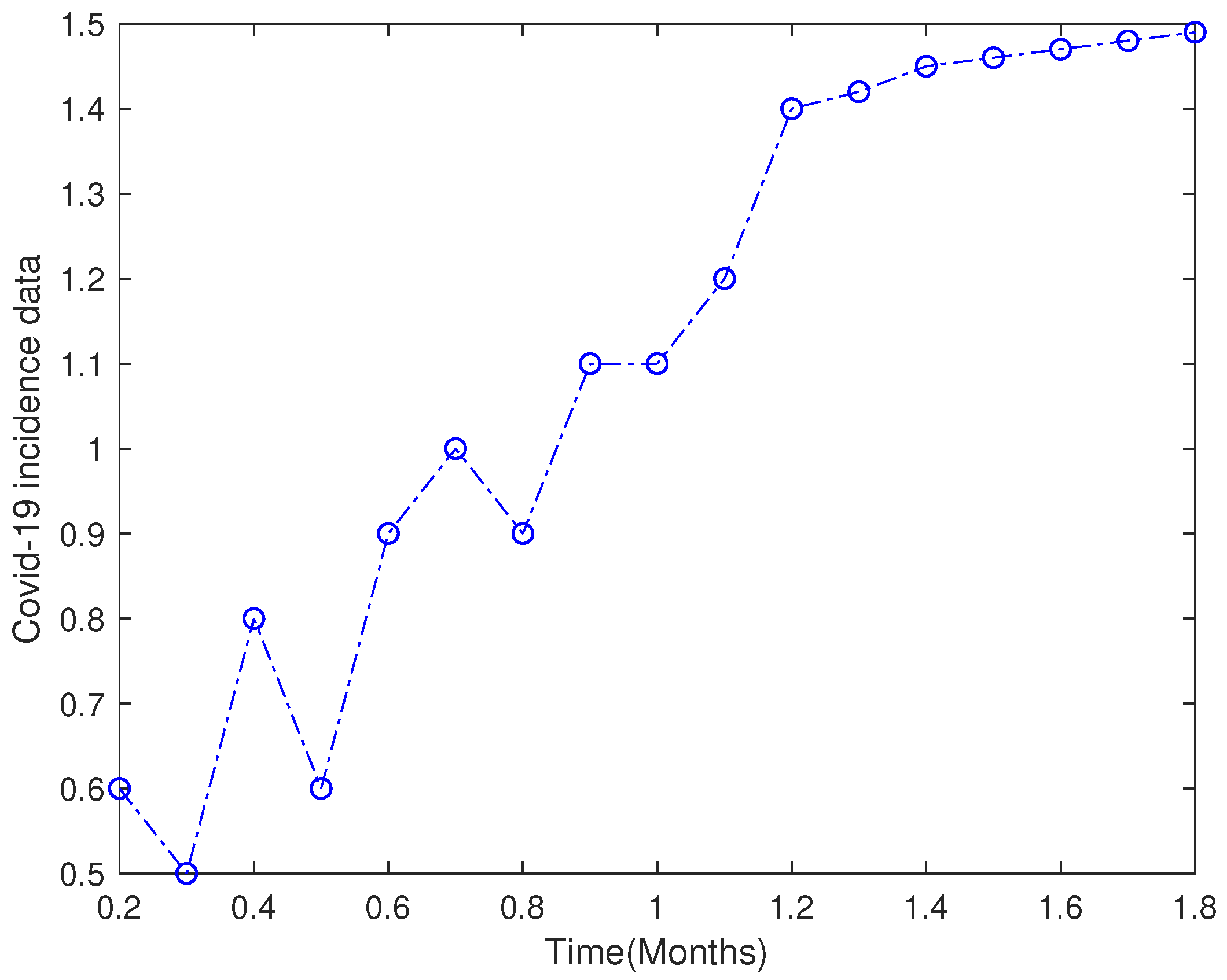
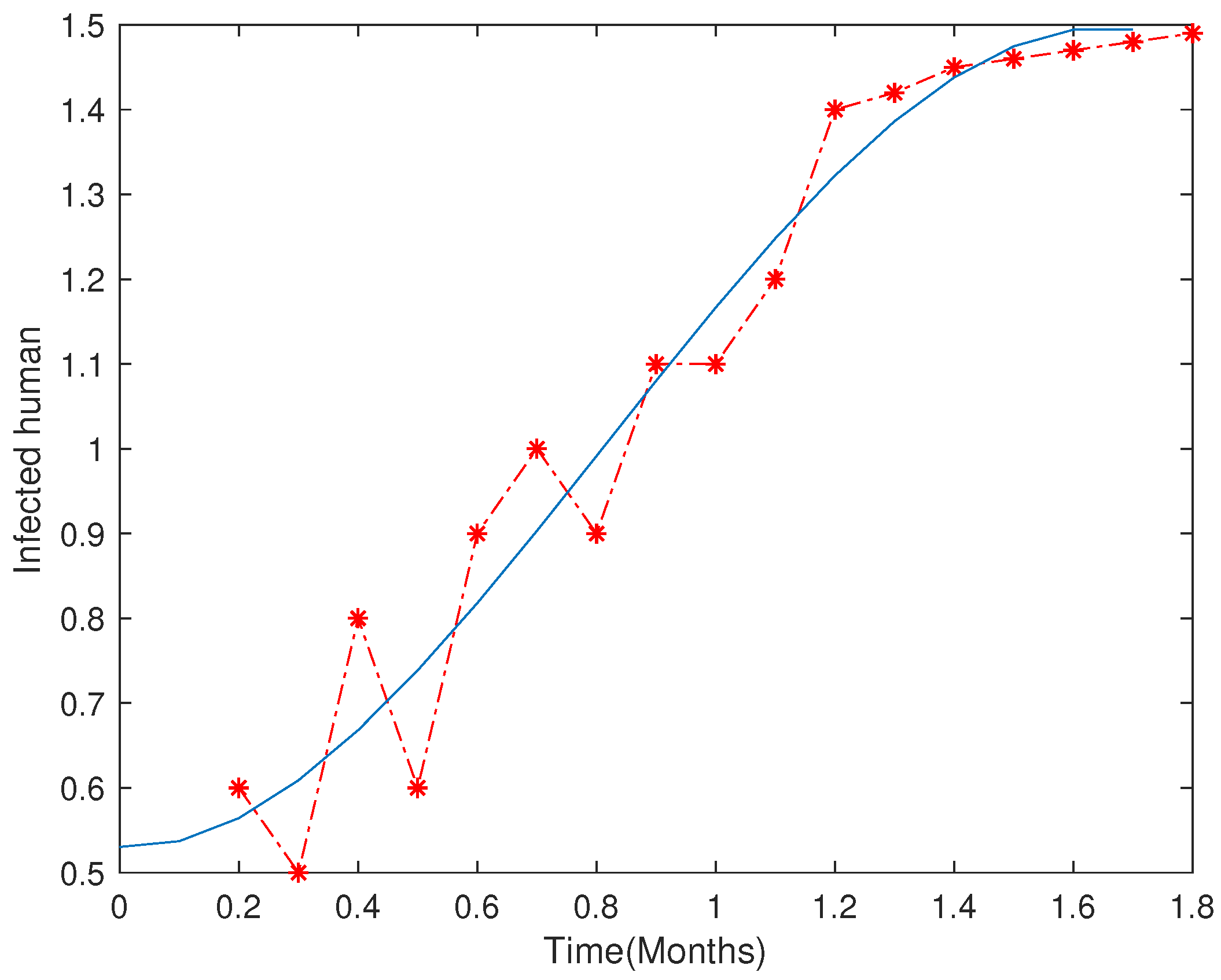
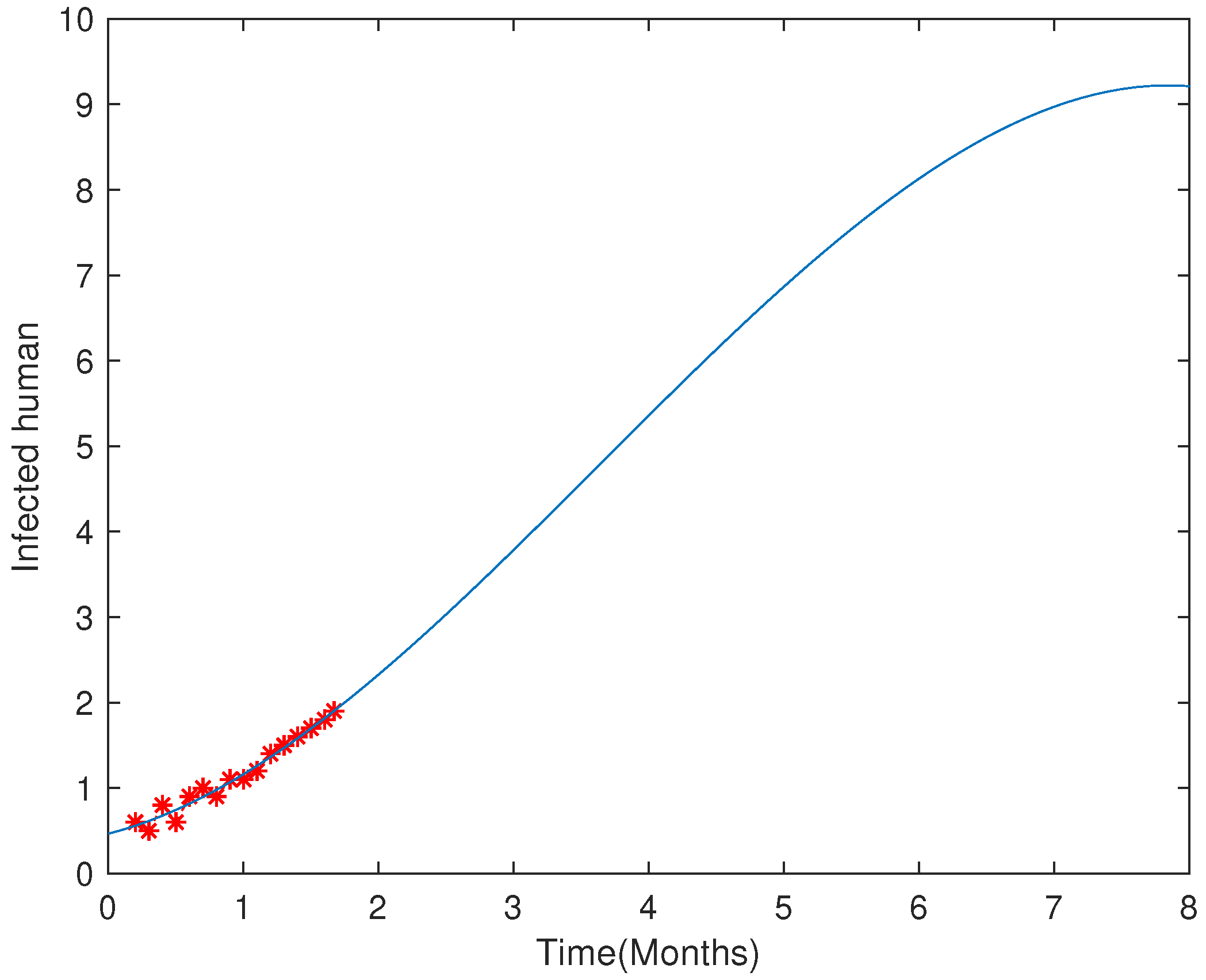
6.1. Case Study with Real Data: Khyber Pakhtunkhawa (Pakistan)
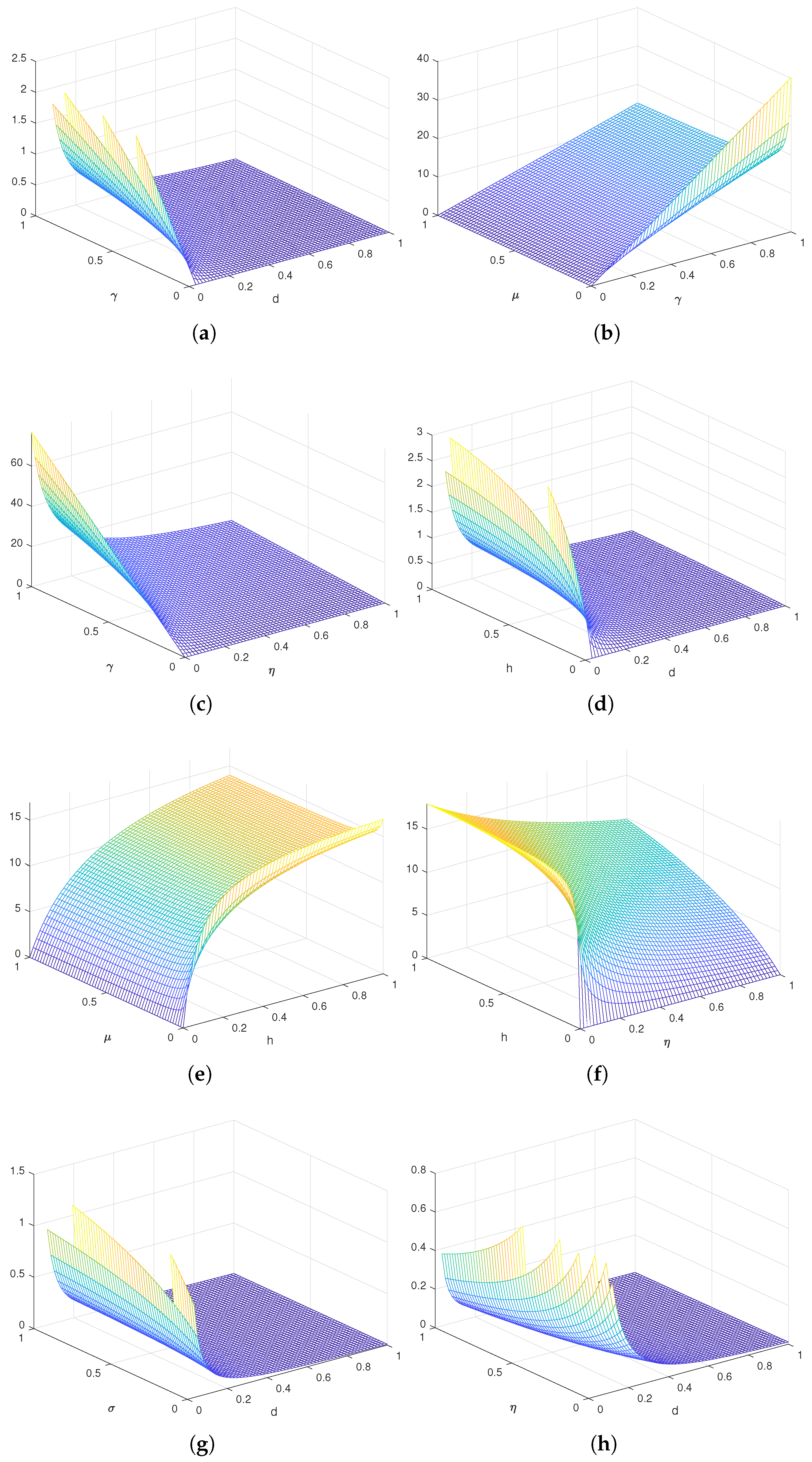
7. Sensitivity Analysis
8. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Din, A.; Li, Y.; Khan, T.; Zaman, G. Mathematical analysis of spread and control of the novel corona virus (COVID-19) in China. Chaos Solitons Fractals 2020, 141, 110286. [Google Scholar] [CrossRef] [PubMed]
- Din, A.; Khan, A.; Baleanu, D. Stationary distribution and extinction of stochastic coronavirus (COVID-19) epidemic model. Chaos Solitons Fractals 2020, 139, 110036. [Google Scholar] [CrossRef] [PubMed]
- Koopmans, M.; Daszak, P.; Dedkov, V.G.; Dwyer, D.E.; Farag, E.; Fischer, T.K.; Hayman, D.T.S.; Leendertz, F.; Maeda, K.; Nguyen-Viet, H.; et al. Origins of SARS-CoV-2: Window is closing for key scientific studies. Nature 2021, 596, 482–485. [Google Scholar] [CrossRef] [PubMed]
- Ndaïrou, F.; Area, I.; Nieto, J.J.; Silva, C.J.; Torres, D.F.M. Fractional model of COVID-19 applied to Galicia, Spain and Portugal. Chaos Solitons Fractals 2021, 144, 110652. [Google Scholar] [CrossRef] [PubMed]
- Lemos-Paião, A.P.; Silva, C.J.; Torres, D.F.M. A New Compartmental Epidemiological Model for COVID-19 with a Case Study of Portugal. Ecol. Complex. 2020, 44, 100885. [Google Scholar] [CrossRef]
- Zine, H.; Boukhouima, A.; Lotfi, E.M.; Mahrouf, M.; Torres, D.F.M.; Yousfi, N. A stochastic time-delayed model for the effectiveness of Moroccan COVID-19 deconfinement strategy. Math. Model. Nat. Phenom. 2020, 15, 50. [Google Scholar] [CrossRef]
- Mahrouf, M.; Boukhouima, A.; Zine, H.; Lotfi, E.M.; Torres, D.F.M.; Yousfi, N. Modeling and Forecasting of COVID-19 Spreading by Delayed Stochastic Differential Equations. Axioms 2021, 10, 18. [Google Scholar] [CrossRef]
- Ndaïrou, F.; Torres, D.F.M. Mathematical Analysis of a Fractional COVID-19 Model Applied to Wuhan, Spain and Portugal. Axioms 2021, 10, 135. [Google Scholar] [CrossRef]
- Murray, J.D. Mathematical Biology I. An Introduction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Stewart, I.W. The Static and Dynamic Continuum Theory of Liquid Crystals; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives; Gordon and Breach Science Publishers: Yverdon, Switzerland, 1993. [Google Scholar]
- Toledo-Hernandez, R.; Rico-Ramirez, V.; Iglesias-Silva, G.A.; Diwekar, U.M. A Fractional calculus approach to the dynamic optimization of biological reactive systems. Part I: Fractional models for biological reactions. Chem. Eng. Sci. 2014, 117, 217–228. [Google Scholar] [CrossRef]
- Miller, K.S.; Bertram, R. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley-Interscience: New York, NY, USA, 1993. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies; Elsevier Science B.V.: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Rahimy, M. Applications of fractional differential equations. Appl. Math. Sci. 2010, 4, 2453–2461. [Google Scholar] [CrossRef]
- Rossikhin, Y.A.; Shitikova, M.V. Applications of fractional calculus to dynamic problems of linear and nonlinear hereditary mechanics of solids. Appl. Mech. Rev. 1997, 50, 15–67. [Google Scholar] [CrossRef]
- Magin, R.L. Fractional Calculus in Bioengineering; Begell House: Redding, CA, USA, 2006. [Google Scholar]
- Kamal, S.; Jarad, F.; Abdeljawad, T. On a nonlinear fractional order model of dengue fever disease under Caputo-Fabrizio derivative. Alex. Eng. J. 2020, 59, 2305–2313. [Google Scholar]
- Biazar, J. Solution of the epidemic model by Adomian decomposition method. Appl. Math. Comput. 2006, 173, 1101–1106. [Google Scholar] [CrossRef]
- Rafei, M.; Ganji, D.D.; Daniali, H. Solution of the epidemic model by homotopy perturbation method. Appl. Math. Comput. 2007, 187, 1056–1062. [Google Scholar] [CrossRef]
- Abdelrazec, A. Adomian Decomposition Method: Convergence Analysis and Numerical Approximations. Master’s Thesis, McMaster University, Hamilton, ON, Canada, 2008. [Google Scholar]
- Rezapour, S.; Mohammadi, H.; Jajarmi, A. A new mathematical model for Zika virus transmission. Adv. Differ. Equ. 2020, 2020, 1–15. [Google Scholar] [CrossRef]
- Baleanu, D.; Ghanbari, B.; Asad, J.H.; Jajarmi, A.; Pirouz, H.M. Planar System-Masses in an Equilateral Triangle: Numerical Study within Fractional Calculus. Comput. Model. Eng. Sci. 2020, 124, 953–968. [Google Scholar] [CrossRef]
- Jajarmi, A.; Baleanu, D. A New Iterative Method for the Numerical Solution of High-Order Non-linear Fractional Boundary Value Problems. Front. Phys. 2020, 8, 220. [Google Scholar] [CrossRef]
- Sajjadi, S.S.; Baleanu, D.; Jajarmi, A.; Pirouz, H.M. A new adaptive synchronization and hyperchaos control of a biological snap oscillator. Chaos Solitons Fractals 2020, 138, 109919. [Google Scholar] [CrossRef]
- Baleanu, D.; Jajarmi, A.; Sajjadi, S.S.; Asad, J.H. The fractional features of a harmonic oscillator with position-dependent mass. Commun. Theor. Phys. 2020, 72, 055002. [Google Scholar] [CrossRef]
- Jajarmi, A.; Baleanu, D. On the fractional optimal control problems with a general derivative operator. Asian J. Control 2021, 23, 1062–1071. [Google Scholar] [CrossRef]
- Azhar, I.; Siddiqui, M.J.; Muhi, I.; Abbas, M.; Akram, T. Nonlinear waves propagation and stability analysis for planar waves at far field using quintic B-spline collocation method. Alex. Eng. J. 2020, 59, 2695–2703. [Google Scholar]
- Khalid, N.; Abbas, M.; Iqbal, M.K.; Singh, J.; Ismail, A.I. A computational approach for solving time fractional differential equation via spline functions. Alex. Eng. J. 2020, 59, 3061–3078. [Google Scholar] [CrossRef]
- Akram, T.; Abbas, M.; Iqbal, A.; Baleanu, D.; Asad, J.H. Novel Numerical Approach Based on Modified Extended Cubic B-Spline Functions for Solving Non-Linear Time-Fractional Telegraph Equation. Symmetry 2020, 12, 1154. [Google Scholar] [CrossRef]
- Din, A.; Li, Y. Controlling heroin addiction via age-structured modeling. Adv. Differ. Equ. 2020, 2020, 1–17. [Google Scholar] [CrossRef]
- Akram, T.; Abbas, M.; Ali, A.; Iqbal, A.; Baleanu, D. A Numerical Approach of a Time Fractional Reaction–Diffusion Model with a Non-Singular Kernel. Symmetry 2020, 12, 1653. [Google Scholar] [CrossRef]
- Amin, M.; Abbas, M.; Iqbal, M.K.; Baleanu, D. Numerical Treatment of Time-Fractional Klein–Gordon Equation Using Redefined Extended Cubic B-Spline Functions. Front. Phys. 2020, 8, 288. [Google Scholar] [CrossRef]
- Amin, M.; Abbas, M.; Iqbal, M.K.; Ismail, A.I.M.; Baleanu, D. A fourth order non-polynomial quintic spline collocation technique for solving time fractional superdiffusion equations. Adv. Differ. Equ. 2019, 2019, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Khalid, N.; Abbas, M.; Iqbal, M.K. Non-polynomial quintic spline for solving fourth-order fractional boundary value problems involving product terms. Appl. Math. Comput. 2019, 349, 393–407. [Google Scholar] [CrossRef]
- Iqbal, M.K.; Abbas, M.; Wasim, I. New cubic B-spline approximation for solving third order Emden-Flower type equations. Appl. Math. Comput. 2018, 331, 319–333. [Google Scholar] [CrossRef]
- Akram, T.; Abbas, M.; Riaz, M.B.; Ismail, A.I.; Norhashidah, M.A. An efficient numerical technique for solving time fractional Burgers equation. Alex. Eng. J. 2020, 59, 2201–2220. [Google Scholar] [CrossRef]
- Khalid, N.; Abbas, M.; Iqbal, M.K.; Baleanu, D. A numerical investigation of Caputo time fractional Allen-Cahn equation using redefined cubic B-spline functions. Adv. Differ. Equ. 2020, 2020, 1–22. [Google Scholar] [CrossRef]
- Ndaïrou, F.; Torres, D.F.M. Pontryagin Maximum Principle for Distributed-Order Fractional Systems. Mathematics 2021, 9, 1883. [Google Scholar] [CrossRef]
- Sabatier, J.; Agrawal, O.P.; Machado, J.A.T. Advances in Fractional Calculus; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar] [CrossRef]
- Baleanu, D.; Machado, J.A.T.; Albert, C.J. Fractional Dynamics and Control; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Torres, D.F.M. Cauchy’s formula on nonempty closed sets and a new notion of Riemann-Liouville fractional integral on time scales. Appl. Math. Lett. 2021, 121, 107407. [Google Scholar] [CrossRef]
- Al-Refai, M.; Abdeljawad, T. Analysis of the fractional diffusion equations with fractional derivative of non-singular kernel. Adv. Differ. Equ. 2017, 2017, 1–12. [Google Scholar] [CrossRef]
- Mozyrska, D.; Torres, D.F.M.; Wyrwas, M. Solutions of systems with the Caputo-Fabrizio fractional delta derivative on time scales. Nonlinear Anal. Hybrid Syst. 2019, 32, 168–176. [Google Scholar] [CrossRef] [Green Version]
- Abdeljawad, T. Fractional operators with exponential kernels and a Lyapunov type inequality. Adv. Differ. Equ. 2017, 2017, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Hasan, S.; El-Ajou, A.; Hadid, S.; Al-Smadi, M.; Momani, S. Atangana-Baleanu fractional framework of reproducing kernel technique in solving fractional population dynamics system. Chaos Solitons Fractals 2020, 133, 109624. [Google Scholar] [CrossRef]
- Khan, S.A.; Shah, K.; Zaman, G.; Jarad, F. Existence theory and numerical solutions to smoking model under Caputo-Fabrizio fractional derivative. Chaos 2019, 29, 013128. [Google Scholar] [CrossRef] [PubMed]
- Sidi Ammi, M.R.; Tahiri, M.; Torres, D.F.M. Necessary optimality conditions of a reaction-diffusion SIR model with ABC fractional derivatives. arXiv 2021, arXiv:2106.15055. [Google Scholar]
- Din, A.; Li, Y.; Liu, Q. Viral dynamics and control of hepatitis B virus (HBV) using an epidemic model. Alex. Eng. J. 2020, 59, 667–679. [Google Scholar] [CrossRef]
- Din, A.; Liang, J.; Zhou, T. Detecting critical transitions in the case of moderate or strong noise by binomial moments. Phys. Rev. E 2018, 98, 012114. [Google Scholar] [CrossRef]
- Lai, C.C.; Shih, T.P.; Ko, W.C.; Tang, H.J.; Hsueh, P.R. Severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) and coronavirus disease-2019 (COVID-19): The epidemic and the challenges. Int. J. Antimicrob. Agents 2020, 55, 105924. [Google Scholar] [CrossRef] [PubMed]
- Din, A.; Li, Y. Lévy noise impact on a stochastic hepatitis B epidemic model under real statistical data and its fractal–fractional Atangana–Baleanu order model. Phys. Scr. 2021, 96, 124008. [Google Scholar] [CrossRef]
- Wang, J.; Shah, K.; Ali, A. Existence and Hyers-Ulam stability of fractional nonlinear impulsive switched coupled evolution equations. Math. Methods Appl. Sci. 2018, 41, 2392–2402. [Google Scholar] [CrossRef]
- Ahmed, E.; El-Sayed, A.M.A.; El-Saka, H.A.A.; Ashry, G.A. On applications of Ulam-Hyers stability in biology and economics. arXiv 2010, arXiv:1004.1354. [Google Scholar]
- Pakistan, G. COVID-19 Situation. Know about COVID-19, See the Realtime Pakistan and Worldwide. Available online: https://covid.gov.pk (accessed on 28 October 2021).
- Rodrigues, H.S.; Monteiro, M.T.T.; Torres, D.F.M. Seasonality effects on dengue: Basic reproduction number, sensitivity analysis and optimal control. Math. Methods Appl. Sci. 2016, 39, 4671–4679. [Google Scholar] [CrossRef] [Green Version]
- Rosa, S.; Torres, D.F.M. Parameter estimation, sensitivity analysis and optimal control of a periodic epidemic model with application to HRSV in Florida. Stat. Optim. Inf. Comput. 2018, 6, 139–149. [Google Scholar] [CrossRef] [Green Version]
| Notation | Description |
|---|---|
| Rate of recruitment | |
| Transmission rate of disease | |
| Natural death rate | |
| Transmission rate of infected to quarantine | |
| Deaths in quarantined zone | |
| Transmission flow of quarantined to become infectious | |
| h | Rate of deaths in infected zone |
| Notation | Parameters Description | Numerical Value |
|---|---|---|
| Rate of recruitment | ||
| Transmission rate of disease | ||
| Natural death rate | ||
| Transmission rate of infected to quarantine | ||
| Death rate in quarantine | ||
| Transmission flow of quarantined to infectious | ||
| h | Rate of death for infected | |
| Initial population of susceptible | 10 millions | |
| Initially infected population | millions | |
| Quarantined population at | millions |
| Notation | Value | Reference |
|---|---|---|
| 0.028 | [55] | |
| 0.2 | Estimated | |
| 0.011 | [55] | |
| 0.2 | Estimated | |
| h | 0.06 | [55] |
| 0.04 | Estimated | |
| 0.3 | Estimated |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Din, A.; Khan, A.; Zeb, A.; Sidi Ammi, M.R.; Tilioua, M.; Torres, D.F.M. Hybrid Method for Simulation of a Fractional COVID-19 Model with Real Case Application. Axioms 2021, 10, 290. https://doi.org/10.3390/axioms10040290
Din A, Khan A, Zeb A, Sidi Ammi MR, Tilioua M, Torres DFM. Hybrid Method for Simulation of a Fractional COVID-19 Model with Real Case Application. Axioms. 2021; 10(4):290. https://doi.org/10.3390/axioms10040290
Chicago/Turabian StyleDin, Anwarud, Amir Khan, Anwar Zeb, Moulay Rchid Sidi Ammi, Mouhcine Tilioua, and Delfim F. M. Torres. 2021. "Hybrid Method for Simulation of a Fractional COVID-19 Model with Real Case Application" Axioms 10, no. 4: 290. https://doi.org/10.3390/axioms10040290
APA StyleDin, A., Khan, A., Zeb, A., Sidi Ammi, M. R., Tilioua, M., & Torres, D. F. M. (2021). Hybrid Method for Simulation of a Fractional COVID-19 Model with Real Case Application. Axioms, 10(4), 290. https://doi.org/10.3390/axioms10040290








