Error Compensation of Strapdown Inertial Navigation System for the Boom-Type Roadheader under Complex Vibration
Abstract
:1. Introduction
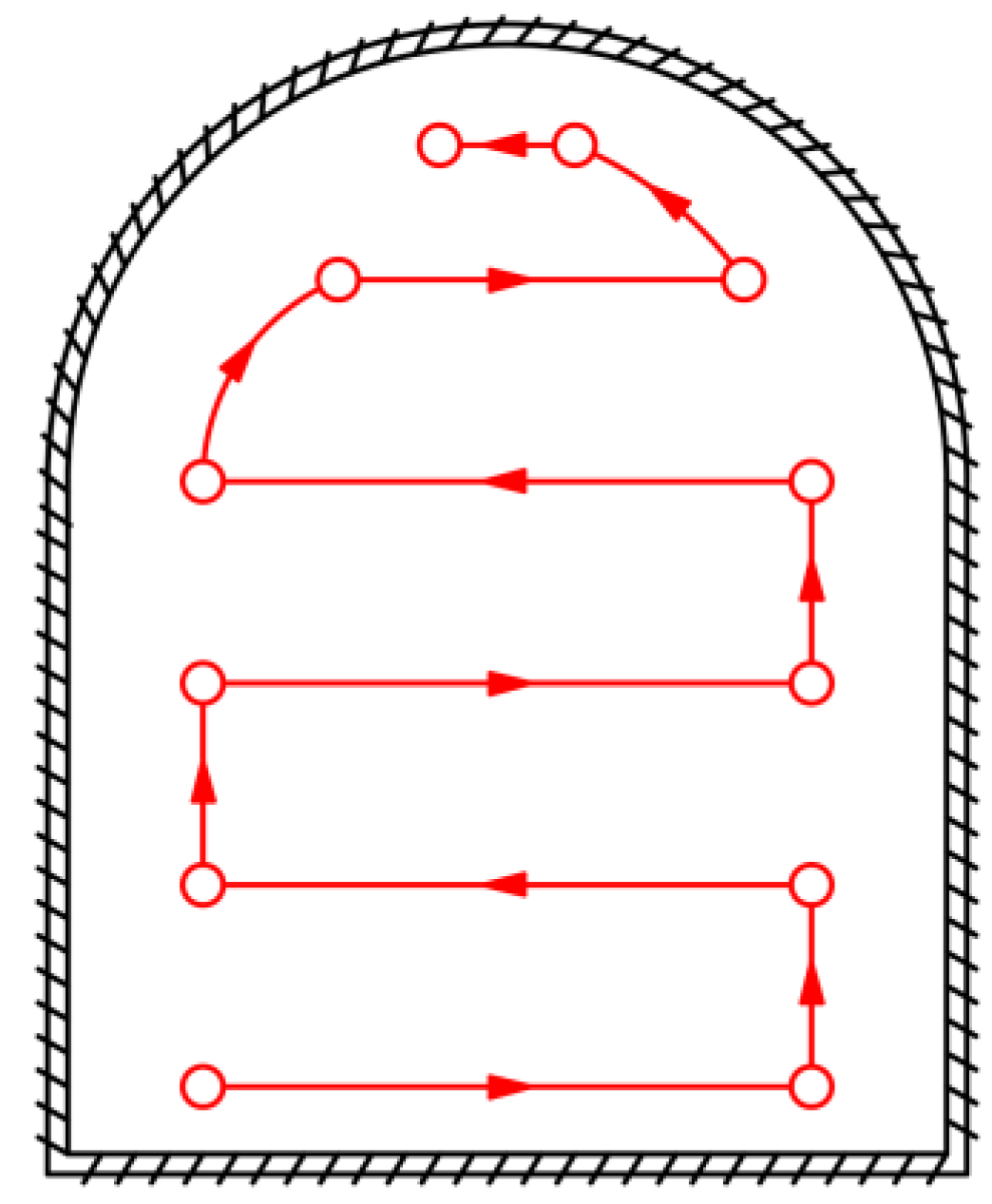
2. Dynamic Analysis of Roadheader
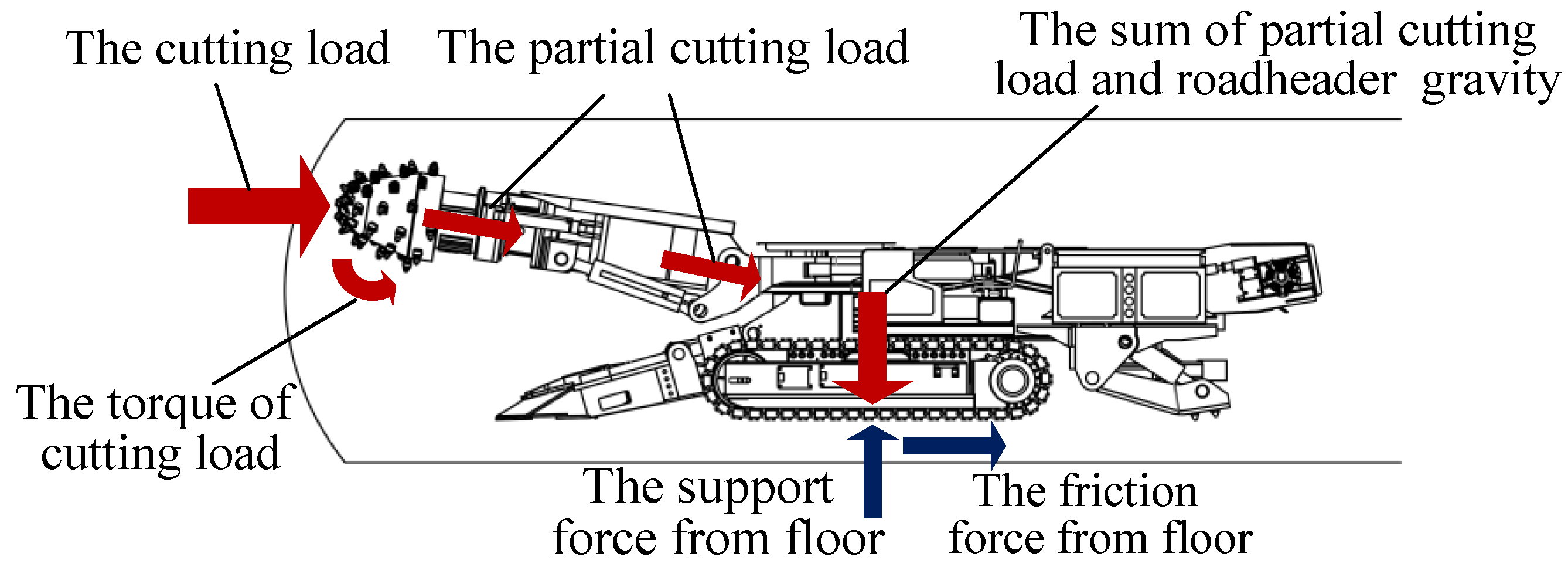
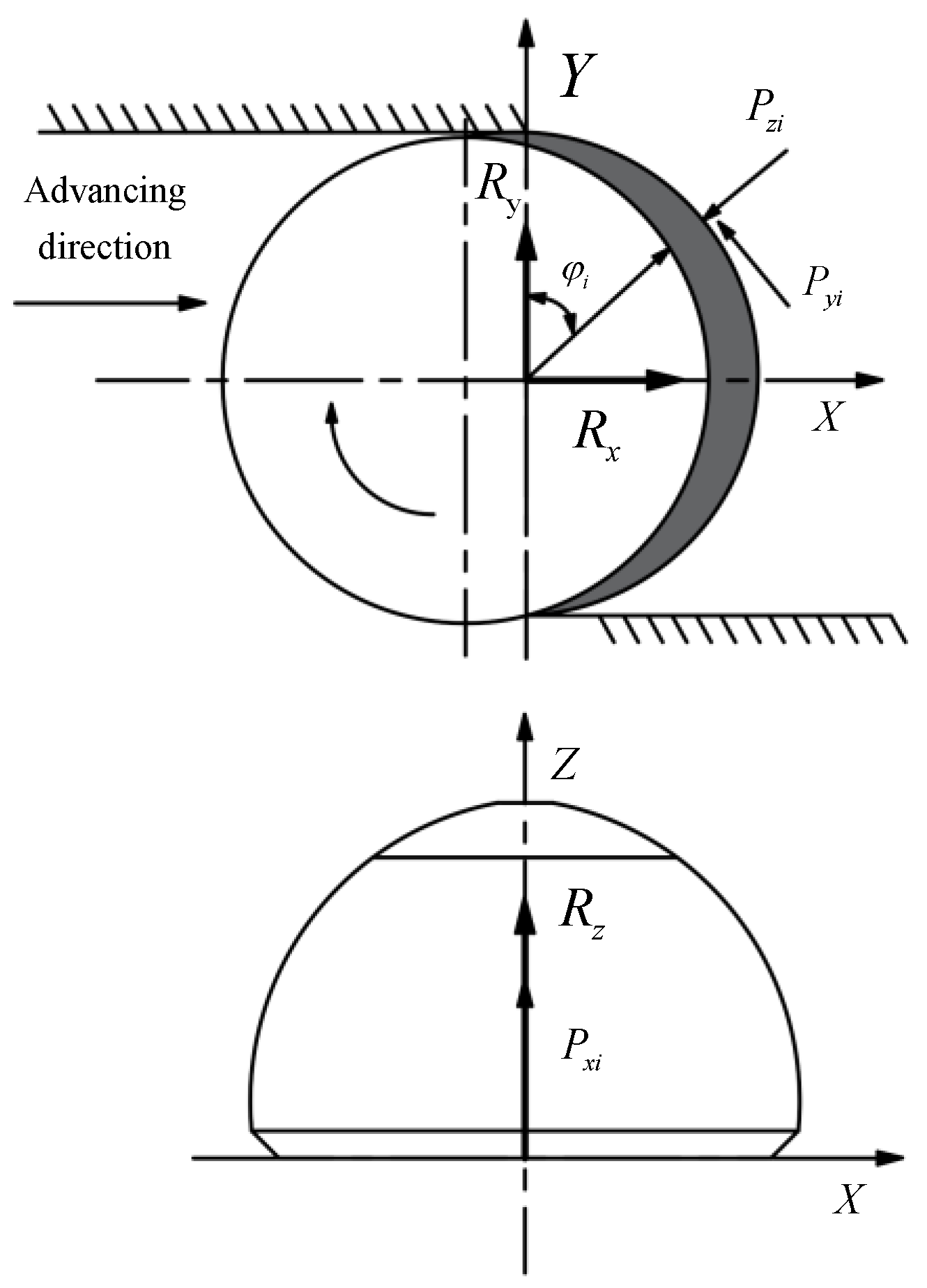
2.1. Force Analysis of Roadheader
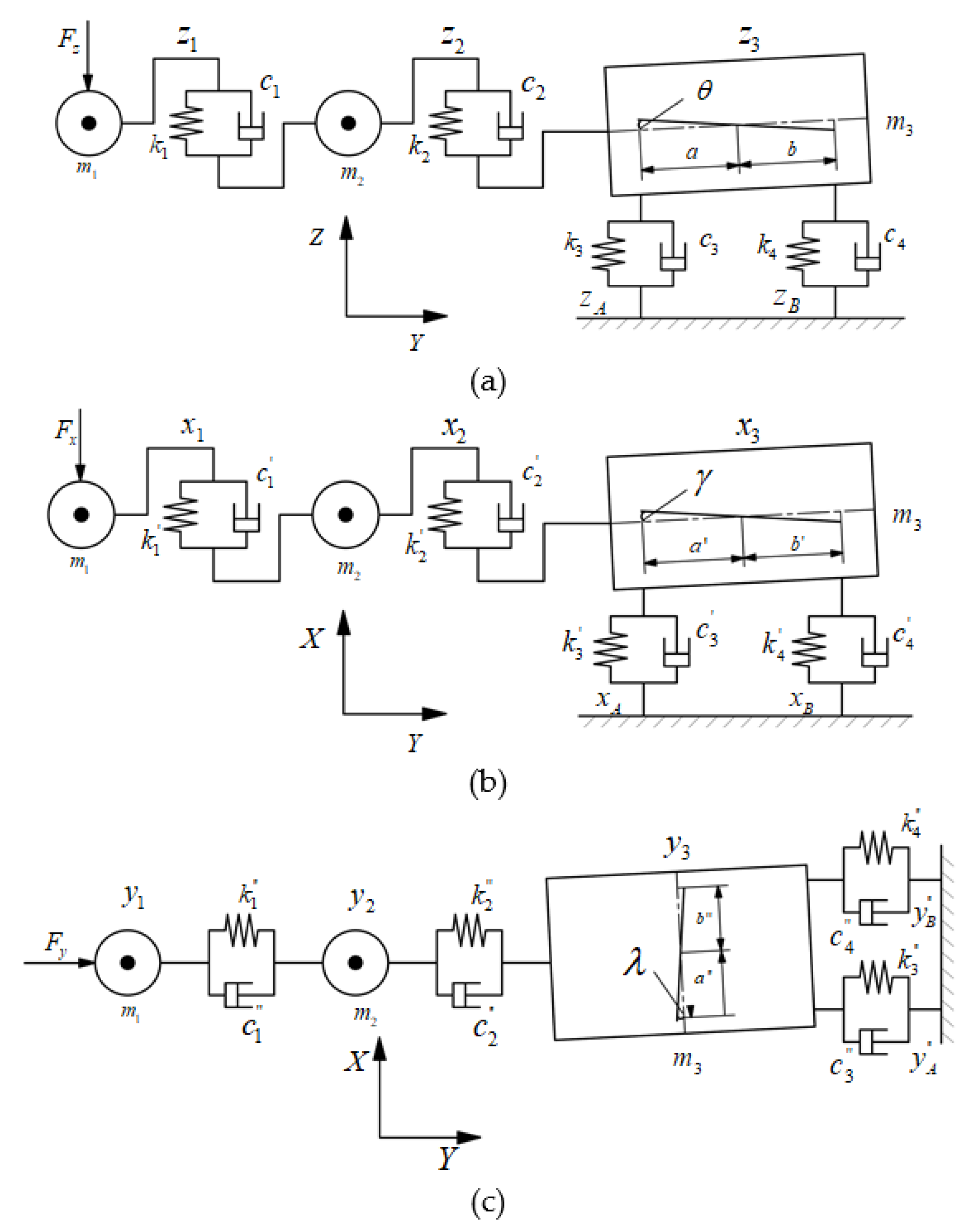
2.2. Dynamic Model of Roadheader
- The mass distribution of each part of the roadheader is even, and the elasticity is minimal. It is simplified to concentrated mass m1, , and m3 (the mass of the cutting head, cutting arm, and fuselage, respectively). J represents the moment of inertia of the fuselage;
- The parts of the roadheader are connected by massless elastic elements. The stiffness between the cutting head and the cutting arm, the cutting arm, and the fuselage, and the fuselage and the bottom floor are represented by , k2, k3, and , respectively;
- The damping between each part of the roadheader is viscous damping. The damping between the cutting head and the cutting arm, the cutting arm, and the fuselage, and the fuselage and the bottom floor are represented by c1, c2, c3, and c4 respectively;
- The roadheader operates normally, and there is no fault causing vibration of the roadheader.
2.3. Solution to Dynamic Model of Roadheader
3. Errors Compensation for Roadheader SINS
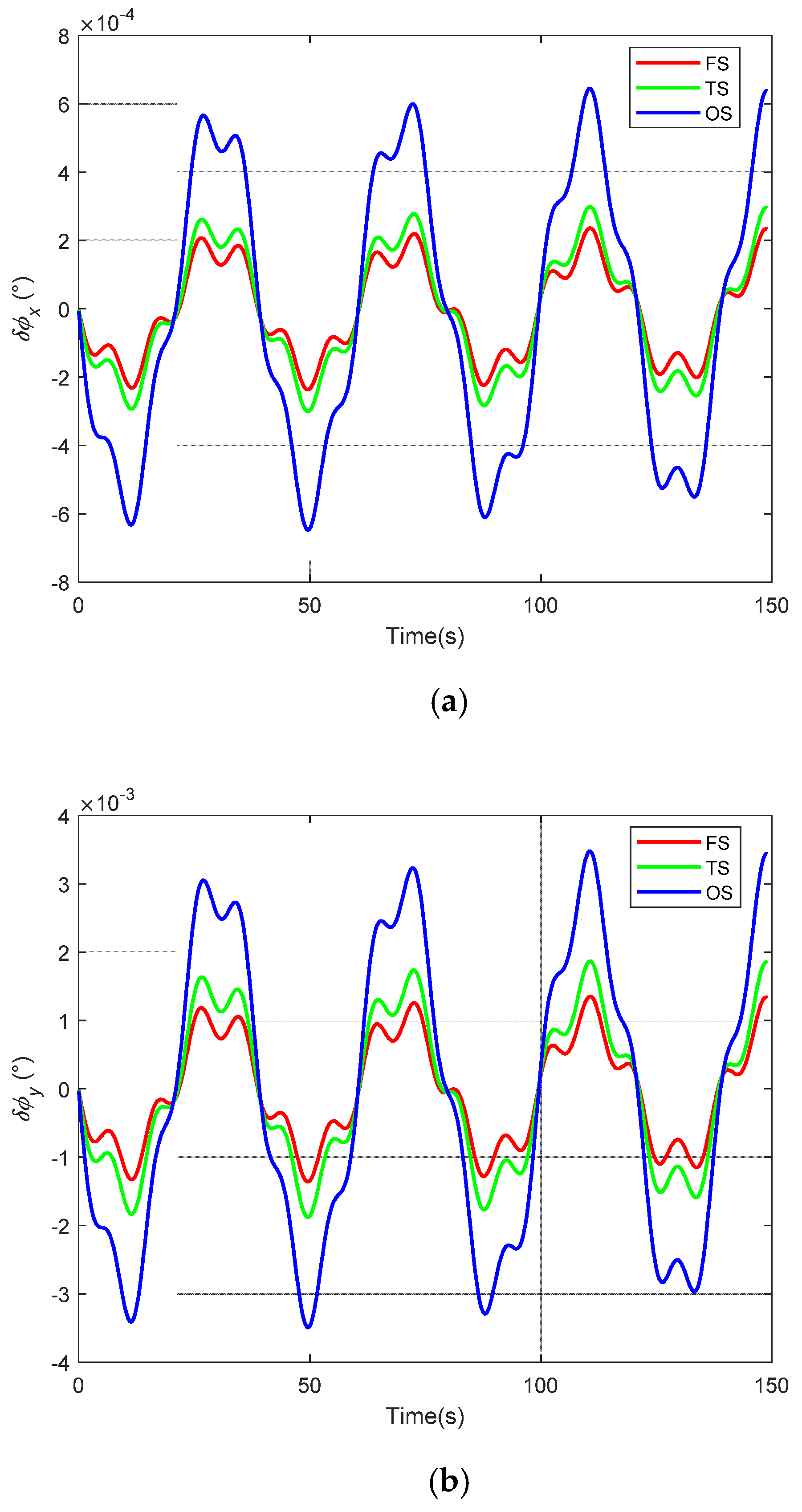
3.1. Calculation Error Compensation for Angular Vibration
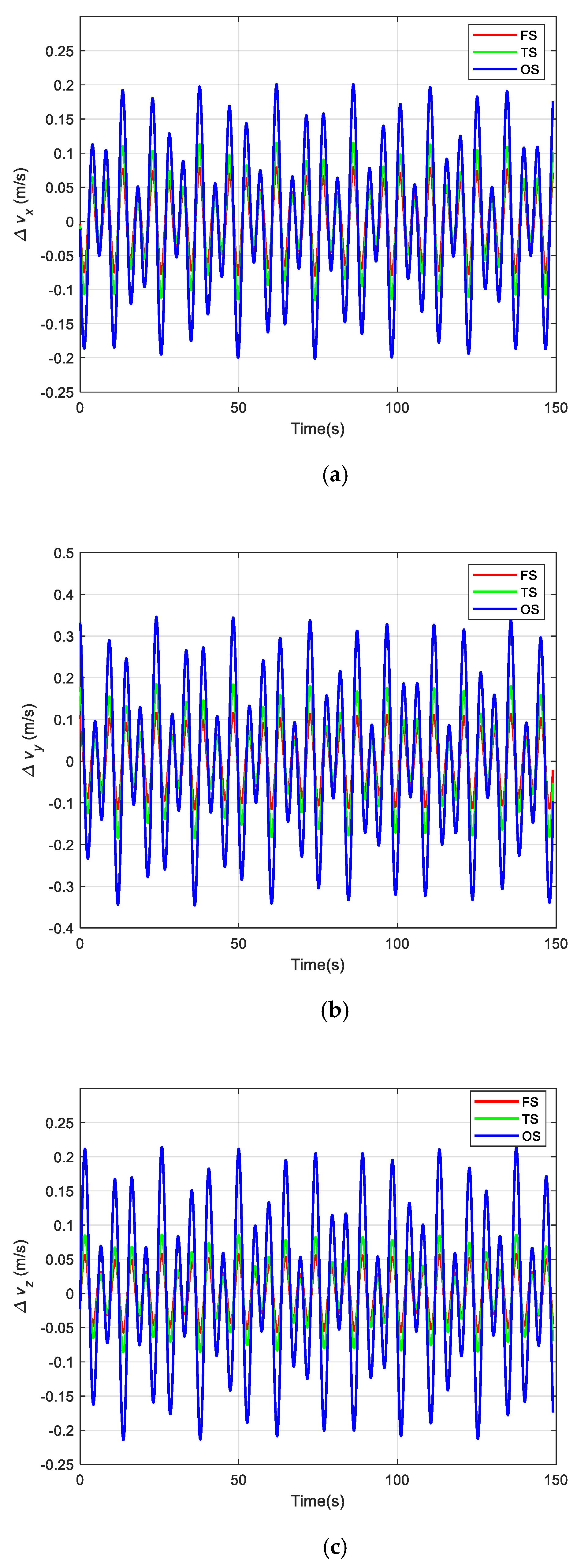
3.2. Calculation Error Compensation for Linear Vibration
4. Simulation and Analysis for Compensation Algorithms
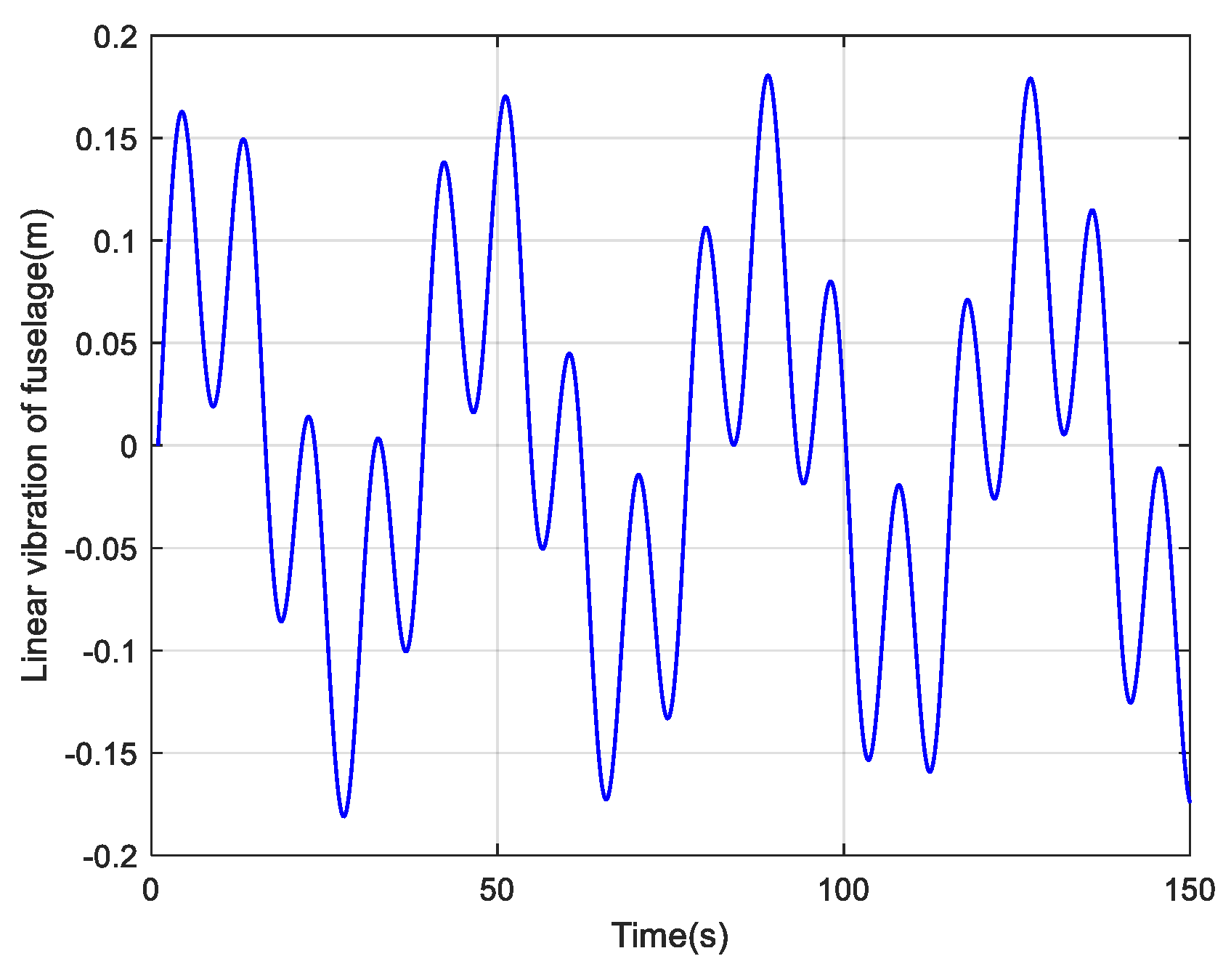
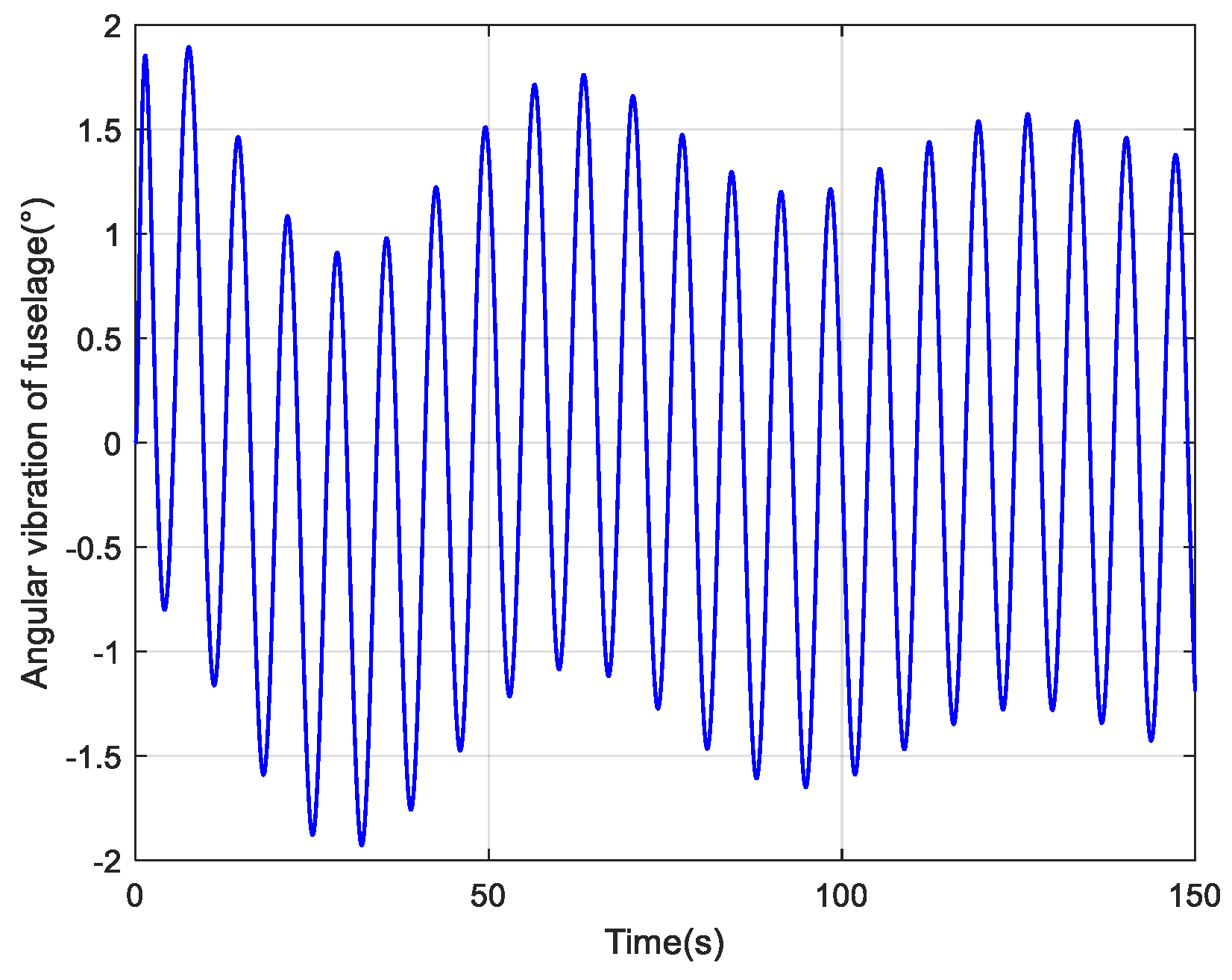
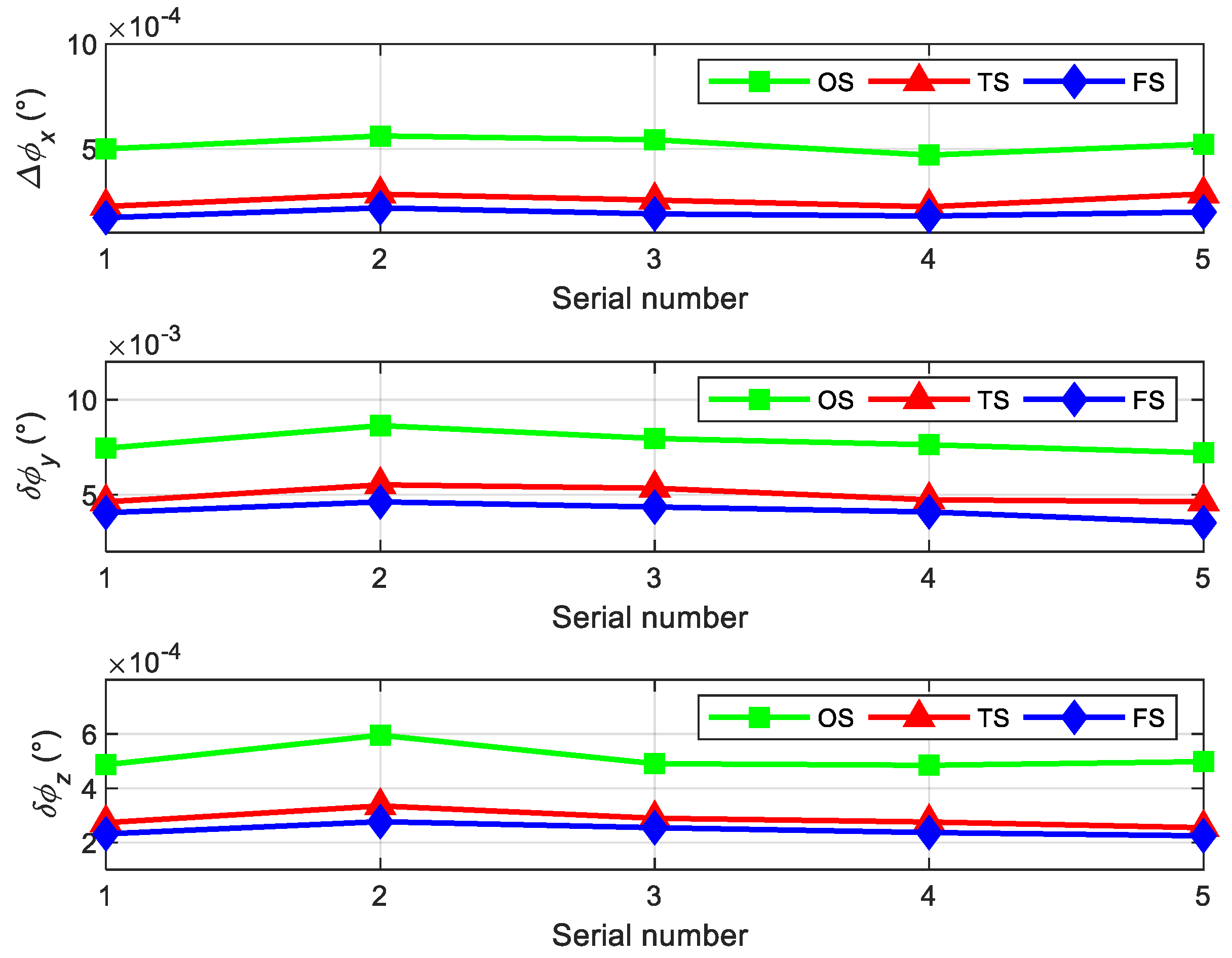
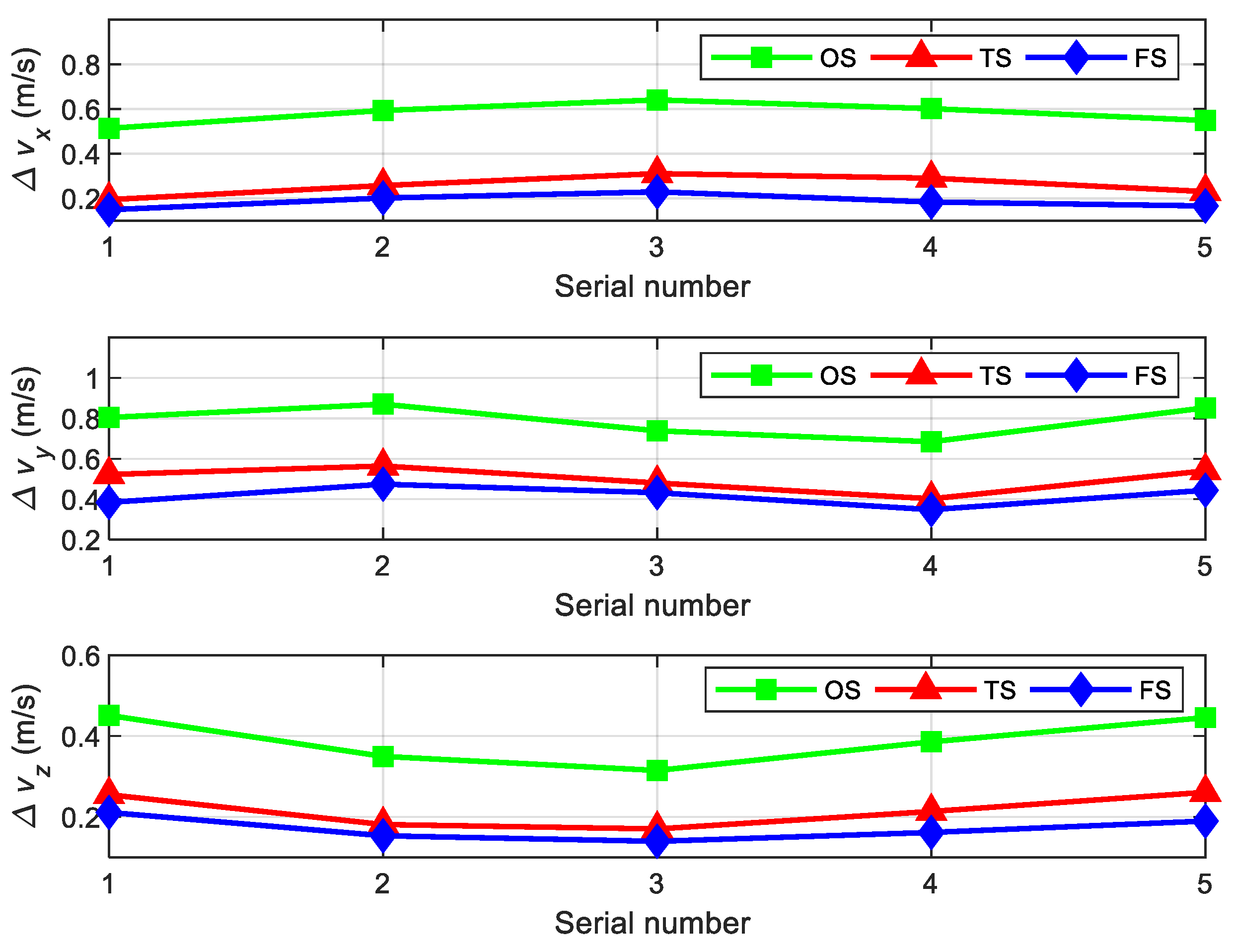
4.1. Simulation for Calculation Error Using Multi-Samples Compensation Algorithms
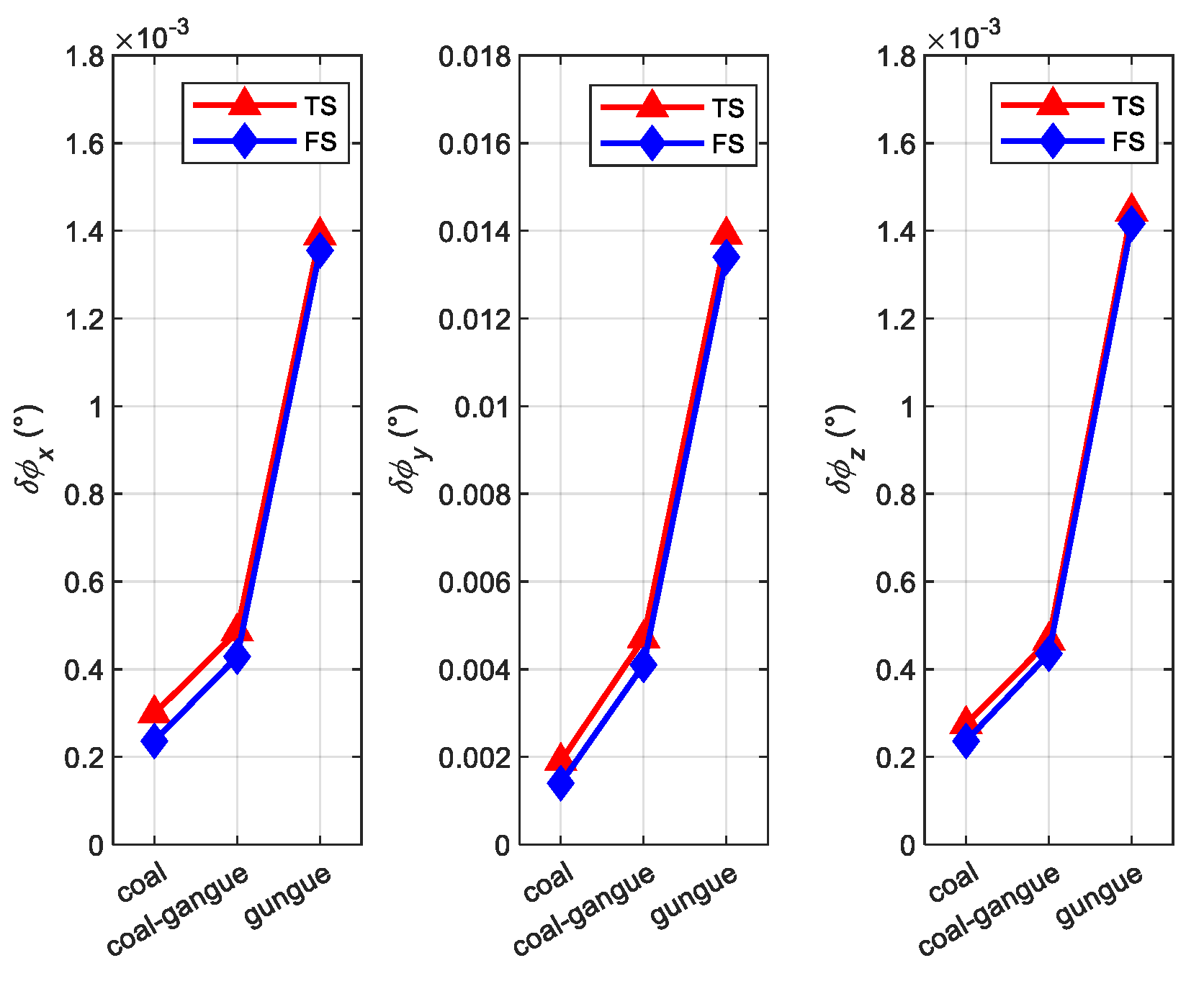
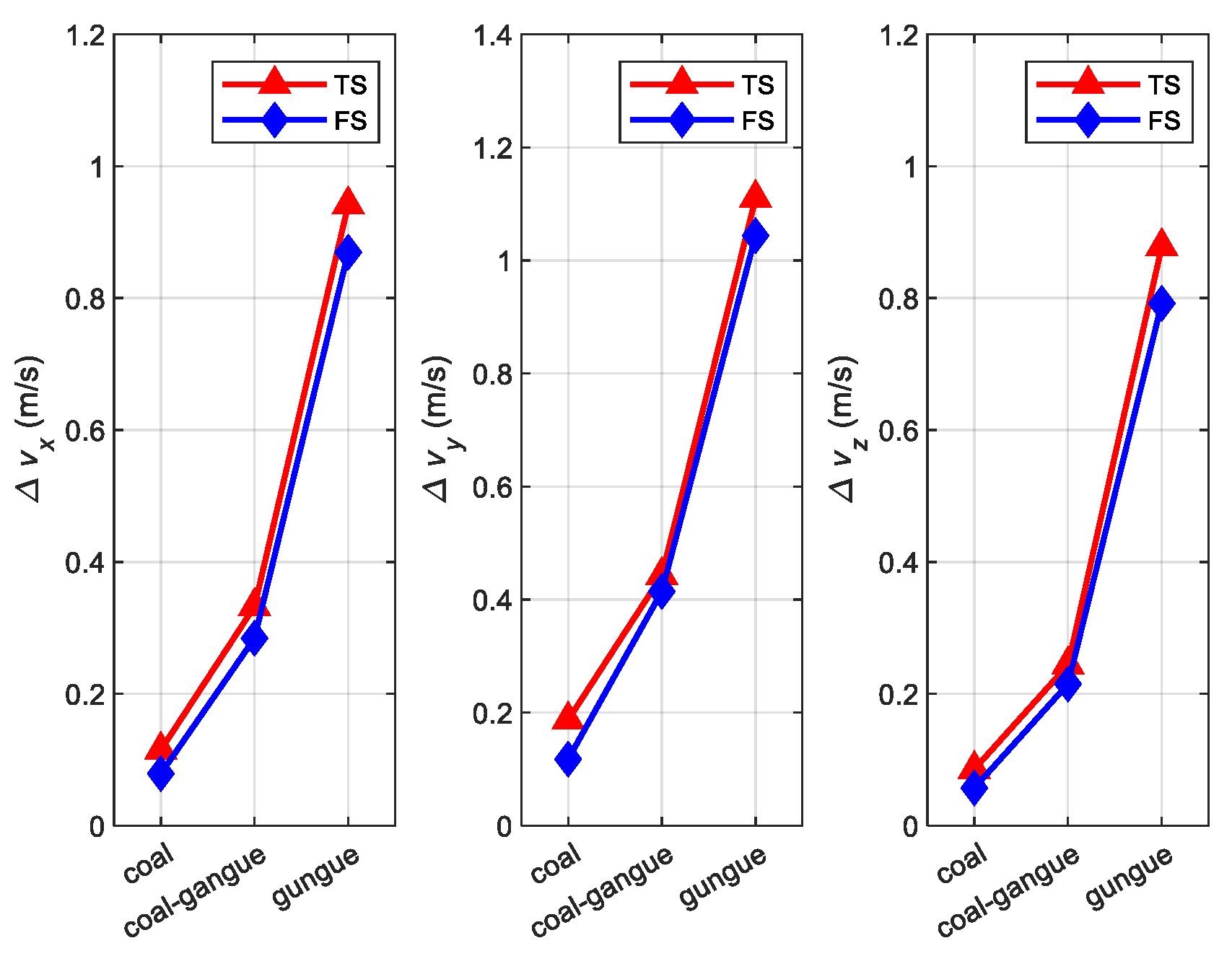
4.2. Simulation for Calculation Error under Different Coal and Rock Characteristics
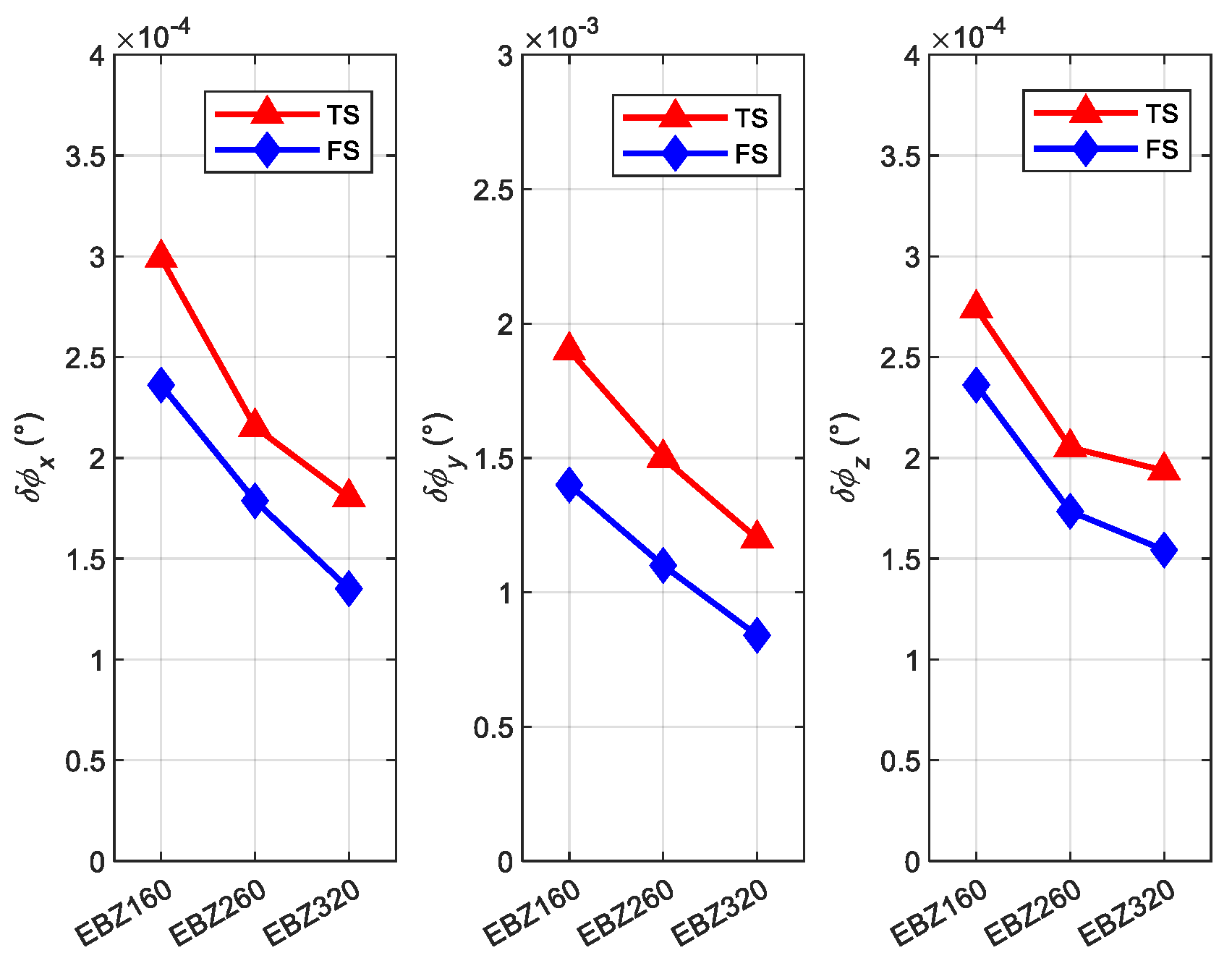
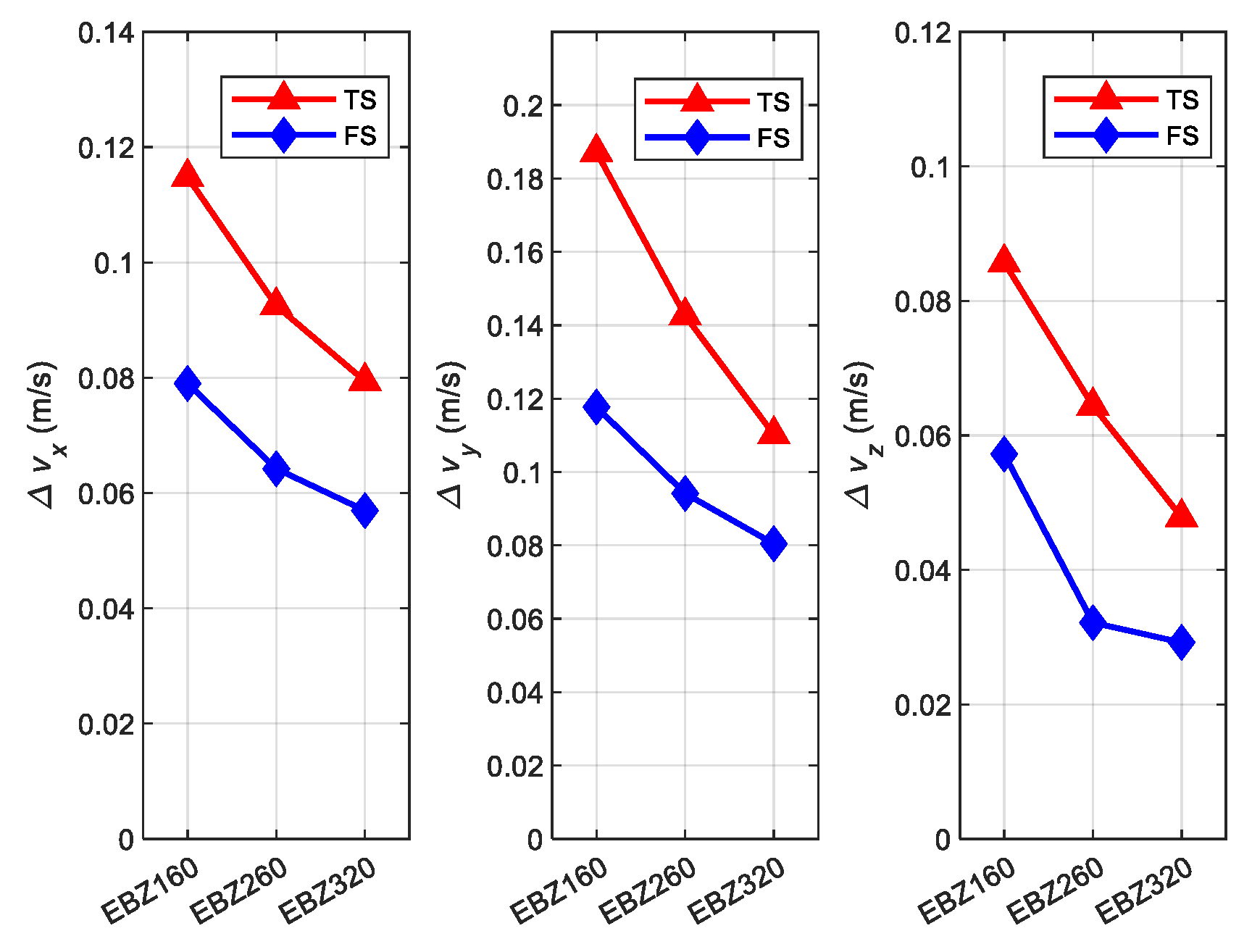
4.3. Simulation for Calculation Error under Different Types of Roadheaders
5. Experiment
5.1. Experiment Scheme
5.2. Experiment Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IEA (International Energy Agency). Coal 2019 Analysis and Forecasts to 2024; IEA: Paris, France, 2019. [Google Scholar]
- He, A.H.; Li, Y.B. A brief discussion on the characteristics and prevention measures of geological disasters in coal mines. West-China Explor. Eng. 2010, 32, 165–166. [Google Scholar]
- Bai, Y.L.; Li, H.L.; Chen, Y.; Zhou, Q.; Bai, C.J.; Xi, L. Statistical Analysis of coal mine accident cases in China in 2019. Policy Res. Explor. 2020, 9, 17–18. [Google Scholar]
- Wang, G.F.; Wang, H.; Ren, H.W. 2025 scenarios and development path of intelligent coal mine. J. China Coal Soc. 2018, 43, 295–305. [Google Scholar]
- Ge, S.R. Present situation and development direction of coal mine robots. China Coal 2019, 45, 18–27. [Google Scholar]
- Yang, J.J.; Zhang, Q.; Wang, C.; Chang, B.S.; Wang, X.L.; Ge, S.R.; Wu, M. Status quo and development of robotization research of coal mine China Coal. J. China Coal Soc. 2020, 45, 2995–3005. [Google Scholar]
- Zong, K.; Zhang, P.; Wang, P.J.; Fu, S.; Zhang, M.; Wu, M. Multifactor Analysis of Roadheader’s Body Pose Responses during the Horizontal Cutting Process. Shock Vib. 2018, 2018, 2387408. [Google Scholar] [CrossRef] [Green Version]
- Zong, K.; Fu, S.C.; Li, Y.M. Analysis of Influence Regularity of Cutting Head Load to Roadheader’s Deviation Angle. Ind. Mine Autom. 2018, 44, 46–51. [Google Scholar]
- Fu, S.C. Research on Pose Detection Method of Boom-Type Roadheader Based on UWB Distance Measurement. Ph.D. Thesis, Mechanical Electronic and Information Engineering, China University of Mining & Technology (Beijing), Beijing, China, 2018. [Google Scholar]
- Fu, S.C.; Li, Y.M.; Zhang, M.J. Ultra-wideband pose detection system for boom-type roadheader based on Caffery transform and Taylor series expansion. Meas. Sci. Technol. 2017, 29, 015101. [Google Scholar] [CrossRef] [Green Version]
- Tao, Y.F. Research on Automatic Measurement Method and System of Position and Attitude of Roadheader Based on Laser Measurement System. Ph.D. Thesis, Mechanical Electronic and Information Engineering, China University of Mining & Technology (Beijing), Beijing, China, 2017. [Google Scholar]
- Tao, Y.F.; Zong, K.; Zhang, M.J. A position and orientation measurement method of single-station, multipoint and time-sharing for roadheader body based on iGPS. J. China Coal Soc. 2015, 40, 2611–2616. [Google Scholar]
- Du, Y.X.; Tong, M.M.; Liu, T.; Dong, H.B. Visual measurement system for roadheaders pose detection in mines. Opt. Eng. 2016, 55, 104107. [Google Scholar] [CrossRef]
- David, H.T.; John, L.W. Basic Principles of Strapdown Inertial Navigation Systems, in Strapdown Inertial Navigation Technology, 2nd ed.; The Institution of Electrical Engineers: Herts, UK, 2004; Chapter 2; pp. 17–25. [Google Scholar]
- Miller, R.B. A new strapdown attitude algorithm, Journal of Guidance. Control Dyn. 1983, 40, 287–291. [Google Scholar] [CrossRef]
- Musoff, H.; Murphy, J.H. Study of strapdown navigation attitude algorithms. J. Guid. Control Dyn. 1995, 28, 287–290. [Google Scholar] [CrossRef]
- Savage, P.G. Strapdown inertial navigation integration algorithm design part 1: Attitude algorithms. J. Guid. Control Dyn. 1998, 21, 19–28. [Google Scholar] [CrossRef]
- Savage, P.G. Strapdown inertial navigation integration algorithm design part 2: Velocity and position algorithms. J. Guid. Control Dyn. 1998, 21, 208–229. [Google Scholar] [CrossRef]
- Yang, H. Research on Accurate Position and Pose Perception Theory and Technology for Shearer with SINS/WSN Integrated Localization. Ph.D. Thesis, School of Mechatronic Engineering, China University of Mining and Technology, Xuzhou, China, 2016. [Google Scholar]
- Lai, J.; Lv, P.; Liu, J.; Jiang, B. Noncommutativity error analysis of strapdown inertial navigation system under the vibration in UAVs. Int. J. Adv. Robot. Syst. 2012, 9, 1–8. [Google Scholar] [CrossRef]
- Li, X.H.; He, Y.; Li, T.; Yu, T.T. Analysis of horizontal and vertical random vibration responses of longitudinal roadheader. J. China Coal Soc. 2014, 33, 1484–1488. [Google Scholar]
- Hou, X.M. The Analysis About the Load on Cutting Head and Vibration of Transverse Roadheader. Master’s Thesis, Department of Mechanical Engineering, AnHui University of Science and Technology, Huaian, China, 2008. [Google Scholar]
- Kang, C.W.; Cho, N.L.; Park, C.G. Approach to direct coning/sculling error compensation based on the sinusoidal modelling of IMU signal. IET Radar Sonar Navig. 2013, 7, 527–534. [Google Scholar] [CrossRef]
- Qin, Y.Y. Strapdown Inertial Navigation System. In Inertial Navigation, 2nd ed.; Science Press: Beijing, China, 2014; Chapter 7; pp. 259–298. [Google Scholar]



| k1 | k2 | k3 | k4 | |
|---|---|---|---|---|
| 1 | - | |||
| 2 | 2/3 | |||
| 3 | 27/20 | 9/20 | ||
| 4 | 214/105 | 92/105 | 54/105 | |
| 5 | 1375/504 | 650/504 | 525/504 | 250/504 |
| Coning Error (°) | ||||
|---|---|---|---|---|
| X-Direction | Y-Direction | Z-Direction | ||
| OS | Avg | 1.5805 × 10−7 | −1.4956 × 10−4 | −2.4478 × 10−5 |
| Var | −2.7737 × 10−5 | 4.5951 × 10−6 | 1.2309 × 10−7 | |
| Max | 6.4484 × 10−4 | 0.0035 | 5.6906 × 10−4 | |
| TS | Avg | −1.2161 × 10−5 | −7.6007 × 10−5 | −1.1058 × 10−5 |
| Var | 3.0743 × 10−8 | 1.2008 × 10−6 | 2.5415 × 10−8 | |
| Max | 2.9909 × 10−4 | 0.0019 | 2.7194 × 10−4 | |
| FS | Avg | −9.3025 × 10−6 | −5.3294 × 10−5 | −9.3039 × 10−6 |
| Var | 1.8212 × 10−8 | 5.9773 × 10−7 | 1.827 × 10−8 | |
| Max | 2.3614 × 10−4 | 0.0014 | 2.3618 × 10−4 | |
| Sculling Error (m/s) | ||||
|---|---|---|---|---|
| X-Direction | Y-Direction | Z-Direction | ||
| OS | Avg | −0.0019 | −4.1859 × 10−4 | 0.0021 |
| Var | 0.0107 | 0.0322 | 0.0123 | |
| Max | 0.2010 | 0.3509 | 0.2142 | |
| TS | Avg | −0.0011 | −2.2325 × 10−4 | −8.2219 × 10−4 |
| Var | 0.0035 | 0.0091 | 0.0020 | |
| Max | 0.1148 | 0.1872 | 0.0857 | |
| FS | Avg | −0.6876 × 10−4 | −1.9588 × 10−4 | −5.2169 × 10−4 |
| Var | 0.0019 | 0.0042 | 0.0010 | |
| Max | 0.0790 | 0.1177 | 0.0572 | |
| EBZ160 | EBZ260 | EBZ320 | |
|---|---|---|---|
| Mass (kg) | 45,000 | 95,000 | 120,000 |
| Dimension (m) | 9.3 × 2.3 × 1.7 | 12.05 × 2.8 × 2.0 | 13.0 × 2.9 × 22.0 |
| Cutting power (kw) | 160 | 260 | 320 |
| Grounding pressure (MPa) | 0.135 | 0.139 | 0.139 |
| Fiber Optic Gyro | Accelerometer | |
|---|---|---|
| Zero bias drift | 0.01°/h | 30 μg |
| Random drift | 0.005°/h | 50 ppm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Y.; Wang, P.; Zheng, W.; Ji, X.; Jiang, H.; Wu, M. Error Compensation of Strapdown Inertial Navigation System for the Boom-Type Roadheader under Complex Vibration. Axioms 2021, 10, 224. https://doi.org/10.3390/axioms10030224
Shen Y, Wang P, Zheng W, Ji X, Jiang H, Wu M. Error Compensation of Strapdown Inertial Navigation System for the Boom-Type Roadheader under Complex Vibration. Axioms. 2021; 10(3):224. https://doi.org/10.3390/axioms10030224
Chicago/Turabian StyleShen, Yang, Pengjiang Wang, Weixiong Zheng, Xiaodong Ji, Hai Jiang, and Miao Wu. 2021. "Error Compensation of Strapdown Inertial Navigation System for the Boom-Type Roadheader under Complex Vibration" Axioms 10, no. 3: 224. https://doi.org/10.3390/axioms10030224
APA StyleShen, Y., Wang, P., Zheng, W., Ji, X., Jiang, H., & Wu, M. (2021). Error Compensation of Strapdown Inertial Navigation System for the Boom-Type Roadheader under Complex Vibration. Axioms, 10(3), 224. https://doi.org/10.3390/axioms10030224






