Location of Urban Logistics Spaces (ULS) for Two-Echelon Distribution Systems
Abstract
:1. Introduction
2. Related Literature
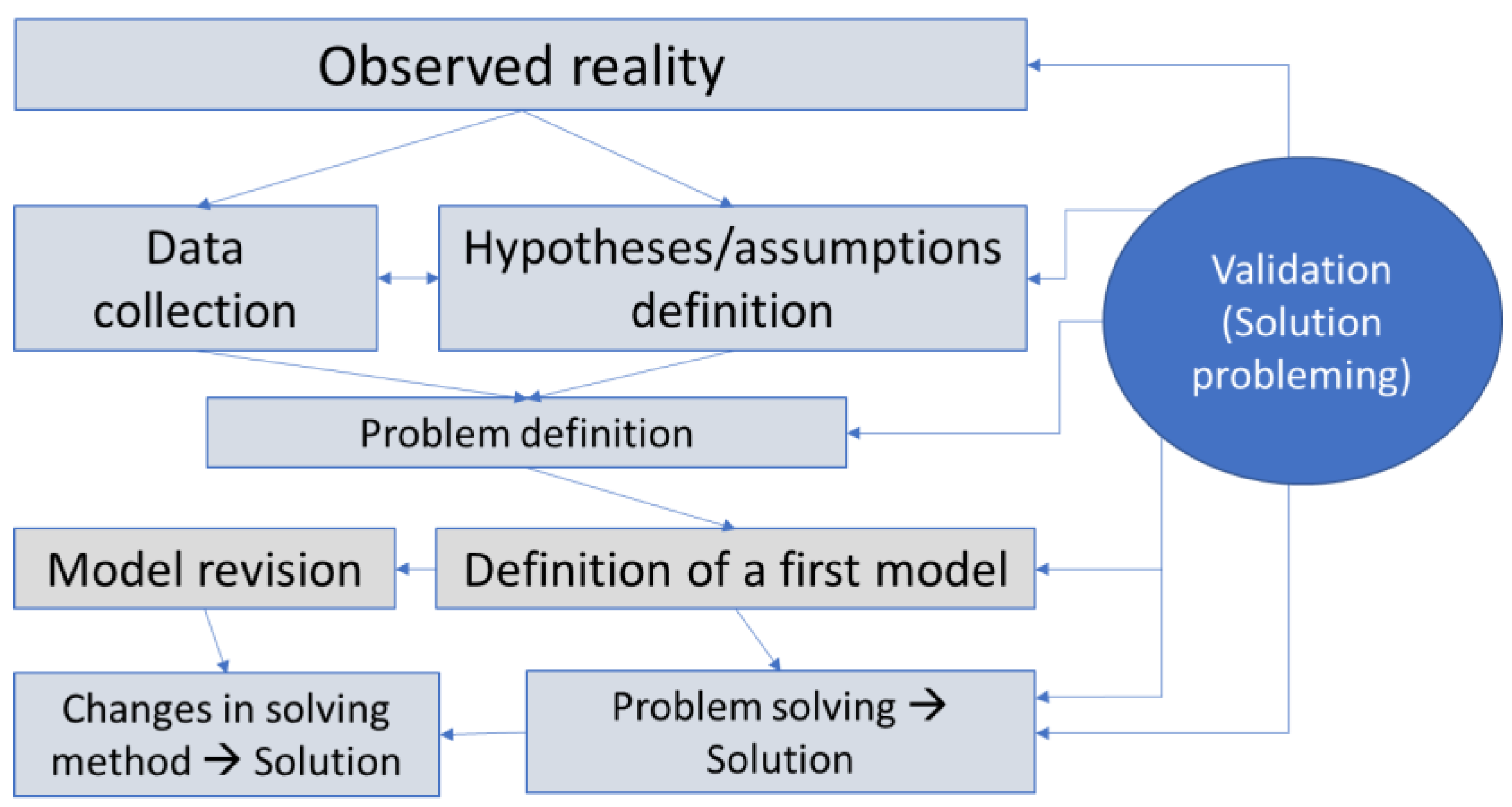
3. Materials and Methods
3.1. Problem Description
3.2. Mathematical Model
4. Results
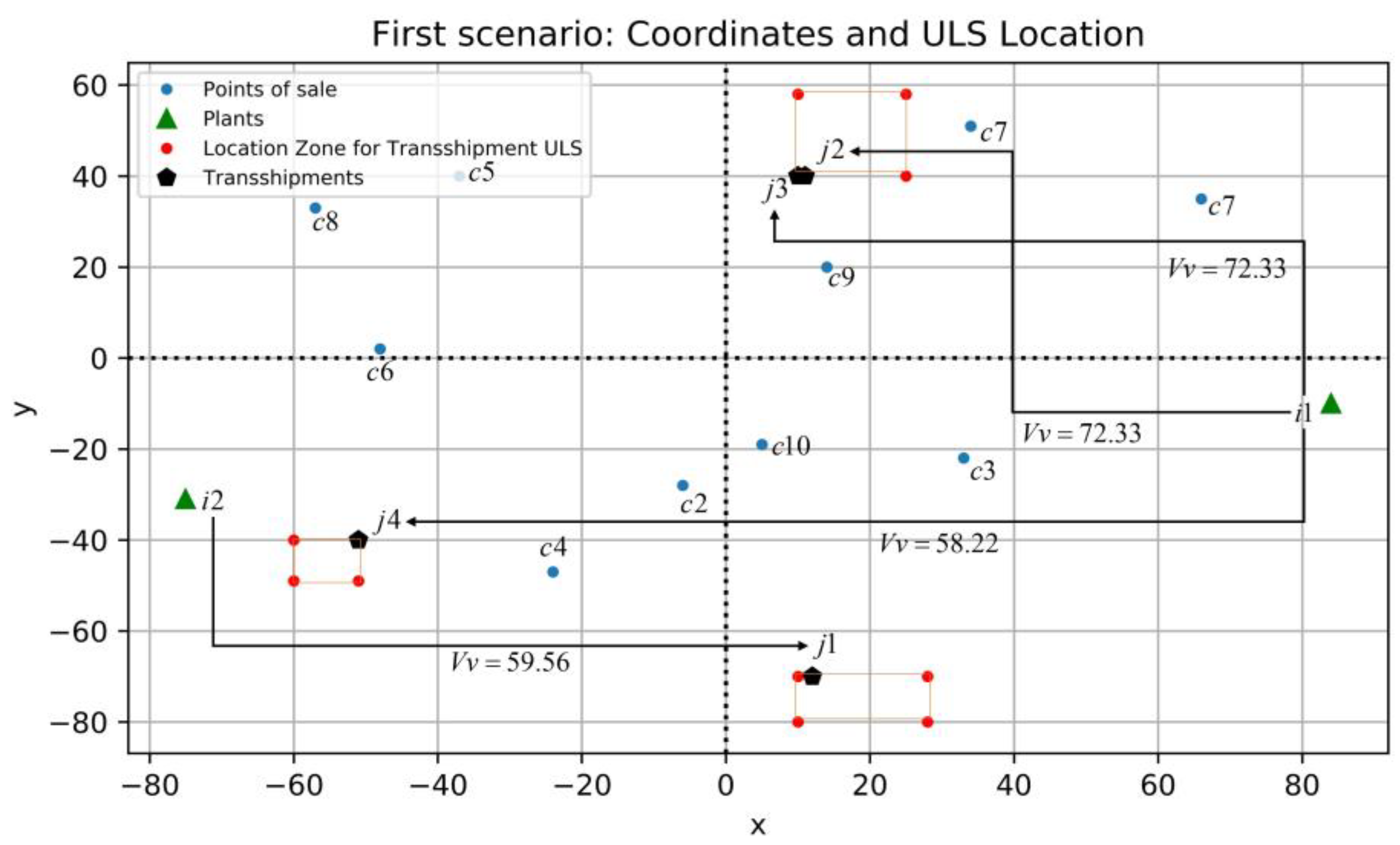
4.1. Analysis of the First Scenario
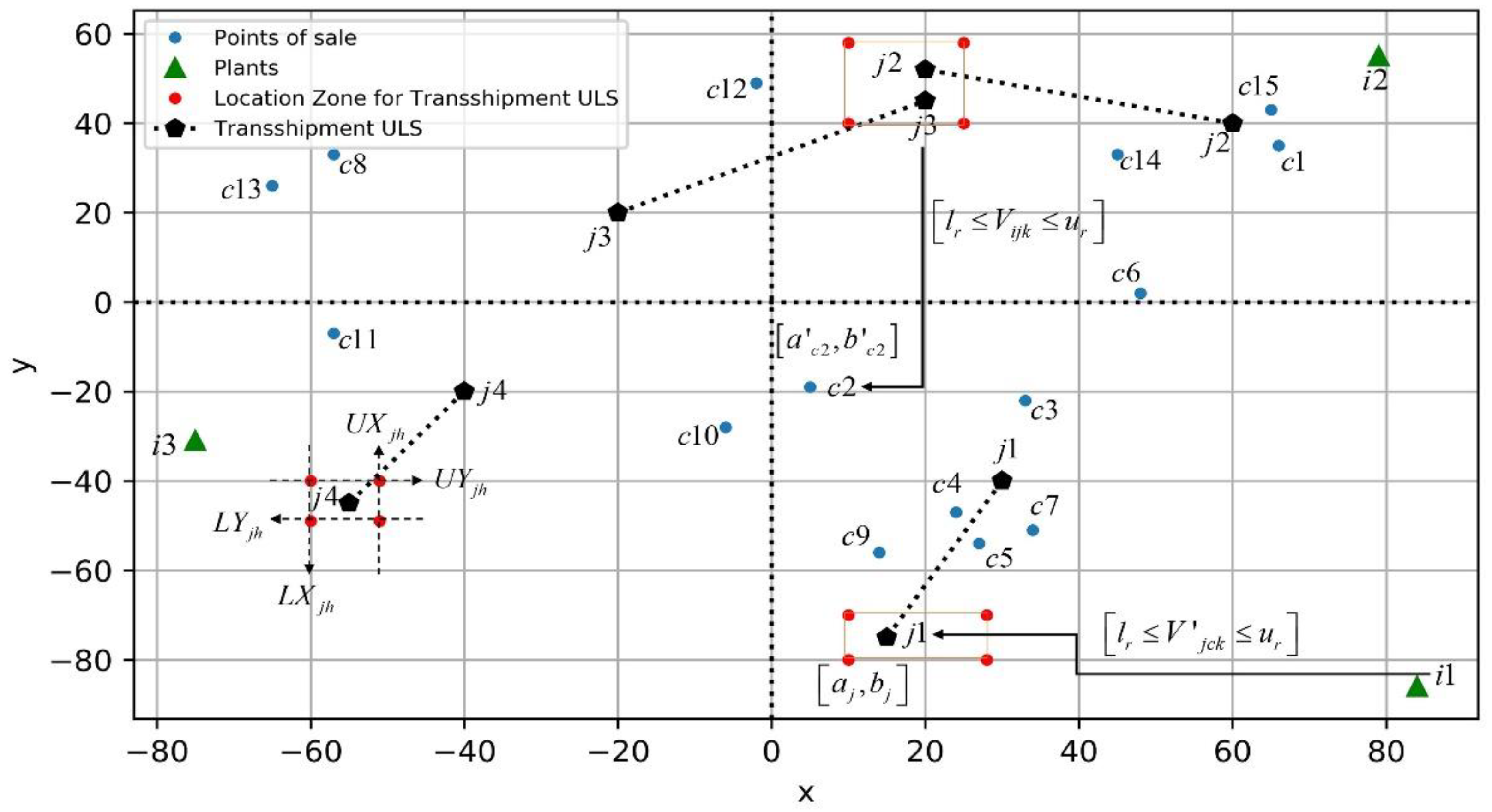
4.2. Analysis of the Second Scenario
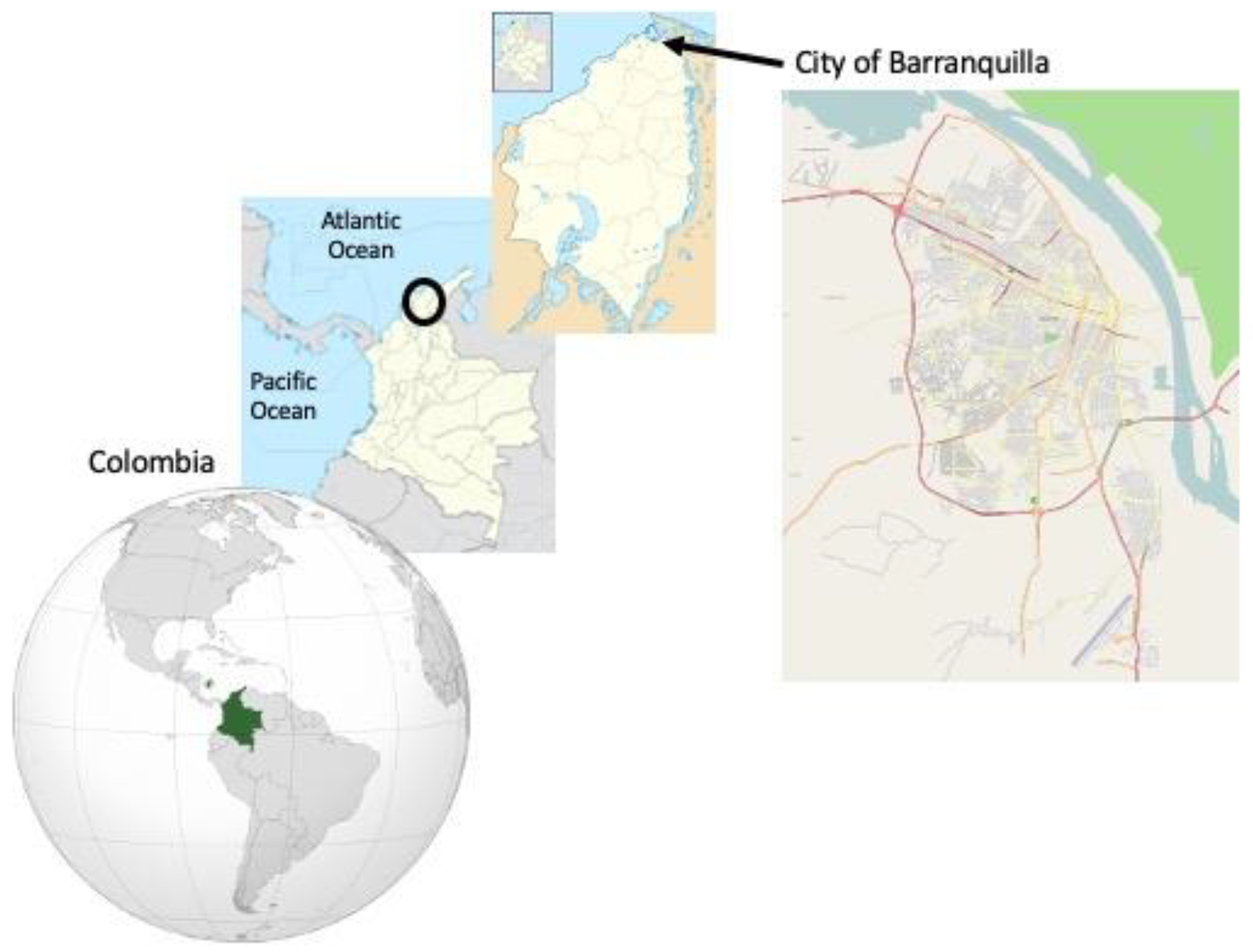
4.3. Analysis of the Case Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cattaruzza, D.; Absi, N.; Feillet, D.; González-Feliu, J. Vehicle routing problems for city logistics. EURO J. Transp. Logist. 2017, 6, 51–79. [Google Scholar] [CrossRef]
- Rześny-Cieplińska, J.; Szmelter-Jarosz, A. Assessment of the Crowd Logistics Solutions—The Stakeholders’ Analysis Approach. Sustainability 2019, 11, 5361. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez-Feliu, J.; Peris-Pla, C. Impacts of retailing attractiveness on freight and shopping trip attraction rates. Res. Transp. Bus. Manag. 2017, 24, 49–58. [Google Scholar] [CrossRef]
- Nathanail, E.; Adamos, G.; Gogas, M. A novel approach for assessing sustainable city logistics. Transp. Res. Procedia 2017, 25, 1036–1045. [Google Scholar] [CrossRef]
- Österle, I.; Aditjandra, P.T.; Vaghi, C.; Grea, G.; Zunder, T.H. The role of a structured stakeholder consultation process within the establishment of a sustainable urban supply chain. Supply Chain Manag. An Int. J. 2015, 20, 284–299. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez-Feliu, J.; Pronello, C.; Grau, J.M.S. Multi-stakeholder collaboration in urban transport: State-of-the-art and research opportunities. Transport 2018, 33, 1079–1094. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez-Feliu, J. Sustainable Urban Logistics: Planning and Evaluation; Wiley-ISTE: Hoboken, NJ, USA, 2018; ISBN 978-1-119-42194-8. [Google Scholar]
- Dorta-González, P. Transporte y Logística Internacional, Universidad de Las Palmas de Gran Canaria. 2014. Available online: http://hdl.handle.net/10553/11886 (accessed on 22 August 2021).
- Bowersox, D.J.; Closs, D.J.; Helferich, O.K. Logistical Management: A Systems Integration of Physical Distribution, Manufacturing Support, and Materials Procurement; Macmillan: London, UK, 1986; ISBN 9780023130908. [Google Scholar]
- Sachan, A.; Datta, S. Review of supply chain management and logistics research. Int. J. Phys. Distrib. Logist. Manag. 2005, 35, 664–705. [Google Scholar] [CrossRef]
- Davis-Sramek, B.; Fugate, B.S. State of logistics: A visionary perspective. J. Bus. Logist. 2007, 28, 1–34. [Google Scholar] [CrossRef]
- Muñoz-Villamizar, A.; Montoya-Torres, J.R.; Moreno-Camacho, C.A. Simulation-based optimization approach for vehicle allocation in a private transport service: A case study. Manag. Sci. Lett. 2019, 193–204. [Google Scholar] [CrossRef]
- Rai, H.B.; Van Lier, T.; Meers, D.; Macharis, C. Improving urban freight transport sustainability: Policy assessment framework and case study. Res. Transp. Econ. 2017, 64, 26–35. [Google Scholar]
- Russo, F.; Comi, A. Investigating the Effects of City Logistics Measures on the Economy of the City. Sustainability 2020, 12, 1439. [Google Scholar] [CrossRef] [Green Version]
- Villa, R.; Monzón, A. A Metro-Based System as Sustainable Alternative for Urban Logistics in the Era of E-Commerce. Sustainability 2021, 13, 4479. [Google Scholar] [CrossRef]
- Gonzalez-Feliu, J. Sustainability Evaluation of Green Urban Logistics Systems: Literature Overview and Proposed Framework. In Green Initiatives for Business Sustainability and Value Creation; Paul, A.K., Bhattacharyya, D.K., Anand, S., Eds.; IGI Global: Hershey, PA, USA, 2018; pp. 103–134. [Google Scholar] [CrossRef]
- Van Duin, J.H.R.; Quak, H.J.; Muñuzuri, J. Revival of cost benefit analysis for evaluating the city distribution centre concept? In Innovations in City Logistics; Nova Science: New York, NY, USA, 2008; pp. 97–114. ISBN 9781604567250. [Google Scholar]
- Battaia, G.; Faure, L.; Marqués, G.; Guillaume, R.; Montoya-Torres, J.R. A Methodology to Anticipate the Activity Level of Collaborative Networks: The Case of Urban Consolidation. Supply Chain Forum An Int. J. 2014, 15, 70–82. [Google Scholar] [CrossRef] [Green Version]
- Nimtrakool, K.; Gonzalez-Feliu, J.; Capo, C. Barriers to the Adoption of an Urban Logistics Collaboration Process: A Case Study of the Saint-Etienne Urban Consolidation Centre. In City Logistics 2; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2018; pp. 313–332. [Google Scholar] [CrossRef]
- Melo, S.; Costa, A. Definition of a Set of Indicators to Evaluate the Performance of Urban Goods Distribution Initiatives. In City Distribution and Urban Freight Transport; Macharis, C., Melo, S., Eds.; Edward Elgar Publishing: Northampton, MA, USA, 2011; pp. 120–147. [Google Scholar]
- Antún, J.P. Distribución Urbana de Mercancías: Estrategias con Centros Logísticos. 2013. Available online: https://publications.iadb.org/publications/spanish/document/Distribuci%C3%B3n-urbana-de-mercanc%C3%ADas-Estrategias-con-centros-log%C3%ADsticos.pdf (accessed on 22 August 2021).
- Boudoin, D.; Morel, C.; Gardat, M. Supply Chains and Urban Logistics Platforms. In Sustainable Urban Logistics: Concepts, Methods and Information Systems; Gonzalez-Feliu, J., Semet, F., Routhier, J., Eds.; Springer: Berlin, Heidelberg, 2014; p. 272. ISBN 9783642317873. [Google Scholar] [CrossRef] [Green Version]
- Crainic, T.G. City Logistics. In State-of-the-Art Decision-Making Tools in the Information-Intensive Age; Chen, Z.L., Raghavan, S., Gray, P., Greenberg, H.J., Eds.; INFORMS: Catonsville, MD, USA, 2008; pp. 181–212. [Google Scholar] [CrossRef] [Green Version]
- Boudouin, D. Urban Logistics Spaces: Methodological Guide; La Documentation française: Paris, France, 2012. [Google Scholar]
- Meza-Peralta, K.; Gonzalez-Feliu, J.; Montoya-Torres, J.R.; Khodadad-Saryazdi, A. A unified typology of urban logistics spaces as interfaces for freight transport. Supply Chain Forum Int. J. 2020, 21, 274–289. [Google Scholar] [CrossRef]
- Crainic, T.G.; Sgalambro, A. Service network design models for two-tier city logistics. Optim. Lett. 2014, 8, 1375–1387. [Google Scholar] [CrossRef]
- Rao, C.; Goh, M.; Zhao, Y.; Zheng, J. Location selection of city logistics centers under sustainability. Transp. Res. Part D Transp. Environ. 2015, 36, 29–44. [Google Scholar] [CrossRef]
- Combes, F. Equilibrium and Optimal Location of Warehouses in Urban Areas: A Theoretical Analysis with Implications for Urban Logistics. Transp. Res. Rec. J. Transp. Res. Board 2019, 2673, 262–271. [Google Scholar] [CrossRef]
- Laporte, G.; Nickel, S.; Saldanha da Gama, F. Location Science; Laporte, G., Nickel, S., Saldanha da Gama, F., Eds.; Springer International Publishing: Cham, Switzerlad, 2019; ISBN 978-3-319-13110-8. [Google Scholar] [CrossRef]
- Ortiz-Astorquiza, C.; Contreras, I.; Laporte, G. Multi-level facility location problems. Eur. J. Oper. Res. 2018, 267, 791–805. [Google Scholar] [CrossRef] [Green Version]
- Farahani, R.Z.; Fallah, S.; Ruiz, R.; Hosseini, S.; Asgari, N. OR models in urban service facility location: A critical review of applications and future developments. Eur. J. Oper. Res. 2019, 276, 1–27. [Google Scholar] [CrossRef]
- Henriques de Gusmão, A.P.; Aragão Pereira, R.M.; Silva, M.M.; da Costa Borba, B.F. The Use of a Decision Support System to Aid a Location Problem Regarding a Public Security Facility. In Proceedings of the Decision Support Systems IX: Main Developments and Future Trends Volume 348 (5th International Conference on Decision Support System Technology, EmC-ICDSST 2019, Funchal, Portugal, 27–29 May 2019; pp. 15–27. [Google Scholar] [CrossRef]
- Csiszár, C.; Csonka, B.; Földes, D.; Wirth, E.; Lovas, T. Urban public charging station locating method for electric vehicles based on land use approach. J. Transp. Geogr. 2019, 74, 173–180. [Google Scholar] [CrossRef]
- Myagmartseren, P.; Buyandelger, M.; Brandt, S.A. Implications of a Spatial Multicriteria Decision Analysis for Urban Development in Ulaanbaatar, Mongolia. Math. Probl. Eng. 2017, 2017, 1–16. [Google Scholar] [CrossRef]
- Prodhon, C.; Prins, C. A survey of recent research on location-routing problems. Eur. J. Oper. Res. 2014, 238, 1–17. [Google Scholar] [CrossRef]
- Martinho, A.; Alves, E.; Rodrigues, A.M.; Ferreira, J.S. Multicriteria Location-Routing Problems with Sectorization. In Operational Research; Springer Proceedings in Mathematics & Statistics, APDIO 2017; Vaz, A., Almeida, J., Oliveira, J., Pinto, A., Eds.; Springer: Cham, Switzerland; Berlin/Heidelberg, Germany; Valença, Portugal, 2018; pp. 215–234. [Google Scholar] [CrossRef]
- Fatimah, I.; Jun, Y.B.; Mustafa, S. Modelling the logistic processes using fuzzy decision approach. Hacettepe J. Math. Stat. 2018, 48. [Google Scholar] [CrossRef]
- Awasthi, A.; Adetiloye, T.; Crainic, T.G. Collaboration partner selection for city logistics planning under municipal freight regulations. Appl. Math. Model. 2016, 40, 510–525. [Google Scholar] [CrossRef]
- Shavarani, S.M.; Mosallaeipour, S.; Golabi, M.; İzbirak, G. A congested capacitated multi-level fuzzy facility location problem: An efficient drone delivery system. Comput. Oper. Res. 2019, 108, 57–68. [Google Scholar] [CrossRef]
- Canevaro, E.; Ingaramo, R.; Lami, I.M.; Morena, M.; Robiglio, M.; Saponaro, S.; Sezenna, E. Strategies for the Sustainable Reindustrialization of Brownfields. IOP Conf. Ser. Earth Environ. Sci. 2019, 296, 012010. [Google Scholar] [CrossRef]
- Koç, Ç.; Bektaş, T.; Jabali, O.; Laporte, G. The impact of depot location, fleet composition and routing on emissions in city logistics. Transp. Res. Part B Methodol. 2016, 84, 81–102. [Google Scholar] [CrossRef]
- Aljohani, K.; Thompson, R.G. Impacts of logistics sprawl on the urban environment and logistics: Taxonomy and review of literature. J. Transp. Geogr. 2016, 57, 255–263. [Google Scholar] [CrossRef]
- Rabe, M.; Gonzalez-Feliu, J.; Chicaiza-Vaca, J.; Tordecilla, R.D. Simulation-Optimization Approach for Multi-Period Facility Location Problems with Forecasted and Random Demands in a Last-Mile Logistics Application. Algorithms 2021, 14, 41. [Google Scholar] [CrossRef]
- Chase, R.; Jacobs, R.; Aquilano, N. Administración de Operaciones. Producción y Cadena de Suministros, 12th ed.; McGraw Hill: New York, NY, USA, 2016; ISBN 9789701070277. [Google Scholar]
- Heitz, A.; Launay, P.; Beziat, A. Heterogeneity of logistics facilities: An issue for a better understanding and planning of the location of logistics facilities. Eur. Transp. Res. Rev. 2019, 11, 5. [Google Scholar] [CrossRef] [Green Version]
- Yang, K.; Roca-Riu, M.; Menéndez, M. An auction-based approach for prebooked urban logistics facilities. Omega 2019, 89, 193–211. [Google Scholar] [CrossRef] [Green Version]
- Ndhaief, N.; Bistorin, O.; Rezg, N. A modelling approach for city locating logistic platforms based on combined forward and reverse flows. IFAC-PapersOnLine 2017, 50, 11701–11706. [Google Scholar] [CrossRef]
- Ambrosino, D.; Sciomachen, A. A capacitated hub location problem in freight logistics multimodal networks. Optim. Lett. 2016, 10, 875–901. [Google Scholar] [CrossRef]
- Kostrzewski, M.; Varjan, P. The issue of parking areas conditions in surrounding of logistics and production facilities in Slovakia and Poland. In Proceedings of the 22nd International Scientific Conference Transport Means 2018, TRANSPORT MEANS, Kaunas, Lithuania, 3–5 October 2018; Robertas, K., Ed.; Transport Means: Kaunas, Lithuania, 2018. [Google Scholar]
- Benhida, K.; Azougagh, Y.; Elfezazi, S. Modelling a flows in supply chain with analytical models: Case of a chemical industry. IOP Conf. Ser. Mater. Sci. Eng. 2016, 114, 012066. [Google Scholar] [CrossRef] [Green Version]
- Guyon, O.; Absi, N.; Feillet, D.; Garaix, T. A Modeling Approach for Locating Logistics Platforms for Fast Parcels Delivery in Urban Areas. Procedia-Soc. Behav. Sci. 2012, 39, 360–368. [Google Scholar] [CrossRef] [Green Version]
- Sakai, T.; Kawamura, K.; Hyodo, T. The relationship between commodity types, spatial characteristics, and distance optimality of logistics facilities. J. Transp. Land Use 2018, 11. [Google Scholar] [CrossRef] [Green Version]
- Oudouar, F.; El Fallahi, A.; Zaoui, E.M. An improved heuristic based on clustering and genetic algorithm for solving the multi-depot vehicle routing problem. Int. J. Recent Technol. Eng. 2019, 8, 6535–6540. [Google Scholar] [CrossRef]
- Mousavi Optimal Design of the Cross-docking in Distribution Networks: Heuristic Solution Approach. Int. J. Eng. 2014, 27. [CrossRef]
- Cortinhal, M.J.; Lopes, M.J.; Melo, M.T. Dynamic design and re-design of multi-echelon, multi-product logistics networks with outsourcing opportunities: A computational study. Comput. Ind. Eng. 2015, 90, 118–131. [Google Scholar] [CrossRef]
- Zhen, L.; Sun, Q.; Wang, K.; Zhang, X. Facility location and scale optimisation in closed-loop supply chain. Int. J. Prod. Res. 2019, 7567–7585. [Google Scholar] [CrossRef]
- Teye, C.; Bell, M.G.H.; Bliemer, M.C.J. Urban intermodal terminals: The entropy maximising facility location problem. Transp. Res. Part B Methodol. 2017, 100, 64–81. [Google Scholar] [CrossRef]
- Wu, T.; Xiao, F.; Zhang, C.; Zhang, D.; Liang, Z. Regression and extrapolation guided optimization for production–distribution with ship–buy–exchange options. Transp. Res. Part E Logist. Transp. Rev. 2019, 129, 15–37. [Google Scholar] [CrossRef]
- Jeet, V.; Kutanoglu, E. Part commonality effects on integrated network design and inventory models for low-demand service parts logistics systems. Int. J. Prod. Econ. 2018, 206, 46–58. [Google Scholar] [CrossRef]
- Essaadi, I.; Grabot, B.; Féniès, P. Location of global logistic hubs within Africa based on a fuzzy multi-criteria approach. Comput. Ind. Eng. 2019, 132, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Vahdani, B.; Dehbari, S.; Naderi-Beni, M.; Zeinali Kh, E. An artificial intelligence approach for fuzzy possibilistic-stochastic multi-objective logistics network design. Neural Comput. Appl. 2014, 25, 1887–1902. [Google Scholar] [CrossRef]
- Ocampo, L.A.; Himang, C.M.; Kumar, A.; Brezocnik, M. A novel multiple criteria decision-making approach based on fuzzy DEMATEL, fuzzy ANP and fuzzy AHP for mapping collection and distribution centers in reverse logistics. Adv. Prod. Eng. Manag. 2019, 14, 297–322. [Google Scholar] [CrossRef] [Green Version]
- Moreno-Camacho, C.A.; Montoya-Torres, J.R.; Jaegler, A.; Gondran, N. Sustainability metrics for real case applications of the supply chain network design problem: A systematic literature review. J. Clean. Prod. 2019, 231, 600–618. [Google Scholar] [CrossRef]
- Gonzalez-Feliu, J. Multi-stage LTL transport systems in supply chain management. In Logistics: Perspectives, Approaches and Challenges; Cheung, J., Song, H., Eds.; Nova Science Publishers: New York, NY, USA, 2013; pp. 65–86. ISBN 9781626180871. [Google Scholar]
- Ambrosino, D.; Grazia Scutellà, M. Distribution network design: New problems and related models. Eur. J. Oper. Res. 2005, 165, 610–624. [Google Scholar] [CrossRef]
- Farahani, R.Z.; Hekmatfar, M.; Fahimnia, B.; Kazemzadeh, N. Hierarchical facility location problem: Models, classifications, techniques, and applications. Comput. Ind. Eng. 2014, 68, 104–117. [Google Scholar] [CrossRef]
- Combes, F. A theoretical analysis of the cost structure of urban logistics. In Proceedings of the ILS 2016—6th International Conference on Information Systems, Logistics and Supply Chain, Bordeaux, France, 1–4 June 2016. [Google Scholar]
- Gonzalez-Feliu, J. Viability and potential demand capitation of urban freight tramway systemss via demand-supply modelling and cost benefit analysis. In Proceedings of the ILS 2016—6th International Conference on Information Systems, Logistics and Supply Chain, Bordeaux, France, 1–4 June 2016; pp. 1–9. [Google Scholar]
- Ackoff, R.L. Optimization + objectivity = optout. Eur. J. Oper. Res. 1977, 1, 1–7. [Google Scholar] [CrossRef]
- Gonzalez-Feliu, J. Logistics and Transport Modeling in Urban Goods Movement; Advances in Logistics, Operations, and Management Science; IGI Global: Hershey, PA, USA, 2019; ISBN 9781522582922. [Google Scholar] [CrossRef]
- Varela, I. Importancia de los Centros Logísticos y sus Efectos Sobre la Competitividad Territorial. Master’s Thesis, Pointificia Universidad Javeriana, Bogotá, Colombia, 2010. [Google Scholar]
- Plan De Ordenamiento Territorial. 2012, pp. 1–166. Available online: https://www.uninorte.edu.co/documents/73923/1041591/DTS_POT_2012_gral.pdf/9b0ea384-bb12-429c-a215-a43f7aafb339?version=1.0 (accessed on 22 August 2021).
- Tricoire, F.; Parragh, S.N. Investing in logistics facilities today to reduce routing emissions tomorrow. Transp. Res. Part B Methodol. 2017, 103, 56–67. [Google Scholar] [CrossRef]
- Raimbault, N. From regional planning to port regionalization and urban logistics. The inland port and the governance of logistics development in the Paris region. J. Transp. Geogr. 2019, 78, 205–213. [Google Scholar] [CrossRef]
- Sakai, T.; Kawamura, K.; Hyodo, T. Evaluation of the spatial pattern of logistics facilities using urban logistics land-use and traffic simulator. J. Transp. Geogr. 2019, 74, 145–160. [Google Scholar] [CrossRef]
- Monios, J. Identifying Governance Relationships Between Intermodal Terminals and Logistics Platforms. Transp. Rev. 2015, 35, 767–791. [Google Scholar] [CrossRef]
- Heitz, A.; Dablanc, L. Logistics Spatial Patterns in Paris. Transp. Res. Rec. J. Transp. Res. Board 2015, 2477, 76–84. [Google Scholar] [CrossRef]
- Krzysztofik, R.; Kantor-Pietraga, I.; Spórna, T.; Dragan, W.; Mihaylov, V. Beyond ‘logistics sprawl’ and ‘logistics anti-sprawl’. Case of the Katowice region, Poland. Eur. Plan. Stud. 2019, 27, 1646–1660. [Google Scholar] [CrossRef]
- Rao, W.; Jin, C. A Model of Vehicle Routing Problem Minimizing Energy Consumption in Urban Environment. In Proceedings of the 2012 Asian Conference of Management Science and Applications, Chengdu, China, 7–8 September 2012; pp. 21–29. [Google Scholar]
- Mora-Garcia, R.-T.; Marti-Ciriquian, P.; Perez-Sanchez, R.; Cespedes-Lopez, M. A comparative analysis of Manhattan, Euclidean and network distances. Why are network distances more useful to urban professionals? In Proceedings of the International Multidisciplinary Scientific GeoConference Surveying Geology and Mining Ecology Man-agement SGEM, Albena, Bulgaria, 30 June–9 July 2018. [Google Scholar] [CrossRef]
- Czyzyk, J.; Mesnier, M.P.; Moré, J.J. The NEOS Server. IEEE J. Comput. Sci. Eng. 1998, 5, 68–75. [Google Scholar] [CrossRef]






| Type of ULS | Receive from: | Send to: |
|---|---|---|
| Plants i | Transshipment | |
| Transshipment ULS j | Plant | Point of sale |
| Points of sale c | Transshipment |
| Item | Number in First Scenario | Number in Second Scenario |
|---|---|---|
| Plants | 2 | 3 |
| Transshipment ULS | 4 | 6 |
| Point of sale | 10 | 15 |
| Location zone for transshipment ULS | 3 | 3 |
| Products | 2 | 2 |
| Speed range | 2 | 2 |
| Trips/vehicle | 20 | 30 |
| Weights | First Scenario | Second Scenario | |||
|---|---|---|---|---|---|
| α | β | Cost | Gap | Cost | Gap |
| 0.90 | 0.10 | 8410.67 | 28.81% | 15,174.32 | 22.04% |
| 0.80 | 0.20 | 7143.97 | 27.52% | 15,079.73 | 26.11% |
| 0.70 | 0.30 | 7468.16 | 24.25% | 15,079.73 | 29.75% |
| 0.60 | 0.40 | 8250.76 | 26.72% | 13,653 | 31.71% |
| 0.50 | 0.50 | 7684.8 | 4% | 12,468.81 | 4% |
| 0.45 | 0.55 | 8232.75 | 4% | 12,215.5 | 4% |
| 0.40 | 0.60 | 7750.53 | 4% | 12,253.54 | 4% |
| 0.35 | 0.65 | 8250.76 | 25.36% | 13,802.88 | 33.58% |
| 0.30 | 0.70 | 7783.7 | 4% | 13,598.73 | 4% |
| 0.25 | 0.75 | 7874.24 | 4% | 13,163.2 | 4% |
| 0.20 | 0.80 | 8564.03 | 4% | 12,308.91 | 4% |
| 0.15 | 0.85 | 7755.9 | 4% | 12,578.33 | 4% |
| 0.10 | 0.90 | 8136.26 | 4% | 12,682.07 | 4% |
| 0.05 | 0.95 | 8021.24 | 4% | 13,039.1 | 4% |
| Variables | Point of Sales | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 41 | 82 | 89 | 68 | 53 | 96 | 74 | 79 | 119 | 87 | |
| 71 | 112 | 119 | 98 | 83 | 126 | 104 | 109 | 149 | 117 | |
| 71 | 112 | 119 | 98 | 83 | 126 | 104 | 109 | 149 | 117 | |
| 13 | 11 | 10 | 16 20 | 18 | 15 | 9 | 19 | 17 | 12 | |
| 59 | 62.33 | 65.83 | 68.5 55.67 | 69.5 | 65 | 57.22 | 57.78 | 62.33 | 50.44 | |
| Variables | Point of Sales | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| 82 | 94 | 64 | 116 | 49 | 33 | 37 | 63 | 112 | 85 | 101 | 59 | 59 | 95 | 88 | |
| 112 | 124 | 94 | 146 | 79 | 63 | 67 | 93 | 142 | 115 | 131 | 89 | 59 | 125 | 118 | |
| 112 | 124 | 94 | 146 | 79 | 63 | 67 | 93 | 142 | 115 | 131 | 89 | 89 | 125 | 118 | |
| 28 | 26 | 18 | 9 20 | 29 | 19 | 30 | 27 | 10 | 13 | 24 | 15 | 23 | 11 | 25 8 | |
| 59.44 | 63 | 65.83 | 68.5 55.67 | 56.78 | 65 | 57.22 | 57.78 | 68.33 | 60.67 | 67.33 | 53.44 | 57.89 | 69.67 | 59.78 59.78 | |
| Vehicle Type | Preparation Costs (COP$) | Fuel Costs (COP$/km) | Load Capacity (Units) |
|---|---|---|---|
| 35 Ton | 215,730 | 1058.292 | 1410 |
| 32 Ton | 215,730 | 857.773 | 1410 |
| 20 Ton | 135,405 | 679.071 | 885 |
| 8 Ton | 120,105 | 417.889 | 785 |
| 4 Ton | 62,530 | 626.834 | 412 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruiz-Meza, J.; Meza-Peralta, K.; Montoya-Torres, J.R.; Gonzalez-Feliu, J. Location of Urban Logistics Spaces (ULS) for Two-Echelon Distribution Systems. Axioms 2021, 10, 214. https://doi.org/10.3390/axioms10030214
Ruiz-Meza J, Meza-Peralta K, Montoya-Torres JR, Gonzalez-Feliu J. Location of Urban Logistics Spaces (ULS) for Two-Echelon Distribution Systems. Axioms. 2021; 10(3):214. https://doi.org/10.3390/axioms10030214
Chicago/Turabian StyleRuiz-Meza, José, Karen Meza-Peralta, Jairo R. Montoya-Torres, and Jesus Gonzalez-Feliu. 2021. "Location of Urban Logistics Spaces (ULS) for Two-Echelon Distribution Systems" Axioms 10, no. 3: 214. https://doi.org/10.3390/axioms10030214
APA StyleRuiz-Meza, J., Meza-Peralta, K., Montoya-Torres, J. R., & Gonzalez-Feliu, J. (2021). Location of Urban Logistics Spaces (ULS) for Two-Echelon Distribution Systems. Axioms, 10(3), 214. https://doi.org/10.3390/axioms10030214









