Semilocal Convergence of the Extension of Chun’s Method
Abstract
1. Introduction
2. Recurrence Relations
- (C1)
- ,
- (C2)
- ,
- (C3)
- ,
Preliminary Results
- (In)
- ,
- (IIn)
- ,
- (IIIn)
- ,
- (IVn)
- .
- (II1):
- By means of the Taylor’s expansion of around , we get
- (III1):
- using () and (),
- (IV1):
- for it has been proven in (9).
3. Convergence Analysis
- (i)
- is increasing and for ,
- (ii)
- and are increasing for .
- (i)
- for ,
- (ii)
- for ,
- (iii)
- the sequence is decreasing and for
4. Numerical Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ortega, J.M.; Rheinboldt, W.C. Iterative Solution of Nonlinear Equations in Several Variables; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Petković, M.S.; Neta, B.; Petković, L.D.; DŽunić, J. Multipoint Methods for Solving Nonlinear Equations; Academic Press: New York, NY, USA, 2012. [Google Scholar]
- Amat, S.; Busquier, S. Advances in Iterative Methods for Nonlinear Equations; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Ezquerro, J.A.; Grau-Sánchez, M.; Hernández, M.A.; Noguera, M. A study of optimization for Steffensen-type methods with frozen divided differences. SeMA 2015, 70, 23–46. [Google Scholar] [CrossRef]
- Hernández-Verón, M.A.; Martínez, E.; Teruel, C. Semilocal convergence of a k-step iterative process and its application for solving a special kind of conservative problems. Numer. Algor. 2017, 6, 309–331. [Google Scholar] [CrossRef]
- Hernández, M.A.; Rubio, M.J. On the local convergence of a Newton-Kurchatov-type method for non-differentiable operators. Appl. Math. Comput. 2017, 304, 1–9. [Google Scholar] [CrossRef]
- Argyros, I.K. A new convergence theorem for Steffensen’s method on Banach spaces and applications. Southwest Pure Appl. Math. 1997, 1, 23–29. [Google Scholar]
- Alarcón, V.; Amat, S.; Busquier, S.; López, D.J. A Steffensen’s type method in Banach spaces with applications on boundary-value problems. Comput. Appl. Math. 2008, 216, 243–250. [Google Scholar] [CrossRef]
- Amat, S.; Busquier, S. A two-step Steffensen’s method under modified convergence conditions. Math. Anal. Appl. 2006, 324, 1084–1092. [Google Scholar] [CrossRef][Green Version]
- Amat, S.; Busquier, S. On a Steffensen’s type method and its behavior for semismooth equations. Appl. Math. Comput. 2006, 177, 819–823. [Google Scholar] [CrossRef]
- Potra, F.A. On a modified Secant method. Anal. Number. Theor. Approx. 1979, 8, 203–214. [Google Scholar]
- Potra, F.A.; Ptak, V. Nondiscrete Induction and Iterative Processes; Research Notes in Mathematics 103; Pitman: Boston, MA, USA, 1984. [Google Scholar]
- Argyros, I.K.; Cordero, A.; Magreñán, Á.A.; Torregrosa, J.R. On the convergence of a damped Secant-like method with modified right hand side vector. Appl. Math. Comput. 2015, 252, 315–323. [Google Scholar]
- Balazs, M.; Goldner, G. On existence of divided differences in linear spaces. Rev. Anal. Numer. Theor. Approx. 1973, 2, 3–6. [Google Scholar]
- Grau-Sánchez, M.; Noguera, M.; Amat, S. On the approximation of derivatives using divided difference operators preserving the local convergence order of iterative methods. J. Comput. Appl. Math. 2013, 237, 363–372. [Google Scholar] [CrossRef]
- Dehghan, M.; Hajarian, M. Some derivative free quadratic and cubic convergence iterative formulas for solving nonlinear equations. Comput. Appl. Math. 2010, 29, 19–30. [Google Scholar] [CrossRef]
- Cordero, A.; García-Maimó, J.; Torregrosa, J.R.; Vassileva, M.P. Solving nonlinear problems by Ostrowski-Chun type parametric families. J. Math. Chem. 2015, 53, 430–449. [Google Scholar] [CrossRef]
- Abad, M.F.; Cordero, A.; Torregrosa, J.R. A family of seventh-order schemes for solving nonlinear systems. Bull. Math. Soc. Sci. Math. Roum. 2014, 57, 133–145. [Google Scholar]
- Candela, V.; Marquina, A. Recurrence relations for rational cubic models I: The Halley method. Computing 1990, 44, 169–184. [Google Scholar] [CrossRef]
- Candela, V.; Marquina, A. Recurrence relations for rational cubic models II: The Chebyshev method. Computing 1990, 45, 355–367. [Google Scholar] [CrossRef]
- Ezquerro, J.A.; Hernández, M.A. Generalized differentiability conditions for Newton’s method. IMA Numer. Anal. 2002, 22, 187–205. [Google Scholar] [CrossRef]
- Ezquerro, J.A.; Hernández, M.A. Halley’s method for operators with unbounded second derivative. Appl. Numer. Math. 2007, 57, 354–360. [Google Scholar] [CrossRef]
- Ezquerro, J.A.; Hernández, M.A. An optimization of Chebyshev’s method. Complexity 2009, 25, 343–361. [Google Scholar] [CrossRef]
- Cordero, A.; Hernández-Verón, M.A.; Romero, N.; Torregrosa, J.R. Semilocal convergence by using recurrence relations for a fifth-order method in Banach spaces. Comput. Appl. Math. 2015, 273, 205–213. [Google Scholar] [CrossRef]
- Hu, S.; Khavanin, M.; Zhuang, W. Integral equations arising in the kinetic theory of gases. Appl. Anal. 1989, 34, 261–266. [Google Scholar] [CrossRef]
- Maleknejad, K.; Torabi, P. Application of fixed point method for solving nonlinear Volterra-Hammerstein Integral Equation. Univ. Politeh. Buchar. Sci. Bull. Ser. A 2012, 74, 45–56. [Google Scholar]
- Cordero, A.; Torregrosa, J.R. Variants of Newton’s method using fifth-order quadrature formulas. Appl. Math. Comput. 2007, 190, 686–698. [Google Scholar] [CrossRef]
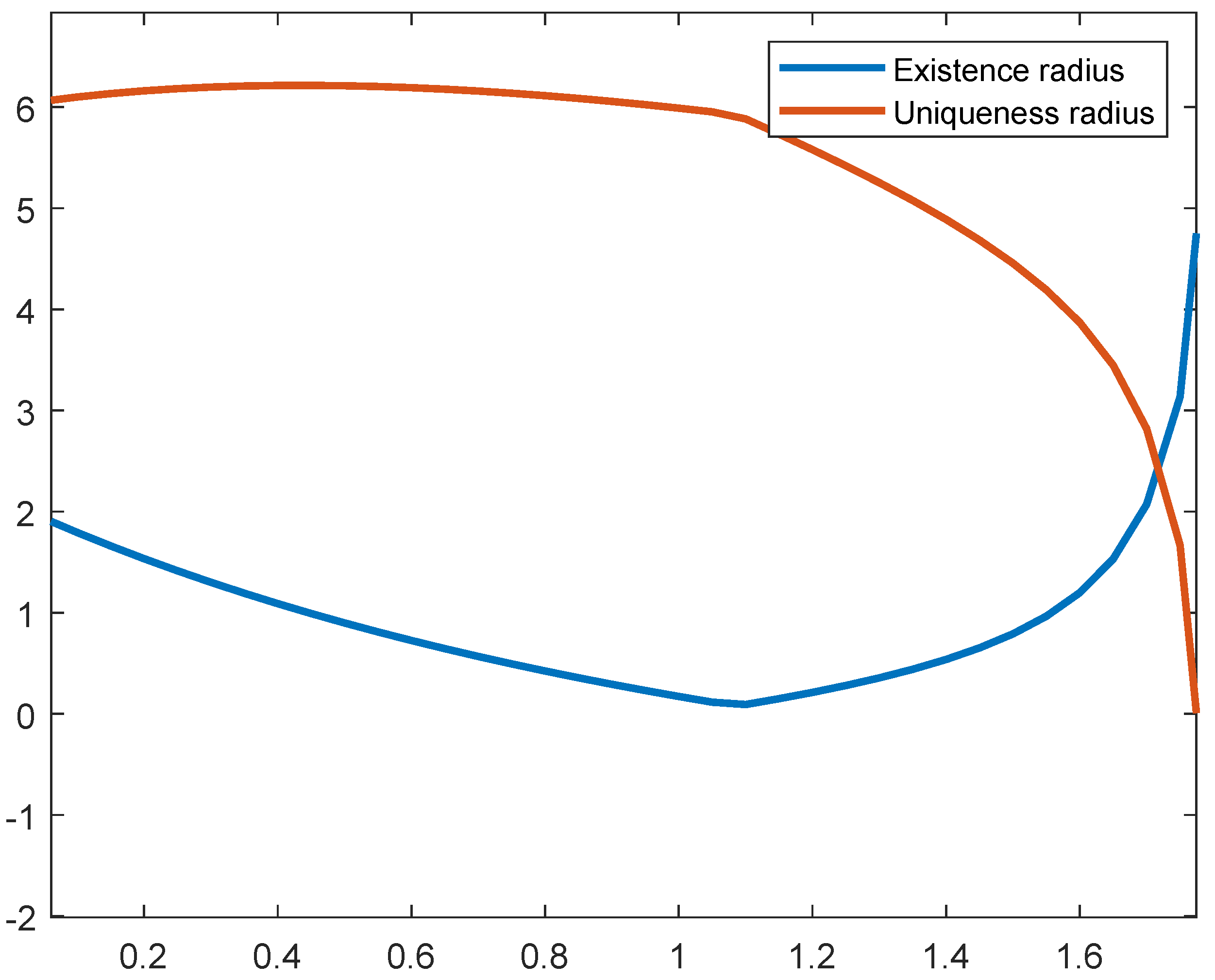
| 0 | 1.0000 | 1.0000 | 0.2471 | 2.0825 | 6.0108 |
| 0.2 | 1.0516 | 0.8465 | 0.2200 | 1.5346 | 6.1614 |
| 0.4 | 1.1080 | 0.6864 | 0.1879 | 1.0901 | 6.2142 |
| 0.6 | 1.1699 | 0.5189 | 0.1500 | 0.7256 | 6.1925 |
| 0.8 | 1.2380 | 0.3428 | 0.1049 | 0.4238 | 6.1134 |
| 1.0 | 1.3134 | 0.1567 | 0.0509 | 0.1720 | 5.9899 |
| 1.2 | 1.3973 | 0.1879 | 0.0649 | 0.2123 | 5.5796 |
| 1.4 | 1.4912 | 0.3889 | 0.1433 | 0.5380 | 4.8892 |
| 1.6 | 1.5969 | 0.5911 | 0.2333 | 1.1986 | 3.8694 |
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 1.0122… | 1.0584… | 1.1181… | 1.1598… | 1.1598… | 1.1181… | 1.0584… | 1.0122… |
| iter | ||||
|---|---|---|---|---|
| 0.2 | 5 | 4.0 | ||
| 0.4 | 5 | 4.0 | ||
| 0.6 | 5 | 4.0 | ||
| 0.8 | 5 | 4.0 | ||
| 1.0 | 5 | 4.0 | ||
| 1.2 | 5 | 4.0 | ||
| 1.4 | 5 | 4.0 | ||
| 1.6 | 5 | 4.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cordero, A.; Maimó, J.G.; Martínez, E.; Torregrosa, J.R.; Vassileva, M.P. Semilocal Convergence of the Extension of Chun’s Method. Axioms 2021, 10, 161. https://doi.org/10.3390/axioms10030161
Cordero A, Maimó JG, Martínez E, Torregrosa JR, Vassileva MP. Semilocal Convergence of the Extension of Chun’s Method. Axioms. 2021; 10(3):161. https://doi.org/10.3390/axioms10030161
Chicago/Turabian StyleCordero, Alicia, Javier G. Maimó, Eulalia Martínez, Juan R. Torregrosa, and María P. Vassileva. 2021. "Semilocal Convergence of the Extension of Chun’s Method" Axioms 10, no. 3: 161. https://doi.org/10.3390/axioms10030161
APA StyleCordero, A., Maimó, J. G., Martínez, E., Torregrosa, J. R., & Vassileva, M. P. (2021). Semilocal Convergence of the Extension of Chun’s Method. Axioms, 10(3), 161. https://doi.org/10.3390/axioms10030161








