L-Fuzzy Rough Approximation Operators Based on Co-Implication and Their (Single) Axiomatic Characterizations

Abstract

For L a complete co-residuated lattice and R an L-fuzzy relation, an L-fuzzy upper approximation operator based on co-implication adjoint with L is constructed and discussed. It is proved that, when L is regular, the new approximation operator is the dual operator of the Qiao–Hu L-fuzzy lower approximation operator defined in 2018. Then, the new approximation operator is characterized by using an axiom set (in particular, by single axiom). Furthermore, the L-fuzzy upper approximation operators generated by serial, symmetric, reflexive, mediate, transitive, and Euclidean L-fuzzy relations and their compositions are characterize through axiom set (single axiom), respectively.

1. Introduction

The theory of rough sets [1,2] is an effective mathematical tool to handle uncertainty. Nowadays, many kinds of generalized rough sets have been developed [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17], and some of them have been successfully applied in many areas including approximate classification, machine learning, conflict analysis, pattern recognition, data mining, and automated knowledge acquisition [2,8,13,14,18,19,20,21,22]. The theoretical core of generalized rough sets is a pair of approximate operators. There are usually two approaches to study these approximate operators: constructive approach and axiomatic approach. The constructive approach is to construct the approximation operators from binary relations, coverings, neighborhoods, and other structures [3,4,5,6,7,9,11,13,14]; the axiomatic approach is to find the axiom (set) for a given operator such that the operator is precisely an approximation operator defined through the constructive approach [10,15,16,17].

Fuzzy rough sets are important generalized rough sets. The constructive and axiomatic approach are also extensively used in the study of fuzzy rough sets (see [20,21,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47]). In recent years, complete residuated (respectively, co-residuated) lattice-valued fuzzy rough sets (L-fuzzy rough sets for short) have attracted much attention for their extreme universality and strongly logical background—complete (co-)residuated lattice includes left (right) continuous triangular (co-)norm as a special case and can be regarded as a truth table of generalized multi-valued logic. In the following, we list some work on this regard.

⋄

Let $L=(L,\ast ,\to )$ be a complete residuated lattice. Based on L-fuzzy relations, Radzikowska [40] defined an L-fuzzy upper (respectively, lower) approximation operator by using ∗ (respectively, →). Then, She [41] characterized these approximation operators by an axiomatic set. Bao [24] and Wang [42] further characterized them by single axiom. Wang [48] gave a comparative study on variable precision L-fuzzy rough sets. Based on L-fuzzy coverings, Li [49] defined and characterized four L-fuzzy approximation operators. Based on L-fuzzy neighborhood systems, Zhao [45,46,47] proposed a pair of L-fuzzy approximation operators and discussed their axiomatic characterizations and the generated L-fuzzy topology. Song [50] studied the lattice structure induced by the approximation operators.

⋄

Let $L=(L,\odot ,⇝)$ be a complete co-residuated lattice. Based on L-fuzzy relations, Qiao [38] defined and characterized an L-fuzzy lower approximation operator by using ⊙. He [37] also introduced a granular variable precision L-fuzzy upper approximation operator by using ⊙. Based on distance functions, Oh [51] investigated an L-fuzzy upper approximation operator and discussed the related L-fuzzy topology.

It is well known that fuzzy rough sets based on triangle norm and those based on triangle conorm can be studied dually [32,52,53]. The cases for fuzzy rough sets based on complete (co-)residuated lattice should be similar. As mentioned above, the research on fuzzy rough sets based on complete residuated lattice is much more abundant than that on complete co-residuated lattice. Therefore, fuzzy rough sets based on complete co-residuated lattice should be further studied. Particularly, note that, in the definition of L-fuzzy approximation operators, the co-implication ⇝ is not used. The main aim of this paper is to investigate an L-fuzzy approximation operator based on ⇝ from both constructive and axiomatic approaches.

The contents are arranged as follows. In Section 2, we recall some basic concepts as preliminary. In Section 3, we investigate an L-fuzzy upper approximation operator based on co-implication ⇝ from a constructive approach. We verify that, when L is regular, the proposed L-fuzzy upper approximation operator is the dual operator of the Qiao–Hu L-fuzzy lower approximation operator defined in 2018. We further discuss the L-fuzzy upper approximation operators generated by serial, symmetric, reflexive, mediate, transitive, and Euclidean L-fuzzy relations and their compositions. In Section 4 and Section 5, we characterize the mentioned L-fuzzy upper approximation operators by axiomatic set and single axiom, respectively. In Section 5, we make a conclusion.

2. Preliminaries

A complete co-residuated lattice [38,54] is an algebra $(L,\bigwedge ,\bigvee ,\odot ,0,1)$ that fulfills:

(i) $(L,\bigwedge ,\bigvee ,0,1)$ is a complete lattice with the bottom (respectively, top) element 0 (respectively, 1).

(ii) $(L,\odot ,0)$ is a commutative monoid with 0 as the unit element.

(iii) ⊙ distributes over arbitrary meets, i.e., $\forall a,a_j(j\in J)\in L$, $a\odot {\displaystyle \underset{j\in J}{\bigwedge }}{a}_j={\displaystyle \underset{j\in J}{\bigwedge }}(a\odot a_j)$.

The function $\to :L\times L⟶L$ determined by

$$a⇝b=\bigwedge \{c\in L|a\odot c\ge b\}$$

is called the co-implication of ⊙.

Complete co-residuated lattice is the extension of right continuous triangle co-norm [55]; for more examples, please see the work of Oh-Kim [51].

Proposition 1.

(Qiao–Hu [37] [Proposition 2.1]) Let L be a complete co-residuated lattice.

(1) $b\le a\odot c\iff a⇝b\le c$.

(2) $0⇝a=a$.

(3) $a\ge b⇝a$.

(4) $a\ge b\iff a⇝b=0$, especially $a⇝a=0$.

(5) $a⇝(b⇝c)=b⇝(a⇝c)=(a\odot b)⇝c$.

(6) $a\odot (a⇝b)\ge b$.

(7) $(a⇝b)\odot (b⇝c)\ge a⇝c$.

(8) $a\odot (b⇝c)\ge b⇝(a\odot c)$.

(9) $a⇝{\displaystyle \underset{j\in J}{\bigvee }}{b}_j={\displaystyle \underset{j\in J}{\bigvee }}(a⇝b_j)$.

(10) $({\displaystyle \underset{j\in J}{\bigwedge }}{b}_j)⇝a={\displaystyle \underset{j\in J}{\bigvee }}(a⇝b_j)$.

(11) $a⇝b={\displaystyle \underset{c\in L}{\bigvee }}(c⇝a)⇝(c⇝b)={\displaystyle \underset{c\in L}{\bigvee }}(b⇝c)⇝(a⇝c)$.

L is said to be regular whenever $\forall a\in L$, $(a⇝1)⇝1=a$.

A function $\mathcal{N}:L⟶L$ is said to be an involutive negation if it is decreasing and fulfills $\forall a\in L$, $\mathcal{N}\left(\mathcal{N}\right(a\left)\right)=a$. If $\mathcal{N}:L⟶L$ is an involutive negation, then the following De Morgan laws hold: $\forall a_j(j\in J)\in L$,

$$\mathcal{N}\left(\underset{j\in J}{\bigvee }{a}_j\right)=\underset{j\in J}{\bigwedge }\mathcal{N}\left(a_j\right),\mathcal{N}\left(\underset{j\in J}{\bigwedge }{a}_j\right)=\underset{j\in J}{\bigvee }\mathcal{N}\left(a_j\right).$$

For a nonempty set U, a function $A:U⟶L$ is called an L-fuzzy set on U. All L-fuzzy sets on U are denoted by $L^U$. For $a\in L$, we also use a to denote the constant value L-fuzzy set values a. For $A\subseteq U$, we use $1_A$ to denote the L-fuzzy set values 1 at A and 0 otherwise; when $A=\left\{x\right\}$, we simplify $1_{\left\{x\right\}}$ as $1_x$.

For $A_j(j\in J)\in L^U$, $A\in L^U$ and $a\in L$, the L-fuzzy sets ${\displaystyle \underset{j\in J}{\bigvee }}{A}_j,{\displaystyle \underset{j\in J}{\bigwedge }}{A}_j,a\odot A,a⇝A,NA$ are defined pointwise.

Definition 1.

(Qiao–Hu [38]) Let $U,V$ be nonempty sets. An L-fuzzy set $\mathfrak{R}:U\times V⟶L$ is called an L-fuzzy relation from U to V, and the triple $(U,V,\mathfrak{R})$ is called an L-fuzzy approximation space (L-FAS for short). When $U=V$, $\mathfrak{R}$ is called an L-fuzzy relation on U and $(U,V,\mathfrak{R})$ is simplified as $(U,\mathfrak{R})$.

Definition 2.

(Qiao–Hu [38]) Let $(U,V,\mathfrak{R})$ be an L-FAS.

(1) $\mathfrak{R}$ is called serial ((SR) for short) if $\forall x\in U$, ${\displaystyle \underset{y\in V}{\bigvee }}\mathfrak{R}(x,y)=1$.

Furthermore, let $U=V$.

(2) $\mathfrak{R}$ is called symmetric ((SY) for short) provided $\forall x,y\in U$, $\mathfrak{R}(x,y)=\mathfrak{R}(y,x)$.

(3) $\mathfrak{R}$ is called reflexive ((RF) for short) provided $\forall x\in X$, $\mathfrak{R}(x,x)=1$.

Definition 3.

Let $(U,\mathfrak{R})$ be an L-FAS.

(1) $\mathfrak{R}$ is called transitive ((TR) for short) provided $\forall x,y,z\in U$, $\mathcal{N}\mathfrak{R}(x,y)\odot \mathcal{N}\mathfrak{R}(y,z)\ge \mathcal{N}\mathfrak{R}(x,z)$.

(2) $\mathfrak{R}$ is called mediate ((ME) for short) provided $\forall x,z\in U$, ${\displaystyle \underset{y\in U}{\bigwedge }}\left[\mathcal{N}\mathfrak{R}(x,y)\odot \mathcal{N}\mathfrak{R}(y,z)\right]\le \mathcal{N}\mathfrak{R}(x,z)$.

(3) $\mathfrak{R}$ is called Euclidean ((EU) for short) provided $\forall x,y,z\in U$, $\mathcal{N}\mathfrak{R}(x,y)\odot \mathcal{N}\mathfrak{R}(x,z)\ge \mathcal{N}\mathfrak{R}(y,z)$.

(4) $\mathfrak{R}$ is called similar provided it is reflexive and symmetric.

(5) $\mathfrak{R}$ is called an L-fuzzy preorder provided it is reflexive and transitive.

(6) $\mathfrak{R}$ is called equivalent provided it is reflexive, symmetric and transitive.

It is not difficult to see that $\mathfrak{R}$ being reflexive implies that $\mathfrak{R}$ is mediate.

Remark 1.

Let $\odot =\vee$.

(1) $\mathfrak{R}$ is transitive iff $\forall x,y,z\in U$, $\mathfrak{R}(x,y)\wedge \mathfrak{R}(y,z)\le \mathfrak{R}(x,z)$, a well-known definition.

(2) $\mathfrak{R}$ is mediate iff $\forall x,z\in U$, ${\displaystyle \underset{y\in U}{\bigvee }}\left[\mathfrak{R}(x,y)\wedge \mathfrak{R}(y,z)\right]\ge \mathfrak{R}(x,z)$, i.e., $\mathfrak{R}$ is mediate in the sense of Pang [35] ([Definition 3.6]).

(3) $\mathfrak{R}$ is Euclidean iff $\forall x,y,z\in U$, $\mathfrak{R}(x,y)\wedge \mathfrak{R}(x,z)\le \mathfrak{R}(y,z)$, a well-known definition.

In [38], Qiao and Hu defined an L-fuzzy rough lower approximation operator via ⊙.

Let $(U,V,\mathfrak{R})$ be an L-FAS. Then, the function $\underline{\mathfrak{R}}:L^V⟶L^U$ defined by: $\forall A\in L^V,\forall x\in U$,

$$\underline{\mathfrak{R}}\left(A\right)\left(x\right)=\underset{y\in V}{\bigwedge }\left(\mathcal{N}\mathfrak{R}(x,y)\odot A\left(y\right)\right),$$

is said to be an L-fuzzy lower approximation operator of $(U,V,\mathfrak{R})$.

3. $\mathit{L}$-Fuzzy Upper Approximation Operator via ⇝: The Constructive Approach

In this section, we introduce an L-fuzzy upper approximation operator via ⇝, and prove that operator is the dual operator of the Qiao–Hu L-fuzzy lower approximation operator when L is regular. We further study the L-fuzzy upper approximation operators associated with serial, symmetric, reflexive, mediate, transitive, and Euclidean L-fuzzy relations.

Definition 4.

Let $(U,V,\mathfrak{R})$ be an L-FAS. Then, the function $\underline{\mathfrak{R}}:L^V⟶L^U$ determined by

$$\forall A\in L^V,\forall x\in U,\overline{\mathfrak{R}}\left(A\right)\left(x\right)=\underset{y\in V}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,y)⇝A\left(y\right)\right),$$

is said to be an L-fuzzy upper approximation operator of $(U,V,\mathfrak{R})$. The pair $(\underline{\mathfrak{R}}\left(A\right),\overline{\mathfrak{R}}\left(A\right))$ is said to be L-fuzzy $(\odot ,⇝)$-rough set of A.

At first, we show that our operator and the Qiao–Hu operator satisfy the following dual theorem.

Theorem 1.

Let $(U,V,\mathfrak{R})$ be an L-FAS. If L is regular and $\mathcal{N}\left(a\right)=a⇝1$, then $\forall A\in L^V$,

$$\overline{\mathfrak{R}}\left(A\right)=\mathcal{N}\underline{\mathfrak{R}}\left(\mathcal{N}A\right),\underline{\mathfrak{R}}\left(A\right)=\mathcal{N}\overline{\mathfrak{R}}\left(\mathcal{N}A\right).$$

Proof. 

For any $A\in L^V$ and $x\in U$,

$$\begin{array}{ccc}\hfill \mathcal{N}\underline{\mathfrak{R}}\left(\mathcal{N}A\right)\left(x\right)& =& \mathcal{N}\left[\underset{z\in V}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,z)\odot \mathcal{N}A\left(z\right)\right)\right]=\underset{z\in V}{\bigwedge }\left[\left(\mathcal{N}\mathfrak{R}(x,z)\odot \mathcal{N}A\left(z\right)\right)⇝1\right]\hfill \\ & =& \underset{z\in V}{\bigwedge }\left[\mathcal{N}\mathfrak{R}(x,z)⇝\left(\left(A\right(z)⇝1)⇝1\right)\right]\hfill \\ & =& \underset{z\in V}{\bigwedge }\left[\mathcal{N}\mathfrak{R}(x,z)⇝A\left(z\right)\right]=\overline{\mathfrak{R}}\left(A\right)\left(x\right).\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \mathcal{N}\overline{\mathfrak{R}}\left(\mathcal{N}A\right)\left(x\right)& =& \mathcal{N}\left[\underset{z\in V}{\bigwedge }\left(\mathcal{N}\mathfrak{R}(x,z)⇝\mathcal{N}A\left(z\right)\right)\right]=\underset{z\in V}{\bigvee }\left[\left(\mathcal{N}\mathfrak{R}(x,z)⇝\left(A\right(z)⇝1)\right)⇝1\right]\hfill \\ & =& \underset{z\in V}{\bigvee }\left[\left(\left(\mathcal{N}\mathfrak{R}\right(x,z)\odot A(z\left)\right)⇝1\right)⇝1\right]\hfill \\ & =& \underset{z\in V}{\bigvee }\left[\mathcal{N}\mathfrak{R}(x,z)\odot A\left(z\right)\right]=\underline{\mathfrak{R}}\left(A\right)\left(x\right).\hfill \end{array}$$

□

Example 1.

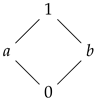Let L be the complete lattice defined by and$\odot =\vee$. It is easily seen that$L=(L,\bigwedge ,\bigvee ,\odot ,0,1)$forms a complete co-residuated lattice and

⇝	0	a	b	1
0	0	a	b	1
a	0	0	b	b
b	0	a	0	a
1	0	0	0	0

Put $\mathcal{N}\left(0\right)=1,\mathcal{N}\left(1\right)=0,\mathcal{N}\left(a\right)=b,\mathcal{N}\left(b\right)=a$, and then $\mathcal{N}$ is an involutive negation.

Let $U=\{x,y\}$ and $\mathfrak{R}$ be the L-fuzzy relation defined by

Take $A=\frac{a}{x}+\frac{b}{y}$; then,

$\mathfrak{R}$	x	y
x	1	a
y	0	a

	x	y
$\underline{\mathfrak{R}}\left(A\right)$	0	b
$\overline{\mathfrak{R}}\left(A\right)$	a	0

The next proposition collects the basic properties of L-fuzzy upper approximation operator.

Proposition 2.

Let $(U,V,\mathfrak{R})$ be an L-FAS and $A,B,A_t(t\in T)\in L^V$.

(1) If $A\le B$, then $\overline{\mathfrak{R}}\left(A\right)\le \overline{\mathfrak{R}}\left(B\right)$.

(2) $\overline{\mathfrak{R}}\left(0\right)=0$.

(3) $\forall x\in U,y\in V$, $\overline{\mathfrak{R}}\left(1_y\right)\left(x\right)=\mathcal{N}\mathfrak{R}(x,y)⇝1$.

(4) $\forall a\in L$, $\overline{\mathfrak{R}}\left(a\right)\le a$ and $\overline{\mathfrak{R}}(1_{V-\left\{y\right\}}⇝a)\left(x\right)=\mathcal{N}\mathfrak{R}(x,y)⇝a$.

(5) $\forall A,B,A_t(t\in T)\in L^V$, $\overline{\mathfrak{R}}\left({\displaystyle \underset{t\in T}{\bigvee }}{A}_t\right)={\displaystyle \underset{t\in T}{\bigvee }}\overline{\mathfrak{R}}\left(A_t\right)$.

(6) $\forall a\in L,A\in L^V$, $\overline{\mathfrak{R}}(a⇝A)=a⇝\overline{\mathfrak{R}}\left(A\right)$.

Proof. 

(1) It is obvious.

(2) For any $x\in U$, $\overline{\mathfrak{R}}\left(0\right)\left(x\right)={\displaystyle \underset{y\in V}{\bigvee }}(\mathcal{N}\mathfrak{R}(x,y)⇝0)=0.$

(3) For any $x\in U,y\in V$,

$$\begin{array}{ccc}\hfill \overline{\mathfrak{R}}\left(1_y\right)\left(x\right)& =& \underset{z\in V}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,z)⇝1_y\left(z\right)\right)\hfill \\ & =& \underset{z\ne y}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,z)⇝0\right)\vee \left(\mathcal{N}\mathfrak{R}(x,y)⇝1\right),\mathrm{by}\mathcal{N}\mathfrak{R}(x,z)\ge 0\hfill \\ & =& 0\vee \left(\mathcal{N}\mathfrak{R}(x,y)⇝1\right)=\mathcal{N}\mathfrak{R}(x,y)⇝1.\hfill \end{array}$$

(4) For any $x\in U$,

$$\overline{\mathfrak{R}}\left(a\right)\left(x\right)=\underset{y\in V}{\bigvee }(\mathcal{N}\mathfrak{R}(x,y)⇝a)\le \underset{y\in V}{\bigvee }(0⇝a)=a.$$

$$\begin{array}{ccc}\hfill \overline{\mathfrak{R}}(1_{V-\left\{y\right\}}⇝a)\left(x\right)& =& \underset{z\in V}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,z)⇝(1_{V-\left\{y\right\}}\left(z\right)⇝a)\right)\hfill \\ & =& \underset{z\ne y}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,z)⇝(1⇝a)\right)\vee \left(\mathcal{N}\mathfrak{R}(x,y)⇝(0⇝a)\right)\hfill \\ & =& \underset{z\ne y}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,z)⇝0\right)\vee \left(\mathcal{N}\mathfrak{R}(x,y)⇝a\right)\hfill \\ & =& 0\vee \left(\mathcal{N}\mathfrak{R}(x,y)⇝a\right)=\mathcal{N}\mathfrak{R}(x,y)⇝a.\hfill \end{array}$$

(5) For any $x\in U$,

$$\overline{\mathfrak{R}}(\underset{t\in T}{\bigvee }{A}_t)\left(x\right)=\underset{y\in V}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,y)⇝\underset{t\in T}{\bigvee }{A}_t\left(y\right)\right)=\underset{y\in V}{\bigvee }\underset{t\in T}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,y)⇝A_t\left(y\right)\right)=\underset{t\in T}{\bigvee }\overline{\mathfrak{R}}\left(A_t\right)\left(x\right).$$

(6) For any $x\in U$,

$$\begin{array}{ccc}\hfill \overline{\mathfrak{R}}(a⇝A)\left(x\right)& =& \underset{y\in V}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,y)⇝[a⇝A(x\left)\right]\right)\hfill \\ & =& \underset{y\in V}{\bigvee }\left(a⇝\left[\mathcal{N}\mathfrak{R}\right(x,y)⇝A(x\left)\right]\right)\hfill \\ & =& a⇝\underset{y\in V}{\bigvee }\left(\left[\mathcal{N}\mathfrak{R}\right(x,y)⇝A(x\left)\right]\right)\hfill \\ & =& a⇝\overline{\mathfrak{R}}A\left(x\right).\hfill \end{array}$$

□

The next proposition shows that L-fuzzy relations and L-fuzzy upper approximation operators are determined uniquely from each other.

Proposition 3.

$\forall \mathfrak{R},\mathfrak{S}\in L^{U\times V}$, $\mathfrak{R}\le \mathfrak{S}$ iff $\overline{\mathfrak{R}}\le \overline{\mathfrak{S}}$. Hence, $\mathfrak{R}=\mathfrak{S}$ iff $\overline{\mathfrak{R}}=\overline{\mathfrak{S}}$.

Proof. 

⟹. It is obvious.

⟸. Let $\overline{\mathfrak{R}}\le \overline{\mathfrak{S}}$. For any $x\in U,y\in V$, it follows by Proposition 2 (4) that $\forall a\in L$

$$\mathcal{N}\mathfrak{R}(x,y)⇝a=\overline{\mathfrak{R}}(1_{V-\left\{y\right\}}⇝a)\left(x\right)\le \overline{\mathfrak{S}}(1_{V-\left\{y\right\}}⇝a)\left(x\right)=\mathcal{N}\mathfrak{S}(x,y)⇝a.$$

Taking $a=\mathcal{N}\mathfrak{S}(x,y)$, we obtain $0=\mathcal{N}\mathfrak{R}(x,y)⇝\mathcal{N}\mathfrak{S}(x,y)$, i.e., $\mathcal{N}\mathfrak{R}(x,y)\ge \mathcal{N}\mathfrak{S}(x,y)$, and thus $\mathfrak{R}(x,y)\le \mathfrak{S}(x,y)$ since $\mathcal{N}$ is involutive. Hence, $\mathfrak{R}\le \mathfrak{S}$. □

In the following, we consider the L-fuzzy upper approximation operators generated by serial, symmetric, reflexive, mediate, transitive, and Euclidean L-fuzzy relations, respectively.

Proposition 4.

Let $(U,V,\mathfrak{R})$ be an L-FAS. Then, $\mathfrak{R}$ is serial iff $\forall a\in L$, $\overline{\mathfrak{R}}\left(a\right)=a$.

Proof. 

⟹. For any $x\in U$,

$$\overline{\mathfrak{R}}\left(a\right)\left(x\right)=\underset{y\in V}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,y)⇝a\right)=\mathcal{N}\left(\underset{y\in V}{\bigvee }\mathfrak{R}(x,y)\right)⇝a\stackrel{\left(SR\right)}{=}\mathcal{N}\left(1\right)⇝a=0⇝a=a.$$

⟸. For any $x\in U$, it follows by $\overline{\mathfrak{R}}\left(a\right)=a$ that we have

$$a=\overline{\mathfrak{R}}\left(a\right)\left(x\right)=\underset{y\in V}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,y)⇝a\right)=\mathcal{N}\left(\underset{y\in V}{\bigvee }\mathfrak{R}(x,y)\right)⇝a,$$

take $a=\mathcal{N}\left({\displaystyle \underset{y\in V}{\bigvee }}\mathfrak{R}(x,y)\right)$, then

$$\mathcal{N}\left(\underset{y\in V}{\bigvee }\mathfrak{R}(x,y)\right)=a⇝a=0,$$

i.e., ${\displaystyle \underset{y\in V}{\bigvee }}\mathfrak{R}(x,y)=1$, so $\mathfrak{R}$ is serial. □

Proposition 5.

Let $(U,\mathfrak{R})$ be an L-FAS. Then, $\mathfrak{R}$ is symmetric iff $\overline{\mathfrak{R}}(1_{U-\left\{y\right\}}⇝a)\left(x\right)=\overline{\mathfrak{R}}(1_{U-\left\{x\right\}}⇝a)\left(y\right),\forall x,y\in U,\forall a\in L$.

Proof. 

⟹. For any $x,y\in U,a\in L$,

$$\begin{array}{ccc}\hfill \overline{\mathfrak{R}}(1_{X-\left\{y\right\}}⇝a)\left(x\right)& =& \underset{z\in V}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,z)⇝[1_{X-\left\{y\right\}}\left(z\right)⇝a]\right)\hfill \\ & =& \left[\underset{z\ne y}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,z)⇝(1⇝a)\right)\right]\vee \left[\mathcal{N}\mathfrak{R}(x,y)⇝(0⇝a)\right]\hfill \\ & =& 0\vee \left[\mathcal{N}\mathfrak{R}(x,y)⇝a\right]\hfill \\ & =& \mathcal{N}\mathfrak{R}(x,y)⇝a\hfill \\ & \stackrel{\left(SR\right)}{=}& \mathcal{N}\mathfrak{R}(y,x)⇝a\hfill \\ & =& \overline{\mathfrak{R}}(1_{U-\left\{x\right\}}⇝a)\left(y\right).\hfill \end{array}$$

⟸. For any $x,y\in U$, $a\in L$,

$$\begin{array}{ccc}& & \overline{\mathfrak{R}}(1_{U-\left\{y\right\}}⇝a)\left(x\right)=\overline{\mathfrak{R}}(1_{U-\left\{x\right\}}⇝a)\left(y\right)\hfill \\ & ⟹& \mathcal{N}\mathfrak{R}(x,y)⇝a=\mathcal{N}\mathfrak{R}(y,x)⇝a,\mathrm{by}\mathrm{taking}a=\mathcal{N}\mathfrak{R}(x,y),\mathcal{N}\mathfrak{R}(y,x),\mathrm{respectively}\hfill \\ & ⟹& \mathcal{N}\mathfrak{R}(x,y)\ge \mathcal{N}\mathfrak{R}(y,x)\mathrm{and}\mathcal{N}\mathfrak{R}(y,x)\ge \mathcal{N}\mathfrak{R}(x,y)\hfill \\ & ⟹& \mathcal{N}\mathfrak{R}(x,y)=\mathcal{N}\mathfrak{R}(y,x)\hfill \\ & ⟹& \mathfrak{R}(x,y)=\mathfrak{R}(y,x),\hfill \end{array}$$

i.e., $\mathfrak{R}$ is symmetric. □

Proposition 6.

Let $(U,\mathfrak{R})$ be an L-FAS. Then, $\mathfrak{R}$ is reflexive iff $\forall A\in L^U$, $A\le \overline{\mathfrak{R}}\left(A\right)$.

Proof. 

⟹. For any $x\in U$,

$$\overline{\mathfrak{R}}\left(A\right)\left(x\right)=\underset{y\in V}{\bigvee }(\mathcal{N}\mathfrak{R}(x,y)⇝A\left(y\right))\ge \mathcal{N}\mathfrak{R}(x,x)⇝A\left(x\right)\stackrel{\left(RF\right)}{=}0⇝A\left(x\right)=A\left(x\right).$$

⟸. For any $x\in U$, $a\in L$,

$$\begin{array}{ccc}\hfill \overline{\mathfrak{R}}(1_{X-\left\{x\right\}}⇝a)\left(x\right)& =& \underset{y\in V}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,y)⇝(1_{X-\left\{x\right\}}\left(y\right)⇝a)\right)\hfill \\ & =& \left[\underset{y\ne x}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,y)⇝(1⇝a)\right)\right]\vee \left[\mathcal{N}\mathfrak{R}(x,x)⇝(0⇝a)\right]\hfill \\ & =& 0\vee \left[\mathcal{N}\mathfrak{R}(x,x)⇝a\right]\hfill \\ & =& \mathcal{N}\mathfrak{R}(x,x)⇝a,\hfill \end{array}$$

it follows by

$$\overline{\mathfrak{R}}(1_{X-\left\{x\right\}}⇝a)\left(x\right)\ge (1_{X-\left\{x\right\}}⇝a)\left(x\right)=0⇝a=a$$

that we have $\mathcal{N}\mathfrak{R}(x,x)⇝a\ge a$. Take $a=\mathcal{N}\mathfrak{R}(x,x)$, we have $\mathcal{N}\mathfrak{R}(x,x)\le 0$, i.e., $\mathfrak{R}(x,x)=1$, hence $\mathfrak{R}$ is reflexive. □

Proposition 7.

Let $(U,\mathfrak{R})$ be an L-FAS. Then, $\mathfrak{R}$ is transitive iff $\forall A\in L^U$, $\overline{\mathfrak{R}}\left(A\right)\ge \overline{\mathfrak{R}}\overline{\mathfrak{R}}\left(A\right)$.

Proof. 

⟹. For any $x\in U$,

$$\begin{array}{ccc}\hfill \overline{\mathfrak{R}}\overline{\mathfrak{R}}\left(A\right)\left(x\right)& =& \underset{y\in U}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,y)⇝\overline{\mathfrak{R}}\left(A\right)\left(y\right)\right)\hfill \\ & =& \underset{y\in U}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,y)⇝\underset{z\in U}{\bigvee }(\mathcal{N}\mathfrak{R}(y,z)⇝A\left(z\right))\right)\hfill \\ & =& \underset{y,z\in U}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,y)⇝\left(\mathcal{N}\mathfrak{R}\right(y,z)⇝A(z\left)\right)\right)\hfill \\ & =& \underset{y,z\in U}{\bigvee }\left(\left[\mathcal{N}\mathfrak{R}\right(x,y)\odot \mathcal{N}\mathfrak{R}(y,z\left)\right]⇝A\left(z\right)\right)\hfill \\ & \stackrel{\left(TR\right)}{\le }& \underset{z\in U}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,z)⇝A\left(z\right)\right)\hfill \\ & =& \overline{\mathfrak{R}}\left(A\right)\left(x\right).\hfill \end{array}$$

⟸. For any $x,y,z\in U$, $a\in L$,

$$\begin{array}{ccc}\hfill \overline{\mathfrak{R}}\overline{\mathfrak{R}}(1_{U-\left\{z\right\}}⇝a)\left(x\right)& =& \underset{y\in U}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,y)⇝\overline{\mathfrak{R}}(1_{U-\left\{z\right\}}⇝a)\left(y\right)\right)\hfill \\ & =& \underset{y\in U}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,y)⇝\underset{w\in U}{\bigvee }\left[\mathcal{N}\mathfrak{R}(y,w)⇝(1_{U-\left\{z\right\}}\left(w\right)⇝a)\right]\right)\hfill \\ & =& \underset{y\in U}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,y)⇝\left[\mathcal{N}\mathfrak{R}(y,z)⇝a\right]\right)\hfill \\ & =& \underset{y\in U}{\bigvee }\left(\left[\mathcal{N}\mathfrak{R}(x,y)\odot \mathcal{N}\mathfrak{R}(y,z)\right]⇝a\right)\hfill \\ & \le & \overline{\mathfrak{R}}(1_{U-\left\{z\right\}}⇝a)\left(x\right)\hfill \\ & =& \mathcal{N}\mathfrak{R}(x,z)⇝a.\hfill \end{array}$$

It follows that $\forall x,y,z\in U$, $a\in L$,

$$\left[\mathcal{N}\mathfrak{R}\right(x,y)\odot \mathcal{N}\mathfrak{R}(y,z\left)\right]⇝a\le \mathcal{N}\mathfrak{R}(x,z)⇝a.$$

Putting $a=\mathcal{N}\mathfrak{R}(x,z)$, we have $\left[\mathcal{N}\mathfrak{R}\right(x,y)\odot \mathcal{N}\mathfrak{R}(y,z\left)\right]⇝\mathcal{N}\mathfrak{R}(x,z)=0$, i.e., $\mathcal{N}\mathfrak{R}(x,y)\odot \mathcal{N}\mathfrak{R}(y,z)\ge \mathcal{N}\mathfrak{R}(x,z)$, hence $\mathfrak{R}$ is transitive. □

Proposition 8.

Let $(U,\mathfrak{R})$ be an L-FAS. Then, $\mathfrak{R}$ is mediate iff $\forall A\in L^U$, $\overline{\mathfrak{R}}\left(A\right)\le \overline{\mathfrak{R}}\overline{\mathfrak{R}}\left(A\right)$.

Proof. 

⟹. For any $x\in U$,

$$\begin{array}{ccc}\hfill \overline{\mathfrak{R}}\overline{\mathfrak{R}}\left(A\right)\left(x\right)& =& \underset{y\in U}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,y)⇝\overline{\mathfrak{R}}\left(A\right)\left(y\right)\right)\hfill \\ & =& \underset{y\in U}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,y)⇝\underset{z\in U}{\bigvee }\left[\mathcal{N}\mathfrak{R}(y,z)⇝A\left(z\right)\right]\right)\hfill \\ & =& \underset{y,z\in U}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,y)⇝\left[\mathcal{N}\mathfrak{R}(y,z)⇝A\left(z\right)\right]\right)\hfill \\ & =& \underset{y,z\in U}{\bigvee }\left(\left[\mathcal{N}\mathfrak{R}(x,y)\odot \mathcal{N}\mathfrak{R}(y,z)\right]⇝A\left(z\right)\right)\hfill \\ & =& \underset{z\in U}{\bigvee }\left(\left[\underset{y\in U}{\bigwedge }\left(\mathcal{N}\mathfrak{R}(x,y)\odot \mathcal{N}\mathfrak{R}(y,z)\right)\right]⇝A\left(z\right)\right)\hfill \\ & \stackrel{\left(ME\right)}{\ge }& \underset{z\in U}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,z)⇝A\left(z\right)\right)\hfill \\ & =& \overline{\mathfrak{R}}\left(A\right)\left(x\right).\hfill \end{array}$$

⟸. For any $x,z\in U$, $a\in L$,

$$\begin{array}{ccc}\hfill \overline{\mathfrak{R}}\overline{\mathfrak{R}}(1_{U-\left\{z\right\}}⇝a)\left(x\right)& =& \underset{y\in U}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,y)⇝\overline{\mathfrak{R}}(1_{U-\left\{z\right\}}⇝a)\left(y\right)\right)\hfill \\ & =& \underset{y\in U}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,y)⇝\underset{w\in U}{\bigvee }[\mathcal{N}\mathfrak{R}(y,w)⇝(1_{U-\left\{z\right\}}\left(w\right)⇝a)]\right)\hfill \\ & =& \underset{y\in U}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,y)⇝\left[\mathcal{N}\mathfrak{R}\right(y,z)⇝a]\right)\hfill \\ & =& \underset{y\in U}{\bigvee }\left(\left[\mathcal{N}\mathfrak{R}\right(x,y)\odot \mathcal{N}\mathfrak{R}(y,z\left)\right]⇝a\right)\hfill \\ & =& \left(\underset{y\in U}{\bigwedge }[\mathcal{N}\mathfrak{R}(x,y)\odot \mathcal{N}\mathfrak{R}(y,z)]\right)⇝a\hfill \\ & \ge & \overline{\mathfrak{R}}(1_{U-\left\{z\right\}}⇝a)\left(x\right)\hfill \\ & =& \underset{y\in U}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,y)⇝(1_{U-\left\{z\right\}}\left(y\right)⇝a)\right)\hfill \\ & =& \mathcal{N}\mathfrak{R}(x,z)⇝a.\hfill \end{array}$$

It follows that $\forall x,z\in U$, $a\in L$,

$$\left(\underset{y\in U}{\bigwedge }[\mathcal{N}\mathfrak{R}(x,y)\odot \mathcal{N}\mathfrak{R}(y,z)]\right)⇝a\ge \mathcal{N}\mathfrak{R}(x,z)⇝a.$$

Putting $a={\displaystyle \underset{y\in U}{\bigwedge }}[\mathcal{N}\mathfrak{R}(x,y)\odot \mathcal{N}\mathfrak{R}(y,z)]$, we have

$$\mathcal{N}\mathfrak{R}(x,z))⇝\underset{y\in U}{\bigwedge }[\mathcal{N}\mathfrak{R}(x,y)\odot \mathcal{N}\mathfrak{R}(y,z)]=0⟹\mathcal{N}\mathfrak{R}(x,z)\ge \underset{y\in U}{\bigwedge }[\mathcal{N}\mathfrak{R}(x,y)\odot \mathcal{N}\mathfrak{R}(y,z)],$$

hence $\mathfrak{R}$ is mediate. □

Proposition 9.

Let $(U,\mathfrak{R})$ be an L-FAS. Then, $\mathfrak{R}$ is Euclidean iff $\forall A\in L^U$, $\overline{\mathfrak{R}}\left(A\right)\ge \overline{{\mathfrak{R}}^{op}}\overline{\mathfrak{R}}\left(A\right)$, where ${\mathfrak{R}}^{op}$ is defined by ${\mathfrak{R}}^{op}(x,y)=\mathfrak{R}(y,x)$.

Proof. 

⟹. For any $x\in U$,

$$\begin{array}{ccc}\hfill \overline{{\mathfrak{R}}^{op}}\overline{\mathfrak{R}}\left(A\right)\left(x\right)& =& \underset{y\in U}{\bigvee }\left(\mathcal{N}{\mathfrak{R}}^{op}(x,y)⇝\overline{\mathfrak{R}}\left(A\right)\left(y\right)\right)\hfill \\ & =& \underset{y\in U}{\bigvee }\left(\mathcal{N}\mathfrak{R}(y,x)⇝\underset{z\in U}{\bigvee }[\mathcal{N}\mathfrak{R}(y,z)⇝A\left(z\right)]\right)\hfill \\ & =& \underset{y,z\in U}{\bigvee }\left(\mathcal{N}\mathfrak{R}(y,x)⇝\left[\mathcal{N}\mathfrak{R}\right(y,z)⇝A(z\left)\right]\right)\hfill \\ & =& \underset{y,z\in U}{\bigvee }\left(\left[\mathcal{N}\mathfrak{R}\right(y,x)\odot \mathcal{N}\mathfrak{R}(y,z\left)\right]⇝A\left(z\right)\right)\hfill \\ & \stackrel{\left(EU\right)}{\le }& \underset{z\in U}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,z)⇝A\left(z\right)\right)\hfill \\ & =& \overline{\mathfrak{R}}\left(A\right)\left(x\right).\hfill \end{array}$$

⟸. For any $x,y,z\in U$, $a\in L$,

$$\begin{array}{ccc}\hfill \overline{{\mathfrak{R}}^{op}}\overline{\mathfrak{R}}(1_{U-\left\{z\right\}}⇝a)\left(x\right)& =& \underset{y\in U}{\bigvee }\left(\mathcal{N}{\mathfrak{R}}^{op}(x,y)⇝\overline{\mathfrak{R}}(1_{U-\left\{z\right\}}⇝a)\left(y\right)\right)\hfill \\ & =& \underset{y\in U}{\bigvee }\left(\mathcal{N}\mathfrak{R}(y,x)⇝\left[\mathcal{N}\mathfrak{R}\right(y,z)⇝a]\right)\hfill \\ & =& \underset{y\in U}{\bigvee }\left(\left[\mathcal{N}\mathfrak{R}\right(y,x)\odot \mathcal{N}\mathfrak{R}(y,z\left)\right]⇝a\right)\hfill \\ & \le & \overline{\mathfrak{R}}(1_{U-\left\{z\right\}}⇝a)\left(x\right)\hfill \\ & =& \mathcal{N}\mathfrak{R}(x,z)⇝a.\hfill \end{array}$$

It follows that $\forall x,y,z\in U$, $a\in L$,

$$\left[\mathcal{N}\mathfrak{R}\right(y,x)\odot \mathcal{N}\mathfrak{R}(y,z\left)\right]⇝a\le \mathcal{N}\mathfrak{R}(x,z)⇝a.$$

Putting $a=\mathcal{N}\mathfrak{R}(x,z)$, we have $\left[\mathcal{N}\mathfrak{R}\right(y,x)\odot \mathcal{N}\mathfrak{R}(y,z\left)\right]⇝\mathcal{N}\mathfrak{R}(x,z))=0$, i.e., $\mathcal{N}\mathfrak{R}(y,x)\odot \mathcal{N}\mathfrak{R}(y,z)\ge \mathcal{N}\mathfrak{R}(x,z)$, hence $\mathfrak{R}$ is Euclidean. □

4. Axiomatic Characterization on $\mathit{L}$-Fuzzy Upper Approximation Operators: By Axiomatic Set

In this section, we characterize the L-fuzzy upper approximation operators generated by serial, symmetric, reflexive, mediate, transitive, and Euclidean L-fuzzy relations and their compositions through axiomatic sets.

Definition 5.

A function $\mathsf{\Omega }:L^V⟶L^U$ is called an L-fuzzy upper approximation operator (L-FUAPO for short) whenever

(U1) $\mathsf{\Omega }\left({\displaystyle \underset{j\in J}{\bigvee }}{A}_j\right)={\displaystyle \underset{j\in J}{\bigvee }}\mathsf{\Omega }\left(A_j\right)$ for any $A_j(j\in J)\in L^V$ and any index set J; and

(U2) $\mathsf{\Omega }(a⇝A)=a⇝\mathsf{\Omega }\left(A\right)$ for any $A\in L^V$ and $a\in L$.

We fix a lemma for later use.

Lemma 1.

Let $A\in L^V$ and the function $(-)⇝1:L\to L$ is a surjective function. Then, for any $y\in V$, there is an $a^y\in L$ s.t. $A\left(y\right)=a^y⇝1$, and $A={\displaystyle \underset{y\in V}{\bigvee }}(a^y⇝1_y)$.

Proof. 

Since $(-)⇝1:L\to L$ is surjective, $\forall y\in V$, $A\left(y\right)=a^y⇝1$ for some $a^y\in L$. It follows that

$$a^y⇝1_y\left(y\right)=a^y⇝1=A\left(y\right)=1_y\left(y\right)\wedge A\left(y\right)⟹a^y⇝1_y=1_y\wedge A\left(y\right),$$

and thus

$$A=\underset{y\in V}{\bigvee }(1_y\wedge A\left(y\right))=\underset{y\in V}{\bigvee }(a^y⇝1_y).$$

□

Remark 2.

There are natural examples satisfy the surjective condition in the above lemma"

(1) When L is regular, $\forall a\in L$, $(a⇝1)⇝1=a$, so $(-)⇝1$ is surjective.

(2) When $L=[0,1]$ and the co-implication ⇝ is continuous, $(-)⇝1$ is surjective.

In the following, we always assume that $(-)⇝1$ is a surjective function without further statement.

Theorem 2.

$\mathsf{\Omega }:L^V⟶L^U$ is an L-FUAPO ⟺ there is a unique L-fuzzy relation $\mathfrak{R}$ s.t. $\mathsf{\Omega }=\overline{\mathfrak{R}}$.

Proof. 

⟸. It is established by Proposition 2 (5),(6).

⟹. Let $\mathfrak{R}\in L^{U\times V}$ be defined by

$$\forall x\in U,\forall y\in V,\mathfrak{R}(x,y)=\bigvee \left\{a\in L|\mathcal{N}\left(a\right)⇝1=\mathsf{\Omega }\left(1_y\right)\left(x\right)\right\}.$$

Then,

$$\begin{array}{ccc}\hfill \mathcal{N}\mathfrak{R}(x,y)⇝1& =& \mathcal{N}\left[\bigvee \left\{a|a\in L,\mathcal{N}\left(a\right)⇝1=\mathsf{\Omega }\left(1_y\right)\left(x\right)\right\}\right]⇝1\hfill \\ & =& \left[\bigwedge \left\{\mathcal{N}\left(a\right)|a\in L,\mathcal{N}\left(a\right)⇝1=\mathsf{\Omega }\left(1_y\right)\left(x\right)\right\}\right]⇝1\hfill \\ & =& \bigvee \left\{\mathcal{N}\left(a\right)⇝1|a\in L,\mathcal{N}\left(a\right)⇝1=\mathsf{\Omega }\left(1_y\right)\left(x\right)\right\}\hfill \\ & =& \mathsf{\Omega }\left(1_y\right)\left(x\right).\hfill \end{array}$$

For any $A\in L^V$ and any $x\in U$,

$$\begin{array}{ccc}\hfill \overline{\mathfrak{R}}\left(A\right)\left(x\right)& =& \underset{y\in V}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,y)⇝A\left(y\right)\right)\hfill \\ & \stackrel{\mathrm{Lemma}1}{=}& \underset{y\in V}{\bigvee }\left(\mathcal{N}\mathfrak{R}(x,y)⇝[a^y⇝1]\right)\hfill \\ & =& \underset{y\in V}{\bigvee }\left(a^y⇝[\mathcal{N}\mathfrak{R}(x,y)⇝1]\right)\hfill \\ & =& \underset{y\in V}{\bigvee }\left(a^y⇝\mathsf{\Omega }\left(1_y\right)\left(x\right)\right)\hfill \\ & =& \underset{y\in V}{\bigvee }\left([a^y⇝\mathsf{\Omega }\left(1_y\right)]\left(x\right)\right)\hfill \\ & \stackrel{\left(U2\right)}{=}& \underset{y\in V}{\bigvee }\left(\mathsf{\Omega }(a^y⇝1_y)\left(x\right)\right)\hfill \\ & \stackrel{\left(U1\right)}{=}& \mathsf{\Omega }\left(\underset{y\in V}{\bigvee }(a^y⇝1_y)\right)\left(x\right)\hfill \\ & \stackrel{\mathrm{Lemma}1}{=}& \mathsf{\Omega }\left(A\right)\left(x\right).\hfill \end{array}$$

Hence, $\overline{\mathfrak{R}}=\mathsf{\Omega }$.

The uniqueness of $\mathfrak{R}$ follows by Proposition 3. □

Theorem 3.

Let $\mathsf{\Omega }:L^V⟶L^U$ be an L-FUAPO.

(1) There is a unique serial L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills:

(U3) $\forall a\in L$, $\mathsf{\Omega }\left(a\right)=a$.

Furthermore, let $U=V$.

(2) There is a unique symmetric L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills:

(U4) $\mathsf{\Omega }(1_{U-\left\{y\right\}}⇝a)\left(x\right)=\mathsf{\Omega }(1_{U-\left\{x\right\}}⇝a)\left(y\right),\forall x,y\in U,a\in L$.

(3) There is a unique reflexive L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills:

(U5) $\forall A\in L^U$, $A\le \mathsf{\Omega }\left(A\right)$.

(4) There is a unique transitive L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills:

(U6) $\forall A\in L^U$, $\mathsf{\Omega }\left(A\right)\ge \mathsf{\Omega }\mathsf{\Omega }\left(A\right)$.

(5) There is a unique mediate L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills:

(U7) $\forall A\in L^U$, $\mathsf{\Omega }\left(A\right)\le \mathsf{\Omega }\mathsf{\Omega }\left(A\right)$.

Proof. 

(1) It is established by Proposition 4 and Theorem 2.

(2) It is established by Proposition 5 and Theorem 2.

(3) It is established by Proposition 6 and Theorem 2.

(4) It is established by Proposition 7 and Theorem 2.

(5) It is established by Proposition 8 and Theorem 2. □

From the above theorem, we easily obtain the characterizations on L-fuzzy upper approximation operator generated by the composition of L-fuzzy relations mentioned early.

Theorem 4.

(The composition of two L-fuzzy relations) Let $\mathsf{\Omega }:L^U⟶L^U$ be an L-FUAPO.

(1) There is a unique similar L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills (U4) and (U5).

(2) There is a unique L-fuzzy preorder$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills (U5) and (U6). Furthermore, the “≥” in (U6) can be changed as “=”.

(3) There is a unique serial and symmetric L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills (U3) and (U4).

(4) There is a unique serial and transitive L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills (U3) and (U6).

(5) There is a unique serial and mediate L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills (U3) and (U7).

(6) There is a unique symmetric and transitive L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills (U4) and (U6).

(7) There is a unique symmetric and mediate L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills (U4) and (U7).

(8) There is a unique transitive mediate L-fuzzy relation $\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills (U6) and (U7), or, equivalently, $\forall A\in L^U$, $\mathsf{\Omega }\left(A\right)=\mathsf{\Omega }\mathsf{\Omega }\left(A\right)$.

Theorem 5.

(The composition of three L-fuzzy relations) Let $\mathsf{\Omega }:L^U⟶L^U$ be an L-FUAPO.

(1) There is a unique equivalent L-fuzzy relation $\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills (U4), (U5), and (U6).

(2) There is a unique serial, symmetric, and transitive L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills (U3), (U4), and (U6).

(3) There is a unique serial, symmetric, and mediate L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills (U3), (U4), and (U7).

(4) There is a unique serial, transitive, and mediate L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills (U3), (U6), and (U7).

(5) There is a unique symmetric, transitive, and mediate L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills (U4), (U6), and (U7).

5. Axiomatic Characterization on L-Fuzzy Upper Approximation Operators: By Single Axiom

In this section, we characterize the mentioned L-fuzzy upper approximation operators by single axiom.

5.1. The Case of One L-Fuzzy Relation

Theorem 6.

$\mathsf{\Omega }:L^V⟶L^U$ is an L-FUAPO ⟺ that fulfills:

(UG ) For any index set J and any $a_j\in L,A_j\in L^V(j\in J)$,

$$\mathsf{\Omega }\left(\underset{j\in J}{\bigvee }(a_j⇝A_j)\right)=\underset{j\in J}{\bigvee }\left(a_j⇝\mathsf{\Omega }\left(A_j\right)\right).$$

Proof. 

We prove (U1) + (U2)⟺ (UG).

⟹. It is obtained by

$$\mathsf{\Omega }\left(\underset{j\in J}{\bigvee }(a_j⇝A_j)\right)\stackrel{\left(U1\right)}{=}\underset{j\in J}{\bigvee }\mathsf{\Omega }\left(a_j⇝A_j\right)\stackrel{\left(U2\right)}{=}\underset{j\in J}{\bigvee }\left(a_j⇝\mathsf{\Omega }\left(A_j\right)\right).$$

⟸. Taking $a_j\equiv 0$ in (UG), we have $\mathsf{\Omega }\left({\displaystyle \underset{j\in J}{\bigvee }}{A}_j\right)\stackrel{\left(UG\right)}{=}{\displaystyle \underset{j\in J}{\bigvee }}\mathsf{\Omega }\left(A_j\right),$ i.e., (U1) holds.

Taking $a_j\equiv a$ and $A_j\equiv A$ in (UG), we have $\mathsf{\Omega }(a⇝A)\stackrel{\left(UG\right)}{=}a⇝\mathsf{\Omega }\left(A\right),$ i.e., (U2) holds. □

Theorem 7.

Let $\mathsf{\Omega }:L^V⟶L^U$ be an L-FUAPO. Then, there is a unique serial L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills:

(USR) For any $a\in L$, any index set J, and any $a_j\in L,A_j\in L^V(j\in J)$,

$$\mathsf{\Omega }\left(\underset{j\in J}{\bigvee }\left[a\vee (a_j⇝A_j)\right]\right)=\underset{j\in J}{\bigvee }\left(a\vee \left[a_j⇝\mathsf{\Omega }\left(A_j\right)\right]\right).$$

Proof. 

We prove (UG) + (U3)⟺ (USR). Note that (UG)⟺ (U1)+(U3).

⟹. It is obtained by

$$\mathsf{\Omega }\left(\underset{j\in J}{\bigvee }\left[a\vee (a_j⇝A_j)\right]\right)\stackrel{\left(U1\right)}{=}\underset{j\in J}{\bigvee }\left(\mathsf{\Omega }\left(a\right)\vee \mathsf{\Omega }(a_j⇝A_j)\right)\stackrel{(U2,U3)}{=}\underset{j\in J}{\bigvee }\left(a\vee \left[a_j⇝\mathsf{\Omega }\left(A_j\right)\right]\right).$$

⟸. Taking $a_j\equiv 1$ in (USR), we have

$$\mathsf{\Omega }\left(a\right)=\mathsf{\Omega }(a\vee 0)=\mathsf{\Omega }\left(\underset{j\in J}{\bigvee }\left[a\vee (1⇝A_j)\right]\right)\stackrel{\left(USR\right)}{=}\underset{j\in J}{\bigvee }\left(a\vee \left[1⇝\mathsf{\Omega }\left(A_j\right)\right]\right)=a,$$

i.e., (U3) holds.

Taking $a=0$ in (USR), we obtain (UG). □

Lemma 2.

For any $A\in L^U$, $A=\underset{y\in U}{\bigvee }(1_{U-\left\{y\right\}}⇝A\left(y\right))$.

Proof. 

For any $x,y\in U$, $1_{U-\left\{y\right\}}\left(x\right)=0$ if $x=y$ and $1_{U-\left\{y\right\}}\left(x\right)=1$ otherwise. Then,

$$\underset{y\in U}{\bigvee }(1_{U-\left\{y\right\}}⇝A\left(y\right))\left(x\right)=\underset{y\in U}{\bigvee }(1_{U-\left\{y\right\}}\left(x\right)⇝A\left(y\right))=(0⇝A\left(x\right))\vee \underset{y\ne x}{\bigvee }(1⇝A\left(y\right))=A\left(x\right)\vee 0=A\left(x\right).$$

Hence, $A=\underset{y\in U}{\bigvee }(1_{U-\left\{y\right\}}⇝A\left(y\right))$. □

Theorem 8.

Let $\mathsf{\Omega }:L^U⟶L^U$ be an L-FUAPO. Then, there is a unique symmetric L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills:

(USY) For any $x,y\in U$, any $A\in L^U$, any index set J, and any $a_j\in L,A_j\in L^U(j\in J)$,

$$\mathsf{\Omega }\left(A\right)\left(x\right)\vee \mathsf{\Omega }\left(\underset{j\in J}{\bigvee }(a_j⇝A_j)\right)=\underset{y\in A}{\bigvee }\mathsf{\Omega }\left(1_{U-\left\{x\right\}}⇝A\left(y\right)\right)\left(y\right)\vee \underset{j\in J}{\bigvee }\left(a_j⇝\mathsf{\Omega }\left(A_j\right)\right),$$

where $y\in A$ means that $A\left(y\right)>0$.

Proof. 

We prove (UG) + (U4)⟺ (USY).

⟹. For $A\in L^X$, note that

$$\begin{array}{ccc}\hfill \underset{y\in A}{\bigvee }\mathsf{\Omega }\left(1_{U-\left\{x\right\}}⇝A\left(y\right)\right)\left(y\right)& \stackrel{\left(U4\right)}{=}& \underset{y\in A}{\bigvee }\mathsf{\Omega }\left(1_{U-\left\{y\right\}}⇝A\left(y\right)\right)\left(x\right)\hfill \\ & \stackrel{\left(U1\right)}{=}& \mathsf{\Omega }\left(\underset{y\in A}{\bigvee }\left(1_{U-\left\{y\right\}}⇝A\left(y\right)\right)\right)\left(x\right)\stackrel{\mathrm{Lemma}2}{=}\mathsf{\Omega }\left(A\right)\left(x\right),\hfill \end{array}$$

it follows by (UG) we get (USY).

⟸. Take $A=0$ and $J=\varnothing$ in (USY); then, by $\bigvee \varnothing =0$ for $\varnothing \subseteq L$, we have, for any $x\in U$,

$$\mathsf{\Omega }\left(0\right)\left(x\right)\vee \mathsf{\Omega }\left(0\right)=0\vee 0=0,$$

which implies $\mathsf{\Omega }\left(0\right)=0$.

For any $x,y\in U$, $a\in L$. If $a=0$, then

$$\mathsf{\Omega }(1_{U-\left\{y\right\}}⇝a)\left(x\right)=\mathsf{\Omega }\left(0\right)\left(x\right)=0=\mathsf{\Omega }\left(0\right)\left(y\right)=\mathsf{\Omega }(1_{U-\left\{x\right\}}⇝a)\left(y\right).$$

If $a>0$, then, taking $A=1_{U-\left\{y\right\}}⇝a$ and $J=\varnothing$ in (USY), we have $A\left(y\right)=a$ and $A\left(z\right)=0$ for any $z\in U,z\ne y$,

$$\mathsf{\Omega }(1_{U-\left\{y\right\}}⇝a)\left(x\right)=\underset{z\in A}{\bigvee }\mathsf{\Omega }\left(1_{U-\left\{x\right\}}⇝A\left(z\right)\right)\left(z\right)=\mathsf{\Omega }(1_{U-\left\{x\right\}}⇝a)\left(y\right).$$

Thus, (U4) holds.

Taking $A=0$ in (USY), followed by $\mathsf{\Omega }\left(0\right)=0$, we obtain (UG). □

Theorem 9.

Let $\mathsf{\Omega }:L^U⟶L^U$ be an L-FUAPO. Then, there is a unique reflexive L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills:

(URF) For any index set J and any $a_j\in L,A_j\in L^U(j\in J)$,

$$\underset{j\in J}{\bigvee }\left((a_j⇝A_j)\vee (a_j⇝\mathsf{\Omega }\left(A_j\right))\right)=\mathsf{\Omega }\left(\underset{j\in J}{\bigvee }(a_j⇝A_j)\right).$$

Proof. 

We prove (UG) + (U5)⟺ (URF).

⟹. It is established by

$$\underset{j\in J}{\bigvee }\left((a_j⇝A_j)\vee (a_j⇝\mathsf{\Omega }\left(A_j\right)\right)\stackrel{\left(U5\right)}{=}\underset{j\in J}{\bigvee }\left(a_j⇝\mathsf{\Omega }\left(A_j\right)\right)\stackrel{\left(UG\right)}{=}\mathsf{\Omega }\left(\underset{j\in J}{\bigvee }(a_j⇝A_j)\right).$$

⟸. Taking $a_j\equiv 0$ and $A_j\equiv A$ in (URF), we have

$$A\vee \mathsf{\Omega }\left(A\right)=(0⇝A)\vee (0⇝\mathsf{\Omega }\left(A\right))\stackrel{\left(URF\right)}{=}\mathsf{\Omega }(0⇝A)=\mathsf{\Omega }\left(A\right),$$

which means $A\le \mathsf{\Omega }\left(A\right)$, i.e., (U5) holds. Then, by applying (U5) in (URF), we obtain (UG). □

Theorem 10.

Let $\mathsf{\Omega }:L^U⟶L^U$ be an L-FUAPO. Then, there is a unique transitive L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills:

(UTR) For any index set J and any $a_j\in L,A_j\in L^U(j\in J)$,

$$\underset{j\in J}{\bigvee }\left([a_j⇝\mathsf{\Omega }\mathsf{\Omega }\left(A_j\right)]\vee [a_j⇝\mathsf{\Omega }\left(A_j\right)]\right)=\mathsf{\Omega }\left(\underset{j\in J}{\bigvee }(a_j⇝A_j)\right).$$

Proof. 

We prove (UG) + (U6)⟺ (UTR).

⟹. It is established by

$$\underset{j\in J}{\bigvee }\left([a_j⇝\mathsf{\Omega }\mathsf{\Omega }\left(A_j\right)]\vee [a_j⇝\mathsf{\Omega }\left(A_j\right)]\right)\stackrel{\left(U6\right)}{=}\underset{j\in J}{\bigvee }\left(a_j⇝\mathsf{\Omega }\left(A_j\right)\right)\stackrel{\left(UG\right)}{=}\mathsf{\Omega }\left(\underset{j\in J}{\bigvee }(a_j⇝A_j)\right).$$

⟸. Taking $a_j\equiv 0$ and $A_j\equiv A$ in (UTR), we have

$$\mathsf{\Omega }\mathsf{\Omega }\left(A\right)\vee \mathsf{\Omega }\left(A\right)=[0⇝\mathsf{\Omega }\mathsf{\Omega }\left(A\right)]\vee [0⇝\mathsf{\Omega }\left(A\right)]\stackrel{\left(UTR\right)}{=}\mathsf{\Omega }(0⇝A)=\mathsf{\Omega }\left(A\right),$$

which means $\mathsf{\Omega }\mathsf{\Omega }\left(A\right)\le \mathsf{\Omega }\left(A\right)$, i.e., (U6) holds. Then, by applying (U6) in (UTR), we obtain (UG). □

Theorem 11.

Let $\mathsf{\Omega }:L^U⟶L^U$ be an L-FUAPO. Then, there is a unique mediate L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills:

(UME) For any index set J and any $a_j\in L,A_j\in L^U(j\in J)$,

$$\underset{j\in J}{\bigvee }\left([a_j⇝\mathsf{\Omega }\mathsf{\Omega }\left(A_j\right)]\wedge [a_j⇝\mathsf{\Omega }\left(A_j\right)]\right)=\mathsf{\Omega }\left(\underset{j\in J}{\bigvee }(a_j⇝A_j)\right).$$

Proof. 

We prove (UG) + (U7)⟺ (UME).

⟹. It is established by

$$\underset{j\in J}{\bigvee }\left([a_j⇝\mathsf{\Omega }\mathsf{\Omega }\left(A_j\right)]\wedge [a_j⇝\mathsf{\Omega }\left(A_j\right)]\right)\stackrel{\left(U7\right)}{=}\underset{j\in J}{\bigvee }\left(a_j⇝\mathsf{\Omega }\left(A_j\right)\right)\stackrel{\left(UG\right)}{=}\mathsf{\Omega }\left(\underset{j\in J}{\bigvee }(a_j⇝A_j)\right).$$

⟸. Take $a_j\equiv 0$ and $A_j\equiv A$ in (UME), we have

$$\mathsf{\Omega }\mathsf{\Omega }\left(A\right)\wedge \mathsf{\Omega }\left(A\right)=[0⇝\mathsf{\Omega }\mathsf{\Omega }\left(A\right)]\wedge [0⇝\mathsf{\Omega }\left(A\right)]\stackrel{\left(UME\right)}{=}\mathsf{\Omega }(0⇝A)=\mathsf{\Omega }\left(A\right),$$

which means $\mathsf{\Omega }\mathsf{\Omega }\left(A\right)\ge \mathsf{\Omega }\left(A\right)$, i.e., (U7) holds. Then, by applying (U7) in (UME), we obtain (UG). □

5.2. The Case of Composition of Two L-Fuzzy Relations

Theorem 12.

Let $\mathsf{\Omega }:L^U⟶L^U$ be an L-FUAPO. Then, there is a unique similar L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills:

(USM) For any $x,y\in U$, any $A\in L^U$, any index set J, and any $a_j\in L,A_j\in L^U(j\in J)$,

$$\mathsf{\Omega }\left(A\right)\left(x\right)\vee \mathsf{\Omega }\left(\underset{j\in J}{\bigvee }(a_j⇝A_j)\right)=\underset{y\in A}{\bigvee }\mathsf{\Omega }\left(1_{U-\left\{x\right\}}⇝A\left(y\right)\right)\left(y\right)\vee \underset{j\in J}{\bigvee }\left([a_j⇝A_j]\vee [a_j⇝\mathsf{\Omega }\left(A_j\right)]\right).$$

Proof. 

We prove (USY) + (U5)⟺ (USM).

⟹. It is obvious.

⟸. Taking $A=0$ and $J=\varnothing$ in (USM), we have $\mathsf{\Omega }\left(0\right)=0$.

Take $A=0$ in (USM); then, by $\mathsf{\Omega }\left(0\right)=0$, we obtain (URF), which means that (U5) holds.

By applying (U5) in (USM), we get (USY). □

Theorem 13.

Let $\mathsf{\Omega }:L^U⟶L^U$ be an L-FUAPO. Then, there is a unique L-fuzzy order$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills:

(UFO) For any index set J and any $a_j\in L,A_j\in L^U(j\in J)$,

$$\underset{j\in J}{\bigvee }\left([a_j⇝\mathsf{\Omega }\mathsf{\Omega }\left(A_j\right)]\vee [a_j⇝\mathsf{\Omega }\left(A_j\right)]\vee [a_j⇝A_j]\right)=\mathsf{\Omega }\left(\underset{j\in J}{\bigvee }(a_j⇝A_j)\right).$$

Proof. 

We prove (UTR) + (U5)⟺ (UFO).

⟹. It is obvious.

⟸. Taking $a_j\equiv 0$ and $A_j\equiv A$ in (UFO), we have $\mathsf{\Omega }\mathsf{\Omega }\left(A\right)\vee \mathsf{\Omega }\left(A\right)\vee A=\mathsf{\Omega }\left(A\right)$, which means that (U5) holds.

By applying (U5) in (UFO), we get (UTR). □

Theorem 14.

Let $\mathsf{\Omega }:L^U⟶L^U$ be an L-FUAPO. Then, there is a unique serial and symmetric L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills:

(USR-SY) For any $x,y\in U$, any $A\in L^U$, any $a\in L$, any index set J, and any $a_j\in L,A_j\in L^U(j\in J)$,

$$\mathsf{\Omega }\left(A\right)\left(x\right)\vee \mathsf{\Omega }\left(\underset{j\in J}{\bigvee }\left[a\vee (a_j⇝A_j)\right]\right)=\underset{y\in A}{\bigvee }\mathsf{\Omega }\left(1_{U-\left\{x\right\}}⇝A\left(y\right)\right)\left(y\right)\vee \underset{j\in J}{\bigvee }\left(a\vee \left[a_j⇝\mathsf{\Omega }\left(A_j\right)\right]\right).$$

Proof. 

We prove (USY) + (U3)⟺ (USR-SY).

⟹. It is obvious.

⟸. Taking $A=0$ and $J=\varnothing$ in (USR-SY), we have $\mathsf{\Omega }\left(0\right)=0$.

Take $A=0$, $a_j\equiv 1$ in (USR-SY); then, by $\mathsf{\Omega }\left(0\right)=0$, we obtain (U3).

Taking $a=0$ in (USR-SY), we obtain (USY). □

Theorem 15.

Let $\mathsf{\Omega }:L^U⟶L^U$ be an L-FUAPO. Then, there is a unique serial and transitive L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills:

(USR-TR) For any $a\in L$, any index set J, and any $a_j\in L,A_j\in L^U(j\in J)$,

$$\underset{j\in J}{\bigvee }\left(a\vee [a_j⇝\mathsf{\Omega }\mathsf{\Omega }\left(A_j\right)]\vee [a_j⇝\mathsf{\Omega }\left(A_j\right)]\right)=\mathsf{\Omega }\left(\underset{j\in J}{\bigvee }\left[a\vee (a_j⇝A_j)\right]\right).$$

Proof. 

We prove (USR) + (U6)⟺ (USR-TR).

⟹. It is obvious.

⟸. Taking $a=0$, $a_j\equiv 0$, and $A_j\equiv A$ in (USR-TR), we obtain (U6).

By using (U6) in (USR-TR), we obtain (USR). □

Theorem 16.

Let $\mathsf{\Omega }:L^U⟶L^U$ be an L-FUAPO. Then, there is a unique serial and mediate L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills:

(USR-ME) For any $a\in L$, any index set J, and any $a_j\in L,A_j\in L^U(j\in J)$,

$$\underset{j\in J}{\bigvee }\left(a\vee \left[\left(a_j⇝\mathsf{\Omega }\mathsf{\Omega }\left(A_j\right)\right)\wedge \left(a_j⇝\mathsf{\Omega }\left(A_j\right)\right)\right]\right)=\mathsf{\Omega }\left(\underset{j\in J}{\bigvee }\left[a\vee (a_j⇝A_j)\right]\right).$$

Proof. 

We prove (USR) + (U7)⟺ (USR-ME).

⟹. It is obvious.

⟸. Take $a=0$, $a_j\equiv 0$, and $A_j\equiv A$ in (USR-ME), we obtain (U7).

By using (U7) in (USR-ME), we obtain (USR). □

Theorem 17.

Let $\mathsf{\Omega }:L^U⟶L^U$ be an L-FUAPO. Then, there is a unique symmetric and transitive L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills:

(USY-TR) For any $x,y\in U$, any $A\in L^U$, any index set J, and any $a_j\in L,A_j\in L^U(j\in J)$,

$$\mathsf{\Omega }\left(A\right)\left(x\right)\vee \mathsf{\Omega }\left(\underset{j\in J}{\bigvee }(a_j⇝A_j)\right)=\underset{y\in A}{\bigvee }\mathsf{\Omega }\left(1_{U-\left\{x\right\}}⇝A\left(y\right)\right)\left(y\right)\vee \underset{j\in J}{\bigvee }\left([a_j⇝\mathsf{\Omega }\mathsf{\Omega }\left(A_j\right)]\vee [a_j⇝\mathsf{\Omega }\left(A_j\right)]\right),$$

Proof. 

We prove (USY) + (U6)⟺ (USY-TR).

⟹. It is obvious.

⟸. Taking $A=0$ and $J=\varnothing$ in (USY-TR), we have $\mathsf{\Omega }\left(0\right)=0$.

Take $A=0$, $a_j\equiv 0$, and $A_j\equiv A$ in (USY-TR); then, by $\mathsf{\Omega }\left(0\right)=0$, we obtain (U6).

By applying (U6) in (USY-TR), we get (USY). □

Theorem 18.

Let $\mathsf{\Omega }:L^U⟶L^U$ be an L-FUAPO. Then, there is a unique symmetric and mediate L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills:

(USY-ME) For any $x,y\in U$, any $A\in L^U$, any index set J, and any $a_j\in L,A_j\in L^U(j\in J)$,

$$\mathsf{\Omega }\left(A\right)\left(x\right)\vee \mathsf{\Omega }\left(\underset{j\in J}{\bigvee }(a_j⇝A_j)\right)=\underset{y\in A}{\bigvee }\mathsf{\Omega }\left(1_{U-\left\{x\right\}}⇝A\left(y\right)\right)\left(y\right)\vee \underset{j\in J}{\bigvee }\left([a_j⇝\mathsf{\Omega }\mathsf{\Omega }\left(A_j\right)]\wedge [a_j⇝\mathsf{\Omega }\left(A_j\right)]\right).$$

Proof. 

We prove (USY) + (U7)⟺ (USY-ME).

⟹. It is obvious.

⟸. Taking $A=0$ and $J=\varnothing$ in (USY-ME), we have $\mathsf{\Omega }\left(0\right)=0$.

Take $A=0$, $a_j\equiv 0$ and $A_j\equiv A$ in (USY-ME); then, by $\mathsf{\Omega }\left(0\right)=0$, we obtain (U7).

By applying (U7) in (USY-ME), we get (USY). □

Theorem 19.

Let $\mathsf{\Omega }:L^U⟶L^U$ be an L-FUAPO. Then, there is a unique transitive and mediate L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills:

(UTR-ME) For any index set J and any $a_j\in L,A_j\in L^U(j\in J)$,

$$\underset{j\in J}{\bigvee }\left(a_j⇝\mathsf{\Omega }\mathsf{\Omega }\left(A_j\right)\right)=\mathsf{\Omega }\left(\underset{j\in J}{\bigvee }(a_j⇝A_j)\right).$$

Proof. 

We prove (UG) + (U6) + (U7)⟺ (UTR-ME).

⟹. It is obvious.

⟸. Taking $a_j\equiv 0$ and $A_j\equiv A$ in (UTR-ME), we have $\mathsf{\Omega }\mathsf{\Omega }\left(A\right)=\mathsf{\Omega }\left(A\right)$, which means that (U6) and (U7) hold.

By (U6) + (U7), we have $\mathsf{\Omega }\mathsf{\Omega }\left(A_j\right)=\mathsf{\Omega }\left(A_j\right)(\forall j\in J)$; then, by applying it in (UTR-ME), we get (UG). □

5.3. The Case of Composition of Three L-Fuzzy Relations

Theorem 20.

Let $\mathsf{\Omega }:L^U⟶L^U$ be an L-FUAPO. Then, there is a unique equivalent L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills:

(UEQ) For any $x,y\in U$, any $A\in L^U$, any index set J, and any $a_j\in L,A_j\in L^U(j\in J)$,

$$\mathsf{\Omega }\left(A\right)\left(x\right)\vee \mathsf{\Omega }\left(\underset{j\in J}{\bigvee }(a_j⇝A_j)\right)=\underset{y\in A}{\bigvee }\mathsf{\Omega }\left(1_{U-\left\{x\right\}}⇝A\left(y\right)\right)\left(y\right)\vee \underset{j\in J}{\bigvee }\left([a_j⇝\mathsf{\Omega }\mathsf{\Omega }\left(A_j\right)]\vee [a_j⇝\mathsf{\Omega }\left(A_j\right)]\vee [a_j⇝A_j]\right).$$

Proof. 

We prove (USM) + (U6)⟺ (UEQ).

⟹. It is obvious.

⟸. Taking $A=0$ and $J=\varnothing$ in (UEQ), we have $\mathsf{\Omega }\left(0\right)=0$.

Take $A=0$, $a_j\equiv 0$, and $A_j\equiv A$ in (UEQ); then, by $\mathsf{\Omega }\left(0\right)=0$, we obtain (U6).

By applying (U6) in (UEQ), we obtain (USM). □

Theorem 21.

Let $\mathsf{\Omega }:L^U⟶L^U$ be an L-FUAPO. Then, there is a unique serial, symmetric, and transitive L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills:

(USR-SY-TR) For any $x,y\in U$, any $A\in L^U$, any $a\in L$, any index set J, and any $a_j\in L,A_j\in L^U(j\in J)$,

$$\mathsf{\Omega }\left(A\right)\left(x\right)\vee \mathsf{\Omega }\left(\underset{j\in J}{\bigvee }[a\vee (a_j⇝A_j)]\right)=\underset{y\in A}{\bigvee }\mathsf{\Omega }\left(1_{U-\left\{x\right\}}⇝A\left(y\right)\right)\left(y\right)\vee \underset{j\in J}{\bigvee }\left(a\vee [a_j⇝\mathsf{\Omega }\mathsf{\Omega }\left(A_j\right)]\vee [a_j⇝\mathsf{\Omega }\left(A_j\right)]\right).$$

Proof. 

We prove (USR-SY) + (U6)⟺ (USR-SY-TR).

⟹. It is obvious.

⟸. Taking $A=0$ and $J=\varnothing$ in (USY-SY-TR), we have $\mathsf{\Omega }\left(0\right)=0$.

Take $A=0$, $a=0$, $a_j\equiv 0$, and $A_j\equiv A$ in (USR-SY-TR); then, by $\mathsf{\Omega }\left(0\right)=0$, we obtain (U6).

Applying (U6) in (USR-SY-TR), we obtain (USR-SY). □

Theorem 22.

Let $\mathsf{\Omega }:L^U⟶L^U$ be an L-FUAPO. Then, there is a unique serial, symmetric, and mediate L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills:

(USR-SY-ME) For any $x,y\in U$, any $A\in L^U$, any $a\in L$, any index set J, and any $a_j\in L,A_j\in L^U(j\in J)$,

$$\mathsf{\Omega }\left(A\right)\left(x\right)\vee \mathsf{\Omega }\left(\underset{j\in J}{\bigvee }\left[a\vee (a_j⇝A_j)\right]\right)=\underset{y\in A}{\bigvee }\mathsf{\Omega }\left(1_{U-\left\{x\right\}}⇝A\left(y\right)\right)\left(y\right)\vee \underset{j\in J}{\bigvee }\left(a\vee \left[\left(a_j⇝\mathsf{\Omega }\mathsf{\Omega }\left(A_j\right)\right)\wedge \left(a_j⇝\mathsf{\Omega }\left(A_j\right)\right)\right]\right).$$

Proof. 

We prove (USR-SY) + (U7)⟺ (USR-SY-ME).

⟹. It is obvious.

⟸. Taking $A=0$ and $J=\varnothing$ in (USY-SY-ME), we have $\mathsf{\Omega }\left(0\right)=0$.

Take $A=0$, $a=0$, $a_j\equiv 0$, and $A_j\equiv A$ in (USR-SY-ME); then, by $\mathsf{\Omega }\left(0\right)=0$, we obtain (U7).

Applying (U7) in (USR-SY-ME), we obtain (USR-SY). □

Theorem 23.

Let $\mathsf{\Omega }:L^U⟶L^U$ be an L-FUAPO. Then, there is a unique serial, transitive, and mediate L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills:

(USR-TR-ME) For any $a\in L$, any index set J, and any $a_j\in L,A_j\in L^U(j\in J)$,

$$\mathsf{\Omega }\left(\underset{j\in J}{\bigvee }\left[a\vee (a_j⇝A_j)\right]\right)=\underset{j\in J}{\bigvee }\left(a\vee \left[a_j⇝\mathsf{\Omega }\mathsf{\Omega }\left(A_j\right)\right]\right).$$

Proof. 

We prove (UTR-ME) + (U3)⟺ (USR-TR-ME).

⟹. It is obvious.

⟸. Taking $a=0$ in (USR-TR-ME), we obtain (UTR-ME).

Taking $a_j\equiv 1$ in (USR-TR-ME), we obtain (U3). □

Theorem 24.

Let $\mathsf{\Omega }:L^U⟶L^U$ be an L-FUAPO. Then, there is a unique symmetric, transitive, and mediate L-fuzzy relation$\mathfrak{R}$s.t.$\mathsf{\Omega }=\overline{\mathfrak{R}}$⟺ Ω fulfills:

(USY-TR-ME) For any $x,y\in U$, any $A\in L^U$, any index set J, and any $a_j\in L,A_j\in L^U(j\in J)$,

$$\mathsf{\Omega }\left(A\right)\left(x\right)\vee \mathsf{\Omega }\left(\underset{j\in J}{\bigvee }(a_j⇝A_j)\right)=\underset{y\in A}{\bigvee }\mathsf{\Omega }\left(1_{U-\left\{x\right\}}⇝A\left(y\right)\right)\left(y\right)\vee \underset{j\in J}{\bigvee }\left(a_j⇝\mathsf{\Omega }\mathsf{\Omega }\left(A_j\right)\right).$$

Proof. 

We prove (UTR-ME) + (U4)⟺ (USY-TR-ME).

⟹. It is obvious.

⟸. Taking $A=0$ and $J=\varnothing$ in (USY-TR-ME), we have $\mathsf{\Omega }\left(0\right)=0$.

Take $A=0$ in (USY-TR-ME); then, by $\mathsf{\Omega }\left(0\right)=0$, we obtain (UTR-ME).

Taking $A=1_{U-\left\{y\right\}}⇝a$ and $J=\varnothing$ in (USY-TR-ME), we obtain (U4). □

Remark 3.

It is easily seen that the results in Section 5 also hold if we assume that $\mathsf{\Omega }:L^U⟶L^U$ is an arbitrary function since each single axiom implies (UG).

6. Concluding Remarks

In this paper, we construct a new L-fuzzy upper approximation operator based on co-implication of a complete co-residuated lattice L. We prove that, when L is regular, the new approximation operator is the dual operator of the Qiao–Hu L-fuzzy lower approximation operator [38]. Then, through axiom sets (single axiom), we characterize the L-fuzzy upper approximation operators generated by serial, symmetric, reflexive, mediate, transitive, and Euclidean L-fuzzy relations and their compositions, respectively.

Notice that the theory of complete co-reisiduated lattice-valued fuzzy rough sets based on L-fuzzy coverings and L-fuzzy neighborhood systems has not been established. In future work, we will do some study on that area.