Transdisciplinary Scientific Strategies for Soft Computing Development: Towards an Era of Data and Business Analytics
Abstract
1. Introduction
2. SWOT Analysis of Computational Intelligence towards Data and Business Analytics
- -
- The Fuzzy disciplines consideration as sciences of vagueness is probably one of the most relevant strengths of Soft Computing.
- -
- -
- Certain advances towards natural language interpretability, like computing with words (CWW) [23,24,25,26,27,28], linguistic data summarization (LDS) [29,30,31,32], linguistic integration of membership functions by operators (LIMFO) [31,32,33,34,35,36,37,38,39,40], and Mamdani fuzzy systems (MFS) constitute a powerful strength [41,42,43,44,45,46,47,48,49,50].
- -
- -
- However, those advances have not been enough for meaningful achievements in natural language recognition and processing. This condition is a relevant weakness in comparison with the natural expectations of the first decades of soft computing development and the extraordinary results obtained by other ways like deep learning [14,15,16].
- -
- Another two important strengths are the graphical interpretability of fuzzy logic and the development of evolutionary algorithms and metaheuristics [14,15,16,60]. They could be especially important together as ways to get synergically promising approaches for the usual hybridization employed in knowledge discovery: A way of representation, a way of evaluation and a method of searching.
- -
- The two other principal weaknesses of fuzzy systems as part of soft computing are probably the evolution of fuzzy control towards functional adjustment techniques not interpretable by natural languages, like the classical Mamdani systems, which principal limitation have been the lack of accuracy [41,42,43,44,45,46,47,48,49,50].
- -
- These two weaknesses combination has produced the myth that interpretability and accuracy are not compatible. That is possible because the traditional concept of Interpretability in fuzzy logic is associated with different measures highly connected with simplicity. The authors of this paper consider that interpretability by natural language, like any interpretation, is practical just because it contributes by the interpretation to efficacy and efficiency of modeling and analysis. Accuracy is one of the essential properties of those two attributes. This treatment of interpretability should be considered another critical weakness. The formal treatment of the concept of interpretability in science is not associated with the possibility to be understood directly by a person, but it relates to a translation process disconnected with the participation of individuals [61,62,63,64,65].
- -
- The consensus of the scientific communities of artificial intelligence, machine learning as well as data and business analytics concerning the importance of augmented intelligence and augmented analytics paradigms constitute a relevant opportunity to fuzzy logic and soft computing associated with its relationship with natural language, as a clear need towards comprehensive or integrative computational cognitive models which are not available yet [1,2,3,4,5].
- -
- -
- -
- The extraordinary accuracy results of deep learning in different applications constitute a threat to the use of other models.
- -
- However, the black box characteristic of those models is an opportunity because of the possible creation of hybrid models combining accuracy arising from deep learning and interpretability stemming from fuzzy logic.
- -
- Strengths: 1. Recognition of fuzzy logic as the science of vagueness (SciV), 2. the growing role of mathematical fuzzy logic (RMFL), 3. advances towards interpretability by natural language (ATNLI), 4. graphical interpretability by trees, graphs, and networks (GIFL), 5. development of evolutionary algorithms and metaheuristics (DEA).
- -
- Weaknesses: 1. Non-appreciable results in natural language treatment from fuzzy sets and fuzzy logic (NARNLT), 2. fuzzy control deviation towards functional adjustment techniques. Limitations of Mamdani fuzzy systems (FCD).
- -
- Opportunities: 1. Transdisciplinary science and scientific and logical pluralism (TS-SLP), 2. lack of general cognitive models (LGCM), 3. lack of interpretability of deep learning (LIDL), 4. existence of universal transformational generative grammar, a consensual scientific linguistic model (TGG).
- -
- Threads: 1. Deep learning extraordinary accuracy results (DLAR).
3. Wide Knowledge Discovery Strategy towards AA Paradigm: Philosophical, Cognitive and Strategic Arguments
- The way to represent knowledge should be general; then, all the knowledge could be represented. That general way of representation can be transformed easily to natural language and different graphical representations, facilitating the understanding and illustration of the knowledge represented
- The way to evaluate knowledge should be a hybrid approach that joins important theoretical elements used in knowledge processing and is represented by natural language and different graphical approaches.
- The way to search for knowledge could be in the form of optimization, and particularly, through heuristics associated with different ways of representation.
- The accomplishment of more directly oriented to the decision-making tools,
- Better participation of experts and decision-makers in the analytics process, by the suggestion of hypotheses, concepts, and decision-making alternatives evaluation.
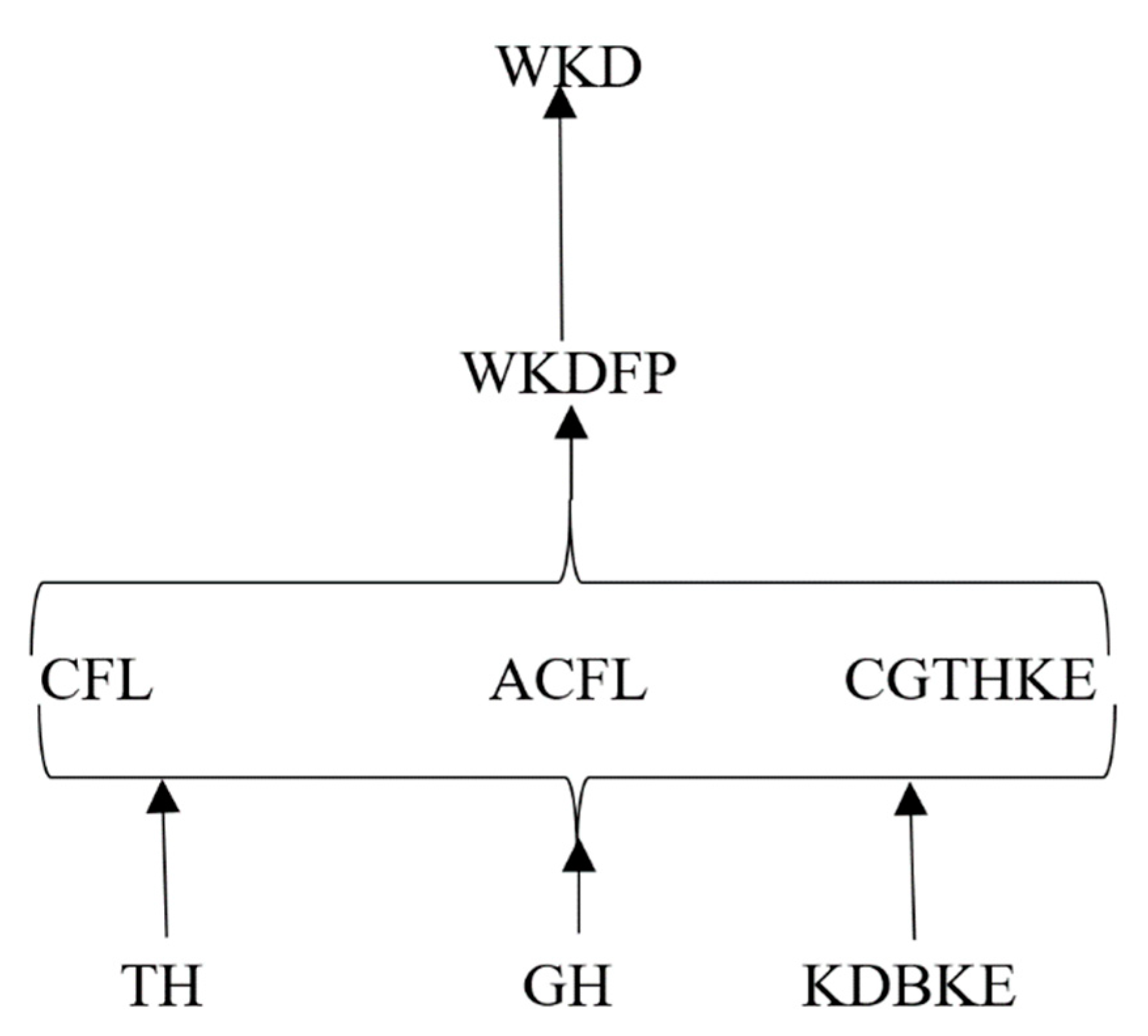
4. Scientific Strategies of Soft Computing towards Wide Knowledge Discovery
4.1. Theoretical Hybridization
4.1.1. Examples of Strategic Results
Compensatory Fuzzy Logic
Archimedean Compensatory Fuzzy Logic
Cooperative N-Personal Game Solution by Knowledge Engineering
4.2. General Hybridization (GH)
4.2.1. Examples of Strategic Results
Definition of Universal Proposition over Cartesian Products of Intervals in CFL
Wide Knowledge Discovery by Fuzzy Predicates (WKDFP)
Strategic Fundamentals
Examples and Explanation of Strategic Results
5. Related and Future Work
5.1. Emergence and Development of CFL (From 2005)
5.2. Creation and Development of ACFL (From 2014)
5.3. Developments of Business Analytics by CFL and ACFL (From 2014)
5.4. Future Works
- -
- -
- Necessary and sufficient conditions theorems for a special free context grammar have been planned to be obtained from the use of generalized continue linguistic variables.
- -
- Elaboration of semantic models for syntactic expressions based on the minimalist program
- -
- Mixing with neural networks as a strategy to new more effective forms of representation and searching is planned. An initial neural network already implemented by using ACFL operators and generalized linguistic variables will be used as a point of departure to get advances in deep learning towards advances in fuzzy predicates analytics and neural networks interpreted by them.
- -
- -
- The use of new genetic algorithms and other ways of searching towards wider classes of fuzzy logic predicates should have a meaningful development and impact in interpretability and inference accuracy.
- -
- Advances towards compensatory morphology in the treatment of color images are planned. The pluralism of ACFL will be used to get a model by integration of different windows using specific ACFL logics.
- -
- New models for decision making in different areas of management should be obtained, for example: internationalization of companies, social enterprises, supply chain management, human capital and competencies, etc.
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Three Dimensions Research Program in Course
- Creating a new theoretical approach interpretable by bivalent logic, and compatible with selected elements of decision-making theories and statistics
- Elaboration of computational tools
- Applications to different fields
- 3.1.
- Application to different fields of business and management
- 3.2.
- Application to images and signals treatment
- 3.3.
- Application to other fields
- Elaboration and application of experiments testing the following elements:
- 4.1.
- Compatibility with human behavior
- 4.2.
- Compatibility with knowledge discovery methods for particular problems
- 4.3.
- Compatibility with Mamdani approach in simple cases
- 4.4.
- Performance of different deductive structures as heuristics in knowledge discovery as a way of approximate reasoning
- 4.5.
- Accuracy improvement in complex and high dimensional cases of fuzzy control
- 4.6.
- Compatibility with protoforms used in CWW and LDS
- 4.7.
- Compatibility with utility theory under risk and prospect theory
- 4.8.
- Study of operators robustness
- Elaboration of a pluralist theoretical approach for fuzzy logic which allows the values compatibility between CFL and the usual very common and extended approach of Fuzzy Logic, the norm and co-norm approach.
- Elaboration of generalizations of important concepts of fuzzy logic, which can be associated by parameters to different ACFL systems with the purpose to include them as searching parameters for knowledge discovery, as way of contextual pluralism.
- 2.1.
- Generalization of modifiers, sigmoid membership functions and linguistic continue variables for each logic.
- 2.2.
- Study of negations, implications, equivalence, and similarities in ACFL.
- 2.3.
- Elaborate interpretations of exigence level and risk attitude from Archimedean compensatory fuzzy logic. as way of achievement of individual and groups pluralism.
- 2.4.
- Elaborate formulas for dual, intuitionistic, and neutrosophic fuzzy logic using archimedean compensatory fuzzy logic as point of departure.
- Creation and development of Eureka Universe.
- Elaboration of procedures for the association of fuzzy predicates forms from universal grammar syntactical structures.
- Elaboration of a way of representation of fuzzy predicates by neural networks which could join the interpretability properties of CFL to the use of the extraordinary results of deep learning in data analysis by fuzzy predicates.
- Elaboration of models and cognitive flows for relevant decision-making problems in business.
- Elaborate an ACFL games theory-based approach useful for business analysis and negotiation.
- Development of Hybridization with other relevant mathematical methods.
- 6.1.
- Hybridization with simulation
- 6.2.
- Hybridization with constructive decision-making approaches
- 6.3.
- Development of fuzzy prospect theory by ACFL
- 6.4.
- Hybridization with statistical and stochastic approaches
- 6.5.
- Hybridization with optimization and evolutionary searching
- Development of logic-statistical inference methods by CFL and ACFL.
- Development of the Generalized Linguistic Continue Variables as a Free Context Grammar theoretically developed from ACFL results.
- Implementation of the new elements in Eureka Universe.
Appendix B. List of Acronyms
- i.
- Advances towards interpretability by natural language (ATNLI)
- ii.
- Augmented analytics (AA)
- iii.
- Archimedean compensatory fuzzy logic (ACFL)
- iv.
- Compensatory fuzzy logic (CFL)
- v.
- Computing with words (CWW)
- vi.
- Deep learning extraordinary accuracy results (DLAR)
- vii.
- Development of evolutionary algorithms and metaheuristics (DEA)
- viii.
- Education 4.0 (E4.0)
- ix.
- Eureka Universe (EU)
- x.
- Existence of universal transformational generative grammar, a consensual scientific linguistic model (TGG)
- xi.
- Fuzzy logic as the science of vagueness (SciV)
- xii.
- Fuzzy control deviation towards functional adjustment techniques (FCD)
- xiii.
- General phase (GPh)
- xiv.
- Graphical interpretability by trees, graphs, and networks (GIFL)
References
- Zheng, N.N.; Liu, Z.Y.; Ren, P.J.; Ma, Y.Q.; Chen, S.T.; Yu, S.Y.; Xue, J.-R.; Chen, B.-D.; Wang, F.Y. Hybrid-augmented intelligence: Collaboration and cognition. Front. Inf. Technol. Electron. Eng. 2017, 18, 153–179. [Google Scholar] [CrossRef]
- Leyva-Vázquez, M.Y.; Bello-Lara, R.; Espín-Andrade, R.A. Compensatory fuzzy logic for intelligent social network analysis. Rev. Cuba. Cienc. Inf. 2014, 8, 74–85. [Google Scholar]
- Zhang, F.Q.; Mao, Z.J.; Ding, G.Y.; Xu, L. Design of chinese natural language in fuzzy boundary determination algorithm based on big data. J. Inf. Hiding Multimed. Signal Process. 2017, 8, 423–434. [Google Scholar]
- Yan, H.; Wan, J.; Zhang, C.; Tang, S.; Hua, Q.; Wang, Z. Industrial Big Data Analytics for Prediction of Remaining Useful Life Based on Deep Learning. IEEE Access 2018, 6, 17190–17197. [Google Scholar] [CrossRef]
- Prat, N. Augmented analytics. Bus. Inf. Syst. Eng. 2019, 61, 375–380. [Google Scholar] [CrossRef]
- Andrade, R.A.E.; Fernández, E.; González, E. Compensatory Fuzzy Logic: A frame for reasoning and modeling preference knowledge in Intelligent Systems. In Soft Computing for Business Intelligence; Springer: Berlin/Heidelberg, Germany, 2014; pp. 3–23. [Google Scholar]
- Espin-Andrade, R.A.; Chao Bataller, A. Methodology for Knowledge Management and Decision Making based on Fuzzy Logic. In Inteligencia Organizacional; Pomim-Valentim, M.L., Más-Basnuevo, A., Eds.; Cultura Académica: Sao Paulo, Brazil, 2015; pp. 163–194. [Google Scholar]
- Salas, F.G.; Del toro, R.J.; Espín-Andrade, R.A.; Jimenez, J.M. An Approach to Knowledge Discovery for Fault Detection by Using Compensatory Fuzzy Logic. In Advances in Soft Computing, Proceedings of the Mexican International Conference on Artificial Intelligence, Xalapa, Mexico, 27 October–2 November 2019; Martínez-Villaseñor, L., Batyrshin, I., Marín-Hernández, A., Eds.; Springer: Cham, Switzerland, 2019; pp. 391–402. [Google Scholar] [CrossRef]
- Espin-Andrade, R.; González, E.; Pedrycz, W.; Fernández, E. An interpretable logical theory: The case ofcompensatory fuzzy logic. Int. J. Comput. Intell. Syst. 2016, 9, 612–626. [Google Scholar] [CrossRef]
- Rodríguez-Cándido, N.P.; Espin-Andrade, R.A.; Solares, E.; Pedrycz, W. A Compensatory Fuzzy Logic Model in Technical Trading. Axioms 2021, 10, 36. [Google Scholar] [CrossRef]
- Espin-Andrade, R.A.; González Caballero, E.; Pedrycz, W.; Fernández González, E.R. Archimedean-compensatory fuzzy logic systems. Int. J. Comput. Intell. Syst. 2015, 8 (Suppl. 2), 54–62. [Google Scholar] [CrossRef]
- Gonzalez, E.; Espin-Andrade, R.A.; Martinez, L.; Guerrero-ramos, L.A. Continuous Linguistic Variables and Their Applications to Data Mining and Time Series Prediction. Int. J. Fuzzy Syst. 2021, 1–22. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. The legacy of 50 years of fuzzy sets: A discussion. In Fuzzy Sets and Systems; Elsevier: Amsterdam, The Netherlands, 2015; Volume 281, pp. 21–31, ISSN 0165-0114; Available online: https://www.sciencedirect.com/science/article/pii/S0165011415004169 (accessed on 1 May 2021). [CrossRef]
- Laengle, S.; Lobos, V.; Merigó, J.M.; Herrera-Viedma, E.; Cobo, M.J.; De Baets, B. Forty years of Fuzzy Sets and Systems: A bibliometric analysis. Fuzzy Sets Syst. 2021, 402, 155–183. [Google Scholar] [CrossRef]
- Elkan, C.; Berenji, H.R.; Chandrasekaran, B.; De Silva CJ, S.; Attikiouzel, Y.; Dubois, D.; Prade, H.; Smets, P.; Freksa, C.; Garcia, O.N.; et al. The paradoxical success of fuzzy logic. IEEE Expert 1994, 9, 3–49. [Google Scholar] [CrossRef]
- Hájek, P. Metamathematics of Fuzzy Logic (4); Springer: Dordrecht, The Netherlands, 1998. [Google Scholar] [CrossRef]
- Hájek, P. Comments on Interpretability and Decidability in Fuzzy Logic. J. Log. Comput. 2011, 21, 823–828. [Google Scholar] [CrossRef]
- Anh, N.T.; Ho, N.C. On the real-world-semantics interpretability of fuzzy rule based systems under fuzzy set approach and hedge algebra approach. J. Comput. Sci. Cybern. 2017, 33, 89–109. [Google Scholar] [CrossRef]
- Dubois, D.; Esteva, F.; Godo, L.; Prade, H. Fuzzy-set based logics-an history-oriented presentation of their main developments. Many Valued Nonmonotonic Turn Log. 2007, 8, 325–449. [Google Scholar]
- Gabbay, D.M.; Woods, J.H. (Eds.) Handbook of the History of Logic; Elsevier: Amsterdam, The Netherlands, 2007; pp. 325–449. [Google Scholar]
- Esteva, F.; Flaminio, T.; Godo, L. From Fuzzy Sets to Mathematical Fuzzy Logic. Arch. Soft Comput. 2019, 2, 26–59. Available online: http://hdl.handle.net/10261/237339 (accessed on 30 April 2021).
- Pedrycz, W.; Kwak, K.C. Boosting of granular models. Fuzz Sets Syst. 2006, 157, 2934–2953. [Google Scholar] [CrossRef]
- Pedrycz, W.; Vasilakos, A.V. Linguistic models and linguistic modeling. IEEE Trans. Syst. Man Cybern. Part B Cybern. 1999, 29, 745–757. [Google Scholar] [CrossRef]
- Zadeh, L.A. Precisiated natural language (PNL). Ai Mag. 2004, 25, 74–91. [Google Scholar]
- Zadeh, L.A. Precisiated natural language. Stud. Fuzziness Soft Comput. 2007, 209, 33–59. [Google Scholar] [CrossRef]
- Zadeh, L.A. A prototype-centered approach to adding deduction capability to search engines-the concept of protoform. In Proceedings of the 2002 Annual Meeting of the North American Fuzzy Information Processing Society Proceedings. NAFIPS-FLINT 2002 (Cat. No. 02TH8622), New Orleans, LA, USA, 27–29 June 2002; pp. 523–525. [Google Scholar]
- Zadeh, L.A. A prototype-centered approach to adding deduction capability to search engines—The concept of protoform. In Proceedings of the Proceedings First International IEEE Symposium Intelligent Systems, Varna, Bulgaria, 10–12 September 2002; pp. 2–3. [Google Scholar] [CrossRef]
- Kacprzyk, J.; Zadrożny, S. Linguistic database summaries and their protoforms: Towards natural language based knowledge discovery tools. Inf. Sci. 2005, 173, 281–304. [Google Scholar] [CrossRef]
- Kacprzyk, J.; Wilbik, A.; Zadrożny, S. Linguistic summarization of time series using a fuzzy quantifier driven aggregation. Fuzzy Sets Syst. 2008, 159, 1485–1499. [Google Scholar] [CrossRef]
- Kacprzyk, J.; Zadrożny, S. Soft computing and web intelligence for supporting consensus reaching. Soft Comput. 2010, 14, 833–846. [Google Scholar] [CrossRef]
- Kacprzyk, J.; Zadrozny, S. Computing with words is an implementable paradigm: Fuzzy queries, linguistic data summaries, and natural-language generation. IEEE Trans. Fuzzy Syst. 2010, 18, 461–472. [Google Scholar] [CrossRef]
- Herrera, F.; Herrera-Viedma, E. A model of consensus in group decision making under linguistic assessments. Fuzzy Sets Syst. 1996, 78, 73–87. [Google Scholar] [CrossRef]
- Herrera, F.; Herrera-Viedma, E. Linguistic decision analysis: Steps for solving decision problems under linguistic information. Fuzzy Sets Syst. 2000, 115, 67–82. [Google Scholar] [CrossRef]
- Herrera-Viedma, E.; Herrera, F.; Chiclana, F.; Luque, M. Some issues on consistency of fuzzy preference relations. Eur. J. Oper. Res. 2004, 154, 98–109. [Google Scholar] [CrossRef]
- Herrera, F.; Herrera-Viedma, E.; Chiclana, F. A study of the origin and uses of the ordered weighted geometric operator in multicriteria decision making. Int. J. Intell. Syst. 2003, 18, 689–707. [Google Scholar] [CrossRef]
- Herrera, F.; Herrera-Viedma, E.; Martínez, L. A fuzzy linguistic methodology to deal with unbalanced linguistic term sets. IEEE Trans. Fuzzy Syst. 2008, 16, 354–370. [Google Scholar] [CrossRef]
- Martínez, L.; Herrera, F. An overview on the 2-tuple linguistic model for computing with words in decision making: Extensions, applications and challenges. Inf. Sci. 2012, 207, 1–18. [Google Scholar] [CrossRef]
- Rodríguez, R.M.; Martínez, L.; Herrera, F. A group decision making model dealing with comparative linguistic expressions based on hesitant fuzzy linguistic term sets. Inf. Sci. 2013, 241, 28–42. [Google Scholar] [CrossRef]
- Rodríguez, R.M.; Martínez, L. An analysis of symbolic linguistic computing models in decision making. Int. J. Gen. Syst. 2013, 42, 121–136. [Google Scholar] [CrossRef]
- Alonso, J.M.; Magdalena, L. An Experimental Study on the Interpretability of Fuzzy Systems. In Proceedings of the Joint 2009 International Fuzzy Systems Association World Congress and 2009 European Society of Fuzzy Logic and Technology Conference, Lisbon, Portugal, 20–24 July 2009; pp. 125–130. [Google Scholar]
- Razak, T.R.; Garibaldi, J.M.; Wagner, C.; Pourabdollah, A.; Soria, D. Towards a Framework for Capturing Interpretability of Hierarchical Fuzzy Systems—A Participatory Design Approach. IEEE Trans. Fuzzy Syst. 2020. [Google Scholar] [CrossRef]
- Gacto, M.J.; Galende, M.; Alcalá, R.; Herrera, F. METSK-HDe: A multiobjective evolutionary algorithm to learn accurate TSK-fuzzy systems in high-dimensional and large-scale regression problems. Inf. Sci. 2014, 276, 63–79. [Google Scholar] [CrossRef]
- Gacto, M.J.; Alcalá, R.; Herrera, F. Interpretability of linguistic fuzzy rule-based systems: An overview of interpretability measures. Inf. Sci. 2011, 181, 4340–4360. [Google Scholar] [CrossRef]
- Guillaume, S.; Charnomordic, B. Generating an interpretable family of fuzzy partitions from data. IEEE Trans. Fuzzy Syst. 2004, 12, 324–335. [Google Scholar] [CrossRef]
- Guillaume, S. Designing fuzzy inference systems from data: An interpretability-oriented review. IEEE Trans. Fuzzy Syst. 2001, 9, 426–443. [Google Scholar] [CrossRef]
- Layne, J.R.; Passino, K.M. Fuzzy model reference learning control. J. Int. Fuzzy Syst. 1996, 4, 33–47. [Google Scholar] [CrossRef]
- Layne, J.R.; Passino, K.M.; Yurkovich, S. Fuzzy learning control for antiskid braking systems. IEEE Trans. Control Syst. Technol. 1993, 1, 122–129. [Google Scholar] [CrossRef]
- Passino, K.; Yurkovich, C. Fuzzy Control; Laura, C., Ed.; Addison Wesley: Menlo Park, CA, USA, 1998. [Google Scholar]
- Yager, R.; Filev, D. Essentials of Fuzzy Modeling and Control; John Wiley and Sons: New York, NY, USA, 1994. [Google Scholar]
- Dhimish, M.; Holmes, V.; Mehrdadi, B.; Dales, M. Comparing Mamdani Sugeno fuzzy logic and RBF ANN network for PV fault detection. Renew. Energy 2018, 117, 257–274. [Google Scholar] [CrossRef]
- Ma, X.; Hu, Z.; Liu, J.; Peng, N.; Neubig, G.; Hovy, E. Stack-pointer networks for dependency parsing. arXiv 2018, arXiv:1805.01087. [Google Scholar]
- Hu, Z.; Yang, Z.; Salakhutdinov, R.; Xing, E. Deep neural networks with massive learned knowledge. In Proceedings of the 2016 Conference on Empirical Methods in Natural Language Processing, Austin, TX, USA, 1–5 November 2016; pp. 1670–1679. [Google Scholar]
- Chen, L.; Zhou, M.; Wu, M.; She, J.; Liu, Z.; Dong, F.; Hirota, K. Three-layer weighted fuzzy support vector regression for emotional intention understanding in human–robot interaction. IEEE Trans. Fuzzy Syst. 2018, 26, 2524–2538. [Google Scholar] [CrossRef]
- Hu, Z.; Ma, X.; Liu, Z.; Hovy, E.; Xing, E. Harnessing deep neural networks with logic rules. In Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics 2016, Berlin, Germany, 7–12 August 2016. arXiv:1603.06318.. [Google Scholar]
- Fan, L. Revisit fuzzy neural network: Demystifying batch normalization and ReLU with generalized hamming network. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Tanaka, H.; Fan, L.T.; Lai, F.S.; Toguchi, K. Fault-tree analysis by fuzzy probability. IEEE Trans. Reliab. 1983, 32, 453–457. [Google Scholar] [CrossRef]
- Fan, L. Deep Epitome for Unravelling Generalized Hamming Network: A Fuzzy Logic Interpretation of Deep Learning. arXiv 2017, arXiv:1711.05397. [Google Scholar]
- Chomsky, N. Minimalist Inquiries: The Framework. In Step by Step: Essays on Minimalist Syntax in Honor of Howard Lasnik; Martin, R., Michaels, D., Uriagereka, J., Eds.; MIT Press: Cambridge, MA, USA, 2000; pp. 89–156. ISBN 026213361X. [Google Scholar]
- Fortin, F.A.; De Rainville, F.M.; Gardner MA, G.; Parizeau, M.; Gagné, C. DEAP: Evolutionary algorithms made easy. J. Mach. Learn. Res. 2012, 13, 2171–2175. [Google Scholar]
- Bozorg-Haddad, O.; Solgi, M.; Loáiciga, H.A. Meta-Heuristic and Evolutionary Algorithms for Engineering Optimization; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Poizat, B. A Course in Model Theory: An Introduction to Contemporary Mathematical Logic; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Harrie, D.S. Philosophical and Mathematical Logic; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Tarski, A.; Mostowski, A.; Robinson, R.M. (Eds.) Undecidable Theories; Elsevier: Amsterdam, The Netherlands, 1953. [Google Scholar]
- Day, J.D.; Ganesh, V.; He, P.; Manea, F.; Nowotka, D. The satisfiability of word equations: Decidable and undecidable theories. In International Conference on Reachability Problems; Springer: Cham, Switzerland, 2018; pp. 15–29. [Google Scholar]
- Nicolescu, B.; Ertas, A. Transdisciplinary Theory, and Practice; The ATLAS Publishing: Lubbock, TX, USA, 2013. [Google Scholar]
- Fam, D.; Neuhauser, L.; Gibbs, P. Transdisciplinary Theory, Practice and Education; Springer International Publishing AG: Cham, Switzerland, 2018. [Google Scholar]
- Hinkel, J. Transdisciplinary Knowledge Integration; Wageningen University: Wageningen, The Netherlands, 2008. [Google Scholar]
- Sun, Y.; Wang, S.; Li, Y.; Feng, S.; Chen, X.; Zhang, H.; Tian, X.; Zhu, D.; Tian, H.; Wu, H. Ernie: Enhanced representation through knowledge integration. arXiv 2019, arXiv:1904.09223. [Google Scholar]
- Hylton, P. Russell, Idealism and the Emergence of Analytic Philosophy; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Lebens, S. Russell and Bradley: Rehabilitating the Creation Narrative of Analytic Philosophy. J. Hist. Anal. Philos. 2017, 5. [Google Scholar] [CrossRef]
- Hanna, R. Kant and nonconceptual content. Eur. J. Philos. 2005, 13, 247–290. [Google Scholar] [CrossRef]
- Hanna, R. Kant and the Foundations of Analytic Philosophy; Clarendon Press: Oxford UK, 2001. [Google Scholar]
- Beall, J.; Restall, G. Logical Pluralism; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Kouri Kissel, T. Logical pluralism from a pragmatic perspective. Australas. J. Philos. 2018, 96, 578–591. [Google Scholar] [CrossRef]
- Wittgenstein, L. Tractatus Logico-Philosophicus [TLP]; Ogden, C.K., Translator; Harcourt, Brace and Company: New York, NY, USA, 1922. [Google Scholar]
- Wittgenstein, L.; dos Santos, L.H.L. Tractatus Logico-Philosophicus; Edusp.: New York, NY, USA, 1994. [Google Scholar]
- Carnap, R. Meaning and Necessity: A Study in Semantics and Modal Logic; University of Chicago Press: Chicago, IL, USA; London, UK, 1988; Volume 30. [Google Scholar]
- Carnap, R. The Logical Syntax of Language; Open Court Publishing: London, UK, 2002. [Google Scholar]
- Allchin, D. Values in Science and in Science Education. In International Handbook of Science Education; Fraser, B.J., Tobin, K.G., Eds.; Kluwer Academic Publishers: Amsterdam, The Netherlands, 1988; Volume 2, pp. 1083–1092. [Google Scholar]
- White, J.M.; Martin, T.F.; Adamsons, K. Family Theories: An Introduction; Sage Publications: Thousand Oaks, CA, USA, 2018. [Google Scholar]
- Liu, X.F.; Jiang, X.J.; Liu, S.H.; Tse, C.K. Knowledge discovery in cryptocurrency transactions: A survey. IEEE Access 2021, 9, 37229–37254. [Google Scholar] [CrossRef]
- Frawley, W.J.; Piatetsky-Shapiro, G.; Matheus, C.J. Knowledge discovery in databases: An overview. Ai Mag. 1992, 13, 57. [Google Scholar]
- Studer, R.; Benjamins, V.R.; Fensel, D. Knowledge engineering: Principles and methods. Data Knowl. Eng. 1998, 25, 161–197. [Google Scholar] [CrossRef]
- Keeney, R.L. Decision analysis: An overview. Oper. Res. 1982, 30, 803–838. [Google Scholar] [CrossRef] [PubMed]
- Llorente-Peralta, C.E.; Cruz-Reyes, L.; Espín-Andrade, R.A. Knowledge Discovery Using an Evolutionary Algorithm and Compensatory Fuzzy Logic. Fuzzy Log. Hybrid Ext. Neural Optim. Algorithms: Theory Appl. 2021, 940, 363. [Google Scholar]
- González-Caballero, E.; Espín-Andrade, R.A. Aplicación de solución difusa de la negociación a tres casos de estudio. Ing. Ind. 2014, 35, 199–213. [Google Scholar]
- Espin, R.; Fernandez, E.; Mazcorro, G.; Lecich, M.I. A fuzzy approach to cooperative n-person games. Eur. J. Oper. Res. 2007, 176, 1735–1751. [Google Scholar] [CrossRef]
- Espin Andrade, R.A. A fuzzy logic model to predict a negotiation result. Comput. Y Sist. 1999, 3, 15–28. [Google Scholar]
- González, E.; Espín, R.A.; Mazcorro, G. Fuzzy negotiation solutions of N-person cooperative games by knowledge engineering in bargaining. Group Decis. Negot. 2012, 21, 133–152. [Google Scholar] [CrossRef]
- González, E.; Andrade, R.A.E.; Fernández, E. Negotiation based on Fuzzy Logic and Knowledge Engineering: Some Case Studies. Group Decis. Negot. 2016, 25, 373–397. Available online: http://link.springer.com/article/10.1007/s10726-015-9446-6 (accessed on 30 April 2021). [CrossRef]
- González, E.; Espín, R.A.; Mazcorro, G.; Muñoz, S. Rationality of two fuzzy negotiation solutions by knowledge engineering to n-person cooperative games. In Fourth International Workshop on Knowledge Discovery; Knowledge Management and Decision Support; Atlantis Press: Paris, France, 2013. [Google Scholar]
- Andrade, R.A.E.; González, E.; Fernández, E.; Alonso, M.M. Compensatory Fuzzy Logic Inference. In Soft computing for Business Intelligence; Espin, R., Pérez, R.B., Cobo, A., Marx Gómez, J., Valdés, A.R., Eds.; Studies on Computational Intelligence Series; Springer: Berlin/Heidelberg, Germany, 2014; pp. 23–42. ISBN 978-3-642-53737-0. [Google Scholar]
- Solares, E.; Coello, C.A.C.; Fernandez, E.; Navarro, J. Handling uncertainty through confidence intervals in portfolio optimization. Swarm Evol. Comput. 2019, 44, 774–787. [Google Scholar] [CrossRef]
- Meschino, G.J.; Nabte, M.; Gesualdo, S.; Monjeau, A.; Passoni, L.I. Fuzzy Tree Studio: A tool for the design of the Scorecard for the Management of Protected Areas. In Soft Computing for Business Intelligence; Springer: Berlin/Heidelberg, Germany, 2014; pp. 99–112. [Google Scholar]
- Espín, R.; Gomez, J.M.; Hernández, M.; Leeich, M. Logical management: Fuzzy logic integrated models for decision making in enterprises. In Proceedings of the World Automation Congress, Seville, Spain, 28 June–1 July 2004; IEEE: New York, NY, USA, 2004; Volume 17, pp. 369–378. [Google Scholar]
- Universe. Available online: https://www.eurekascommunity.org/eureka-universe-eu (accessed on 28 April 2021).
- Padron-Tristan, J.F.; Cruz-Reyes, L.; Espin-Andrade, R.A.; Fraire-Huacuja, H.J.; Castellanos-Alvarez, A.; Llorente-Peralta, C.E. Eureka-Universe (2.8.4_1). 2020. Available online: https://www.dropbox.com/s/tfer1ac5ftx2yjw/eureka-client-2.8.4_1.jar?dl=0 (accessed on 28 April 2021).
- Cruz-Reyes, L.; Espin-Andrade, R.A.; Irrarragorri, F.L.; Medina-Trejo, C.; Tristán, J.F.P.; Martinez-Vega, D.A.; Peralta, C.E. Use of Compensatory Fuzzy Logic for Knowledge Discovery Applied to the Warehouse Order Picking Problem for Real-Time Order Batching. In Handbook of Research on Metaheuristics for Order Picking Optimization in Warehouses to Smart Cities; Ochoa Ortiz-Zezzati, A., Rivera, G., Gómez-Santillán, C., Sánchez–Lara, B., Eds.; IGI Global: Hershey, PA, USA, 2019; pp. 62–88. Available online: https://www.igiglobal.com/book/handbookresearchmetaheuristics-order-picking/214899 (accessed on 1 May 2021).
- Fernandez, E.; Navarro, J.; Solares, E.; Coello, C.C. Using evolutionary computation to infer the decision maker’s preference model in presence of imperfect knowledge: A case study in portfolio optimization. Swarm Evol. Comput. 2020, 54, 100648. [Google Scholar] [CrossRef]
- Eureka Universe Real Case Studies. Available online: https://www.eurekascommunity.org/eureka-universe-eu/learning-about-eu/other-documents (accessed on 29 April 2021).
- Espin-Andrade, R.A. (n.d.). Eurekas Community. Cases of Use. Available online: https://www.eurekascommunity.org/eureka-universe-eu/learning-about-eu/cases-of-use/cases-of-use-documents (accessed on 20 April 2021).
- Gonzalez, M. Classification of over-segmented regions result of the watershed transform through Compensatory Fuzzy Logic. In Towards a Trans-disciplinarian Technology for Business Intelligence: Gathering Knowledge Discovery, Knowledge Management and Decision Making; Espin, R., Marx, J., Racet, A., Eds.; Editorial Shaker Verlag: Düren, Germany, 2011; pp. 161–168. ISBN 9783832297183. [Google Scholar]
- González, M.A.; Ballarin, V.L.; Espin Andrade, R.A.; Meschino, G.J. Classification of over-segmented regions result of the Watershed Transform through Compensatory Fuzzy Logic. Alio-Inf. Jt. Int. Meet. 2011, 161–168. [Google Scholar] [CrossRef]
- Meschino, G.J.; Ballarin, V.L.; Espin-Andrade, R.A. Image segmentation with predicates analysis and Compensatory Fuzzy Logic. In Towards a Transdisciplinary Technology for Business Intelligence: Gathering Knowledge Discovery, Knowledge Management and Decision Making; Shaker Verlag: Düren, Germany, 2011; pp. 210–225. [Google Scholar]
- Comas, D.S.; Pastore, J.I.; Bouchet, A.; Ballarin, V.L.; Passoni, L.I.; Meschino, G.J. Diseño automático de Sistemas de Lógica Difusa Tipo 2 mediante Mapas Auto-organizados. In Proceedings of the Quinto Torneo Regional De Inteligencia Computacional, Cordova, Argentina, 1 April 2012; pp. 1–8. [Google Scholar]
- Meschino, G.J.; Andrade, R.E.; Ballarin, V.L. A framework for tissue discrimination in Magnetic Resonance brain images based on predicates analysis and Compensatory Fuzzy Logic. Int. J. Intell. Comput. Med. Sci. Image Process. 2008, 2, 207–222. [Google Scholar] [CrossRef]
- Bouchet, A.; Pastore, J.I.; Andrade, R.E.; Brun, M.; Ballarin, V. Arithmetic mean based compensatory fuzzy logic. Int. J. Comput. Intell. Appl. 2011, 10, 231–243. [Google Scholar] [CrossRef]
- Bouchet, A.; Pastore, J.I.; Espin-Andrade, R.A.; Brun, M.; Ballarin, V.L. Compensatory Logic applied to Digital Image Processing. In Towards a Transdisciplinary Technology for Business Intelligence: Gathering Knowledge Discovery, Knowledge Management and Decision Making; Shaker Verlag: Düren, Germany, 2011; pp. 226–235. [Google Scholar]
- Bouchet, A.; Meschino, G.J.; Brun, M.; Espín, R.A.; Ballarin, V. Linguistic Interpretation of Mathematical Morphology. In Studies on Knowledge Discovery, Knowledge Management, and Decision Making; Advances in Intelligent Systems Research Series; Atlantis Press: Paris, France, 2013. [Google Scholar]
- Meschino, G.J. Modelos Híbridos de Inteligencia Computacional aplicados en la Segmentación de Imágenes de Resonancia Magnética. Ph.D. Thesis, Universidad nacional de Mar del Plata, Facultad de Ingenierıa, Deán Funes, Argentina, 10 October 2008. [Google Scholar]
- Ortega, P.M.M.; Andrade, R.E.; Gómez, J.M. Multivalued Fuzzy Logics: A Sensitive Analysis. In Fourth International Workshop on Knowledge Discovery, Knowledge Management and Decision Support; Atlantis Press: Paris, France, 2013; pp. 1–7. [Google Scholar]
- Andrade, R.A.E.; Vanti, A.A. Administración Lógica: Un estudio de caso en una empresa de Comercio Exterior. Rev. Base (Adm. E Contab.) Da Unisinos 2005, 2, 69–77. [Google Scholar]
- Espin-Andrade, R.A. SWOT-OA Fuzzy Analysis for Strategic Plan Evaluation and Decision Making Support. In Towards a Trans-disciplinarian Technology for Business Intelligence: Gathering Knowledge Discovery, Knowledge Management and Decision Making; Espin, R., Marx, J., Racet, A., Eds.; Editorial Shaker Verlag: Düren, Germany, 2011; pp. 89–111. ISBN 9783832297183. [Google Scholar]
- Vanti, A.; Espin-Andrade, R.A. The importance of objectives and strategic lagging and leading indicators definition in the chain import and export process in the light of strategic planning through the use of Fuzzy Logic System. In Proceedings of the 2006 ACM SIGMIS CPR Session 6.2, Claremont, CA, USA, 13–15 April 2006; pp. 190–197. [Google Scholar]
- Vanti, A.A.; Espin, R. Metodologia multivalente para priorização estratégica em construção de Balanced Scorecard (BSC). Rev. Ccei 2007, 11, 54–67. [Google Scholar]
- Vanti, A.A.; Espin, R.; Perez-Soltero, A.; Ciotta, D. Strategic Themes for Balanced Scorecard Construction Based on Fuzzy Logic. Int. J. Appl. Manag. Technol. 2008, 6, 4–39. [Google Scholar]
- Cárdenas, M.L.S.; del Rio, D.R.P.; Fernández, T.D.; Fernández, M.D. Enfoque de Integración Basado en Datos Enlazados Empresariales. Rev. Cubana Adm. Pública Empresarial 2018, 2, 268–279. [Google Scholar]
- Delgado-Fernández, T.; Lance, K.; Buck, M.; Onsrud, H. Assessing an SDI Readiness Index. FIG Working Week and GSDI-8. 2005, pp. 16–21. Available online: https://www.fig.net/pub/cairo/papers/ts_36/ts36_03_delgado_etal.pdf (accessed on 28 April 2021).
- Fernández, T.D.; Fernández, M.D.; Andrade, R.E. The Spatial Data Infrastructure Readiness model and its worldwide application. In Multi-View Framew. Assess SDIs; Crompvoets, J., Rajabifard, A., Van Loenen, B., Fernández, T.D., Eds.; Geo-Information (RGI); The University of Melbourne: Melbourne, Australia, 2008; pp. 117–134. [Google Scholar]
- Dechkova, D.; Miranda, R. Introduction of Sustainability Report in an Enterprise: Decision Making Model Based on Compensatory Fuzzy Logic. In Soft Computing for Business Intelligence; Espin, R., Pérez, R.B., Cobo, A., Marx Gómez, J., Valdés, A.R., Eds.; Series Studies in Business Intelligence; Springer: Berlin/Heidelberg, Germany, 2014; pp. 247–272. [Google Scholar]
- Fernandez, E.; Navarro, J.; Solares, E.; Coello, C.C. A novel approach to select the best portfolio considering the preferences of the decision maker. Swarm Evol. Comput. 2019, 46, 140–153. [Google Scholar] [CrossRef]
- Espín-Andrade, R.A.; Fernández, E.; González, E. A logic system for reasoning and decision making: Compensatory Fuzzy Logic on Geometric Mean. Rev. Investig. Oper. 2012, 32, 230–245. (In Spanish) [Google Scholar]
- Espín-Andrade, R.A.; González, E.; Fernández, E.; Gutiérrez, S.M. A Fuzzy Approach to Prospect theory. In Soft Computing for Business Intelligence; Espin, R., Pérez, R.B., Cobo, A., Marx Gómez, J., Valdés, A.R., Eds.; Studies on Computational Intelligence Series; Springer: Berlin/Heidelberg, Germany, 2014; pp. 43–64. [Google Scholar]
- Gu, J.; Wang, Z.; Xu, Z.; Chen, X. A decision-making framework based on the prospect theory under an intuitionistic fuzzy environment. Technol. Econ. Dev. Econ. 2018, 24, 2374–2396. [Google Scholar] [CrossRef]
- Fernández, E.R.; Navarro, J.A.; Picos, J.C.; Espín, R.A. Un nuevo modelo para agregación de preferencias multicriterio basado en lógica difusa. Investig. Oper. 2018, 38, 216–237. [Google Scholar]
- Alonso, M.M.; Andrade, R.E. Knowledge discovery by Compensatory Fuzzy Logic predicates using a metaheuristic approach. In Fourth International Workshop on Knowledge Discovery, Knowledge Management and Decision Support; Atlantis Press: Paris, France, 2013; pp. 17–26. [Google Scholar]
- Cordovés, T.C.; Suárez, A.R.; Andrade, R.A.E. Knowledge Discovery by Fuzzy Predicates. In Soft Computing for Business Intelligence; Espin, R., Pérez, R.B., Cobo, A., Marx Gómez, J., Valdés, A.R., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 187–196. [Google Scholar]
- Ambriola, V.; Gervasi, V. Processing natural language requirements. In Proceedings of the 12th IEEE International Conference Automated Software Engineering, Lake Tahoe, CA, USA, 2–5 November 1997; pp. 36–45. [Google Scholar]
- Tuomi, I. Ontological Expansion. In Handbook of Anticipation: Theoretical and Applied Aspects of the Use of the Future in Decision Making; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]

| 1 TS-SLP | 2 LGCM | 3 LIDL | 4 TGG | 5 DLAR | |
|---|---|---|---|---|---|
| 1 SciV | x | x | x | ||
| 2. RMFL | x | x | |||
| 3 ATNLI | x | x | x | ||
| 4 GIFL | x | x | x | ||
| 5 DEA | x | x | |||
| 6 NARNLT | x | x | x | ||
| 7 FCD | x | x |
| 1 TS-SLP | 2 LGCM | 3 LIDL | 4 TGG | 5 DLAR | |
|---|---|---|---|---|---|
| 1 SciV | WKDFLP | WKDFLP | WKDFLP | ||
| 2. RMFL | THy | THy | |||
| 3 ATNLI | WKDFLP | WKDFLP | WKDFLP | ||
| 4 GIFL | THy | THy | THy | ||
| 5 DEA | THy | THy | |||
| 6 NARNLT | WKDFLP | WKDFLP | WKDFLP | ||
| 7 FCD | THy | THy |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Espin-Andrade, R.A.; Pedrycz, W.; Solares, E.; Cruz-Reyes, L. Transdisciplinary Scientific Strategies for Soft Computing Development: Towards an Era of Data and Business Analytics. Axioms 2021, 10, 93. https://doi.org/10.3390/axioms10020093
Espin-Andrade RA, Pedrycz W, Solares E, Cruz-Reyes L. Transdisciplinary Scientific Strategies for Soft Computing Development: Towards an Era of Data and Business Analytics. Axioms. 2021; 10(2):93. https://doi.org/10.3390/axioms10020093
Chicago/Turabian StyleEspin-Andrade, Rafael A., Witold Pedrycz, Efrain Solares, and Laura Cruz-Reyes. 2021. "Transdisciplinary Scientific Strategies for Soft Computing Development: Towards an Era of Data and Business Analytics" Axioms 10, no. 2: 93. https://doi.org/10.3390/axioms10020093
APA StyleEspin-Andrade, R. A., Pedrycz, W., Solares, E., & Cruz-Reyes, L. (2021). Transdisciplinary Scientific Strategies for Soft Computing Development: Towards an Era of Data and Business Analytics. Axioms, 10(2), 93. https://doi.org/10.3390/axioms10020093







