1. Introduction
Recently, the so-called Parrondo’s paradox (see, e.g., [
1,
2,
3]) has received the attention of many researchers. Although it appears in game theory, the dynamic version can be stated in terms of chaotic and non-chaotic behavior. Briefly (see, e.g., [
4]), we consider two discrete dynamical systems given by continuous maps
,
, on a metric space
X, usually a subset of
,
. The Parrondo’s paradox appears when the dynamical behavior of both maps is simple (respectively, chaotic) and that of
is chaotic (respectively, simple). Of course, this paradox can involve more maps (see, e.g., [
5]). Mathematical examples includes interval dynamics (see [
5,
6]), dynamics of complex maps (see [
7,
8]), local stability problems ([
9,
10]), etc. In addition, we can find applications of this paradox to physics (see [
11,
12]), biology (see [
13,
14,
15]) and social sciences (see [
16,
17]).
In this paper, we study this paradox for interval continuous maps which are piecewise linear. More precisely, we consider continuous interval maps
for which there is a finite partition
P given by
such that the restriction
is linear. Note that
f is piecewise monotone because there is a subpartition of
P such that
,
, is monotone. We denote by
the number of monotone pieces of
f. Then, the topological entropy of
f is given by (see, e.g., [
18] [Chapter 4])
where
, for
,
. It is well-known that positive topological entropy implies the existence of some kind of complex behavior. For instance, for positive entropy maps, there exists an uncountable subset
such that for each pair of distinct points
we have that
This is the well-known definition of chaos in the sense of Li and Yorke (see [
19]).
The Parrondo’s paradox appears in terms of topological entropy when two zero (respectively, positive) topological entropy maps
holds that
(respectively,
). This paradox has been shown in several models (see, e.g., [
11,
20]). Now, we analyze it for continuous piecewise linear maps. The results and necessary background can be find in the next section. A section with conclusions finishes the paper.
2. The Results
By a discrete dynamical system we mean the pair , where X is a metric space and is continuous. For , its orbit is given by the recursive sequence . In this paper, .
Let
be the tent map given by
The parameter
is called the slope of
. A piecewise continuous linear map is called of constant slope
s if the slope of its linear pieces is either
s or
. It is known (see, e.g., [
18], Chapter 4) that piecewise continuous linear maps with constant slope
have topological entropy
. Therefore,
if
and zero otherwise.
It is easy to see that , , is a piecewise linear continuous map with constant slope . Then, . Thus, if both and are smaller than or equal to one, and if they are greater than one . The conclusion is that there is no Parrondo’s paradox of any type. This is true for any piecewise linear continuous map with constant slope.
Thus, we consider maps with two different slopes. Namely, let
be the map
where
and
. This map is strictly increasing, and then
and the property
holds. We say that the map
is of Type 1 if
and of Type 2 if
. Note that
for Type 1 and
for Type 2 when
.
Next, we fix
,
and
and consider the maps
and
. These maps have the same topological entropy (see [
21]), and then we can work with both of them producing the same results. Let us analyze if the Parrondo’s paradox “simple + simple = complex” happens for these maps. More precisely, we study the relationship between the topological entropies of
and
. We start by proving the following easy lemmas.
Lemma 1. The map has a unique maximum .
Proof. It is straightforward. □
Lemma 2. Assume that . Then, has constant slope .
Proof. Note that
. Then,
and the proof concludes. □
The above lemma suggests that working with
instead of
is a good idea. We can compute its topological entropy in this particular case. On the other hand, the maximum is always 1/2, and, then, programming the algorithm from Block et al. [
22] used for numerical computation of the topological entropy of
is slightly simplified.
2.1. Maps of Type 1
First, we consider that . We can prove the following result.
Proposition 1. Let . Then, for all .
Proof. If
, the result follows by Lemma 2 since
. Thus, let
and let
be such that
. Note that
. On the other hand,
. Since
is piecewise linear, we have that
. Since, by [
18] [Chapter 4],
and
is increasing, we have that
, and the proof concludes. □
The above proposition shows that Parrondo’s paradox is not possible for maps of Type 1. It can be generalized for maps with as follows.
Proposition 2. Let and let and p be such that . Then, .
Proof. It is analogous to that of Proposition 1. □
At this moment, we have obtained that, if the hypothesis of Propositions 1 or 2 are fulfilled, then
. One might think that this inequality holds for any map
.
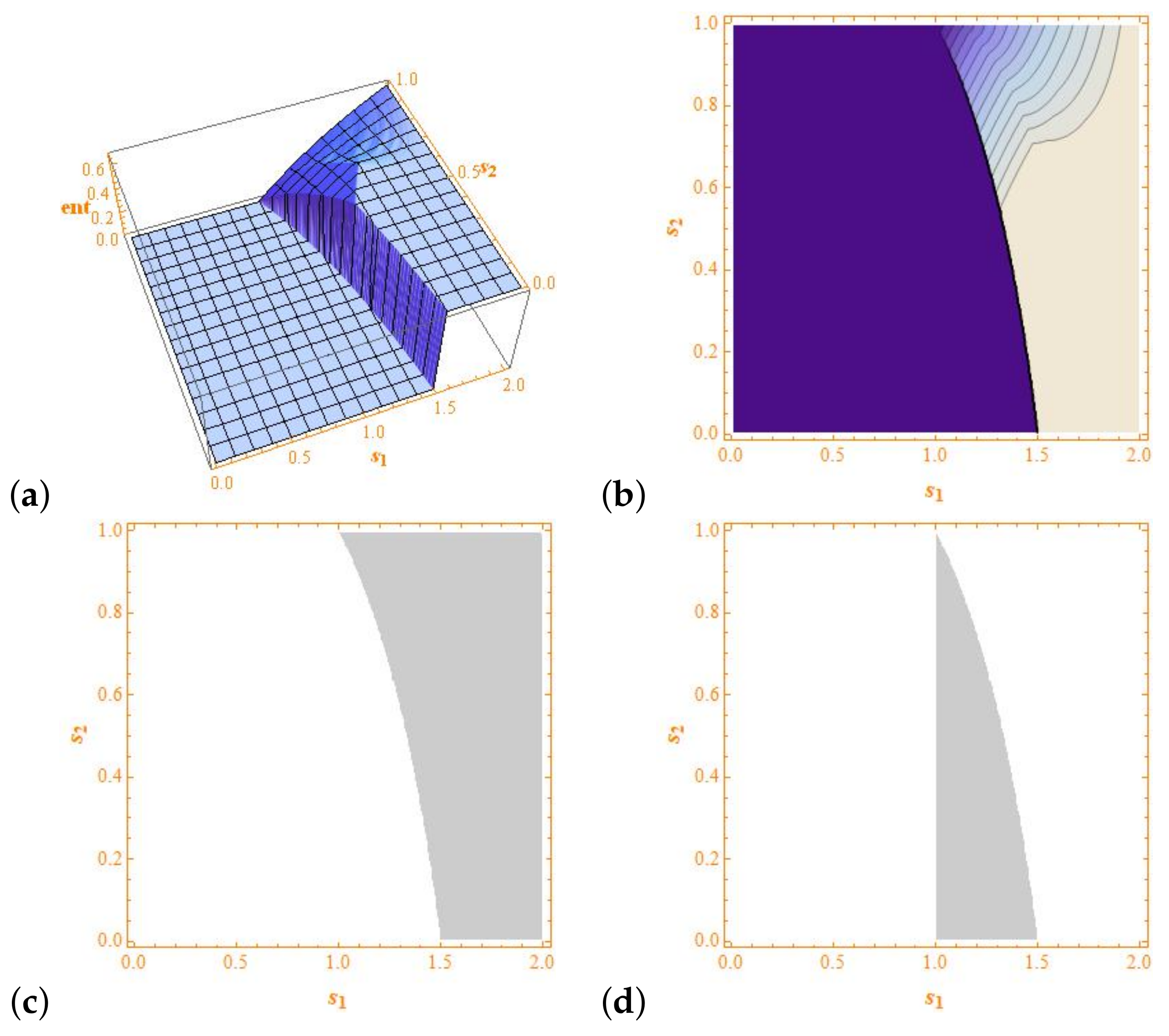
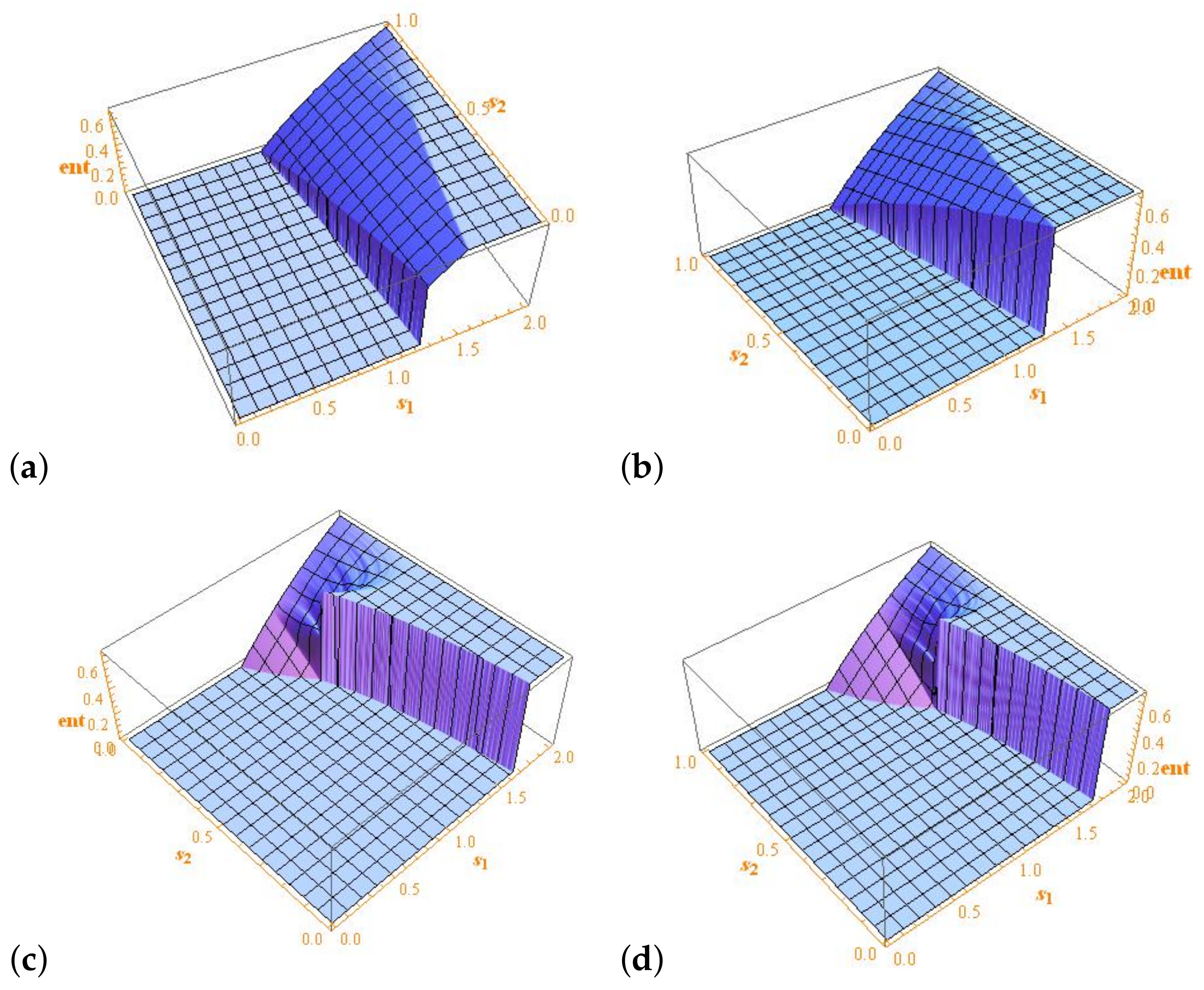
Figure 1 shows the computation of the topological entropy of
with prescribed accuracy using the algorithm from [
22]. We use Mathematica, which can work properly with infinite precision with linear maps, and, thus, our computations are not affected by round-off effects. Note that there is not a clear relationship between the topological entropies of the tent and the modified tent maps. In
Figure 2, we explore the variation of the parameter
p.
It is important to realize what it means that the algorithm from Block et al. [
22] is free of round-off effects. This algorithm depends on the so-called kneading sequences. For a unimodal map
f with maximum at
c, its kneading sequence is
such that, for
,
if
,
if
and
if
. Since we work without round-off effects, this kneading sequence is free of them. The set of possible kneading sequences can be endowed with order relationship such that, if
g is another unimodal map with kneading sequence
and
, then
. Thus, when we are able to state that either
or
for some
, as, in
Figure 1c,d, we give a computed-assisted proof of that inequalities.
2.2. Maps of Type 2
Next, we consider the case . We can prove the following result.
Theorem 1. Let be such that . Then, .
Proof. By Lemma 2, the map has constant slope . Then, the proof follows easily. □
The above result shows that it is possible to combine two zero topological entropy maps to obtain positive topological entropy, and therefore Parrondo’s paradox is possible. Moreover, as
, we have that
and hence
whenever
. Note that otherwise
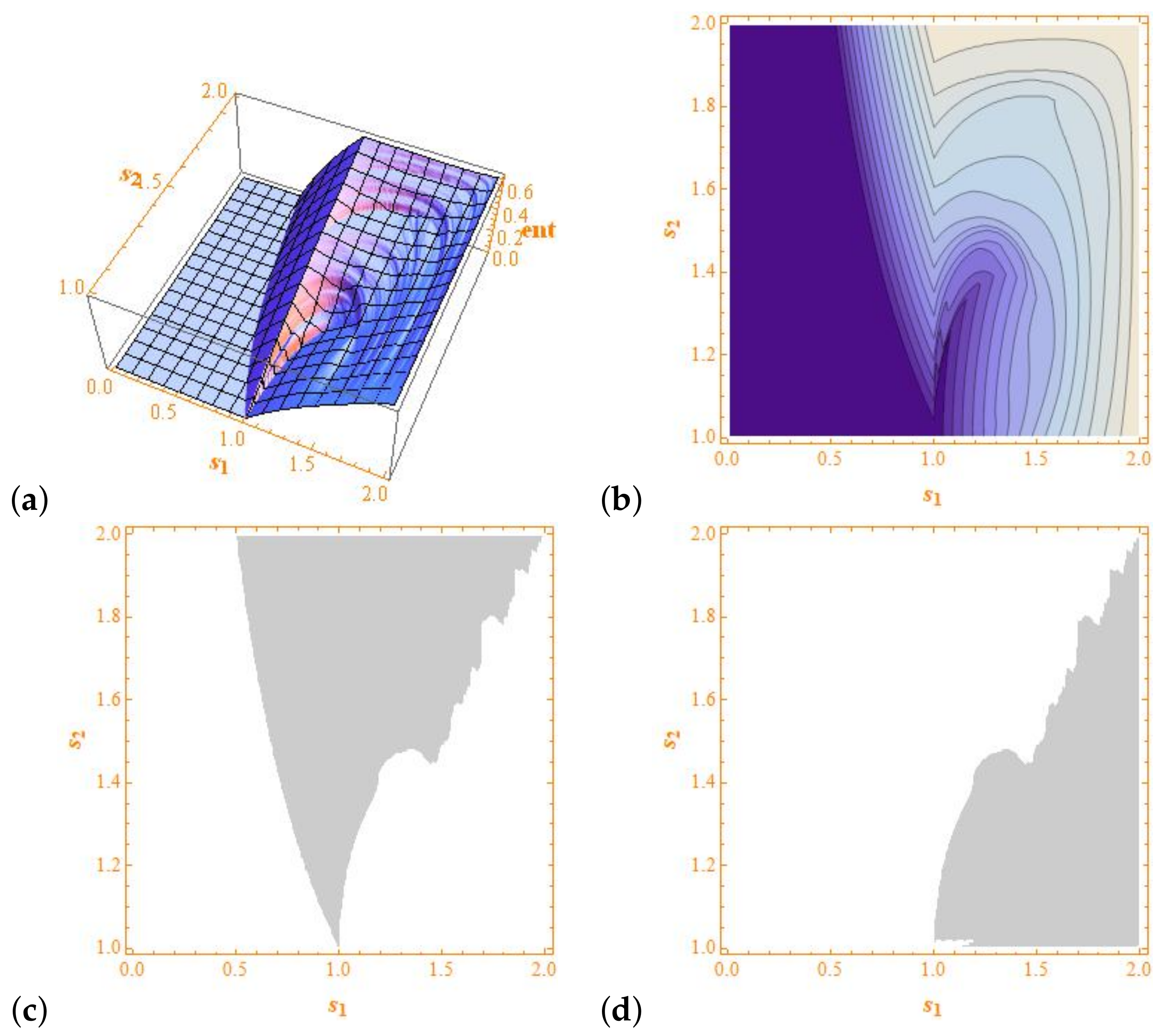
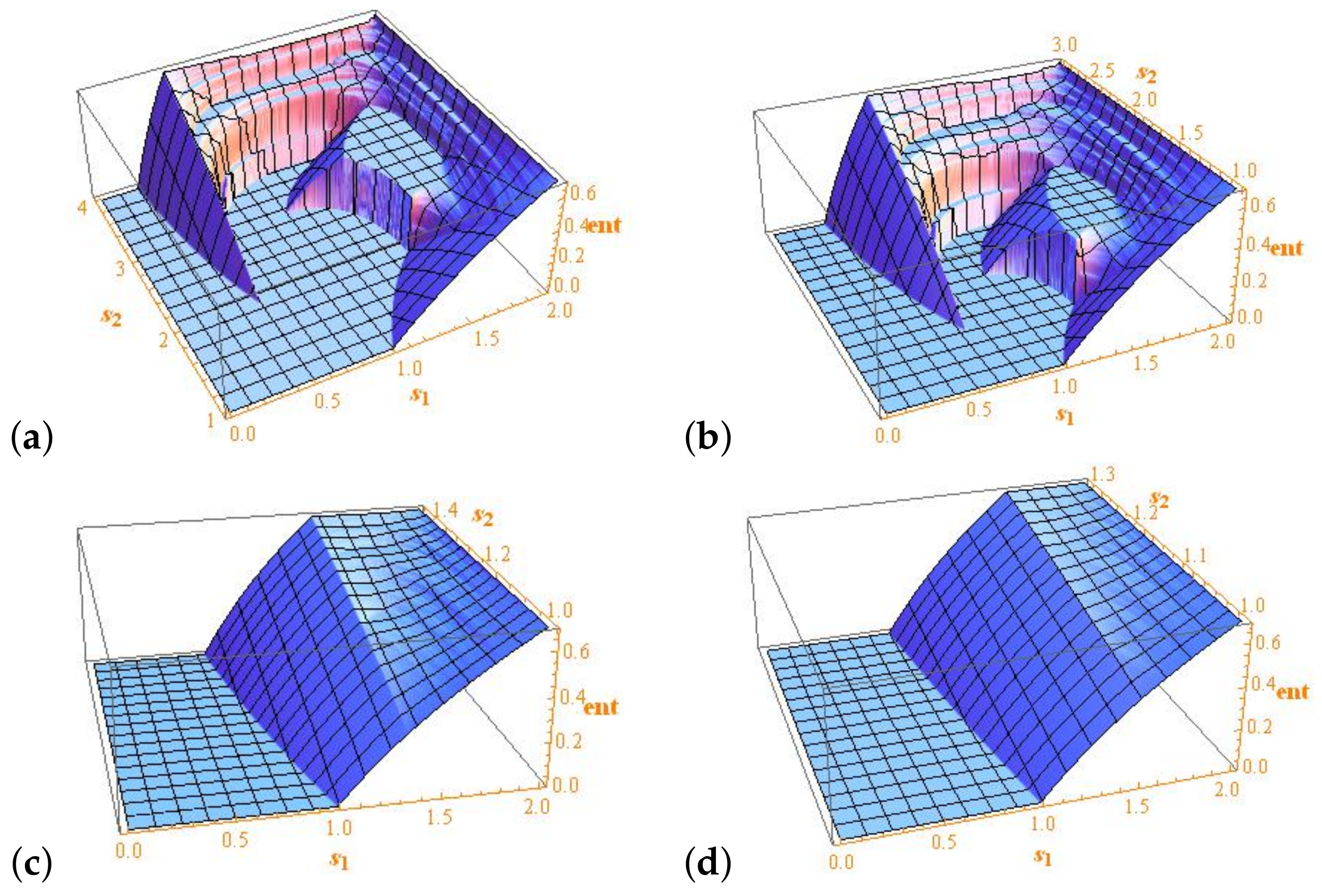
. Numerical computations with prescribed accuracy are shown in
Figure 3. Note that
can be greater and lower than
when
. Note that, as above, our computations are free of round-off errors. In
Figure 4, we explore the variation of the parameter
p.
3. Conclusions
We analyze the Parrondo’s paradox for the family of tent maps proving that no paradox is possible if we combine two maps in the family. However, the paradox “simple + simple = complex” is possible when we combine a tent map with a homeomorphism consisting on two linear pieces with different slopes changing the slope at
. Numerical computations show that there is not a clear relationship between the topological entropies of the tent and modified tent maps. We also find numerical evidence showing that as
p increases the topological entropy of the modified tent map decreases. The computations are made using an algorithm depending on kneading sequences, which can be computed without round off effects, and, therefore, they can be taken as a computer-assisted proof of the above-mentioned facts. It is unclear whether, for instance, the boundaries of the regions depicted in
Figure 1c,d and
Figure 3c,d can be obtained in an analytical way.