Singular Integral Neumann Boundary Conditions for Semilinear Elliptic PDEs

Abstract

In this article, we discuss semilinear elliptic partial differential equations with singular integral Neumann boundary conditions. Such boundary value problems occur in applications as mathematical models of nonlocal interaction between interior points and boundary points. Particularly, we are interested in the uniqueness of solutions to such problems. For the sublinear and subcritical case, we calculate, on the one hand, illustrative, rather explicit solutions in the one-dimensional case. On the other hand, we prove in the general case the existence and—via the strong solution of an integro-PDE with a kind of fractional divergence as a lower order term—uniqueness up to a constant.

1. Introduction

The aim of this article is to discuss (possibly singular) semilinear elliptic PDEs of the form

$$-\Delta u+c(·,u)=0\mathrm{in}\Omega \mathrm{with}c(x,u):={\int }_{\partial \Omega }b(x,y,u)dS\left(y\right)$$

(1)

on bounded $C^2$-domains $\Omega \subset {\mathbb{R}}^N$ subject to (possibly singular) integral Neumann boundary conditions

$$\frac{\partial u}{\partial \overrightarrow{n}}=Iu\mathrm{on}\partial \Omega \mathrm{with}\left(Iu\right)\left(y\right):={\int }_{\Omega }b(x,y,u\left(x\right))dx$$

(2)

for a (possibly singular) kernel $b:\Omega \times \partial \Omega \times \mathbb{R}\to \mathbb{R}$. Such integral boundary value problems occur in applications as mathematical models of nonlocal interaction between interior points and boundary points [1] and have been abstractly studied in the non-singular case by [2]. The linear case of Poisson’s problem and (non-integral) singular Neumann boundary conditions has been discussed in [3]; see [4] for the general linear case and [5] for nonlinear boundary conditions involving a measure. The existence of positive solutions to semilinear singular elliptic problems has been studied in [6] for homogeneous Dirichlet boundary conditions; for (non-integral) homogeneous Neumann boundary conditions, see [7]. For the semilinear problem (1) with (possibly singular) integral Neumann boundary condition (2), existence of very weak solutions $u\in L^p(\Omega )$, $1<p<\infty$, with zero average ${\int }_{\Omega }udx=0$ has been shown in [8] under the assumptions on b that

(A1)

$b:\Omega \times \partial \Omega \times \mathbb{R}\to \mathbb{R}$ is a Carathéodory function; i.e., $b(x,y,u)$ is measurable w.r.t. $(x,y)\in \Omega \times \partial \Omega$ for every $u\in \mathbb{R}$ and continuous w.r.t. u for a.e. $(x,y)\in \Omega \times \partial \Omega$.

(A2)

b is bounded by $\left|b(x,y,u)\right|\le b_0(x,y)+b_1(x,y){\left|u\right|}^r$ with non-negative functions satisfying $b_0(x,y){|x-y|}^{s+\frac{N-1}{q}}\in L^{q^{\prime }}(\Omega \times \partial \Omega )$ and $b_1(x,y){|x-y|}^{s+\frac{N-1}{q}}\in L^{\frac{p{q}^{\prime }}{p-r{q}^{\prime }}}(\Omega \times \partial \Omega )$ for some $1\le q<{\left(p^{\prime }\right)}^{*}$, $0\le r<max(p/q^{\prime },1)$ and $0<s<1$,

I.e., in the subcritical (w.r.t. $x,y$) and sublinear (w.r.t. u) case.

In this article, on the one hand, we discuss one-dimensional examples, which illustrate that without fixing the average ${\int }_{\Omega }udx$ the problem (1) and (2), has a one-dimensional continuum of solutions; on the other hand, we show that if the average ${\int }_{\Omega }udx$ is fixed, then problems (1) and (2), have a unique very weak solution under the additional assumption.

(A3)

$b(x,y,u)$ is monotone w.r.t. u for a.e. $(x,y)\in \Omega \times \partial \Omega$ with derivative $0\le \frac{\partial b}{\partial u}(x,y,u)\le b_2(x,y)$ bounded by a function satisfying $b_2(x,y){|x-y|}^{s+\frac{N-1}{q}}\in L^{\frac{p{q}^{\prime }}{p-q^{\prime }}}(\Omega \times \partial \Omega )$; particularly, we require $p^{\prime }<q<{\left(p^{\prime }\right)}^{*}$.

For example, $b(x,y,u):=b_0(x,y)+b_2(x,y)f\left(u\right)$ with $f\left(u\right):=\left\{\begin{array}{cc}u\hfill & \left|u\right|\le 1\hfill \\ \frac{1}{r}{\left|u\right|}^{r-1}u\hfill & \left|u\right|\ge 1\hfill \end{array}\right.$ for $0\le r<1$ and functions $b_0,b_2$ as in (A2), (A3), satisfies all three conditions. A main difference to previous results of other authors like [1,2] regarding PDEs with integral boundary conditions is that, here, the equation as well as the boundary condition may be singular.

2. Preliminaries

Let $\Omega \subset {\mathbb{R}}^N$ be a bounded domain. For an exponent $p\in [1,\infty ]$, we denote the dual exponent by $p^{\prime }:=\frac{p}{p-1}$, and the Sobolev conjugate by $p^{*}:=\frac{Np}{N-p}$ for $1\le p<N$ resp. Consider $p^{*}\in \mathbb{R}$ as arbitrary large for $p=N$ resp. Let $p^{*}:=\infty$ for $p>N$. Particularly, the dual of the Banach space $L^p(\Omega )$ of the p-integrable function u on $\Omega$ can be identified with $L^{p^{\prime }}(\Omega )$, the Sobolev embedding $W_0^{1,p}(\Omega )\subset L^{p^{*}}(\Omega )$ holds for $p\in [1,\infty ]$, and the embedding $W_0^{1,p}(\Omega )\subset \subset L^q(\Omega )$ is compact for $1\le q<p^{*}$ due to the Rellich–Kondrachov theorem. Hereby, $W^{1,p}(\Omega )$ denotes the Sobolev space of functions u on $\Omega$ having a p-integrable weak gradient $\nabla u$, and functions in $W_0^{1,p}(\Omega )$ additionally satisfy Dirichlet boundary conditions $u=0$ on $\partial \Omega$ in the sense of traces [9]. Similarly, $W^{2,p}(\Omega )$ denotes the Sobolev space of functions u on $\Omega$ having p-integrable second-order derivatives.

Let us exemplify the difference between strong, weak, and very weak solutions of linear elliptic partial differential equations (PDEs) by considering Poisson’s equation $-\Delta u=f$ for a right hand side (r.h.s.) f. If $u\in W^{2,p}(\Omega )$, then $-\Delta u=-div(\nabla u)=-{\displaystyle \sum _{i=1}^N}\frac{{\partial }^{2}u}{\partial x_i^2}$ is a p-integrable function; thus, for $f\in L^p(\Omega )$ it makes sense to require $-\Delta u=f$ almost everywhere (a.e.) in $\Omega$, and in this case, $u\in W^{2,p}(\Omega )$ is called a strong solution Poisson’s equation. Correspondingly, $A:W^{2,p}(\Omega )\to L^p(\Omega )$, $Au:=-\Delta u$, is called the strong realization of the negative Laplacian.

However, if the r.h.s. is merely a distribution $f\in {\left(W_0^{1,p^{\prime }}(\Omega )\right)}^{*}$, then the existence of strong solutions cannot be guaranteed. However, weak solutions $u\in W_0^{1,p}(\Omega )$ of Poisson’s equation subject to Dirichlet boundary conditions on $\partial \Omega$ may exist in the sense that

$$⟨Au,v⟩:={\int }_{\Omega }\nabla u·\nabla vdx=⟨f,v⟩$$

(3)

holds for every $v\in W_0^{1,p^{\prime }}(\Omega )$, and the operator $A:W_0^{1,p}(\Omega )\to {\left(W_0^{1,p^{\prime }}(\Omega )\right)}^{*}$ defined on the left hand side (l.h.s.) is called the weak realization of the negative Dirichlet–Laplacian. Note that the l.h.s. arises from ${\int }_{\Omega }(-\Delta u)vdx$ via partial integration using $v=0$ on $\partial \Omega$. If the r.h.s. is an even worse distribution $f\in {\left(\{v\in W^{2,p^{\prime }}(\Omega )|v=0\mathrm{on}\partial \Omega \}\right)}^{*}$, then another partial integration leads to the notion of a very weak solution.

Definition 1.

A function $u\in L^p(\Omega )$ is called a very weak solution of Poisson’s equation subject to Dirichlet boundary condition, if

$${\int }_{\Omega }u(-\Delta v)dx=⟨f,v⟩$$

(4)

is valid for every $v\in W^{2,p^{\prime }}(\Omega )$ with $v=0$ on $\partial \Omega$, and $A:L^p(\Omega )\to {\left(\{v\in W^{2,p^{\prime }}(\Omega )|v=0on\partial \Omega \}\right)}^{*}$ defined by letting $⟨Au,v⟩$ be the l.h.s. of (4) is called the very weak realization of the negative Dirichlet–Laplacian.

Note that during partial integration the term ${\int }_{\partial \Omega }u\frac{\partial v}{\partial \overrightarrow{n}}dx$ arises, but as the derivative of v in direction of the outer normal vector $\overrightarrow{n}$ along the boundary $\partial \Omega$ can be arbitrary, for functions f, validity of (4) ensures formally that u satisfies Dirichlet boundary conditions. Particularly, if ${\left(p^{\prime }\right)}^{*}>N$, then $\{v\in W^{2,p^{\prime }}(\Omega )|v=0\mathrm{on}\partial \Omega \}\subset W_0^{1,{\left(p^{\prime }\right)}^{*}}(\Omega )\subset C^{0,\alpha }\left(\overline{\Omega }\right)$ holds with $\alpha =1-\frac{N}{{\left(p^{\prime }\right)}^{*}}$ by Sobolev embeddings into Hölder spaces. Thus, if $b:\Omega \times \partial \Omega \to \mathbb{R}$ is a non-negative kernel not integrable over $\Omega \times \partial \Omega$, but satisfying ${b(x,y)|x-y|}^{\alpha }\in L^1(\Omega \times \partial \Omega )$, then for the possibly non-integrable function $f\left(x\right):={\int }_{\partial \Omega }b(x,y)dy$ on $\Omega$ it still makes sense to consider very weak solutions of (4), where the definition $⟨f,v⟩:={\int }_{\Omega }f\left(x\right)v\left(x\right)dx$ of the r.h.s. makes sense due to

$${\int }_{\Omega }\left|f\left(x\right)v\left(x\right)\right|dx={\int }_{\Omega }\left|{\int }_{\partial \Omega }b(x,y){|x-y|}^{\alpha }\frac{v\left(x\right)-v\left(y\right)}{{|x-y|}^{\alpha }}dy\right|dx\le \left({\int }_{\Omega }{\int }_{\partial \Omega }b(x,y){|x-y|}^{\alpha }dydx\right){\parallel v\parallel }_{C^{0,\alpha }},$$

where $v\left(y\right)=0$ for $y\in \partial \Omega$ is used. This case is very similar to Brézis problem, where Poisson’s equation $-\Delta u=f$ subject to Dirichlet boundary conditions $u=0$ on $\partial \Omega$ is considered for a measurable function $f\notin L^1(\Omega )$ satisfying ${\int }_{\Omega }\left|f\left(x\right)\right|dist(x,\partial \Omega )dx<+\infty$. Brézis et al. [10] (see also [11]) have proved the existence and uniqueness of a very weak solution $u\in L^1(\Omega )$ to this problem, and there is the notion of a very weak solution that prominently occurred for the first time. In this article, we are mainly interested in the very weak solution for the case of singular integral Neumann boundary conditions (instead of homogeneous Dirichlet boundary conditions) and semilinear (instead of linear) elliptic PDEs. To prove the existence and uniqueness, considering the above mentioned facts about Sobolev spaces, we used functional analytic methods like topological degree theory [12].

3. One-Dimensional Examples

In this section, we illustrate by one-dimensional examples—one example is linear but inhomogeneous; another one is sublinear but has vanishing r.h.s—that without fixing the average ${\int }_{\Omega }udx$, the problem (1) and (2), has a one-dimensional continuum of solutions.

3.1. A Linear Example with Singular Right Hand Side

Example 1

(in [8]). In the one-dimensional case of the interval $\Omega :=(0,1)$, where the boundary $\partial \Omega =\{0,1\}$ consists of two points, and for the kernel $b(x,0,u):=\frac{a(a-1)}{x^s}(u-1)$ containing a parameter $a\in \mathbb{R}$, $b(x,1,u):=0$, which is affine linear w.r.t. u and has a singularity of order $s>0$ as $x\searrow 0$, Equation (1) reads as $-u^{″}\left(x\right)+\frac{a(a-1)}{x^s}u\left(x\right)=\frac{a(a-1)}{x^s}$. In the special case $s=2$, this is an inhomogeneous Cauchy–Euler ODE, and every solution has the form

$$u\left(x\right)=C_1{x}^a+C_2{x}^{1-a}+1,C_1,C_2\in \mathbb{R}.$$

(5)

Note that u does not admit a classical derivative $-u^{\prime }\left(0\right)$ at $x=0$ for parameters $-1\le a<\frac{1}{2}$ except for $a=0$, or $a<0$ and $C_1=0$. The integral Neumann boundary conditions (2) read in this example formally as $-u^{\prime }\left(0\right)={\int }_0^1\frac{a(a-1)}{x^2}(u\left(x\right)-1)dx$ and $u^{\prime }\left(1\right)=0$. In other words, the outflow through the boundary point 0 is given by the integral ${\int }_0^1\frac{a(a-1)}{x^2}(u\left(x\right)-1)dx$; i.e., there is a nonlocal dependence of the outflow on a singularly weighted average of u over the domain, while there is no flow through the boundary point 1. Note that for every solution u of the form (5), the integral ${\int }_0^1\frac{a(a-1)}{x^2}(u\left(x\right)-1)dx$ is infinite within the parameter range $-1\le a<\frac{1}{2}$, except for $a=0$, or $a<0$ and $C_1=0$. Therefore, the integral Neumann boundary condition at the boundary point 0 reads formally as $\pm \infty =\pm \infty$ and thus is singular; i.e., there is an explosive inflow or outflow. Nonetheless, Equation (1) together with the singular integral Neumann boundary condition (2) at $x=0$ as well as the classical Neumann boundary condition $u^{\prime }\left(1\right)=0$ at $x=1$ (corresponding to $b(x,1,u):=0$) is satisfied for $-1<a<\frac{1}{2}$ by the integrable functions $u\left(x\right):=C((1-a)x^a-a{x}^{1-a})+1$ for arbitrary $C\in \mathbb{R}$ in the very weak sense that

$$-\underset{0}{\overset{1}{\int }}u\left(x\right)v^{″}\left(x\right)dx+\underset{0}{\overset{1}{\int }}\frac{a(a-1)}{x^2}(u\left(x\right)-1)(v\left(x\right)-v\left(0\right))dx=0$$

(6)

holds for every $v\in C^2\left([0,1]\right)$ with $v^{\prime }\left(0\right)=0=v^{\prime }\left(1\right)$. Thus, the very weak solutions of this singular integral boundary value problem form a one-dimensional affine linear subspace. Finally, fixing the average ${\int }_0^{1}u\left(x\right)dx$ determines the constant C and hence the solution uniquely.

3.2. A Semilinear Example with Sublinear Kernel

Example 2.

Again, consider the one-dimensional case $\Omega :=(0,1)$, now for the kernel $b(x,0,u):=\frac{1}{x^s}{u}^r$ with signed power $u^r:={\left|u\right|}^{r-1}u$, $b(x,1,u):=0$, which is sublinear for $0<r<1$ and has a singularity of order $s>0$ as $x\searrow 0$. Then, Equation (1) reads as $-u^{″}\left(x\right)+\frac{1}{x^s}{\left(u\left(x\right)\right)}^r=0$ and is called an Emden–Fowler or Thomas–Fermi equation. As this equation is a second-order ODE, its general solution contains two constants. The boundary condition $u^{\prime }\left(1\right)=0$ relates these constants by one equation. However, as the integral Neumann boundary condition $-u^{\prime }\left(0\right)={\int }_0^1\frac{1}{x^s}{\left(u\left(x\right)\right)}^{r}dx$ is simply implied by integrating the ODE $u^{″}\left(x\right)=\frac{1}{x^s}{\left(u\left(x\right)\right)}^r$ over Ω, it does not provide another equation for the constants. Hence, there is a one-dimensional continuum of solutions.

It remains to show that these solutions satisfy a singular Neumann BC at $x=0$ for $u^{\prime }\left(1\right)=0$ and $u\left(1\right)>0$ (and similarly for $u\left(1\right)<0$). Elementarily, $u\left(x\right)>0$ for $0<x\le 1$ implies due to $u^{″}\left(x\right)=\frac{1}{x^s}{\left(u\left(x\right)\right)}^r$ that $u^{″}$ is positive near x; i.e., u is strictly convex near x. Hence, $u^{\prime }\left(x\right)$ is strictly monotone increasing and, thus, due to $u^{\prime }\left(1\right)=0$ negative for $0<x<1$, so that $u\left(x\right)$ is strictly monotone decreasing and positive for $0<x\le 1$. In the weak formulation ${\int }_0^1{u}^{\prime }{v}^{\prime }dx+{\int }_0^1\frac{1}{x^s}{\left(u\left(x\right)\right)}^r(v\left(x\right)-v\left(0\right))dx=0$, put $v\left(x\right):=x^{s-1}$ to obtain ${\int }_0^1\frac{1}{x}{\left(u\left(x\right)\right)}^{r}dx=(s-1){\int }_0^1\frac{1}{x^{2-s}}(-u^{\prime }\left(x\right))dx$. As $u\left(x\right)\ge u\left(1\right)$, we obtain $+\infty =u{\left(1\right)}^r\left({\int }_0^1\frac{1}{x}dx\right)\le (s-1){\int }_0^1\frac{1}{x^{2-s}}(-u^{\prime }\left(x\right))dx$, and, hence, $|u^{\prime }\left(x\right)|=-u^{\prime }\left(x\right)$ tends to $+\infty$ as $x\to 0$ due to $2-s<1$ Therefore, for $s>1$ and $0<r<1$, every solution $u\not\equiv 0$ of $-u^{″}\left(x\right)+\frac{1}{x^s}{\left(u\left(x\right)\right)}^r=0$ on $\Omega =(0,1)$ to the boundary value $u^{\prime }\left(1\right)=0$ satisfies a singular Neumann boundary condition at $x=0$.

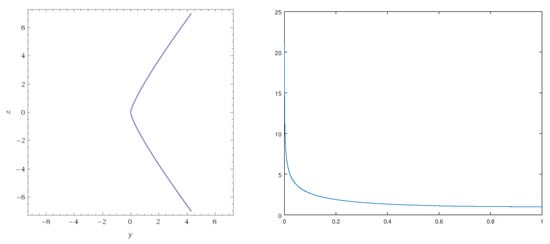
In the special case of $s=2$, solutions can be more precisely described by $u\left(x\right):=y(ln(x\left)\right)$, where $y\left(t\right)$ solves the autonomous ODE $-y^{″}\left(t\right)+y^{\prime }\left(t\right)+{\left(y\left(t\right)\right)}^r=0$ and t is related to x by $t:=ln\left(x\right)\le 0$. This autonomous ODE can principally be solved by substituting $z\left(y\right):=y^{\prime }\left(t\left(y\right)\right)$, which leads to the first-order ODE $z^{\prime }\left(y\right)=1+{\left|z\left(y\right)\right|}^{r-1}$. In the case $r=\frac{1}{2}$, we obtain by separation of variables the equation $\left|z\left(y\right)\right|-{2\left|z\left(y\right)\right|}^r{+2ln(1+|z\left(y\right)|}^r)=y-C$ with a constant $C\in \mathbb{R}$. As $z\left(y\left(t\right)\right)=y^{\prime }\left(t\right)$ holds, $y\left(t\right)$ satisfies the implicit ODE $|y^{\prime }\left(t\right)|-2|y^{\prime }{\left(t\right)|}^r+2ln(1+|y^{\prime }\left(t\right){|}^r)=y\left(t\right)-C$. A phase plot of y is shown in the left of Figure 1 for $C=0$, and a numerical solution u with $u^{\prime }\left(1\right)=0$ and $u\left(1\right)=1$ showing singularity at $x=0$ is plotted to the right in Figure 1.

Figure 1. Left: phase portrait; right: solution curve.

4. Existence

In this section, for dimensions $N>1$, let us briefly extend the proof of existence of very weak solutions from [8] to functions with an arbitrary pregiven average.

Theorem 1.

Let $\Omega \subset {\mathbb{R}}^N$ be a bounded $C^2$-domain and let $b:\Omega \times \partial \Omega \times \mathbb{R}\to \mathbb{R}$ be a kernel satisfying (A1) and (A2) for some $1<p<\infty$. Then, for every constant $a\in \mathbb{R}$, there exists $u\in L^p(\Omega )$, satisfying ${\int }_{\Omega }u\left(x\right)dx=a$, which solves (1) and (2) in the very weak sense that

$${\int }_{\Omega }u(-\Delta v)dx+{\int }_{\Omega }{\int }_{\partial \Omega }b(x,y,u\left(x\right))(v\left(x\right)-v\left(y\right))dS\left(y\right)dx=0$$

is valid for every $v\in W^{2,p^{\prime }}(\Omega )$ with $\frac{\partial v}{\partial \overrightarrow{n}}=0$ on $\partial \Omega$.

In the following, denote by

• D the subspace

  $$D:=\{v\in W^{2,p^{\prime }}(\Omega )|\frac{\partial v}{\partial \overrightarrow{n}}=0\mathrm{on}\partial \Omega \}\subset W^{2,p^{\prime }}(\Omega )$$

  (7)

  which has a compact embedding $D\subset \subset W^{1,q}(\Omega )$ for $q<{\left(p^{\prime }\right)}^{*}$.
• $W^{s,q}(\Omega ;\partial \Omega )$, the mixed fractional Sobolev space of order s and exponent q, which can be considered a space of functions v on $\overline{\Omega }$ such that ${v|}_{\Omega }$ is q-integrable over $\Omega$ and ${\displaystyle \frac{v\left(x\right)-v\left(y\right)}{{|x-y|}^{s+(N-1)/q}}}$ is q-integrable over $\Omega \times \partial \Omega$ (particularly, ${v|}_{\partial \Omega }\in L^q(\partial \Omega )$), where functions on $\overline{\Omega }$ are identified if they coincide a.e. on $\Omega$ and a.e. on $\partial \Omega$.
• $A:L^p(\Omega )\to D^{*}$,

  $$⟨Au,v⟩:={\int }_{\Omega }u(-\Delta v)dx,$$

  (8)

  the very weak realization of the negative Neumann–Laplacian $-\Delta$.
• $B:L^p(\Omega )\to {\left(W^{s,q}(\Omega ;\partial \Omega )\right)}^{*}$,

  $$⟨Bu,v⟩:={\int }_{\Omega }{\int }_{\partial \Omega }b(x,y,u\left(x\right))(v\left(x\right)-v\left(y\right))dS\left(y\right)dx$$

  the realization of the nonlinearity and the integral Neumann boundary conditions, which may be singular.

Proof of Theorem 1.

Restrict A and B to the closed affine linear subspace $U:=\{u\in L^p(\Omega )|{\int }_{\Omega }udx=a\}$ of $L^p(\Omega )$ (of codimension 1) so that A becomes injective. By (A1) and (A2), $B:L^p(\Omega )\to {\left(W^{s,q}(\Omega ;\partial \Omega )\right)}^{*}\subset {\left(W^{1,q}(\Omega )\right)}^{*}$ is a bounded continuous mapping which becomes compact when viewed as mapping into $D^{*}$ due to the compactness of $D\subset \subset W^{1,q}(\Omega )$. Thus, we can view $A+B$ as a perturbation of A by a compact operator B. To conclude, regarding the existence of very weak solutions $u\in L^p(\Omega )$ with ${\int }_{\Omega }udx=a$, we may apply topological degree theory as in [8], but for this, we need to exclude the existence of solutions with an arbitrarily large $L^p$-norm:

For $u\in L^p(\Omega )$ with ${\int }_{\Omega }udx=a$ let $v\in D$ be a strong solution of

$$-\Delta v={\left|u\right|}^{p-2}u-\lambda$$

(9)

subject to homogeneous Neumann boundary conditions $\frac{\partial v}{\partial \overrightarrow{n}}=0$ on $\partial \Omega$, where the constant $\lambda :=\frac{1}{|\Omega |}{\int }_{\Omega }{\left|u\right|}^{p-2}udx$ is chosen such that the right hand side of (9) has zero integral. Thus, the compatibility condition is satisfied, and there exists a strong solution v of (9) subject to homogeneous Neumann boundary conditions, which is unique up to an additive constant. Moreover, such a solution v satisfies

$${\left[v\right]}_{s,q,\Omega ,\partial \Omega }\le {C\parallel \nabla v\parallel }_{q,\Omega }\le {C\parallel \left|u\right|}^{p-2}{u-\lambda \parallel }_{p^{\prime },\Omega }\le {C(\parallel u\parallel }_{p,\Omega }^{p-1}+{\parallel \lambda \parallel }_{p^{\prime },\Omega }{)\le C\parallel u\parallel }_{p,\Omega }^{p-1}$$

(10)

with a constant $C<\infty$ independent of u, as ${\parallel \lambda \parallel }_{p^{\prime },\Omega }={\left|\lambda \right||\Omega |}^{1/p^{\prime }}\le \frac{{|\Omega |}^{1/p^{\prime }}}{{|\Omega |}^{1/p^{\prime }}}{\parallel u\parallel }_{p,\Omega }^{p-1}={\parallel u\parallel }_{p,\Omega }^{p-1}$ holds by the definition of $\lambda$. Further, by the definition of v we have

$$⟨Au,v⟩={\int }_{\Omega }{\left|u\right|}^{p}dx-\lambda {\int }_{\Omega }udx\ge {\parallel u\parallel }_{p,\Omega }^p-\frac{a}{{|\Omega |}^{1/p^{\prime }}}{\parallel u\parallel }_{p,\Omega }^{p-1}$$

due to $\lambda \le \frac{1}{|\Omega |}{\int }_{\Omega }{\left|u\right|}^{p-1}dx$ and Jensen’s inequality ${\left(\frac{1}{|\Omega |}{\int }_{\Omega }{\left|u\right|}^{p-1}dx\right)}^{p^{\prime }}\le \frac{1}{|\Omega |}{\int }_{\Omega }{\left|u\right|}^{p}dx$. From (A2) we can conclude

$$\left|⟨Bu,v⟩\right|\le (C_1+C_2{\parallel u\parallel }_{p,\Omega }^r{)\left[v\right]}_{s,q,\Omega ,\partial \Omega }$$

with $0\le r<max(p/q^{\prime },1)$, and together with (10) both inequalities imply

$$⟨(A+B)u,v⟩\ge {\parallel u\parallel }_{p,\Omega }^p-\frac{a}{{|\Omega |}^{1/p^{\prime }}}{\parallel u\parallel }_{p,\Omega }^{p-1}-(C_1+C_2{\parallel u\parallel }_{p,\Omega }^r{)\parallel u\parallel }_{p,\Omega }^{p-1}.$$

As the right hand side tends to infinity for ${\parallel u\parallel }_{p,\Omega }\to \infty$ due to $r<1$, the equation $(A+B)u=0$ has no solution $u\in L^p(\Omega )$ satisfying ${\int }_{\Omega }udx=a$ on the boundary of a sufficiently large ball around zero in $L^p(\Omega )$. Therefore, like $Au=0$, $(A+B)u=0$ also has a solution $u\in L^p(\Omega )$ with ${\int }_{\Omega }udx=a$. □

Remark 1.

Existence even holds in the linear case $r=1$, $p^{\prime }<q<{\left(p^{\prime }\right)}^{*}$, provided that $C_2<1$ or equivalently $\parallel b_1{(x,y)|x-y|}^{s+\frac{N-1}{q}}{\parallel }_{\frac{p{q}^{\prime }}{p-q^{\prime }},\Omega \times \partial \Omega }$ is sufficiently small.

5. Duality

To prepare the proof of uniqueness of very weak solutions to (1) and (2), let us consider in this section the affine linear case $b(x,y,u)=\tilde{b}(x,y)u-\frac{1}{|\partial \Omega |}\tilde{f}\left(x\right)$, where the sublinearity required in (A2) as well as the smallness condition mentioned in Remark 1 are not satisfied, but instead $\tilde{b}$ satisfies the same condition as $b_2$ in (A3); i.e., $\tilde{b}\ge 0$ and $\tilde{b}(x,y){|x-y|}^{s+\frac{N-1}{q}}\in L^{\frac{p{q}^{\prime }}{p-q^{\prime }}}(\Omega \times \partial \Omega )$ and $\tilde{f}\in L^p(\Omega )$ have average ${\int }_{\Omega }\tilde{f}dx=0$. Then problems (1) and (2) become linear and read (with w instead of u) as

$$\begin{array}{cc}\hfill & -\Delta w+\tilde{c}(·)w=\tilde{f}\mathrm{in}\Omega \mathrm{with}\tilde{c}\left(x\right):={\int }_{\partial \Omega }\tilde{b}(x,y)dS\left(y\right),\hfill \\ \hfill & \frac{\partial w}{\partial \overrightarrow{n}}\left(y\right)={\int }_{\Omega }\tilde{b}(x,y)w\left(x\right)dx\mathrm{for}y\in \partial \Omega .\hfill \end{array}$$

(11)

The dual to this linear problem is

$$-\Delta v+\tilde{B}v=f-\lambda \mathrm{in}\Omega ,\frac{\partial v}{\partial \overrightarrow{n}}=0\mathrm{on}\partial \Omega ,$$

(12)

where $f\in L^{p^{\prime }}(\Omega )$, $\lambda \in \mathbb{R}$ and

$$\left(\tilde{B}v\right)\left(x\right):={\int }_{\partial \Omega }\tilde{b}(x,y)(v\left(x\right)-v\left(y\right))dS\left(y\right)$$

(13)

is a kind of fractional divergence of the function v with kernel $\tilde{b}(x,y)$.

Example 3.

In the one-dimensional nonsingular case $\tilde{b}\equiv -\frac{1}{2}$, $f\equiv 0$, (12) with (13) reads as $-v^{″}+v-\frac{1}{2}(v\left(0\right)+v\left(1\right))=0$ or equivalently as $-v^{″}+v+{\int }_0^1\left((\frac{1}{2}-t)v^{\prime }\left(t\right)-v\left(t\right)\right)dt=0$, which is an integro-ODE. Differentiating $-v^{″}+v-\frac{1}{2}(v\left(0\right)+v\left(1\right))=0$ gives $-v^{‴}+v^{\prime }=0$ with fundamental system $v\left(x\right)=C_{1}cosh\left(x\right)+C_{2}sinh\left(x\right)+C_3$, but the constant functions $v\left(x\right)=C_3$ simply satisfy the homogeneous Neumann boundary conditions $v^{\prime }\left(0\right)=0=v^{\prime }\left(1\right)$; i.e., we have uniqueness up to constants.

Lemma 1.

For $\tilde{b}\ge 0$ satisfying $\tilde{b}(x,y){|x-y|}^{s+\frac{N-1}{q}}\in L^{\frac{p{q}^{\prime }}{p-q^{\prime }}}(\Omega \times \partial \Omega )$ with $p^{\prime }<q<{\left(p^{\prime }\right)}^{*}$ and every $f\in L^{p^{\prime }}(\Omega )$, there exists a $\lambda \in \mathbb{R}$ such that (12) and (13) have, with the addition of constants, a unique strong solution $v\in W^{2,p^{\prime }}(\Omega )$.

Proof. 

With the strong realization $A_s:D\to L^{p^{\prime }}$, $A_{s}v:=-\Delta v$, of the Neumann–Laplacian and the compact operator $\tilde{B}:D\subset \subset W^{1,q}(\Omega )\subset W^{s,q}(\Omega ;\partial \Omega )\to L^{p^{\prime }}(\Omega )$, we seek a solution $v\in D$ of $(A_s+\tilde{B})v=f-\lambda$, i.e., a strong solution satisfying homogeneous Neumann boundary conditions. A problem closely related to (12) is

$$-\Delta \tilde{v}+\tilde{B}\tilde{v}=f-\tilde{\lambda }\mathrm{in}\Omega ,\frac{\partial \tilde{v}}{\partial \overrightarrow{n}}={\int }_{\Omega }\tilde{b}(x,y)(\tilde{v}\left(x\right)-\tilde{v}\left(y\right))dx\mathrm{on}\partial \Omega$$

(14)

with $\tilde{\lambda }:=\frac{1}{|\Omega |}{\int }_{\Omega }fdx$. In fact, note that the weak formulation of this problem is the identification of a $\tilde{v}\in W^{1,2}(\Omega )$ such that

$${\int }_{\Omega }\nabla \tilde{v}·\nabla wdx+{\int }_{\Omega }{\int }_{\partial \Omega }\tilde{b}(x,y)(\tilde{v}\left(x\right)-\tilde{v}\left(y\right))(w\left(x\right)-w\left(y\right))dS\left(y\right)dx={\int }_{\Omega }(f-\tilde{\lambda })wdx$$

(15)

for every $w\in W^{1,2}(\Omega )$. For $\tilde{b}(x,y)\ge 0$ with $\tilde{b}(x,y){|x-y|}^{2s+(N-1)}\in L^{\infty }(\Omega \times \partial \Omega )$, the existence and uniqueness of the solution $\tilde{v}\in W^{1,2}(\Omega )$ with ${\int }_{\Omega }\tilde{v}dx=0$ follows Lax–Milgram and Poincáre inequality. In fact, the second term in (15) has the potential $\Phi \left(v\right):=\frac{1}{2}{\int }_{\Omega }{\int }_{\partial \Omega }\tilde{b}(x,y){|v\left(x\right)-v\left(y\right)|}^{2}dS\left(y\right)dx$, and due to $\tilde{b}\ge 0$, the whole operator on the l.h.s. of the weak formulation has a coercive and weakly lower semicontinuous potential on $W^{1,2}(\Omega )/\mathbb{R}$.

Further, solving Poisson’s equation $-\Delta \overline{v}=\overline{\lambda }$ subject to inhomogeneous Neumann BC $\frac{\partial \overline{v}}{\partial \overrightarrow{n}}={\int }_{\Omega }\tilde{b}(x,y)(\tilde{v}\left(x\right)-\tilde{v}\left(y\right))dx$ on $\partial \Omega$, where $\overline{\lambda }:=-{\int }_{\Omega }{\int }_{\partial \Omega }\tilde{b}(x,y)(\tilde{v}\left(x\right)-\tilde{v}\left(y\right))dS\left(y\right)dx$ is such that a (strong) solution $\overline{v}$ exists. Then $v:=\tilde{v}-\overline{v}$ satisfies $-\Delta v+\tilde{B}v=f-\lambda$ in $\Omega$ with $\lambda :=\tilde{\lambda }+\overline{\lambda }$ and $\frac{\partial v}{\partial \overrightarrow{n}}=0$ on $\partial \Omega$, i.e., (12), in a weak sense. Finally, due to $\tilde{B}v\in L^{p^{\prime }}(\Omega )$ and $f\in L^{p^{\prime }}(\Omega )$, the weak solution v is in fact a strong solution, and, by approximation, this also holds true under the regularity assumptions on $\tilde{b}\ge 0$ in Lemma 1. □

6. Uniqueness

To prove the uniqueness of very weak solutions to (1) and (2), we additionally require b to satisfy (A3); i.e. the derivative $\frac{\partial b}{\partial u}$ is bounded by a function $b_2(x,y)$ independent of u satisfying $b_2(x,y){|x-y|}^{s+\frac{N-1}{q}}\in L^{\frac{p{q}^{\prime }}{p-q^{\prime }}}(\Omega \times \partial \Omega )$. As a consequence, the difference quotient $(x,y,u,\tilde{u})\mapsto \frac{b(x,y,u)-b(x,y,\tilde{u})}{u-\tilde{u}}$ is continuous w.r.t. $(u,\tilde{u})$ for a.e. $(x,y)\in \Omega \times \partial \Omega$ and thus a Carathéodory function.

Theorem 2.

Let $\Omega \subset {\mathbb{R}}^N$ be a bounded $C^2$-domain and let $b:\Omega \times \partial \Omega \times \mathbb{R}\to \mathbb{R}$ be a kernel satisfying (A1)–(A3) for some $1<p<\infty$. Then, for every constant $a\in \mathbb{R}$, the very weak solution $u\in L^p(\Omega )$ of (1) and (2) satisfying ${\int }_{\Omega }u\left(x\right)dx=a$ is unique.

Proof. 

Let $u,\tilde{u}\in L^p(\Omega )$ be two very weak solutions of (1) and (2), with identical averages ${\int }_{\Omega }udx={\int }_{\Omega }\tilde{u}dx$. Let $v\in W^{2,p^{\prime }}(\Omega )$ be a strong solution of

$$-\Delta v+\tilde{B}v={|u-\tilde{u}|}^{p-2}(u-\tilde{u})-\lambda \mathrm{in}\Omega ,\frac{\partial v}{\partial \overrightarrow{n}}=0\mathrm{on}\partial \Omega ,$$

where

$$\tilde{B}v\left(x\right):={\int }_{\partial \Omega }\tilde{b}(x,y)(v\left(x\right)-v\left(y\right))dS\left(y\right)$$

(16)

is a kind of fractional divergence of the function v with kernel $\tilde{b}(x,y):=\frac{b(x,y,u\left(x\right))-b(x,y,\tilde{u}\left(x\right))}{u\left(x\right)-\tilde{u}\left(x\right)}$, and $\lambda \in \mathbb{R}$ is chosen such that there exists a solution v satisfying homogeneous Neumann boundary conditions $\frac{\partial v}{\partial \overrightarrow{n}}=0$ on $\partial \Omega$. Note that Lemma 1 guarantees the existence of such a strong solution. Now, test the difference between the equations solved by u and $\tilde{u}$ with the test function v to obtain

$$\begin{array}{cc}\hfill & {\int }_{\Omega }{|u\left(x\right)-\tilde{u}\left(x\right)|}^{p}dx-{\int }_{\Omega }{\int }_{\partial \Omega }\tilde{b}(x,y)(u\left(x\right)-\tilde{u}\left(x\right))(v\left(x\right)-v\left(y\right))dS\left(y\right)dx\hfill \\ \hfill & +{\int }_{\Omega }{\int }_{\partial \Omega }(b(x,y,u\left(x\right))-b(x,y,\tilde{u}\left(x\right)))(v\left(x\right)-v\left(y\right))dS\left(y\right)dx=0\hfill \end{array}$$

(17)

and due to $\tilde{b}(x,y)(u\left(x\right)-\tilde{u}\left(x\right))=b(x,y,u\left(x\right))-b(x,y,\tilde{u}\left(x\right))$, ${\int }_{\Omega }{|u-\tilde{u}|}^{p}dx=0$. Hence, $u=\tilde{u}$ holds. □

7. Conclusions

We were able to prove uniqueness up to a constant for very weak solutions to singular semilinear elliptic PDEs subject to singular integral Neumann boundary conditions. Our method to test for two very weak solutions of (1) and (2), with identical averages of the difference in the equations determined by the strong solution of a dual problem (which is an integro-PDE with a kind of fractional divergence as a lower-order term here), seems to be rather promising and may be applicable to show the uniqueness of very weak solutions for many other problems.

However, our results are still not optimal. For example, while we used an intermediate compact embedding $W^{2,p^{\prime }}(\Omega )\subset W^{1,{\left(p^{\prime }\right)}^{*}}(\Omega )$, it seems to be an open question for which $(s,q)$ the direct embedding $W^{2,p^{\prime }}(\Omega )\subset W^{s,q}(\Omega ;\partial \Omega )$ is compact. In fact, the embedding and interpolation properties of mixed fractional Sobolev spaces have not been studied in depth in the literature to date. Therefore, although there are some first steps, as in the Appendix B of [13], for example, how singular a domain-boundary kernel b can be without destroying the existence of solutions is an open question.