Optimal Control Analysis of Cholera Dynamics in the Presence of Asymptotic Transmission
Abstract
1. Introduction
2. Derivation of the Models and Their Analysis
2.1. Deterministic Model of the Transmission Dynamics of the Cholera Model and Its Biological Description
- (i)
- The use of hygiene promotion and social mobilization, ;
- (ii)
- The use of treatment by drug/oral re-hydration solution (ORS), ;
- (iii)
- The use of safe water, hygiene, and sanitation, .
2.2. WHO Recommendation of the Current Cholera Control Interventions Used in the Model
2.3. Positivity of the Solution for the Deterministic Model
2.4. Boundedness of the Solution for the Deterministic Model
2.5. The Invariant Region for the Deterministic Model
2.6. Existence of Disease Free Equilibrium Point (DFE)
2.7. The Effective Reproduction Number
2.8. Global Stability of Disease Free Equilibrium Point (DFE)
2.9. Global Stability of the Endemic Equilibrium Point
3. Sensitivity and Elasticity Analysis
Interpretation of Sensitivity Indices
4. Stochastic Model of the Transmission Dynamics of the Cholera Model and Its Biological Description
Positivity of the Solution for the SDE Model
5. Optimal Control Analysis
Existence of Optimal Control
6. Numerical Simulation and Graphical Illustration of the Model
- Strategy A: Employing hygiene promotion and social mobilisation , only.
- Strategy B: Treatment of the symptomatic individuals with drug/oral re-hydration solution (ORS) , only.
- Strategy C: Employing sanitation, hygiene, and safe water , only.
- Strategy D: Employing the control interventions .
- Strategy E: Employing the control interventions .
- Strategy F: Employing the control interventions .
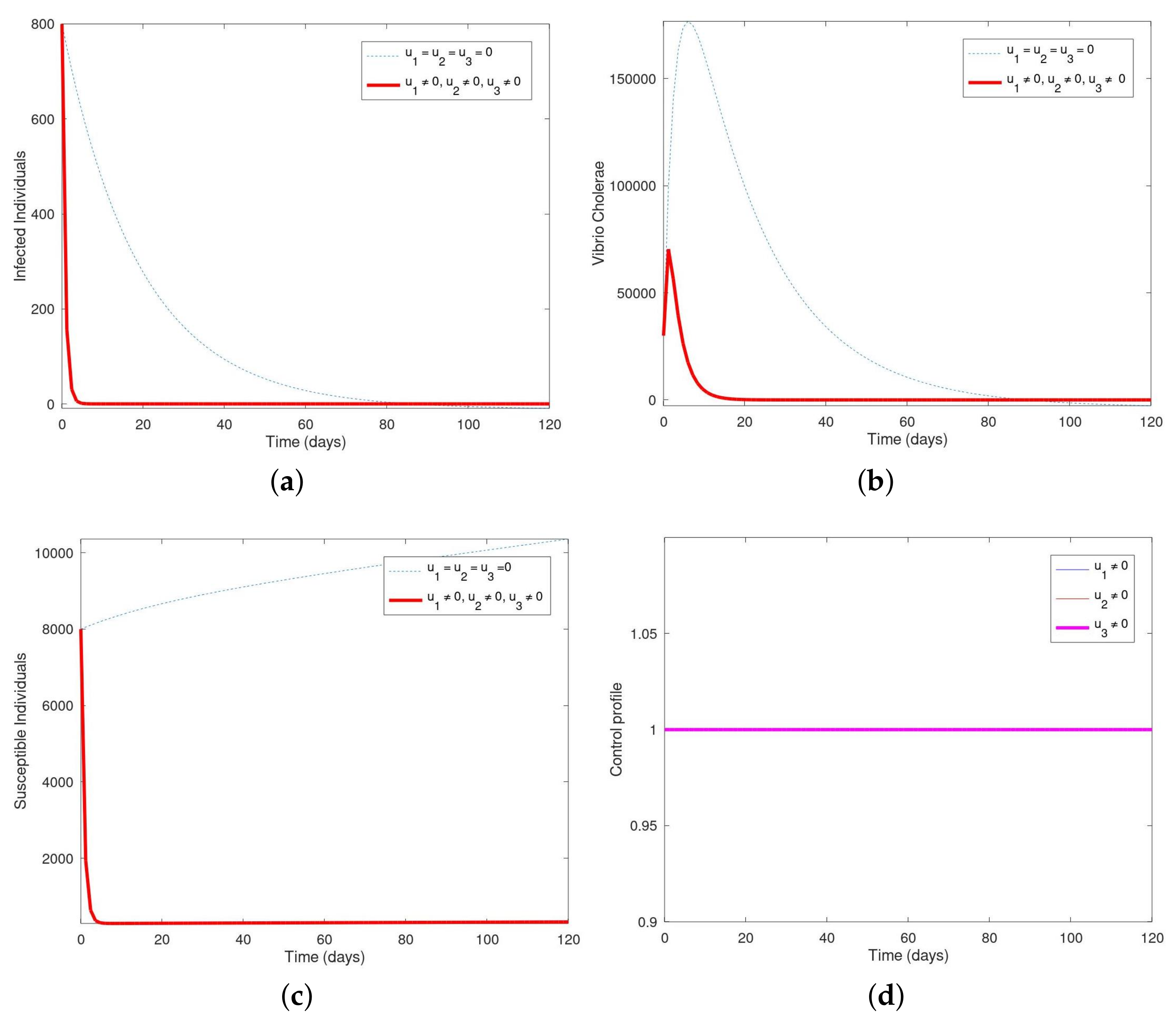
- Strategy G: Employing all three control interventions .
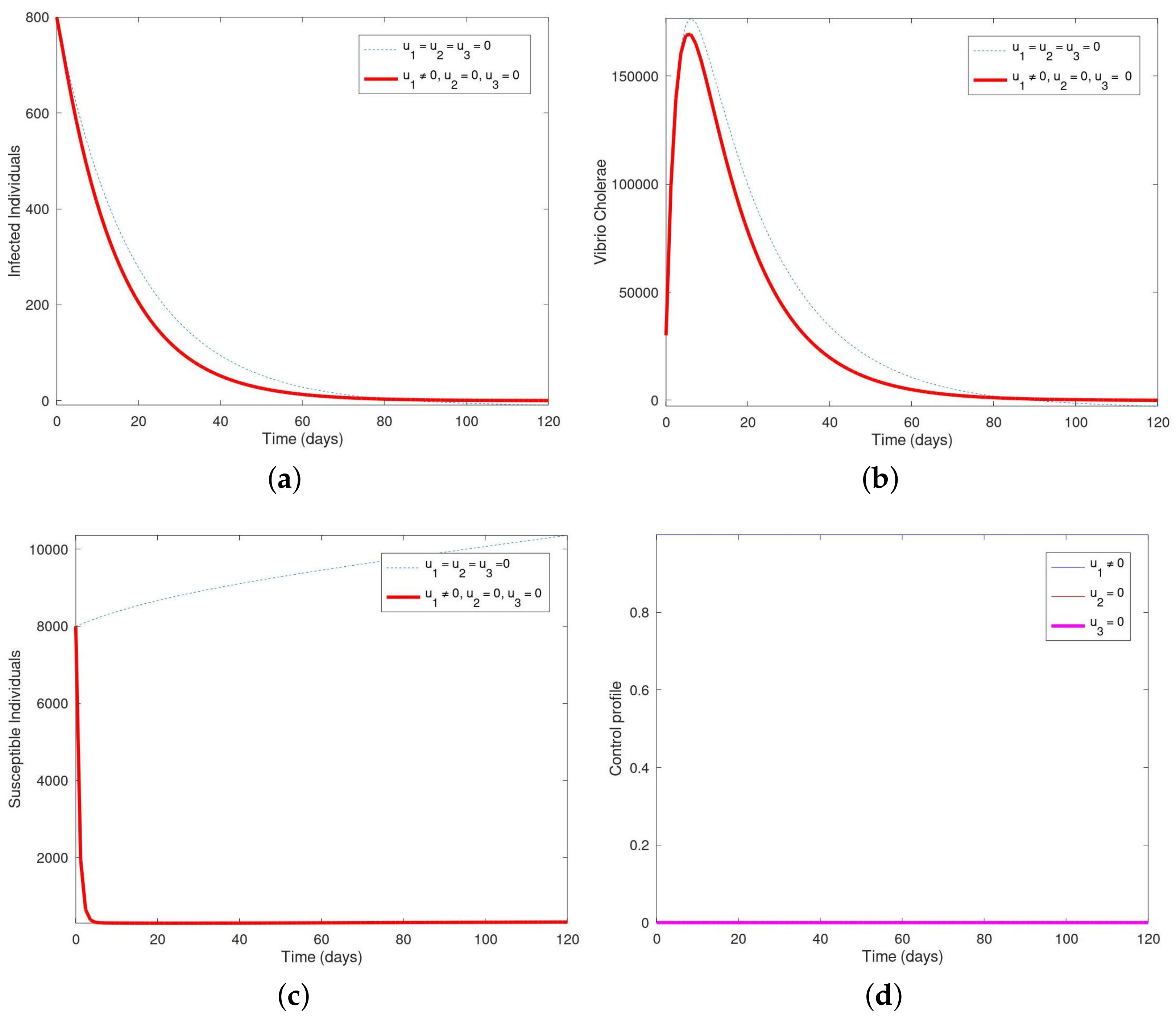
6.1. Strategy A: Employing Hygiene Promotion and Social Mobilization , Only
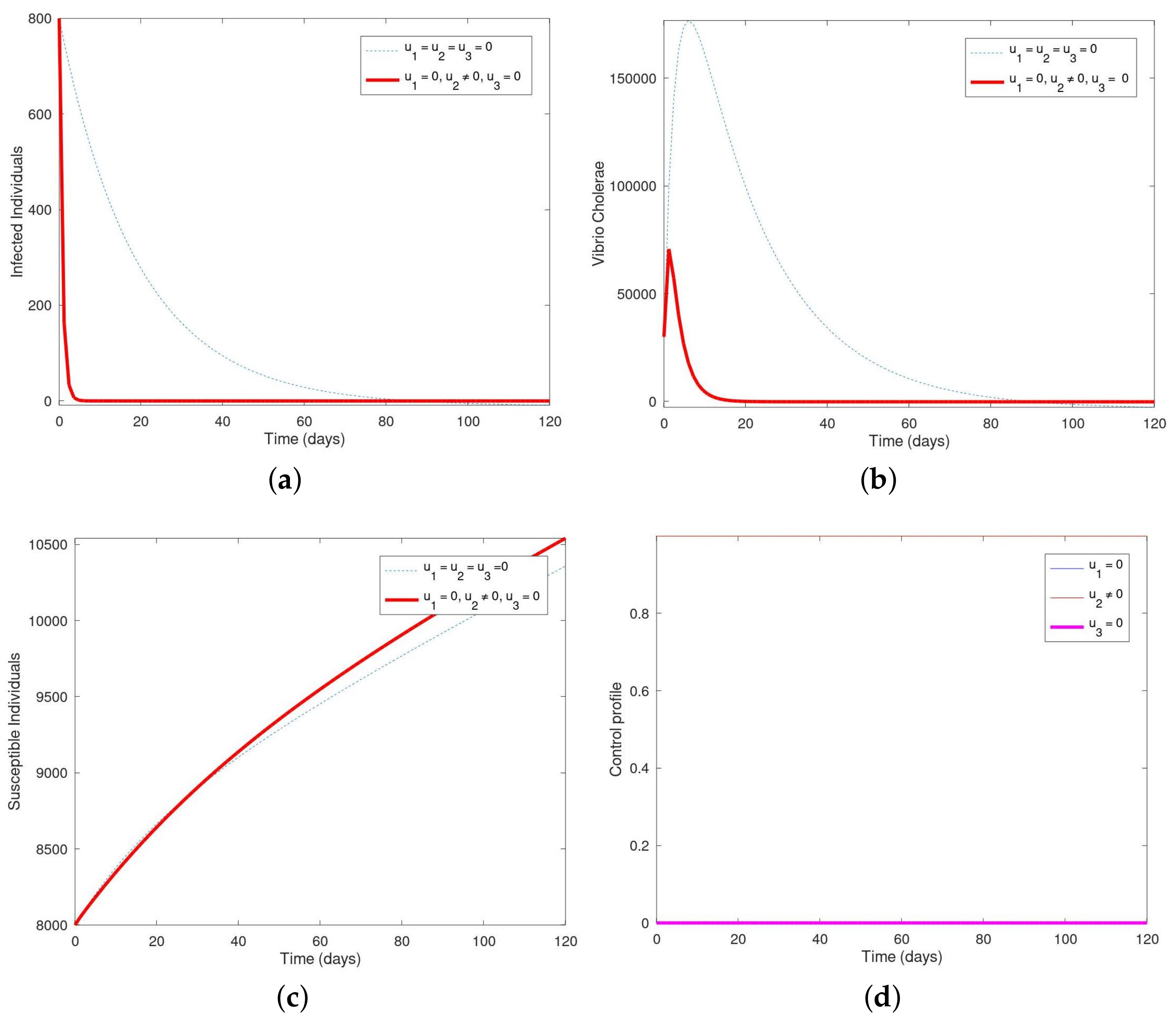
6.2. Strategy B: Treatment of the Symptomatic Individuals with Drug/Oral Re-Hydration Solution (ORS) , Only
6.3. Strategy C: Employing Sanitation, Hygiene, and Safe Water , Only
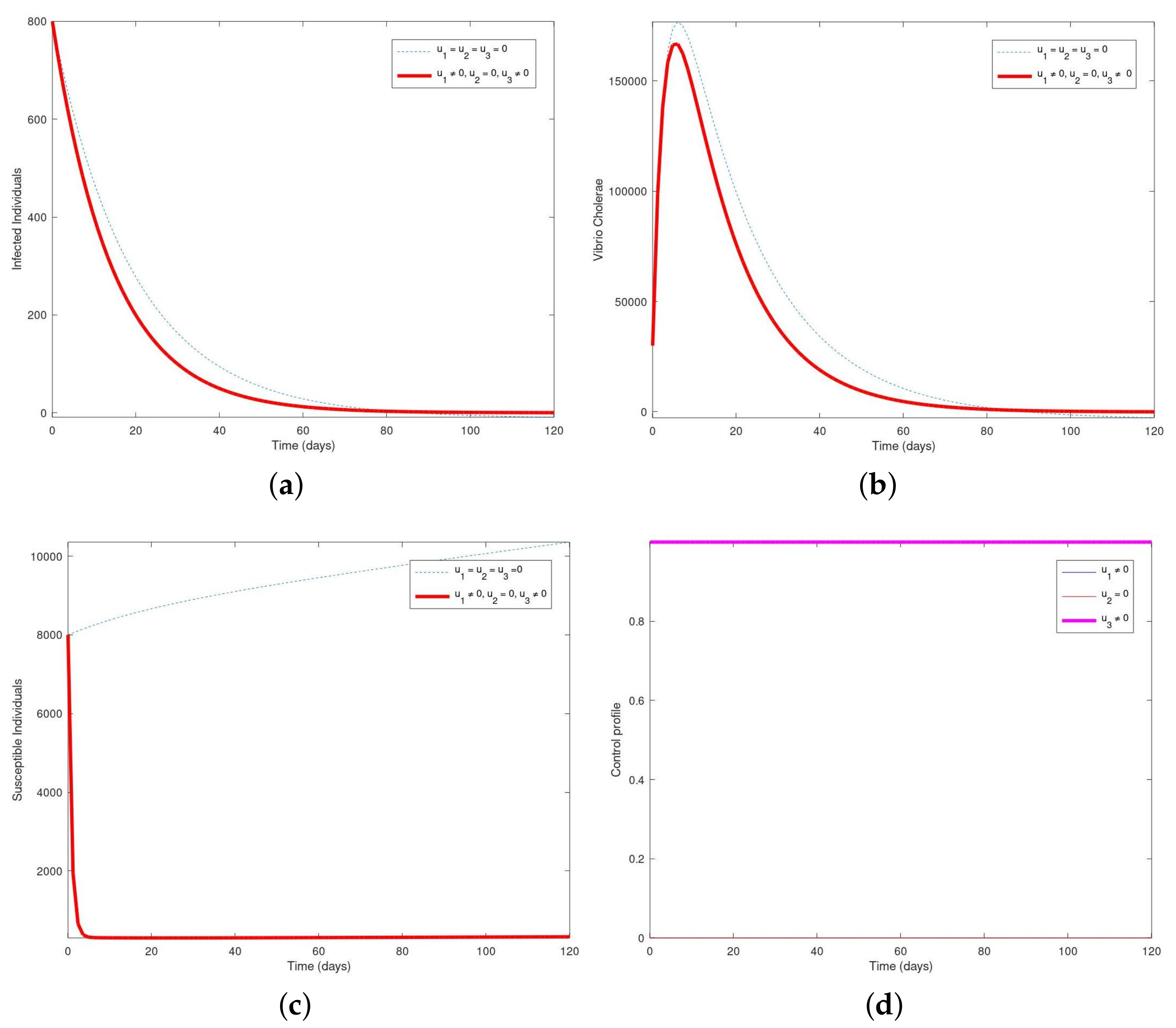
6.4. Strategy D: Employing the Control Interventions (, )
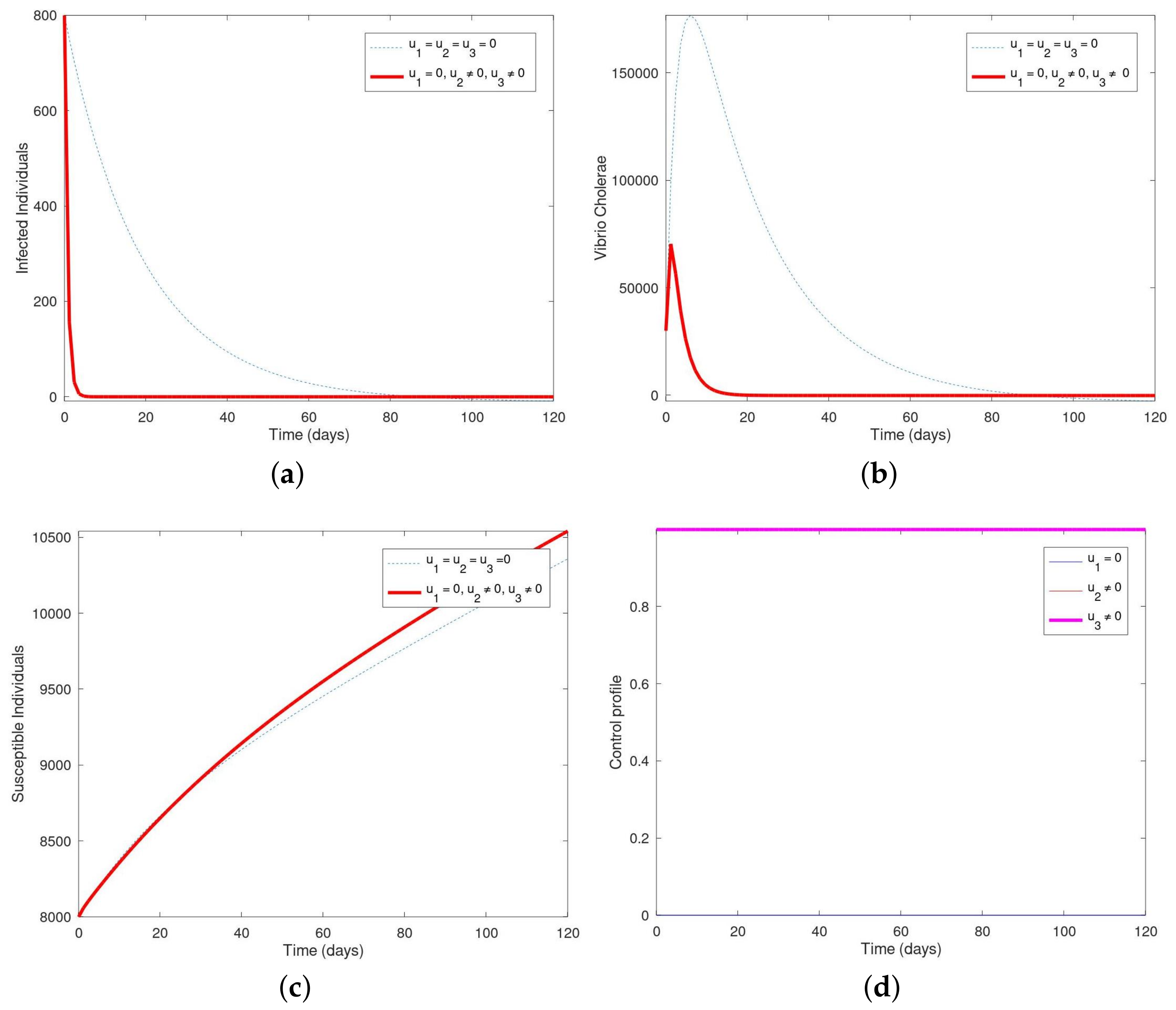
6.5. Strategy E: Employing the Control Interventions (, )
6.6. Strategy F: Employing the Control Interventions (, )
6.7. Strategy G: Employing All the Three Control Interventions (, , )
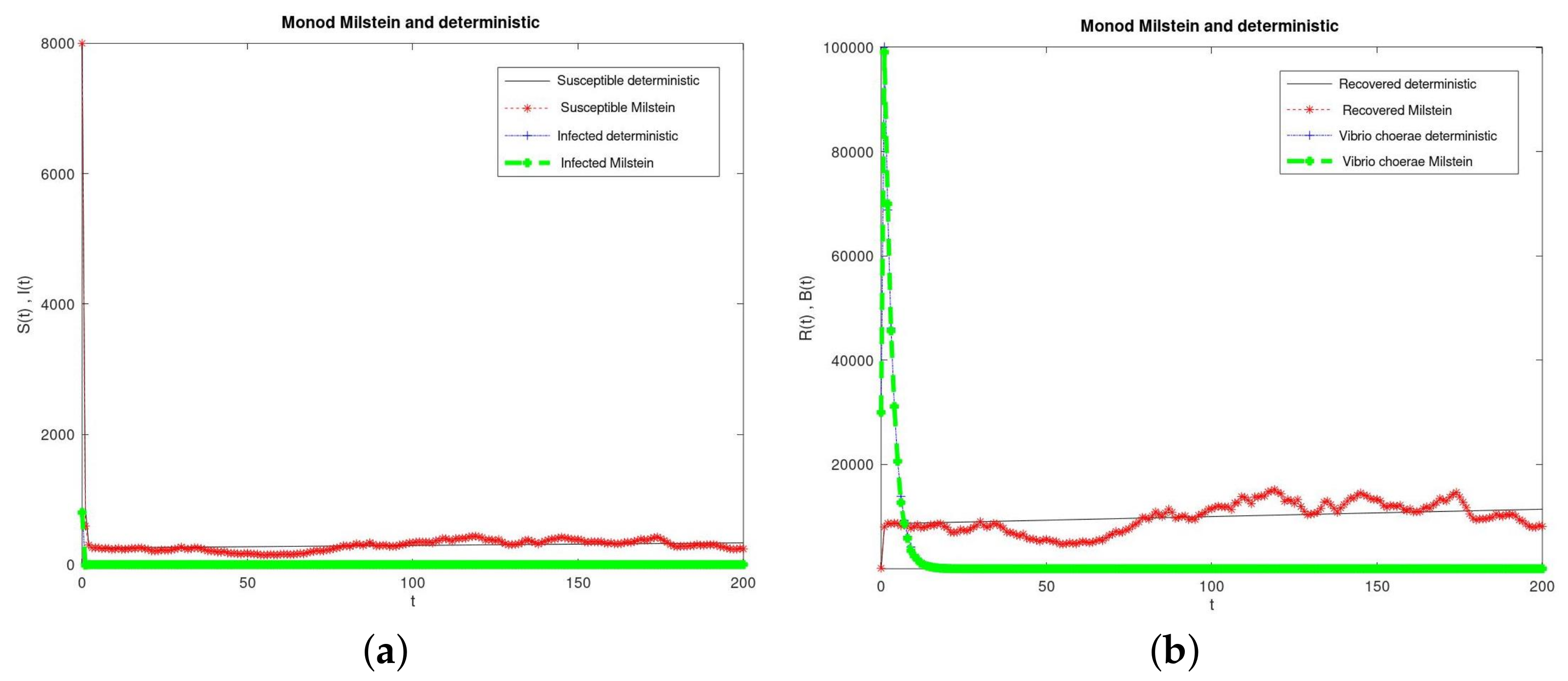
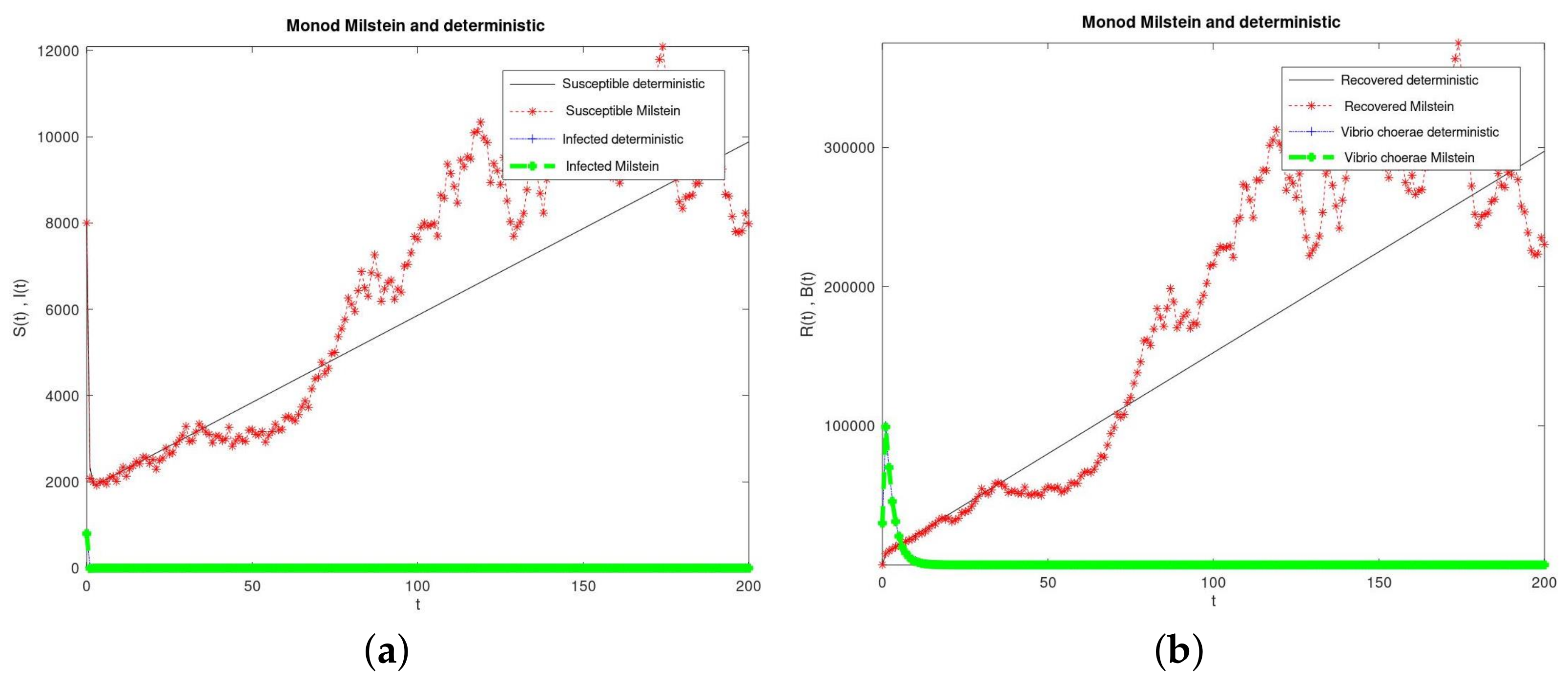
7. Numerical Simulation of the SDE Model
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- WHO. Cholera Country Profiles. Available online: http://www.who.int/cholera/countries/en/ (accessed on 13 January 2021).
- CDC. Cholera—Vibrio Cholera Infection. Available online: https://www.cdc.gov/cholera/ (accessed on 13 January 2021).
- Ngwa, M.C.; Liang, S.; Kracalik, I.T.; Morris, L.; Blackburn, J.K.; Mbam, L.M.; Ba Pouth, S.F.; Teboh, A.; Yang, Y.; Arabi, M.; et al. Cholera in Cameroon, 2000–2012: Spatial and Temporal Analysis at the Operational (Health District) and Sub Climate Levels. PLoS Negl. Trop. Dis. 2016, 10, e0005105. [Google Scholar] [CrossRef]
- Bakare, E.A.; Are, E.B.; Osanyinlusi, S. Impact of multiple control strategies on the Mathematical Modelling of Cholera transmission dynamics with asymptotic transmission. J. Niger. Assoc. Math. Phys. 2016, 36, 107–116. [Google Scholar]
- Ali, M.; Nelson, A.R.; Lopez, A.L.; Sack, D. Updated global burden of cholera in endemic countries. PLoS Negl. Trop. Dis. 2015, 9, e0003832. [Google Scholar] [CrossRef]
- Azman, A.S.; Rudolph, K.E.; Cummings, D.A.; Lessler, J. The incubation period of cholera: A systematic review. J Infect. 2013, 66, 432–438. [Google Scholar] [CrossRef]
- Faruque, S.M.; Naser, I.B.; Islam, M.J.; Faruque, A.S.; Ghosh, A.N.; Nair, G.B.; Sack, D.A.; Mekalanos, J.J. Seasonal epidemics of cholera inversely correlate with the prevalence of environmental cholrea phages. Proc. Natl. Acad. Sci. USA 2005, 102, 1702–1707. [Google Scholar] [CrossRef]
- Agarwal, M.; Verma, V. Modeling and analysis of the spread of an infectious disease cholera with environmental fluctuations. Appl. Appl. Math. 2012, 7, 406–425. [Google Scholar]
- Gil, A.I.; Louis, V.R.; Rivera, I.N.G.; Lipp, E.; Huq, A.; Lanata, C.F.; Taylor, D.N.; Russek-Cohen, E.; Choopun, N.; Sack, R.B.; et al. Occurrence and distribution of vibrio cholerae in the coastal environment of Peru. Environ. Microbiol. 2004, 6, 699–706. [Google Scholar] [CrossRef] [PubMed]
- Liao, S.; Wang, J. Stability analysis and application of a mathematical cholera model. Math. Biosci. Eng. 2011, 8, 733–752. [Google Scholar] [PubMed]
- Eisenberg, M.C.; Shuai, Z.; Tien, J.H.; van den Driessche, P. A cholera model in a patchy environment with water and human movement. Math. Biosci. 2013, 246, 105–112. [Google Scholar] [CrossRef] [PubMed]
- Louis, V.R.; Russek-Cohen, E.; Choopun, N.; Rivera, I.N.G.; Gangle, B.; Jiang, S.C.; Rubin, A.; Patz, J.E.; Huq, A.; Colwell, R.R. Predictability of vibrio cholerae in chesapeake bay. Appl. Environ. Microbiol. 2003, 69, 2773–2785. [Google Scholar] [CrossRef] [PubMed]
- Maheshwari, M.; Kiranmayi, K.N.B. Vibrio cholerae. Vet. World 2011, 4, 423–428. [Google Scholar] [CrossRef]
- Mondiale de la Santé, O.; World Health Organization. Cholera Vaccines: WHO Position Paper—August 2017 Weekly Epidemiological Record 25 August 2017. Wkly. Epidemiol. Rec. = Relevé épidéMiologique Hebdomadaire 2017, 92, 477–498. Available online: http://apps.who.int/iris/bitstream/10665/258764/1/WER9234-477-498.pdf (accessed on 13 January 2021).
- Dangbé, E.; Irépran, D.; Perasso, A.; Békollé, D. Mathematical modelling and numerical simulations of the influence of hygiene and seasons on the spread of cholera. Math. Biosci. 2018, 296, 60–70. [Google Scholar] [CrossRef] [PubMed]
- Mwasa, A.; Tchuenche, J.M. Mathematical analysis of a cholera model with public health interventions. Biosystems 2011, 105, 190–200. [Google Scholar] [CrossRef] [PubMed]
- Capasso, V. What IS First Name? A mathematical model for the 1973 cholera epidemic in the european mediterranean region. Rev. Epidemiol. Sante Publique 1979, 27, 121–132. [Google Scholar]
- Mosley, W.H.; Ahmed, S.; Benenson, A.S.; Ahmed, A. The relationship of vibiriocidal antibody titre to susceptibility to cholera in family contacts of cholera patients. Bull. World Health Organ. 1968, 38, 777–785. [Google Scholar]
- Shuai, Z.; Tien, J.H.; van den Driessche, P. Cholera models with hyperinfectivity and van den Driessche temporary immunity. Bull. Math. Biol. 2012, 74, 2423–2445. [Google Scholar] [CrossRef] [PubMed]
- Shuai, Z.; van den Driessche, P. Global dynamics of cholera models with differential infectivity. Math. Biosci. 2011, 234, 118–126. [Google Scholar] [CrossRef]
- Codeço, C.T. Endemic and epidemic dynamics of cholera: The role of the aquatic reservoir. BMC Infect. Dis. 2001, 1, 1–14. [Google Scholar] [CrossRef]
- Hartley, D.M.; Morris, J.G.; Smith, D.L. Hyperinfectivity: A critical element in the ability of V. cholerae to cause epidemics? PLoS Med. 2006, 3, 63–69. [Google Scholar] [CrossRef]
- Zhou, X.; Cui, J. Threshold dynamics for a cholera epidemic model with periodic transmission rate. Appl. Math. Model. 2013, 37, 3093–3101. [Google Scholar] [CrossRef]
- Tien, J.H.; Earn, D.J.D. Multiple transmission pathways and disease dynamics in a waterborne pathogen model. Bull. Math. Biol. 2010, 72, 1502. [Google Scholar] [CrossRef] [PubMed]
- Jensen, M.A.; Faruque, S.M.; Mekalanos, J.J.; Levin, B.R. Modeling the role of bacteriophage in the control of cholera outbreaks. Proc. Natl. Acad. Sci. USA 2006, 103, 4652–4657. [Google Scholar] [CrossRef]
- Mukandavire, Z.; Liao, S.; Wang, J.; Gaff, H.; Smith, D.L.; Morris, J.G. Estimating the reproductive numbers for the 2008–2009 cholera outbreaks in Zimbabwe. Proc. Natl. Acad. Sci. USA 2011, 108, 8767–8772. [Google Scholar] [CrossRef] [PubMed]
- Fung, I.C.H. Cholera transmission dynamic models for public health practitioners. Emerg. Themes Epidemiol. 2014, 11, 1. [Google Scholar] [CrossRef] [PubMed]
- Fister, K.R.; Gaff, H.; Lenhart, S.; Numfor, E.; Schaefer, E.; Wang, J. Optimal Control of Vaccination in an Age-Structured Cholera Model. Math. Stat. Model. Emerg. Re-Emerg. Infect. Dis. 2016, 221–248. [Google Scholar] [CrossRef]
- Kim, J.H.; Mogasale, V.; Burgess, C.; Wierzba, T.F. Impact of oral cholera vaccines in cholera-endemic countries: A mathematical modeling study. Vaccine 2016, 34, 2113–2120. [Google Scholar] [CrossRef] [PubMed]
- Sun, G.Q.; Xie, J.H.; Huang, S.H.; Jin, Z.; Li, M.T.; Liu, L. Transmission dynamics of cholera: Mathematical modeling and control strategies. Commun. Nonlinear Sci. Numer. Simul. 2017, 45, 235–244. [Google Scholar] [CrossRef]
- LaSalle, J.P. Stability theory of ordinary differential equations. J. Differ. Equs. 1968, 4, 57–65. [Google Scholar] [CrossRef]
- Yavuz, M.; Sene, N. Stability analysis and numerical computation of the fractional predator–prey model with the harvesting rate. Fractal Fract. 2020, 4, 35. [Google Scholar] [CrossRef]
- Parvaiz, A.N.; Mehmet, Y.; Sainat, Q.; Jian, Z.; Stuart, T. Modeling and analysis of COVID-19 epidemics with treatment in fractional derivatives using real data from Pakistan. Eur. Phys. J. Plus 2020, 135, 1–42. [Google Scholar]
- Parvaiz, A.N.; Kolade, M.O.; Mehmet, Y.; Jian, Z. Chaotic dynamics of a fractional order HIV-1 model involving AIDS-related cancer cells. Chaos Solitons Fractals 2020, 140, 110272. [Google Scholar]
- Mehmet, Y.; Necati, O. Analysis of an epidemic spreading model with exponential decay law. Math. Sci. Appl. E-Notes 2020, 8, 142–154. [Google Scholar]
- Hailemariam Hntsa, K.; Nerea Kahsay, B. Analysis of Cholera Epidemic Controlling Using Mathematical Modeling. Int. J. Math. Math. Sci. 2020, 2020, 7369204. [Google Scholar] [CrossRef]
- Shabami, I. Modelling the Effect of Screening on the Spread of HIV Infection in a Homogeneous Population with Infective Immigrants. Master’s Thesis, University of Der es Salaam, Dar es Salaam, Tanzania, 2010. [Google Scholar]
- Nakul, C.; Hyman, J.M.; Cushing, J.M. Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model. Bull. Math. Biol. 2008, 70, 1272–1296. [Google Scholar]
- Zaman, G.; Kang, Y.H.; Jong, H.I. Stability analysis and optimal vaccination of an SIR epidemic model. BioSystems 2008, 93, 240–249. [Google Scholar] [CrossRef] [PubMed]
- Pontryagin, L.S.; Boltyanskii, V.G.; Gamkrelidze, R.V.; Mishchenko, E.F. The Mathematical Theory of Optimal Processes; Wiley: New York, NY, USA, 1962. [Google Scholar]
- Maturo, F. Unsupervised classification of ecological communities ranked according to their biodiversity patterns via a functional principal component decomposition of Hill’s numbers integral functions. Ecol. Indic. 2018, 90, 305–315. [Google Scholar] [CrossRef]
- Ferguson, J.; O’Leary, N.; Maturo, F.; Yusuf, S.; O’Donnell, M. Graphical comparisons of relative disease burden across multiple risk factors. BMC Med. Res. Methodol. 2019, 19, 186. [Google Scholar] [CrossRef] [PubMed]
- Urban, R.; Hoskova-Mayerova, S. Threat life cycle and its dynamics. Deturope 2017, 9, 93–109. [Google Scholar]
- Kudlak, A.; Urban, R.; Hoskova-Mayerova, S. Determination of the Financial Minimum in a Municipal Budget to Deal with Crisis Situations. Soft Comput. 2020, 24, 8607–8616. [Google Scholar] [CrossRef]
- Bekesiene, S.; Hoskova-Mayerova, S. Decision Tree—Based Classification Model for Identification of Effective Leadership Indicators in the Lithuania Army Forces. J. Math. Fund. Sci. 2018, 50, 121–141. [Google Scholar] [CrossRef]
- Tušer, I.; Hošková-Mayerová, Š. Emergency Management in Resolving an Emergency Situation. J. Risk Financ. Manag. 2020, 13, 262. [Google Scholar] [CrossRef]


| Variables | Description |
|---|---|
| S | Susceptible Human |
| I | Infected Human |
| R | Recovered Human |
| B | Vibrio Cholerae |
| Parameter | Symbol |
|---|---|
| Recruitment rate of susceptible population | A |
| Contribution of infected individuals to | |
| the population of Vibrio cholerae | |
| Natural death rate of human | |
| Net death rate of Vibrio cholerae | |
| Acquired temporary immunity | r |
| Disease-induced death rate | d |
| Concentration of Vibrio cholerae in water | K |
| Human spontaneous recovery rate | |
| Use of hygiene promotion and social mobilization | |
| Use of treatment by drug/oral re-hydration solution (ORS) | |
| Use of safe water, hygiene, and sanitation | |
| Rates of ingesting vibrios from the contaminated environment | |
| Rates of ingesting vibrios through human-to-human interaction | |
| loss of immunity |
| Parameter | Parameter Values | Sensitivity to |
|---|---|---|
| 100 | +0.24511 | |
| 0.2143 | +0.24511 | |
| 0.000002 | +0.755 | |
| A | 15 | +0.9999 |
| d | 0.015 | −0.2174 |
| 0.033 | −0.24511 | |
| 0.0000548 | −1.0000 | |
| 0.05 | −0.7245 | |
| r | 0.004 | −0.0579 |
| K | −0.24511 | |
| 0.025 | −0.24511 |
| Parameter | Symbol | Value | Source |
|---|---|---|---|
| Recruitment rate of susceptible population | A | 15/day | Assumed |
| Contribution of infected individuals to | |||
| the population of Vibrio cholerae | 100 cells/L-per day | [5] | |
| Natural death rate of human | 0.0000548/day | [18] | |
| Net death rate of Vibrio cholerae | 0.033/day | [5] | |
| Acquired temporary immunity | r | 0.004/day | [8,26] |
| Disease-induced death rate | d | 0.015/day | [26] |
| Concentration of Vibrio cholerae in water | K | cells/L | [26] |
| Human spontaneous recovery rate | 0.05 | [18] | |
| Use of oral cholera vaccine | 0.9 | Assumed | |
| Use of treatment by ORS | 0.91 | Assumed | |
| Personal hygiene/sanitation | 0.94 | Assumed | |
| Rates of ingesting vibrios from the CO * | 0.2143 | Assumed | |
| Eates of ingesting vibrios through H-H int. * | 0.000002 | Assumed | |
| Loss of immunity | 0.025 | Assumed |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bakare, E.A.; Hoskova-Mayerova, S. Optimal Control Analysis of Cholera Dynamics in the Presence of Asymptotic Transmission. Axioms 2021, 10, 60. https://doi.org/10.3390/axioms10020060
Bakare EA, Hoskova-Mayerova S. Optimal Control Analysis of Cholera Dynamics in the Presence of Asymptotic Transmission. Axioms. 2021; 10(2):60. https://doi.org/10.3390/axioms10020060
Chicago/Turabian StyleBakare, Emmanuel A., and Sarka Hoskova-Mayerova. 2021. "Optimal Control Analysis of Cholera Dynamics in the Presence of Asymptotic Transmission" Axioms 10, no. 2: 60. https://doi.org/10.3390/axioms10020060
APA StyleBakare, E. A., & Hoskova-Mayerova, S. (2021). Optimal Control Analysis of Cholera Dynamics in the Presence of Asymptotic Transmission. Axioms, 10(2), 60. https://doi.org/10.3390/axioms10020060







