An Affine Model of a Riemann Surface Associated to a Schwarz–Christoffel Mapping

Abstract

In this paper, we construct an affine model of a Riemann surface with a flat Riemannian metric associated to a Schwarz–Christoffel mapping of the upper half plane onto a rational triangle. We explain the relation between the geodesics on this Riemann surface and billiard motions in a regular stellated n-gon in the complex plane.

1. Introduction

We give a section by section summary of the contents of this paper.

In §1 we define the Schwarz–Christoffel conformal map $F_Q$ (2) of the complex plane less $\{0,1\}$ onto a quadrilateral Q, which is formed by reflecting a rational triangle $T_{n_0{n}_1{n}_{\infty }}$ in the real axis.

In §2, following Aurell and Itzykson [1] we associate to the map $F_Q$ the affine Riemann surface $\mathcal{S}$ in ${\mathbb{C}}^2$ defined by ${\eta }^n={\xi }^{n-n_0}{(1-\xi )}^{n-n_1}$, where ${\mathbb{C}}^2$ has coordinates $(\xi ,\eta )$ and $n=n_0+n_1+n_{\infty }$. Thinking of $\mathcal{S}$ as a branched covering

$$\pi :\mathcal{S}\to \mathbb{C}\backslash \{0,1\}:(\xi ,\eta )\mapsto \xi$$

with branch points at $(0,0)$, $(1,0)$ and ∞ corresponding to the branch values 0, 1, and ∞, respectively, we show that $\mathcal{S}$ has genus $\frac{1}{2}\left(n+2-(d_0+d_1+d_{\infty })\right)$, where $d_j=gcd(n,n_j)$ for $j=0,1,\infty$. Let ${\mathcal{S}}_{\mathrm{reg}}$ be the set of nonsingular points of $\mathcal{S}$. The map $\widehat{\pi }={\pi }_{|{\mathcal{S}}_{\mathrm{reg}}}:{\mathcal{S}}_{\mathrm{reg}}\to \mathbb{C}\backslash \{0,1\}$ is a holomorphic n-fold covering map with covering group the cyclic group generated by

$$\mathcal{R}:{\mathcal{S}}_{\mathrm{reg}}\subseteq {\mathbb{C}}^2\to {\mathcal{S}}_{\mathrm{reg}}\subseteq {\mathbb{C}}^2:(\xi ,\eta )\mapsto (\xi ,{\mathrm{e}}^{2\pi i/n}\eta ).$$

In §3 we build a model ${\tilde{\mathcal{S}}}_{\mathrm{reg}}$ of the affine Riemann surface ${\mathcal{S}}_{\mathrm{reg}}$. The quadrilateral Q is holomorphically diffeomorphic to a fundamental domain $\mathcal{D}$ of the action of the covering group on ${\mathcal{S}}_{\mathrm{reg}}$. Rotating Q by

$$R:\mathbb{C}\to \mathbb{C}:z\mapsto {\mathrm{e}}^{2\pi i/n}z$$

gives a regular stellated n-gon $K^{*}$, which is invariant under the dihedral group G generated by the mappings R and $U:\mathbb{C}\to \mathbb{C}:z\mapsto \overline{z}$. We study the group theoretic properties of $K^{*}$. We show that $K^{*}$ is invariant under the reflection $S^{(j)}=R^{n_j}U$ in the ray $\{t{\mathrm{e}}^{2\pi i{n}_n/n}\in \mathbb{C}|t\ge 0\}$ for $j=0,1,\infty$. To construct the model ${\tilde{\mathcal{S}}}_{\mathrm{reg}}$ of the affine Riemann surface ${\mathcal{S}}_{\mathrm{reg}}$ from the regular stellated n-gon $K^{*}$ we follow Richens and Berry [2]. We identify two nonadjacent closed edges of $\mathrm{cl}(K^{*})$, the closure of $K^{*}$, if one edge is obtained from the other by a reflection $S_k^{(j)}=R^k{S}^{(j)}{R}^{-k}$ for some $j=0,1,\infty$. The identification space ${(\mathrm{cl}(K^{*})\backslash \mathrm{O})}^{\sim }$, where $\mathrm{O}$ is the center of $K^{*}$, is a complex manifold except at points corresponding to $\mathrm{O}$ or a vertex of $\mathrm{cl}(K^{*})$, where it has a conical singularity. The action of G on $K^{*}\backslash \mathrm{O}$ induces a free and proper action on the identification space ${(K^{*}\backslash \mathrm{O})}^{\sim }$, whose orbit space ${\tilde{\mathcal{S}}}_{\mathrm{reg}}$ is a complex manifold with compact closure in ${\mathbb{CP}}^2$, with genus $\frac{1}{2}\left(n+2-(d_0+d_1+d_{\infty })\right)$. Moreover ${\tilde{\mathcal{S}}}_{\mathrm{reg}}$ is holomorphically diffeomorphic to the affine Riemann surface ${\mathcal{S}}_{\mathrm{reg}}$.

In §4, we construct an affine model ${\tilde{S}}_{\mathrm{reg}}$ of the Riemann surface ${\mathcal{S}}_{\mathrm{reg}}$. In other words, we find a discrete subgroup $\mathfrak{G}$ of the 2-dimensional Euclidean group $\mathrm{E}(2)$, which acts freely and properly on $\mathbb{C}\backslash {\mathbb{V}}^{+}$ such that after forming an identification space ${(\mathbb{C}\backslash {\mathbb{V}}^{+})}^{\sim }$ the $\mathfrak{G}$ orbit space ${(\mathbb{C}\backslash {\mathbb{V}}^{+})}^{\sim }/\mathfrak{G}$ is holomorphically diffeomorphic to ${\mathcal{S}}_{\mathrm{reg}}$. We now describe the group $\mathfrak{G}$. Reflect the regular stellated n-gon $K^{*}$ in its edges, and then in the edges of the reflected regular stellated n-gons, et cetera. We obtain a group $\mathcal{T}$ generated by $2n$ translations ${\tau }_k$ so that ${\tau }_1^{{\ell }_1}\circ \cdots \circ {\tau }_{2n}^{{\ell }_{2n}}$ sends the center $\mathrm{O}$ of $K^{*}$ to the center of a repeatedly reflected reflected n-gon. The set ${\mathbb{V}}^{+}$ is the union of the image under ${\tau }_1^{{\ell }_1}\circ \cdots \circ {\tau }_{2n}^{{\ell }_{2n}}$ of a vertex of $\mathrm{cl}(K^{*})$ and its center $\mathrm{O}$ for every $({\ell }_1,\dots ,{\ell }_{2n})\in {({\mathbb{Z}}_{\ge 0})}^{2n}$. Let $\mathfrak{G}$ be the semi-direct product $G⋉\mathcal{T}$. The fundamental domain of the $\mathfrak{G}$ action on $\mathbb{C}\backslash {\mathbb{V}}^{+}$ is $\mathrm{cl}(K^{*})$ less its vertices and center. Identifying equivalent open edges of $K^{*}\backslash \mathrm{O}$ and then taking G orbits, it follows that the affine model ${\tilde{S}}_{\mathrm{reg}}$ of the affine Riemann surface ${\mathcal{S}}_{\mathrm{reg}}$ is the $\mathfrak{G}$ orbit space ${(C\backslash {\mathbb{V}}^{+})}^{\sim }/\mathfrak{G}$.

In §5 we show that the mapping

$${\delta }_Q:\mathcal{D}\subseteq {\mathcal{S}}_{\mathrm{reg}}\subseteq {\mathbb{C}}^2\to Q\subseteq \mathbb{C}:(\xi ,\eta )\mapsto (F_Q\circ \widehat{\pi })(\xi ,\eta )=z$$

straightens the nowhere vanishing holomorphic vector field X (11) on ${\mathcal{S}}_{\mathrm{reg}}$, that is, $T_{(\xi ,\eta )}{\delta }_{Q}X(\xi ,\eta )=\frac{\partial }{\partial z}|z={\delta }_Q(\xi ,\eta )$ for every $(\xi ,\eta )\in \mathcal{D}$. We pull back the flat metric $\gamma =\mathrm{d}z⨀\mathrm{d}\overline{z}$ on $\mathbb{C}$ by ${\delta }_Q$ to the metric $\Gamma$ on ${\mathcal{S}}_{\mathrm{reg}}$. So ${\delta }_Q$ is a local developing map. Since $\frac{\partial }{\partial z}$ is the geodesic vector field on $(Q,\gamma {|}_Q)$, it follows that X is a holomorphic geodesic vector field on $({\mathcal{S}}_{\mathrm{reg}},\Gamma )$.

In §6 we study the geometry of the developing map ${\delta }_Q$. The dihedral group $\mathcal{G}$ generated by $\mathcal{R}$ and $\mathcal{U}:{\mathcal{S}}_{\mathrm{reg}}\to {\mathcal{S}}_{\mathrm{reg}}:(\xi ,\eta )\mapsto (\overline{\xi },\overline{\eta })$ is a group of isometries of $({\mathcal{S}}_{\mathrm{reg}},\Gamma )$. The group G generated by R and $U:\mathbb{C}\to \mathbb{C}:z\mapsto \overline{z}$ is a group of isometries of $(Q,\gamma {|}_Q)$. Extend the holomorphic map ${\delta }_Q$ to a holomorphic map map ${\delta }_{K^{*}}:{\mathcal{S}}_{\mathrm{reg}}\to K^{*}$ by requiring that $R^j\circ {\delta }_{K^{*}}={\delta }_Q\circ {\mathcal{R}}^j$ on ${\mathcal{R}}^{-j}(\mathcal{D})$. This works since $\mathcal{D}$ is a fundamental domain of the action of the covering group on ${\mathcal{S}}_{\mathrm{reg}}$, which implies ${\mathcal{S}}_{\mathrm{reg}}={⨿}_{0\le j\le n}{\mathcal{R}}^j(\mathcal{D})$. Thus, the local holomorphic diffeomorphism ${\delta }_{K^{*}}$ intertwines the $\mathcal{G}$ action on $({\mathcal{S}}_{\mathrm{reg}},\Gamma )$ with the G action on $(K^{*},\gamma {|}_{K^{*}})$ and intertwines the local geodesic flow of the holomorphic geodesic vector field X with the local geodesic flow of the holomorphic vector field $\frac{\partial }{\partial z}$.

Following Richens and Berry [2] we impose the condition: when a geodesic, starting at a point in $\mathrm{int}(\mathrm{cl}(K^{*})\backslash \mathrm{O})$, meets $\partial K^{*}$ it undergoes a reflection in the edge of $K^{*}$ that it meets. Such geodesics never meet a vertex of $\mathrm{cl}(K^{*})$. Thus, this type of geodesic becomes a billiard motion in $K^{*}\backslash \mathrm{O}$, which is defined for all time. Billiard motions in polygons have been extensively studied. For a nice overview see Berger ([3], chpt. XI) and references therein. An argument shows that $\widehat{\mathcal{G}}$ invariant geodesics on $({\mathcal{S}}_{\mathrm{reg}},\Gamma )$ correspond under the map ${\delta }_{K^{*}\backslash \mathrm{O}}$ to billiard motions on $(K^{*}\backslash \mathrm{O},\gamma {|}_{(K^{*}\backslash \mathrm{O})})$.

Repeatedly reflecting a billiard motion in an edge of $K^{*}\backslash \mathrm{O}$ and suitable edges of suitable $\mathcal{T}$ translations of $K^{*}\backslash \mathrm{O}$ gives a straight line motion $\lambda$ on $\mathbb{C}\backslash {\mathbb{V}}^{+}$. The image of the segment of a billiard motion, where $\lambda$ intersects $K^{*}\backslash \mathrm{O}$, in the orbit space ${(\mathbb{C}\backslash {\mathbb{V}}^{+})}^{\sim }/\mathfrak{G}={\tilde{S}}_{\mathrm{reg}}$, is a geodesic. Here we use the flat Riemannian metric $\widehat{\gamma }$ on ${\tilde{S}}_{\mathrm{reg}}$, which is induced by the $\mathfrak{G}$ invariant Euclidean metric $\gamma$ on $\mathbb{C}\backslash {\mathbb{V}}^{+}$ restricted to $K^{*}\backslash \mathrm{O}$. Consequently, $({\tilde{S}}_{\mathrm{reg}},\widehat{\gamma })$ is an affine analogue of the affine Riemann surface ${\mathcal{S}}_{\mathrm{reg}}$ thought of as the orbit space of a discrete subgroup of $\mathrm{PGl}(2,\mathbb{C})$ acting on $\mathbb{C}$ with the Poincaré metric, see Weyl [4].

2. A Schwarz–Christoffel Mapping

Consider the conformal Schwarz–Christoffel mapping

$$\begin{array}{cc}\hfill F_T:{\mathbb{C}}^{+}& =\{\xi \in \mathbb{C}|\mathrm{Im}\xi \ge 0\}\to T=T_{n_0{n}_1{n}_{\infty }}\subseteq \mathbb{C}:\xi \mapsto {\int }_0^{\xi }\frac{\mathrm{d}w}{w^{1-\frac{n_0}{n}}{(1-w)}^{1-\frac{n_1}{n}}}=z\hfill \end{array}$$

(1)

of the upper half plane ${\mathbb{C}}^{+}$ to the rational triangle $T=T_{n_0{n}_1{n}_{\infty }}$ with interior angles $\frac{n_0}{n}\pi$, $\frac{n_1}{n}\pi$, and $\frac{n_{\infty }}{n}\pi$, see Figure 1. Here $n_0+n_1+n_{\infty }=n$ and $n_j\in {\mathbb{Z}}_{\ge 1}$ for $j=0,1$ and ∞ with $1\le n_0\le n_1\le n_{\infty }$. Because $n_{\infty }$ is greater than or equal to either $n_0$ or $n_1$, it follows that the corresponding side $OC$ is the longest side of the triangle $T=△OCD$.

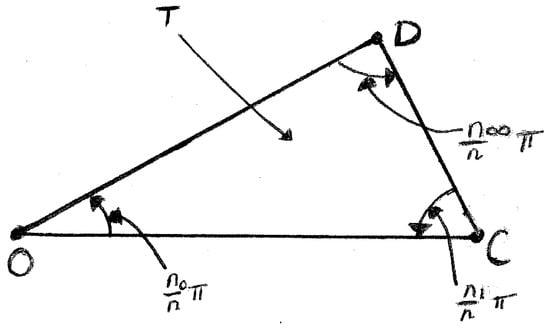
Figure 1. The rational triangle $T=T_{n_0{n}_1{n}_{\infty }}$.

In the integrand of (1) we use the following choice of complex $n\mathrm{th}$ root. Suppose that $w\in \mathbb{C}\backslash \{0,1\}$. Let $w=r_0{\mathrm{e}}^{i{\theta }_0}$ and $1-w=r_1{\mathrm{e}}^{i{\theta }_1}$ where $r_0,$$r_1\in {\mathbb{R}}_{>0}$ and ${\theta }_0$, ${\theta }_1\in [0,2\pi )$. For $w\in (0,1)$ on the real axis we have ${\theta }_0={\theta }_1=0$, $w=r_0>0$, and $1-w=r_1>0$. So ${\left(w^{n-n_0}{(1-w)}^{n-n_1}\right)}^{-2pt1/n}={(r_0^{n-n_0}{r}_1^{n-n_1})}^{1/n}$. In general for $w\in \mathbb{C}\backslash \{0,1\}$, we have

$${\left(w^{n-n_0}{(1-w)}^{n-n_1}\right)}^{-2pt1/n}={(r_0^{n-n_0}{r}_1^{n-n_1})}^{1/n}{\mathrm{e}}^{i((n-n_0){\theta }_0+(n-n_1){\theta }_1)/n}.$$

From (1) we get

$$F_T(0)=0,F_T(1)=C,\mathrm{and}{F}_T(\infty )=D,$$

where $C={\int }_0^1\frac{\mathrm{d}w}{w^{1-\frac{n_0}{n}}{(1-w)}^{1-\frac{n_1}{n}}}$ and $D={\mathrm{e}}^{\frac{n_0}{n}\pi i}(\frac{sin\frac{n_1}{n}\pi }{sin\frac{n_{\infty }}{n}\pi })C$. Consequently, the bijective holomorphic mapping $F_T$ sends $\mathrm{int}({\mathbb{C}}^{+}\backslash \{0,1\})$, the interior of the upper half plane less 0 and 1, onto $\mathrm{int}T$, the interior of the rational triangle $T=T_{n_0{n}_1{n}_{\infty }}$, and sends the boundary of ${\mathbb{C}}^{+}\backslash \{0,1\}$ to the edges of $\partial T$ less their end points O, C and D, see Figure 1. Thus, the image of ${\mathbb{C}}^{+}\backslash \{0,1\}$ under $F_T$ is $\mathrm{cl}(T)\backslash \{O,C,D\}$. Here $\mathrm{cl}(T)$ is the closure of T in $\mathbb{C}$.

Because $F_T{|}_{[0,1]}$ is real valued, we may use the Schwarz reflection principle to extend $F_T$ to the holomorphic diffeomorphism

$$\begin{array}{cc}\hfill & F_Q:\mathbb{C}\backslash \{0,1\}\to Q=T\cup \overline{T}\subseteq \mathbb{C}:\xi \mapsto z=\left\{\begin{array}{cc}\hfill F_T(\xi ),& \mathrm{if}\xi \in {\mathbb{C}}^{+}\backslash \{0,1\}\hfill \\ \hfill \overline{F_T(\overline{\xi })},& \mathrm{if}\xi \in \overline{{\mathbb{C}}^{+}\backslash \{0,1\}}.\hfill \end{array}\right.\hfill \end{array}$$

(2)

Here $Q=Q_{n_0{n}_1{n}_{\infty }}$ is a quadrilateral with internal angles $2\pi \frac{n_0}{n}$, $\pi \frac{n_{\infty }}{n}$, $2\pi \frac{n_1}{n}$, and $\pi \frac{n_{\infty }}{n}$ and vertices at O, D, C, and $\overline{D}$, see Figure 2. The conformal mapping $F_Q$ sends $\mathbb{C}\backslash \{0,1\}$ onto $\mathrm{cl}(Q)\backslash \{O,D,C,\overline{D}\}$.

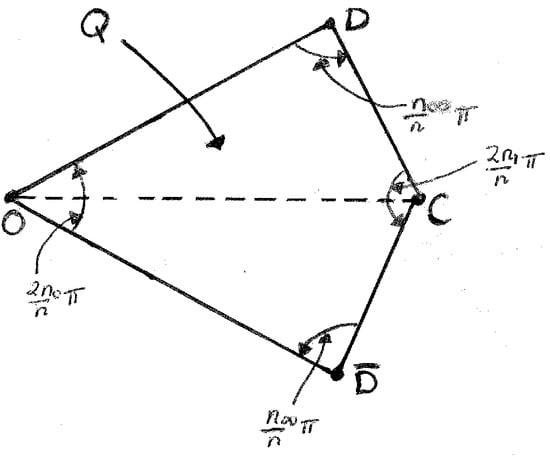
Figure 2. The rational quadrilateral Q.

3. The Geometry of an Affine Riemann Surface

Let $\xi$ and $\eta$ be coordinate functions on ${\mathbb{C}}^2$. Consider the affine Riemann surface $\mathcal{S}={\mathcal{S}}_{n_0,n_1,n_{\infty }}$ in ${\mathbb{C}}^2$, associated to the holomorphic mapping $F_Q$, defined by

$$g(\xi ,\eta )={\eta }^n-{\xi }^{n-n_0}{(1-\xi )}^{n-n_1}=0,$$

(3)

see Aurell and Itzykson [1]. We determine the singular points of $\mathcal{S}$ by solving

$$\begin{array}{cc}\hfill 0& =\mathrm{d}g(\xi ,\eta )\hfill \\ \hfill & =-(n-n_0){\xi }^{n-n_0-1}{(1-\xi )}^{n-n_1-1}(1-\frac{2n-n_0-n_1}{n-n_0}\xi )\mathrm{d}\xi +n{\eta }^{n-1}\mathrm{d}\eta \hfill \end{array}$$

(4)

For $(\xi ,\eta )\in \mathcal{S}$, we have $\mathrm{d}g(\xi ,\eta )=0$ if and only if $(\xi ,\eta )=(0,0)$ or $(1,0)$. Thus, the set ${\mathcal{S}}_{\mathrm{sing}}$ of singular points of $\mathcal{S}$ is $\{(0,0),(1,0)\}$. So the affine Riemann surface ${\mathcal{S}}_{\mathrm{reg}}=\mathcal{S}\backslash {\mathcal{S}}_{\mathrm{sing}}$ is a complex submanifold of ${\mathbb{C}}^2$. Actually, ${\mathcal{S}}_{\mathrm{reg}}\subseteq {\mathbb{C}}^2\backslash \{\eta =0\}$, for if $(\xi ,\eta )\in \mathcal{S}$ and $\eta =0$, then either $\xi =0$ or $\xi =1$.

Lemma 1.

Topologically ${\mathcal{S}}_{\mathrm{reg}}$ is a compact Riemann surface $\overline{\mathcal{S}}\subseteq {\mathbb{C}\mathbb{P}}^2$ of genus $g=\frac{1}{2}\left(n+2-(d_0+d_1+d_{\infty })\right)$ less three points: $[0:0:1]$, $[1:0:1]$, and $[0:1:0]$. Here $d_j=gcd(n_j,n)$ for $j=0,1,\infty$.

Proof. 

Consider the (projective) Riemann surface $\overline{\mathcal{S}}\subseteq {\mathbb{C}\mathbb{P}}^2$ specified by the condition $[\xi :\eta :\zeta ]\in \overline{\mathcal{S}}$ if and only if

$$G(\xi ,\eta ,\zeta )={\zeta }^{n-n_0-n_1}{\eta }^n-{\xi }^{n-n_0}{(\zeta -\xi )}^{n-n_1}=0.$$

(5)

Thinking of G as a polynomial in $\eta$ with coefficients which are polynomials in $\xi$ and $\zeta$, we may view $\overline{\mathcal{S}}$ as the branched covering

$$\overline{\pi }:\overline{\mathcal{S}}\subseteq {\mathbb{C}\mathbb{P}}^2\to \mathbb{C}\mathbb{P}:[\xi :\eta :\zeta ]\mapsto [\xi :\zeta ].$$

(6)

When $\zeta =1$ we get the affine branched covering

$$\pi =\overline{\pi }|\mathcal{S}:\mathcal{S}=\overline{\mathcal{S}}\cap \{\zeta =1\}\subseteq {\mathbb{C}}^2\to \mathbb{C}=\mathbb{C}\mathbb{P}\cap \{\zeta =1\}:(\xi ,\eta )\mapsto \xi .$$

(7)

From (3) it follows that $\eta ={\omega }_k{({\xi }^{n-n_0}{(1-\xi )}^{n-n_1})}^{1/n}$, where ${\omega }_k$ for $k=0,1,\dots ,n-1$ is an nth root of unity with and ${()}^{1/n}$ is the complex nth root used in the definition of the mapping $F_T$ (1). Thus, the branched covering mapping $\overline{\pi }$ (6) has n “sheets” except at its branch points. Since

$$\begin{array}{cc}\hfill \eta & ={\xi }^{1-\frac{n_0}{n}}{(1-\xi )}^{1-\frac{n_1}{n}}={\xi }^{1-\frac{n_0}{n}}\left(1-(1-\frac{n_1}{n})\xi +\cdots \right)\hfill \end{array}$$

(8a)

and

$$\begin{array}{cc}\hfill \eta & ={(1-\xi )}^{1-\frac{n_1}{n}}{\left(1-(1-\xi )\right)}^{1-\frac{n_0}{n}}\hfill \\ \hfill & ={(1-\xi )}^{1-\frac{n_1}{n}}\left(1-(1-\frac{n_0}{n})(1-\xi )+\cdots \right),\hfill \end{array}$$

(8b)

it follows that $\xi =0$ and $\xi =1$ are branch points of the mapping $\overline{\pi }$ of degree $\frac{n}{d_0}$ and $\frac{n}{d_1}$, since $d_j=\gcd (n,n_j)=\gcd (n-n_j,n_j)$ for $j=0,1$, see McKean and Moll ([5], p. 39). Because

$$\begin{array}{cc}\hfill \eta & ={(\frac{1}{\xi })}^{-(1-\frac{n_0}{n})}{(1-\frac{1}{\frac{1}{\xi }})}^{1-\frac{n_1}{n}}={(-1)}^{1-\frac{n_1}{n}}{\xi }^{2-\frac{n_0+n_1}{n}}{(1-\frac{1}{\xi })}^{1-\frac{n_1}{n}}\hfill \\ \hfill & ={(-1)}^{1-\frac{n_1}{n}}{\xi }^{1+\frac{n_{\infty }}{n}}(1-(1-\frac{n_1}{n})\frac{1}{\xi }+\cdots ),\hfill \end{array}$$

(8c)

∞ is a branch point of the mapping $\overline{\pi }$ of degree $\frac{n}{d_{\infty }}$, where $d_{\infty }=\gcd (n,n_{\infty })$. Hence the ramification index of 0, 1, ∞ is $d_0(\frac{n}{d_0}-1)=n-d_0$, $n-d_1$, and $n-d_{\infty }$, respectively. Thus, the map $\overline{\pi }$ has $d_0$ fewer sheets at 0, $d_1$ fewer at 1, and $d_{\infty }$ fewer at ∞ than an n-fold covering of $\mathbb{C}\mathbb{P}$. Thus, the total ramification index r of the mapping $\overline{\pi }$ is $r=(n-d_0)+(n-d_1)+(n-d_{\infty })$. By the Riemann–Hurwitz formula, the genus g of $\overline{\mathcal{S}}$ is $r=2n+2g-2$. In other words,

$$\begin{array}{c}\hfill g=\frac{1}{2}\left(n+2-(d_0+d_1+d_{\infty })\right).\end{array}$$

(9)

Consequently, the affine Riemann surface $\mathcal{S}$ is the compact connected surface $\overline{\mathcal{S}}$ less the point at ∞, namely, $\mathcal{S}=\overline{\mathcal{S}}\backslash \{[0:1:0]\}$. So ${\mathcal{S}}_{\mathrm{reg}}$ is the compact connected surface $\overline{\mathcal{S}}$ less three points: $[0:0:1]$, $[1:0:1]$, and $[0:1:0]$. □

Examples of $\overline{\mathcal{S}}={\overline{\mathcal{S}}}_{n_0,n_1,n_{\infty }}$

• $n_0=1$, $n_0=1$, $n_{\infty }=4$; $n=6$. So $d_0=1$, $d_1=1$, $d_{\infty }=2$. Hence $2g=8-4=4$. So $g=2$.
• $n_0=2$, $n_1=2$, $n_{\infty }=3$; $n=7$. So $d_0=d_1=d_{\infty }=1$. Hence $2g=9-3=6$. So $g=3$.

Table 1 below lists all the partitions $\{n_1,n_0,n_{\infty }\}$ of n, which give a low genus Riemann surface $\overline{\mathcal{S}}={\overline{\mathcal{S}}}_{n_0,n_1,n_{\infty }}$

Table 1. Based on the table in Aurell and Itzykson ([1], p. 193).

g	${\mathit{n}}_0,{\mathit{n}}_1,{\mathit{n}}_{\mathit{\infty }};\mathit{n}$	g	${\mathit{n}}_0,{\mathit{n}}_1,{\mathit{n}}_{\mathit{\infty }};\mathit{n}$
1	$1,1,1;3$	3	$2,2,3;7$
1	$1,1,2;4$	3	$1,3,3;7$
1	$1,2,3;6$	3	$1,1,5;7$
2	$1,2,2;5$	3	$2,3,3;8$
2	$1,1,3;5$	3	$1,2,5;8$
2	$1,1,4;6$	3	$1,1,6;8$
2	$1,3,4;8$	3	$2,3,4;9$
2	$2,3,5;10$	3	$1,3,5;9$
2	$1,4,5;10$	3	$1,2,6;9$
		3	$3,4,5;12$
		3	$1,5,6;12$
		3	$1,3,8;12$
		3	$2,5,7;14$
		3	$1,6,7;14$

Corollary 1.

If n is an odd prime number and $\{n_1,n_0,n_{\infty }\}$ is a partition of n into three parts, then the genus of $\overline{\mathcal{S}}$ is $\frac{1}{2}(n-1)$.

Proof. 

Because n is prime, we get $d_0=d_1=d_{\infty }=1$. Using the formula $g=\frac{1}{2}\left(n+2-(d_0+d_1+d_{\infty })\right)$ we obtain $g=\frac{1}{2}(n-1)$. □

Corollary 2.

The singular points of the Riemann surface $\overline{\mathcal{S}}$ are $[0:0:1]$, $[1:0:1]$, and if $n_{\infty }>1$ then also $[0:1:0]$.

Proof. 

A point $[\xi :\eta :\zeta ]\in {\overline{\mathcal{S}}}_{\mathrm{sing}}$ if and only if $[\xi :\eta :\zeta ]\in \overline{\mathcal{S}}$, that is,

$$0=G(\xi ,\eta ,\zeta )={\zeta }^{n-(n_0+n_1)}{\eta }^n-{\xi }^{n-n_0}{(\zeta -\xi )}^{n-n_1}$$

(10a)

and

$$\begin{array}{cc}\hfill (0,0,0)& =DG(\xi ,\eta ,\zeta )\hfill \\ \hfill & =(-{\xi }^{n-n_0-1}{(\zeta -\xi )}^{n-n_1-1}\left((n-n_0)(\zeta -\xi )-(n-n_1)\xi \right),\hfill \\ \hfill & n{\eta }^{n-1}{\zeta }^{n-(n_0+n_1)},(n-(n_0+n_1)){\eta }^n{\zeta }^{n-n_0-n_1-1}\hfill \\ \hfill & -(n-n_1){\xi }^{n-n_0}{(\zeta -\xi )}^{n-n_1-1})\hfill \end{array}$$

(10b)

We need only check the points $[0:0:1]$, $[1:0:1]$ and $[0:1:0]$. Since the first two points are singular points of $\mathcal{S}=\overline{\mathcal{S}}\backslash \{[0:1:0]\}$, they are singular points of $\overline{\mathcal{S}}$. Thus, we need to see if $[0:1:0]$ is a singular point of $\overline{\mathcal{S}}$. Substituting $(0,1,0)$ into the right hand side of (10b) we get $\left\{\begin{array}{c}(0,0,1),\mathrm{if}{n}_{\infty }=n-(n_0+n_1)=1\hfill \\ (0,0,0),\mathrm{if}{n}_{\infty }>1.\hfill \end{array}\right.$ Thus, $[0:1:0]$ is a singular point of $\overline{\mathcal{S}}$ only if $n_{\infty }>1$. □

Lemma 2.

The mapping

$$\widehat{\pi }=\pi |{\mathcal{S}}_{\mathrm{reg}}:{\mathcal{S}}_{\mathrm{reg}}\subseteq {\mathbb{C}}^2\to \mathbb{C}\backslash \{0,1\}:(\xi ,\eta )\mapsto \xi$$

(11)

is a surjective holomorphic local diffeomorphism.

Proof. 

Let $(\xi ,\eta )\in {\mathcal{S}}_{\mathrm{reg}}$ and let

$$X(\xi ,\eta )=\eta \frac{\partial }{\partial \xi }+\frac{n-n_0}{n}\frac{{\xi }^{n-n_0-1}{(1-\xi )}^{n-n_1-1}(1-\frac{2n-n_0-n_1}{n-n_0}\xi )}{{\eta }^{n-2}}\frac{\partial }{\partial \eta }.$$

(12)

By hypothesis $(\xi ,\eta )\in {\mathcal{S}}_{\mathrm{reg}}$ implies that $\eta \ne 0$. The vector $X(\xi ,\eta )$ is defined and is nonzero. From $(X⌟\mathrm{d}g)(\xi ,\eta )=0$ and $T_{(\xi ,\eta )}{\mathcal{S}}_{\mathrm{reg}}=ker\mathrm{d}g(\xi ,\eta )$, it follows that $X(\xi ,\eta )\in T_{(\xi ,\eta )}{\mathcal{S}}_{\mathrm{reg}}$. Using the definition of $X(\xi ,\eta )$ (12) and the definition of the mapping $\pi$ (7), we see that the tangent of the mapping $\widehat{\pi }$ (11) at $(\xi ,\eta )\in {\mathcal{S}}_{\mathrm{reg}}$ is given by

$$T_{(\xi ,\eta )}\widehat{\pi }:T_{(\xi ,\eta )}{\mathcal{S}}_{\mathrm{reg}}\to T_{\xi }(\mathbb{C}\backslash \{0,1\})=\mathbb{C}:X(\xi ,\eta )\mapsto \eta \frac{\partial }{\partial \xi }.$$

(13)

Since $X(\xi ,\eta )$ and $\eta \frac{\partial }{\partial \xi }$ are nonzero vectors, they form a complex basis for $T_{(\xi ,\eta )}{\mathcal{S}}_{\mathrm{reg}}$ and $T_{\xi }(\mathbb{C}\backslash \{0,1\})$, respectively. Thus, the complex linear mapping $T_{(\xi ,\eta )}\widehat{\pi }$ is an isomorphism. Hence $\widehat{\pi }$ is a local holomorphic diffeomorphism. □

Corollary 3.

$\widehat{\pi }$ (11) is a surjective holomorphic n to 1 covering map.

Proof. 

We only need to show that $\widehat{\pi }$ is a covering map. First we note that every fiber of $\widehat{\pi }$ is a finite set with n elements, since for each fixed $\xi \in \mathbb{C}\backslash \{0,1\}$ we have ${\widehat{\pi }}^{-1}(\xi )=\{(\xi ,\eta )\in {\mathcal{S}}_{\mathrm{reg}}|\eta ={\omega }_k{({\xi }^{n-n_0}{(1-\xi )}^{n-n_1})}^{1/n}\}$. Here ${\omega }_k$ for $k=0,1,\dots ,n-1$, is an $n^{\mathrm{th}}$ root of 1 and ${()}^{1/n}$ is the complex $n^{\mathrm{th}}$ root used in the definition of the Schwarz–Christoffel map $F_Q$ (2). Hence the map $\widehat{\pi }$ is a proper surjective holomorphic submersion, because each fiber is compact. Thus, the mapping $\widehat{\pi }$ is a presentation of a locally trivial fiber bundle with fiber consisting of n distinct points. In other words, the map $\widehat{\pi }$ is a n to 1 covering mapping. □

Consider the group $\widehat{\mathcal{G}}$ of linear transformations of ${\mathbb{C}}^2$ generated by

$$\mathcal{R}:{\mathbb{C}}^2\to {\mathbb{C}}^2:(\xi ,\eta )\mapsto (\xi ,{\mathrm{e}}^{2\pi i/n}\eta ).$$

Clearly ${\mathcal{R}}^n={\mathrm{id}}_{{\mathbb{C}}^2}=e$, the identity element of $\widehat{\mathcal{G}}$ and $\widehat{\mathcal{G}}=\{e,\mathcal{R},\dots ,{\mathcal{R}}^{n-1}\}$. For each $(\xi ,\eta )\in \mathcal{S}$ we have

$$\begin{array}{cc}\hfill {({\mathrm{e}}^{2\pi i/n}\eta )}^n-{\xi }^{n-n_0}{(1-\xi )}^{n-n_1}& ={\eta }^n-{\xi }^{n-n_0}{(1-\xi )}^{n-n_1}=0.\hfill \end{array}$$

So $\mathcal{R}(\xi ,\eta )\in \mathcal{S}$. Thus, we have an action of $\widehat{\mathcal{G}}$ on the affine Riemann surface $\mathcal{S}$ given by

$$\Phi :\widehat{\mathcal{G}}\times \mathcal{S}\to \mathcal{S}:\left(g,(\xi ,\eta )\right)\mapsto g(\xi ,\eta ).$$

(14)

Since $\widehat{\mathcal{G}}$ is finite, and hence is compact, the action $\Phi$ is proper. For every $g\in \widehat{\mathcal{G}}$ we have ${\Phi }_g(0,0)=(0,0)$ and ${\Phi }_g(1,0)=(1,0)$. So ${\Phi }_g$ maps ${\mathcal{S}}_{\mathrm{reg}}$ into itself. At $(\xi ,\eta )\in {\mathcal{S}}_{\mathrm{reg}}$ the isotropy group ${\widehat{\mathcal{G}}}_{(\xi ,\eta )}$ is $\{e\}$, that is, the $\widehat{\mathcal{G}}$-action $\Phi$ on ${\mathcal{S}}_{\mathrm{reg}}$ is free. Thus, the orbit space ${\mathcal{S}}_{\mathrm{reg}}/\widehat{\mathcal{G}}$ is a complex manifold.

Corollary 4.

Consider the holomorphic mapping

$$\rho :{\mathcal{S}}_{\mathrm{reg}}\subseteq {\mathbb{C}}^2\to {\mathcal{S}}_{\mathrm{reg}}/\widehat{\mathcal{G}}\subseteq {\mathbb{C}}^2:(\xi ,\eta )\mapsto [(\xi ,\eta )],$$

where $[(\xi ,\eta )]$ is the $\widehat{\mathcal{G}}$-orbit $\{{\Phi }_g(\xi ,\eta )\in {\mathcal{S}}_{\mathrm{reg}}|g\in \widehat{\mathcal{G}}\}$ of $(\xi ,\eta )$ in ${\mathcal{S}}_{\mathrm{reg}}$. The $\widehat{\mathcal{G}}$ principal bundle presented by the mapping ρ is isomorphic to the bundle presented by the mapping $\widehat{\pi }$ (11).

Proof. 

We use invariant theory to determine the orbit space $\mathcal{S}/\widehat{\mathcal{G}}$. The algebra of polynomials on ${\mathbb{C}}^2$, which are invariant under the $\widehat{\mathcal{G}}$-action $\Phi$, is generated by ${\pi }_1=\xi \mathrm{and}{\pi }_2={\eta }^n$. Since $(\xi ,\eta )\in \mathcal{S}$, these polynomials are subject to the relation

$${\pi }_2-{\pi }_1^{n-n_0}{(1-{\pi }_1)}^{n-n_1}={\eta }^n-{\xi }^{n-n_0}{(1-\xi )}^{n-n_1}=0.$$

(15)

Equation (15) defines the orbit space $\mathcal{S}/\widehat{\mathcal{G}}$ as a complex subvariety of ${\mathbb{C}}^2$. This subvariety is homeomorphic to $\mathbb{C}$, because it is the graph of the function ${\pi }_1\mapsto {\pi }_1^{n-n_0}{(1-{\pi }_1)}^{n-n_1}$. Consequently, the orbit space ${\mathcal{S}}_{\mathrm{reg}}/\widehat{\mathcal{G}}$ is holomorphically diffeomorphic to $\mathbb{C}\backslash \{0,1\}$.

It remains to show that $\widehat{\mathcal{G}}$ is the group of covering transformations of the bundle presented by the mapping $\widehat{\pi }$ (11). For each $\xi \in \mathbb{C}\backslash \{0,1\}$ look at the fiber ${\widehat{\pi }}^{-1}(\xi )$. If $(\xi ,\eta )\in {\widehat{\pi }}^{-1}(\xi )$, then ${\mathcal{R}}^{\pm 1}(\xi ,\eta )=(\xi ,{\mathrm{e}}^{\pm 2\pi i/n}\eta )\in {\mathcal{S}}_{\mathrm{reg}}$, since $(\xi ,{\mathrm{e}}^{\pm 2\pi i/n}\eta )\ne (0,0)$ or $(1,0)$ and $(\xi ,{\mathrm{e}}^{\pm 2\pi i/n}\eta )\in \mathcal{S}$. Thus, ${\Phi }_{{\mathcal{R}}^{\pm 1}}\left({\widehat{\pi }}^{-1}(\xi )\right)\subseteq {\widehat{\pi }}^{-1}(\xi )$. So ${\widehat{\pi }}^{-1}(\xi )\subseteq {\Phi }_{\mathcal{R}}\left({\widehat{\pi }}^{-1}(\xi )\right)\subseteq {\widehat{\pi }}^{-1}(\xi )$. Hence ${\Phi }_{\mathcal{R}}\left({\widehat{\pi }}^{-1}(\xi )\right)={\widehat{\pi }}^{-1}(\xi )$. Thus, ${\Phi }_{\mathcal{R}}$ is a covering transformation for the bundle presented by the mapping $\widehat{\pi }$. So $\widehat{\mathcal{G}}$ is a subgroup of the group of covering transformations. These groups are equal because $\widehat{\mathcal{G}}$ acts transitively on each fiber of the mapping $\widehat{\pi }$. □

4. Another Model for ${\mathcal{S}}_{\mathbf{reg}}$

We construct another model ${\tilde{\mathcal{S}}}_{\mathrm{reg}}$ for the smooth part ${\mathcal{S}}_{\mathrm{reg}}$ of the affine Riemann surface $\mathcal{S}$ (3) as follows. Let $\mathcal{D}\subseteq {\mathcal{S}}_{\mathrm{reg}}$ be a fundamental domain for the $\widehat{\mathcal{G}}$ action $\Phi$ (14) on ${\mathcal{S}}_{\mathrm{reg}}$. So $(\xi ,\eta )\in \mathcal{D}$ if and only if for $\xi \in \mathbb{C}\backslash \{0,1\}$ we have $\eta ={\left({\xi }^{n-n_0}{(1-\xi )}^{n-n_1}\right)}^{-2pt1/n}$. Here ${()}^{1/n}$ is the $n^{\mathrm{th}}$ root used in the definition of the mapping $F_Q$ (2). The domain $\mathcal{D}$ is a connected subset of ${\mathcal{S}}_{\mathrm{reg}}$ with nonempty interior. Its image under the map $\widehat{\pi }$ (11) is $\mathbb{C}\backslash \{0,1\}$. Thus, $\mathcal{D}$ is one “sheet” of the covering map $\widehat{\pi }$. So $\widehat{\pi }{|}_{\mathcal{D}}$ is one to one.

Using the extended Schwarz–Christoffel mapping $F_Q$ (2), we give a more geometric description of the fundamental domain $\mathcal{D}$. Consider the mapping

$$\delta :\mathcal{D}\subseteq {\mathcal{S}}_{\mathrm{reg}}\to Q\subseteq \mathbb{C}:(\xi ,\eta )\mapsto F_Q\left(\widehat{\pi }(\xi ,\eta )\right),$$

(16)

where the map $\widehat{\pi }$ is given by Equation (11). The map $\delta$ is a holomorphic diffeomorphism of $\mathrm{int}\mathcal{D}$ onto $\mathrm{int}Q$, which sends $\partial \mathcal{D}$ homeomorphically onto $\partial Q$. Look at $\mathrm{cl}(Q)$, which is a closed quadrilateral with vertices O, D, C, and $\overline{D}$. The set $\delta (\mathcal{D})$ contains the open edges $OD$, $DC$, and $C\overline{D}$ but not the open edge $O\overline{D}$ of $\mathrm{cl}(Q)$, see Figure 3 above.

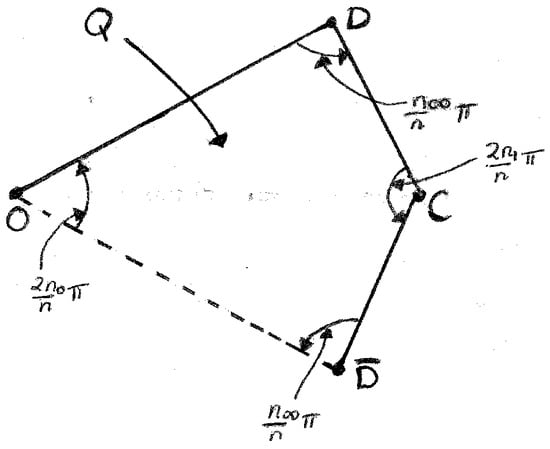
Figure 3. The image Q of the fundamental domain $\mathcal{D}$ under the mapping $\delta$. The open edges $OD$, $C\overline{D}$, and $CD$ of the quadrilateral are included; while the open edge $O\overline{D}$ is excluded.

Let $K^{*}=K_{n_0,n_1,n_{\infty }}^{*}={⨿}_{0\le j\le n-1}{R}^j\left(\delta (\mathcal{D})\right)$ be the region in $\mathbb{C}$ formed by repeatedly rotating $Q=\delta (\mathcal{D})$ through an angle $2\pi /n$. Here R is the rotation $\mathbb{C}\to \mathbb{C}:z\mapsto {\mathrm{e}}^{2\pi i/n}z$. We say that the quadrilateral $Q=Q_{2n_0,n_{\infty },2n_1,n_{\infty }}$forms$K^{*}$, see Figure 4 above.

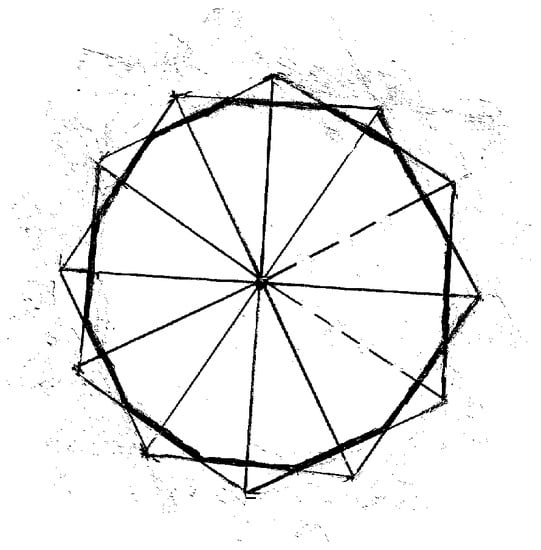
Figure 4. The regular duodecagon K and the stellated regular duodecagon $K^{*}=K_{4,4,4}^{*}$ formed by rotating the quadrilateral $Q_{4,4,4}$ through an angle 2$\pi$/12 around the origin.

Theorem 1.

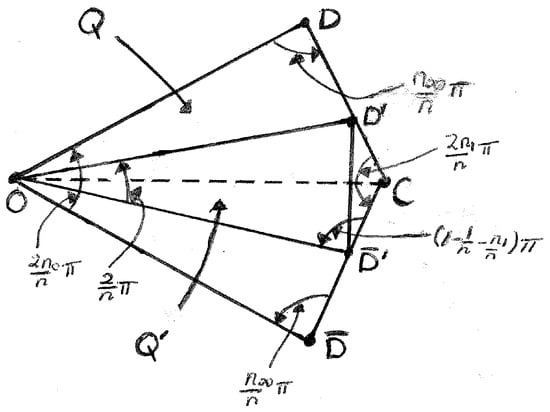
The connected set $K^{*}$ is a regular stellated n-gon with its $2n$ vertices omitted, which is formed from the quadrilateral $Q^{\prime }=O{D}^{\prime }C\overline{D^{\prime }}$, see Figure 5.

Figure 5. The dart in the figure is the quadrilateral $Q^{\prime }=O{D}^{\prime }C\overline{D^{\prime }}$, which is the union of the triangles $T=\Delta O{D}^{\prime }C$ and the triangle $\overline{T^{\prime }}$.

Proof. 

By construction the quadrilateral $Q^{\prime }=O{D}^{\prime }C\overline{D^{\prime }}$ is contained in the quadrilateral $Q=ODC\overline{D}$. Note that $Q\subseteq {\bigcup }_{j=[-\frac{n_1+1}{2}]}^{[\frac{n_1+1}{2}]}{R}^j(Q^{\prime })$. Thus,

$$K^{*}=\bigcup _{j=0}^n{R}^j(Q)\subseteq \bigcup _{j=0}^n{R}^j(Q^{\prime })\subseteq \bigcup _{j=0}^n{R}^j(Q)=K^{*}.$$

So $K^{*}={\bigcup }_{j=0}^n{R}^j(Q^{\prime })$. Thus, $K^{*}$ is the regular stellated n-gon less its vertices, one of whose open sides is the diagonal $D^{\prime }\overline{D^{\prime }}$ of $Q^{\prime }$. □

We would like to extend the mapping $\delta$ (16) to a mapping of ${\mathcal{S}}_{\mathrm{reg}}$ onto $K^{*}$. Let

$${\delta }_{{\Phi }_{{\mathcal{R}}^j}(\mathcal{D})}:{\Phi }_{{\mathcal{R}}^j}(\mathcal{D})\subseteq {\mathcal{S}}_{\mathrm{reg}}\to R^j\left(\delta (\mathcal{D})\right)\subseteq K^{*}:(\xi ,\eta )\mapsto R^j\delta \left({\Phi }_{{\mathcal{R}}^{-j}}(\xi ,\eta )\right),$$

where $\Phi$ is the $\widehat{\mathcal{G}}$ action defined in Equation (14). So we have a mapping

$${\delta }_{K^{*}}:{\mathcal{S}}_{\mathrm{reg}}\subseteq {\mathbb{C}}^2\to K^{*}\subseteq \mathbb{C}$$

(17)

defined by $({\delta }_{K^{*}}){{|}_{{\Phi }_{{\mathcal{R}}^j}(\mathcal{D})}=\delta |}_{{\Phi }_{{\mathcal{R}}^j}(\mathcal{D})}$. The mapping ${\delta }_{K^{*}}$ is defined on ${\mathcal{S}}_{\mathrm{reg}}$, because ${\mathcal{S}}_{\mathrm{reg}}={⨿}_{0\le j\le n-1}{\Phi }_{{\mathcal{R}}^j}(\mathcal{D})$, since $\mathcal{D}$ is a fundamental domain for the $\widehat{\mathcal{G}}$-action $\Phi$ (14) on ${\mathcal{S}}_{\mathrm{reg}}$. Because $K^{*}={⨿}_{0\le j\le n-1}{R}^j\left(\delta (\mathcal{D})\right)$, the mapping ${\delta }_{K^{*}}$ is surjective. Hence ${\delta }_{K^{*}}$ is holomorphic, since it is continuous on ${\mathcal{S}}_{\mathrm{reg}}$ and is holomorphic on the dense open subset ${⨿}_{0\le j\le n-1}{\mathcal{R}}^j(\mathrm{int}\mathcal{D})$ of ${\mathcal{S}}_{\mathrm{reg}}$. Let $U:\mathbb{C}\to \mathbb{C}:z\mapsto \overline{z}$ and let G be the group generated by the rotation R and the reflection U subject to the relations $R^n=U^2=e$ and $RU=U{R}^{-1}$. Shorthand $G=⟨U,R|U^2=e=R^n\&RU=U{R}^{-1}⟩$. Then $G=\{e;R^p{U}^{\ell },\ell =0,1\&p=0,1,\dots ,n-1\}$. The group G is the dihedral group $D_{2n}$. The closure $\mathrm{cl}(K^{*})$ of $K^{*}={⨿}_{0\le j\le n-1}{R}^j(Q)$ in $\mathbb{C}$ is invariant under $\widehat{G}$, the subgroup of G generated by the rotation R. Because the quadrilateral Q is invariant under the reflection $U:z\mapsto \overline{z}$, and $U{R}^j=R^{-j}U$, it follows that $\mathrm{cl}(K^{*})$ is invariant under the reflection U. So $\mathrm{cl}(K^{*})$ is invariant under the group G.

We now look at some group theoretic properties of $K^{*}$.

Lemma 3.

If F is a closed edge of the polygon $\mathrm{cl}(K^{*})$ and ${g|}_F{=\mathrm{id}|}_F$ for some $g\in G$, then $g=e$.

Proof. 

Suppose that $g\ne e$. Then $g=R^p{U}^{\ell }$ for some $\ell \in \{0,1\}$ and some $p\in \{0,1,\dots$, $n-1\}$. Let $g=R^{p}U$ and suppose that F is an edge of $\mathrm{cl}(K^{*})$ such that $\mathrm{int}(F)\cap \mathbb{R}\ne ⌀$, where $\mathbb{R}=\{\mathrm{Re}z|z\in \mathbb{C}\}$. Then $U(F)=F$, but ${U|}_F\ne {\mathrm{id}}_F$. So ${g|}_F=R^p{U|}_F\ne {\mathrm{id}}_F$. Now suppose that $\mathrm{int}(F)\cap \mathbb{R}=⌀$. Then $U(F)\ne F$. So ${U|}_F\ne {\mathrm{id}}_F$. Hence ${g|}_F\ne {\mathrm{id}}_F$. Finally, suppose that $g=R^p$ with $p\ne 0$. Then $g(F)\ne F$. So ${g|}_F{\ne \mathrm{id}|}_F$. □

Lemma 4.

For $j=0,1,\infty$ put $S^{(j)}=R^{n_j}U$. Then $S^{(j)}$ is a reflection in the closed ray ${\ell }^j=\{t{\mathrm{e}}^{i\pi n_j/n}\in \mathbb{C}|t\in OD\}$. The ray ${\ell }^0$ is the closure of the side $OD$ of the quadrilateral $Q=ODC\overline{D}$ in Figure 5.

Proof. 

$S^{(j)}$ fixes every point on the closed ray ${\ell }^j$, because

$$\begin{array}{cc}\hfill S^{(j)}(\{t{\mathrm{e}}^{i\pi n_j/n}|t\in OD\})& =R^{n_j}(\{t{\mathrm{e}}^{-i\pi n_j/n}|t\in OD\})=\{t{\mathrm{e}}^{i\pi n_j/n}|t\in OD\}.\hfill \end{array}$$

Since ${(S^{(j)})}^2=(R^{n_j}U)(R^{n_j}U)=R^{n_j}(UU)R^{-n_j}=e$, it follows that $S^{(j)}$ is a reflection in the closed ray ${\ell }^j$. □

Corollary 5.

For every $j=0,1,\infty$ and every $k\in \{0,1,\dots ,n-1\}$ let $S_k^{(j)}=R^k{S}^{(j)}{R}^{-k}$. Here $S_n^{(j)}=S_0^{(j)}=S^{(j)}$, because $R^n=e$. Then $S_k^{(j)}$ is a reflection in the closed ray $R^k{\ell }^j$.

Proof. 

This follows because ${(S_k^{(j)})}^2=R^k{(S^{(j)})}^2{R}^{-k}=e$ and $S_k^{(j)}$ fixes every point on the closed ray $R^k{\ell }^j$, for

$$\begin{array}{cc}\hfill S_k^{(j)}\left(R^k(\{t{\mathrm{e}}^{i\pi n_j/n}|t\in OD\})\right)& =R^k{S}^{(j)}(\{t{\mathrm{e}}^{i\pi n_j/n}|t\in OD\}))\hfill \\ \hfill & =R^k(\{t{\mathrm{e}}^{i\pi n_j/n}|t\in OD\}).\hfill \end{array}$$

□

Corollary 6.

For every $j=0,1,\infty$, every $S_k^{(j)}$ with $k=0,1,\dots ,n-1$, and every $g\in G$, we have $g{S}_k^{(j)}{g}^{-1}=S_r^{(j)}$ for a unique $r\in \{0,1,\dots ,n-1\}$.

Proof. 

We compute. For every $k=0,1,\dots ,n-1$ we have

$$R{S}_k^{(j)}{R}^{-1}=R(R^k{S}^{(j)}{R}^{-k})R^{-1}=R^{(k+1)}{S}^{(j)}{R}^{-(k+1)}=S_{k+1}^{(j)}$$

(18)

and

$$\begin{array}{cc}\hfill U{S}_k^{(j)}{U}^{-1}& =U(R^{(k+n_j)}U{R}^{-(k+n_j)})U=R^{-(k+n_j)}U{R}^{(k+n_j)}\hfill \\ \hfill & =S_{-(k+2n_j)}^{(j)}=S_t^{(j)},\hfill \end{array}$$

(19)

where $t=-(k+2n_j)modn$. Since R and U generate the group G, the corollary follows. □

Corollary 7.

For $j=0,1,\infty$ let $G^j$ be the group generated by the reflections $S_k^{(j)}$ for $k=0,1,\dots ,n-1$. Then $G^j$ is a normal subgroup of G.

Proof. 

Clearly $G^j$ is a subgroup of G. From Equations (18) and (19) it follows that $g{S}_k^{(j)}{g}^{-1}\in G^j$ for every $g\in G$ and every $k=0,1\dots ,n-1$, since G is generated by R and U. However, $G^j$ is generated by the reflections $S_k^{(j)}$ for $k=0,1,\dots ,n-1$, that is, every $g^{\prime }\in G^j$ may be written as $S_{i_1}^{(j)}\cdots S_{i_p}^{(j)}$, where for $\ell \in \{1,\dots p\}$ we have $i_{\ell }\in \{0,1,\dots ,n-1\}$. So $g{g}^{\prime }{g}^{-1}=g(S_{i_1}^{(j)}\cdots S_{i_p}^{(j)})g^{-1}=(g{S}_{i_1}^{(j)}{g}^{-1})\cdots (g{S}_{i_p}^{(j)}{g}^{-1})\in G^j$ for every $g\in G$, that is, $G^j$ is a normal subgroup of G. □

As a first step in constructing the model ${\tilde{\mathcal{S}}}_{\mathrm{reg}}$ of ${\mathcal{S}}_{\mathrm{reg}}$ from the regular stellated n-gon $K^{*}$ we look at certain pairs of edges of $\mathrm{cl}(K^{*})$. For each $j=0,1,\infty$ we say two distinct closed edges E and $E^{\prime }$ of $\mathrm{cl}(K^{*})$ are adjacent if and only if they intersect at a vertex of $\mathrm{cl}(K^{*})$. For $j=0,1,\infty$ let ${\mathcal{E}}^j$ be the set of unordered pairs of equivalent closed edges E and $E^{\prime }$ of $\mathrm{cl}(K^{*})$, that is, the edges E and $E^{\prime }$ are not adjacent and $E^{\prime }=S_m^{(j)}(E)$ for some generator $S_m^{(j)}$ of $G^j$. Recall that for x and y in some set, the unordered pair $[x,y]$ is precisely one of the ordered pairs $(x,y)$ or $(y,x)$. Note that ${\bigcup }_{j=0,1,\infty }{\mathcal{E}}^j$ is the set of all unordered pairs of nonadjacent edges of $\mathrm{cl}(K^{*})$. Geometrically, two nonadjacent closed edges $E^{\prime }$ and E of $\mathrm{cl}(K^{*})$ are equivalent if and only if $E^{\prime }$ is obtained from E by reflection in the line $R^m{\ell }^j$ for some $m\in \{0,1,\dots ,n-1\}$ and some $j=0,1,\infty$. In Figure 6, where $K^{*},=K_{1,1,4}^{*}$, parallel edges of $K^{*}$, which are labeled with the same letter, are $G^0$-equivalent. This is no coincidence.

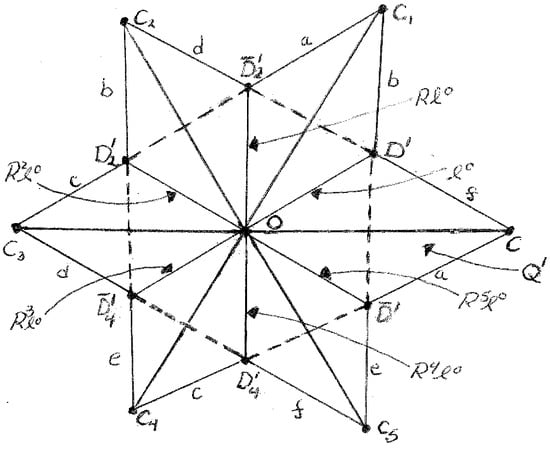
Figure 6. The triangulation ${\mathcal{T}}_{cl}(K^{*})$ of the regular stellated hexagon $K^{*}$. The vertices of cl($K^{*}$) are labeled $X_j=R^{j}X$ for $X=A,B,C$ and equivalent edges by $a,b,c,d,e,f$.

Lemma 5.

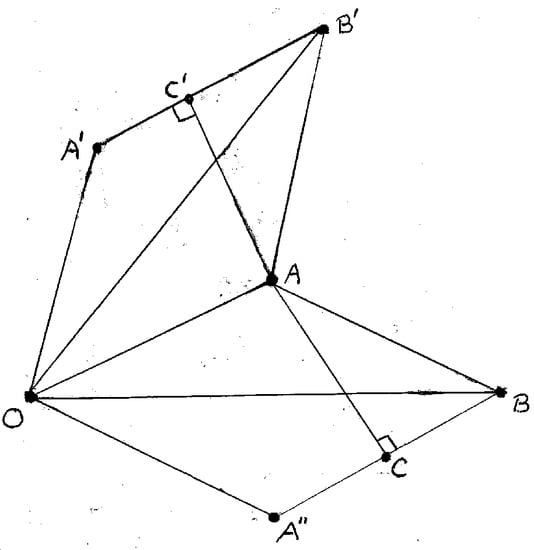
Let $K^{*}$ be formed from the quadrilateral $Q=T\cup \overline{T}$, where T is the isosceles rational triangle $T_{n_0{n}_0{n}_{\infty }}$ less its vertices. Then nonadjacent edges of $\partial \mathrm{cl}(K^{*})$ are $G^0$-equivalent if and only if they are parallel, see Figure 7.

Figure 7. The geometric configuration.

Proof. 

In Figure 7, let $OAB$ be the triangle T with $\angle AOB=\alpha$, $\angle OAB=\beta$, and $\angle ABO=\gamma$. Let $OAB{A}^{″}$ be the quadrilateral formed by reflecting the triangle $OAB$ in its edge $OB$. The quadrilateral $OAB{A}^{″}$ reflected it its edge $OA$ is the quadrilateral $OA{B}^{\prime }{A}^{\prime }$. Let $A{C}^{\prime }$ be perpendicular to $A^{\prime }{B}^{\prime }$ and $AC$ be perpendicular to $A^{″}B$, see Figure 7. Then $CA{C}^{\prime }$ is a straight line if and only if $\angle C^{\prime }A{B}^{\prime }+\angle B^{\prime }AB+\angle BAC=\pi$. By construction $\angle C^{\prime }A{B}^{\prime }=\angle BAC=\pi /2-2\gamma$ and $\angle B^{\prime }AB=2\pi -2\beta$. So

$$\begin{array}{cc}\hfill \pi & =2(\frac{\pi }{2}-2\gamma )+2(\pi -\beta )=3\pi -2(\beta +\gamma )-2\gamma \hfill \\ \hfill & =3\pi -2(\alpha +\beta +\gamma )+2(\alpha -\gamma )=\pi +2(\alpha -\gamma ),\hfill \end{array}$$

if and only if $\alpha =\gamma$. Hence the edges $A^{″}B$ and $A^{\prime }{B}^{\prime }$ are parallel if and only if the triangle $OAB$ is isosceles. □

Theorem 2.

Let $K^{*}$ be the regular stellated n-gon formed from the rational quadrilateral $Q_{n_0{n}_1{n}_{\infty }}$ with $d_j=\gcd (n_j,n)$ for $j=0,1,\infty$. The G orbit space formed by first identifiying equivalent edges of the regular stellated n-gon $K^{*}$ formed from Q less O and then acting on the identification space by the group G is ${\tilde{\mathcal{S}}}_{\mathrm{reg}}$, which is a smooth 2-sphere with g handles, where $g=\frac{1}{2}\left(n+2-(d_0+d_1+d_{\infty })\right)$, less some points corresponding to the image of the vertices of $\mathrm{cl}(K^{*})$.

Example 1.

Before we begin proving Theorem 2 we consider the following special case. Let $K^{*}=K_{1,1,4}^{*}$ be a regular stellated hexagon formed by repeatedly rotating the quadrilateral $Q^{\prime }=O{D}^{\prime }C\overline{D^{\prime }}$ by R through an angle $2\pi /6$, see Figure 6.

Let $G^0$ be the group generated by the reflections $S_k^{(0)}=R^k{S}^{(0)}{R}^{-k}=R^{2k+1}U$ for $k=0,1,\dots ,5$. Here $S^{(0)}=RU$ is the reflection which leaves the closed ray ${\ell }^0=\{t{\mathrm{e}}^{i\rho /6}|t\in O{D}^{\prime }\}$ fixed. Define an equivalence relation on $\mathrm{cl}(K^{*})$ by saying that two points x and y in $\mathrm{cl}(K^{*})$ are equivalent, $x\sim y$, if and only if 1) x and y lie on $\partial \mathrm{cl}(K^{*})$ with x on the closed edge E and $y=S_m^{(0)}(x)\in S_m^{(0)}(E)$ for some reflection $S_m^{(0)}\in G^0$ or 2) if x and y lie in the interior of $\mathrm{cl}(K^{*})$ and $x=y$. Let $\mathrm{cl}{(K^{*})}^{\sim }$ be the space of equivalence classes and let

$$\rho :\mathrm{cl}(K^{*})\to \mathrm{cl}{(K^{*})}^{\sim }:p\mapsto [p]$$

(20)

be the identification map which sends a point $p\in \mathrm{cl}(K^{*})$ to the equivalence class $[p]$, which contains p. Give $\mathrm{cl}(K^{*})$ the topology induced from $\mathbb{C}$. Placing the quotient topology on $\mathrm{cl}{(K^{*})}^{\sim }$ turns it into a connected topological manifold without boundary, whose closure is compact. Let $K^{*}$ be $\mathrm{cl}(K^{*})$ less its vertices. The identification space ${(K^{*}\backslash \mathrm{O})}^{\sim }=\rho (K^{*}\backslash \mathrm{O})$ is a connected 2-dimensional smooth manifold without boundary.

Let $G=⟨R,U|R^6=e=U^2\&RU=U{R}^{-1}⟩$. The usual G-action

$$G\times \mathrm{cl}(K^{*})\subseteq G\times \mathbb{C}\to \mathrm{cl}(K^{*})\subseteq \mathbb{C}:(g,z)\mapsto g(z)$$

preserves equivalent edges of $\mathrm{cl}(K^{*})$ and is free on $K^{*}\backslash \mathrm{O}$. Hence it induces a G action on ${(K^{*}\backslash \mathrm{O})}^{\sim }$, which is free and proper. Thus, its orbit map

$$\sigma :{(K^{*}\backslash \mathrm{O})}^{\sim }\to {(K^{*}\backslash \mathrm{O})}^{\sim }/G={\tilde{\mathcal{S}}}_{\mathrm{reg}}:z\mapsto zG$$

is surjective, smooth, and open. The orbit space ${\tilde{\mathcal{S}}}_{\mathrm{reg}}=\sigma ({(K^{*}\backslash \mathrm{O})}^{\sim })$ is a connected 2-dimensional smooth manifold. The identification space ${(K^{*}\backslash \mathrm{O})}^{\sim }$ has the orientation induced from an orientation of $K^{*}\backslash \mathrm{O}$, which comes from $\mathbb{C}$. So ${\tilde{\mathcal{S}}}_{\mathrm{reg}}$ has a complex structure, since each element of G is a conformal mapping of $\mathbb{C}$ into itself.

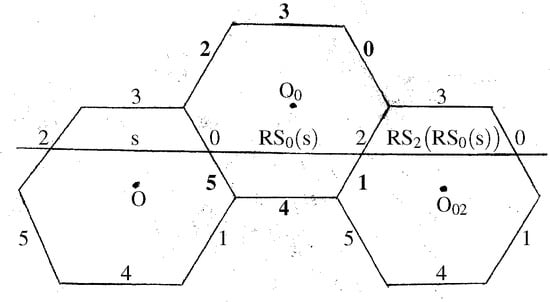
Our aim is to specify the topology of ${\tilde{\mathcal{S}}}_{\mathrm{reg}}$. The regular stellated hexagon $K^{*}\backslash \mathrm{O}$ less the origin has a triangulation ${\mathcal{T}}_{K^{*}\backslash \mathrm{O}}$ made up of 12 open triangles $R^j(△OC{D}^{\prime })$ and $R^j(△OC{\overline{D}}^{\prime })$ for $j=0,1,\dots ,5$; 24 open edges $R^j(OC)$, $R^j(O{\overline{D}}^{\prime })$, $R^j(C{\overline{D}}^{\prime })$, and $R^j(C{D}^{\prime })$ for $j=0,1,\dots ,5$; and 12 vertices $R^j(D^{\prime })$ and $R^j(C)$ for $j=0,1,\dots ,5$, see Figure 6.

Consider the set ${\mathcal{E}}^0$ of unordered pairs of equivalent closed edges of $\mathrm{cl}(K^{*})$, that is, ${\mathcal{E}}^0$ is the set $[E,S_k^{(0)}(E)]$ for $k=0,1,\dots ,5$, where E is a closed edge of $\mathrm{cl}(K^{*})$. Table 2 lists the elements of ${\mathcal{E}}^0$. G acts on ${\mathcal{E}}^0$, namely, $g·[E,S_k^{(0)}(E)]=[g(E),g{S}_k^{(0)}{g}^{-1}\left(g(E)\right)]$, for $g\in G$. Since $G^0$ is the group generated by the reflections $S_k^{(0)}$, $k=0,1,\dots ,5$, it is a normal subgroup of G. Hence the action of G on ${\mathcal{E}}^0$ restricts to an action of $G^0$ on ${\mathcal{E}}^0$ and the G action permutes $G^0$-orbits in ${\mathcal{E}}^0$. Thus, the set of $G^0$-orbits in ${\mathcal{E}}^0$ is G-invariant.

Table 2. The set ${\mathcal{E}}^0$. Here $D_k^{\prime }=R^k(D^{\prime })$ and $\overline{D_k^{\prime }}=R^k(\overline{D^{\prime }})$ for $k=0,2,4$ and $C_k=R^k(C)$ for $k=\{0,1,\dots ,5\}$, see Figure 6.

$a=\left[\overline{D^{\prime }}C,S_0^{(0)}(\overline{D^{\prime }}C)=\overline{D_2^{\prime }}{C}_1\right]$		$b=\left[D^{\prime }{C}_1,S_1^{(0)}(D^{\prime }{C}_1)=D_2^{\prime }{C}_2\right]$
$d=\left[\overline{D_2^{\prime }}{C}_2,S_2^{(0)}(\overline{D_2^{\prime }}{C}_2)=\overline{D_4^{\prime }}{C}_3\right]$		$c=\left[D_2^{\prime }{C}_3,S_3^{(0)}(D_2^{\prime }{C}_3)=D_4^{\prime }{C}_4\right]$
$e=\left[\overline{D_4^{\prime }}{C}_4,S_4^{(0)}(\overline{D_4^{\prime }}{C}_4)=\overline{D^{\prime }}{C}_5\right]$		$f=\left[D_4^{\prime }{C}_5,S_5^{(0)}(D_4^{\prime }{C}_5)=D^{\prime }C\right]$

We now look at the $G^0$-orbits on ${\mathcal{E}}^0$. We compute the $G^0$-orbit of $d\in {\mathcal{E}}^0$ as follows. We have

$$\begin{array}{cc}\hfill (UR)·d& =\left[UR(\overline{D_2^{\prime }}{C}_2),UR(S_2^{(0)}(\overline{D_2^{\prime }}{C}_2))\right]=\left[UR(\overline{D_2^{\prime }}{C}_2),UR(\overline{D_4^{\prime }}{C}_3))\right]\hfill \\ \hfill & =\left[U(D_2^{\prime }{C}_3),U(D_4^{\prime }{C}_4)\right]=\left[\overline{D_4^{\prime }}{C}_5,\overline{D_2^{\prime }}{C}_2\right]=d.\hfill \end{array}$$

Since

$$\begin{array}{cc}\hfill R^2·d& =R^2·\left[\overline{D_2^{\prime }}{C}_2,S_2^{(0)}(\overline{D_2^{\prime }}{C}_2)\right]=\left[R^2(\overline{D_2^{\prime }}{C}_2),R^2{S}_2^{(0)}{R}^{-2}(R^2(\overline{D_2^{\prime }}{C}_2))\right]\hfill \\ \hfill & =\left[\overline{D_4^{\prime }}{C}_4,S_4^{(0)}(\overline{D_4^{\prime }}{C}_4)\right]=\left[\overline{D_4^{\prime }}{C}_4,\overline{D^{\prime }}{C}_5\right]=e\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill R^4·d& =\left[R^4(\overline{D_4^{\prime }}{C}_2),R^4{S}_2^{(0)}{R}^{-4}(R^4(\overline{D_2^{\prime }}{C}_2))\right]\hfill \\ \hfill & =\left[\overline{D^{\prime }}C,S_6^{(0)}(\overline{D^{\prime }}C)\right]=\left[\overline{D^{\prime }}C,S_0^{(0)}(\overline{D^{\prime }}C)\right]=\left[\overline{D^{\prime }}C,\overline{D_2^{\prime }}{C}_1\right]=a,\hfill \end{array}$$

the $G^0$ orbit $G^0·d$ of $d\in {\mathcal{E}}^0$ is $(G^0/⟨UR|{(UR)}^2=e⟩)·d=H^0·d=\{a,d,e\}$. Here $H^0=⟨V=R^2|V^3=e⟩$, since $G^0=⟨V=R^2,UR|V^3=e={(UR)}^2\&V(UR)=(UR)V^{-1}⟩$. Similarly, the $G^0$-orbit $G^0·f$ of $f\in {\mathcal{E}}^0$ is $H^0·f=\{b,c,f\}$. Since $G^0·d\cup G^0·f={\mathcal{E}}^0$, we have found all $G^0$-orbits on ${\mathcal{E}}^0$. The G-orbit of $OC$ is $R^j(OC)$ for $j=0,1,\dots ,5$, since $U(OC)=OC$; while the G-orbit of $O{D}^{\prime }$ is $R^j(O{D}^{\prime })$, $R^j(O\overline{D^{\prime }})$ for $j=0,1,\dots ,5$, since $U(O{D}^{\prime })=O\overline{D^{\prime }}$.

Suppose that B is an end point of the closed edge E of $\mathrm{cl}(K^{*})$. Then E lies in a unique $[E,S_m^{(0)}(E)]$ of ${\mathcal{E}}^0$. Let $G^0·[E,S_m^{(0)}(E)]$ be the $G^0$-orbit of $[E,S_m^{(0)}(E)]$. Then $g^{\prime }·B$ is an end point of the closed edge $g^{\prime }(E)$ of $g^{\prime }·[E,S_m^{(0)}(E)]\in {\mathcal{E}}^0$ for every $g^{\prime }\in G^0$. So $\mathcal{O}(B)=\{g^{\prime }·B|g^{\prime }\in G^0\}$ the $G^0$-orbit of the vertex B. It follows from the classification of $G^0$-orbits on ${\mathcal{E}}^0$ that $\mathcal{O}(D^{\prime })=\{D^{\prime },D_2^{\prime },D_4^{\prime }\}$ and $\mathcal{O}(\overline{D^{\prime }})=\{\overline{D^{\prime }},{\overline{D^{\prime }}}_2,{\overline{D^{\prime }}}_4\}$ are $G^0$-orbits of the vertices of $\mathrm{cl}(K^{*})$, which are permuted by the action of G on ${\mathcal{E}}^0$. Furthermore, $\mathcal{O}(C)=\{C,C_1,\dots ,C_5\}$ and $\mathcal{O}(D^{\prime }\&\overline{D^{\prime }})=\{D^{\prime },\overline{D^{\prime }},D_2^{\prime },{\overline{D^{\prime }}}_2,D_4^{\prime },{\overline{D^{\prime }}}_4\}$ are G-orbits of vertices of $\mathrm{cl}(K^{*})$, which are end points of the G-orbit of the rays $OC$ and $O{D}^{\prime }$, respectively.

To determine the topology of the G orbit space ${\tilde{\mathcal{S}}}_{\mathrm{reg}}$ we find a triangulation of ${\tilde{\mathcal{S}}}_{\mathrm{reg}}$. Note that the triangulation ${\mathcal{T}}_{K^{*}\backslash \mathrm{O}}$ of $K^{*}\backslash \mathrm{O}$, illustrated in Figure 6, is G-invariant. Its image under the identification map $\rho$ is a G-invariant triangulation ${\mathcal{T}}_{{(K^{*}\backslash \mathrm{O})}^{\sim }}$ of ${(K^{*}\backslash \mathrm{O})}^{\sim }$. After identification of equivalent edges, each vertex $\rho (v)$, each open edge $\rho (E)$, having $\rho (O)$ as an end point, or each open edge $\rho ([F,F^{\prime }])$, where $[F,F^{\prime }]$ is a pair of equivalent edges of $\mathrm{cl}(K^{*})$, and each open triangle $\rho (T)$ in ${\mathcal{T}}_{{(K^{*}\backslash \mathrm{O})}^{\sim }}$ lies in a unique G orbit. It follows that $\sigma (\rho (v))$, $\sigma (\rho (E))$ or $\sigma (\rho ([F,F^{\prime }]))$, and $\sigma (\rho (T))$ is a vertex, an open edge, and an open triangle, respectively, of a triangulation ${\mathcal{T}}_{{\tilde{\mathcal{S}}}_{\mathrm{reg}}}=\sigma ({\mathcal{T}}_{{(K^{*}\backslash \mathrm{O})}^{\sim }})$ of ${\tilde{\mathcal{S}}}_{\mathrm{reg}}$. The triangulation ${\mathcal{T}}_{{\tilde{\mathcal{S}}}_{\mathrm{reg}}}$ has 4 vertices, corresponding to the G orbits $\sigma (\rho (\mathcal{O}(D^{\prime })))$, $\sigma (\rho (\mathcal{O}(\overline{D^{\prime }})))$, $\sigma (\rho (\mathcal{O}(C)))$, and $\sigma (\rho (\mathcal{O}(D^{\prime }\&\overline{D^{\prime }})))$; 18 open edges corresponding to $\sigma (\rho (R^j(OC)))$, $\sigma (\rho (R^j(O{D}^{\prime })))$, and $\sigma (\rho (R^j(C{D}^{\prime })))$ for $j=0,1,\dots ,5$; and 12 open triangles $\sigma (\rho (R^j(△OC{D}^{\prime })))$ and $\sigma (\rho (R^j(△OC\overline{D^{\prime }})))$ for $j=0,1,\dots ,5$. Thus, the Euler characteristic $\chi ({\tilde{\mathcal{S}}}_{\mathrm{reg}})$ of ${\tilde{\mathcal{S}}}_{\mathrm{reg}}$ is $4-18+12=-2$. Since ${\tilde{\mathcal{S}}}_{\mathrm{reg}}$ is a 2-dimensional smooth real manifold, $\chi ({\tilde{\mathcal{S}}}_{\mathrm{reg}})=2-2g$, where g is the genus of ${\tilde{\mathcal{S}}}_{\mathrm{reg}}$. Hence $g=2$. So ${\tilde{\mathcal{S}}}_{\mathrm{reg}}$ is a smooth 2-sphere with 2 handles, less a finite number of points, which lies in a compact topological space $\tilde{S}=\mathrm{cl}{(K^{*})}^{\sim }/G$, that is its closure, see Figure 8. This completes the example.

Figure 8. The G-orbit space ${\tilde{\mathcal{S}}}_{\mathrm{reg}}$ is 2-sphere with two handles.

Proof of Theorem 2.

We now begin the construction of ${\tilde{\mathcal{S}}}_{\mathrm{reg}}$ by identifying equivalent edges of $\mathrm{cl}(K^{*})$. For each $j=0,1,\infty$ let $[E,S_m^{(j)}(E)]$ be an unordered pair of equivalent closed edges of $\mathrm{cl}(K^{*})$. We say that x and y in $\mathrm{cl}(K^{*})$ are equivalent, $x\sim y$, if 1) x and y lie in $\partial \mathrm{cl}(K^{*})$ with $x\in E$ and $y=S_m^{(j)}(x)\in S_m^{(0)}(E)$ for some $m\in \{0,1,\dots ,n-1\}$ and some $j=0,1,\infty$ or 2) x and y lie in $\mathrm{int}\mathrm{cl}(K^{*})$ and $x=y$. The relation ∼ is an equivalence relation on $\mathrm{cl}(K^{*})$. Let $\mathrm{cl}{(K^{*})}^{\sim }$ be the set of equivalence classes and let

$$\rho :\mathrm{cl}(K^{*})\to \mathrm{cl}{(K^{*})}^{\sim }:p\mapsto [p]$$

(21)

be the map which sends p to the equivalence class $[p]$, that contains p. Compare this argument with that of Richens and Berry [2]. Give $\mathrm{cl}(K^{*})$ the topology induced from $\mathbb{C}$ and put the quotient topology on $\mathrm{cl}{(K^{*})}^{\sim }$. □

Theorem 3.

Let $K^{*}$ be $\mathrm{cl}(K^{*})$ less its vertices. Then ${(K^{*}\backslash \mathrm{O})}^{\sim }=\rho (K^{*}\backslash \mathrm{O})$ is a smooth manifold. Furthermore, $\mathrm{cl}{(K^{*})}^{\sim }$ is a topological manifold.

Proof. 

To show that ${(K^{*}\backslash \mathrm{O})}^{\sim }$ is a smooth manifold, let $E_{+}$ be an open edge of $K^{*}$. For $p_{+}\in E_{+}$ let $D_{p_{+}}$ be a disk in $\mathbb{C}$ with center at $p_{+}$, which does not contain a vertex of $\mathrm{cl}(K^{*})$. Set $D_{p_{+}}^{+}=K^{*}\cap D_{p_{+}}$. For each $j=0,1,\infty$ let $E_{-}$ be an open edge of $K^{*}$, which is equivalent to $E_{+}$ via the reflection $S_m^{(j)}$, that is, $[\mathrm{cl}(E_{+}),\mathrm{cl}(E_{-})=S_m^{(j)}(\mathrm{cl}(E_{+}))]\in {\mathcal{E}}^j$ is an unordered pair of $S_m^{(j)}$ equivalent edges. Let $p_{-}=S_m^{(j)}(p_{+})$ and set $D_{p_{-}}^{-}=S_m^{(j)}(D_{p_{+}}^{+})$. Then $V_{[p]}=\rho (D_{p_{+}}^{+}\cup D_{p_{-}}^{-})$ is an open neighborhood of $[p]=[p_{+}]=[p_{-}]$ in ${(K^{*}\backslash \mathrm{O})}^{\sim }$, which is a smooth 2-disk, since the identification mapping $\rho$ is the identity on $\mathrm{int}{K}^{*}$. It follows that ${(K^{*}\backslash \mathrm{O})}^{\sim }$ is a smooth 2-dimensional manifold without boundary.

We now handle the vertices of $\mathrm{cl}(K^{*})$. Let $v_{+}$ be a vertex of $\mathrm{cl}(K^{*})$ and set $D_{v_{+}}=\tilde{D}\cap \mathrm{cl}(K^{*})$, where $\tilde{D}$ is a disk in $\mathbb{C}$ with center at the vertex $v_{+}=r_0{\mathrm{e}}^{i\pi {\theta }_0}$. The map

$$W_{v_{+}}:D_{+}\subseteq \mathbb{C}\to D_{v_{+}}\subseteq \mathbb{C}:r{\mathrm{e}}^{i\pi \theta }\mapsto |r-r_0|{\mathrm{e}}^{i\pi s(\theta -{\theta }_0)}$$

with $r\ge 0$ and $0\le \theta \le 1$ is a homeomorphism, which sends the wedge with angle $\pi$ to the wedge with angle $\pi s$. The latter wedge is formed by the closed edges $E_{+}^{\prime }$ and $E_{+}$ of $\mathrm{cl}(K^{*})$, which are adjacent at the vertex $v_{+}$ such that ${\mathrm{e}}^{i\pi s}{E}_{+}^{\prime }=E_{+}$ with the edge $E_{+}^{\prime }$ being swept out through $\mathrm{int}\mathrm{cl}(K^{*})$ during its rotation to the edge $E_{+}$. Because $\mathrm{cl}(K^{*})$ is a rational regular stellated n-gon, the value of s is a rational number for each vertex of $\mathrm{cl}(K^{*})$. For each $j=0,1,\infty$ let $E_{-}=S_m^{(j)}(E_{+})$ be an edge of $\mathrm{cl}(K^{*})$, which is equivalent to $E_{+}$ and set $v_{-}=S_m^{(j)}(v_{+})$. Then $v_{-}$ is a vertex of $\mathrm{cl}(K^{*})$, which is the center of the disk $D_{v_{-}}=S_m^{(j)}(D_{v_{+}})$. Set $D_{-}={\overline{D}}_{+}$. Then $D=D_{+}\cup D_{-}$ is a disk in $\mathbb{C}$. The map $W:D\to \rho (D_{v_{+}}\cup D_{v_{-}})$, where ${W|}_{D_{+}}=\rho \circ W_{v_{+}}$ and ${W|}_{D_{-}}=\rho \circ S_m^{(0)}\circ W_{v_{+}}\circ {}^{\overline{5pt0pt}}$, is a homeomorphism of D into a neighborhood $\rho (D_{v_{+}}\cup D_{v_{-}})$ of $[v]=[v_{+}]=[v_{-}]$ in $\mathrm{cl}{(K^{*})}^{\sim }$. Consequently, the identification space $\mathrm{cl}{(K^{*})}^{\sim }$ is a topological manifold. □

We now describe a triangulation of $K^{*}\backslash \mathrm{O}$. Let $T^{\prime }=T_{1,n_1,n-(1+n_1)}$ be the open rational triangle $△OC{D}^{\prime }$ with vertex at the origin O, longest side $OC$ on the real axis, and interior angles $\frac{1}{n}\pi$, $\frac{n_1}{n}\pi$, and $\frac{n-1-n_1}{n}\pi$. Let $Q^{\prime }$ be the quadrilateral $T^{\prime }\cup \overline{T^{\prime }}$. Then $Q^{\prime }$ is a subset of the quadrilateral $Q=ODC\overline{D}$, see Figure 5. Moreover $K^{*}={\bigcup }_{\ell =0}^{n-1}{R}^{\ell }(Q^{\prime })$. The $2n$ triangles $\mathrm{cl}(R^j(T^{\prime }))\backslash \{O\}$ and $\mathrm{cl}(R^k(\overline{T^{\prime }}))\backslash \mathrm{O}$ with $k=0,1,\dots ,n-1$ form a triangulation ${\mathcal{T}}_{K^{*}\backslash \mathrm{O}}$ of $K^{*}\backslash \mathrm{O}$ with $2n$ vertices $R^k(C)$ and $R^k(D^{\prime })$ for $k=0,1,\dots ,n-1$; $4n$ open edges $R^k(OC)$, $R^k(O{D}^{\prime })$, $R^k(C{D}^{\prime })$, and $R^k(C\overline{D^{\prime }})$ for $k=0,1,\dots ,n-1$; and $2n$ open triangles $R^k(T^{\prime })$, $R^k(\overline{T^{\prime }})$ with $k=0,1,\dots ,n-1$. The image of the triangulation ${\mathcal{T}}_{K^{*}\backslash \mathrm{O}}$ under the identification map $\rho$ (21) is a triangulation ${\mathcal{T}}_{{(K^{*}\backslash \mathrm{O})}^{\sim }}$ of the identification space ${(K^{*}\backslash \mathrm{O})}^{\sim }$.

The action of G on $\mathrm{cl}(K^{*})$ preserves the set of unordered pairs of $S_m^{(j)}$ equivalent edges of $\mathrm{cl}(K^{*})$ for each $j=0,1,\infty$. Hence G induces an action on $\mathrm{cl}{(K^{*})}^{\sim }$, which is proper, since G is finite. The G action is free on $K^{*}\backslash \mathrm{O}$ and thus on ${(K^{*}\backslash \mathrm{O})}^{\sim }$ by Lemma A2. We have proved

Lemma 6.

The G-orbit space $\tilde{\mathcal{S}}=\mathrm{cl}{(K^{*})}^{\sim }/G$ is a compact connected topological manifold with ${\tilde{\mathcal{S}}}_{\mathrm{reg}}={(K^{*}\backslash \mathrm{O})}^{\sim }/G$ being a smooth manifold. Let

$$\sigma :\mathrm{cl}{(K^{*})}^{\sim }\to \tilde{\mathcal{S}}=\mathrm{cl}{(K^{*})}^{\sim }/G:z\mapsto zG.$$

Then σ is the G orbit map, which is surjective, continuous, and open. The restriction of σ to $K^{*}\backslash \mathrm{O}$ has image ${\tilde{\mathcal{S}}}_{\mathrm{reg}}$ and is a smooth open mapping.

We now determine the topology of the orbit space ${\tilde{\mathcal{S}}}_{\mathrm{reg}}$. For each $j=0,1,\infty$ and ${\ell }_j=0,1,\dots ,d_j-1$ let $A_{{\ell }_j}^j$ be an end point of a closed edge E of $\mathrm{cl}(K^{*})$, which lies on the unordered pair $[E,S_{{\ell }_j}^{(j)}(E)]\in {\mathcal{E}}^j$. Then $H^j·A_{{\ell }_j}^{(j)}$ is an end point of the edge $H^j·E$ of the unordered pair $H^j·[E,S_{{\ell }_j}^{(j)}(E)]$ of ${\mathcal{E}}^j$. See Appendix A for the definition of the group $H_j$. The sets $\mathcal{O}(A_{\ell }^{(j)})=\{H^j·A_{{\ell }_j}^{(j)}\}$ with ${\ell }_j=0,1,\dots ,d_j-1$ are permuted by G. The action of G on $K^{*}\backslash \mathrm{O}$ preserves the set of open edges of the triangulation ${\mathcal{T}}_{K^{*}\backslash \mathrm{O}}$. There are $3n$-orbits: $R^k(OC)$; $R^k(O\overline{D^{\prime }})$, since $O{D}^{\prime }=R(O\overline{D^{\prime }})$; and $R^k(CD)$, since $C\overline{D^{\prime }}=U(CD)$ for $k=0,1,\dots ,n-1$. So the image of the triangulation ${\mathcal{T}}_{K^{*}\backslash \mathrm{O}}$ under the continuous open map

$${\mu =\sigma \circ \pi |}_{K^{*}\backslash \mathrm{O}}:K^{*}\backslash \mathrm{O}\to {\tilde{\mathcal{S}}}_{\mathrm{reg}}$$

(22)

is a triangulation ${\mathcal{T}}_{{\tilde{\mathcal{S}}}_{\mathrm{reg}}}$ of the G-orbit space ${\tilde{\mathcal{S}}}_{\mathrm{reg}}$ with $d_0+d_1+d_{\infty }$ vertices $\mu (\mathcal{O}(A_{{\ell }_j}^{(j)}))$, where $j=0,1,\infty$ and ${\ell }_j=0,1,\dots ,d_j-1$; $3n$ open edges $\mu (R^k(OC))$, $\mu (R^j(O\overline{D^{\prime }}))$, and $\mu (R^k(CD))$ for $k=0,1,\dots ,n-1$; and $2n$ open triangles $\mu (R^k(T^{\prime }))$ and $\mu (R^k(\overline{T^{\prime }}))$ for $k=0,1,\dots n-1$. Thus, the Euler characteristic $\chi ({\tilde{\mathcal{S}}}_{\mathrm{reg}})$ of ${\tilde{\mathcal{S}}}_{\mathrm{reg}}$ is $d_0+d_1+d_{\infty }-3n+2n=d_0+d_1+d_{\infty }-n$. However, ${\tilde{\mathcal{S}}}_{\mathrm{reg}}$ is a smooth manifold. So $\chi ({\tilde{\mathcal{S}}}_{\mathrm{reg}})=2-2g$, where g is the genus of ${\tilde{\mathcal{S}}}_{\mathrm{reg}}$. Hence $g=\frac{1}{2}\left(n+2-(d_0+d_1+d_{\infty })\right)$. Compare this argument with that of Weyl ([4], p. 174). This proves Theorem 2.

Since the quadrilateral Q is a fundamental domain for the action of G on $K^{*}$, the G orbit map $\overline{\mu }=\sigma \circ \pi :K^{*}\subseteq \mathbb{C}\to \tilde{\mathcal{S}}$ restricted to Q is a bijective continuous open mapping. However, ${\delta }_Q:\mathcal{D}\subseteq \mathcal{S}\to Q\subseteq \mathbb{C}$ is a bijective continous open mapping of the fundamental domain $\mathcal{D}$ of the $\mathcal{G}$ action on $\mathcal{S}$. Consequently, the $\mathcal{G}$ orbit space is homeomorphic to the G orbit space $\tilde{\mathcal{S}}$. The mapping $\overline{\mu }$ is holomorphic except possibly at 0 and the vertices of $\mathrm{cl}(K^{*})$. So the mapping $\overline{\mu }\circ {\delta }_{K^{*}}:{\mathcal{S}}_{\mathrm{reg}}\to {\tilde{\mathcal{S}}}_{\mathrm{reg}}$ is a holomorphic diffeomorphism.

5. An Affine Model of ${\mathcal{S}}_{\mathbf{reg}}$

We construct an affine model of the affine Riemann surface ${\mathcal{S}}_{\mathrm{reg}}$ as follows. Return to the regular stellated n-gon $K^{*}=K_{n_0{n}_1{n}_{\infty }}^{*}$, which is formed from the quadrilateral $Q=Q_{n_0{n}_1{n}_{\infty }}$ less its vertices. Repeatedly reflecting in the edges of $K^{*}$ and then in the edges of the resulting reflections of $K^{*}$ et cetera, we obtain a covering of $\mathbb{C}\backslash {\mathbb{V}}^{+}$ by certain translations of $K^{*}$. Here ${\mathbb{V}}^{+}$ is the union of the translates of the vertices of $\mathrm{cl}(K^{*})$ and its center O. Let $\mathfrak{T}$ be the group generated by these translations. The semidirect product $\mathfrak{G}=G⋉\mathfrak{T}$ acts freely, properly and transitively on $\mathbb{C}\backslash {\mathbb{V}}^{+}$. It preserves equivalent edges of $\mathbb{C}\backslash {\mathbb{V}}^{+}$ and it acts freely and properly on ${(\mathbb{C}\backslash {\mathbb{V}}^{+})}^{\sim }$, the space formed by identifying equivalent edges in $\mathbb{C}\backslash {\mathbb{V}}^{+}$. The orbit space ${(\mathbb{C}\backslash {\mathbb{V}}^{+})}^{\sim }/\mathfrak{G}$ is holomorphically diffeomorphic to ${\tilde{\mathcal{S}}}_{\mathrm{reg}}$ and is the desired affine model of ${\mathcal{S}}_{\mathrm{reg}}$. We now justify these assertions.

First we determine the group $\mathcal{T}$ of translations.

Lemma 7.

Each of the $2n$ sides of the regular stellated n-gon $K^{*}$ is perpendicular to exactly one of the directions

$${\mathrm{e}}^{[\frac{1}{2}-\frac{n_1}{n}+2k\frac{1}{n}]\pi i}\mathrm{or}{\mathrm{e}}^{[-\frac{1}{2}-\frac{1}{n}+\frac{n_1}{n}+(2k+1)\frac{1}{n}]\pi i},$$

(23)

for $k=0,1,\dots ,n-1$.

Proof. 

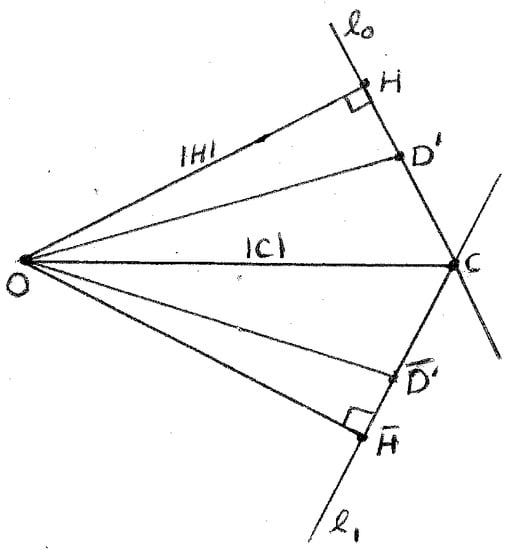
From Figure 9 we have $\angle D^{\prime }CO=\frac{n_1}{n}\pi$. So $\angle COH=\frac{1}{2}\pi -\frac{n_1}{n}\pi$. Hence the line ${\ell }_0$, containing the edge $C{D}^{\prime }$ of $K^{*}$, is perpendicular to the direction ${\mathrm{e}}^{[\frac{1}{2}-\frac{n_1}{n}]\pi }$. Since $△CO\overline{D^{\prime }}$ is the reflection of $△CO{D}^{\prime }$ in the line segment $OC$, the line ${\ell }_1$, containing the edge $C\overline{D^{\prime }}$ of $K^{*}$, is perpendicular to the direction ${\mathrm{e}}^{[-\frac{1}{2}+\frac{n_1}{n}]\pi }$. Because the regular stellated n-gon $K^{*}$ is formed by repeatedly rotating the quadrilateral $Q^{\prime }=O{D}^{\prime }C\overline{D^{\prime }}$ through an angle $\frac{2\pi }{n}$, we find that Equation (23) holds. □

Figure 9. The regular stellated n-gon $K^{*}$ two of whose sides are $C{D}^{\prime }$ and $C\overline{D^{\prime }}$.

Since $\angle COH=\frac{1}{2}\pi -\frac{n_1}{n}\pi$, it follows that $\left|H\right|=\left|C\right|sin\pi \frac{n_1}{n}$ is the distance from the center O of $K^{*}$ to the line ${\ell }_0$ containing the side $C{D}^{\prime }$, or to the line ${\ell }_1$ containing the side $C\overline{D^{\prime }}$. So $u_0=(|C|sin\pi \frac{n_1}{n}){\mathrm{e}}^{[\frac{1}{2}-\frac{n_1}{n}]\pi i}$ is the closest point H on ${\ell }_0$ to O and $u_1=(|C|sin\pi \frac{n_1}{n}){\mathrm{e}}^{[-\frac{1}{2}+\frac{n_1}{n}]\pi i}$ is the closest point $\overline{H}$ on ${\ell }_1$ to O. Since the regular stellated n-gon $K^{*}$ is formed by repeatedly rotating the quadrilateral $Q^{\prime }=O{D}^{\prime }C\overline{D^{\prime }}$ through an angle $\frac{2\pi }{n}$, the point

$$u_{2k}=R^k{u}_0=(|C|sin\pi \frac{n_1}{n}){\mathrm{e}}^{[\frac{1}{2}-\frac{n_1}{n}+2k\frac{1}{n}]\pi i}$$

(24)

lies on the line ${\ell }_{2k}=R^k{\ell }_0$, which contains the edge $R^k(C{D}^{\prime })$ of $K^{*}$; while

$$u_{2k+1}=R^k{u}_1=(|C|sin\pi \frac{n_1}{n}){\mathrm{e}}^{[-\frac{1}{2}+\frac{n_1}{n}-\frac{1}{n}+(2k+1)\frac{1}{n}]\pi i}$$

(25)

lies on the line ${\ell }_{2k+1}=R^k{\ell }_1$, which contains the edge $R^k(C\overline{D^{\prime }})$ of $K^{*}$ for every $k\in \{0,1,\dots ,n-1\}$. Furthermore, the line segments $O{u}_{2k}$ and $O{u}_{2k+1}$ are perpendicular to the line ${\ell }_{2k}$ and ${\ell }_{2k+1}$, respectively, for $k\in \{0,1,\dots ,n-1\}$.

Corollary 8.

For $k=0,1,\dots ,n-1$ we have

$$\overline{u_{2k}}=u_{2(n-k)+1}\mathrm{and}\overline{u_{2k+1}}=u_{2(n-k)}.$$

(26)

Proof. 

We compute. From (24) it follows that

$$\begin{array}{cc}\hfill \overline{u_{2k}}& =U(u_{2k})=U{R}^k(u_0)=R^{-k}(U(u_0))\hfill \\ \hfill & =R^{-k}(u_1)=R^{n-k}(u_1)=u_{2(n-k)+1},\mathrm{using} (25);\hfill \end{array}$$

while from (25) we get

$$\begin{array}{cc}\hfill \overline{u_{2k+1}}& =U(u_{2k+1})=U{R}^k(u_1)=R^{-k}(U(u_1))=R^{n-k}(u_0)=u_{2(n-k)}.\hfill \end{array}$$

□

Corollary 9.

For k, $\ell \in \{0,1,\dots ,2n-1\}$ we have

$$u_{(k+2\ell )mod2n}=R^{\ell }{u}_k.$$

(27)

Proof. 

If $k=2i$, then $u_k=R^i{u}_0$, by definition. So

$$R^{\ell }{u}_k=R^{\ell +i}{u}_0=u_{(2i+2\ell )mod2n}=u_{(k+2\ell )mod2n}.$$

If $k=2i+1$, then $u_{\ell }=R^i{u}_1$, by definition. So

$$\begin{array}{c}\hfill R^{\ell }{u}_k=R^{\ell +i}{u}_1=u_{(2(i+\ell )+1)mod2n}=u_{(k+2\ell )mod2n}.\end{array}$$

□

For $k=0,1,\dots ,2n-1$ let ${\tau }_k$ be the translation

$${\tau }_k:\mathbb{C}\to \mathbb{C}:z\mapsto z+2u_k.$$

(28)

Corollary 10.

For k, $\ell \in \{0,1,\dots ,2n-1\}$ we have

$${\tau }_{(k+2\ell )mod2n}\circ R^{\ell }=R^{\ell }\circ {\tau }_k.$$

(29)

Proof. 

For every $z\in \mathbb{C}$, we have

$$\begin{array}{cc}\hfill {\tau }_{(k+2\ell )mod2n}(z)& =z+2u_{(k+2\ell )mod2n},\mathrm{using}(28)\hfill \\ \hfill & =z+2R^{\ell }{u}_k\mathrm{by}(27)\hfill \\ \hfill & =R^{\ell }(R^{-\ell }z+2u_k)=R^{\ell }\circ {\tau }_k(R^{-\ell }z).\hfill \end{array}$$

□

Reflecting the regular stellated n-gon $K^{*}$ in its edge $C{D}^{\prime }$ contained in ${\ell }_0$ gives a congruent regular stellated n-gon $K_0^{*}$ with the center O of $K^{*}$ becoming the center $2u_0$ of $K_0^{*}$.

Lemma 8.

The collection of all the centers of the regular stellated n-gons, formed by reflecting $K^{*}$ in its edges and then reflecting in the edges of the reflected regular stellated n-gons et cetera, is

$$\begin{array}{cc}\hfill \{{\tau }_0^{{\ell }_0}\circ \cdots \circ {\tau }_{2n-1}^{{\ell }_{2n-1}}(0)\in \mathbb{C}|({\ell }_0,\dots ,{\ell }_{2n-1})\in {({\mathbb{Z}}_{\ge 0})}^{2n}\}& =\hfill \\ \hfill & =\left\{2\sum _{{\ell }_0,\dots ,{\ell }_{2n-1}=0}^{\infty }\left({\ell }_0{u}_0+\cdots {\ell }_{2n-1}{u}_{2n-1}\right)\right\},\hfill \end{array}$$

where for $k=0,1,\dots ,2n-1$ we have

$${\tau }_k^{{\ell }_k}=\stackrel{{\ell }_k}{\overbrace{{\tau }_k\circ \cdots \circ {\tau }_k}}:\mathbb{C}\to \mathbb{C}:z\mapsto z+2{\ell }_j{u}_k.$$

Proof. 

For each $k_0=0,1,\dots ,2n-1$ the center of the $2n$ regular stellated congruent n-gon $K_{k_0}^{*}$ formed by reflecting in an edge of $K^{*}$ contained in the line ${\ell }_{k_0}$ is ${\tau }_{k_0}(0)=2u_{k_0}$. Repeating the reflecting process in each edge of $K_{k_0}^{*}$ gives $2n$ congruent regular stellated n-gons $K_{k_0{k}_1}^{*}$ with center at ${\tau }_{k_1}\left({\tau }_{k_0}(0)\right)=2(u_{k_1}+u_{k_0})$, where $k_1=0,1,\dots 2n-1$. Repeating this construction proves the lemma. □

The set $\mathbb{V}$ of vertices of the regular stellated n-gon $K^{*}$ is

$$\{V_{2k}=C{\mathrm{e}}^{2k(\frac{1}{n}\pi i)},V_{2k+1}=D^{\prime }{\mathrm{e}}^{(2k+1)(\frac{1}{n}\pi i)}for0\le k\le n-1\},$$

see Figure 5. Clearly the set $\mathbb{V}$ is G invariant.

Corollary 11.

The set

$$\begin{array}{cc}\hfill {\mathbb{V}}^{+}& =\{v_{{\ell }_0\cdots {\ell }_{2n-1}}={\tau }_0^{{\ell }_0}\circ \cdots \circ {\tau }_{2n-1}^{{\ell }_{2n-1}}(V)|\hfill \\ \hfill & V\in \mathbb{V}\cup \{\mathrm{O}\}\&({\ell }_0,\dots ,{\ell }_{2n-1})\in {({\mathbb{Z}}_{\ge 0})}^{2n}\}\hfill \end{array}$$

(30)

is the collection of vertices and centers of the congruent regular stellated n-gons $K^{*}$, $K_{k_1}^{*}$, $K_{k_0{k}_1}^{*},\dots$.

Proof. 

This follows immediately from Lemma 8. □

Corollary 12.

The union of $K^{*},K_{k_0}^{*},K_{k_0{k}_1}^{*},\dots K_{k_0{k}_1\cdots k_{\ell }}^{*},\dots$, where $\ell \ge 0$, $0\le j\le \ell$, and $0\le k_j\le 2n-1$, covers $\mathbb{C}\backslash {\mathbb{V}}^{+}$, that is,

$$K^{*}\cup \bigcup _{\ell \ge 0}\bigcup _{0\le j\le \ell }\bigcup _{0\le k_j\le 2n-1}{K}_{k_0{k}_1\cdots k_{\ell }}^{*}=\mathbb{C}\backslash {\mathbb{V}}^{+}.$$

Proof. 

This follows immediately from $K_{k_0{k}_1\cdots k_{\ell }}^{*}={\tau }_{k_{\ell }}\circ \cdots \circ {\tau }_{k_0}(K^{*})$. □

Let $\mathcal{T}$ be the abelian subgroup of the 2-dimensional Euclidean group $\mathrm{E}(2)$ generated by the translations ${\tau }_k$ (28) for $k=0,1,\dots 2n-1$. It follows from Corollary 12 that the regular stellated n-gon $K^{*}$ with its vertices and center removed is the fundamental domain for the action of the abelian group $\mathcal{T}$ on $\mathbb{C}\backslash {\mathbb{V}}^{+}$. The group $\mathcal{T}$ is isomorphic to the abelian subgroup $\mathfrak{T}$ of $(\mathbb{C},+)$ generated by ${\{2u_k\}}_{k=0}^{2n-1}$.

Next we define the group $\mathfrak{G}$ and show that it acts freely, properly, and transitively on $\mathbb{C}\backslash {\mathbb{V}}^{+}$. Consider the group $\mathfrak{G}=G⋉\mathfrak{T}\subseteq G\times \mathfrak{T}$, which is the semidirect product of the dihedral group G, generated by the rotation R through $2\pi /n$ and the reflection U subject to the relations $R^n=e=U^2$ and $RU=U{R}^{-1}$, and the abelian group $\mathfrak{T}$. An element $(R^j{U}^{\ell },2u_k)$ of $\mathfrak{G}$ is the affine linear map

$$(R^j{U}^{\ell },2u_k):\mathbb{C}\to \mathbb{C}:z\mapsto R^j{U}^{\ell }z+2u_k.$$

Multiplication in $\mathfrak{G}$ is defined by

$$(R^j{U}^{\ell },2u_k)·(R^{j^{\prime }}{U}^{{\ell }^{\prime }},2u_{k^{\prime }})=\left(R^{j+j^{\prime }}{U}^{\ell +{\ell }^{\prime }},(R^j{U}^{\ell })(2u_{k^{\prime }})+2u_k\right),$$

(31)

which is the composition of the affine linear map $(R^{j^{\prime }}{U}^{{\ell }^{\prime }},2u_{k^{\prime }})$ followed by $(R^j{U}^{\ell },2u_k)$. The mappings $G\to \mathfrak{G}:R^j\mapsto (R^j{U}^{\ell },0)$ and $\mathfrak{T}\to \mathfrak{G}:2u_k\mapsto (e,2u_k)$ are injective, which allows us to identify the groups G and $\mathfrak{T}$ with their image in $\mathfrak{G}$. Using (31) we may write an element $(R^j{U}^{\ell },2u_k)$ of $\mathfrak{G}$ as $(e,2u_k)·(R^j{U}^{\ell },0)$. So

$$(e,2u_{(j+2k)mod2n})·(R^k{U}^{\ell },0)=(R^k{U}^{\ell },2u_{(j+2k)mod2n}),$$

For every $z\in \mathbb{C}$ we have

$$\begin{array}{cc}\hfill R^k{U}^{\ell }z+2u_{(j+2k)mod2n}& =R^k{U}^{\ell }z+R^k{U}^{\ell }(2u_j),\mathrm{using}(27),\hfill \end{array}$$

that is,

$$(R^k{U}^{\ell },2u_{(j+2k)mod2n})=(R^k{U}^{\ell },R^k{U}^{\ell }(2u_j))=(R^k{U}^{\ell },0)·(e,2u_j).$$

Hence

$$(e,2u_{(j+2k)mod2n})·(R^k{U}^{\ell },0)=(R^k{U}^{\ell },0)·(e,2u_j),$$

(32)

which is just Equation (29). The group $\mathfrak{G}$ acts on $\mathbb{C}$ as $\mathrm{E}(2)$ does, namely, by affine linear orthogonal mappings. Denote this action by

$$\psi :\mathfrak{G}\times \mathbb{C}\to \mathbb{C}:((g,\tau ),z)\mapsto \tau (g(z)).$$

Lemma 9.

The set ${\mathbb{V}}^{+}$ (30) is invariant under the $\mathfrak{G}$ action.

Proof. 

Let $v\in {\mathbb{V}}^{+}$. Then for some $({\ell }_0^{\prime },\dots ,{\ell }_{2n-1}^{\prime })\in {\mathbb{Z}}_{\ge 0}^{2n}$ and some $w\in \mathbb{V}\cup \{\mathrm{O}\}$

$$v={\tau }_0^{{\ell }_0^{\prime }}\circ \cdots \circ {\tau }_{2n-1}^{{\ell }_{2n-1}^{\prime }}(w)={\psi }_{(e,2u^{\prime })}(w),$$

where $u^{\prime }={\sum }_{k=0}^{2n-1}{\ell }_k^{\prime }{u}_k$. For $(R^j{U}^{\ell },2u)\in \mathfrak{G}$ with $j=0,1,\dots ,n-1$ and $\ell =0,1$ we have

$$\begin{array}{cc}\hfill {\psi }_{(R^j{U}^{\ell },2u)}v& ={\psi }_{(R^j{U}^{\ell },2u)}\circ {\psi }_{(e,2u^{\prime })}(w)={\psi }_{(R^j{U}^{\ell },2u)·(e,2u^{\prime })}(w)\hfill \\ \hfill & ={\psi }_{(R^j{U}^{\ell },R^j{U}^{\ell }(2u^{\prime })+2u)}(w)={\psi }_{(e,2(R^j{U}^{\ell }{u}^{\prime }+u))·(R^j{U}^{\ell },0)}(w)\hfill \\ \hfill & ={\psi }_{(e,2(R^j{U}^{\ell }{u}^{\prime }+u))}\left({\psi }_{(R^j{U}^{\ell },0)}(w)\right)={\psi }_{(e,2(R^j{U}^{\ell }{u}^{\prime }+u))}(w^{\prime }),\hfill \end{array}$$

(33)

where $w^{\prime }={\psi }_{(R^j{U}^{\ell },0)}(w)=R^j{U}^{\ell }(w)\in \mathbb{V}\cup \{\mathrm{O}\}$. If $\ell =0$, then

$$\begin{array}{cc}\hfill R^j{u}^{\prime }& =R^j(\sum _{k=0}^{2n-1}{\ell }_k^{\prime }{u}_k)=\sum _{k=0}^{2n-1}{\ell }_k^{\prime }{R}^j(u_k)=\sum _{k=0}^{2n-1}{\ell }_k^{\prime }{u}_{(k+2j)mod2n};\hfill \end{array}$$

while if $\ell =1$, then

$$\begin{array}{cc}\hfill R^{j}U(u^{\prime })& =\sum _{k=0}^{2n-1}{\ell }_k^{\prime }{R}^j(U(u_k))=\sum _{k=0}^{2n-1}{\ell }_k^{\prime }{R}^j(u_{k^{\prime }(k)})=\sum _{k=0}^{2n-1}{\ell }_k^{\prime }{u}_{(k^{\prime }(k)+2j)mod2n}.\hfill \end{array}$$

Here $k^{\prime }(k)=$$\left\{\begin{array}{cc}2n-k+1,& \mathrm{if}k\mathrm{is}\mathrm{even}\hfill \\ 2n-k-1,& \mathrm{if}k\mathrm{is}\mathrm{odd},\hfill \end{array}\right.$ see Corollary 8. So $(e,2(R^j{U}^{\ell }{u}^{\prime }+u))\in \mathfrak{T}$, which implies ${\psi }_{(e,2(R^j{U}^{\ell }{u}^{\prime }+u))}(w^{\prime })\in {\mathbb{V}}^{+}$, as desired. □

Lemma 10.

The action of $\mathfrak{G}$ on $\mathbb{C}\backslash {\mathbb{V}}^{+}$ is free.

Proof. 

Suppose that for some $v\in \mathbb{C}\backslash {\mathbb{V}}^{+}$ and some $(R^j{U}^{\ell },2u)\in \mathfrak{G}$ we have $v={\psi }_{(R^j{U}^{\ell },2u)}(v)$. Then v lies in some $K_{k_0{k}_1\cdots k_{\ell }}^{*}$. So for some $v^{\prime }\in K^{*}$ we have

$$\begin{array}{cc}\hfill v& ={\tau }_0^{{\ell }_0^{\prime }}\circ \cdots {\tau }_{2n-1}^{{\ell }_{2n-1}^{\prime }}(v^{\prime })={\psi }_{(e,2u^{\prime })}(v^{\prime }),\hfill \end{array}$$

where $u^{\prime }={\sum }_{j=0}^{2n-1}{\ell }_j^{\prime }{u}_j$ for some $({\ell }_0^{\prime },\dots ,{\ell }_{2n-1}^{\prime })\in {({\mathbb{Z}}_{\ge 0})}^{2n}$. Thus,

$${\psi }_{(e,2u^{\prime })}(v^{\prime })={\psi }_{(R^j{U}^{\ell },2u)·(e,2u^{\prime })}(v^{\prime })={\psi }_{(R^j{U}^{\ell },2R^j{U}^{\ell }{u}^{\prime }+2u)}(v^{\prime }).$$

This implies $R^j{U}^{\ell }=e$, that is, $j=\ell =0$. So $2u^{\prime }=2R^j{U}^{\ell }{u}^{\prime }+2u=2u^{\prime }+2u$, that is, $u=0$. Hence $(R^j{U}^{\ell },u)=(e,0)$, which is the identity element of $\mathfrak{G}$. □

Lemma 11.

The action of $\mathcal{T}$ (and hence $\mathfrak{G}$) on $\mathbb{C}\backslash {\mathbb{V}}^{+}$ is transitive.

Proof. 

Let $K_{k_0\cdots k_{\ell }}^{*}$ and $K_{k_0^{\prime }\cdots k_{{\ell }^{\prime }}^{\prime }}^{*}$ lie in

$$\mathbb{C}\backslash {\mathbb{V}}^{+}=K^{*}\cup \bigcup _{\ell \ge 0}\bigcup _{0\le j\le \ell }\bigcup _{0\le k_j\le 2n-1}{K}_{k_0{k}_1\cdots k_{\ell }}^{*}.$$

Since $K_{k_0\cdots k_{\ell }}^{*}={\tau }_{k_{\ell }}\circ \cdots \circ {\tau }_{k_0}(K^{*})$ and $K_{k_0^{\prime }\cdots k_{{\ell }^{\prime }}^{\prime }}^{*}={\tau }_{k_{{\ell }^{\prime }}^{\prime }}\circ \cdots \circ {\tau }_{k_0^{\prime }}(K^{*})$, it follows that $({\tau }_{k_{{\ell }^{\prime }}^{\prime }}\circ \cdots \circ {\tau }_{k_0^{\prime }})\circ {({\tau }_{k_{\ell }}\circ \cdots \circ {\tau }_{k_0})}^{-1}(K_{k_0\cdots k_{\ell }}^{*})=K_{k_0^{\prime }\cdots k_{{\ell }^{\prime }}^{\prime }}^{*}$. □

The action of $\mathfrak{G}$ on $\mathbb{C}\backslash {\mathbb{V}}^{+}$ is proper because $\mathfrak{G}$ is a discrete subgroup of $\mathrm{E}(2)$ with no accumulation points.

We now define an edge of $\mathbb{C}\backslash {\mathbb{V}}^{+}$ and what it means for an unordered pair of edges to be equivalent. We show that the group $\mathfrak{G}$ acts freely and properly on the identification space of equivalent edges.

Let E be an open edge of $K^{*}$. Since $E_{k_0\cdots k_{\ell }}={\tau }_{k_0}\cdots {\tau }_{k_{\ell }}(E)\in K_{k_0\cdots k_{\ell }}^{*}$, it follows that $E_{k_0\cdots k_{\ell }}$ is an open edge of $K_{k_0\cdots k_{\ell }}^{*}$. Let

$$\mathfrak{E}=\{E_{k_0\cdots k_{\ell }}|\ell \ge 0,0\le j\le \ell \&0\le k_j\le 2n-1\}.$$

Then $\mathfrak{E}$ is the set of open edges of $\mathbb{C}\backslash {\mathbb{V}}^{+}$ by 12. Since ${\tau }_{k_{\ell }}\circ \cdots \circ {\tau }_{k_0}(0)$ is the center of $K_{k_0\cdots k_{\ell }}^{*}$, the element $(e,{\tau }_{k_{\ell }}\circ \cdots \circ {\tau }_{k_0})·(g,{({\tau }_{k_{\ell }}\circ \cdots \circ {\tau }_{k_0})}^{-1})$ of $\mathfrak{G}$ is a rotation-reflection of $K_{k_0\cdots k_{\ell }}^{*}$, which sends an edge of $K_{k_0\cdots k_{\ell }}^{*}$ to another edge of $g*K_{k_0\cdots k_{\ell }}^{*}$. Thus, $\mathfrak{G}$ sends $\mathfrak{E}$ into itself. For $j=0,1,\infty$ let ${\mathfrak{E}}_{k_0\cdots k_{\ell }}^j$ be the set of unordered pairs $[E_{k_0\cdots k_{\ell }},E_{k_0\cdots k_{\ell }}^{\prime }]$ of equivalent open edges of $K_{k_0\cdots k_{\ell }}^{*}$, that is, $E_{k_0\cdots k_{\ell }}\cap E_{k_0\cdots k_{\ell }}^{\prime }=⌀$, so the open edges $E_{k_0\cdots k_{\ell }}={\tau }_{k_0}\cdots {\tau }_{k_{\ell }}(E)$ and $E_{k_0\cdots k_{\ell }}^{\prime }={\tau }_{k_0}\cdots {\tau }_{k_{\ell }}(E^{\prime })$ of $\mathrm{cl}(K_{k_0\cdots k_{\ell }}^{*})$ are not adjacent, which implies that the open edges E and $E^{\prime }$ of $K^{*}$ are not adjacent, and for some generator $S_m^{(j)}$ of the group $G^j$ of reflections with $j=0,1,\infty$ we have

$$E_{k_0\cdots k_{\ell }}^{\prime }=({\tau }_{k_0}\circ \cdots \circ {\tau }_{k_0})\left(S_m^{(j)}({({\tau }_{k_{\ell }}\circ \cdots \circ {\tau }_{k_0})}^{-1}(E_{k_0\cdots k_{\ell }}))\right).$$

Let ${\mathfrak{E}}^j={\cup }_{\ell \ge 0}{\cup }_{0\le j\le \ell }{\cup }_{0\le k_j\le 2n-1}{\mathfrak{E}}_{k_0\cdots k_{\ell }}^j$. So ${\bigcup }_{j=0,1,\infty }{\mathfrak{E}}^j$ is the set of unordered pairs of equivalent edges of $\mathbb{C}\backslash {\mathbb{V}}^{+}$. Define an action * of $\mathfrak{G}$ on ${\bigcup }_{j=0,1,\infty }{\mathcal{E}}^j$ by

$$\begin{array}{cc}\hfill (g,\tau )*[E_{k_0\cdots k_{\ell }},E_{k_0\cdots k_{\ell }}^{\prime }]& =\left([({\tau }^{\prime }\circ \tau )(g{({\tau }^{\prime })}^{-1}(E_{k_0\cdots k_{\ell }})),({\tau }^{\prime }\circ \tau )(g({({\tau }^{\prime })}^{-1}(E_{k_0\cdots k_{\ell }}^{\prime }))]\right)\hfill \\ \hfill & =[(g,\tau )*E_{k_0\cdots k_{\ell }},(g,\tau )*E_{k_0\cdots k_{\ell }}^{\prime }],\hfill \end{array}$$

where ${\tau }^{\prime }={\tau }_{k_{\ell }}\circ \cdots {\tau }_{k_0}$.

Define a relation ∼ on $\mathbb{C}\backslash {\mathbb{V}}^{+}$ as follows. We say that x and $y\in \mathbb{C}\backslash {\mathbb{V}}^{+}$ are related, $x\sim y$, if 1) $x\in F=\tau (E)\in {\mathfrak{E}}^j$ and $y\in F^{\prime }=\tau (E^{\prime })\in {\mathfrak{E}}^j$ such that $[F,F^{\prime }]=[\tau (E),\tau (E^{\prime })]\in {\mathfrak{E}}^0$, where $[E,E^{\prime }]\in {\mathcal{E}}^j$ with $E^{\prime }=S_m^{(j)}(E)$ for some $S_m^{(j)}\in G^j$ and $y=\tau \left(S_m^{(j)}({\tau }^{-1}(x))\right)$ for some $j=0,1,\infty$, or 2) x, $y\in \left(\mathbb{C}\backslash {\mathbb{V}}^{+}\right)\backslash \mathfrak{E}$ and $x=y$. Then ∼ is an equivalence relation on $\mathbb{C}\backslash {\mathbb{V}}^{+}$. Let ${(\mathbb{C}\backslash {\mathbb{V}}^{+})}^{\sim }$ be the set of equivalence classes and let $\Pi$ be the map

$$\Pi :\mathbb{C}\backslash {\mathbb{V}}^{+}\to {(\mathbb{C}\backslash {\mathbb{V}}^{+})}^{\sim }:p\mapsto [p],$$

(34)

which assigns to every $p\in \mathbb{C}\backslash {\mathbb{V}}^{+}$ the equivalence class $[p]$ containing p.

Lemma 12.

${\Pi |}_{K^{*}}$ is the map ρ (20).

Proof. 

This follows immediately from the definition of the maps $\Pi$ and $\rho$. □

Lemma 13.

The usual action of $\mathfrak{G}$ on $\mathbb{C}$, restricted to $\mathbb{C}\backslash {\mathbb{V}}^{+}$, is compatible with the equivalence relation ∼, that is, if x, $y\in \mathbb{C}\backslash \mathbb{V}$ and $x\sim y$, then $(g,\tau )(x)\sim (g,\tau )(y)$ for every $(g,\tau )\in \mathfrak{G}$.

Proof. 

Suppose that $x\in F={\tau }^{\prime }(E)$, where ${\tau }^{\prime }\in \mathcal{T}$. Then $y\in F^{\prime }={\tau }^{\prime }(E^{\prime })$, since $x\sim y$. So for some $S_m^{(j)}\in G^j$ with $j=0,1,\infty$, we have ${({\tau }^{\prime })}^{-1}(y)=S_m^{(j)}({\tau }^{-1}(x))$. Let $(g,\tau )\in \mathfrak{G}$. Then

$$(g,\tau )\left({({\tau }^{\prime })}^{-1}(y)\right)=g({({\tau }^{\prime })}^{-1}(y))+u_{\tau }=g\left(S_m^{(j)}({\tau }^{-1}(x))\right)+u_{\tau }.$$

So $(g,\tau )(y)\in (g,\tau )*F^{\prime }$. However, $(g,\tau )(x)\in (g,\tau )*F$ and $[(g,\tau )*F,(g,\tau )*F^{\prime }]=(g,\tau )*[F,F^{\prime }]$. Hence $(g,\tau )(x)\sim (g,\tau )(y)$. □

Because of Lemma 13, the usual $\mathfrak{G}$-action on $\mathbb{C}\backslash {\mathbb{V}}^{+}$ induces an action of $\mathfrak{G}$ on ${(\mathbb{C}\backslash {\mathbb{V}}^{+})}^{\sim }$.

Lemma 14.

The action of $\mathfrak{G}$ on ${(\mathbb{C}\backslash {\mathbb{V}}^{+})}^{\sim }$ is free and proper.

Proof. 

The following argument shows that it is free. Using Lemma A2 we see that an element of $\mathfrak{G}$, which lies in the isotropy group ${\mathfrak{G}}_{[F,F^{\prime }]}$ for $[F,F^{\prime }]\in {\mathfrak{E}}^0$, interchanges the edge F with the equivalent edge $F^{\prime }$ and thus fixes the equivalence class $[p]$ for every $p\in F$. Hence the $\mathfrak{G}$ action on ${(\mathbb{C}\backslash {\mathbb{V}}^{+})}^{\sim }$ is free. It is proper because $\mathfrak{G}$ is a discrete subgroup of the Euclidean group $\mathrm{E}(2)$ with no accumulation points. □

Theorem 4.

The $\mathfrak{G}$-orbit space ${(\mathbb{C}\backslash {\mathbb{V}}^{+})}^{\sim }/\mathfrak{G}$ is holomorphically diffeomorphic to the G-orbit space ${(K^{*}\backslash \mathrm{O})}^{\sim }/G={\tilde{\mathcal{S}}}_{\mathrm{reg}}$.

Proof. 

The claim follows because the fundamental domain of the $\mathfrak{G}$-action on $\mathbb{C}\backslash {\mathbb{V}}^{+}$ is $K^{*}\backslash \mathrm{O}$ is the fundamental domain of the G-action on $K^{*}\backslash \mathrm{O}$. Thus, $\Pi (\mathbb{C}\backslash {\mathbb{V}}^{+})$ is a fundamental domain of the $\mathfrak{G}$-action on ${(\mathbb{C}\backslash {\mathbb{V}}^{+})}^{\sim }$, which is equal to $\rho (K^{*}\backslash \mathrm{O})$ = ${(K^{*}\backslash \mathrm{O})}^{\sim }$ by Lemma 12. Hence the $\mathfrak{G}$-orbit space ${(\mathbb{C}\backslash {\mathbb{V}}^{+})}^{\sim }/\mathfrak{G}$ is equal to the G-orbit space ${\tilde{\mathcal{S}}}_{\mathrm{reg}}$. So the identity map from $\Pi (\mathbb{C}\backslash {\mathbb{V}}^{+})$ to ${(K^{*}\backslash \mathrm{O})}^{\sim }$ induces a holomorphic diffeomorphism of orbit spaces. □

Because the group $\mathfrak{G}$ is a discrete subgroup of the 2-dimensional Euclidean group $\mathrm{E}(2)$, the Riemann surface ${(\mathbb{C}\backslash {\mathbb{V}}^{+})}^{\sim }/\mathfrak{G}$ is an affine model of the affine Riemann surface ${\mathcal{S}}_{\mathrm{reg}}$.

6. The Developing Map and Geodesics

In this section, we show that the mapping

$$\delta :\mathcal{D}\subseteq {\mathcal{S}}_{\mathrm{reg}}\to Q\subseteq \mathbb{C}:(\xi ,\eta )\to (F_Q\circ \widehat{\pi })(\xi ,\eta ))$$

(35)

straightens the holomorphic vector field X (12) on the fundamental domain $\mathcal{D}\subseteq {\mathcal{S}}_{\mathrm{reg}}$, see [6] and Flaschka [7]. We also verify that X is the geodesic vector field for a flat Riemannian metric $\Gamma$ on $\mathcal{D}$.

First we rewrite Equation (13) as

$$T_{(\xi ,\eta )}\widehat{\pi }\left(X(\xi ,\eta )\right)=\eta \frac{\partial }{\partial \xi },\mathrm{for} (\xi ,\eta )\in \mathcal{D}.$$

(36)

From the definition of the mapping $F_Q$ (2) we get

$$\mathrm{d}z=\mathrm{d}{F}_Q=\frac{1}{{\left({\xi }^{n-n_0}{(1-\xi )}^{n-n_1}\right)}^{-2pt1/n}}\mathrm{d}\xi =\frac{1}{\eta }\mathrm{d}\xi ,$$

where we use the same complex nth root as in the definition of $F_Q$. This implies

$$\frac{\partial }{\partial z}=T_{\xi }{F}_Q\left(\eta \frac{\partial }{\partial \xi }\right),\mathrm{for}(\xi ,\eta )\in \mathcal{D}$$

(37)

For each $(\xi ,\eta )\in \mathcal{D}$ using (36) and (37) we get

$$\begin{array}{cc}\hfill & T_{(\xi ,\eta )}\delta \left(X(\xi ,\eta )\right)=\left(T_{\xi }{F}_Q\circ T_{(\xi ,\eta )}\widehat{\pi }\right)\left(X(\xi ,\eta )\right)=T_{\xi }{F}_Q(\eta \frac{\partial }{\partial \xi })=\frac{\partial }{\partial z}{|}_{z=\delta (\xi ,\eta )}.\hfill \end{array}$$

So the holomorphic vector field X (12) on $\mathcal{D}$ and the holomorphic vector field $\frac{\partial }{\partial z}$ on Q are $\delta$-related. Hence $\delta$ sends an integral curve of the vector field X starting at $(\xi ,\eta )\in \mathcal{D}$ onto an integral curve of the vector field $\frac{\partial }{\partial z}$ starting at $z=\delta (\xi ,\eta )\in Q$. Since an integral curve of $\frac{\partial }{\partial z}$ is a horizontal line segment in Q, we have proved

Theorem 5.

The holomorphic mapping δ (35) straightens the holomorphic vector field X (12) on the fundamental domain $\mathcal{D}\subseteq {\mathcal{S}}_{\mathrm{reg}}$.

We can say more. Let $u=\mathrm{Re}z$ and $v=\mathrm{Im}z$. Then

$$\gamma =\mathrm{d}u⨀\mathrm{d}u+\mathrm{d}v⨀\mathrm{d}v=\mathrm{d}z⨀\overline{\mathrm{d}z}$$

(38)

is the flat Euclidean metric on $\mathbb{C}$. Its restriction ${\gamma |}_{\mathbb{C}\backslash {\mathbb{V}}^{+}}$ to $\mathbb{C}\backslash {\mathbb{V}}^{+}$ is invariant under the group $\mathfrak{G}$, which is a subgroup of the Euclidean group $\mathrm{E}(2)$.

Consider the flat Riemannian metric ${\gamma |}_Q$ on Q, where $\gamma$ is the metric (38) on $\mathbb{C}$. Pulling back ${\gamma |}_Q$ by the mapping $F_Q$ (2) gives a metric

$$\tilde{\gamma }=F_Q^{*}(\gamma {|}_Q)={|{\xi }^{n-n_0}{(1-\xi )}^{n-n_1}|}^{-2/n}\mathrm{d}\xi ⨀\overline{\mathrm{d}\xi }$$

on $\mathbb{C}\backslash \{0,1\}$. Pulling the metric $\tilde{\gamma }$ back by the projection mapping $\tilde{\pi }:{\mathbb{C}}^2\to \mathbb{C}:(\xi ,\eta )\mapsto \xi$ gives

$$\tilde{\Gamma }={\tilde{\pi }}^{*}\tilde{\gamma }={|{\xi }^{n-n_0}{(1-\xi )}^{n-n_1}|}^{-2/n}\mathrm{d}\xi ⨀\overline{\mathrm{d}\xi }$$

on ${\mathbb{C}}^2$. Restricting $\tilde{\Gamma }$ to the affine Riemann surface ${\mathcal{S}}_{\mathrm{reg}}$ gives $\Gamma =\frac{1}{\eta }\mathrm{d}\xi ⨀\frac{1}{\overline{\eta }}\overline{\mathrm{d}\xi }$.

Lemma 15.

Γ is a flat Riemannian metric on ${\mathcal{S}}_{\mathrm{reg}}$.

Proof. 

We compute. For every $(\xi ,\eta )\in {\mathcal{S}}_{\mathrm{reg}}$ we have

$$\begin{array}{cc}\hfill \Gamma (\xi ,\eta )(X(\xi ,\eta ),X(\xi ,\eta ))& =\hfill \\ \hfill & =\frac{1}{\eta }\mathrm{d}\xi (\eta \frac{\partial }{\partial \xi }+\frac{n-n_0}{n}\frac{\xi (1-\xi )(1-\frac{2n-n_0-n_1}{n}\xi )}{{\eta }^{n-2}}\frac{\partial }{\partial \eta })·\frac{1}{\overline{\eta }}\overline{\mathrm{d}\xi }(\overline{\eta }\overline{\frac{\partial }{\partial \xi }}+\frac{n-n_0}{n}\frac{\overline{\xi (1-\xi )(1-\frac{2n-n_0-n_1}{n}\xi )}}{{\overline{\eta }}^{n-2}}\overline{\frac{\partial }{\partial \eta }})\hfill \\ \hfill & =\frac{1}{\eta }\mathrm{d}\xi (\eta \frac{\partial }{\partial \xi })·\frac{1}{\overline{\eta }}\overline{\mathrm{d}\xi }(\overline{\eta }\overline{\frac{\partial }{\partial \xi }})=1.\hfill \end{array}$$

Thus, $\Gamma$ is a Riemannian metric on ${\mathcal{S}}_{\mathrm{reg}}$. It is flat by construction. □

Because $\mathcal{D}$ has nonempty interior and the map $\delta$ (35) is holomorphic, it can be analytically continued to the map

$$\begin{array}{cc}\hfill & {\delta }_Q:{\mathcal{S}}_{\mathrm{reg}}\subseteq {\mathbb{C}}^2\to Q\subseteq \mathbb{C}:(\xi ,\eta )\mapsto F_Q\left(\widehat{\pi }(\xi ,\eta )\right),\hfill \end{array}$$

(39)

since $\delta ={\delta }_Q{|}_{\mathcal{D}}$. By construction ${\delta }_Q^{*}(\gamma {|}_Q)=\Gamma$. So the mapping ${\delta }_Q$ is an isometry of $({\mathcal{S}}_{\mathrm{reg}},\Gamma )$ onto $(Q,\gamma {|}_Q)$. In particular, the map $\delta$ is an isometry of $(\mathcal{D},\Gamma {|}_{\mathcal{D}})$ onto $(Q,\gamma {|}_Q)$. Moreover, $\delta$ is a local holomorphic diffeomorphism, because for every $(\xi ,\eta )\in \mathcal{D}$, the complex linear mapping $T_{(\xi ,\eta )}\delta$ is an isomorphism, since it sends $X(\xi ,\eta )$ to $\frac{\partial }{\partial z}|z=\delta (\xi ,\eta )$. Thus, $\delta$ is a developing map in the sense of differential geometry, see Spivak ([8], p. 97) note on §12 of Gauss [9]. The map $\delta$ is local because the integral curves of $\frac{\partial }{\partial z}$ on Q are only defined for a finite time, since they are horizontal line segments in Q. Thus, the integral curves of X (12) on $\mathcal{D}$ are defined for a finite time. Since the integral curves of $\frac{\partial }{\partial z}$ are geodesics on $(Q,\gamma {|}_Q)$, the image of a local integral curve of $\frac{\partial }{\partial z}$ under the local inverse of the mapping $\delta$ is a local integral curve of X. This latter local integral curve is a geodesic on $(\mathcal{D},\Gamma {|}_{\mathcal{D}})$, since $\delta$ is an isometry. Thus, we have proved

Theorem 6.

The holomorphic vector field X (12) on the fundamental domain $\mathcal{D}$ is the geodesic vector field for the flat Riemannian metric ${\Gamma |}_{\mathcal{D}}$ on $\mathcal{D}$.

Corollary 13.

The holomorphic vector field X on the affine Riemann surface ${\mathcal{S}}_{\mathrm{reg}}$ is the geodesic vector field for the flat Riemannian metric Γ on ${\mathcal{S}}_{\mathrm{reg}}$.

Proof. 

The corollary follows by analytic continuation from the conclusion of Theorem 6, since $\mathrm{int}\mathcal{D}$ is a nonempty open subset of ${\mathcal{S}}_{\mathrm{reg}}$ and both the vector field X and the Riemannian metric $\Gamma$ are holomorphic on ${\mathcal{S}}_{\mathrm{reg}}$. □

7. Discrete Symmetries and Billiard Motions

Let $\mathcal{G}$ be the group of homeomorphisms of the affine Riemann surface $\mathcal{S}$ (3) generated by the mappings

$$\mathcal{R}:\mathcal{S}\to \mathcal{S}:(\xi ,\eta )\mapsto (\xi ,{\mathrm{e}}^{2\pi i/n}\eta )\mathrm{and}\mathcal{U}:\mathcal{S}\to \mathcal{S}:(\xi ,\eta )\mapsto (\overline{\xi },\overline{\eta }).$$

Clearly, the relations ${\mathcal{R}}^n={\mathcal{U}}^2=e$ hold. For every $(\xi ,\eta )\in \mathcal{S}$ we have

$$\begin{array}{cc}\hfill \mathcal{U}{\mathcal{R}}^{-1}(\xi ,\eta )& =\mathcal{U}(\xi ,{\mathrm{e}}^{-2\pi i/n}\eta )=(\overline{\xi },{\mathrm{e}}^{2\pi i/n}\overline{\eta })=\mathcal{R}(\overline{\xi },\overline{\eta })=\mathcal{R}\mathcal{U}(\xi ,\eta ).\hfill \end{array}$$

So the additional relation $\mathcal{U}{\mathcal{R}}^{-1}=\mathcal{R}\mathcal{U}$ holds. Thus, $\mathcal{G}$ is isomorphic to the dihedral group.

Lemma 16.

$\mathcal{G}$ is a group of isometries of $({\mathcal{S}}_{\mathrm{reg}},\Gamma )$.

Proof. 

For every $(\xi ,\eta )\in {\mathcal{S}}_{\mathrm{reg}}$ we get

$$\begin{array}{cc}\hfill {\mathcal{R}}^{*}\Gamma (\xi ,\eta )\left(X(\xi ,\eta ),X(\xi ,\eta )\right)& =\Gamma \left(\mathcal{R}(\xi ,\eta )\right)\left(T_{(\xi ,\eta )}\mathcal{R}\left(X(\xi ,\eta )\right),T_{(\xi ,\eta )}\mathcal{R}\left(X(\xi ,\eta )\right)\right)\hfill \\ \hfill & =\Gamma (\xi ,{\mathrm{e}}^{2\pi i/n}\eta )({\mathrm{e}}^{2\pi i/n}\eta \frac{\partial }{\partial \xi }+\frac{n-n_0}{n}\frac{\xi (1-\xi )(1-\frac{2n-n_0-n_1}{n-n_0}\xi )}{{\eta }^{n-2}}{\mathrm{e}}^{2\pi i/n}\frac{\partial }{\partial \eta },\hfill \\ \hfill & {\mathrm{e}}^{2\pi i/n}\eta \frac{\partial }{\partial \xi }+\frac{n-n_0}{n}\frac{\xi (1-\xi )(1-\frac{2n-n_0-n_1}{n-n_0}\xi )}{{\eta }^{n-2}}{\mathrm{e}}^{2\pi i/n}\frac{\partial }{\partial \eta })\hfill \\ \hfill & =\frac{1}{|{\mathrm{e}}^{2\pi i/n}{\eta |}^2}\mathrm{d}\xi \left({\mathrm{e}}^{2\pi i/n}\eta \frac{\partial }{\partial \xi }\right)·\overline{\mathrm{d}\xi }(\overline{{\mathrm{e}}^{2\pi i/n}\eta \frac{\partial }{\partial \xi }})=1\hfill \\ \hfill & =\frac{1}{{\left|\eta \right|}^2}\mathrm{d}\xi (\eta \frac{\partial }{\partial \xi })·\overline{\mathrm{d}\xi }(\overline{\eta \frac{\partial }{\partial \xi }})=\Gamma (\xi ,\eta )\left(X(\xi ,\eta ),X(\xi ,\eta )\right)\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\mathcal{U}}^{*}\Gamma (\xi ,\eta )\left(X(\xi ,\eta ),X(\xi ,\eta )\right)& =\Gamma \left(\mathcal{U}(\xi ,\eta )\right)\left(T_{(\xi ,\eta )}\mathcal{U}\left(X(\xi ,\eta )\right),T_{(\xi ,\eta )}\mathcal{U}\left(X(\xi ,\eta )\right)\right)\hfill \\ \hfill & =\frac{1}{{\left|\eta \right|}^2}\overline{\mathrm{d}\xi }(\overline{\eta \frac{\partial }{\partial \xi }})·\overline{\overline{\mathrm{d}\xi }}(\overline{\overline{\eta \frac{\partial }{\partial \xi }}})=\Gamma (\xi ,\eta )\left(X(\xi ,\eta ),X(\xi ,\eta )\right).\hfill \end{array}$$

□

Recall that the group G, generated by the linear mappings

$$R:\mathbb{C}\to \mathbb{C}:z\mapsto {\mathrm{e}}^{2\pi i/n}z\mathrm{and}U:\mathbb{C}\to \mathbb{C}:z\mapsto \overline{z},$$

is isomorphic to the dihedral group.

Lemma 17.

G is a group of isometries of $(\mathbb{C},\gamma )$.

Proof. 

This follows because R and U are Euclidean motions. □

We would like the developing map ${\delta }_Q$ (39) to intertwine the actions of $\mathcal{G}$ and G and the geodesic flows on $({\mathcal{S}}_{\mathrm{reg}},\Gamma )$ and $(Q,\gamma {|}_Q)$. There are several difficulties. The first is: the group G does not preserve the quadrilateral Q. To overcome this difficulty we extend the mapping ${\delta }_Q$ (39) to the mapping ${\delta }_{K^{*}}$ (17) of the affine Riemann surface ${\mathcal{S}}_{\mathrm{reg}}$ onto the regular stellated n-gon $K^{*}$.

Lemma 18.

The mapping ${\delta }_{K^{*}}$ (17) intertwines the action Φ (14) of $\mathcal{G}$ on ${\mathcal{S}}_{\mathrm{reg}}$ with the action

$$\Psi :G\times K^{*}\to K^{*}:(g,z)\mapsto g(z)$$

(40)

of G on the regular stellated n-gon $K^{*}$.

Proof. 

From the definition of the mapping ${\delta }_{K^{*}}$ we see that for each $(\xi ,\eta )\in \mathcal{D}$ we have ${\delta }_{K^{*}}\left({\mathcal{R}}^j(\xi ,\eta )\right)=R^j{\delta }_{K^{*}}(\xi ,\eta )$ for every $j\in \mathbb{Z}$. By analytic continuation we see that the preceding equation holds for every $(\xi ,\eta )\in {\mathcal{S}}_{\mathrm{reg}}$. Since $F_Q(\overline{\xi })=\overline{F_Q(\xi )}$ by construction and $\widehat{\pi }(\overline{\xi },\overline{\eta })=\overline{\xi }$ (11), from the definition of the mapping $\delta$ (35) we get $\delta (\overline{\xi },\overline{\eta })=\overline{\delta (\xi ,\eta )}$ for every $(\xi ,\eta )\in \mathcal{D}$. In other words, ${\delta }_{K^{*}}\left(\mathcal{U}(\xi ,\eta )\right)=U{\delta }_{K^{*}}(\xi ,\eta )$ for every $(\xi ,\eta )\in \mathcal{D}$. By analytic continuation we see that the preceding equation holds for all $(\xi ,\eta )\in {\mathcal{S}}_{\mathrm{reg}}$. Hence on ${\mathcal{S}}_{\mathrm{reg}}$ we have

$${\delta }_{K^{*}}\circ {\Phi }_g={\Psi }_{\phi (g)}\circ {\delta }_{K^{*}}\mathrm{for}\mathrm{every}g\in \mathcal{G}.$$

(41)

The mapping $\phi :\mathcal{G}\to G$ sends the generators $\mathcal{R}$ and $\mathcal{U}$ of the group $\mathcal{G}$ to the generators R and U of the group G, respectively. So it is an isomorphism. □

There is a second more serious difficulty: the integral curves of $\frac{\partial }{\partial z}$ run off the quadrilateral Q in finite time. We fix this by requiring that when an integral curve reaches a point P on the boundary $\partial Q$ of Q, which is not a vertex, it undergoes a specular reflection at P. (If the integral curve reaches a vertex of Q in forward or backward time, then the motion ends). This motion can be continued as a straight line motion, which extends the motion on the original segment in Q.

To make this precise, we give Q the orientation induced from $\mathbb{C}$ and suppose that the incoming (and hence outgoing) straight line motion has the same orientation as $\partial Q$. If the incoming motion makes an angle $\alpha$ with respect to the inward pointing normal N to $\partial Q$ at P, then the outgoing motion makes an angle $\alpha$ with the normal N, see Richens and Berry [2]. Specifically, if the incoming motion to P is an integral curve of $\frac{\partial }{\partial z}$, then the outgoing motion, after reflection at P, is an integral curve of $R^{-1}\frac{\partial }{\partial z}={\mathrm{e}}^{-2\pi i/n}\frac{\partial }{\partial z}$. Thus, the outward motion makes a turn of $-2\pi /n$ at P towards the interior of Q, see Figure 10 (left). In Figure 10 (right) the incoming motion has the opposite orientation from $\partial Q$. This extended motion on Q is called a billiard motion. A billiard motion starting in the interior of $\mathrm{cl}(Q)\backslash (\mathrm{cl}(Q)\cap \mathbb{R})$ is defined for all time and remains in $\mathrm{cl}(Q)$ less its vertices, since each of the segments of the billiard motion is a straight line parallel to an edge of $\mathrm{cl}(Q)$ and does not hit a vertex of $\mathrm{cl}(Q)$, see Figure 11.

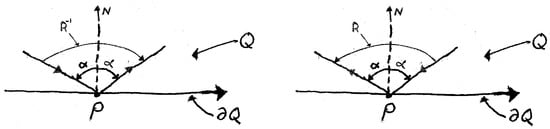
Figure 10. Reflection at a point P on $\partial Q$.

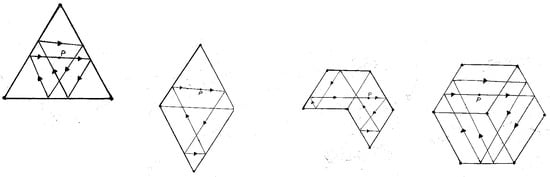
Figure 11. A periodic billiard motion in the equilateral triangle $T=T_{1,1,1}$ starting at P. First, extended by the reflection U to a periodic billiard motion in the quadrilateral $Q=T\cup U(T)$. Second, extended by the relection S to a periodic billiard motion in $Q\cup S(Q)$. Third, extended by the reflection $SR$ to a periodic billiard motion in the stellated equilateral triangle $H=K_{1,1,1}^{*}=Q\cup S(Q)SR(S(Q))$.

We can do more. If we apply a reflection S in the edge of Q in its boundary $\partial Q$, which contains the reflection point P, to the initial reflected motion at P, see Figure 12.

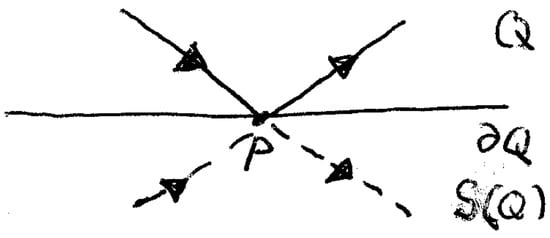
Figure 12. Continuation of a billiard motion in the quadrilateral Q to a billiard motion in the quarilateral $S(Q)$ obtained by the reflection S in an edge of Q.

The motion in $S(Q)$ when it reaches $\partial S(Q)$, et cetera, the extended motion becomes a billiard motion in the regular stellated n-gon $K^{*}=Q\cup {⨿}_{0\le k\le n-1}S{R}^k(Q))$, see Figure 11. So we have verified

Theorem 7.

A billiard motion in the regular stellated n-gon $K^{*}$, which starts at a point in the interior of $K^{*}\backslash \mathrm{O}$ and does not hit a vertex of $\mathrm{cl}(K^{*})$, is invariant under the action of the isometry subgroup $\widehat{G}$ of the isometry group G of $(K^{*},\gamma {|}_{K^{*}})$ generated by the rotation R.

Let $\widehat{\mathcal{G}}$ be the subgroup of $\mathcal{G}$ generated by the rotation $\mathcal{R}$. We now show

Lemma 19.

The holomorphic vector field X (12) on ${\mathcal{S}}_{\mathrm{reg}}$ is $\widehat{\mathcal{G}}$-invariant.

Proof. 

We compute. For every $(\xi ,\eta )\in {\mathcal{S}}_{\mathrm{reg}}$ and for $\mathcal{R}\in \widehat{\mathcal{G}}$ we have

$$\begin{array}{cc}\hfill T_{(\xi ,\eta )}{\Phi }_{\mathcal{R}}\left(X(\xi ,\eta )\right)& ={\mathrm{e}}^{2\pi i/n}\left[\eta \frac{\partial }{\partial \xi }+\frac{n-n_0}{n}\frac{\xi (1-\xi )(1-\frac{2n-n_0-n_1}{n}\xi )}{{\eta }^{n-2}}\frac{\partial }{\partial \eta }\right]\hfill \\ \hfill & =({\mathrm{e}}^{2\pi i/n}\eta )\frac{\partial }{\partial \xi }+\frac{n-n_0}{n}\frac{\xi (1-\xi )(1-\frac{2n-n_0-n_1}{n}\xi )}{{({\mathrm{e}}^{2\pi i/n}\eta )}^{n-2}}\frac{\partial }{\partial ({\mathrm{e}}^{2\pi i/n}\eta )}\hfill \\ \hfill & =X(\xi ,{\mathrm{e}}^{2\pi i/n}\eta )=X\circ {\Phi }_{\mathcal{R}}(\xi ,\eta ).\hfill \end{array}$$

Hence for every $j\in \mathbb{Z}$ we get

$$T_{(\xi ,\eta )}{\Phi }_{{\mathcal{R}}^j}\left(X(\xi ,\eta )\right)=X\circ {\Phi }_{{\mathcal{R}}^j}(\xi ,\eta )$$

(42)

for every $(\xi ,\eta )\in {\mathcal{S}}_{\mathrm{reg}}$. In other words, the vector field X is invariant under the action of $\widehat{\mathcal{G}}$ on ${\mathcal{S}}_{\mathrm{reg}}$. □

Corollary 14.

For every $(\xi ,\eta )\in \mathcal{D}$ we have

$${X|}_{{\Phi }_{{\mathcal{R}}^j}(\mathcal{D})}=T{\Phi }_{{\mathcal{R}}^j}{\circ X|}_{\mathcal{D}}.$$

(43)

Proof. 

Equation (43) is a rewrite of Equation (42). □

Corollary 15.

Every geodesic on $({\mathcal{S}}_{\mathrm{reg}},\Gamma )$ is $\widehat{\mathcal{G}}$-invariant.

Proof. 

This follows immediately from the lemma. □

Lemma 20.

For every $(\xi ,\eta )\in {\mathcal{S}}_{\mathrm{reg}}$ and every $j\in \mathbb{Z}$ we have

$$T_{{\Phi }_{{\mathcal{R}}^j}(\xi ,\eta )}{\delta }_{K^{*}}\left(X(\xi ,\eta )\right)=\frac{\partial }{\partial z}{|}_{{\delta }_{K^{*}}({\Phi }_{{\mathcal{R}}^j}(\xi ,\eta ))=R^{j}z.}$$

(44)

Proof. 

From Equation (41) we get ${\delta }_{K^{*}}\circ {\Phi }_{\mathcal{R}}={\Psi }_R\circ {\delta }_{K^{*}}$ on ${\mathcal{S}}_{\mathrm{reg}}$. Differentiating the preceding equation and then evaluating the result at $X(\xi ,\eta )\in T_{(\xi ,\eta )}{\mathcal{S}}_{\mathrm{reg}}$ gives

$$\left(T_{{\Phi }_{\mathcal{R}}(\xi ,\eta )}{\delta }_{K^{*}}\circ T_{(\xi ,\eta )}{\Phi }_{\mathcal{R}}\right)X(\xi ,\eta )=\left(T_{{\delta }_{K^{*}}(\xi ,\eta )}{\Psi }_R\circ T_{(\xi ,\eta )}{\delta }_{K^{*}}\right)X(\xi ,\eta )$$

for all $(\xi ,\eta )\in {\mathcal{S}}_{\mathrm{reg}}$. When $(\xi ,\eta )\in \mathcal{D}$, by definition ${\delta }_{K^{*}}(\xi ,\eta )=\delta (\xi ,\eta )$. So for every $(\xi ,\eta )\in {\mathcal{S}}_{\mathrm{reg}}$

$$T_{(\xi ,\eta )}{\delta }_{K^{*}}\left(X(\xi ,\eta )\right)=T_{(\xi ,\eta )}\delta \left(X(\xi ,\eta )\right)=\frac{\partial }{\partial z}{|}_{z=\delta (\xi ,\eta )}=\frac{\partial }{\partial z}{|}_{z={\delta }_{K^{*}}(\xi ,\eta )}.$$

Thus,

$$T_{{\Phi }_{\mathcal{R}}(\xi ,\eta )}{\delta }_{K^{*}}\left(T_{(\xi ,\eta )}{\Phi }_{\mathcal{R}}X(\xi ,\eta )\right)=T_{{\delta }_{K^{*}}(\xi ,\eta )}{\Psi }_R(\frac{\partial }{\partial z}{|}_{z={\delta }_{K^{*}}(\xi ,\eta )}),$$

(45)

for every $(\xi ,\eta )\in \mathcal{D}$. By analytic continuation (45) holds for every $(\xi ,\eta )\in {\mathcal{S}}_{\mathrm{reg}}$. Now $T_{(\xi ,\eta )}{\Phi }_{\mathcal{R}}$ sends $T_{(\xi ,\eta )}{\mathcal{S}}_{\mathrm{reg}}$ to $T_{{\Phi }_{\mathcal{R}}(\xi ,\eta )}{\mathcal{S}}_{\mathrm{reg}}$. Since $T_{(\xi ,\eta )}{\Phi }_{\mathcal{R}}X(\xi ,\eta )={\mathrm{e}}^{2\pi i/n}X(\xi ,\eta )$ for every $(\xi ,\eta )\in {\mathcal{S}}_{\mathrm{reg}}$, it follows that ${\mathrm{e}}^{2\pi i/n}X(\xi ,\eta )$ is in $T_{{\Phi }_{\mathcal{R}}(\xi ,\eta )}{\mathcal{S}}_{\mathrm{reg}}$. Furthermore, since $T_{{\delta }_{K^{*}}(\xi ,\eta )}{\Psi }_R$ sends $T_{{\delta }_{K^{*}}(\xi ,\eta )}{K}^{*}$ to $T_{{\Psi }_R({\delta }_{K^{*}}(\xi ,\eta )}{K}^{*}$, we get

$$T_{{\delta }_{K^{*}}(\xi ,\eta )}{\Psi }_R(\frac{\partial }{\partial z}|z={\delta }_{K^{*}(\xi ,\eta )})=R\frac{\partial }{\partial z}{|}_{Rz={\Psi }_R({\delta }_{K^{*}}(\xi ,\eta ))}.$$

For every $(\xi ,\eta )\in {\mathcal{S}}_{\mathrm{reg}}$ we obtain

$$T_{{\Phi }_{\mathcal{R}}(\xi ,\eta )}{\delta }_{K^{*}}\left(X(\xi ,\eta )\right)=\frac{\partial }{\partial z}{|}_{Rz={\Psi }_{\mathcal{R}}({\delta }_{K^{*}}(\xi ,\eta ))},$$

(46)

that is, Equation (44) holds with $j=0$. A similar calculation shows that Equation (46) holds with $\mathcal{R}$ replaces by ${\mathcal{R}}^j$. This verifies Equation (44). □

We now show

Theorem 8.

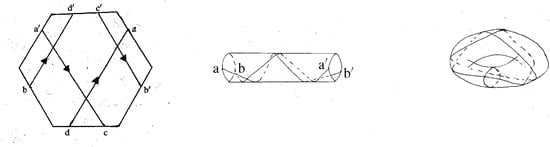
The image of a $\widehat{\mathcal{G}}$ invariant geodesic on $({\mathcal{S}}_{\mathrm{reg}},\Gamma )$ under the developing map ${\delta }_{K^{*}}$ (17) is a billiard motion in $K^{*}$, see Figure 13.

Figure 13. (left) A billiard motion in $K^{*}=K_{1,1,1}^{*}$. (center) The points c, $c^{\prime }$ and d, $d^{\prime }$ in $K^{*}$ are identified, which results in motion on a cylinder. (right) After identifying the points a, $a^{\prime }$ and b, $b^{\prime }$ on the cylinder the motion becomes a periodic geodesic on ${\tilde{S}}_{\mathrm{reg}}={(K^{*}\backslash \{O\})}^{\sim }/G$ on a smooth 2-torus less three points.

Proof. 

Because ${\Phi }_{{\mathcal{R}}^j}$ and ${\Psi }_{R^j}$ are isometries of $({\mathcal{S}}_{\mathrm{reg}},\Gamma )$ and $(K^{*},\gamma {|}_{K^{*}})$, respectively, it follows from equation (41) that the surjective map ${\delta }_{K^{*}}:({\mathcal{S}}_{\mathrm{reg}},\Gamma )\to (K^{*},\gamma {|}_{K^{*}})$ (17) is an isometry. Hence ${\delta }_{K^{*}}$ is a local developing map. Using the local inverse of ${\delta }_{K^{*}}$ and Equation (44), it follows that a billiard motion in $\mathrm{int}(K^{*}\backslash \mathrm{O})$ is mapped onto a geodesic in $({\mathcal{S}}_{\mathrm{reg}},\Gamma )$, which is possibly broken at the points $({\xi }_i,{\eta }_i)={\delta }_{K^{*}}^{-1}(p_i)$. Here $p_i\in \partial K^{*}$ are the points where the billiard motion undergoes a reflection. However, the geodesic on ${\mathcal{S}}_{\mathrm{reg}}$ is smooth at $({\xi }_i,{\eta }_i)$ since the geodesic vector field X is holomorphic on ${\mathcal{S}}_{\mathrm{reg}}$. Thus, the image of the geodesic under the developing map ${\delta }_{K^{*}}$ is a billiard motion. □

Theorem 9.

Under the restriction of the mapping

$$\nu =\sigma \circ \Pi :\mathbb{C}\backslash {\mathbb{V}}^{+}\to {(\mathbb{C}\backslash {\mathbb{V}}^{+})}^{\sim }/\mathfrak{G}={\tilde{S}}_{\mathrm{reg}}$$

(47)

to $K^{*}\backslash \mathrm{O}$ the image of a billiard motion ${\lambda }_z$ is a smooth geodesic ${\widehat{\lambda }}_{\nu (z)}$ on $({\tilde{S}}_{\mathrm{reg}},\widehat{\gamma })$, where ${\nu }^{*}(\widehat{\gamma }){=\gamma |}_{\mathbb{C}\backslash {\mathbb{V}}^{+}}$.

Proof. 

Since the Riemannian metric $\gamma$ on $\mathbb{C}$ is invariant under the group of Euclidean motions, the Riemannian metric ${\gamma |}_{K^{*}\backslash \mathrm{O}}$ on $K^{*}\backslash \mathrm{O}$ is $\widehat{G}$-invariant. Hence ${\gamma }_{K^{*}\backslash \mathrm{O}}$ is invariant under the reflection $S_m$ for $m\in \{0,1,\dots ,n-1\}$. So ${\gamma |}_{K^{*}\backslash \mathrm{O}}$ pieces together to give a Riemannian metric ${\gamma }^{\sim }$ on the identification space ${(K^{*}\backslash \mathrm{O})}^{\sim }$. In other words, the pull back of ${\gamma }^{\sim }$ under the map ${\Pi |}_{K^{*}\backslash \mathrm{O}}:K^{*}\backslash \mathrm{O}\to {(K^{*}\backslash \mathrm{O})}^{\sim }$, which identifies equivalent edges of $K^{*}$, is the metric ${\gamma |}_{K^{*}\backslash \mathrm{O}}$. Since ${\Pi |}_{K^{*}\backslash \mathrm{O}}$ intertwines the G-action on $K^{*}\backslash \mathrm{O}$ with the G-action on ${(K^{*}\backslash \mathrm{O})}^{\sim }$, the metric ${\gamma }^{\sim }$ is $\widehat{G}$-invariant. It is flat because the metric $\gamma$ is flat. So ${\gamma }^{\sim }$ induces a flat Riemannian metric $\widehat{\gamma }$ on the orbit space ${(K^{*}\backslash \mathrm{O})}^{\sim }/G={\tilde{S}}_{\mathrm{reg}}$. Since the billiard motion ${\lambda }_z$ is a $\widehat{G}$-invariant broken geodesic on $(K^{*}\backslash \mathrm{O},{\gamma }_{K^{*}\backslash \mathrm{O}})$, it gives rise to a continuous broken geodesic ${\lambda }_{\Pi (z)}^{\sim }$ on $({(K^{*}\backslash \mathrm{O})}^{\sim },{\gamma }^{\sim })$, which is $\widehat{G}$-invariant. Thus, ${\widehat{\lambda }}_{\nu (z)}=\nu ({\lambda }_z)$ is a piecewise smooth geodesic on the smooth G-orbit space $({(K^{*}\backslash \mathrm{O})}^{\sim }/G={\tilde{S}}_{\mathrm{reg}},\widehat{\gamma })$.

We need only show that ${\widehat{\lambda }}_{\nu (z)}$ is smooth. To see this we argue as follows. Let $s\subseteq K^{*}$ be a closed segment of a billiard motion ${\gamma }_z$, that does not meet a vertex of $\mathrm{cl}(K^{*})$. Then s is a horizontal straight line motion in $\mathrm{cl}(K^{*})$. Suppose that $E_{k_0}$ is the edge of $K^{*}$, perpendicular to the direction $u_{k_0}$, which is first met by s and let $P_{k_0}$ be the meeting point. Let $S_{k_0}$ be the reflection in $E_{k_0}$. The continuation of the motion s at $P_{k_0}$ is the horizontal line $R{S}_{k_0}(s)$ in $K_{k_0}^{*}$. Recall that $K_{k_0}^{*}$ is the translation of $K^{*}$ by ${\tau }_{k_0}$. Using a suitable sequence of reflections in the edges of a suitable $K_{k_0\cdots k_{\ell }}^{*}$ each followed by a rotation R and then a translation in $\mathcal{T}$ corresponding to their origins, we extend s to a smooth straight line $\lambda$ in $\mathbb{C}\backslash {\mathbb{V}}^{+}$, see Figure 14. The line $\lambda$ is a geodesic in $(\mathbb{C}\backslash {\mathbb{V}}^{+},\gamma {|}_{\mathbb{C}\backslash {\mathbb{V}}^{+}})$, which in $K^{*}$ has image ${\widehat{\lambda }}_{\nu (z)}$ under the $\mathfrak{G}$-orbit map $\nu$ (47) that is a smooth geodesic on $({\tilde{S}}_{\mathrm{reg}},\widehat{\gamma })$. The geodesic $\nu (\lambda )$ starts at $\nu (z)$. Thus, the smooth geodesic $\nu (\lambda )$ and the geodesic ${\widehat{\lambda }}_{\nu (z)}$ are equal. In other words, ${\widehat{\lambda }}_{\nu (z)}$ is a smooth geodesic. □

Figure 14. The billiard motion ${\gamma }_z$ in the stellated regular 3-gon $K_{1,1,1}^{*}$ meets the edge 0, isreflected in this edge by $S_0$, and then is rotated by R. This gives an extended motion $R{S}_0{\gamma }_z$, which is a straight line that is the same as reflecting ${\gamma }_z$ by U and then translating by ${\tau }_0$.

Thus, the affine orbit space ${\tilde{S}}_{\mathrm{reg}}={(\mathbb{C}\backslash {\mathbb{V}}^{+})}^{\sim }/\mathfrak{G}$ with flat Riemannian metric $\widehat{\gamma }$ is the affine analogue of the Poincaré model of the affine Riemann surface ${\mathcal{S}}_{\mathrm{reg}}$ as an orbit space of a discrete subgroup of $\mathrm{PGl}(2,\mathbb{C})$ acting on the unit disk in $\mathbb{C}$ with the Poincaré metric.