A Finitely Axiomatized Non-Classical First-Order Theory Incorporating Category Theory and Axiomatic Set Theory

Abstract

It is well known that Zermelo-Fraenkel Set Theory (ZF), despite its usefulness as a foundational theory for mathematics, has two unwanted features: it cannot be written down explicitly due to its infinitely many axioms, and it has a countable model due to the Löwenheim–Skolem theorem. This paper presents the axioms one has to accept to get rid of these two features. For that matter, some twenty axioms are formulated in a non-classical first-order language with countably many constants: to this collection of axioms is associated a universe of discourse consisting of a class of objects, each of which is a set, and a class of arrows, each of which is a function. The axioms of ZF are derived from this finite axiom schema, and it is shown that it does not have a countable model—if it has a model at all, that is. Furthermore, the axioms of category theory are proven to hold: the present universe may therefore serve as an ontological basis for category theory. However, it has not been investigated whether any of the soundness and completeness properties hold for the present theory: the inevitable conclusion is therefore that only further research can establish whether the present results indeed constitute an advancement in the foundations of mathematics.

1. Introduction

1.1. Motivation

Zermelo–Fraenkel set theory, which emerged from the axiomatic set theory proposed by Zermelo in [1] by implementing improvements suggested independently by Skolem and Fraenkel, is without a doubt the most widely accepted foundational theory for mathematics. However, it has two features that we may call “unwanted” or “pathological”. Let us, in accordance with common convention, use ZFC to denote the full theory, ZF for the full theory minus the axiom of choice (AC), and let us use ZF(C) in statements that are to hold for both ZF and ZFC; in a sentence, the two pathological features are then the following:

(i)

The number of axioms of ZF(C) is infinite, as a result of which ZF(C) cannot be written down explicitly;

(ii)

A corollary of the downward Löwenheim–Skolem theorem [2,3] is that ZF(C) has a countable model (if it has a model at all), as a result of which we have to swallow that there is a model of ZF(C) in which the powerset of the natural numbers is countable.

However, let us be more specific, starting with the infinite axiomatization of ZF(C). One might have the impression that ZF(C) has just eight or nine axioms—that is eight for ZF and nine for ZFC which includes AC. This impression, however, is false. The crux is that ZF(C) contains two axiom schemata, which are sometimes colloquially referred to as “axioms”: each axiom schema consists of infinitely many axioms. The first of these is the separation axiom schema, usually abbreviated by SEP. A standard formulation of SEP is the following:

$$\forall X\exists Y\forall z(z\in Y\iff z\in X\wedge \Phi )$$

(1)

This means: for any set X there is a set Y, such that any z is an element of Y if and only if z is an element of X and $\Phi$ is true. With such an axiom, we can construct a subset Y of X. The fact is, however, that $\Phi$ is a metavariable: it is a variable that stands for any well-formed formula not open in X. So, in fact, we have a separation axiom for every suitable well-formed formula that we substitute for $\Phi$ in Equation (1). For example, if we substitute “$z=\varnothing$” for “$\Phi$” in Equation (1), then we have a separation axiom. The second axiom schema of ZF(C) is the replacement axiom schema, usually abbreviated by REP. A standard formulation of REP is the following:

$$\forall x\exists !y\Phi (x,y)\Rightarrow \forall X\exists Y\forall y(y\in Y\iff \exists x\in X(\Phi (x,y)\left)\right)$$

(2)

This means: if for every set x there is a unique set y such that the relation $\Phi (x,y)$ is true, then for any set X there is a set Y made up of all the elements y for which there is an element x in X such that the relation $\Phi (x,y)$ is true. Again, $\Phi$ is a metavariable but now it stands for any well-formed functional relation. So, in fact, we have a replacement axiom for every well-formed functional relation that we substitute for $\Phi$ in Equation (2). For example, if we substitute “$y=\{x,\varnothing \}$" for “$\Phi (x,y)$” in Equation (2), then we have a replacement axiom. Ergo, ZF(C) is infinitely axiomatized: as a consequence, ZF(C) cannot ever be written down explicitly—that is our first pathological feature of ZF(C).

Now let us turn to the corollary of the downward Löwenheim–Skolem theorem that if ZF(C) has a model, it has a countable model—of all people, Zermelo himself considered this a pathological feature of the theory [4]. This countable model, let us call it “M”, thus consists of a universe $\left|M\right|$, which is a countable family of sets $m_1,m_2,m_3,\dots$ such that for every axiom A of ZF(C), its translation $A^{*}$ in the language of the model M is valid in M. That is, we have

$${\vDash }_M{A}^{*}$$

(3)

for the translation $A^{*}$ of any axiom A of ZF(C) in the language of M. Elaborating, the countable universe $\left|M\right|$ contains at least the following sets:

(i)

The natural numbers $0,1,2,\dots$ defined as sets;

(ii)

The countable set of natural numbers $\mathbb{N}=\{0,1,2,\dots \}$;

(iii)

Countably many subsets $S_1,S_2,S_3,\dots$ of the set $\mathbb{N}$;

(iv)

A countable set K that contains the above subsets of $\mathbb{N}$, so $K=\{S_1,S_2,S_3,\dots \}$.

Now the powerset axiom of ZF(C), usually abbreviated POW, is the following:

$$\forall X\exists Y\forall z(z\in Y\iff z\subset X)$$

(4)

This means: for any set X there is a set Y made up of the subsets of X. The set Y is then usually denoted by $Y=\mathcal{P}\left(X\right)$. However, in our model M, this translates as: for any set X in $\left|M\right|$ there is a set Y in $\left|M\right|$ made up of all the subsets of X in $\left|M\right|$. As a result, we have

$${\vDash }_{M}K=\mathcal{P}\left(\mathbb{N}\right)$$

(5)

So, in our model M the powerset of the natural numbers is a countable set. Intuitively we think that the powerset of $\mathbb{N}$ is uncountable and contains subsets of $\mathbb{N}$ other than the $S_j$’s in the universe $\left|M\right|$ of the model M. However, the crux is that these “other” subsets of $\mathbb{N}$ are not in $\left|M\right|$. Löwenheim and Skolem have proven that the existence of such a model M is an inevitable consequence of the standard first-order axiomatization of ZF. This is a famous result in the foundations of mathematics and one that is completely counterintuitive to boot. The proof is not constructive, that is, there exists no specification of how the set K can be constructed, but nevertheless we have to swallow that ZF(C) has a model M in which a countable set K is the powerset of the natural numbers. This is the second pathological feature of ZF(C).

The purpose of this paper is to present the axioms one has to accept such that the axioms of ZF can be derived from the new axioms—we omit a discussion of AC—but such that these two pathological features are both removed. The collection of these new axioms will henceforth be referred to with the symbol $\mathfrak{T}$ (a Gothic “T”): it is thus the case that $\mathfrak{T}$ has a finite number of non-logical axioms of finite length.

1.2. Related Works

While it is emphasized that it is not the purpose of this paper to review every idea ever published in set theory, it is true that at least one set theory that can be finitely axiomatized has already been suggested, namely Von Neumann–Gödel–Bernays set theory (NGB). NGB is provably a mere conservative extension of ZF and as such “it seems to be no stronger than ZF” [5]. However, NGB shares the second of the two aforementioned unwanted features with ZF: if it has a model at all, it also has a countable model. In that regard, Von Neumann has been quoted stating

“At present we can do no more than note that we have one more reason here to entertain reservations about set theory and that for the time being no way of rehabilitating this theory is known”.

[6]

That shows that Von Neumann too considered the countable model a pathological feature. That being said, a finite theory in the same language as ZF (without extra objects) and as strong as ZF has already in the 1950s been proved impossible by Montague [7]. This result is a landmark in the historical development of the foundations of mathematics: even though it may not be stated anywhere explicitly, it has ever since become accepted that there is no standard solution to “our” problem identified in the beginning. That is, the general consensus is that it is impossible to develop a foundational theory for mathematics in standard first-order language that lacks both pathological features of ZF—all the more so because the downward Löwenheim–Skolem theorem pertains to standard first-order theories in general. It is therefore not surprising that this is not an active research field: those working in the foundations of mathematics are well aware of “our” problem, but ongoing research in set theory focuses on other topics such as, for example, large cardinals, forcing, and inner models—see, e.g., [8,9,10] for some recent works. That being said, the finitely axiomatized theory $\mathfrak{T}$ that we present here is a nonstandard solution to “our” problem: it entails a rather drastic departure from the language, ontology, and logic of ZF. Earlier, a radical departure was already suggested by Lawvere, who formulated a theory of the category of sets: here the ∈-relation has been defined in terms of the primitive notions of category theory, that is, in terms of mappings, domains, and codomains [11]. The present theory $\mathfrak{T}$, however, is more of a “marriage”—for lack of a better term—between set theory and category theory: the ∈-relation is maintained as an atomic expression, while the notion of a category is built in as the main structural element. So, regarding the philosophical position on the status of category theory, here neither Lawvere’s position, that category theory provides the foundation for mathematics [12], Mayberry’s position, that category theory requires set theory as a foundation [13], nor Landry’s position, that category theory provides (all of) the language for mathematics [14], is taken: instead, the present position is that category theory is incorporated in the foundations.

1.3. Informal Overview of the Main Result

Category theory being incorporated means that the universe of (mathematical) discourse is not Cantor’s paradise of sets, but a category:

Definition 1.

The universe of discourse is a category $\mathcal{C}$ consisting of:

(i)

A proper class of objects, each of which is a set;

(ii)

A proper class of arrows, each of which is a function.

□

As to the meaning of the term “universe of discourse” in Definition 1, the following quote from a standard textbook is interesting:

“Instead of having to say the entities to which the predicates might in principle apply, we can make things easier for ourselves by collectively calling these entities the universe of discourse”.

[15]

So, a theory without a universe of discourse is nothing but a schema of meaningless strings of symbols, which are its axioms; an inference rule is then nothing but a rule by which (other) meaningless strings of symbols can be “deduced” from those axioms. Such a notion of “theory” might be acceptable from the perspective of a formalist, but here the position is taken that theories c.q. strings of symbols without meaning are not interesting. So, to the present theory $\mathfrak{T}$ is associated a Platonic universe of discourse—in case of the category $\mathcal{C}$ of Definition 1—which we can think of as being made up of the things that satisfy the axioms of $\mathfrak{T}$. That does not mean that for every thing in the universe of discourse a constant needs to be included in the formal language: the vocabulary contains only countably many constants. However, $\mathfrak{T}$ has been formulated with an intended model in mind: its universe is then a “Platonic imitation” of the universe of discourse. Below we briefly elaborate on the universe of discourse using set-builder notation: strictly speaking this is not a part of the formal language, but given its status as a widely used tool for the description of sets it is suitable for an informal introductory exposition that one can hold in the back of one’s mind.

For starters, the primitive notion of a set is, of course, that it is an object made up of elements: a thing $\alpha$ being an element of a set S is formalized by an irreducible ∈-relation, that is, by an atomic expression of the form $\alpha \in S$. The binary predicate “∈” is part of the language for $\mathfrak{T}$: there is no need to express it in the language of category theory, since that does not yield a simplification. (Hence the language of the present theory is not reduced to the language of category theory.) In ZF we then have the adage “everything is a set”, meaning that if we have $x\in y$, then x is a set too. Here, however, that adage remains valid in this proper class of objects only to the extent that all the objects are sets—the adage does not hold for all elements of all sets. That is, we will assume that every object of the category is either the empty set or an object that contains elements, but an element of an object—if any—can either be the empty set, or again an object made up of elements, or a function: a function is then not a set. A number of constructive set-theoretical axioms then describe in terms of the ∈-relation which sets there are at least in this proper class of sets; these axioms are very simple theorems of ZF that hardly need any elaboration.

As to the notion of a function, in the framework of ZF a function is identified with its graph. However, as hinted at above, here we reject that set-theoretical reduction. First of all, functions are objects sui generis. If we use simple symbols like X and Y for sets, then a composite symbol $f_X$—to be pronounced “f-on-X”—can be used for a function on X: in the intended model, a function is a thing $f_X$ where the “f” in “$f_X$” stands for the graph of the function and the “X” in “$f_X$” for its domain. To give an example, let the numbers 0 and 1 be defined as sets, e.g., by $0:=\varnothing$ and $1:=\{\varnothing \}$, and let, for sets x and y, a two-tuple $⟨x,y⟩$ be defined as a set, e.g., by $⟨x,y⟩:=\{x,\{x,y\left\}\right\}$; then the composite symbol ${\{⟨0,1⟩,⟨1,0⟩\}}_{\{0,1\}}$ refers to the function on the set $\{0,1\}$ whose graph is the set $\{⟨0,1⟩,⟨1,0⟩\}$. However, we have $f_X\ne Y$ for any function on any domain X and for any set Y, so

$${\{⟨0,1⟩,⟨1,0⟩\}}_{\{0,1\}}\ne \{⟨0,1⟩,⟨1,0⟩\}$$

(6)

That is, the function ${\{⟨0,1⟩,⟨1,0⟩\}}_{\{0,1\}}$ is not identical to its graph $\{⟨0,1⟩,⟨1,0⟩\}$—nor, in fact, to any other set Y. At this point one might be inclined to think that the whole idea of functions on a set as objects sui generis is superfluous and should be eliminated in favor of the idea that functions are identified with their graphs (which are sets). That, however, has already been tried in an earlier stage of this investigation: it turned out to lead to unsolvable difficulties with the interpretation of the formalism, cf. [16]. The crux is that the main constructive axiom of the theory—here a constructive axiom is an axiom that, when certain things are given (e.g., one or two sets or a set and a predicate), states the existence of a uniquely determined other thing [17]—“produces” things referred to by a symbol $F_X$: one gets into unsolvable difficulties if one tries to interpret these things as sets.

However, functions are not completely different than sets. Contrary to a set, a function in addition has a domain and a codomain—both are sets—and it also does something: namely, it maps every element in its domain to an element in its codomain. This first aspect, that a function “has” a domain and a codomain, can be expressed in the language of category theory: an atomic formula $f_X:Y\twoheadrightarrow Z$ expresses that the function $f_X$ has domain Y and codomain Z. In accordance with existing convention, the two-headed arrow “↠” expresses that $f_X$ is a surjection: the codomain is always the set of the images of the elements of the domain under $f_X$. Since such an expression $f_X:Y\twoheadrightarrow Z$ is irreducible in the present framework, it requires some function-theoretical axioms to specify when such an atomic formula is true and when it is not. For example, for the function ${\{⟨0,1⟩,⟨1,0⟩\}}_{\{0,1\}}$ discussed above we have

$${\{⟨0,1⟩,⟨1,0⟩\}}_{\{0,1\}}:\{0,1\}\twoheadrightarrow \{0,1\}$$

(7)

while other expressions ${\{⟨0,1⟩,⟨1,0⟩\}}_{\{0,1\}}:Y\twoheadrightarrow Z$ are false. Again, at this point one might be inclined to think that these expressions $f_X:Y\twoheadrightarrow Z$ are superfluous, because the notation $f_X$ already indicates that X is the domain of $f_X$. The crux, however, is that these expressions are essential to get to a finite axiomatization: we may, then, have the opinion that it is obvious from the notation $f_X$ that X is the domain of $f_X$, but only an expression $f_X:X\twoheadrightarrow Z$ expresses this fact—it is, thus, an axiom of the theory that $f_X:Y\twoheadrightarrow Z$ is only true if $Y=X$. In particular, this expression is not true if $Y⊊X$.

The second aspect, that for any set X any function $f_X$ “maps” an element y of its domain to an element z of its codomain, is expressed by another atomic formula $f_X:y\mapsto z$. In the framework of ZF this is just a notation for $⟨y,z⟩\in f_X$, but in the present framework this is also an irreducible expression: therefore, it requires some more function-theoretical axioms to specify when such an atomic formula is true and when not. The idea, however, is this: given a set X and a function $f_X$, precisely one expression $f_X:y\mapsto z$ is true for each element y in the domain of $f_X$. For example, we have

$$\begin{array}{c}{\{⟨0,1⟩,⟨1,0⟩\}}_{\{0,1\}}:0\mapsto 1\end{array}$$

(8)

$$\begin{array}{c}{\{⟨0,1⟩,⟨1,0⟩\}}_{\{0,1\}}:1\mapsto 0\end{array}$$

(9)

for the above function ${\{⟨0,1⟩,⟨1,0⟩\}}_{\{0,1\}}$. Importantly, each function is thus a total function. However, for any set X, any total function $f_X$ with codomain Y, and any set Z for which $X⊊Z$, we may view $f_X$ as a partial function on Z. We might express that with a formula $f_X:Z\nrightarrow Y$, which we may define in the language of our theory $\mathfrak{T}$ by

$$f_X:Z\nrightarrow Y\iff f_X:X\twoheadrightarrow Y\wedge X\subset Z$$

(10)

We then have $f_X:z\mapsto y$ for some $y\in Y$ if $z\in X$, and $\forall u(f_X:z\nrightarrow u)$ if $z\in Z/X$. We will not use the notion of a partial function to build our theory $\mathfrak{T}$, but this shows that we can still use the notion of a partial function in the framework of $\mathfrak{T}$.

All the above can be expressed with a dozen and a half very simple axioms—these can, in fact, all be reformulated in the framework of ZF. The present axiomatic schema does, however, contain “new mathematics” in the form of the second axiom of a pair of constructive, function-theoretical axioms. The first one is again very simple and merely states that given any two singletons $X=\left\{x\right\}$ and $Y=\left\{y\right\}$, there exists an “ur-function” that maps the one element x of X to the one element y of Y. An ur-function is thus a function with a singleton domain and a singleton codomain. The above function ${\{⟨0,1⟩,⟨1,0⟩\}}_{\{0,1\}}$ is thus not an ur-function but the function referred to by the symbol ${\left\{⟨0,1⟩\right\}}_{\left\{0\right\}}$ is: we have

$$\begin{array}{c}{\left\{⟨0,1⟩\right\}}_{\left\{0\right\}}:\left\{0\right\}\twoheadrightarrow \left\{1\right\}\end{array}$$

(11)

$$\begin{array}{c}{\left\{⟨0,1⟩\right\}}_{\left\{0\right\}}:0\mapsto 1\end{array}$$

(12)

That said, the second of the pair of constructive, function-theoretical axioms is a new mathematical principle: it states that given any family of ur-functions $f_{\left\{j\right\}}$ indexed in a set Z, there exists a sum function $F_Z$ such that the sum function maps an element j of Z to the same image as the corresponding ur-function $f_{\left\{j\right\}}$. The formulation of this principle requires, however, a new non-classical concept that can be called a “multiple quantifier”. This new concept can be explained as follows. Suppose we have defined the natural numbers $0,1,2,\dots$ as sets, suppose the singletons $\left\{0\right\},\left\{1\right\},\left\{2\right\},\dots$ exist as well, and suppose we also have the set of natural numbers $\omega =\{0,1,2,\dots \}$. We can, then, consider variables $f_{\left\{0\right\}},f_{\left\{1\right\}},f_{\left\{2\right\}},\dots$ ranging over all ur-functions on a singleton of a natural number as indicated by the subscript—so, $f_{\left\{0\right\}}$ is a variable that ranges over all ur-functions on the singleton of 0. In the standard first-order language of ZF, we have the possibility to quantify over all ur-functions on a singleton $\left\{a\right\}$ by using a quantifier $\forall f_{\left\{a\right\}}$, and we have the possibility to use any finite number of such quantifiers in a sentence. For example, we can have a formula

$$\forall f_{\left\{0\right\}}\forall f_{\left\{1\right\}}\forall f_{\left\{2\right\}}\Psi$$

(13)

meaning: for all ur-functions on $\left\{0\right\}$, for all ur-functions on $\left\{1\right\}$, and for all ur-functions on $\left\{2\right\}$, $\Psi$. We can then introduce a new notation by the following postulate of meaning:

$${(\forall f_{\left\{j\right\}})}_{j\in \{0,1,2\}}\Psi \iff \forall f_{\left\{0\right\}}\forall f_{\left\{1\right\}}\forall f_{\left\{2\right\}}\Psi$$

(14)

This formula can be read as: for any family of ur-functions indexed in $\{0,1,2\}$, $\Psi$. So ${(\forall f_{\left\{i\right\}})}_{i\in \{0,1,2\}}$ is then a multiple quantifier that, in this case, is equivalent to three quantifiers in standard first-order language. The next step is now that we lift the restriction that a multiple quantifier has to be equivalent to a finite number of standard quantifiers: with that step we enter into non-classical territory. In the language of $\mathfrak{T}$ we can consider a formula like

$${(\forall f_{\left\{i\right\}})}_{i\in \omega }\Psi$$

(15)

The multiple quantifier is equivalent to a sequence $\forall f_{\left\{0\right\}}\forall f_{\left\{1\right\}}\forall f_{\left\{2\right\}}\cdots$ of infinitely many standard quantifiers in this case. However, in the present framework the constant $\omega$ in Formula (15) can be replaced by any constant, yielding non-classical multiple quantifiers equivalent to an uncountably infinite number of standard quantifiers.

To yield meaningful theorems, the subformula $\Psi$ of Formula (15) has to be open in infinitely many variables $f_{\left\{0\right\}},f_{\left\{1\right\}},f_{\left\{2\right\}},\dots$, each of which ranges over all ur-functions on a singleton of a natural number. This is achieved by placing a conjunctive operator${\bigwedge }_{i\in \omega }$ in front of a standard first-order formula $\Psi \left(f_{\left\{i\right\}}\right)$ that is open in a composite variable $f_{\left\{i\right\}}$, yielding an expression

$${\bigwedge }_{i\in \omega }\Psi \left(f_{\left\{i\right\}}\right)$$

(16)

Syntactically this is a formula of finite length, but semantically it is the conjunction of a countably infinite family of formulas $\Psi \left(f_{\left\{0\right\}}\right),\Psi \left(f_{\left\{1\right\}}\right),\Psi \left(f_{\left\{2\right\}}\right),\dots$. Together with the multiple quantifier from Formula (15) it yields a sentence${(\forall f_{\left\{i\right\}})}_{i\in \omega }{\bigwedge }_{i\in \omega }\Psi \left(f_{\left\{i\right\}}\right)$: semantically it contains a bound occurrence of the variables $f_{\left\{0\right\}},f_{\left\{1\right\}},f_{\left\{2\right\}},\dots$. The non-classical “sum function axiom” constructed with these formal language elements is so powerful that it allows one to derive the infinite schemas SEP and REP of ZF from just a finite number of axioms.

That said, the literature already contains a plethora of so-called infinitary logics; see [18] for a general overview and [19,20] for an example of some recent work. In the framework of such an infinitary logic, one typically can form infinitary conjunctions of a collection $\Sigma$ of standard first-order formulas indexed by some set S. So, if $\Sigma =\left\{{\varphi }_j\right|j\in S\}$ is such a collection of formulas, then a formula $\bigwedge \Sigma$ stands for ${\wedge }_{j\in S}{\varphi }_j$, which resembles Formula (16). That way, one can, for example, form the conjunction of all the formulas of the SEP schema of ZF: that yields a finite axiomatization of set theory. However, such an infinitary conjunction cannot be written down explicitly: the string of symbols “${\wedge }_{j\in S}{\varphi }_j$” is an informal abbreviation that is not part of the formal language—that is, it is not a well-formed formula. In the present case, however, we are only interested in well-formed formulas of finite length, which can be written down explicitly. This is achieved by building restrictions in the definition of the syntax, so that a conjunctive operator like ${\bigwedge }_{x\in \omega }$ only forms a well-formed formula if it is put in front of an atomic expression of the type $f_{\left\{x\right\}}:x\mapsto t\left(x\right)$ where both $f_{\left\{x\right\}}$ and $t\left(x\right)$ are terms with an occurrence of the same variable x that occurs in the conjunctive operator: the way typographically finite expressions obtain that semantically is infinitary conjunctions. So, the language for our theory $\mathfrak{T}$ is much more narrowly defined than the language of (overly?) general infinitary logics: as it turns out, that suffices for our present aims.

That brings us to the next point, which is to discuss the (possible) practical use of the new finite theory $\mathfrak{T}$ as a foundational theory for mathematics, that is, as a framework for proofs in mathematics. The practical usefulness of the schema lies therein that it (i) provides an easy way to construct sets and (ii) that categories like Top, Mon, Grp, etc., which are subjects of study in category theory, can be viewed as subcategories of the category of sets and functions of Definition 1, thus providing a new approach to the foundational problem identified in [21]. While that latter point (ii) hardly needs elaboration, the former (i) does. The crux is that one does not need to apply the non-classical sum function axiom directly: what one uses is the theorem—or rather: the theorem schema—that given any set X, we can construct a new function on X by giving a function prescription. So, this is a philosophical nuance: in ZF one constructs a new object with the ∈-relation, but in the present framework one can construct a new function $f_X$ not with the ∈-relation but by simply defining which expressions $f_X:y\mapsto z$ are true for the elements y in the domain. On account of the sum function axiom, it is then a guarantee that the function $f_X$ exists. So, given any set X one can simply give a defining function prescription

$$f_X:y\stackrel{\mathrm{def}}{⟼}ız\Phi (y,z)$$

(17)

(where the iota-term $ız\Phi (y,z)$ denotes the unique thing z for which the functional relation $\Phi (y,z)$ holds) and it is then a guarantee that $f_X$ exists. Furthermore, having constructed the function, we have implicitly constructed its graph and its image set. Ergo, giving a function prescription is constructing a set. The non-classical axiom, which may be cumbersome to use directly, stays thus in the background: one uses the main theorem of $\mathfrak{T}$.

What remains to be discussed is that $\mathfrak{T}$, as mentioned in the first paragraph, entails the axioms of ZF and does not have a countable model. As to the first-mentioned property, it will be proven that the infinite axiom schemas SEP and SUP of ZF, translated in the formal language of $\mathfrak{T}$, can be derived from the finitely axiomatized theory $\mathfrak{T}$: that provides an argument for considering $\mathfrak{T}$ to be not weaker than ZF. Secondly, even though the language of $\mathfrak{T}$ has only countably many constants, it will be shown that the validity of the non-classical sum function axiom in a model $\mathcal{M}$ of $\mathfrak{T}$ has the consequence that the downward Löwenheim–Skolem theorem does not hold: if $\mathfrak{T}$ has a model $\mathcal{M}$, then $\mathcal{M}$ is uncountable. This is a significant result that does not hold in the framework of ZF: it provides, therefore, an argument for considering $\mathfrak{T}$ to be stronger than ZF.

1.4. Point-by-Point Overview

(i)

Zermelo–Fraenkel set theory is the most widely accepted foundational theory for mathematics, but the problem is that it has two unwanted features:

–

It has infinitely many axioms;

–

It has a countable model in which the powerset of the naturals is countable;

(ii)

Since the 1950s it has been generally accepted that this problem has no standard solution;

(iii)

This paper presents a nonstandard solution, which opens up an entirely new research field that may be called “infinitary mathematical logic”;

(iv)

The main result, the non-classical theory $\mathfrak{T}$, incorporates category theory and axiomatic set theory in a single framework;

(v)

Category theory is incorporated by the ontological assumption that the universe of $\mathfrak{T}$ is a class of sets and a class of functions: this universe satisfies the axioms of category theory;

(vi)

Set theory is incorporated in the sense that the axioms of ZF can be derived from the axioms of $\mathfrak{T}$;

(vii)

$\mathfrak{T}$ can be considered stronger than ZF since it lacks the two unwanted features:

–

$\mathfrak{T}$ has finitely many axioms of finite length;

–

If $\mathfrak{T}$ has a model, it is uncountable;

(viii)

$\mathfrak{T}$ is introduced here as a candidate for a foundational theory for mathematics, the corresponding philosophy of mathematics being that mathematics—i.e., all of mathematics—can be viewed as the collection of valid inferences within the framework of $\mathfrak{T}$;

(ix)

The true merit of $\mathfrak{T}$ as a foundational theory for mathematics has yet to be established by a program for further research: negative results may invalidate the idea that $\mathfrak{T}$ is suitable as a foundational theory for mathematics.

This concludes the introductory discussion. The remainder of this paper is organized as follows. The next section axiomatically introduces this finitely axiomatized non-classical theory $\mathfrak{T}$. The section thereafter discusses the theory $\mathfrak{T}$ (i) by deriving its main theorem, (ii) by deriving the axiom schemas SEP and REP of ZF, (iii) by showing that the downward Löwenheim–Skolem theorem does not hold for the non-classical theory $\mathfrak{T}$, (iv) by showing the axioms of category theory hold for the class of arrows of the universe of discourse meant in Definition 1, and (v) by addressing the main concerns for inconsistency. The final section states the conclusions.

2. Axiomatic Introduction

2.1. Formal language

First of all a remark. In standard first-order logic, the term “quantifier” refers both to the logical symbols “∀” and “∃” and to combinations like $\forall x$, $\exists y$ consisting of such a symbol and a variable. While that may be unproblematic in standard logic, here the logical symbols “∀” and “∃” are applied in different kinds of quantifiers. Therefore, to avoid confusion we will refer to the symbol “∀” by the term “universal quantification symbol” and to the symbol “∃” by the term “existential quantification symbol”.

Definition 2.

The vocabulary of the language $L_{\mathfrak{T}}$ of $\mathfrak{T}$ consists of the following:

(i)

The constants ∅ and $\mathbf{\omega }$, to be interpreted as the empty set and the first infinite ordinal;

(ii)

The constants $1_{\varnothing }$, to be interpreted as the inactive function;

(iii)

Simple variables $x,X,y,Y,\dots$ ranging over sets;

(iv)

For any constant $\widehat{\mathbf{X}}$ referring to an individual set, composite symbols $f_{\widehat{\mathbf{X}}},g_{\widehat{\mathbf{X}}},\dots$ with an occurrence of the constant $\widehat{\mathbf{X}}$ as the subscript are simple variables ranging over functions on that set $\widehat{\mathbf{X}}$;

(v)

For any simple variable X ranging over sets, composite symbols $f_X,g_X,\cdots$ with an occurrence of the variable X as the subscript are composite variables ranging over functions on a set X;

(vi)

Simple variables $\alpha ,\beta ,\dots$ ranging over all things (sets and functions);

(vii)

The binary predicates “∈” and “=”, and the ternary predicates “$(.):(.)\twoheadrightarrow (.)$” and “$(.):(.)\mapsto (.)$”;

(viii)

The logical connectives of first-order logic $\neg ,\wedge ,\vee ,\Rightarrow ,\iff$;

(ix)

The universal and existential quantification symbols $\forall ,\exists$;

(x)

The brackets “(’ and ‘)". □

Remark 1.

To distinguish between the theory $\mathfrak{T}$ and its intended model, boldface symbols with a hat like $\widehat{\mathbf{X}}$, $\widehat{\mathbf{\alpha }}$, etc., will be used to denote constants in the vocabulary of the theory $\mathfrak{T}$, while underlined boldface symbols like $\underline{\mathbf{X}}$, $\underline{\mathbf{\alpha }}$, etc., will be used to denote individuals in the intended model of $\mathfrak{T}$. □

Definition 3.

The syntax of the language $L_{\mathfrak{T}}$ is defined by the following clauses:

(i)

If t is a constant, or a simple or a composite variable, then t is a term;

(ii)

If $t_1$ and $t_2$ are terms, then $t_1=t_2$ and $t_1\in t_2$ are atomic formulas;

(iii)

If $t_1$, $t_2$, and $t_3$ are terms, then $t_1:t_2\twoheadrightarrow t_3$ and $t_1:t_2\mapsto t_3$ are atomic formulas;

(iv)

If $\Phi$ and $\Psi$ are formulas, then $\neg \Phi$, $(\Phi \wedge \Psi )$, $(\Phi \vee \Psi )$, $(\Phi \Rightarrow \Psi )$, $(\Phi \iff \Psi )$ are formulas;

(v)

If $\Psi$ is a formula and t a simple variable ranging over sets, over all things, or over functions on a constant set, then $\forall t\Psi$ and $\exists t\Psi$ are formulas;

(vi)

If X and $f_{\widehat{\mathbf{X}}}$ are simple variables ranging respectively over sets and over functions on the set $\widehat{\mathbf{X}}$, $f_X$ a composite variable with an occurrence of X as the subscript, and $\Psi$ a formula with an occurrence of a quantifier $\forall f_{\widehat{\mathbf{X}}}$ or $\exists f_{\widehat{\mathbf{X}}}$ but with no occurrence of X, then $\forall X[X\backslash \widehat{\mathbf{X}}]\Psi$ and $\exists X[X\backslash \widehat{\mathbf{X}}]\Psi$ are formulas. □

Remark 2.

Regarding clause (vi) of Definition 3, $[u\backslash t]\Psi$ is the formula obtained from $\Psi$ by replacing t everywhere by u. This definition will be used throughout this paper. Note that if $\Psi$ is a formula with an occurrence of the simple variable $f_{\widehat{\mathbf{X}}}$, then $[X\backslash \widehat{\mathbf{X}}]\Psi$ is a formula with an occurrence of the composite variable $f_X$. □

Definition 4.

The language $L_{\mathfrak{T}}$ contains the following special language elements:

(i)

If t is a simple variable ranging over sets, over all things, or over functions on a constant set, then $\forall t$ and $\exists t$ are quantifiers with a simple variable;

(ii)

If $f_X$ is a composite variable, then $\forall f_X$ and $\exists f_X$ are a quantifiers with a composite variable.

A sequence like $\forall X\forall f_X$ can be called a double quantifier. □

The scope of a quantifier is defined as usual: note that a quantifier with a composite variable can only occur in the scope of a quantifier with a simple variable. A free occurrence and a bounded occurrence of a simple variable is also defined as usual; these notions can be simply defined for formulas with a composite variable.

Definition 5.

Let $f_X$ be a composite variable with an occurrence of the simple variable X; then

(i)

An occurrence of $f_X$ in a formula $\Psi$ is free if that occurrence is neither in the scope of a quantifier with the composite variable $f_X$ nor in the scope of a quantifier with the simple variable X;

(ii)

An occurrence of $f_X$ in a formula $\Psi$ is bounded if that occurrence is in the scope of a quantifier with the composite variable $f_X$.

A sentence is a formula with no free variables—simple or composite. A formula is open in a variable if there is a free occurrence of that variable. A formula that is open in a composite variable $f_X$ is also open in the simple variable X. □

Definition 6.

The semantics of any sentence without a quantifier with a composite variable is as usual. Furthermore,

(i)

A sentence $\forall X\Psi$ with an occurrence of a quantifier $\forall f_X$ or $\exists f_X$ with the composite variable $f_X$ is valid in a model $\mathcal{M}$ if and only if for every assignment g that assigns an individual set $g\left(X\right)=\underline{\mathbf{X}}$ in $\mathcal{M}$ as a value to the variable X, the sentence $[\underline{\mathbf{X}}\backslash X]\Psi$ is valid in $\mathcal{M}$;

(ii)

The sentence $[\underline{\mathbf{X}}\backslash X]\Psi$ obtained in clause (i) is a sentence without a quantifier with a composite variable, hence with usual semantics.

The semantics of a sentence $\exists X\Psi$ with an occurrence of a quantifier $\forall f_X$ or $\exists f_X$ is left as an exercise. □

After the introduction of the “standard” first-order axioms of $\mathfrak{T}$, the language $L_{\mathfrak{T}}$ will be extended to enable the formulation of the desired non-classical formulas.

2.2. Set-Theoretical Axioms

Below the set-theoretical axioms are listed; these are all standard first-order formulas. Due to the simplicity of the axioms, comments are kept to a bare minimum.

Axiom 1.

Extensionality Axiom for Sets (EXT): two sets X and Y are identical if they have the same things (sets and functions) as elements.

$$\forall X\forall Y(X=Y\iff \forall \alpha (\alpha \in X\iff \alpha \in Y\left)\right)$$

(18)

□

Axiom 2.

For any set X, any function $f_X$ is not identical to any set Y:

$$\forall X\forall f_X\forall Y(f_X\ne Y)$$

(19)

□

Axiom 3.

A set X has no domain or codomain, nor does it map any thing to an image:

$$\forall X\forall \alpha \forall \beta (X:\alpha \cancel{\twoheadrightarrow }\beta \wedge X:\alpha \cancel{\mapsto }\beta )$$

(20)

□

These latter two axioms establish that sets are different from functions on a set and do not have the properties of functions on a set.

Axiom 4.

Empty Set Axiom (EMPTY): there exists a set X, designated by the constant ∅, that has no elements.

$$\exists X(X=\varnothing \wedge \forall \alpha (\alpha \notin X\left)\right)$$

(21)

□

Axiom 5.

Axiom of Pairing (PAIR): for every thing $\alpha$ and every thing $\beta$ there exists a set X that has precisely the things $\alpha$ and $\beta$ as its elements.

$$\forall \alpha \forall \beta \exists X\forall \gamma (\gamma \in X\iff \gamma =\alpha \vee \gamma =\beta )$$

(22)

□

Remark 3.

Using set-builder notation, the empty set can be interpreted as the individual $\left\{\right\}$ in the intended model. Furthermore, given individual things $\underline{\mathbf{\alpha }}$ and $\underline{\mathbf{\beta }}$ in the universe of the intended model, the pair set of $\underline{\mathbf{\alpha }}$ and $\underline{\mathbf{\beta }}$ can then be identified with the individual $\{\underline{\mathbf{\alpha }},\underline{\mathbf{\beta }}\}$. Note that this is a singleton if $\underline{\mathbf{\alpha }}=\underline{\mathbf{\beta }}$. □

Remark 4.

The sets in the present theory cannot be viewed as multisets, the objects of multiset theory [22]. In the framework of our theory $\mathfrak{T}$, we have for any thing $\alpha$ in the category of sets and functions that $\left\{\alpha \right\}=\{\alpha ,\alpha \}=\{\alpha ,\alpha ,\alpha \}$. In multiset theory, this is not the case: an element may occur more than once in a multiset. We then have $\{\alpha ,\alpha \}\ne \{\alpha ,\alpha ,\alpha \}$ for multisets $\{\alpha ,\alpha \}$ and $\{\alpha ,\alpha ,\alpha \}$. □

Definition 7. (Extension of vocabulary of $L_{\mathfrak{T}}$.)

If t is a term, then ${\left(t\right)}^{+}$ is a term, to be called “the singleton of t”—which may be written as $t^{+}$ if no confusion arises. In particular, if $\alpha$ is a variable ranging over all things and x a variable ranging over all sets, then ${\alpha }^{+}$ is a variable ranging over all singletons and $x^{+}$ a variable ranging over all singletons of sets. We thus have

$$\forall \alpha \forall \beta (\beta ={\alpha }^{+}\iff \exists X(\beta =X\wedge \forall \gamma (\gamma \in X\iff \gamma =\alpha )))$$

(23)

Likewise for $x^{+}$. □

Notation 1.

On account of Definition 7, the constants ${\varnothing }^{+},{\varnothing }^{++},{\varnothing }^{+++},\dots$ are contained in the language $L_{\mathfrak{T}}$. Therefore, we can introduce the (finite) Zermelo ordinals at this point as a notation for these singletons:

$$\left\{\begin{array}{c}0:=\varnothing \hfill \\ 1:={\varnothing }^{+}\hfill \\ 2:={\varnothing }^{++}\hfill \\ ⋮\hfill \end{array}\right.$$

(24)

According to the literature, the idea stems from unpublished work by Zermelo in 1916 [23]. □

Remark 6.

Sum Set Axiom (SUM): for every set X there exists a set Y made up of the elements of the elements of X.

$$\forall X\exists Y\forall \alpha (\alpha \in Y\iff \exists Z(Z\in X\wedge \alpha \in Z\left)\right)$$

(25)

□

Remark 5.

Given an individual set $\underline{\mathbf{X}}$ in the universe of the intended model, the sum set of $\underline{\mathbf{X}}$ can be denoted by the symbol $\bigcup \underline{\mathbf{X}}$ and, using set-builder notation, can be identified with the individual $\left\{\alpha \right|\exists Z\in \underline{\mathbf{X}}(\alpha \in Z)\}$. □

Remark 7.

Powerset Axiom (POW): for every set X there is a set Y made up of the subsets of X.

$$\forall X\exists Y\forall \alpha (\alpha \in Y\iff \exists Z(Z\subset X\wedge \alpha =Z\left)\right)$$

(26)

□

Remark 6.

Given an individual set $\underline{\mathbf{X}}$ in the universe of the intended model, the powerset of $\underline{\mathbf{X}}$ can be denoted by the symbol $\mathcal{P}\left(\underline{\mathbf{X}}\right)$ and, using set-builder notation, be identified with the individual $\left\{x\right|x\subset \underline{\mathbf{X}}\}$. □

Remark 8.

Infinite Ordinal Axiom (INF): the infinite ordinal $\mathbf{\omega }$ is the set of all finite Zermelo ordinals.

$$0\in \mathbf{\omega }\wedge \forall \alpha (\alpha \in \mathbf{\omega }\Rightarrow {\alpha }^{+}\in \mathbf{\omega })\wedge \forall \beta \in \mathbf{\omega }(\cancel{\exists }\gamma \in \mathbf{\omega }(\beta ={\gamma }^{+})\iff \beta =\varnothing ))$$

(27)

□

Remark 7.

The set $\mathbf{\omega }$ in INF is uniquely determined. In the intended model, the set $\mathbf{\omega }$ can be denoted by the symbol $\mathbb{N}$ and, using set-builder notation, be identified with the individual $\mathbb{N}:=\left\{\right\{\},\{\left\{\right\}\},\{\left\{\right\{\left\}\right\}\},\dots \}$. □

Axiom 9.

Axiom of Regularity (REG): every nonempty set X contains an element $\alpha$ that has no elements in common with X.

$$\forall X\ne \varnothing \exists \alpha (\alpha \in X\wedge \forall \beta (\beta \in \alpha \Rightarrow \beta \notin X\left)\right)$$

(28)

□

Definition 8.

For any things that are $\alpha$ and $\beta$, the two-tuple$⟨\alpha ,\beta ⟩$ is the pair set of $\alpha$ and the pair set of $\alpha$ and $\beta$; using the iota-operator we get

$$⟨\alpha ,\beta ⟩:=ıx(\forall \gamma (\gamma \in x\iff \gamma =\alpha \vee \exists Z(\gamma =Z\wedge \forall \eta (\eta \in Z\iff \eta =\alpha \vee \eta =\beta \left)\right))$$

(29)

□

A simple corollary of Definition 8 is that for any things that are $\alpha$ and $\beta$, the two-tuple $⟨\alpha ,\beta ⟩$ always exists. There is, thus, no danger of nonsensical terms involved in the use of the iota-operator in Definition 8.

Remark 8.

Given individual things $\underline{\mathbf{\alpha }}$ and $\underline{\mathbf{\beta }}$ in the universe of the intended model, the two-tuple $⟨\underline{\mathbf{\alpha }},\underline{\mathbf{\beta }}⟩$ can, using set-builder notation, be identified with the individual $\{\underline{\mathbf{\alpha }},\{\underline{\mathbf{\alpha }},\underline{\mathbf{\beta }}\}\}$. □

In principle, these set-theoretical axioms suffice: the function-theoretical axioms in the next section provide other means for the construction of sets.

2.3. Standard Function-Theoretical Axioms

Axiom 10.

A function $f_X$ on a set X has no elements:

$$\forall X\forall f_X\forall \alpha (\alpha \notin f_X)$$

(30)

□

Remark 9.

One might think that Axiom 10 destroys the uniqueness of the empty set. However, that is not true. It is true that a function on a set X and the empty set share the property that they have no elements, but the empty set is the only set that has this property: Axiom 2 guarantees, namely, that a function on a set X is not a set! □

Axiom 11.

General Function-Theoretical Axiom (GEN-F): for any nonempty set X, any function $f_X$ has a set Y as domain and a set Z as codomain, and maps every element $\alpha$ in Y to a unique image $\beta$:

$$\forall X\forall f_X(X\ne \varnothing \Rightarrow \exists Y\exists Z(f_X:Y\twoheadrightarrow Z\wedge \forall \alpha \in Y\exists !\beta (f_X:\alpha \mapsto \beta )))$$

(31)

□

Axiom 12.

For any set X, any function $f_X$ has no other domain than X:

$$\forall X\forall f_X\forall \alpha (\alpha \ne X\Rightarrow \forall \xi (f_X:\alpha \cancel{\twoheadrightarrow }\xi ))$$

(32)

□

Axiom 13.

For any set X, any function $f_X$ does not take a thing outside X as argument:

$$\forall X\forall f_X\forall \alpha \notin X\forall \beta (f_X:\alpha \cancel{\mapsto }\beta )$$

(33)

□

Remark 10.

Axiom 11 dictates that precisely one expression $f_X:\alpha \mapsto \beta$ is true for each $\alpha \in X$. This does not a priori exclude that such an expression can also be true for another thing $\alpha$ not in X. However, by Axiom 13 this is excluded. □

Axiom 14.

For any nonempty set X and any function $f_X$, the image set is the only codomain:

$$\forall X\forall f_X(X\ne \varnothing \Rightarrow \forall \beta (f_X:X\twoheadrightarrow \beta \Rightarrow \exists Z(\beta =Z\wedge \forall \gamma (\gamma \in Z\iff \exists \eta \in X(f_X:\eta \mapsto \gamma )))))$$

(34)

(This is the justification for the use of the two-headed arrow “↠”, commonly used for surjections.) □

Remark 11.

Note that these first function-theoretical axioms already provide a tool to construct a set: if we can construct a new function $f_X$ on a set X from existing functions (an axiom will be given further below), then these axioms guarantee the existence of a unique codomain made up of all the images of the elements of X under $f_X$. □

Remark 12.

Given an individual set $\underline{\mathbf{X}}$ and an individual function ${\underline{\mathbf{f}}}_{\underline{\mathbf{X}}}$ in the universe of the intended model, this unique codomain can be denoted by ${\underline{\mathbf{f}}}_{\underline{\mathbf{X}}}\left[\underline{\mathbf{X}}\right]$ or $\mathrm{cod}\left({\underline{\mathbf{f}}}_{\underline{\mathbf{X}}}\right)$, and, using set-builder notation, be identified with the individual $\left\{\beta \right|\exists \alpha \in \underline{\mathbf{X}}({\underline{\mathbf{f}}}_{\underline{\mathbf{X}}}:\alpha \mapsto \beta )\}$ in the universe of the intended model. Furthermore, given a thing $\underline{\mathbf{\alpha }}$ in $\underline{\mathbf{X}}$, its unique image under ${\underline{\mathbf{f}}}_{\underline{\mathbf{X}}}$ can be denoted by the symbol ${\underline{\mathbf{f}}}_{\underline{\mathbf{X}}}\left(\underline{\mathbf{\alpha }}\right)$. □

Notation 2.

At this point we can introduce expressions $f_X:X\to Y$, to be read as “the function f-on-X is a function from the set X to the set Y”, by the postulate of meaning

$$f_X:X\to Y\iff \exists Z(f_X:X\twoheadrightarrow Z\wedge Z\subset Y)$$

(35)

This provides a connection to existing mathematical practices. □

Axiom 15.

Inverse Image Set Axiom (INV): for any nonempty set X and any function $f_X$ with domain X and any co-domain Y, there is for any thing $\alpha$ a set $Z\subset X$ that contains precisely the elements of X that are mapped to $\alpha$ by $f_X$:

$$\forall X\ne \varnothing \forall f_X\forall Y(f_X:X\twoheadrightarrow Y\Rightarrow \forall \beta \exists Z\forall \alpha (\alpha \in Z\iff \alpha \in X\wedge f_X:\alpha \mapsto \beta ))$$

(36)

□

Remark 13.

Note that INV, in addition to GEN-F, also provides a tool to construct a set: if we have constructed a new function $f_X$ with domain X from existing functions, then with this axiom guarantees that the inverse image set exists of any thing $\beta$ in the codomain of $f_X$. □

Remark 14.

Given an individual set $\underline{\mathbf{X}}$, an individual function ${\underline{\mathbf{f}}}_{\underline{\mathbf{X}}}$, and an individual thing $\underline{\mathbf{\beta }}$ in the universe of the intended model, the unique inverse image set can be denoted by the symbol ${\underline{\mathbf{f}}}_{\underline{\mathbf{X}}}^{-1}\left(\underline{\mathbf{\beta }}\right)$ and can, using set-builder notation, be identified with the individual $\left\{\alpha \right|\alpha \in \underline{\mathbf{X}}\wedge {\underline{\mathbf{f}}}_{\underline{\mathbf{X}}}:\alpha \mapsto \underline{\mathbf{\beta }}\}$ in the universe of the intended model. □

Axiom 16.

Extensionality Axiom for Functions (EXT-F): for any set X and any function $f_X$, and for any set Y and any function $g_Y$, the function $f_X$ and the function $g_Y$ are identical if and only if their domains are identical and their images are identical for every argument:

$$\forall X\forall f_X\forall Y\forall g_Y(f_X=g_Y\iff X=Y\wedge \forall \alpha \forall \beta (f_X:\alpha \mapsto \beta \iff g_Y:\alpha \mapsto \beta ))$$

(37)

□

Axiom 17.

Inactive Function Axiom (IN-F): there exists a function $f_{\varnothing }$, denoted by the constant $1_{\varnothing }$, which has the empty set as domain and codomain, and which does not map any argument to any image:

$$\exists f_{\varnothing }(f_{\varnothing }=1_{\varnothing }\wedge f_{\varnothing }:\varnothing \twoheadrightarrow \varnothing \wedge \forall \alpha \forall \beta (f_{\varnothing }:\alpha \cancel{\mapsto }\beta ))$$

(38)

□

Note that there can be no other functions on the empty set than the inactive function $1_{\varnothing }$, since the image set is always empty: the atomic expression $f_{\varnothing }:\varnothing \twoheadrightarrow A$ cannot be true for any nonempty set A.

Axiom 18.

Ur-Function Axiom (UFA): for any things $\alpha$ and $\beta$ there exists an ur-function $f_{{\alpha }^{+}}$ with domain ${\alpha }^{+}$ and codomain ${\beta }^{+}$ that maps $\alpha$ to $\beta$:

$$\forall \alpha \forall \beta \exists f_{{\alpha }^{+}}(f_{{\alpha }^{+}}:{\alpha }^{+}\twoheadrightarrow {\beta }^{+}\wedge f_{{\alpha }^{+}}:\alpha \mapsto \beta )$$

(39)

□

Remark 15.

Given individual things $\underline{\mathbf{\alpha }}$ and $\underline{\mathbf{\beta }}$ in the universe of the intended model, the ur-function on $\left\{\underline{\mathbf{\alpha }}\right\}$ that maps $\underline{\mathbf{\alpha }}$ to $\underline{\mathbf{\beta }}$ can, using set-builder notation, be identified with the individual ${\left\{⟨\underline{\mathbf{\alpha }},\underline{\mathbf{\beta }}⟩\right\}}_{\left\{\underline{\mathbf{\alpha }}\right\}}$ in the universe of the intended model. Note that the graph of the ur-function is guaranteed to exist. □

Axiom 19.

Axiom of Regularity for Functions (REG-F): for any set X and any function $f_X$ with any codomain Y, $f_X$ does not take itself as argument or has itself as image:

$$\forall X\forall f_X\forall Y(f_X:X\twoheadrightarrow Y\Rightarrow \forall \alpha (f_X:f_X\cancel{\mapsto }\alpha \wedge f_X:\alpha \cancel{\mapsto }{f}_X))$$

(40)

□

Remark 16.

As to the first part, Wittgenstein already mentioned that a function cannot have itself as argument [24]. The second part is to exclude the existence of pathological “Siamese twin functions”, e.g., the ur-function $f_X$ and $g_Y$ given, using set-builder notation, by

$$\begin{array}{c}{f}_X:\left\{h_Y\right\}\twoheadrightarrow \left\{f_X\right\},f_X:h_Y\mapsto f_X\end{array}$$

(41)

$$\begin{array}{c}{h}_Y:\left\{f_X\right\}\twoheadrightarrow \left\{h_Y\right\},g_Y:f_X\mapsto g_Y\end{array}$$

(42)

We thus have $\mathrm{dom}\left(f_X\right)=X=\left\{h_Y\right\}$ and $\mathrm{dom}\left(h_Y\right)=Y=\left\{f_X\right\}$; if one tries to substitute that in the above equations, then one gets “infinite towers”. These functions may not be constructible from the axioms, but they could exist a priori in the category of sets and functions: to avoid that, we practice mathematical eugenics and prevent them from occurring with REG-F. See Figure 1 for an illustration. The name “Siamese twin functions” is derived from the name “Siamese twin sets” for sets A and B satisfying $A\in B\wedge B\in A$, as published by Muller in [25]. □

Figure 1. Venn diagram of the Siamese twin functions $f_X$ and $h_Y$. The left oval together with the black point inside it is a Venn diagram representing the singleton $\left\{f_X\right\}$; the right oval together with the black point inside it is a Venn diagram representing the singleton $\left\{h_y\right\}$. The upper arrow represents the mapping of $f_X$ to $h_Y$ by $h_Y$, the lower arrow the mapping of $h_Y$ to $f_X$ by $f_X$.

2.4. The Non-Classical Function-Theoretical Axiom and Inference Rules

Definition 9.

The vocabulary of $L_{\mathfrak{T}}$ as given by Definition 2 is extended:

(i)

With symbols “ı”, the iota-operator, and “⋀”, the conjunctor;

(ii)

For any constant $\widehat{\mathbf{X}}$ denoting a set, with enough composite symbols ${\widehat{\mathbf{f}}}_{{\alpha }^{+}}$, ${\widehat{\mathbf{h}}}_{{\beta }^{+}}$, … such that each of these is a variable that ranges over a family of ur-functions indexed in $\widehat{\mathbf{X}}$.

The syntax of $L_{\mathfrak{T}}$ as given by Definition 3 is extended with the following clauses:

(iii)

If ${\widehat{\mathbf{f}}}_{{\alpha }^{+}}$ is a variable as in clause (ii) of Definition 9, then ${\widehat{\mathbf{f}}}_{{\alpha }^{+}}$ is a term;

(iv)

If t is a term and $u_{t^{+}}$ is a composite term with an occurrence of t, and $\beta$ is a variable ranging over all things, then $ı\beta (u_{t^{+}}:t\mapsto \beta )$ is a iota-term denoting the image of t under the ur-function $u_{t^{+}}$;

(v)

If $\widehat{\mathbf{X}}$ is a constant designating a set, $\alpha$ a simple variable ranging over all things, and $\Psi \left(\alpha \right)$ an atomic formula of the type $t:t^{\prime }\mapsto t^{\prime \prime }$ that is open in $\alpha$, then ${\bigwedge }_{\alpha \in \widehat{\mathbf{X}}}\Psi \left(\alpha \right)$ is a formula;

(vi)

If $\Phi$ is a formula with a subformula ${\bigwedge }_{\alpha \in \widehat{\mathbf{X}}}\Psi \left(\alpha \right)$ as in (v) with an occurrence of a composite variable $f_{{\alpha }^{+}}$, then ${(\forall f_{{\alpha }^{+}})}_{\alpha \in \widehat{\mathbf{X}}}\Phi$ and ${(\exists f_{{\alpha }^{+}})}_{\alpha \in \widehat{\mathbf{X}}}\Phi$ are formulas;

(vii)

If X is a simple variable ranging over sets, and $\Psi$ a formula with no occurrence of X but with a subformula ${(\forall f_{{\alpha }^{+}})}_{\alpha \in \widehat{\mathbf{X}}}\Phi$ as in (vi), then $\forall X[X\backslash \widehat{\mathbf{X}}]\Psi$ and $\exists X[X\backslash \widehat{\mathbf{X}}]\Psi$ are formulas with a subformula ${(\forall f_{{\alpha }^{+}})}_{\alpha \in X}[X\backslash \widehat{\mathbf{X}}]\Phi$;

(viii)

If X is a simple variable ranging over sets, and $\Psi$ a formula with no occurrence of X but with a subformula ${(\exists f_{{\alpha }^{+}})}_{\alpha \in \widehat{\mathbf{X}}}\Phi$ as in (vi), then $\forall X[X\backslash \widehat{\mathbf{X}}]\Psi$ and $\exists X[X\backslash \widehat{\mathbf{X}}]\Psi$ are formulas with a subformula ${(\exists f_{{\alpha }^{+}})}_{\alpha \in X}[X\backslash \widehat{\mathbf{X}}]\Phi$. □

Remark 17.

Concerning the iota-operator in clause (iv) of Definition 9, we thus have

$$\forall \alpha \forall f_{{\alpha }^{+}}\forall \gamma (\gamma =ı\beta (f_{{\alpha }^{+}}:\alpha \mapsto \beta )\iff f_{{\alpha }^{+}}:\alpha \mapsto \gamma )$$

(43)

Note that upon assigning constant values to $\alpha$ and $f_{{\alpha }^{+}}$, the term $ı\beta (f_{{\alpha }^{+}}:\alpha \mapsto \beta )$ always refers to an existing, unique thing: there is thus no danger of nonsensical terms involved in this use of the iota-operator. □

Definition 10.

The following special language elements are added:

(i)

If $\widehat{\mathbf{X}}$ is a constant designating a set, X and $\alpha$ simple variables ranging over sets c.q. things, and $f_{{\alpha }^{+}}$ a composite variable ranging over ur-functions on ${\alpha }^{+}$, then

• ${(\forall f_{{\alpha }^{+}})}_{\alpha \in \widehat{\mathbf{X}}}$ is a multiple universal quantifier;
• ${(\exists f_{{\alpha }^{+}})}_{\alpha \in \widehat{\mathbf{X}}}$ is a multiple existential quantifier;
• ${(\forall f_{{\alpha }^{+}})}_{\alpha \in X}$ in the scope of a quantifier $\forall X$ is a universally generalized multiple universal quantifier;
• ${(\forall f_{{\alpha }^{+}})}_{\alpha \in X}$ in the scope of a quantifier $\exists X$ is an existentially generalized multiple universal quantifier;
• ${(\exists f_{{\alpha }^{+}})}_{\alpha \in X}$ in the scope of a quantifier $\forall X$ is a universally generalized multiple existential quantifier;
• ${(\exists f_{{\alpha }^{+}})}_{\alpha \in X}$ in the scope of a quantifier $\exists X$ is an existentially generalized multiple existential quantifier;

(ii)

If $\widehat{\mathbf{X}}$ is a constant designating a set, X a simple variable ranging over sets, and $\alpha$ a simple variable ranging over all things, then

• ${\bigwedge }_{\alpha \in \widehat{\mathbf{X}}}$ is a conjunctive operator with constant range;
• ${\bigwedge }_{\alpha \in X}$ is a conjunctive operator with variable range. □

Concerning the language elements in clause (i), if ʞ and ${ʞ}^{\prime }$ are existential or universal quantification symbols, then we can generally say that ${(ʞf_{{\alpha }^{+}})}_{\alpha \in \widehat{\mathbf{X}}}$ is a multiple quantifier and that ${(ʞf_{{\alpha }^{+}})}_{\alpha \in X}$ in the scope of a quantifier ${ʞ}^{\prime }X$ is a generalized multiple quantifier.

Definition 11.

If $\widehat{\mathbf{X}}$ is a constant designating a set and ${\bigwedge }_{\alpha \in \widehat{\mathbf{X}}}\Psi$ is a subformula of a formula $\Phi$, then $\Psi$ is the scope of the conjunctive operator; furthermore,

(i)

If there is an occurrence of a variable $\alpha$ and/or ${\widehat{\mathbf{f}}}_{{\alpha }^{+}}$ in the scope of the conjunctive operator, then a formula ${\bigwedge }_{\alpha \in \widehat{\mathbf{X}}}\Psi$ has a semantic occurrence of each of the constants $\widehat{\alpha }$ referring to a thing in the range of the variable $\alpha$, and/or of each of the constant ur-functions ${\widehat{\mathbf{u}}}_{{\widehat{\alpha }}^{+}}$ over which the variable ${\widehat{\mathbf{f}}}_{{\alpha }^{+}}$ ranges—a subformula ${\bigwedge }_{\alpha \in \widehat{\mathbf{X}}}\Psi$ has thus to be viewed as the conjunction of all the formulas $[\widehat{\alpha }\backslash \alpha ]{[{\widehat{\mathbf{u}}}_{{\widehat{\alpha }}^{+}}\backslash \widehat{\mathbf{f}}]}_{{\alpha }^{+}}]\Psi$ with $\widehat{\alpha }\in \widehat{\mathbf{X}}$.

(ii)

If there is an occurrence of a composite variable $f_{{\alpha }^{+}}$ in the scope of the conjunctive operator, then the subformula ${\bigwedge }_{\alpha \in \widehat{\mathbf{X}}}\Psi \left(f_{{\alpha }^{+}}\right)$ has a free semantic occurrence of each of the simple variables $f_{{\widehat{\alpha }}^{+}}$ ranging over ur-functions on the singleton of $\widehat{\alpha }$ with $\widehat{\alpha }\in \widehat{\mathbf{X}}$—the formula ${\bigwedge }_{\alpha \in \widehat{\mathbf{X}}}\Psi \left(f_{{\alpha }^{+}}\right)$ has thus to be viewed as the conjunction of all the formulas $[\widehat{\alpha }\backslash \alpha ][f_{{\widehat{\alpha }}^{+}}\backslash f_{{\alpha }^{+}}]\Psi$. □

Definition 12.

If $\widehat{\mathbf{X}}$ is a constant designating a set, ʞ an existential or universal quantification symbol, and ${(ʞf_{{\alpha }^{+}})}_{\alpha \in \widehat{\mathbf{X}}}\Psi$ a subformula of a formula $\Phi$, then $\Psi$ is the scope of the multiple quantifier; likewise for the scope of the generalized multiple quantifiers of Definition 10. If a formula $\Psi$ has a free semantic occurrence of each of the simple variables $f_{{\widehat{\alpha }}^{+}}$ with a constant $\widehat{\alpha }\in \widehat{\mathbf{X}}$, then a formula ${(ʞf_{{\alpha }^{+}})}_{\alpha \in \widehat{\mathbf{X}}}\Psi$ has a bounded semantic occurrence of each of the simple variables $f_{{\widehat{\alpha }}^{+}}$ with a constant $\widehat{\alpha }\in \widehat{\mathbf{X}}$. A non-classical formula $\Psi$ without free occurrences of variables is a sentence. If X is a simple variable ranging over sets and $\Psi$ is a sentence with an occurrence of a multiple quantifier ${(ʞf_{{\alpha }^{+}})}_{\alpha \in \widehat{\mathbf{X}}}$ and with no occurrence of X, then $\forall X[X\backslash \widehat{\mathbf{X}}]\Psi$ and $\exists X[X\backslash \widehat{\mathbf{X}}]\Psi$ are sentences with an occurrence of a generalized multiple quantifier ${(ʞf_{{\alpha }^{+}})}_{\alpha \in X}$. □

Axiom 20.

Sum Function Axiom (SUM-F): for any nonempty set X and for any family of ur-functions $f_{{\alpha }^{+}}$ indexed in X, there is a sum function $F_X$ with some codomain Y such that the conjunction of all mappings by $F_X$ of $\alpha$ to its image under the ur-function $f_{{\alpha }^{+}}$ holds for $\alpha$ ranging over X:

$$\forall X\ne \varnothing {(\forall f_{{\alpha }^{+}})}_{\alpha \in X}\exists F_X\exists Y\left(F_X:X\twoheadrightarrow Y\wedge {\bigwedge }_{\alpha \in X}{F}_X:\alpha \mapsto ı\beta (f_{{\alpha }^{+}}:\alpha \mapsto \beta )\right)$$

(44)

□

With SUM-F, all non-logical axioms of the present non-classical theory have been introduced. However, still, rules of inference must be given to derive meaningful theorems from SUM-F. So, the rules of inference that follow have to be seen as part of the logic.

Inference Rule 1.

Nonstandard Universal Elimination:

$$\forall X\Psi \left({(ʞf_{{\alpha }^{+}})}_{\alpha \in X},{\bigwedge }_{\alpha \in X}\right)⊢[\widehat{\mathbf{X}}\backslash X]\Psi \mathrm{for}\mathrm{any}\mathrm{constant}\widehat{\mathbf{X}}$$

(45)

where $\Psi \left({(ʞf_{{\alpha }^{+}})}_{\alpha \in X},{\bigwedge }_{\alpha \in X}\right)$ is a formula with an occurrence of a generalized multiple quantifier and of a conjunctive operator with variable range, and where $[\widehat{\mathbf{X}}\backslash X]\Psi$ is a formula with an occurrence of a multiple quantifier ${(ʞf_{{\alpha }^{+}})}_{\alpha \in \widehat{\mathbf{X}}}$ and of a conjunctive operator ${\bigwedge }_{\alpha \in \widehat{\mathbf{X}}}$ with constant range. □

Thus speaking, from SUM-F we can deduce a formula

$${(\forall f_{{\alpha }^{+}})}_{\alpha \in \widehat{\mathbf{X}}}\exists F_{\widehat{\mathbf{X}}}\exists Y\left(F_{\widehat{\mathbf{X}}}:\widehat{\mathbf{X}}\twoheadrightarrow Y\wedge {\bigwedge }_{\alpha \in \widehat{\mathbf{X}}}{F}_{\widehat{\mathbf{X}}}:\alpha \mapsto ı\beta (f_{{\alpha }^{+}}:\alpha \mapsto \beta )\right)$$

(46)

for any constant $\widehat{\mathbf{X}}$ designating a set.

Inference Rule 2.

Multiple Universal Elimination:

$${(\forall f_{{\alpha }^{+}})}_{\alpha \in \widehat{\mathbf{X}}}\Phi \left(f_{{\alpha }^{+}}\right)⊢[{\widehat{\mathbf{f}}}_{{\alpha }^{+}}\backslash f_{{\alpha }^{+}}]\Phi$$

(47)

where $\Phi \left(f_{{\alpha }^{+}}\right)$ is a formula with an occurrence of the same composite variable $f_{{\alpha }^{+}}$ that also occurs in the preceding multiple universal quantifier ${(\forall f_{{\alpha }^{+}})}_{\alpha \in \widehat{\mathbf{X}}}$, and where ${\widehat{\mathbf{f}}}_{{\alpha }^{+}}$ is a variable as meant in clause (ii) of Definition 9. □

Thus speaking, from a sentence (46), which is an instance of SUM-F derived by inference rule 1, we can derive a formula

$$\exists F_{\widehat{\mathbf{X}}}\exists Y\left(F_{\widehat{\mathbf{X}}}:\widehat{\mathbf{X}}\twoheadrightarrow Y\wedge {\bigwedge }_{\alpha \in \widehat{\mathbf{X}}}{F}_{\widehat{\mathbf{X}}}:\alpha \mapsto ı\beta ({\widehat{\mathbf{f}}}_{{\alpha }^{+}}:\alpha \mapsto \beta )\right)$$

(48)

for each variable ${\widehat{\mathbf{f}}}_{{\alpha }^{+}}$ ranging over a family of ur-functions indexed in $\widehat{\mathbf{X}}$. Note that the range of such a variable ${\widehat{\mathbf{f}}}_{{\alpha }^{+}}$ is constructed by assigning to each of the simple variables $f_{{\widehat{\alpha }}^{+}}$ semantically occurring in Formula (46) a constant value ${\widehat{\mathbf{u}}}_{{\widehat{\alpha }}^{+}}$.

Inference Rule 3.

Nonstandard Rule-C:

$$\exists t\Phi ⊢[\widehat{\mathbf{t}}\backslash t]\Phi$$

(49)

where t is a simple variable x ranging over sets or a simple variable $f_{\widehat{\mathbf{X}}}$ ranging over functions on a constant set, and where $\widehat{\mathbf{t}}$ is a constant in the range of t that does not occur in $\Phi$ but for which $[\widehat{\mathbf{t}}\backslash t]\Phi$ holds. If $\Phi$ has an occurrence of a generalized multiple quantifier ${(ʞf_{{\alpha }^{+}})}_{\alpha \in t}$, then $[\widehat{\mathbf{t}}\backslash t]\Phi$ has an occurrence of a multiple quantifier ${(ʞf_{{\alpha }^{+}})}_{\alpha \in \widehat{\mathbf{t}}}$; if $\Phi$ has an occurrence of a conjunctive operator ${\bigwedge }_{\alpha \in t}$ with variable range, then $[\widehat{\mathbf{t}}\backslash t]\Phi$ has an occurrence of a conjunctive operator ${\bigwedge }_{\alpha \in \widehat{\mathbf{t}}}$ with constant range. □

Thus speaking, from SUM-F we can deduce a formula

$$\exists Y({\widehat{\mathbf{F}}}_{\widehat{\mathbf{X}}}:\widehat{\mathbf{X}}\twoheadrightarrow Y)\wedge {\bigwedge }_{\alpha \in \widehat{\mathbf{X}}}{\widehat{\mathbf{F}}}_{\widehat{\mathbf{X}}}:\alpha \mapsto ı\beta ({\widehat{\mathbf{f}}}_{{\alpha }^{+}}:\alpha \mapsto \beta )$$

(50)

which is a conjunction of a standard first-order formula and a non-classical formula with an occurrence of the new constant ${\widehat{\mathbf{F}}}_{\widehat{\mathbf{X}}}$, designating the sum function on $\widehat{\mathbf{X}}$, in the scope of a conjunctive operator. Of course, this conjunction $\Psi \wedge \Phi$ is true if and only if both its members are true. This requires one more inference rule.

Inference Rule 4.

Conjunctive Operator Elimination:

$${\bigwedge }_{\alpha \in \widehat{\mathbf{X}}}\Psi \left(\alpha \right)⊢[\widehat{\alpha }\backslash \alpha ]\Psi \left(\alpha \right)$$

(51)

where $\Psi \left(\alpha \right)$ is a formula of the type $t:t^{\prime }\mapsto t^{\prime \prime }$ that is open in $\alpha$, and $\widehat{\alpha }$ any constant designating an element of $\widehat{\mathbf{X}}$. □

Thus speaking, from the right member of the conjunction (50) we can derive an entire schema, consisting of one standard first-order formula

$${\widehat{\mathbf{F}}}_{\widehat{\mathbf{X}}}:\widehat{\alpha }\mapsto ı\beta ({\widehat{\mathbf{u}}}_{{\widehat{\alpha }}^{+}}:\widehat{\alpha }\mapsto \beta )$$

(52)

for each constant ${\widehat{\mathbf{u}}}_{{\widehat{\alpha }}^{+}}$. So given an infinitary conjunction ${\bigwedge }_{\alpha \in \widehat{\mathbf{X}}}{\widehat{\mathbf{F}}}_{\widehat{\mathbf{X}}}:\alpha \mapsto ı\beta ({\widehat{\mathbf{f}}}_{{\alpha }^{+}}:\alpha \mapsto \beta )$, the sentences (52) derived by rule 4 are true for each constant ${\widehat{\mathbf{u}}}_{{\widehat{\alpha }}^{+}}$ semantically occurring in Equation (50).

Remark 18.

Given an individual set $\underline{\mathbf{X}}$ and a variable ${\underline{\mathbf{f}}}_{{\alpha }^{+}}$ that ranges over a family of ur-functions indexed in $\underline{\mathbf{X}}$ in the universe of the intended model, the unique sum function ${\underline{\mathbf{F}}}_{\underline{\mathbf{X}}}$ for which

$${\bigwedge }_{\alpha \in \underline{\mathbf{X}}}{\underline{\mathbf{F}}}_{\underline{\mathbf{X}}}:\alpha \mapsto ı\beta ({\underline{\mathbf{f}}}_{{\alpha }^{+}}:\alpha \mapsto \beta )$$

(53)

can, using set-builder notation, be identified with the individual

$${\underline{\mathbf{F}}}_{\underline{\mathbf{X}}}={\left\{⟨\alpha ,\beta ⟩\right|\alpha \in \underline{\mathbf{X}}\wedge \beta ={\underline{\mathbf{f}}}_{{\alpha }^{+}}\left(\alpha \right)\}}_{\underline{\mathbf{X}}}$$

(54)

in the universe of the intended model. The graph of ${\underline{\mathbf{F}}}_{\underline{\mathbf{X}}}$, which can be identified with the set $\left\{⟨\alpha ,\beta ⟩\right|\alpha \in \underline{\mathbf{X}}\wedge \beta ={\underline{\mathbf{f}}}_{{\alpha }^{+}}\left(\alpha \right)\}$, is certain to exist, see Theorem 1 (next section). So, constructing a sum function is a means to constructing a set. □

Example 1.

Consider the infinite ordinal $\mathbf{\omega }$ from Axiom 8: its elements are the finite ordinals 0, 1, 2, … Applying Nonstandard Universal Elimination, we thus deduce from SUM-F that

$${(\forall f_{{\alpha }^{+}})}_{\alpha \in \mathbf{\omega }}\exists F_{\mathbf{\omega }}\exists Y\left(F_{\mathbf{\omega }}:\mathbf{\omega }\twoheadrightarrow Y\wedge {\bigwedge }_{\alpha \in \mathbf{\omega }}{F}_{\mathbf{\omega }}:\alpha \mapsto ı\beta (f_{\left\{\alpha \right\}}:\alpha \mapsto \beta )\right)$$

(55)

On account of the ur-function Axiom 18 we have

$$\forall x\in \mathbf{\omega }\exists f_{x^{+}}(f_{x^{+}}:x\mapsto x)$$

(56)

That is, for any finite ordinal x there is an ur-function that on the singleton of x that maps x to itself. Let the variable ${\widehat{\mathbf{f}}}_{{\alpha }^{+}}^1$ range over these identity ur-functions; applying Multiple Universal Elimination to the sentence (55) then yields a sentence

$$\exists F_{\mathbf{\omega }}\exists Y\left(F_{\mathbf{\omega }}:\mathbf{\omega }\twoheadrightarrow Y\wedge {\bigwedge }_{\alpha \in \mathbf{\omega }}{F}_{\mathbf{\omega }}:\alpha \mapsto ı\beta ({\widehat{\mathbf{f}}}_{{\alpha }^{+}}^1:\alpha \mapsto \beta )\right)$$

(57)

Introducing the new constant $1_{\mathbf{\omega }}$ by applying Rule-C to the sentence (57) and substituting $ı\beta ({\widehat{\mathbf{f}}}_{{\alpha }^{+}}^1:\alpha \mapsto \beta )=\alpha$ then yields the conjunction

$$1_{\mathbf{\omega }}:\mathbf{\omega }\twoheadrightarrow \mathbf{\omega }\wedge {\bigwedge }_{\alpha \in \mathbf{\omega }}{1}_{\mathbf{\omega }}:\alpha \mapsto \alpha )$$

(58)

By applying Conjunctive Operator Elimination to the right member of this conjunction (58), we obtain the countable schema

$$\left\{\begin{array}{c}{1}_{\mathbf{\omega }}:0\mapsto 0\hfill \\ 1_{\mathbf{\omega }}:1\mapsto 1\hfill \\ 1_{\mathbf{\omega }}:2\mapsto 2\hfill \\ ⋮\hfill \end{array}\right.$$

(59)

This example demonstrates, strictly within the language of $\mathfrak{T}$, how SUM-F and the inference rules can be used to construct the identity function on $\mathbf{\omega }$ from a family of ur-functions indexed in $\mathbf{\omega }$. □

Remark 19.

Summarizing, it has thus to be taken:

(i)

That SUM-F is a typographically finite sentence;

(ii)

That an instance (46) of SUM-F, deduced by applying Nonstandard Universal Elimination, is a typographically finite sentence;

(iii)

That a Formula (48), deduced from an instance of SUM-F by applying Multiple Universal Elimination, is a typographically finite sentence;

(iv)

That a conjunction (50), deduced by applying Rule-C to a sentence deduced from SUM-F by successively applying Nonstandard Universal Elimination and Multiple Universal Elimination, is a typographically finite sentence.

We thus get that SUM-F being true means that every instance (46) of SUM-F obtained by Nonstandard Universal Elimination is true; that an instance (46) of SUM-F being true means that for any variable ${\widehat{\mathbf{f}}}_{{\alpha }^{+}}$ ranging over a family of ur-functions indexed in $\widehat{\mathbf{X}}$, Formula (48) is true; and that a non-classical Formula (48) with an occurrence of a variable ${\widehat{\mathbf{f}}}_{{\alpha }^{+}}$ being true means that, after applying Rule-C, the schema of standard formulas (52) obtained by Conjunctive Operator Elimination is true—one true standard formula obtains for every ur-function ${\widehat{\mathbf{u}}}_{{\widehat{\alpha }}^{+}}$ in the range of the variable ${\widehat{\mathbf{f}}}_{{\alpha }^{+}}$. □

This concludes the axiomatic introduction of the non-classical theory $\mathfrak{T}$. Since we are primarily interested in the theorems that can be derived from the axioms of $\mathfrak{T}$, no rules have been given for the introduction of (multiple) quantifiers or conjunctive operators. Below such rules are given for the sake of completeness, but these will not be discussed. (These rules are not a part of the current axiomatic system, but we can consider adding these rules if we want to extend the current system.)

Inference Rule 5.

Conjunctive Operator Introduction:

$${\left\{\right[I\left(\alpha \right)\backslash \alpha ]\Psi (\alpha \left)\right\}}_{I\left(\alpha \right)\in \widehat{\mathbf{X}}}⊢{\bigwedge }_{\alpha \in \widehat{\mathbf{X}}}\Psi \left(\alpha \right)$$

(60)

where $\Psi \left(\alpha \right)$ is a formula of the type $t:t^{\prime }\mapsto t^{\prime \prime }$ that is open in $\alpha$, and ${\left\{\right[I\left(\alpha \right)\backslash \alpha ]\Psi (\alpha \left)\right\}}_{I\left(\alpha \right)\in \widehat{\mathbf{X}}}$ is a possibly infinite collection of formulas, each of which is obtained by interpreting the variable $\alpha$ as a constant $I\left(\alpha \right)\in \widehat{\mathbf{X}}$ and replacing $\alpha$ in $\Psi \left(\alpha \right)$ everywhere by $I\left(\alpha \right)$. □

Note that the collection of formulas ${\left\{\right[I\left(\alpha \right)\backslash \alpha ]\Psi (\alpha \left)\right\}}_{I\left(\alpha \right)\in \widehat{\mathbf{X}}}$ in Equation (60) is itself not a well-formed formula of the language $L_{\mathfrak{T}}$, but each of the formulas in the collection is.

Inference Rule 6.

Multiple Universal Introduction:

$$\Phi \left({\bigwedge }_{\alpha \in \widehat{\mathbf{X}}}\Psi \left({\widehat{\mathbf{f}}}_{{\alpha }^{+}}\right)\right)⊢{(\forall f_{{\alpha }^{+}})}_{\alpha \in \widehat{\mathbf{X}}}[f_{{\alpha }^{+}}\backslash {\widehat{\mathbf{f}}}_{{\alpha }^{+}}]\Phi$$

(61)

where $\Phi \left({\bigwedge }_{\alpha \in \widehat{\mathbf{X}}}\Psi \left({\widehat{\mathbf{f}}}_{{\alpha }^{+}}\right)\right)$ denotes a formula $\Phi$ with a subformula ${\bigwedge }_{\alpha \in \widehat{\mathbf{X}}}\Psi \left({\widehat{\mathbf{f}}}_{{\alpha }^{+}}\right)$ (implying that $\Psi$ is an atomic formula of the type $t:t^{\prime }\mapsto t^{\prime \prime }$), and where the variable ${\widehat{\mathbf{f}}}_{{\alpha }^{+}}$ ranges over an arbitrary family of ur-functions indexed in $\widehat{\mathbf{X}}$. □

Inference Rule 7.

Multiple Existential Introduction:

$$\Phi \left({\bigwedge }_{\alpha \in \widehat{\mathbf{X}}}\Psi \left({\widehat{\mathbf{f}}}_{{\alpha }^{+}}\right)\right)⊢{(\exists f_{{\alpha }^{+}})}_{\alpha \in \widehat{\mathbf{X}}}[f_{{\alpha }^{+}}\backslash {\widehat{\mathbf{f}}}_{{\alpha }^{+}}]\Phi$$

(62)

where $\Phi \left({\bigwedge }_{\alpha \in \widehat{\mathbf{X}}}\Psi \left({\widehat{\mathbf{f}}}_{{\alpha }^{+}}\right)\right)$ denotes a formula $\Phi$ with a subformula ${\bigwedge }_{\alpha \in \widehat{\mathbf{X}}}\Psi \left({\widehat{\mathbf{f}}}_{{\alpha }^{+}}\right)$ (implying that $\Psi$ is an atomic formula of the type $t:t^{\prime }\mapsto t^{\prime \prime }$), and where the variable ${\widehat{\mathbf{f}}}_{{\alpha }^{+}}$ ranges over a specific family of ur-functions indexed in $\widehat{\mathbf{X}}$. □

Remark 20.

Nonstandard Universal Quantification, i.e., the rule

$$\Psi \left(\widehat{\mathbf{X}}\right)⊢\forall X[X\backslash \widehat{\mathbf{X}}]\Psi$$

(63)

for a non-classical formula $\Psi$ with an occurrence of an arbitrary constant $\widehat{\mathbf{X}}$, and Nonstandard Existential Quantification, i.e., the rule

$$\Psi \left(\widehat{\mathbf{X}}\right)⊢\exists X[X\backslash \widehat{\mathbf{X}}]\Psi$$

(64)

for a non-classical formula $\Psi$ with an occurrence of a specific constant $\widehat{\mathbf{X}}$, are the same as in the standard case, but with the understanding that upon quantification a multiple quantifier ${(ʞf_{{\alpha }^{+}})}_{\alpha \in \widehat{\mathbf{X}}}$ in $\Psi$ becomes a generalized multiple quantifier ${(ʞf_{{\alpha }^{+}})}_{\alpha \in X}$ in $[X\backslash \widehat{\mathbf{X}}]\Psi$, and a conjunctive operator ${\bigwedge }_{\alpha \in \widehat{\mathbf{X}}}$ with constant range in $\Psi$ becomes a conjunctive operator ${\bigwedge }_{\alpha \in X}$ with variable range in $[X\backslash \widehat{\mathbf{X}}]\Psi$. □

3. Discussion

3.1. Main theorems

Theorem 1.

Graph Theorem: for any set X and any function $f_X$ with any codomain Y, there is a set Z that is precisely the graph of the function $f_X$—that is, there is a set Z whose elements are precisely the two-tuples $⟨\alpha ,\beta ⟩$ made up of arguments and images of the function $f_X$. In a formula:

$$\forall X\forall f_X\forall Y\left(f_X:X\twoheadrightarrow Y\Rightarrow \exists Z\forall \zeta (\zeta \in Z\iff \exists \alpha \exists \beta (\zeta =⟨\alpha ,\beta ⟩\wedge f_X:\alpha \mapsto \beta )))\right)$$

(65)

□

Proof. 

Let $\widehat{\mathbf{X}}$ be an arbitrary set, and let the function ${\widehat{\mathbf{f}}}_{\widehat{\mathbf{X}}}$ be an arbitrary function on $\widehat{\mathbf{X}}$. On account of GEN-F (Axiom 11), for any $\alpha \in X$ there is then precisely one $\beta$ such that ${\widehat{\mathbf{f}}}_{\widehat{\mathbf{X}}}:\alpha \mapsto \beta$. Using Definition 8, there exists then for each $\alpha \in \widehat{\mathbf{X}}$ a singleton ${⟨\alpha ,\beta ⟩}^{+}$ such that ${\widehat{\mathbf{f}}}_{\widehat{\mathbf{X}}}:\alpha \mapsto \beta$. On account of the ur-function axiom (Axiom 18), there exists then also an ur-function $u_{{\alpha }^{+}}:{\alpha }^{+}\twoheadrightarrow {⟨\alpha ,\beta ⟩}^{+},u_{{\alpha }^{+}}:\alpha \mapsto ⟨\alpha ,\beta ⟩$ for each $\alpha \in \widehat{\mathbf{X}}$. Thus, on account of SUM-F there is a sum function ${\widehat{\mathbf{G}}}_{\widehat{\mathbf{X}}}$ with some codomain Z such that ${\widehat{\mathbf{G}}}_{\widehat{\mathbf{X}}}$ maps every $\alpha \in X$ precisely to the two-tuple $⟨\alpha ,\beta ⟩$ for which ${\widehat{\mathbf{f}}}_{\widehat{\mathbf{X}}}:\alpha \mapsto \beta$. On account of GEN-F, the codomain Z of ${\widehat{\mathbf{G}}}_{\widehat{\mathbf{X}}}$ exists, and on account of Axiom 14 it is unique: this codomain is precisely the graph of ${\widehat{\mathbf{f}}}_{\widehat{\mathbf{X}}}$. Since $\widehat{\mathbf{X}}$ and ${\widehat{\mathbf{f}}}_{\widehat{\mathbf{X}}}$ were arbitrary, the Graph Theorem follows from universal generalization. □

In the intended model of $\mathfrak{T}$, there is thus no risk involved in identifying a function f with the individual $\mathrm{graph}{\left(f\right)}_{\mathrm{dom}\left(f\right)}$, where $\mathrm{graph}\left(f\right)$ is the graph of f and $\mathrm{dom}\left(f\right)$ the domain of f, cf. Remark 18.

Theorem 2.

Main Theorem: for any nonempty set X, if there is a functional relation $\Phi (\alpha ,\beta )$ that relates every $\alpha$ in X to precisely one $\beta$, then there is a function $F_X$ with some codomain Y that maps every $\eta \in X$ to precisely that $\xi \in Y$ for which $\Phi (\eta ,\xi )$. In a formula, using the iota-operator:

$$\forall X\ne \varnothing (\forall \alpha \in X\exists !\beta \Phi (\alpha ,\beta )\Rightarrow \exists F_X\exists Y(F_X:X\twoheadrightarrow Y\wedge \forall \eta \in X(F_X:\eta \mapsto ı\xi \Phi (\eta ,\xi ))))$$

(66)

□

Proof. 

Let $\widehat{\mathbf{X}}$ be an arbitrary nonempty set. Suppose then, that for every $\alpha \in \widehat{\mathbf{X}}$ we have precisely one $\beta$ such that $\Phi (\alpha ,\beta )$. On account of the ur-function axiom (Axiom 18), for an arbitrary constant $\widehat{\mathit{\alpha }}\in \widehat{\mathbf{X}}$ there exists then also an ur-function ${\widehat{\mathbf{u}}}_{{\widehat{\mathit{\alpha }}}^{+}}$ for which

$${\widehat{\mathbf{u}}}_{{\widehat{\mathit{\alpha }}}^{+}}:\widehat{\mathit{\alpha }}\mapsto ı\beta \Phi (\widehat{\mathit{\alpha }},\beta )$$

(67)

Let the variable ${\widehat{\mathbf{f}}}_{{\alpha }^{+}}$ range over these ur-functions. We then deduce from SUM-F by applying Nonstandard Universal Elimination and subsequently Multiple Universal Elimination that

$$\exists F_{\widehat{\mathbf{X}}}\exists Y\left(F_{\widehat{\mathbf{X}}}:\widehat{\mathbf{X}}\twoheadrightarrow Y\wedge {\bigwedge }_{\alpha \in \widehat{\mathbf{X}}}{F}_{\widehat{\mathbf{X}}}:\alpha \mapsto ı\beta ({\widehat{\mathbf{f}}}_{{\alpha }^{+}}:\alpha \mapsto \beta )\right)$$

(68)

By subsequently applying Rule-C and Conjunctive Operator Elimination we then deduce the schema

$${\widehat{\mathbf{F}}}_{\widehat{\mathbf{X}}}:\widehat{\alpha }\mapsto ı\beta \Phi (\widehat{\alpha },\beta )$$

(69)

for the sum function ${\widehat{\mathbf{F}}}_{\widehat{\mathbf{X}}}$. Generalizing this schema we obtain

$$\forall \eta \in \widehat{\mathbf{X}}({\widehat{\mathbf{F}}}_{\widehat{\mathbf{X}}}:\eta \mapsto ı\xi \Phi (\eta ,\xi )))$$

(70)

We thus obtain

$$\exists F_{\widehat{\mathbf{X}}}\exists Y\left(F_{\widehat{\mathbf{X}}}:\widehat{\mathbf{X}}\twoheadrightarrow Y\wedge \forall \eta \in \widehat{\mathbf{X}}(F_{\widehat{\mathbf{X}}}:\eta \mapsto ı\xi \Phi (\eta ,\xi )))\right)$$

(71)

Since the functional relation was assumed, we get $\forall \alpha \in \widehat{\mathbf{X}}\exists !\beta \Phi (\alpha ,\beta )\Rightarrow \Psi$ where $\Psi$ is Formula (71). Since $\widehat{\mathbf{X}}$ was an arbitrary nonempty set, we can quantify over nonempty sets. This gives precisely the requested Formula (66). □

Remark 21.

Theorem 2 is an infinite schema, with one formula for every functional relation $\Phi$. The point is this: given a set X, on account of this theorem we can construct a function $f_X$ by giving a function prescription—what we then actually do is define an ur-function for every $\alpha \in X$; the function $f_X$ then exists on account of SUM-F. Furthermore, by constructing the function we construct its graph, which exists on account of Theorem 1. Generally speaking, if we define an ur-function for each singleton ${\alpha }^{+}\subset X$, then we do not yet have the graphs of these ur-functions in a set. However, in the present framework, the set of these graphs is guaranteed to exist. Ergo, giving a function prescription is constructing a set! □

3.2. Derivation of SEP and REP of ZF

We start by proving that the infinite axiom schema SEP of ZF is a theorem (schema) of our theory $\mathfrak{T}$:

Theorem 3.

Separation Axiom Scheme of ZF:

$\forall X\exists Y\forall \alpha (\alpha \in Y\iff \alpha \in X\wedge \Phi (\alpha \left)\right)$

Proof. 

Let $\widehat{\mathbf{X}}$ be an arbitrary set and let $\Phi$ be an arbitrary unary relation on $\widehat{\mathbf{X}}$. On account of the ur-function axiom (Axiom 18), for an arbitrary constant $\widehat{\alpha }\in \widehat{\mathbf{X}}$ there exists then an ur-function ${\widehat{\mathbf{u}}}_{{\widehat{\alpha }}^{+}}$ for which

$$\left\{\begin{array}{c}{\widehat{\mathbf{u}}}_{{\widehat{\alpha }}^{+}}:\widehat{\alpha }\mapsto 1if\Phi \left(\widehat{\alpha }\right)\hfill \\ {\widehat{\mathbf{u}}}_{{\widehat{\alpha }}^{+}}:\widehat{\alpha }\mapsto 0if\neg \Phi \left(\widehat{\alpha }\right)\hfill \end{array}\right.$$

(72)

Let the variable ${\widehat{\mathbf{f}}}_{{\eta }^{+}}$ range over these ur-functions. On account of Theorem 2 we then get

$$\exists F_{\widehat{\mathbf{X}}}\forall \eta \in \widehat{\mathbf{X}}(F_{\widehat{\mathbf{X}}}:\eta \mapsto ı\beta ({\widehat{\mathbf{f}}}_{{\eta }^{+}}:\eta \mapsto \beta ))$$

(73)

Let this sum function be designated by the constant ${\widehat{\mathbf{F}}}_{\widehat{\mathbf{X}}}$. On account of INV (Axiom 15), the inverse image set ${\widehat{\mathbf{F}}}_{\widehat{\mathbf{X}}}^{-1}\left(1\right)$ exists: we then have $\forall \alpha (\alpha \in {\widehat{\mathbf{F}}}_{\widehat{\mathbf{X}}}^{-1}\left(1\right)\iff \alpha \in \widehat{\mathbf{X}}\wedge \Phi \left(\alpha \right))$. Theorem 3 then obtains from here by existential generalization and universal generalization. □

Proceeding, we prove that the infinite axiom schema REP of ZF is a theorem (schema) of our theory $\mathfrak{T}$:

Theorem 4.

Replacement Axiom Scheme of ZF:

$\forall X(\forall \alpha \in X\exists !\beta \Phi (\alpha ,\beta )\Rightarrow \exists Z\forall \gamma (\gamma \in Z\iff \exists \xi (\xi \in X\wedge \Phi (\xi ,\gamma \left)\right)\left)\right)$

Proof. 

Let $\widehat{\mathbf{X}}$ be an arbitrary set and let there for every $\alpha \in \widehat{\mathbf{X}}$ be precisely one $\beta$ such that $\Phi (\alpha ,\beta )$. Then on account of Theorem 2, a sum function ${\widehat{\mathbf{F}}}_{\widehat{\mathbf{X}}}$ exists for which

$$\forall \alpha \in X({\widehat{\mathbf{F}}}_{\widehat{\mathbf{X}}}:\alpha \mapsto ı\beta \Phi (\alpha ,\beta ))$$

(74)

On account of Axiom 14, the codomain of ${\widehat{\mathbf{F}}}_{\widehat{\mathbf{X}}}$ is the image set; denoting this by ${\widehat{\mathbf{F}}}_{\widehat{\mathbf{X}}}\left[\widehat{\mathbf{X}}\right]$ we then have

$$\forall \gamma (\gamma \in {\widehat{\mathbf{F}}}_{\widehat{\mathbf{X}}}\left[\widehat{\mathbf{X}}\right]\iff \exists \xi (\xi \in X\wedge \Phi (\xi ,\gamma )))$$

(75)

Since the functional relation $\Phi$ on the arbitrary set $\widehat{\mathbf{X}}$ was assumed, this is implied by $\forall \alpha \in \widehat{\mathbf{X}}\exists !\beta \Phi (\alpha ,\beta )$. We write out this implication: Theorem 4 then obtains by existential generalization and universal generalization. □

These two theorems’ schemas provide an argument for considering our theory $\mathfrak{T}$ to be not weaker than ZF. However, we have strictly speaking not yet proven that every result in ZF about sets automatically translates to the present framework, in which not all things are sets.

Remark 22.

Should further research on $\mathfrak{T}$ reveal unintended consequences that render it inconsistent or otherwise useless, there is still the possibility to remove SUM-F from $\mathfrak{T}$ and add the above theorem schemas 3 and 4 as axioms to $\mathfrak{T}$. That still gives a theory—although a standard one with infinitely many axioms—that incorporates set theory and category theory into a single framework. □

3.3. Model theory

Definition 13.

A model $\mathcal{M}$ of the present theory $\mathfrak{T}$ consists of the universe$\left|\mathcal{M}\right|$ of $\mathcal{M}$, which is a concrete category made up of a nonempty collection of objects (sets) and a nonempty collection of arrows (functions on sets), and the language$L_{\mathcal{M}}$ of $\mathcal{M}$, which is the language $L_{\mathfrak{T}}$ of $\mathfrak{T}$ extended with a constant for every object and for every arrow in $\left|\mathcal{M}\right|$, such that the axioms of $\mathfrak{T}$ are valid in $\mathcal{M}$. □

In standard first-order logic it is well defined what it means that a formula is “valid” in a model M. This notion of validity translates to the framework of $\mathfrak{T}$ for all standard formulas. However, it remains to be established what it means that SUM-F and non-classical consequences thereof are valid in a model $\mathcal{M}$ of $\mathfrak{T}$. Recall that symbols referring to individuals in $\left|\mathcal{M}\right|$ will be underlined to distinguish these individuals from constants of $\mathfrak{T}$.

Definition 14. (Validity of non-classical formulas):

(i)

A sentence $\forall X\ne \varnothing \Psi$ with a non-classical subformula $\Psi$, such as the sum function axiom, is valid in a model $\mathcal{M}$ of $\mathfrak{T}$ if and only if for every assignment g that assigns an individual nonempty set $g\left(X\right)=\underline{\mathbf{X}}$ in $\left|\mathcal{M}\right|$ as a value to the variable X, $[\underline{\mathbf{X}}\backslash X]\Psi$ is valid in $\mathcal{M}$;

(ii)

A sentence ${(\forall f_{{\alpha }^{+}})}_{\alpha \in \underline{\mathbf{X}}}\Phi$ with an occurrence of an individual nonempty set $\underline{\mathbf{X}}$ of $\left|\mathcal{M}\right|$, such as an instance of SUM-F, is valid in a model $\mathcal{M}$ of $\mathfrak{T}$ if and only if for every “team assignment” g that assigns an individual ur-function $g\left(f_{{\underline{\mathbf{\alpha }}}^{+}}\right)={\underline{\mathbf{u}}}_{{\underline{\mathbf{\alpha }}}^{+}}$ in $\left|\mathcal{M}\right|$ as a value to each variable $f_{{\underline{\mathbf{\alpha }}}^{+}}$ semantically occurring in $\Phi$, the sentence $[{\underline{\mathbf{f}}}_{{\alpha }^{+}}^g\backslash f_{{\alpha }^{+}}]\Phi$ with the variable ${\underline{\mathbf{f}}}_{{\alpha }^{+}}^g$ ranging over the family of ur-functions ${\left({\underline{\mathbf{u}}}_{{\alpha }^{+}}\right)}_{\alpha \in \underline{\mathbf{X}}}$ is valid in $\mathcal{M}$;

(iii)

A sentence $\exists t{\rm Y}$ with an occurrence of a simple variable t ranging over sets or over functions on a set $\underline{\mathbf{X}}$ and with ${\rm Y}$ being a non-classical formula, such as the sentences that can be obtained by successively applying Nonstandard Universal Elimination and Multiple Universal Elimination to SUM-F, is valid in a model $\mathcal{M}$ of $\mathfrak{T}$ if and only if for at least one assignment g that assigns an individual function $g\left(t\right)={\underline{\mathbf{F}}}_{\underline{\mathbf{X}}}$ or an individual nonempty set $g\left(t\right)=\underline{\mathbf{Y}}$ as value to the variable t, the sentence $\left[g\right(t)\backslash t]{\rm Y}$ is valid in $\mathcal{M}$;

(iv)

A sentence ${\bigwedge }_{\alpha \in \underline{\mathbf{X}}}\Psi ({\underline{\mathbf{f}}}_{{\alpha }^{+}},\alpha )$ is valid in a model $\mathcal{M}$ of $\mathfrak{T}$ if and only if for every assignment g that assigns an individual ur-function $g\left({\underline{\mathbf{f}}}_{{\alpha }^{+}}\right)={\underline{\mathbf{u}}}_{{\underline{\mathbf{\alpha }}}^{+}}$ from the range ${\left({\underline{\mathbf{u}}}_{{\alpha }^{+}}\right)}_{\alpha \in \underline{\mathbf{X}}}$ of the variable ${\underline{\mathbf{f}}}_{{\alpha }^{+}}$ and an individual $\underline{\mathbf{\alpha }}$ as values to the variables ${\underline{\mathbf{f}}}_{{\alpha }^{+}}$ and $\alpha$ respectively, the sentence $[\underline{\mathbf{\alpha }}\backslash \alpha ][{\underline{\mathbf{u}}}_{{\underline{\mathbf{\alpha }}}^{+}}\backslash {\underline{\mathbf{f}}}_{{\alpha }^{+}}]\Psi$ is valid in $\mathcal{M}$.

This defines the validity of the non-classical formulas that can be deduced from SUM-F in terms of the well-established validity of standard first-order formulas. □

Proposition 1.

If $\mathfrak{T}$ has a model $\mathcal{M}$, then $\mathcal{M}$ is not countable.

Proof. 

Suppose $\mathfrak{T}$ has a model $\mathcal{M}$, and $\mathcal{M}$ is countable. That means that there are only countably many subsets of $\mathbb{N}=\{0,1,2,\dots \}$ in $\mathcal{M}$, and that the powerset $\mathcal{P}\left(\mathbb{N}\right)$ in $\mathcal{M}$ contains those subsets: we thus assume that there are subsets of $\mathbb{N}$ that are “missing” in $\mathcal{M}$. Let $\underline{\mathbf{A}}$ be any subset of $\mathbb{N}$ that is not in $\mathcal{M}$, and let $\underline{\mathbf{h}}\in \underline{\mathbf{A}}$. All numbers $0,1,2,\dots$ are in $\mathcal{M}$ (including $\underline{\mathbf{h}}$), so for an arbitrary number $\underline{\mathbf{n}}\in \mathbb{N}$ there is thus on account of the ur-function axiom (Axiom 18) an ur-function on $\left\{\underline{\mathbf{n}}\right\}$ that maps $\underline{\mathbf{n}}$ to $\underline{\mathbf{n}}$ and an ur-function on $\left\{\underline{\mathbf{n}}\right\}$ that maps $\underline{\mathbf{n}}$ to $\underline{\mathbf{h}}$. Since $\mathbb{N}$ is in $\mathcal{M}$, we get on account of SUM-F and Nonstandard Universal Elimination that

$${\vDash }_{\mathcal{M}}{(\forall f_{p^{+}})}_{p\in \mathbb{N}}\exists F_{\mathbb{N}}\exists Y\left(F_{\mathbb{N}}:\mathbb{N}\twoheadrightarrow Y\wedge {\bigwedge }_{p\in \mathbb{N}}{F}_{\mathbb{N}}:p\mapsto ıq(f_{p^{+}}:p\mapsto q)\right)$$

(76)

Equation (76) being valid in $\mathcal{M}$ means thus that for any team assignment g, there is a sum function ${\underline{\mathbf{F}}}_{\mathbb{N}}^g$ in $\left|\mathcal{M}\right|$ for which

$$\forall p\in \mathbb{N}({\underline{\mathbf{F}}}_{\mathbb{N}}^g:p\mapsto ıq({\underline{\mathbf{f}}}_{p^{+}}^g:p\mapsto q))$$

(77)

where the variable ${\underline{\mathbf{f}}}_{p^{+}}^g$ ranges over ur-functions $g\left(f_{0^{+}}\right),g\left(f_{1^{+}}\right),g\left(f_{2^{+}}\right),\dots$ That said, the crux is that there is a team assignment $g^{*}$ which assigns to the variables $f_{0^{+}},f_{1^{+}},f_{2^{+}},\dots$, the constants $g^{*}\left(f_{0^{+}}\right),g^{*}\left(f_{1^{+}}\right),g^{*}\left(f_{2^{+}}\right),\dots$ such that for all $n\in \mathbf{\omega }$ we have

$$\left\{\begin{array}{c}{g}^{*}\left(f_{n^{+}}\right):n\mapsto nifn\in \underline{\mathbf{A}}\hfill \\ g^{*}\left(f_{n^{+}}\right):n\mapsto \underline{\mathbf{h}}ifn\notin \underline{\mathbf{A}}\hfill \end{array}\right.$$

(78)

To see that, note that it is a certainty that there is at least one team assignment $g^0$ such that Equation (78) is satisfied for $n=0$. Namely, there is (i) at least one team assignment g such that $g\left(f_{0^{+}}\right)={\left\{⟨0,0⟩\right\}}_{\left\{0\right\}}$ so that $g\left(f_{0^{+}}\right):0\mapsto 0$, and (ii) at least one team assignment $g^{\prime }$ such that $g^{\prime }\left(f_{0^{+}}\right)={\left\{⟨0,\underline{\mathbf{h}}⟩\right\}}_{\left\{0\right\}}$ so that $g^{\prime }\left(f_{0^{+}}\right):0\mapsto \underline{\mathbf{h}}$. Now assume that there is a team assignment $g^k$ such that Equation (78) is satisfied for $n\in \{0,1,\dots ,k\}$: it is then a certainty that there is at least one team assignment $g^{k+1}$ such that Equation (78) is satisfied for $n\in \{0,1,\dots ,k+1\}$. Namely, there is (i) at least one team assignment $g_{k+1}^k$ such that for $n\in \{0,1,\dots ,k\}$ we have $g_{k+1}^k\left(f_{n^{+}}\right)=g^k\left(f_{n^{+}}\right)$ and such that for $n=k+1$ we have $g_{k+1}^k\left(f_{n^{+}}\right)={\left\{⟨n,n⟩\right\}}_{\left\{n\right\}}$ so that $g_{k+1}^k\left(f_{{(k+1)}^{+}}\right):k+1\mapsto k+1$, and (ii) at least one team assignment $g_{\underline{\mathbf{h}}}^k$ such that for $n\in \{0,1,\dots ,k\}$ we have $g_{\underline{\mathbf{h}}}^k\left(f_{n^{+}}\right)=g^k\left(f_{n^{+}}\right)$ but such that for $n=k+1$ we have $g_{\underline{\mathbf{h}}}^k\left(f_{{\left(n\right)}^{+}}\right)={\left\{⟨n,\underline{\mathbf{h}}⟩\right\}}_{\left\{n\right\}}$ so that $g_{\underline{\mathbf{h}}}^k\left(f_{{(k+1)}^{+}}\right):k+1\mapsto \underline{\mathbf{h}}$. By induction, there is thus a team assignment $g^{*}$ such that Equation (78) is satisfied for all $n\in \mathbf{\omega }$. Ergo, there is a sum function ${\underline{\mathbf{F}}}_{\mathbf{\omega }}^{*}$ for which

$$\forall p\in \mathbf{\omega }({\underline{\mathbf{F}}}_{\mathbf{\omega }}^{*}:p\mapsto g^{*}\left(f_{p^{+}}\right)\left(p\right))$$

(79)

However, then we get ${\underline{\mathbf{F}}}_{\mathbf{\omega }}^{*}\left[\mathbf{\omega }\right]=\underline{\mathbf{A}}$, so $\underline{\mathbf{A}}$ is in $\mathcal{M}$, contrary to what was assumed. Ergo, if $\mathfrak{T}$ has a model, it is not countable. □

Remark 23.

Proposition 1 is a significant result that does not hold in ZF: given Theorems 3 and 4, this provides an argument for considering the present theory $\mathfrak{T}$ to be stronger than ZF. The crux here is that the non-classical sentence (76) has to be valid in $\mathcal{M}$: the notion of validity of Definition 14 entails that there are uncountably many variables ${\underline{\mathbf{f}}}_{p^{+}}^g$, ranging over a family of individual ur-functions indexed in $\mathbb{N}$, in the language of the model. As a result, the subsets of $\mathbb{N}$ that can be constructed within the model are non-denumerable—a model of $\mathfrak{T}$ in which Multiple Universal Elimination, inference rule 2, applies for at most countably many variables ${\underline{\mathbf{f}}}_{p^{+}}^g$ is thus nonexistent. Thus speaking, the Löwenheim–Skolem theorem does not apply because $\mathfrak{T}$ is a non-classical first-order theory, meaning that $\mathfrak{T}$ cannot be reformulated as a standard first-order theory. □

Proposition 2.

$\mathfrak{T}$ is not a second-order theory.

Proof. 

Let us assume that $\mathfrak{T}$ is a second-order theory. That is, let us assume that the use of a multiple quantifier ${(\forall f_{\left\{\alpha \right\}})}_{\alpha \in \widehat{\mathbf{X}}}$ amounts to second-order quantification. With such a multiple quantifier, we de facto quantify over all functional relations on the set $\widehat{\mathbf{X}}$—note, however, that we do not quantify over all functional relations on the universe of sets! However, this has an equivalent in ZF: if $\widehat{\mathbf{X}}$ is a constant (a set), and ${\widehat{\mathbf{Y}}}^{\widehat{\mathbf{X}}}$ is the set of all functions from $\widehat{\mathbf{X}}$ to a set $\widehat{\mathbf{Y}}$, then with the quantifier $\forall B\forall f\in B^{\widehat{\mathbf{X}}}$ in a sentence

$$\forall B\forall f\in B^{\widehat{\mathbf{X}}}\Psi$$

(80)

we de facto quantify over all functional relations on the set $\widehat{\mathbf{X}}$ too. Ergo, if $\mathfrak{T}$ is a second-order theory, then ZF is a second-order theory too. However, ZF is a first-order theory and not a second-order theory. So by modus tollens, $\mathfrak{T}$ is not a second-order theory. □

As an additional heuristic argument, we can also directly compare second-order quantification and the present non-classical first-order quantification with a multiple quantifier ${(\forall f_{\left\{\alpha \right\}})}_{\alpha \in \widehat{\mathbf{X}}}$. Let us first look at second-order quantification with a quantifier $\forall \Phi$ where the variable $\Phi$ ranges over functional relations on the class of sets. An arbitrary individual functional relation $\widehat{\Phi }$ has the entire proper class of things as its “domain”, so $\widehat{\Phi }$ corresponds to a proper class of ur-functions: for an arbitrary thing $\widehat{\alpha }$ there is a $\widehat{\Phi }$-related ur-function ${\widehat{\mathbf{u}}}_{{\widehat{\alpha }}^{+}}$ for which ${\widehat{\mathbf{u}}}_{{\widehat{\alpha }}^{+}}:\widehat{\alpha }\mapsto ı\beta \widehat{\Phi }(\widehat{\alpha },\beta )$. A quantifier $\forall \Phi$ is thus equivalent to a proper class of simple quantifiers $f_{{\widehat{\alpha }}^{+}}$ ranging over ur-functions on the singleton of a thing $\widehat{\alpha }$. The universe of $\mathfrak{T}$, however, does not contain a set $\widehat{\mathbf{U}}$ of all things, so there is no multiple quantifier ${(\forall f_{{\alpha }^{+}})}_{\alpha \in \widehat{\mathbf{U}}}$ which would be equivalent to quantifier $\forall \Phi$: a multiple quantifier ${(\forall f_{{\alpha }^{+}})}_{\alpha \in \widehat{\mathbf{X}}}$ is at most equivalent to an infinite set of simple quantifiers $f_{{\widehat{\alpha }}^{+}}$ and the degree of infinity is then bounded by the notion of a set. Thus, since a set does not amount to a proper class, a multiple quantifier ${(\forall f_{{\alpha }^{+}})}_{\alpha \in \widehat{\mathbf{X}}}$ does not amount to second-order quantification. See Figure 2 for an illustration.

Figure 2. Illustration of the heuristic argument. In both diagrams (a,b), all things in the universe of T are for illustrative purposes represented on the horizontal and vertical axes. In diagram (a), the dotted black line represents an arbitrary functional relation $\widehat{\Phi }$: each dot corresponds to a constant ur-function as indicated, so the dotted line is equivalent to a proper class of ur-functions. In diagram (b) it is indicated of which things on the horizontal axis the set $\widehat{\mathbf{X}}$ is made up, and each of the black dots within the red oval corresponds to a constant ur-functions: the dotted line segment is thus equivalent to a set of ur-functions. So, a multiple quantifier ${(\forall f_{{\alpha }^{+}})}_{\alpha \in \widehat{\mathbf{X}}}$ cannot be equivalent to a quantifier $\forall \Phi$.

This heuristic argument can also be formulated in another way. Let $\widehat{\mathbf{U}}$ and $\widehat{\mathbf{X}}$ be two nonempty disjoint sets, and let us then compare a truly second-order quantification $\forall \Phi$ over all functional relations on the class of sets with our non-classical first-order quantification with a multiple quantifier ${(\forall f_{\left\{\alpha \right\}})}_{\alpha \in \widehat{\mathbf{X}}}$. In the first case, given any individual functional relation $\widehat{\Phi }$ we can construct image sets of both $\widehat{\mathbf{U}}$ and $\widehat{\mathbf{X}}$ that contain precisely the images of the elements of $\widehat{\mathbf{U}}$ c.q. $\widehat{\mathbf{X}}$ under the functional relation $\widehat{\Phi }$. In the second case, however, given any family of ur-functions ${\left({\widehat{\mathbf{f}}}_{\left\{\alpha \right\}}\right)}_{\alpha \in \widehat{\mathbf{X}}}$ we can construct the image set of $\widehat{\mathbf{X}}$ that for each element $\alpha$ of $\widehat{\mathbf{X}}$ contains the image of $\alpha$ under the ur-function ${\widehat{\mathbf{f}}}_{{\alpha }^{+}}$, but we cannot construct any image set of $\widehat{\mathbf{U}}$. That shows that our non-classical first-order quantification is not the same as second-order quantification.

3.4. The Axioms of Category Theory

In Definition 1 it has been assumed that the universe of sets and functions is a category. In this section we prove that the axioms of category theory for the arrows indeed hold for the functions (which are the arrows of the present category). That means that we must prove the following:

(i)

That domain and codomain of any function on any set are unique;

(ii)

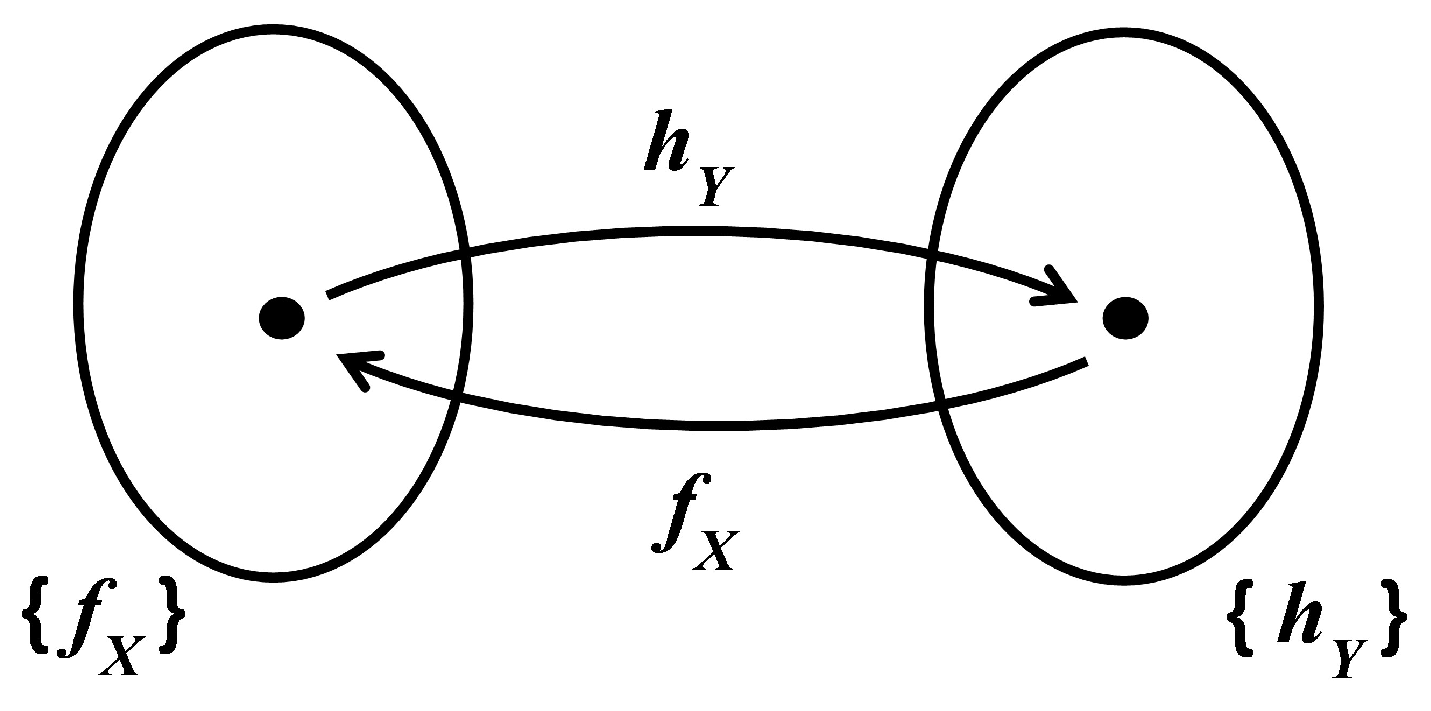
That, given sets X and Y and functions $f_X$ and $g_Y$ with $Y=f_X\left[X\right]$, there is a function $h_X=g_Y\circ f_X$ such that $h_X$ maps every $\alpha \in X$ to the image under $g_Y$ of its image under $f_X$;

(iii)

That for any set X there is a function $1_X$ such that $f_X\circ 1_X=f_X$ and $1_{f_X\left[X\right]}\circ f_X=f_X$ for any function $f_X$ on X.

Ad(i): domain and codomain of a function $f_X$ are unique

This has already been proven in Section 2.3. GEN-F (Axiom 11) guarantees that for any set X, any function $f_X$ has at least one domain and at least one codomain. Axiom 12 guarantees that no other thing (set or function) than X is a domain of $f_X$. Furthermore, Axiom 14 guarantees that no other thing (set or function) than the image set $f_X\left[X\right]$ is a codomain of $f_X$. That proves uniqueness of domain and codomain.

Ad(ii): existence of the composite of two functions

Given a set X, a function $f_X$ and a function $g_Y$ with $Y=f_X\left[X\right]$, there is for every $\alpha \in X$ precisely one ur-function $h_{{\alpha }^{+}}$ such that

$$h_{{\alpha }^{+}}:\alpha \mapsto ı\beta (g_Y:f_X\left(\alpha \right)\mapsto \beta )$$

(81)

So, there is a sum function $H_X$ that maps each $\alpha \in X$ precisely to its image under the ur-function $h_{{\alpha }^{+}}$ for which $ı\xi (h_{{\alpha }^{+}}:\alpha \mapsto \xi )=ı\beta (g_Y:f_X\left(\alpha \right)\mapsto \beta )$. This sum function is precisely the composite $H_X=g_Y\circ f_X$. The proof that function composition is associative is omitted.

Ad(iii): existence of an identity function on any set X

Given a set X, there is for every $\alpha \in X$ precisely one ur-function $1_{{\alpha }^{+}}$ for which

$$1_{{\alpha }^{+}}:\alpha \mapsto \alpha$$

(82)

Therefore, there is a sum function $F_X$ that maps every $\alpha \in X$ to $ı\xi (1_{{\alpha }^{+}}:\alpha \mapsto \xi )=\alpha$. This sum function is the requested function $1_X$. The proof that this sum function $1_X$ satisfies the properties that $g_X\circ 1_X=g_X$ and $1_{g_X\left[X\right]}\circ g_X=g_X$ for any function $g_X$ on X, is omitted.

This shows that the axioms for a category hold for the proper class of functions.

3.5. Concerns Regarding Inconsistency

We address the main concerns regarding inconsistency, which are in particular that the existence of a set of all sets or a set of all functions can be derived from $\mathfrak{T}$.

Conjecture 1.

The category of sets and functions does not contain a set of all sets.

Heuristic argument:

A set $\widehat{\mathbf{U}}$ of all sets does not exist (i) because REG (Axiom 9) excludes that $\widehat{\mathbf{U}}$ exists a priori, and (ii) because SUM-F, the only constructive axiom of $\mathfrak{T}$ that is not a theorem of ZF, excludes that $\widehat{\mathbf{U}}$ exists by construction. The crux is that one must first have constructed the set X before one can construct a sum function $F_X$: the set X is thus a regular set, and by applying SUM-F one cannot create a new set with a higher cardinality than the set X because the graph of $F_X$ contains precisely one element for each element of X. It is the same for the image set $F_X\left[X\right]$: it cannot have a higher cardinality than X. Therefore, SUM-F does not allow the construction of a set $\widehat{\mathbf{U}}$ of all sets. □

Conjecture 2.

The category of sets and functions on sets does not contain a set $\widehat{\Omega }$ of all functions.

Heuristic argument:

Suppose that we have a set $\widehat{\Omega }$ such that

$$\forall X\forall f_X(f_X\in \widehat{\Omega })$$

(83)

Then on account of Theorem 3 we can single out the subset ${\widehat{\Omega }}_1$ of all identity functions:

$$\forall \alpha (\alpha \in {\widehat{\Omega }}_1\iff \alpha \in \widehat{\Omega }\wedge \exists X(\alpha =1_X))$$

(84)

However, then there also exists the identity function $1_{{\widehat{\Omega }}_1}$, for which

$$1_{{\widehat{\Omega }}_1}:{\widehat{\Omega }}_1\twoheadrightarrow {\widehat{\Omega }}_1,1_{{\widehat{\Omega }}_1}:1_{{\widehat{\Omega }}_1}\mapsto 1_{{\widehat{\Omega }}_1}$$

(85)

This latter feature that $1_{{\widehat{\Omega }}_1}$ maps itself to itself contradicts the axiom of regularity for functions, REG-F (Axiom 19). Ergo, there is no set $\widehat{\Omega }$ of all functions. □

4. Concluding Remarks

4.1. Limitations of the Present Study

First of all, the syntax of the formal language for the theory $\mathfrak{T}$ has been defined in such a way that the axioms of $\mathfrak{T}$ are well-formed formulas. While this definition of the syntax has been checked for obvious mistakes, a limitation of the present study is that it has not been checked exhaustively for unintended consequences. That is, it may turn out that details of the present definition of the syntax require revision to avoid the situation that this or that “weird” formula becomes a well-formed formula.

As to the axioms of $\mathfrak{T}$, the axiom of regularity for functions, Axiom 19, has been formulated to rule out the existence of the pathological functions mentioned in its formulation. While the existence of certain other pathological objects, such as a set X and a function $f_X$ for which $X=\left\{f_X\right\}$, is also ruled out as a corollary of this axiom, it cannot be excluded that a creative mind can come up with even more pathological objects that are not ruled out by the two axioms of regularity of $\mathfrak{T}$. That is, it may turn out that the axioms of regularity require revision to avoid the situation that $\mathfrak{T}$ has a model in which certain pathological objects exist a priori.

Furthermore, since $\mathfrak{T}$ is a non-classical theory there is the obvious risk that $\mathfrak{T}$ is not (relatively) consistent. While the theory $\mathfrak{T}$ has been checked for the most obvious concerns regarding inconsistency—we have argued that the category of sets and functions cannot contain a set of all sets nor a set of all functions—it has not been checked exhaustively for inconsistency. That is, further research may reveal that $\mathfrak{T}$ has unintended consequences which render it inconsistent. In such a case the approach would be to resolve the inconsistency by a revision of the axioms of $\mathfrak{T}$. However, if that fails, we still have the prospect of a fallback position: as outlined in Remark 22, we can remove the non-classical part of $\mathfrak{T}$ and add the infinite theorem schemas for SEP and REP as axioms; the standard first-order theory thus obtained then no longer solves the problem identified in the introduction, but it still incorporates category theory and set theory in a single framework.

A further limitation of this study is that the axiom of choice has been left out. We can easily express AC in the language $L_{\mathfrak{T}}$ as

$$\forall X\ne \varnothing (\Theta \left(X\right)\Rightarrow \exists f_X\forall Z\in X\forall \gamma (f_X:Z\mapsto \gamma \Rightarrow \gamma \in Z)$$

(86)

where $\Theta \left(X\right)$ stands for

$$\forall \alpha \in X\exists Y(\alpha =Y\wedge \exists \eta (\eta \in Y\left)\right)\wedge \forall U\in X\forall V\in X\neg \exists \beta (\beta \in U\wedge \beta \in V)$$

(87)

However, the question is whether this has to be added as an axiom or whether it can be derived as a theorem of $\mathfrak{T}$—we certainly have for any $Z\in X$ that there is an ur-function $f_{Z^{+}}$ such that $ı\xi (f_{Z^{+}}:Z\mapsto \xi )\in Z$. We leave this as a topic for further research.

Last but not least, another limitation of the present study is that the metamathematics of $\mathfrak{T}$ have not been studied. That is, it has not been investigated whether the calculus has any of the various soundness and completeness properties. This is left as a topic for further research—(dis-)proving that these properties hold is a sizeable research project in itself.

4.2. Aesthetic Counterarguments

The present theory $\mathfrak{T}$ gives immediate rise to at least three purely aesthetical arguments for rejection.

First of all, the universe of $\mathfrak{T}$ contains sets and functions, the latter being objects sui generis: this entails a departure from the adage “everything is a set” that holds in the framework of ZF(C) and that will be enough to evoke feelings of dislike among mathematical monists who hold the position that set theory, in particular ZF or ZFC, has to be the foundation for mathematics.

Secondly, although the universe of $\mathfrak{T}$ is a category, the formal language of $\mathfrak{T}$ contains ∈-relations $t_1\in t_2$ as atomic formulas: an ∈-relation is, thus, not reduced to a mapping in the language of category theory and that fact alone will be enough to evoke feelings of dislike among mathematical monists who hold the position that category theory has to be the foundation for mathematics.

Thirdly, the language of $\mathfrak{T}$ entails a rather drastic departure from standard first-order language: that will be enough to evoke feelings of dislike among those who attach a notion of beauty to the standard first-order language of ZF(C) or who consider that the language of category theory is all of the language of mathematics.

These arguments can be dismissed as nonmathematical, but those who experience these feelings of dislike will nevertheless reject the theory $\mathfrak{T}$ straightaway as not suitable as a foundational theory for mathematics.

4.3. Main Conclusions

The main conclusion is that the aim stated in the introduction has been achieved: a theory $\mathfrak{T}$, with a vocabulary containing countably many constants, has been introduced which lacks the two unwanted c.q. pathological features of ZF. Each axiom of $\mathfrak{T}$ is a typographically finite sentence, so contrary to what is the case with infinitary logics, each axiom can be written down explicitly. However, not just that: $\mathfrak{T}$ is finitely axiomatized, so contrary to what is the case with ZF, the entire theory $\mathfrak{T}$ can be written down explicitly on a piece of paper. In addition, it has been shown that $\mathfrak{T}$, contrary to ZF, does not have a countable model—if it has a model at all, that is. This failure of the downward Löwenheim–Skolem theorem for $\mathfrak{T}$ is due to the non-classical nature of $\mathfrak{T}$.

Furthermore, three reasons can be given as to why $\mathfrak{T}$ might be potentially applicable as a foundational theory for mathematics. First of all, it has been proven that the axioms of ZF, translated in the language $L_{\mathfrak{T}}$ of $\mathfrak{T}$, can be derived from $\mathfrak{T}$. While we acknowledge that this result does not automatically imply that all theorems about sets derived within the framework of ZF are necessarily also true in the framework of $\mathfrak{T}$ because in the latter framework sets exist whose elements are not sets, it nevertheless shows that the tools available in the framework ZF for constructing sets are also available in the framework of $\mathfrak{T}$. Secondly, it has been proved that the axioms of a category hold for the universe of discourse that is associated to $\mathfrak{T}$, which is a category of sets and functions: this universe might then serve as the ontological basis for the various (large) categories studied in category theory. Thirdly, $\mathfrak{T}$ is easy to use in everyday mathematical practice because for any set X we can construct a function $f_X$ by giving a defining function prescription $f_X:X\twoheadrightarrow Y,f_X:\alpha \stackrel{\mathrm{def}}{⟼}\iota \beta \Phi (\alpha ,\beta )$ where $\Phi$ is some functional relation: $\mathfrak{T}$ then guarantees that $F_X$ exists, as well as its graph, its image set, and the inverse image sets for every element of its codomain—ergo, giving a defining function prescription is a tool for constructing sets.

That being said, there are also arguments why $\mathfrak{T}$ cannot be generally accepted as a new foundational theory for mathematics right now by a collective act of instant rationality. The strongest of these may be that the methamathematics have not been studied: contrary to the purely aesthetic arguments against $\mathfrak{T}$, negative results in that direction may yield a decisive argument to reject $\mathfrak{T}$ as not suitable as a foundational theory for mathematics. Therefore, this topic should be given highest priority in further research; the prospect is that it should become clear within a few years whether or not the various soundness and completeness properties apply.

The bottom line is that the present results are rather avant-garde and that further research is necessary to establish whether the non-classical theory $\mathfrak{T}$ introduced in this paper constitutes an advancement in the foundations of mathematics. The proven fact that $\mathfrak{T}$ lacks the pathological features of ZF may provide a reason for such further research, but it is emphasized that it may turn out to be a dead end. That is to say: the present marriage of set theory and category theory—as we called it in the introduction—may look promising from a certain perspective, but it still may end in divorce.